
GRE 2024 Quantitative Reasoning Practice Test Set 11 Question Paper with Solutions PDF is available for download. The overall test time is about 1 hour and 58 minutes. GRE has total 5 sections:
- Analytical Writing (One "Analyze an Issue" task, Alloted time 30 minutes)
- Verbal Reasoning (Two Sections, with 12 questions and 15 questions respectively)
- Quantitative Reasoning (Two Sections, with 12 questions and 15 questions respectively)
GRE 2024 Qantitative Reasoning Practice Test Set 11 Question Paper with Solutions PDF
| GRE 2024 Quantitative Reasoning Set 11 Question Paper with Solutions PDF | Check Solutions |

In the figure, two right-angled triangles are given. One triangle has legs of length 4 and 8, and the other has legs of length 4 and \( y \).

The equation \( (x - 2y)(x + 2y) = 4 \) is given.

A certain recipe requires 3 2 cups of sugar and makes 2 dozen cookies. (1 dozen = 12)

A power station is located on the boundary of a square region that measures 10 miles on each side. Three substations are located inside the square region.

Given \( 6 < x < 7 \) and \( y = 8 \).

O is the center of the circle and the perimeter of \( \triangle AOB \) is 6.

The standard deviation of a set of 5 different integers, each of which is between 0 and 10.

Given \( x > 1 \).

Given \( x \neq 0 \).

The system of equations is: \[ 7x + 3y = 12
3x + 7y = 6 \]
If \(x\) and \(y\) satisfy the system of equations, what is the value of \(x - y\)?
In triangle ABC, the measure of angle A is 25° and the measure of angle B is greater than 90°. Which of the following could be the measure of angle C? Indicate all possible values.
What is the least integer \( n \) such that \( 2n < 1001 \)?
In the sunshine, an upright pole 12 feet tall is casting a shadow 8 feet long. At the same time, a nearby upright pole is casting a shadow 10 feet long. If the lengths of the shadows are proportional to the heights of the poles, what is the height, in feet, of the taller pole?
If \( a \) is the smallest prime number greater than 21 and \( b \) is the largest prime number less than 16, then \( ab = ? \)
The total amount of Judy’s water bill for the last quarter of the year was
(40.50. The bill consisted of a fixed charge of)13.50 plus a charge of
(0.0075 per gallon for the water used in the quarter. For how many gallons of water was Judy charged for the quarter?

The median of the numbers in list \( R \) is how much greater than the median of the numbers in list \( S \)?
If \( c \) and \( d \) are positive integers and \( m \) is the greatest common factor of \( c \) and \( d \), then \( m \) must be the greatest common factor of \( c \) and which of the following integers?
Of the 750 participants in a professional meeting, 450 are females and 1/4 of the male participants are less than thirty years old. If one of the participants will be randomly selected to receive a book prize, what is the probability that the person selected will be less than thirty years old?
In the xy-plane, what is the slope of the line whose equation is \( 3x - 2y = 8 \)?
If a group of students having an average age of 16 years joined a class, the average age of all the students in the class reduces from 18 years to 17 years. What is the ratio of the number of students who joined the class to the number of students who were initially in the class?
If \( (a - 3)^2 + |b - 3| = 0 \), \( (a - 3)^2 + |b - 3| = 0 \), what is the value of \( a - b \)?
What is one possible solution to the following equation: \[ \frac{x+1}{x} - \frac{3}{2x^2} = \frac{-5}{2x} \]
If \( 4x + 3x - 2(x + 5) = -9 \), then \( x = ? \)
If the ratio of milk cartons to juice boxes is \( 13:x \) and there are 39 milk cartons and 18 juice boxes, what is the value of \( x \)?
A triangle, RST, is reflected across the y-axis to form the triangle \( R'S'T' \) in the standard \( (x, y) \) coordinate plane; thus, \( R \) reflects to \( R' \). The coordinates of point T are \( (j, k) \). What are the coordinates of point \( T' \)?
How many of the numbers between 20 and 40 are prime?
If \( a = -1 \) and \( b = 4 \), what is the difference between \( a3b + 3b \) and \( a3b + 3b0 \)?
What is the least common multiple (LCM) of 3, 8, and 10?
How many of the numbers between 20 and 40 are prime?
If \( a = -1 \) and \( b = 4 \), what is the difference between \( a3b + 3b \) and \( a3b + 3b0 \)?
What is the least common multiple (LCM) of 3, 8, and 10?

Question 32:
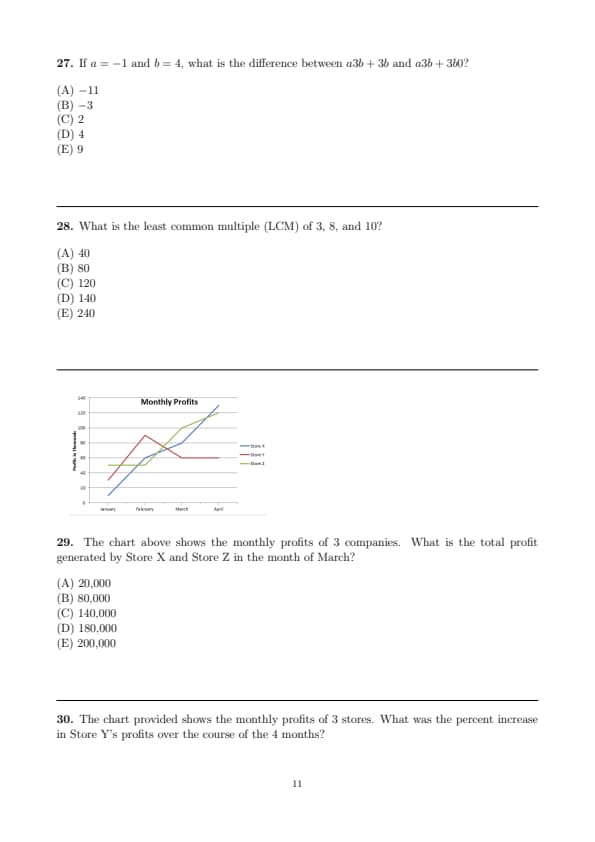
The chart above shows the monthly profits of 3 companies. What is the total profit generated by Store X and Store Z in the month of March?
View Solution
Step 1: Identify the profits for Store X and Store Z in March.
From the graph:
- Store X profit in March is 60,000 (thousands of dollars).
- Store Z profit in March is also 60,000 (thousands of dollars).
Step 2: Add the profits for Store X and Store Z.
The total profit for Store X and Store Z in March is: \[ 60,000 + 60,000 = 120,000 \, thousands of dollars. \]
Step 3: Conclusion.
The total profit generated by Store X and Store Z in March is 120,000. Therefore, the correct answer is: \[ \boxed{140,000}. \]
Final Answer: \[ \boxed{140,000} \] Quick Tip: When calculating total profits, always ensure to sum the individual profits for each company involved in the question.
O is the center of the circle with radius 6.
The greatest prime factor of 144 is \( x \)
The greatest prime factor of 96 is \( y \)
The price of a pair of sneakers was $80 for the last six months of last year. On January first, the price increased by 20%. After the price increase, an employee bought these sneakers with a 10% employee discount. What price did the employee pay?
In how many different ways can 3 identical green shirts and 3 identical red shirts be distributed among 6 children such that each child receives a shirt?
Dharik lives in a house on a straight street. For years, there have been 16 houses on his street to the right of his house and 17 houses on his street to the left of his house. Last year, 5 new houses were built on the same street even further to the left of those houses to the left of Dharik’s house. If these are the only houses on this street, how many houses are on this street?




















Comments