The CAT DILR section requires good analysis skills, critical thinking, and attention to detail, along with a thorough understanding of the Data Analysis. This article provides a set of MCQs on Data Analysis to help you understand the topic and enhance your data interpretation and logical reasoning with the help of detailed solutions, which will help you in the CAT 2025 exam preparation.
Whether you're revising the basics or testing your knowledge, these MCQs will serve as a valuable practice resource.
The CAT 2025 exam is expected to follow a similar trend to the CAT 2024, with 24 questions from the VARC section out of a total of 68 questions.
Also Read

CAT MCQs on Data Analysis
The following additional facts are known about the scores in the project and the test.
1. The minimum, maximum and the average of both project and test scores were identical – 40, 80 and 60 , respectively.
2. The test scores of the students were all multiples of 10 ; four of them were distinct and the remaining two were equal to the average test scores.
3. Amala's score in the project was double that of Koli in the same, but Koli scored 20 more than Amala in the test. Yet Amala had the highest aggregate score.
4. Shyamal scored the second highest in the test. He scored two more than Koli, but two less than Amala in the aggregate.
5. Biman scored the second lowest in the test and the lowest in the aggregate.
6. Mathew scored more than Rini in the project, but less than her in the test.
What was Rini's score in the project?(This Question was asked as TITA)

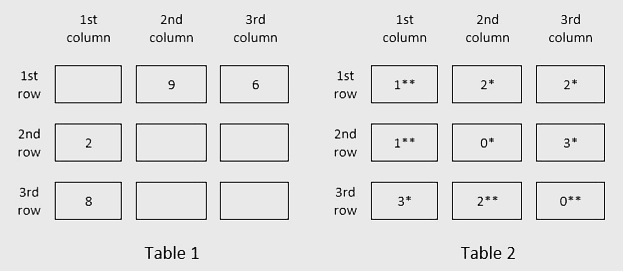
Table 1 gives information regarding the median of the numbers of coins in the three sacks in a box for some of the boxes. In Table 2 each box has a number which represents the number of sacks in that box having more than 5 coins. That number is followed by a * if the sacks in that box satisfy exactly one among the following three conditions, and it is followed by ** if two or more of these conditions are satisfied.
i) The minimum among the numbers of coins in the three sacks in the box is 1.
ii) The median of the numbers of coins in the three sacks is 1.
iii) The maximum among the numbers of coins in the three sacks in the box is 9.
For how many boxes are the average and median of the numbers of coins contained in the three sacks in that box the same? [This Question was asked as TITA]
The following additional facts are known about the scores in the project and the test.
1. The minimum, maximum and the average of both project and test scores were identical – 40, 80 and 60 , respectively.
2. The test scores of the students were all multiples of 10 ; four of them were distinct and the remaining two were equal to the average test scores.
3. Amala's score in the project was double that of Koli in the same, but Koli scored 20 more than Amala in the test. Yet Amala had the highest aggregate score.
4. Shyamal scored the second highest in the test. He scored two more than Koli, but two less than Amala in the aggregate.
5. Biman scored the second lowest in the test and the lowest in the aggregate.
6. Mathew scored more than Rini in the project, but less than her in the test.
What was Mathew's score in the test?(This Question was asked as TITA)

Table 1 gives information regarding the median of the numbers of coins in the three sacks in a box for some of the boxes. In Table 2 each box has a number which represents the number of sacks in that box having more than 5 coins. That number is followed by a * if the sacks in that box satisfy exactly one among the following three conditions, and it is followed by ** if two or more of these conditions are satisfied.
i) The minimum among the numbers of coins in the three sacks in the box is 1.
ii) The median of the numbers of coins in the three sacks is 1.
iii) The maximum among the numbers of coins in the three sacks in the box is 9.
How many sacks have exactly one coin?[This Question was asked as TITA]

Table 1 gives information regarding the median of the numbers of coins in the three sacks in a box for some of the boxes. In Table 2 each box has a number which represents the number of sacks in that box having more than 5 coins. That number is followed by a * if the sacks in that box satisfy exactly one among the following three conditions, and it is followed by ** if two or more of these conditions are satisfied.
i) The minimum among the numbers of coins in the three sacks in the box is 1.
ii) The median of the numbers of coins in the three sacks is 1.
iii) The maximum among the numbers of coins in the three sacks in the box is 9.
In how many boxes do all three sacks contain different numbers of coins? [This Question was asked as TITA]
1. Every dealer sold at least two window ACs.
2. D1 sold 13 inverter ACs, while D3 sold 5 Non-inverter ACs.
3. A total of six Window Non-inverter ACs and 36 Split Inverter ACs were sold in the city. 4. The number of Split ACs sold by D1 was twice the number of Window ACs sold by it. 5. D3 and D4 sold an equal number of Window ACs and this number was one-third of the number of similar ACs sold by D2.
4. D2 and D3 were the only ones who sold Window Non-inverter ACs. The number of these ACs sold by D2 was twice the number of these ACs sold by D3.
5. D3 and D4 sold an equal number of Split Inverter ACs. This number was half the number of similar ACs sold by D2
How many Split Inverter ACs did D2 sell?
1. Every dealer sold at least two window ACs.
2. D1 sold 13 inverter ACs, while D3 sold 5 Non-inverter ACs.
3. A total of six Window Non-inverter ACs and 36 Split Inverter ACs were sold in the city. 4. The number of Split ACs sold by D1 was twice the number of Window ACs sold by it. 5. D3 and D4 sold an equal number of Window ACs and this number was one-third of the number of similar ACs sold by D2.
4. D2 and D3 were the only ones who sold Window Non-inverter ACs. The number of these ACs sold by D2 was twice the number of these ACs sold by D3.
5. D3 and D4 sold an equal number of Split Inverter ACs. This number was half the number of similar ACs sold by D2
What was the total number of ACs sold by D2 and D4? (This Question was asked as TITA)
1. Chitra never waited in the queue and completed her visit by 11 am after spending Rs. 50 to pay for the ticket(s).
2. Anjali took Ride-1 at 11 am after waiting for 30 mins for Chitra to complete it. It was the only ride where Anjali waited.
3. Bipasha began her first of three rides at 11:30 am. All three visitors incurred the same amount of ticket expense by 12:15 pm.
4. The last ride taken by Anjali and Bipasha was the same, where Bipasha waited 30 mins for Anjali to complete her ride. Before standing in the queue for that ride, Bipasha took a 1- hour coffee break after completing her previous ride
How many rides did Anjali and Chitra take in total? [This Question was asked as TITA]
1. Chitra never waited in the queue and completed her visit by 11 am after spending Rs. 50 to pay for the ticket(s).
2. Anjali took Ride-1 at 11 am after waiting for 30 mins for Chitra to complete it. It was the only ride where Anjali waited.
3. Bipasha began her first of three rides at 11:30 am. All three visitors incurred the same amount of ticket expense by 12:15 pm.
4. The last ride taken by Anjali and Bipasha was the same, where Bipasha waited 30 mins for Anjali to complete her ride. Before standing in the queue for that ride, Bipasha took a 1- hour coffee break after completing her previous ride
What was the total amount spent on tickets (in Rs.) by Anjali? [This Question was asked as TITA]
b. 25 patients were treated with type A medicine only. 20 patients were treated with type C medicine only. 10 patients were treated with type D medicine only.
c. 35 patients were treated with type A and type D medicines only. 20 patients were treated with type A and type B medicines only. 30 patients were treated with type A and type C medicines only. 20 patients were treated with type C and type D medicines only.
d. 100 patients were treated with exactly three types of medicines.
e. 40 patients were treated with medicines of types A, B and C, but not with medicines of type D. 20 patients were treated with medicines of types A, C and D, but not with medicines of type B.
f. 50 patients were given all the four types of medicines. 75 patients were treated with exactly one type of medicine.
How many patients were treated with medicine type B? [This Question was asked as TITA]
b. 25 patients were treated with type A medicine only. 20 patients were treated with type C medicine only. 10 patients were treated with type D medicine only.
c. 35 patients were treated with type A and type D medicines only. 20 patients were treated with type A and type B medicines only. 30 patients were treated with type A and type C medicines only. 20 patients were treated with type C and type D medicines only.
d. 100 patients were treated with exactly three types of medicines.
e. 40 patients were treated with medicines of types A, B and C, but not with medicines of type D. 20 patients were treated with medicines of types A, C and D, but not with medicines of type B.
f. 50 patients were given all the four types of medicines. 75 patients were treated with exactly one type of medicine.
The number of patients who were treated with medicine types B, C and D, but not type A was: [This Question was asked as TITA]
b. 25 patients were treated with type A medicine only. 20 patients were treated with type C medicine only. 10 patients were treated with type D medicine only.
c. 35 patients were treated with type A and type D medicines only. 20 patients were treated with type A and type B medicines only. 30 patients were treated with type A and type C medicines only. 20 patients were treated with type C and type D medicines only.
d. 100 patients were treated with exactly three types of medicines.
e. 40 patients were treated with medicines of types A, B and C, but not with medicines of type D. 20 patients were treated with medicines of types A, C and D, but not with medicines of type B.
f. 50 patients were given all the four types of medicines. 75 patients were treated with exactly one type of medicine.
How many patients were treated with medicine types B and D only? [This Question was asked as TITA]
b. 25 patients were treated with type A medicine only. 20 patients were treated with type C medicine only. 10 patients were treated with type D medicine only.
c. 35 patients were treated with type A and type D medicines only. 20 patients were treated with type A and type B medicines only. 30 patients were treated with type A and type C medicines only. 20 patients were treated with type C and type D medicines only.
d. 100 patients were treated with exactly three types of medicines.
e. 40 patients were treated with medicines of types A, B and C, but not with medicines of type D. 20 patients were treated with medicines of types A, C and D, but not with medicines of type B.
f. 50 patients were given all the four types of medicines. 75 patients were treated with exactly one type of medicine.
The number of patients who were treated with medicine type D was: [This Question was asked as TITA]
1.At the end of three rounds, Arun had scored 6 points, Dipak had scored 2 points, Bankim and Charu had scored -2 points each.
2.At the end of six rounds, Arun had scored 7 points, Bankim and Dipak had scored -1 point each, and Charu had scored -5 points.
3.Dipak’s score in the third round was less than his score in the first round but was more than his score in the second round.
4.In exactly two out of the six rounds, Arun was the only player who bid Hi.
In how many rounds did Arun bid Hi? [This Question was asked as TITA]



Comments