UP Board Class 12 Physics Question Paper 2024 PDF (Code 348 FY) is available for download here. The Physics exam was conducted on March 4, 2024 in the Evening Shift from 2 PM to 5:15 PM. The total marks for the theory paper are 70. Students reported the paper to be moderate to tough.
UP Board Class 12 Physics Question Paper 2024 (Code 348 FY) with Solutions
| UP Board Class 12 Physics Question Paper with Answer Key | Check Solution |

UP Board Class 12 Physics Questions with Solutions
(a) A wire is stretched to double of its original length. The value of its resistivity becomes:
View Solution
Step 1: Resistivity (\( \rho \)) is a material property and does not change with stretching.
\[ Resistivity remains constant \]
\[ \boxed{\rho = constant} \] Quick Tip: Resistivity depends only on the material, not on dimensions.
(b) The refracting angle of a prism of refractive index \( \sqrt{3} \) is equal to its angle of minimum deviation. The value of angle of minimum deviation is:
View Solution
Step 1: The formula for minimum deviation is:
\[ \delta_{\min} = 2 \theta - A \]
Step 2: Given \( A = 60^\circ \) and \( \mu = \sqrt{3} \), we solve for \( \delta_{\min} \).
\[ \boxed{\delta_{\min} = 60^\circ} \] Quick Tip: In an equilateral prism with refractive index \( \sqrt{3} \), the minimum deviation angle equals the prism angle.
(c) The unit of \( \sqrt{LC} \) (where \( L \) is inductance and \( C \) is capacitance) is:
View Solution
Step 1: The dimensional formula of inductance \( L \) is \( [ML^2T^{-2}A^{-2}] \) and for capacitance \( C \) is \( [M^{-1}L^{-2}T^{4}A^{2}] \).
Step 2: Their product gives:
\[ \sqrt{LC} \propto T \]
\[ \boxed{Unit: Second} \] Quick Tip: The product of inductance and capacitance represents the square of time dimension.
(d) Threshold wavelength for a photoelectric cell is \( \lambda_0 \). If the work-function of the cathode of some other cell becomes \( n \) times that of the first cell, then threshold wavelength for the other cell will be:
View Solution
Step 1: The work-function \( W \) and threshold wavelength \( \lambda \) are related as:
\[ W \propto \frac{1}{\lambda} \]
Step 2: If the work-function increases \( n \) times:
\[ \lambda' = \frac{\lambda_0}{n} \]
\[ \boxed{\lambda_0 / n} \] Quick Tip: Threshold wavelength is inversely proportional to the work-function.
(e) In the given nuclear process, particle \( W \) is:
\[ ^2He^4 + _zX^A \rightarrow _{z+2}Y^{A+3} + W \]
View Solution
Step 1: By balancing atomic number and mass number:
\[ 4 + A = (A+3) + 1 \]
Step 2: This indicates that the emitted particle is a proton.
\[ \boxed{Proton} \] Quick Tip: Use conservation of mass and atomic number to identify unknown particles.
(f) In order to pass 10% of the main current in a galvanometer of resistance \( R \), the required resistance of shunt should be:
View Solution
Step 1: The shunt resistance is calculated as:
\[ S = \frac{I_G R}{I - I_G} \]
Step 2: Given 10% current passes through the galvanometer, the correct answer is:
\[ \boxed{R/11} \] Quick Tip: Shunt resistance allows a controlled fraction of current to bypass the galvanometer.
(a) Write the expression and unit of magnetic dipole moment.
View Solution
The magnetic dipole moment \( \mu \) is given by:
\[ \mu = I \cdot A \]
where \( I \) is the current and \( A \) is the area of the loop.
The unit of magnetic dipole moment is:
\[ Ampere-meter^2 \, (A \cdot m^2) \] Quick Tip: Magnetic dipole moment quantifies the strength and orientation of a magnetic source.
(b).What are the microwaves? State one use of them.
View Solution
Microwaves are electromagnetic waves with frequencies between \( 1 \) GHz and \( 300 \) GHz.
Use: Microwaves are commonly used in radar systems for detecting objects at a distance.
\[ \boxed{Used in radar systems} \] Quick Tip: Microwaves are widely used in communication and cooking applications.
(c). What is meant by angle of polarisation?
View Solution
The angle of polarisation (\( \theta_p \)) is the angle of incidence at which light is completely polarised upon reflection.
\[ \theta_p = \tan^{-1} (\mu) \] Quick Tip: At Brewster's angle, reflected light is completely plane polarised.
(d).Whether the \( p-n \) junction diode is forward biased or reverse biased in the given figure.
View Solution
The diode is reverse biased.
Step 1: In the given circuit, the negative terminal (\(-5V\)) is connected to the \( p \)-side, and the positive terminal (\(-3V\)) is connected to the \( n \)-side.
Step 2: Since the \( p \)-side is at a lower potential, the junction is reverse biased.
\[ \boxed{Reverse biased} \] Quick Tip: In reverse bias, the depletion region widens, and current flow is minimal.
(e) Define 1 henry of self-inductance.
View Solution
A coil has an inductance of 1 henry if a current change of \( 1 \) ampere per second induces an electromotive force of \( 1 \) volt.
\[ \boxed{1 \, H = 1 \, V \cdot s / A} \] Quick Tip: Inductance measures the opposition to changes in current flow in a circuit.
(f.) Write the definition and unit of current density.
View Solution
Current density (\( J \)) is defined as the current flowing per unit cross-sectional area.
\[ J = \frac{I}{A} \]
The unit of current density is:
\[ Ampere per square meter (A/m^2) \] Quick Tip: Current density indicates how much electric current flows through a given area.
(a) Obtain the formula of the relationship of drift velocity and potential difference.
View Solution
The drift velocity \( v_d \) is related to the applied potential difference \( V \) by the formula:
\[ v_d = \frac{e E \tau}{m} \]
Since \( E = \frac{V}{L} \), the relationship becomes:
\[ v_d = \frac{e \tau}{m} \cdot \frac{V}{L} \] Quick Tip: Drift velocity increases linearly with the applied potential difference.
(b.) Find the ratio of de-Broglie wavelength associated with a proton and an \( \alpha \)-particle having the same kinetic energy.
View Solution
The de-Broglie wavelength is given by:
\[ \lambda = \frac{h}{\sqrt{2mK}} \]
For equal kinetic energy:
\[ \frac{\lambda_p}{\lambda_{\alpha}} = \sqrt{\frac{m_{\alpha}}{m_p}} \]
Since the mass of an alpha particle is four times that of a proton:
\[ \frac{\lambda_p}{\lambda_{\alpha}} = \sqrt{\frac{4m_p}{m_p}} = 2 \]
\[ \boxed{2} \] Quick Tip: For particles with the same kinetic energy, de-Broglie wavelength is inversely proportional to the square root of mass.
(c).Define mass defect and binding energy.
View Solution
Mass defect: The difference between the sum of the masses of individual nucleons and the actual mass of the nucleus.
\[ \Delta m = (Z m_p + N m_n) - M_{nucleus} \]
Binding energy: The energy required to separate the nucleus into its individual nucleons.
\[ E_b = \Delta m \cdot c^2 \]
\[ \boxed{E_b = \Delta m \cdot c^2} \] Quick Tip: Mass defect leads to the release of binding energy according to Einstein's equation.
(d) Current of 5 mA is flowing in the given circuit. Find the value of the resistor \( R \).
View Solution
Using Ohm's Law:
\[ V_{total} = 1.5 \, V - 0.5 \, V = 1.0 \, V \]
\[ I = \frac{V}{R} \]
\[ 5 \times 10^{-3} = \frac{1}{R} \]
\[ R = \frac{1}{5 \times 10^{-3}} = 200 \, \Omega \]
\[ \boxed{200 \, \Omega} \] Quick Tip: Subtract the diode voltage drop before applying Ohm's Law to find resistance.
(a) What is displacement current? A plane electromagnetic wave of 25 MHz frequency is propagating along the x-axis in vacuum. The electric field at any point in the vacuum is \( \vec{E} = 6 \hat{j} \) volt/metre.
What is the magnitude and direction of the magnetic field \( \vec{B} \) at this point?
View Solution
Displacement Current: It is the current that appears in the region where an electric field is changing with time, given by:
\[ I_d = \varepsilon_0 \frac{d\Phi_E}{dt} \]
Step 1: The magnitude of the magnetic field is obtained using the relation:
\[ B = \frac{E}{c} \]
Step 2: Substituting values:
\[ B = \frac{6}{3 \times 10^8} \]
\[ B = 2 \times 10^{-8} \, T \]
Step 3: The direction is along the \( \hat{k} \)-axis due to cross-product rules.
\[ \boxed{B = 2 \times 10^{-8} T, along \hat{k}} \] Quick Tip: The magnetic field is perpendicular to both the electric field and propagation direction.
(b) The equivalent capacitance is 20 \( \mu \)F by joining two capacitors of capacitances \( C_1 \) \( \mu \)F and \( C_2 \) \( \mu \)F in parallel. If they are joined in series, the equivalent capacitance is 4.8 \( \mu \)F. Find the ratio of the capacitances \( C_1 \) and \( C_2 \) ( \( C_1 > C_2 \)).
View Solution
Using the formulas for parallel and series combinations:
\[ C_1 + C_2 = 20 \]
\[ \frac{C_1 C_2}{C_1 + C_2} = 4.8 \]
Solving for the ratio:
\[ C_1 = 16 \, \muF, \quad C_2 = 4 \, \muF \]
\[ \boxed{C_1 : C_2 = 4 : 1} \] Quick Tip: In series, reciprocal capacitances add; in parallel, capacitances sum directly.
(c) When does the force acting between two parallel and straight current carrying conductors become (i) attractive and (ii) repulsive and why?
View Solution
(i) Attractive: When the currents flow in the same direction.
(ii) Repulsive: When the currents flow in opposite directions.
\[ \boxed{Attractive if same direction, repulsive if opposite direction.} \] Quick Tip: Parallel currents attract, anti-parallel currents repel due to the interaction of magnetic fields.
(d) What is meant by a resonant circuit? Write down the required conditions for the L-C-R series resonant circuit and expression for the frequency in the state of resonance.
View Solution
A resonant circuit is an electrical circuit in which resonance occurs at a particular frequency.
Resonance Condition:
\[ \omega L = \frac{1}{\omega C} \]
Resonant Frequency:
\[ f = \frac{1}{2\pi \sqrt{LC}} \]
\[ \boxed{f = \frac{1}{2\pi \sqrt{LC}}} \] Quick Tip: At resonance, impedance is minimum and current is maximum in an L-C-R circuit.
(e) Write down Einstein’s photoelectric equation. Photons of energies 1 eV and 2.5 eV respectively are incident on a metal plate of work function 0.5 eV. If maximum kinetic energies of emitted photoelectrons are \( k_1 \) and \( k_2 \) respectively and their velocities are \( v_1 \) and \( v_2 \), then find the magnitudes of (i) \( k_1/k_2 \) and (ii) \( v_1/v_2 \).
View Solution
Einstein’s Photoelectric Equation:
\[ K_{\max} = h\nu - \phi \]
Step 1: Using given data:
\[ k_1 = 1 - 0.5 = 0.5 \, eV \]
\[ k_2 = 2.5 - 0.5 = 2.0 \, eV \]
\[ \frac{k_1}{k_2} = \frac{0.5}{2.0} = \frac{1}{4} \]
\[ \boxed{\frac{k_1}{k_2} = \frac{1}{4}} \]
Step 2: Since kinetic energy is proportional to the square of velocity:
\[ \frac{v_1}{v_2} = \sqrt{\frac{k_1}{k_2}} \]
\[ = \sqrt{\frac{1}{4}} = \frac{1}{2} \]
\[ \boxed{\frac{v_1}{v_2} = \frac{1}{2}} \] Quick Tip: Kinetic energy is proportional to the square of velocity in photoelectric effect.
(a) Derive the formula for the torque acting on a current-carrying loop in a uniform magnetic field and define the magnetic dipole moment with the help of it.
View Solution
Torque on a current-carrying loop:
The torque \( \tau \) on a current loop in a uniform magnetic field is given by:
\[ \tau = \vec{m} \times \vec{B} \]
where \( \vec{m} \) is the magnetic dipole moment and \( \vec{B} \) is the magnetic field.
Magnetic dipole moment:
\[ m = N I A \]
where:
- \( N \) is the number of turns,
- \( I \) is the current,
- \( A \) is the area of the loop.
\[ \boxed{\tau = N I A B \sin \theta} \] Quick Tip: The torque is maximum when the plane of the loop is perpendicular to the magnetic field.
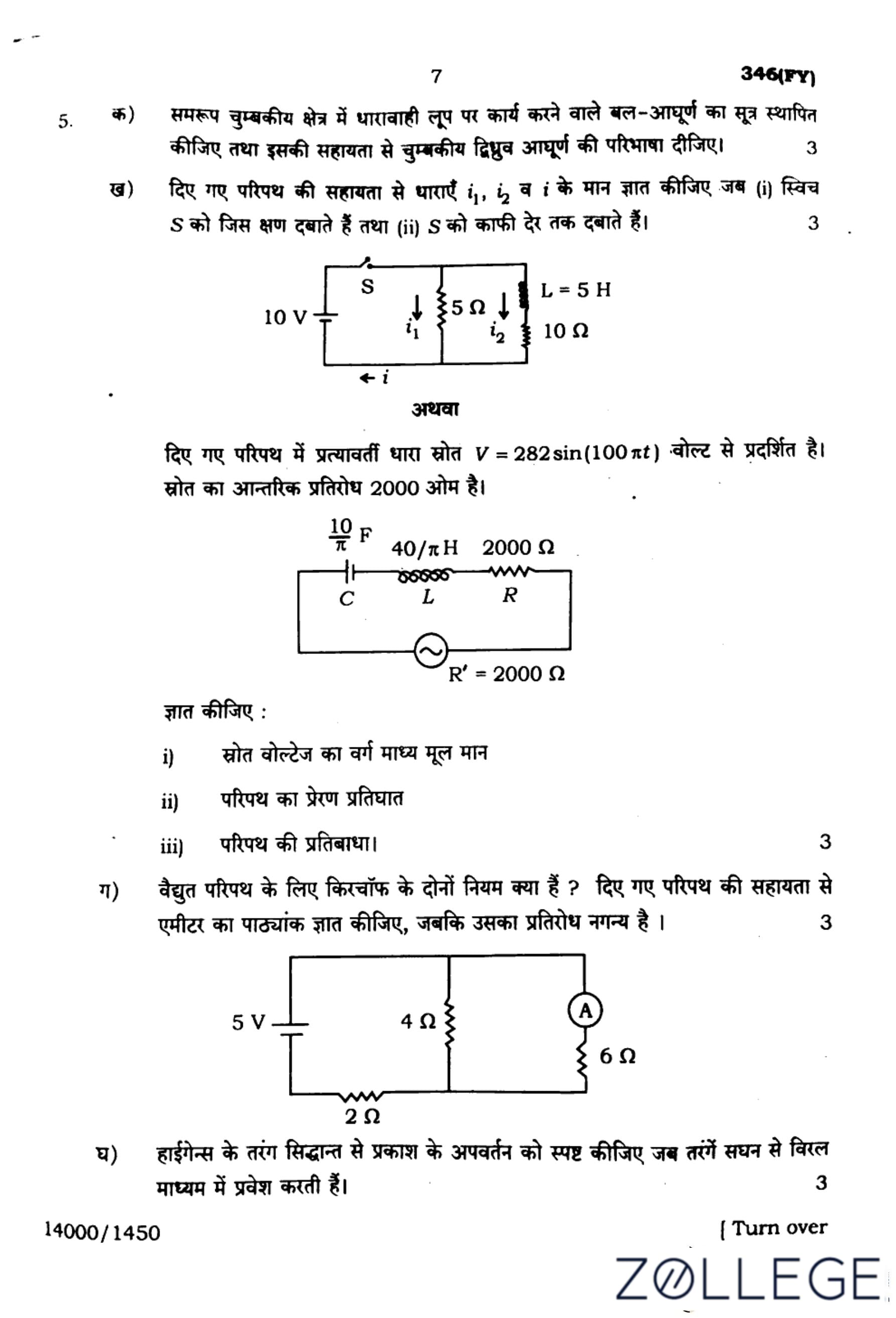
(b) Find the magnitudes of currents \( i_1 \), \( i_2 \), and \( i \) with the help of the given circuit, when (i) just at the moment switch S is pressed and (ii) S is pressed for a long time.
View Solution
(i) Just at the moment switch \( S \) is pressed:
At \( t = 0 \), the inductor opposes any change in current, so the initial current through the inductor is zero.
\[ i_2 = 0, \quad i_1 = \frac{10}{5} = 2 A \]
\[ \boxed{i = i_1 = 2 A} \]
(ii) After a long time:
The inductor acts as a short circuit, and the total resistance becomes:
\[ R_{eq} = 5 + 10 = 15 \, \Omega \]
\[ i = \frac{10}{15} = \frac{2}{3} A \]
Current division:
\[ i_1 = \frac{2}{3} \times \frac{10}{15} = \frac{2}{3} A, \quad i_2 = \frac{2}{3} \times \frac{5}{15} = \frac{1}{3} A \]
\[ \boxed{i_1 = \frac{2}{3} A, \quad i_2 = \frac{1}{3} A} \] Quick Tip: In an RL circuit, the inductor initially resists current flow and allows full current flow after a long time.
OR
Question 5:
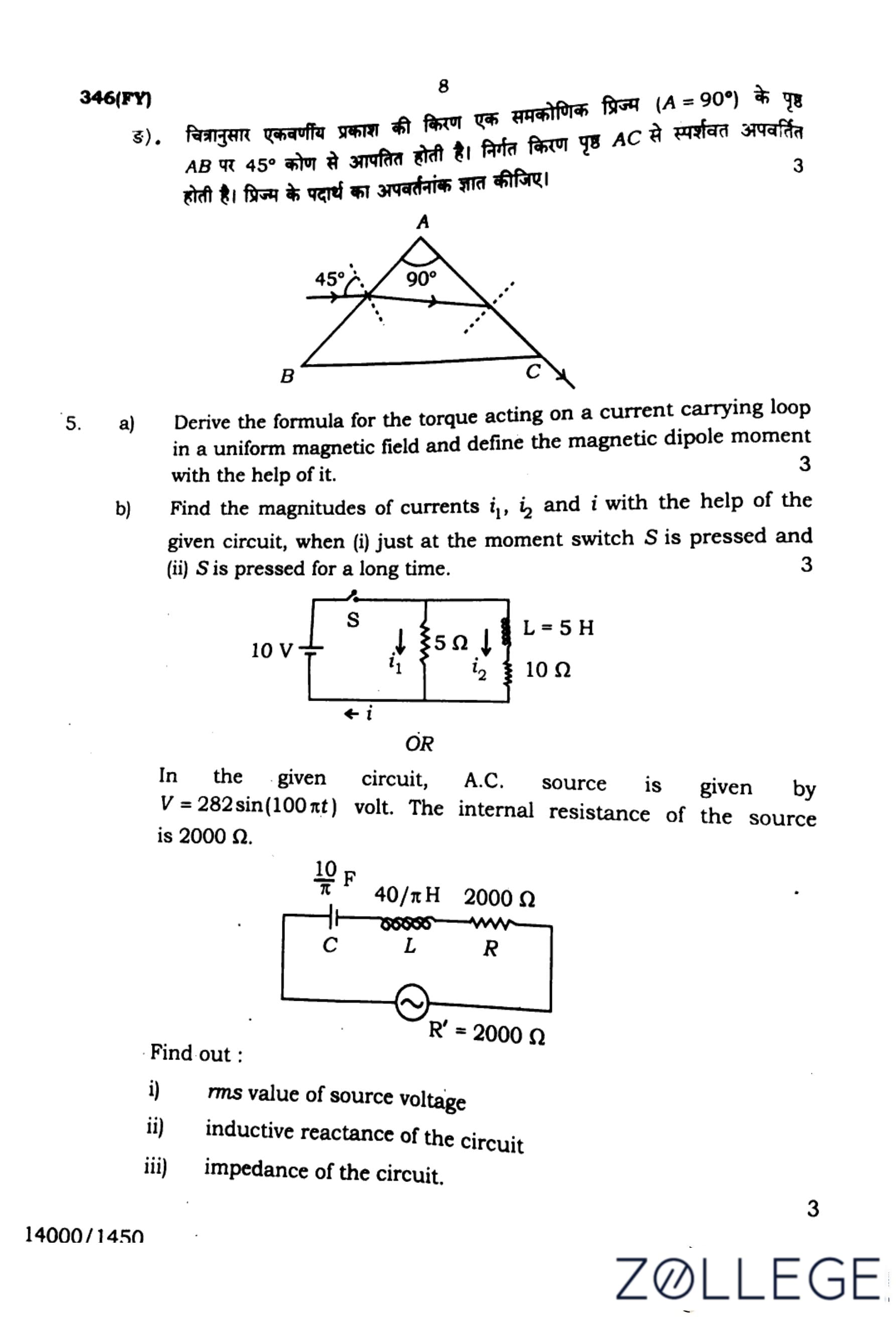
(b) In the given circuit, A.C. source is given by:
\[ V = 282 \sin (100 \pi t) volt \]
The internal resistance of the source is \( 2000 \, \Omega \).
Find out:
(i) rms value of source voltage
(ii)inductive reactance of the circuit
(iii) impedance of the circuit
View Solution
(i) RMS Value of Source Voltage
The given voltage is in peak form:
\[ V_{peak} = 282 V \]
\[ V_{rms} = \frac{V_{peak}}{\sqrt{2}} \]
\[ = \frac{282}{\sqrt{2}} = 199.5 V \]
\[ \boxed{199.5 V} \] Quick Tip: RMS voltage is obtained by dividing peak voltage by \( \sqrt{2} \).
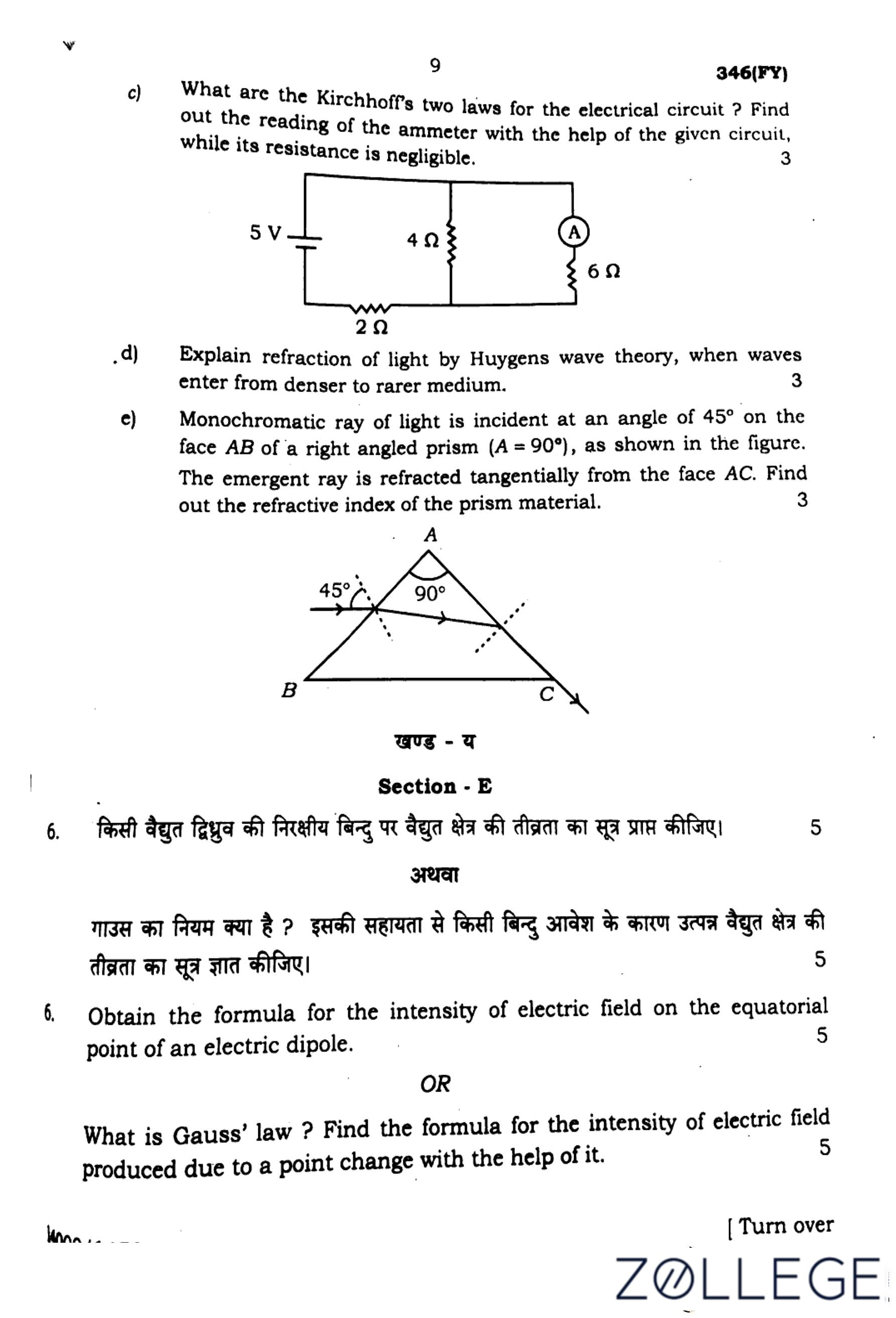
(c) What are Kirchhoff’s two laws for the electrical circuit? Find out the reading of the ammeter with the help of the given circuit, while its resistance is negligible.
View Solution
Kirchhoff's First Law (KCL - Junction Rule):
The sum of currents entering a junction is equal to the sum of currents leaving the junction.
\[ \sum I_{in} = \sum I_{out} \]
Kirchhoff's Second Law (KVL - Loop Rule):
The sum of all voltages around any closed loop in a circuit is zero.
\[ \sum V = 0 \]
Solution for Ammeter Reading:
Applying Kirchhoff's loop rule to the given circuit:
\[ \frac{5}{4 + 2} = \frac{5}{6} \, A \]
The voltage across the parallel resistors is:
\[ V = IR = \frac{5}{6} \times 2 = \frac{10}{6} V \]
Current through the 6Ω resistor:
\[ I = \frac{10}{6} \div 6 = \frac{5}{18} \, A \]
\[ \boxed{Ammeter reading = \frac{5}{18} A} \] Quick Tip: Use Kirchhoff's loop rule to calculate voltages and junction rule for current distribution.
(d) Explain refraction of light by Huygens wave theory, when waves enter from denser to rarer medium.
View Solution
According to Huygens' wave theory:
Each point on a wavefront acts as a secondary source of wavelets.
When light travels from a denser to a rarer medium, the speed of the wave increases.
The wavefront bends away from the normal due to the increase in speed.
The refractive index is given by:
\[ n = \frac{speed in rarer medium}{speed in denser medium} \]
\[ \boxed{\sin i = n \sin r} \] Quick Tip: When light travels to a rarer medium, it bends away from the normal.
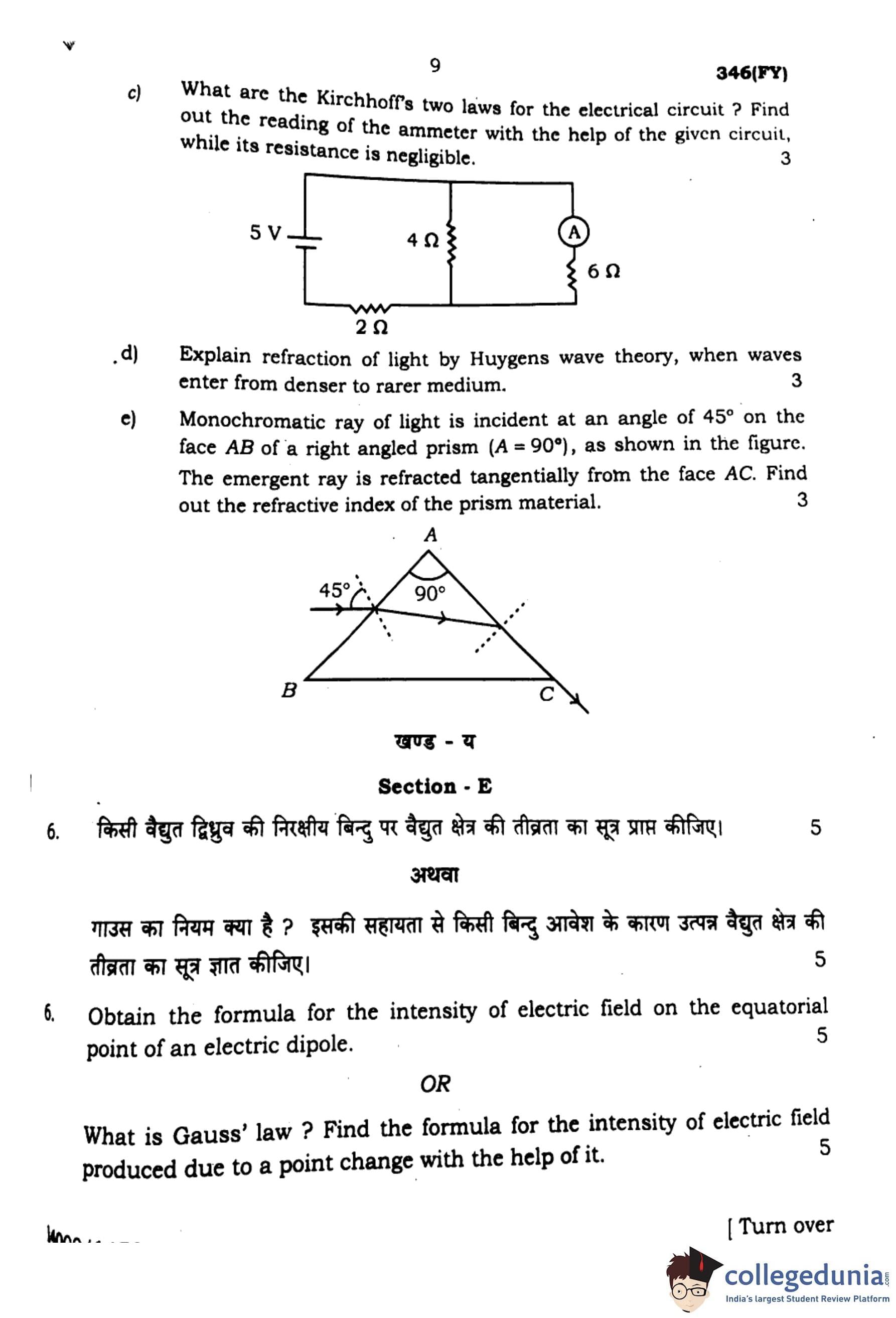
(e) Monochromatic ray of light is incident at an angle of \( 45^\circ \) on the face AB of a right-angled prism (\( A = 90^\circ \)), as shown in the figure. The emergent ray is refracted tangentially from the face AC. Find out the refractive index of the prism material.
View Solution
Step 1: Applying Snell's law at face AB:
\[ n_{air} \sin 45^\circ = n_{prism} \sin r \]
Since \( r = 90^\circ \), the critical angle condition applies:
\[ \sin 45^\circ = \frac{1}{n} \]
\[ n = \frac{1}{\sin 45^\circ} \]
\[ n = \frac{1}{\frac{1}{\sqrt{2}}} = \sqrt{2} \]
\[ \boxed{n = 1.414} \] Quick Tip: At the critical angle, light refracts tangentially along the interface.
Obtain the formula for the intensity of electric field on the equatorial point of an electric dipole.
View Solution
Step 1: Consider an electric dipole consisting of charges \( +q \) and \( -q \) separated by a distance \( 2a \). The dipole moment is:
\[ \vec{p} = q \cdot 2a \]
Step 2: The electric field at an equatorial point (perpendicular bisector) of the dipole at a distance \( r \) from the center is given by the formula:
\[ E_{equatorial} = \frac{1}{4 \pi \varepsilon_0} \cdot \frac{p}{(r^2 + a^2)^{3/2}} \]
Step 3: For large distances (\( r \gg a \)):
\[ E_{equatorial} \approx \frac{1}{4 \pi \varepsilon_0} \cdot \frac{p}{r^3} \]
\[ \boxed{E = \frac{1}{4 \pi \varepsilon_0} \cdot \frac{p}{r^3}} \] Quick Tip: The electric field at the equatorial position is directed opposite to the dipole moment.
OR
Question 6:
What is Gauss' law? Find the formula for the intensity of electric field produced due to a point charge with the help of it.
View Solution
Step 1: Gauss' law states that the total electric flux \( \Phi \) through a closed surface is equal to the charge enclosed divided by the permittivity of free space:
\[ \oint \vec{E} \cdot d\vec{A} = \frac{q}{\varepsilon_0} \]
Step 2: Consider a point charge \( q \) at the center of a spherical surface of radius \( r \):
\[ E \cdot 4 \pi r^2 = \frac{q}{\varepsilon_0} \]
Step 3: Solving for the electric field:
\[ E = \frac{1}{4 \pi \varepsilon_0} \cdot \frac{q}{r^2} \]
\[ \boxed{E = \frac{1}{4 \pi \varepsilon_0} \cdot \frac{q}{r^2}} \] Quick Tip: Gauss' law simplifies calculations for symmetric charge distributions.
State the required conditions for the interference of light. Find the value of maximum resultant intensity of two waves having intensities \( I \) and \( 4I \), when sources are (i) coherent and (ii) non-coherent.
View Solution
Conditions for Interference of Light:
The sources must be coherent (having a constant phase difference).
The sources should emit light waves of the same frequency and wavelength.
The sources must have equal or nearly equal intensity for clear visibility.
The superposition of waves should occur in the same medium.
Step 1: For coherent sources:
\[ I_{max} = (\sqrt{I} + \sqrt{4I})^2 \]
\[ = (1 + 2)^2 I = 9I \]
\[ \boxed{9I} \]
Step 2: For non-coherent sources, the intensities add directly:
\[ I_{total} = I + 4I = 5I \]
\[ \boxed{5I} \] Quick Tip: In coherent interference, amplitudes add; in non-coherent interference, intensities add.
OR
Question 7:
Focal length of each lens is 10 cm as shown in the given figure. Find the distance of the image of point object O from the convex lens and also draw the ray diagram. If both lenses are placed in contact, what will be the power of the combined lens?
View Solution
Step 1: Using the lens formula for the convex lens:
\[ \frac{1}{f} = \frac{1}{v} - \frac{1}{u} \]
\[ \frac{1}{10} = \frac{1}{v} - \frac{1}{-20} \]
\[ \frac{1}{v} = \frac{1}{10} + \frac{1}{20} = \frac{3}{20} \]
\[ v = \frac{20}{3} \approx 6.67 cm \]
Step 2: The image acts as an object for the concave lens. Using the lens formula again:
\[ \frac{1}{-10} = \frac{1}{v'} - \frac{1}{30 - 6.67} \]
\[ \frac{1}{-10} = \frac{1}{v'} - \frac{1}{23.33} \]
\[ v' = -17.5 cm \]
\[ \boxed{Image distance = 17.5 cm behind concave lens.} \]
Step 3: For combined lenses in contact, the effective power is:
\[ P_{total} = P_1 + P_2 \]
\[ = \frac{100}{10} + \frac{100}{-10} \]
\[ = 10 - 10 = 0 \, D \]
\[ \boxed{Total power = 0 D (acts like a plane glass).} \] Quick Tip: When convex and concave lenses of equal focal length are combined, they cancel each other out.
What are the Bohr’s postulates for the hydrogen atom? Write down the following for electrons in the ground state of hydrogen atom:
(i) Binding energy
(ii) Angular momentum
(iii) Total energy
View Solution
Bohr's Postulates for Hydrogen Atom:
Electrons revolve in fixed orbits without emitting energy.
Only certain discrete orbits are allowed where angular momentum is quantized.
Electrons emit or absorb energy when transitioning between orbits.
Step 1: Binding Energy
\[ E_{binding} = 13.6 \, eV \]
\[ \boxed{E_{binding} = 13.6 eV} \]
Step 2: Angular Momentum
According to Bohr's quantization condition:
\[ m v r = n \hbar \]
For ground state \( n = 1 \):
\[ L = \hbar = \frac{h}{2\pi} \]
\[ \boxed{L = \frac{h}{2\pi}} \]
Step 3: Total Energy
Total energy of an electron in the ground state:
\[ E = -\frac{13.6}{n^2} \, eV \]
For \( n = 1 \):
\[ \boxed{E = -13.6 eV} \] Quick Tip: Bohr's model explains discrete energy levels and quantization of angular momentum.
OR
Question 8:
What is the difference between nuclear fission and nuclear fusion? Explain each of them with the help of an appropriate example. Why is in both incidents the nuclear energy released?
View Solution
Step 1: Definition of Nuclear Fission and Fusion
Nuclear Fission: The splitting of a heavy nucleus into two lighter nuclei with the release of energy.
\[ ^{235}U + n \rightarrow ^{141}Ba + ^{92}Kr + 3n + energy \]
Nuclear Fusion: The combining of two light nuclei to form a heavier nucleus with the release of energy.
\[ ^{2}H + ^{3}H \rightarrow ^{4}He + n + energy \]
Step 2: Why Energy is Released?
Energy is released in both processes due to the mass defect, which is converted into energy according to Einstein’s equation:
\[ E = mc^2 \]
Step 3: Key Differences
\begin{tabular{|c|c|c|
\hline
Aspect & Fission & Fusion
\hline
Fuel & Uranium/Plutonium & Hydrogen isotopes
\hline
Temperature & Moderate & Very High
\hline
Energy Yield & High & Very High
\hline
Example & Nuclear reactors & Sun's energy
\hline
\end{tabular
\[ \boxed{Fission releases energy by splitting; Fusion releases energy by combining.} \] Quick Tip: Fusion releases more energy than fission but requires extreme conditions to occur.
Explain the differences between \( n \)-type and \( p \)-type semiconductors. Show that both types of semiconductors are electrically neutral.
View Solution
Differences between \( n \)-type and \( p \)-type semiconductors:
\begin{table[h]
\centering
\begin{tabular{|c|c|c|
\hline
Property & \( n \)-type Semiconductor & \( p \)-type Semiconductor
\hline
Majority Carriers & Electrons & Holes
\hline
Minority Carriers & Holes & Electrons
\hline
Dopant Type & Donor (e.g., Phosphorus) & Acceptor (e.g., Boron)
\hline
Charge Carrier Mobility & Higher & Lower
\hline
Electrical Neutrality & Yes & Yes
\hline
\end{tabular
\end{table
Step 1: Electrical Neutrality
Although \( n \)-type semiconductors have excess electrons and \( p \)-type have excess holes, the total number of positive and negative charges remains equal due to the balance between ionized dopant atoms and charge carriers.
\[ \boxed{Both types of semiconductors are electrically neutral.} \] Quick Tip: Both \( n \)-type and \( p \)-type semiconductors are electrically neutral because the charge of dopants balances the free charge carriers.
OR
Question 9:
Discuss the characteristics of (i) forward biasing and (ii) reverse biasing in \( p\)-\(n \) junction. Explain the cause of origin and direction of current in both conditions.
View Solution
(i) Forward Biasing:
Step 1: In forward bias, the \( p \)-side is connected to the positive terminal and the \( n \)-side to the negative terminal.
Step 2: The depletion region narrows, allowing current to flow.
\[ I_{forward} \approx I_s (e^{\frac{V}{kT}} - 1) \]
Step 3: Current flows from \( p \) to \( n \).
\[ \boxed{Current increases exponentially with voltage.} \]
\hrule
(ii) Reverse Biasing:
Step 1: In reverse bias, the \( p \)-side is connected to the negative terminal and the \( n \)-side to the positive terminal.
Step 2: The depletion region widens, preventing current flow.
Step 3: A small leakage current due to minority carriers flows.
\[ \boxed{Current remains nearly constant.} \] Quick Tip: In forward bias, current flows easily; in reverse bias, only leakage current flows.























Comments