UP Board Class 12 Physics Question Paper 2024 PDF (Code 347 FW) is available for download here. The Physics exam was conducted on March 4, 2024 in the Evening Shift from 2 PM to 5:15 PM. The total marks for the theory paper are 70. Students reported the paper to be moderate to tough.
UP Board Class 12 Physics Question Paper 2024 (Code 347 FW) with Solutions
| UP Board Class 12 Physics Question Paper with Answer Key | Check Solution |

UP Board Class 12 Physics Questions with Solutions
(a) The unit of magnetic field is
View Solution
The unit of magnetic field is derived from the definition of force \( F = q(\mathbf{v} \times \mathbf{B}) \), where magnetic force \( B = \frac{F}{qv} \). In terms of SI units: \[ B = \frac{N}{A \cdot m} \quad \Rightarrow \quad newton \cdot metre^{-1} \cdot ampere^{-1}. \] Quick Tip: The SI unit of the magnetic field (B) is Tesla, which is equivalent to \( newton \cdot metre^{-1} \cdot ampere^{-1} \).
(b) If the radius of the nucleus of \(^{13} Al^{27}\) is 3.6 fermi, then the radius of the nucleus of \(^{52} Te^{125}\) is:
View Solution
The radius of a nucleus is proportional to the cube root of its mass number (\(A\)): \[ R \propto A^{1/3}. \]
For \(^{13} Al^{27}\), \[ R_1 = 3.6 \, fermi, \quad A_1 = 27, \quad A_2 = 125. \] \[ \frac{R_2}{R_1} = \left(\frac{A_2}{A_1}\right)^{1/3} \quad \Rightarrow \quad R_2 = R_1 \cdot \left(\frac{125}{27}\right)^{1/3}. \] \[ R_2 = 3.6 \cdot 2 \quad \Rightarrow \quad R_2 = 6 \, fermi. \] Quick Tip: The nuclear radius is proportional to \( A^{1/3} \), where \(A\) is the mass number.
(c) Which of the following laws of conservation holds in Einstein's photoelectric equation?
View Solution
Einstein's photoelectric equation states that: \[ h\nu = \phi + K_{max}, \]
where \(h\nu\) is the energy of the incident photon, \(\phi\) is the work function, and \(K_{max}\) is the maximum kinetic energy of the ejected electron. This conservation equation explicitly describes the conservation of energy. Quick Tip: The law of conservation of energy is fundamental in all physical processes, including photoelectric emission.
(d) If \( V_L, V_R, V_C \), and \( V_O \) are readings of AC voltmeter across the inductor, resistor, capacitor, and source respectively in a certain L-C-R circuit, then:
View Solution
In an L-C-R circuit, the voltage \(V_O\) of the source is the vector sum of voltages across the resistor (\(V_R\)), inductor (\(V_L\)), and capacitor (\(V_C\)). Due to phase differences, the net voltage satisfies: \[ V_O^2 = (V_L - V_C)^2 + V_R^2. \] Quick Tip: Use the phasor addition technique to derive voltage relationships in L-C-R circuits.
(e) Which of the following ray diagrams is correct, when \( n_1 \) is the refractive index of the medium and \( n_2 \) is of the lens material (\( n_1 > n_2 \))?
View Solution
For \(n_1 > n_2\), light rays bend away from the normal upon passing from a denser to a rarer medium. The first diagram (i) correctly demonstrates this refraction. Quick Tip: The bending of light depends on the refractive index of the materials: it bends towards the normal when entering a denser medium and away when entering a rarer medium.
(f) The sides of two solid cubes of the same material are \(l\) and \(3l\) respectively. The ratio of their resistances will be:
View Solution
The resistance \(R\) of a material is given by: \[ R \propto \frac{1}{Cross-sectional area}. \]
For a cube, the cross-sectional area scales with \(l^2\), and resistance is inversely proportional to the square of the side length: \[ R_1 : R_2 = \frac{1}{l^2} : \frac{1}{(3l)^2} \quad \Rightarrow \quad R_1 : R_2 = 9 : 1. \] Quick Tip: The resistance of a material is inversely proportional to its cross-sectional area.
(a) What is the magnitude of the current \( i \) in the given circuit?
View Solution
Using Kirchhoff’s Current Law (KCL), the sum of currents entering a junction equals the sum of currents leaving it: \[ i = (6 \, A + 3 \, A) - (10 \, A + 3 \, A) = 4 \, A. \] Quick Tip: Kirchhoff’s Current Law states that at any junction, the sum of currents entering equals the sum of currents leaving.
(b) What is Lenz’s law?
View Solution
When the magnetic flux linked with a circuit changes, an electromotive force (EMF) is induced, and the induced current opposes this change. Quick Tip: Lenz’s law is a consequence of the principle of conservation of energy in electromagnetic induction.
(c) What is meant by the depletion layer in a \(p\)-\(n\) junction?
View Solution
In a \(p\)-\(n\) junction, due to diffusion, electrons and holes recombine near the junction, leaving behind a region with immobile ions. This region forms the depletion layer, acting as a potential barrier for current flow. Quick Tip: The depletion layer thickness determines the behavior of the \(p\)-\(n\) junction under different biasing conditions.
(d) Find out the angle of refraction in a medium of refractive index \(\sqrt{3}\), when the angle of incidence is \(60^\circ\).
View Solution
Using Snell's law: \[ n_1 \sin i = n_2 \sin r, \]
where \( n_1 = 1 \) (air), \( n_2 = \sqrt{3} \), \( i = 60^\circ \): \[ \sin r = \frac{n_1 \sin i}{n_2} = \frac{1 \times \sin 60^\circ}{\sqrt{3}} = \frac{\sqrt{3}/2}{\sqrt{3}} = \frac{1}{2}. \]
Thus, \( r = 30^\circ \). Quick Tip: Snell's law helps calculate refraction at the boundary between two media of different refractive indices.
(e) The amplitude of the magnetic field of an electromagnetic wave in vacuum is \(B_0 = 510 \, nT\). What is the amplitude of the electric field of the wave?
View Solution
The amplitude of the electric field (\(E_0\)) and magnetic field (\(B_0\)) are related by: \[ E_0 = c B_0, \]
where \( c = 3 \times 10^8 \, m/s \). Substituting the values: \[ E_0 = 3 \times 10^8 \times 510 \times 10^{-9} = 153 \, V/m. \] Quick Tip: In electromagnetic waves, the electric and magnetic fields are related by the speed of light: \( E_0 = c B_0 \).
(f) What is the main difference between paramagnetic and ferromagnetic substances?
View Solution
- Paramagnetic substances have unpaired electrons and exhibit weak magnetic moments.
- Ferromagnetic substances have domains aligned in a magnetic field and show strong magnetic behavior even when the external field is removed. Quick Tip: The retention of magnetism distinguishes ferromagnetic materials from paramagnetic materials.
(a) Explain the energy bands in solids.
View Solution
1. Valence Band: The energy band filled with the highest energy electrons in a solid.
2. Conduction Band: The energy band above the valence band where electrons can move freely, contributing to conductivity.
3. Forbidden Energy Gap: The region between the valence band and conduction band where no electron can exist.
Classification of solids based on band theory:
- Conductors: Overlapping valence and conduction bands.
- Semiconductors: Small energy gap between valence and conduction bands.
- Insulators: Large energy gap, preventing electron movement. Quick Tip: The nature of the energy gap between bands determines the electrical conductivity of a material.
(b) State the conclusions of Rutherford's \( \alpha \)-particle scattering experiment.
View Solution
Key conclusions from the \( \alpha \)-particle scattering experiment:
1. Most \( \alpha \)-particles passed through the gold foil, indicating atoms are mostly empty space.
2. A few \( \alpha \)-particles were deflected at small angles, suggesting a positively charged region in the atom.
3. Very few were deflected back, confirming that the nucleus is small, massive, and positively charged. Quick Tip: Rutherford’s model of the atom replaced Thomson's "plum pudding" model by introducing the nucleus.
(c) If the corresponding de Broglie wavelengths of a proton and a neutron are obtained as same, then which of the two will have greater kinetic energy?
View Solution
From de Broglie’s wavelength formula: \[ \lambda = \frac{h}{\sqrt{2mK}}, \]
where \(m\) is the mass and \(K\) is the kinetic energy. For the same wavelength: \[ K \propto \frac{1}{m}. \]
Since the proton has less mass than the neutron, its kinetic energy will be greater for the same wavelength. Quick Tip: For the same de Broglie wavelength, a lighter particle will always have higher kinetic energy.
(d) A current is passed in a wire of \( 4 \, \Omega \) resistance by a battery. Find out the internal resistance of the battery, when current is passed in another \( 9 \, \Omega \) resistor by the same battery; while the same heat is produced during the same time in both wires.
View Solution
Let the EMF of the battery be \( E \) and its internal resistance be \( r \).
The heat \( H \) is proportional to \( I^2 R \), where \( I \) is the current and \( R \) is the resistance. For both cases, the heat is equal: \[ I_1^2 \cdot 4 = I_2^2 \cdot 9. \]
Using Ohm’s law: \[ I_1 = \frac{E}{4 + r}, \quad I_2 = \frac{E}{9 + r}. \]
Substituting these: \[ \left( \frac{E}{4 + r} \right)^2 \cdot 4 = \left( \frac{E}{9 + r} \right)^2 \cdot 9. \]
Simplifying: \[ \frac{4}{(4 + r)^2} = \frac{9}{(9 + r)^2}. \]
Taking the square root: \[ \frac{2}{4 + r} = \frac{3}{9 + r}. \]
Cross-multiplying: \[ 2(9 + r) = 3(4 + r). \]
Expanding and solving: \[ 18 + 2r = 12 + 3r \quad \Rightarrow \quad r = 6 \, \Omega. \] Quick Tip: The internal resistance of a battery affects the total current and power delivered to external resistors.
A charge \( Q \) is distributed over two concentric hollow spheres of radii \( r \) and \( R \) (\( R > r \)) such that their surface charge densities are equal. Find the electric potential at their common center.
View Solution
The surface charge density for both spheres is equal: \[ \sigma = \frac{Q_1}{4 \pi r^2} = \frac{Q_2}{4 \pi R^2}. \] This implies that the charge on the inner sphere is: \[ Q_1 = \frac{Q r^2}{R^2}, \quad Q_2 = Q - Q_1 = Q \left( 1 - \frac{r^2}{R^2} \right). \] The potential at the common center is: \[ V = \frac{1}{4 \pi \epsilon_0} \left( \frac{Q_1}{r} + \frac{Q_2}{R} \right). \] Substituting values: \[ V = \frac{3Q}{4 \pi \epsilon_0 R}. \] Quick Tip: When dealing with concentric spheres, use charge distribution rules and superposition principles to calculate the potential.What are electromagnetic waves? Explain two characteristics of these waves.
View Solution
- They travel in a vacuum at the speed of light (\( c = 3 \times 10^8 \, \mathrm{m/s} \)).
- They carry energy and momentum and can exert radiation pressure.
What is Biot-Savart law? Obtain the formula and direction for the intensity of the magnetic field on the axis of an anti-clockwise current-carrying loop with its help.
View Solution
The Biot-Savart law states that the magnetic field \( dB \) due to a small current element \( Idl \) at a point is given by: \[ dB = \frac{\mu_0}{4 \pi} \frac{I \, dl \, \sin \theta}{r^2}. \] For a circular current loop, the magnetic field on its axis is: \[ B = \frac{\mu_0 I R^2}{2 (R^2 + x^2)^{3/2}}, \] where \( R \) is the radius of the loop, \( x \) is the distance from the center, and \( I \) is the current. The direction of the magnetic field follows the right-hand thumb rule. Quick Tip: Use Biot-Savart law for problems involving magnetic fields due to current elements or loops.(d) A graph is shown between the maximum kinetic energy (\( E_k \)) of emitted photoelectrons and frequency (\( \nu \)) of the incident light in an experiment of photoelectric effect. Find:
View Solution
Quick Tip: Use Biot-Savart law for problems involving magnetic fields due to current elements or loops.
(e) Define the coefficient of mutual inductance. If a current \( i = 10 \sin(100 \pi t) \, \mathrm{A} \) is flowing in a primary coil, the maximum induced electromotive force in the secondary coil placed near it is \( 5 \pi \, \mathrm{volt} \). What is the coefficient of mutual induction between these coils?
View Solution
The maximum induced emf is related to mutual inductance \( M \) by:
emfmax = M \frac{di}{dt}.
For \( i = 10 \sin(100 \pi t) \):
\(\frac{di}{dt} = 1000 \pi \cos(100 \pi t).\)
The maximum value of \( \frac{di}{dt} \) is \( 1000 \pi \). Substituting values:
5 \pi = M (1000 \pi) \quad \Rightarrow \quad M = 0.005 \, \mathrm{H}.
Quick Tip: The coefficient of mutual inductance can be calculated using \( \text{emf}_{\text{max}} = M \frac{di}{dt} \). Use the derivative of current to find \( \frac{di}{dt} \).(a) A concave mirror forms a real image 4 times the size of an object. The magnification is 3 times by moving the object 3 cm away from the mirror. Find out the radius of curvature of the mirror.
View Solution
(b) Currents of 10 A and 20 A are passed in two long parallel wires A and B, as shown in the figure. A wire C of 15 cm length is placed just in between these two wires, in which 5 A of current is passed. Then what will be the force acting on the wire C?
What is meant by the transformation ratio of a transformer? In a step-down transformer, the transmission line voltage of 2200 volt is changed to 220 volt. Number of turns in the primary coil is 5000. The efficiency of the transformer is 90 percent and output power is 8kW.
Calculate:
View Solution
For a concave mirror, the magnification \( m = -\frac{v}{u} \), where \( v \) is the image distance and \( u \) is the object distance.
Case 1 (\( m = -4 \)):
\( v = -4u. \)
The mirror formula is:
\( \frac{1}{f} = \frac{1}{u} + \frac{1}{v}. \)
Substituting \( v = -4u \):
\( \frac{1}{f} = \frac{1}{u} + \frac{1}{-4u} = \frac{3}{4u}. \)
Case 2 (\( m = -3 \), object moved by 3 cm):
\( u' = u + 3, \quad v' = -3u'. \)
Using the mirror formula:
\( \frac{1}{f} = \frac{1}{u'} + \frac{1}{v'}. \)
Substituting \( v' = -3u' \):
\( \frac{1}{f} = \frac{1}{u+3} + \frac{1}{-3(u+3)} = \frac{2}{3(u+3)}. \)
Equating \( \frac{1}{f} \) from both cases:
\( \frac{3}{4u} = \frac{2}{3(u+3)}. \)
Solving for \( u \):
\( u = 12 \, \mathrm{cm}, \quad f = 9 \, \mathrm{cm}. \)
The radius of curvature is:
\( R = 2f = 18 \, \mathrm{cm}. \)
Quick Tip: For transformers, use the transformation ratio \( \frac{V_s}{V_p} = \frac{N_s}{N_p} \). Efficiency relates input and output power.(c) What is plane polarized light? How is polarized light obtained by refraction? State the uses of polaroid.
View Solution
Plane polarized light consists of waves oscillating in a single plane perpendicular to the direction of propagation.
Obtaining polarized light by refraction: When unpolarized light is incident at Brewster's angle on a transparent medium, the reflected light becomes plane polarized.
Quick Tip: Polarization can occur by reflection, refraction, or scattering. Brewster's angle is key for obtaining plane polarized light.
(d) Obtain the formula for the internal resistance of a cell in terms of \( E \), \( V \), and \( R \), where \( E \), \( V \), and \( R \) are the electromotive force of the cell, potential difference across the external resistance, and external resistance, respectively.
View Solution
The total current in the circuit is:
I = \frac{E}{R + r}, where \( r \) is the internal resistance.
The terminal voltage is given by:
V = IR = \frac{ER}{R + r}.
Rearranging:
r = R \left( \frac{E}{V} - 1 \right).
Quick Tip: The internal resistance of a cell depends on the electromotive force \( E \), terminal voltage \( V \), and external resistance \( R \).(e) What do you mean by the current sensitivity of a moving coil galvanometer? Resistance of a galvanometer is \( 50 \, \Omega \) and for full-scale deflection, the current is \( 0.05 \, \mathrm{A} \). What would be the required length of a wire to convert it into an ammeter of 5 A range? (Area of cross-section of wire = \( 2.7 \times 10^{-6} \, \mathrm{m^2} \), specific resistance of the wire material = \( 5.0 \times 10^{-7} \, \Omega \cdot \mathrm{m} \))
View Solution
The shunt resistance is:
S = \frac{IG \, G}{I - IG}, where \( G = 50 \, \Omega, I = 5 \, \mathrm{A}, IG = 0.05 \, \mathrm{A}.
Substituting the values:
S = \frac{0.05 \times 50}{5 - 0.05} = 0.5 \, \Omega.
The length of the wire is:
R = \rho \frac{l}{A} \quad \Rightarrow \quad l = \frac{R A}{\rho}.
Substituting \( R = 0.5, A = 2.7 \times 10^{-6}, \rho = 5.0 \times 10^{-7} \):
l = \frac{0.5 \times 2.7 \times 10^{-6}}{5.0 \times 10^{-7}} = 2.7 \, \mathrm{m}.
Quick Tip: The shunt resistance determines the range of an ammeter. Use the formula \( S = \frac{IG \, G}{I - IG} \).Explain the working of forward biased configuration of a p-n junction diode. Draw a graph between forward voltage and forward current, showing the knee voltage.
View Solution
1. Forward Bias Configuration:
- The positive terminal of the power supply is connected to the \( p \)-side (anode), and the negative terminal is connected to the \( n \)-side (cathode).
- This reduces the potential barrier, allowing majority charge carriers (holes in the \( p \)-region and electrons in the \( n \)-region) to cross the junction.
- Once the applied voltage exceeds the **knee voltage** (typically \( \sim 0.7 \, V \) for silicon), a significant current flows due to the reduced barrier potential.
2. Graph:
- The relationship between forward voltage (X-axis) and forward current (Y-axis) shows an exponential increase in current after the knee voltage is reached.
\[ (Graph of forward current vs forward voltage is shown below.) \]
Quick Tip: In forward bias, a p-n junction diode behaves as a low-resistance circuit element, conducting current beyond the knee voltage.
OR Explain the working of reverse biased configuration of a p-n junction diode. Draw a graph between reverse voltage and reverse current, showing the breakdown voltage.
View Solution
1. Reverse Bias Configuration:
- The positive terminal of the power supply is connected to the \( n \)-side (cathode), and the negative terminal is connected to the \( p \)-side (anode).
- This increases the potential barrier, blocking the majority carriers. A small leakage current flows due to minority carriers.
- At the **breakdown voltage**, the junction experiences a sudden increase in reverse current due to mechanisms like Zener breakdown or avalanche breakdown.
2. Graph:
- The graph between reverse voltage (X-axis) and reverse current (Y-axis) shows a small leakage current initially, followed by a sharp increase at the breakdown voltage.
(Graph of reverse current vs reverse voltage is shown below.)
Quick Tip: In reverse bias, a p-n junction diode behaves as a high-resistance circuit element, except at the breakdown voltage.
Show that the circumference of the orbit of an electron revolving in the \( n \)-th orbit is equal to \( n\lambda \) with the help of Bohr's quantum theory. Also, show the emission and absorption spectral lines between energy levels \( n = 1 \) and \( n = 3 \) of hydrogen atom.
View Solution
1. Bohr's Quantum Theory:
- Bohr's quantization condition states that the angular momentum \( mvr \) of an electron in the \( n \)-th orbit is given by:
\[ mvr = \frac{nh}{2\pi}, \quad where n = 1, 2, 3, \dots \]
Here, \( m \) is the mass of the electron, \( v \) is its velocity, \( r \) is the orbital radius, \( h \) is Planck's constant, and \( n \) is the quantum number.
2. Relation with De Broglie Wavelength:
- De Broglie wavelength of the electron is given by \( \lambda = \frac{h}{mv} \).
- Substituting \( \lambda \) in the above expression:
\[ 2\pi r = n\lambda. \]
Thus, the circumference of the orbit is \( n \lambda \).
3. Emission and Absorption Lines:
- The energy difference between two energy levels \( E_n = -\frac{13.6}{n^2} \, eV \) is emitted or absorbed as a photon:
\[ E = E_f - E_i = -\frac{13.6}{n_f^2} + \frac{13.6}{n_i^2}. \]
- For transitions between \( n = 1 \), \( n = 2 \), and \( n = 3 \), the emission and absorption lines correspond to the Lyman and Balmer series in the spectrum.
Quick Tip: The Bohr model combines classical circular orbits with quantum conditions. Emission corresponds to the release of energy, while absorption involves gaining energy.
OR What do you mean by binding energy? The atomic mass of \( \, ^{16}_8O \, \) is \( 16.00000 \, amu \). Find its binding energy per nucleon.
View Solution
1. Binding Energy:
- The mass defect \( \Delta m \) is the difference between the total mass of nucleons and the actual mass of the nucleus.
\[ \Delta m = Zm_p + Nm_n - m_{nucleus}, \]
where \( Z = 8 \), \( N = 8 \), \( m_p = 1.007593 \, amu \), \( m_n = 1.008982 \, amu \), and \( m_{nucleus} = 16.00000 \, amu \).
Substituting:
\[ \Delta m = (8 \times 1.007593) + (8 \times 1.008982) - 16.00000 = 16.13176 - 16.00000 = 0.13176 \, amu. \]
2. Binding Energy:
- The binding energy is \( \Delta m \times 931 \, MeV/amu \):
\[ Binding energy = 0.13176 \times 931 = 122.65 \, MeV. \]
3. Per Nucleon:
- The binding energy per nucleon is:
\[ Binding energy per nucleon = \frac{Binding energy}{Total nucleons} = \frac{122.65}{16} = 7.67 \, MeV. \] Quick Tip: Higher binding energy per nucleon indicates a more stable nucleus. For oxygen-16, it is \( \approx 7.67 \, MeV \).
Differentiate between interference and diffraction of light. Explain qualitatively the diffraction phenomenon of light by a single slit. Light of 6000 Å wavelength is incident normally on a single slit of width \( 3 \times 10^{-4} \, cm \). Find out the angular width of the central maxima.
View Solution
(A) Difference Between Interference and Diffraction:
| Aspect | Interference | Diffraction |
|---|---|---|
| Pattern Origin | Superposition of light waves from coherent sources | Light bends around obstacles or through apertures |
| Fringes | All fringes are equally bright and equally spaced | Central fringe is brighter and wider; others diminish gradually |
| Cause | Interaction of two or more light beams | Single light wave encountering edges of an aperture |
- When light passes through a single slit, it bends and forms a pattern of alternating bright and dark fringes on a screen.
- The intensity distribution is maximum at the center (central maxima) and decreases for higher-order fringes.
- At specific angles, destructive interference occurs due to the path difference, forming dark fringes.
\[ a \sin \theta = n\lambda, \, where a is the slit width, \lambda is the wavelength, and n = \pm 1, \pm 2, \dots \]
3. Angular Width of Central Maximum:
- Central maximum extends between \( -\theta \) and \( +\theta \).
- The angular width \( \Delta \theta \) is:
\[ \Delta \theta = 2\sin^{-1} \left(\frac{\lambda}{a}\right). \]
Substituting \( \lambda = 6000 \, Å = 6 \times 10^{-5} \, cm \) and \( a = 3 \times 10^{-4} \, cm \):
\[ \sin \theta = \frac{\lambda}{a} = \frac{6 \times 10^{-5}}{3 \times 10^{-4}} = 0.2. \]
\[ \Delta \theta = 2\sin^{-1}(0.2) \approx 2 \times 11.54^\circ = 23.08^\circ. \]
(C) Final Answer:
The angular width of the central maxima is approximately \( 23.08^\circ \). Quick Tip: Diffraction and interference demonstrate the wave nature of light. Diffraction is more evident with small apertures or obstacles.
OR Draw a ray diagram of a reflecting telescope. The magnifying power of an astronomical telescope is 5, and the distance between the objective and eyepiece lenses is 36 cm. If the final image is formed at infinity, find the focal lengths of the two lenses.
View Solution
(A) Ray Diagram:
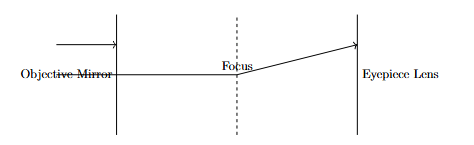
(B) Relation Between Focal Lengths:
- The magnifying power \( M \) for an astronomical telescope is:
\[ M = \frac{f_o}{f_e}, \]
where \( f_o \) is the focal length of the objective lens, and \( f_e \) is the focal length of the eyepiece lens.
- The length of the telescope \( L \) is:
\[ L = f_o + f_e. \]
3. Calculations:
- Given \( M = 5 \) and \( L = 36 \, cm \):
\[ f_o = 5f_e. \]
Substituting \( f_o = 5f_e \) into \( L = f_o + f_e \):
\[ 36 = 5f_e + f_e = 6f_e \quad \Rightarrow \quad f_e = 6 \, cm, \, f_o = 30 \, cm. \]
(C) Final Answer:
- Focal length of the objective lens: \( f_o = 30 \, cm \).
- Focal length of the eyepiece lens: \( f_e = 6 \, cm \). Quick Tip: To achieve a higher magnifying power in telescopes, increase the focal length of the objective lens or decrease that of the eyepiece.
Two parallel plate capacitors of capacitances \( C \) and \( 2C \) are joined with a battery of voltage difference \( V \) as shown in the figure. If the battery is removed and the space between the plates of the capacitor of capacitance \( C \) is completely filled with a material of dielectric constant \( K \), then find out:
i) Total capacitance of the combination
ii) Final voltage difference across the combination
iii) Total energy stored in the combination.
View Solution
(A) [i)] Total Capacitance of the Combination:
The initial total capacitance (without dielectric) is the series combination of \( C \) and \( 2C \):
\[ \frac{1}{C_{total, initial}} = \frac{1}{C} + \frac{1}{2C} = \frac{3}{2C} \quad \Rightarrow \quad C_{total, initial} = \frac{2C}{3}. \]
After inserting the dielectric of constant \( K \) into the capacitor of capacitance \( C \), its new capacitance becomes:
\[ C' = KC. \]
The new total capacitance is the series combination of \( C' = KC \) and \( 2C \):
\[ \frac{1}{C_{total, final}} = \frac{1}{KC} + \frac{1}{2C}. \]
Simplifying:
\[ \frac{1}{C_{total, final}} = \frac{K + 2}{2KC}. \]
Thus:
\[ C_{total, final} = \frac{2KC}{K + 2}. \]
(B) [ii)] Final Voltage Difference Across the Combination:
The charge on the initial combination is given by:
\[ Q_{initial} = C_{total, initial} \cdot V = \frac{2C}{3} \cdot V. \]
Since the battery is removed, the total charge remains the same. The final voltage \( V_{final} \) across the new combination is:
\[ V_{final} = \frac{Q_{initial}}{C_{total, final}}. \]
Substituting the values:
\[ V_{final} = \frac{\frac{2C}{3} \cdot V}{\frac{2KC}{K + 2}} = \frac{V \cdot (K + 2)}{3K}. \]
(C) [iii)] Total Energy Stored in the Combination:
The total energy stored in a capacitor is given by:
\[ U = \frac{1}{2} C_{total, final} \cdot V_{final}^2. \]
Substituting \( C_{total, final} = \frac{2KC}{K + 2} \) and \( V_{final} = \frac{V \cdot (K + 2)}{3K} \):
\[ U = \frac{1}{2} \cdot \frac{2KC}{K + 2} \cdot \left(\frac{V \cdot (K + 2)}{3K}\right)^2. \]
Simplifying:
\[ U = \frac{1}{2} \cdot \frac{2KC}{K + 2} \cdot \frac{V^2 \cdot (K + 2)^2}{9K^2}. \]
\[ U = \frac{C V^2 \cdot (K + 2)}{9K}. \]
Thus, the total energy stored is:
\[ U = \frac{C V^2 (K + 2)}{9K}. \] Quick Tip: In capacitors, the total charge remains constant when a battery is removed, and energy calculations depend on the final capacitance and voltage configuration.
OR Define electric flux and state its unit. Derive the formula for the intensity of electric field outside a uniformly charged thin spherical shell with the help of Gauss' law.
View Solution
(A) [i)] Definition of Electric Flux:
Electric flux is the total number of electric field lines passing through a given surface. Mathematically:
\[ \Phi_E = \int \vec{E} \cdot d\vec{A}, \]
where \( \vec{E} \) is the electric field and \( d\vec{A} \) is the area vector.
Unit of electric flux: \( volt meter (Vm) or Nm^2/C. \)
(B) [ii)] Electric Field Intensity (Using Gauss' Law):
Consider a uniformly charged thin spherical shell of total charge \( Q \) and radius \( R \).
- Outside the Shell \((r > R)\):
By Gauss' law:
\[ \oint \vec{E} \cdot d\vec{A} = \frac{Q}{\epsilon_0}. \]
The Gaussian surface is a sphere of radius \( r \):
\[ E \cdot 4\pi r^2 = \frac{Q}{\epsilon_0}. \]
Thus, the electric field outside the shell is:
\[ E = \frac{Q}{4\pi \epsilon_0 r^2}. \]
- Inside the Shell \((r < R)\):
Since the shell is uniformly charged, no charge is enclosed within the Gaussian surface inside the shell:
\[ E = 0 \quad for r < R. \] Quick Tip: Gauss' law simplifies electric field calculations by utilizing symmetrical Gaussian surfaces.

























Comments