UP Board Class 12 Physics Question Paper 2024 PDF (Code 346 FT) is available for download here. The Physics exam was conducted on March 4, 2024 in the Evening Shift from 2 PM to 5:15 PM. The total marks for the theory paper were 70. According to the appeared students, the difficulty level of the paper was moderate to high.
UP Board Class 12 Physics Question Paper 2024 (Code 346 FT) with Solutions
| UP Board Class 12 Physics Question Paper with Answer Key | Check Solution |

UP Board Class 12 Physics Question Paper 2024
(a) Electric charges are uniformly distributed in a small volume. The flux of electric field through a spherical surface of radius 2 cm surrounding the total charge is 10 V x m. The flux over a sphere of radius 4 cm will be:
View Solution
The flux through a spherical surface depends only on the total charge enclosed, according to Gauss's law:
\[ \Phi_E = \frac{q_{enc}}{\epsilon_0}. \]
Since the total charge \( q_{enc} \) remains constant, the flux through any spherical surface enclosing this charge will be the same. Therefore, the flux through the sphere with a radius of 4 cm is also 10 V x m. Quick Tip: The electric flux through a spherical surface only depends on the enclosed charge, not on the radius of the sphere.
(b) A moving charge produces:
View Solution
A moving charge creates both an electric field (due to its charge) and a magnetic field (due to its motion). This is the foundation of electromagnetism, as described by Maxwell's equations. Quick Tip: A moving charge is the source of both electric and magnetic fields.
(c) An electromagnetic wave propagating through vacuum, described by \( E = E_0 \sin(kx - \omega t) \), \( B = B_0 \sin(kx - \omega t) \), then:
View Solution
For an electromagnetic wave, the electric and magnetic field strengths \( E_0 \) and \( B_0 \) are related by the speed of light in vacuum \( c \):
\[ E_0 = c B_0. \]
The wave number \( k \) and angular frequency \( \omega \) are related to the speed of light as:
\[ c = \frac{\omega}{k}. \]
Combining the two equations, we get:
\[ E_0 \omega = B_0 k. \] Quick Tip: The electric and magnetic field amplitudes in an electromagnetic wave are related by the speed of light, \( c = E_0 / B_0 \).
(d) A double convex lens is made of a material having refractive index 1.2. Both the surfaces of the lens are convex. If it is dipped into water of refractive index 1.33, it will behave like:
View Solution
The focal length of a lens is determined by the refractive index difference between the material of the lens and the medium around it. When the lens is dipped in water, the refractive index of the medium increases, reducing the refractive index difference and causing the lens to behave more like a divergent lens. Quick Tip: When the refractive index of the surrounding medium is greater than that of the lens material, the lens becomes divergent.
(e) The equation \( E = pc \), (where \( E \) and \( p \) are energy and momentum respectively) is valid:
View Solution
The equation \( E = pc \) applies to massless particles like photons, where \( E \) is the energy, \( p \) is the momentum, and \( c \) is the speed of light. For particles with mass, such as electrons, the correct relationship is \( E^2 = (pc)^2 + (mc^2)^2 \). Quick Tip: The equation \( E = pc \) applies only to massless particles such as photons.
(f) Diffusion current in a p-n junction is greater than the drift current in magnitude:
View Solution
In a p-n junction, the diffusion current is due to the movement of charge carriers from high concentration to low concentration, whereas the drift current arises due to the presence of an electric field. When the junction is reverse biased, the depletion region widens, increasing the diffusion current compared to the drift current. Quick Tip: In reverse bias, the diffusion current is greater than the drift current due to the widening of the depletion region.
(a) Write the equation for the relationship between specific conductivity (\( \sigma \)) and drift velocity (\( v_d \)).
View Solution
Specific conductivity (\( \sigma \)) is related to the drift velocity (\( v_d \)) by the equation:
\[ \sigma = nq v_d A, \]
where:
- \( n \) is the number density of charge carriers,
- \( q \) is the charge of the carriers,
- \( A \) is the cross-sectional area of the conductor. Quick Tip: The drift velocity of charge carriers is proportional to the current and the specific conductivity of the material.
(b) State Ampere's Circuital Law.
View Solution
Ampere's Circuital Law states that the magnetic field \( B \) around a closed loop is proportional to the current passing through the loop. The law is expressed mathematically as:
\[ \oint_{loop} \mathbf{B} \cdot d\mathbf{l} = \mu_0 I_{enc}, \]
where:
- \( \oint_{loop} \mathbf{B} \cdot d\mathbf{l} \) is the circulation of the magnetic field around the loop,
- \( \mu_0 \) is the permeability of free space,
- \( I_{enc} \) is the current enclosed by the loop. Quick Tip: Ampere's Circuital Law relates the magnetic field around a closed loop to the current enclosed by that loop.
(c) Find the value of 1 kWh in Joules.
View Solution
1 kWh (kilowatt-hour) is a unit of energy and can be converted to Joules as follows:
\[ 1 \, kWh = 1 \, kW \times 1 \, h = 1000 \, W \times 3600 \, s = 3.6 \times 10^6 \, J. \] Quick Tip: 1 kWh is equivalent to \( 3.6 \times 10^6 \) Joules.
(d) Deduce the dimensional equation of self-inductance.
View Solution
Self-inductance (\( L \)) is defined by the relation:
\[ Emf = -L \frac{dI}{dt}, \]
where \( Emf \) is the induced electromotive force and \( I \) is the current. The dimensional formula of \( Emf \) is:
\[ \left[ Emf \right] = \left[ \frac{ML^2}{T^3 A} \right]. \]
By substituting the dimensional formula of \( \frac{dI}{dt} \) (which is \( T^{-1} A \)):
\[ \left[L \right] = \frac{\left[ Emf \right]}{\left[ \frac{dI}{dt} \right]} = \frac{\left[ ML^2 \right]}{\left[ T^3 A \right] \times \left[ T^{-1} A \right]} = \left[ M L^2 T^{-2} A^{-2} \right]. \] Quick Tip: The dimensional formula of self-inductance is \( \left[ M L^2 T^{-2} A^{-2} \right] \).
(e) Ionisation energy of Hydrogen atom is 13.6 eV. In a state where \( n = 2 \), what will be ionisation energy of its electron?
View Solution
The ionization energy for the \( n \)-th orbit of the hydrogen atom is given by:
\[ E_n = \frac{13.6 \, eV}{n^2}. \]
For \( n = 2 \):
\[ E_2 = \frac{13.6}{2^2} = \frac{13.6}{4} = 3.4 \, eV. \]
The ionization energy required for ionizing the electron from \( n = 2 \) to \( n = \infty \) is the energy needed to remove it from the \( n = 2 \) level, which is 3.4 eV. Quick Tip: The ionization energy decreases with increasing principal quantum number \( n \).
(f) Define 'wavefront' of a wave.
View Solution
A wavefront is the surface over which the phase of the wave is constant. In other words, it is an imaginary surface connecting all points of a wave that are in the same phase, meaning the wave amplitude at every point on this surface is the same. Quick Tip: Wavefronts represent the locus of points having the same phase in a wave, often used to study wave propagation.
(a) Find the current through the 10 Ω resistor when the switch S is open and closed in the given circuit.
View Solution
When the switch S is open, the current flows through the 10 Ω and 30 Ω resistors in series, and the total resistance is:
\[ R_{total} = 10 + 30 = 40 \, \Omega. \]
Using Ohm's law:
\[ I = \frac{V}{R_{total}} = \frac{20}{40} = 0.5 \, A. \]
Thus, the current through the 10 Ω resistor when the switch S is open is 0.5 A.
When the switch S is closed, the 30 Ω resistor is bypassed, and only the 10 Ω resistor remains in the circuit. The current through the 10 Ω resistor is:
\[ I = \frac{V}{R_{total}} = \frac{20}{10} = 2 \, A. \]
Thus, the current through the 10 Ω resistor when the switch S is closed is 2 A. Quick Tip: When the switch is closed, the 30 Ω resistor is bypassed, reducing the total resistance in the circuit.
(b) Calculate the energy equivalence of unified atomic mass unit.
View Solution
The energy equivalence of 1 unified atomic mass unit (1 amu) can be calculated using the relation:
\[ E = mc^2, \]
where \( m \) is the mass of 1 amu, and \( c \) is the speed of light. The value of 1 amu is approximately:
\[ m = 1.660539 \times 10^{-27} \, kg. \]
Substituting the values:
\[ E = \left( 1.660539 \times 10^{-27} \, kg \right) \times (3 \times 10^8 \, m/s)^2 = 1.492 \times 10^{-10} \, J. \]
So, 1 amu is equivalent to \( 1.492 \times 10^{-10} \, J \). Quick Tip: The energy equivalent of an atomic mass unit can be found using \( E = mc^2 \), where \( m \) is the mass in kg and \( c \) is the speed of light.
(c) Two magnets of equal magnetic moment (\( m_1 = m_2 \)) are placed as shown in the figure. If the magnetic field intensity at P due to magnet A1 is \( 2 \times 10^{-3} \, Tesla \), then find out the total magnetic field intensity at P due to both the magnets.
View Solution
Since the magnets have equal magnetic moments, the magnetic fields due to the individual magnets at point P will add vectorially. If both magnets are placed at equal distances from point P and their magnetic fields are in the same direction, then the total magnetic field intensity will be:
\[ B_{total} = B_1 + B_2 = 2 \times 10^{-3} + 2 \times 10^{-3} = 4 \times 10^{-3} \, Tesla. \]
Thus, the total magnetic field intensity at point P due to both magnets is \( 4 \times 10^{-3} \, Tesla \). Quick Tip: When the magnetic moments are equal and the fields are in the same direction, the total field intensity is the sum of the individual field intensities.
(d) In a Silicon p-n junction diode, for 20 V forward voltage, the forward current produced is 10 mA. Calculate its forward resistance.
View Solution
The forward resistance (\( R_{forward} \)) is given by Ohm's law:
\[ R_{forward} = \frac{V}{I}, \]
where \( V = 20 \, V \) and \( I = 10 \, mA = 10 \times 10^{-3} \, A \). Substituting the values:
\[ R_{forward} = \frac{20}{10 \times 10^{-3}} = 2000 \, \Omega. \]
Thus, the forward resistance is \( 2000 \, \Omega \). Quick Tip: Forward resistance is calculated by dividing the forward voltage by the forward current.
(a) Deduce the formula of torque on an electric dipole placed in a uniform electric field.
View Solution
Consider an electric dipole consisting of two charges \( +q \) and \( -q \), separated by a distance \( d \). The dipole moment \( \mathbf{p} \) is given by:
\[ \mathbf{p} = q \cdot \mathbf{d}, \]
where \( \mathbf{d} \) is the vector pointing from the negative to the positive charge.
When the dipole is placed in a uniform electric field \( \mathbf{E} \), it experiences a torque that tends to align the dipole with the electric field. The torque \( \mathbf{T} \) is given by:
\[ \mathbf{T} = \mathbf{p} \times \mathbf{E}, \]
where the cross product ensures that the torque is perpendicular to both the dipole moment and the electric field.
The magnitude of the torque is:
\[ T = pE \sin \theta, \]
where \( \theta \) is the angle between the dipole moment \( \mathbf{p} \) and the electric field \( \mathbf{E} \). Quick Tip: The torque on an electric dipole in a uniform electric field is given by \( T = pE \sin \theta \), where \( p \) is the dipole moment, \( E \) is the electric field, and \( \theta \) is the angle between \( \mathbf{p} \) and \( \mathbf{E} \).
(b) The intensity of the magnetic field \( B \) due to a current-carrying circular coil of radius 12 cm at its center is \( 0.5 \times 10^{-4} \, Tesla \) perpendicular to the plane of the coil upward. Calculate the magnitude and direction of current flowing in the coil.
View Solution
The magnetic field at the center of a circular loop carrying current \( I \) is given by:
\[ B = \frac{\mu_0 I}{2R}, \]
where \( \mu_0 = 4\pi \times 10^{-7} \, T m/A \) is the permeability of free space, \( I \) is the current, and \( R \) is the radius of the coil.
Rearranging for \( I \):
\[ I = \frac{2 B R}{\mu_0}. \]
Substituting the given values (\( B = 0.5 \times 10^{-4} \, T \), \( R = 12 \, cm = 0.12 \, m \)):
\[ I = \frac{2 \times 0.5 \times 10^{-4} \times 0.12}{4\pi \times 10^{-7}} = 3.0 \, A. \]
The direction of the current follows the right-hand rule: when the fingers of the right hand curl in the direction of the current in the coil, the thumb points in the direction of the magnetic field at the center, which is upward. Quick Tip: The magnetic field at the center of a current-carrying circular coil is given by \( B = \frac{\mu_0 I}{2R} \), where \( \mu_0 \) is the permeability, \( I \) is the current, and \( R \) is the radius of the coil.
(c) What is total internal reflection and critical angle? What is the working principle of Optical Fibre.
View Solution
Total Internal Reflection:
Total internal reflection occurs when a light ray traveling from a denser medium to a rarer medium hits the boundary at an angle greater than the critical angle and reflects completely back into the denser medium.
\textit{Critical Angle:
The critical angle \( \theta_c \) is the angle of incidence beyond which total internal reflection occurs. It is given by:
\[ \sin \theta_c = \frac{n_2{n_1}, \]
where \( n_1 \) and \( n_2 \) are the refractive indices of the denser and rarer media, respectively.
\textit{Working Principle of Optical Fibre:
An optical fibre works based on the principle of total internal reflection. Light signals are transmitted through the fibre by multiple total internal reflections within the fibre, which is made of a core with a higher refractive index than the cladding surrounding it. Quick Tip: Total internal reflection occurs when light moves from a denser to a rarer medium and strikes the boundary at an angle larger than the critical angle.
(d) In the given circuit, find the potential difference between \( A \) and \( B \).
View Solution
The circuit consists of three branches connected between points \( A \) and \( B \), each having a \( 1 \, \Omega \) resistor in series with voltage sources of \( 3 \, \mathrm{V} \), \( 2 \, \mathrm{V} \), and \( 1 \, \mathrm{V} \), respectively. The current in each branch can be calculated using Ohm's Law: \[ I = \frac{Voltage}{Resistance}. \]
For the top branch: \( I_1 = \frac{3}{1} = 3 \, \mathrm{A} \),
For the middle branch: \( I_2 = \frac{2}{1} = 2 \, \mathrm{A} \),
For the bottom branch: \( I_3 = \frac{1}{1} = 1 \, \mathrm{A} \).
Since all resistances are equal, the potential difference between \( A \) and \( B \) is determined by the branch with the highest voltage source. Hence, \[ V_{AB} = 3 \, \mathrm{V}. \] Quick Tip: For circuits with parallel branches, the potential difference between two points is primarily influenced by the voltage sources in the branches. Consider the highest voltage source when resistances are equal.
(e) Define Mutual Inductance. Show that Henry = Newton Meter / Ampere².
View Solution
Mutual Inductance:
Mutual inductance \( M \) is the proportionality constant that describes the induced EMF in one coil when the current in a nearby coil changes. If the changing current in coil 1 produces a flux linking coil 2, the induced EMF in coil 2 is given by:
\[ \mathcal{E_2 = -M \frac{dI_1}{dt}, \]
where \( \frac{dI_1}{dt} \) is the rate of change of current in coil 1.
Dimensional Formula for Henry:
The unit of mutual inductance is the Henry (H), and it can be derived from the relationship between induced EMF and the rate of current change:
\[ [M] = \frac{[Induced EMF] \cdot [Time]{[Current]} \]
Since the dimensional formula for EMF is \( [M] = V \cdot s/A \) and voltage (V) has the dimensional formula \( [M L^2 T^{-3} I^{-1}] \), we arrive at the final result for Henry:
\[ Henry = \frac{Newton \cdot Meter}{Ampere^2}. \] Quick Tip: Mutual inductance quantifies the induced EMF in a coil due to a changing current in a nearby coil. Its SI unit, Henry, is derived from the dimensional analysis of voltage, time, and current.
(a) What is the value of resistance of ideal ammeter and ideal voltmeter? Why are an ammeter and a voltmeter respectively connected in series and parallel in a circuit?
View Solution
- \textit{Ideal Ammeter: An ideal ammeter has zero resistance. It is connected in series with the circuit, as the current to be measured flows through the ammeter without affecting the circuit.
- \textit{Ideal Voltmeter: An ideal voltmeter has infinite resistance. It is connected in parallel with the component across which the potential difference is to be measured. This ensures that no current is drawn by the voltmeter, and only the potential difference is measured. Quick Tip: An ideal ammeter has zero resistance and is connected in series, while an ideal voltmeter has infinite resistance and is connected in parallel.
(b) A coil has a resistance of 10 Ω and inductance of 0.4 Henry. It is connected to an AC source of 6.5 V, 30 Hz. Find the average power consumed in the circuit.
View Solution
Given:
- Resistance \( R = 10 \, \Omega \)
- Inductance \( L = 0.4 \, H \)
- AC Voltage \( V = 6.5 \, V \)
- Frequency \( f = 30 \, Hz \)
The inductive reactance \( X_L \) is given by:
\[ X_L = 2\pi f L = 2\pi \times 30 \times 0.4 = 75.4 \, \Omega. \]
The impedance \( Z \) of the coil is:
\[ Z = \sqrt{R^2 + X_L^2} = \sqrt{10^2 + 75.4^2} = \sqrt{100 + 5684.16} = 75.7 \, \Omega. \]
The RMS value of the current \( I_{rms} \) is:
\[ I_{rms} = \frac{V}{Z} = \frac{6.5}{75.7} = 0.086 \, A. \]
The average power consumed is:
\[ P_{avg} = I_{rms}^2 R = (0.086)^2 \times 10 = 0.074 \, W. \] Quick Tip: In an R-L circuit, the average power consumed is given by \( P_{avg} = I_{rms}^2 R \), where \( I_{rms} \) is the RMS current.
(c) Explain Maxwell's displacement current and write its equation. What is the phase difference between it and the conduction current?
View Solution
Maxwell's displacement current is a term added by Maxwell in the Ampere's law to account for the changing electric field in a capacitor or any region where the electric field is changing with time. The displacement current density \( J_D \) is given by:
\[ J_D = \epsilon \frac{\partial E}{\partial t}, \]
where \( \epsilon \) is the permittivity of the medium, and \( \frac{\partial E}{\partial t} \) is the time rate of change of the electric field.
The displacement current causes a magnetic field in the same way as conduction current, ensuring continuity of current even in regions without free charge carriers.
The displacement current and conduction current are in phase, meaning they oscillate together. Quick Tip: Maxwell’s displacement current accounts for the changing electric field and ensures that the magnetic field is continuous even in regions without free charge carriers.
(d) What is interference of light? Mention the condition for (i) constructive and (ii) destructive interference.
View Solution
\textit{Interference of Light:
Interference is the phenomenon that occurs when two or more light waves superpose to form a resultant wave. Depending on the phase relationship between the waves, the interference can be constructive or destructive.
\textit{Condition for Constructive Interference:
When the path difference between the waves is an integer multiple of the wavelength \( m\lambda \), the waves interfere constructively:
\[ \Delta x = m\lambda, \quad m = 0, 1, 2, \dots \]
\textit{Condition for Destructive Interference:
When the path difference is an odd multiple of half the wavelength \( (m + 1/2) \lambda \), the waves interfere destructively:
\[ \Delta x = (m + 1/2)\lambda, \quad m = 0, 1, 2, \dots \] Quick Tip: Interference occurs when two light waves superpose. Constructive interference occurs when the path difference is \( m\lambda \), and destructive interference occurs when the path difference is \( (m + 1/2)\lambda \).
(e) Find the maximum magnitude of velocity and linear momentum of a photoelectron emitted when light of wavelength 4000 Å falls on a metal having work function 2.5 eV.
View Solution
Given:
- Wavelength \( \lambda = 4000 \, Å = 4 \times 10^{-7} \, m \)
- Work function \( \phi = 2.5 \, eV = 2.5 \times 1.6 \times 10^{-19} \, J \)
- Planck's constant \( h = 6.626 \times 10^{-34} \, J \cdot s \)
- Speed of light \( c = 3 \times 10^8 \, m/s \)
The energy of the incoming photon is:
\[ E_{photon} = \frac{hc}{\lambda} = \frac{6.626 \times 10^{-34} \times 3 \times 10^8}{4 \times 10^{-7}} = 4.97 \times 10^{-19} \, J. \]
The kinetic energy of the emitted photoelectron is:
\[ E_k = E_{photon} - \phi = 4.97 \times 10^{-19} - 2.5 \times 1.6 \times 10^{-19} = 2.57 \times 10^{-19} \, J. \]
The maximum velocity of the photoelectron is given by:
\[ v = \sqrt{\frac{2E_k}{m_e}} = \sqrt{\frac{2 \times 2.57 \times 10^{-19}}{9.11 \times 10^{-31}}} = 7.52 \times 10^5 \, m/s. \]
The linear momentum \( p \) of the photoelectron is:
\[ p = m_e v = 9.11 \times 10^{-31} \times 7.52 \times 10^5 = 6.85 \times 10^{-25} \, kg \cdot m/s. \] Quick Tip: The kinetic energy of a photoelectron is the energy of the photon minus the work function. The maximum velocity and linear momentum of the photoelectron can be determined using this energy.
State and explain Gauss's law in electrostatics. Using it, find the electric field due to a uniformly charged thin spherical shell (charge = q and radius = R) at (i) external point of shell (ii) internal point of shell and (iii) on the surface of shell.
View Solution
Gauss’s Law:
Gauss’s law states that the electric flux \( \Phi_E \) through any closed surface is proportional to the charge \( Q_{enclosed \) enclosed by the surface. Mathematically:
\[ \Phi_E = \oint_S \mathbf{E} \cdot d\mathbf{A} = \frac{Q_{enclosed}}{\epsilon_0}, \]
where \( \mathbf{E} \) is the electric field, \( d\mathbf{A} \) is the differential area vector, and \( \epsilon_0 \) is the permittivity of free space.
Now, applying Gauss's law to a uniformly charged thin spherical shell, we can find the electric field at various points:
(i) At an external point (at a distance \( r > R \) from the center of the shell):
Since the charge distribution is spherically symmetric, we can use a spherical Gaussian surface of radius \( r \) (where \( r > R \)). The total charge \( Q \) is enclosed within this Gaussian surface, and the electric field at a distance \( r \) is given by:
\[ E \cdot 4\pi r^2 = \frac{q}{\epsilon_0}, \]
so the electric field is:
\[ E = \frac{q}{4 \pi \epsilon_0 r^2}. \]
(ii) At an internal point (at a distance \( r < R \) from the center of the shell):
For a point inside the uniformly charged spherical shell, the electric flux through the Gaussian surface is zero because no charge is enclosed within the Gaussian surface. Thus, the electric field inside the shell is:
\[ E = 0. \]
(iii) At a point on the surface of the shell (at \( r = R \)):
At the surface, the electric field will have the same magnitude as at any external point on a spherical shell with radius \( r = R \). Thus, the electric field is:
\[ E = \frac{q}{4 \pi \epsilon_0 R^2}. \] Quick Tip: Gauss's law simplifies the calculation of the electric field in situations with spherical symmetry, such as around a uniformly charged spherical shell.
OR
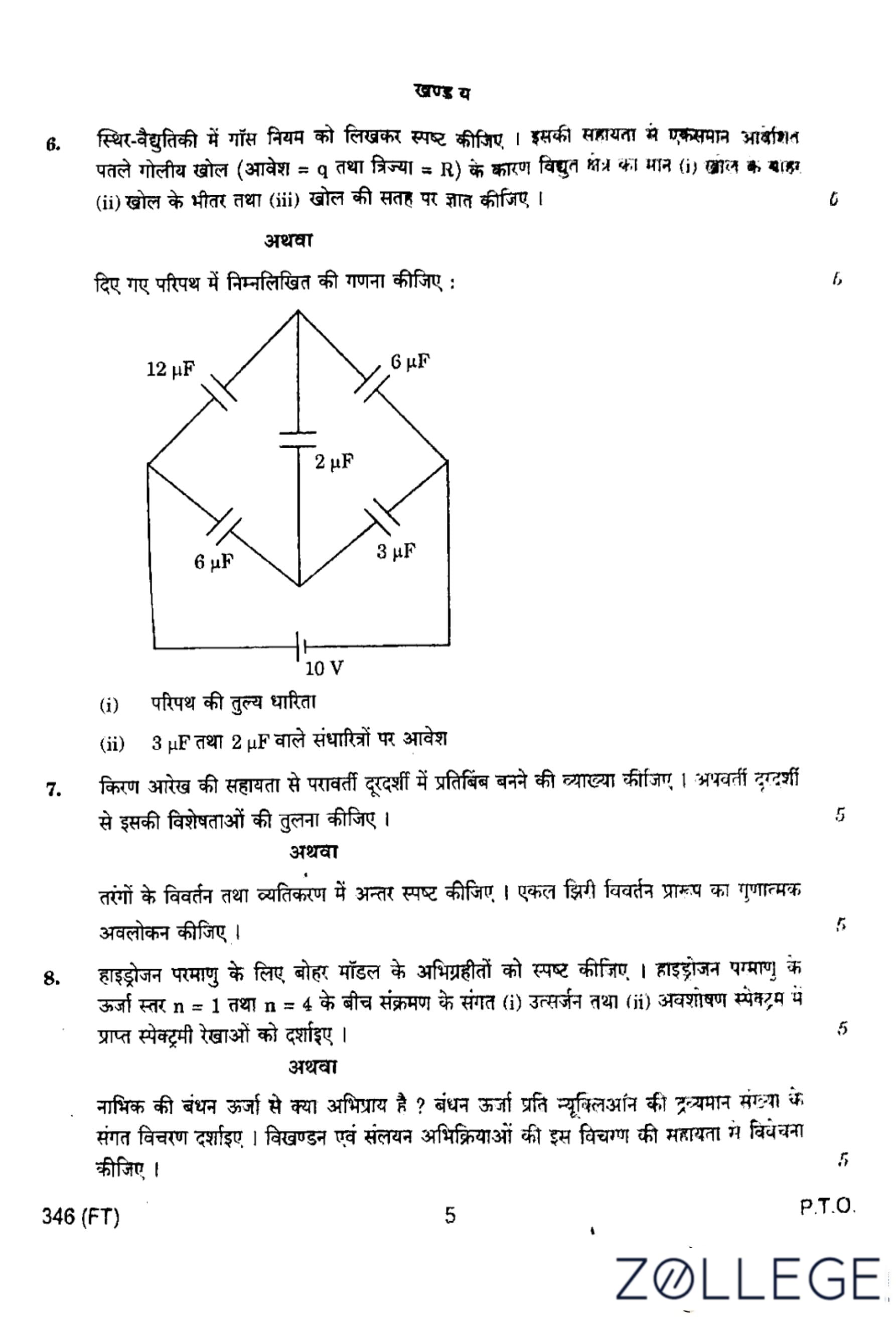
Question 6:
Calculate the following in the given circuit:
(i) The equivalent capacitance of the circuit.
(ii) The charge on \( 3 \, \mu\mathrm{F} \) and \( 2 \, \mu\mathrm{F} \) capacitors.
View Solution
(i) Equivalent Capacitance of the Circuit:
The given circuit has capacitors arranged in a combination of series and parallel connections. Let us simplify step by step:
1. The \( 6 \, \mu\mathrm{F} \) and \( 12 \, \mu\mathrm{F} \) capacitors are in series: \[ \frac{1}{C_1} = \frac{1}{6} + \frac{1}{12} \quad \Rightarrow \quad C_1 = \frac{12}{3} = 4 \, \mu\mathrm{F}. \]
2. The \( 6 \, \mu\mathrm{F} \) and \( 3 \, \mu\mathrm{F} \) capacitors are in series: \[ \frac{1}{C_2} = \frac{1}{6} + \frac{1}{3} \quad \Rightarrow \quad C_2 = 2 \, \mu\mathrm{F}. \]
3. The \( C_1 = 4 \, \mu\mathrm{F} \), \( 2 \, \mu\mathrm{F} \), and \( C_2 = 2 \, \mu\mathrm{F} \) are in parallel: \[ C_{eq} = C_1 + C_2 + 2 \quad \Rightarrow \quad C_{eq} = 4 + 2 + 2 = 8 \, \mu\mathrm{F}. \]
Thus, the equivalent capacitance of the circuit is: \[ \boxed{8 \, \mu\mathrm{F}}. \]
(ii) Charge on \( 3 \, \mu\mathrm{F} \) and \( 2 \, \mu\mathrm{F} \) capacitors:
The total charge in the circuit is given by: \[ Q_{total} = C_{eq} \cdot V = 8 \, \mu\mathrm{F} \cdot 10 \, \mathrm{V} = 80 \, \mu\mathrm{C}. \]
For the \( 3 \, \mu\mathrm{F} \) capacitor, the voltage across \( C_2 = 2 \, \mu\mathrm{F} \) is the same as the voltage across the series combination of \( 6 \, \mu\mathrm{F} \) and \( 3 \, \mu\mathrm{F} \). Using charge conservation: \[ Q = C \cdot V = 3 \, \mu\mathrm{F} \cdot 10 \, \mathrm{V} = 30 \, \mu\mathrm{C}. \]
Similarly, for the \( 2 \, \mu\mathrm{F} \) capacitor: \[ Q = C \cdot V = 2 \, \mu\mathrm{F} \cdot 10 \, \mathrm{V} = 20 \, \mu\mathrm{C}. \]
Thus, the charges are: \[ \boxed{30 \, \mu\mathrm{C} on the 3 \, \mu\mathrm{F} capacitor, and 20 \, \mu\mathrm{C} on the 2 \, \mu\mathrm{F} capacitor.} \] Quick Tip: For capacitors in series, the equivalent capacitance is given by: \[ \frac{1}{C_{eq}} = \frac{1}{C_1} + \frac{1}{C_2} + \cdots \] For capacitors in parallel, the equivalent capacitance is given by: \[ C_{eq} = C_1 + C_2 + \cdots \]
Explain image formation in a reflecting telescope with the help of a ray diagram. Compare its qualities with a refracting telescope.
View Solution
In a reflecting telescope, the image is formed using a concave mirror. When parallel rays of light from a distant object fall on the mirror, they converge at the focal point to form the image. The ray diagram of the image formation is as follows:
\begin {center
A reflecting telescope uses a concave mirror to form the primary image, and the final image is seen through the eyepiece. Unlike a refracting telescope, it avoids the chromatic aberration associated with lenses.
Comparison with a refracting telescope:
Optical Medium: A reflecting telescope uses a mirror, while a refracting telescope uses lenses.
Aberrations: Reflecting telescopes do not suffer from chromatic aberration, whereas refracting telescopes do.
Size: Reflecting telescopes are generally more compact than refracting ones for the same focal length and aperture size.
Cost: Mirrors are easier and cheaper to produce than large lenses, making reflecting telescopes more cost-effective. Quick Tip: Reflecting telescopes do not suffer from chromatic aberrations, making them ideal for astronomical observations, especially for large telescopes.
Explain the differences between diffraction and interference of waves. Observe qualitatively the diffraction pattern of a single slit.
View Solution
Differences Between Diffraction and Interference:
Diffraction: Diffraction refers to the bending of waves around obstacles or through narrow openings. It occurs for all types of waves, including sound, light, and water waves.
Interference: Interference occurs when two or more waves superimpose to form a resultant wave. It occurs only when two coherent waves combine, resulting in constructive or destructive interference.
Pattern: Diffraction produces a pattern of bright and dark regions, while interference produces alternating bands of constructive and destructive regions.
Cause: Diffraction occurs due to the wave nature of light, while interference results from the superposition principle of two or more coherent waves.
\textit{Qualitative Diffraction Pattern of a Single Slit:
When monochromatic light passes through a narrow slit, diffraction occurs, leading to a central bright maximum followed by a series of dark and bright fringes. The intensity of the diffraction pattern decreases as we move away from the central maximum. The angular position of the minima is given by the equation:
\[ a \sin \theta = n \lambda, \quad where \quad a = width of the slit, \, \lambda = wavelength of light, \, n = 1, 2, 3, \dots \] Quick Tip: Diffraction patterns are most prominent when the wavelength of light is comparable to the size of the slit or obstacle.
Explain postulates of Bohr's model for Hydrogen atom. Show the number of lines in the (i) emission and (ii) absorption spectra of Hydrogen atom corresponding to transition between energy states \(n = 1\) and \(n = 4\).
View Solution
Bohr’s Postulates for Hydrogen Atom:
(A) The electron in the atom revolves in specific orbits without radiating energy.
(B) The electron can only occupy discrete energy levels or orbits. The energy of the electron in the \(n\)-th orbit is given by:
\[ E_n = - \frac{k e^2{2r_n}, \]
where \( k \) is Coulomb's constant, \( e \) is the electron charge, and \( r_n \) is the radius of the \(n\)-th orbit.
(C) The transition of the electron between orbits results in emission or absorption of energy corresponding to the difference in energy levels.
For transition between \(n = 1\) and \(n = 4\), the emission and absorption spectra can be derived using the following formulas:
1. For emission, when the electron transitions from higher to lower energy states, the frequency of the emitted radiation is:
\[ f = \frac{E_{higher} - E_{lower}}{h}. \]
2. For absorption, the electron absorbs energy when it moves to a higher energy state.
(i) Emission Spectrum Lines:
The number of lines in the emission spectrum is given by the number of possible transitions from \(n=4\) to \(n=1\), including intermediate states. The transitions are as follows:
\[ 4 \to 3, \, 4 \to 2, \, 4 \to 1, \, 3 \to 2, \, 3 \to 1, \, 2 \to 1. \]
There are a total of 6 emission lines.
(ii) Absorption Spectrum Lines:
Similarly, for absorption, the number of lines will be the same, as absorption also happens when the electron moves from a lower to higher energy state. The number of lines is 6. Quick Tip: The number of spectral lines increases with the number of possible energy level transitions.
OR
Question 8:
What is meant by binding energy of a nucleus? Draw variation of binding energy per nucleon against the mass number. Discuss fission and fusion with the help of this variation.
View Solution
Binding Energy of a Nucleus: The binding energy of a nucleus is the energy required to separate all the nucleons (protons and neutrons) in the nucleus to infinite distance. It is given by the equation:
\[ E_b = \Delta m \cdot c^2, \]
where \( \Delta m \) is the mass defect, and \( c \) is the speed of light. The mass defect is the difference between the mass of the individual nucleons and the mass of the nucleus.
\textit{Variation of Binding Energy per Nucleon:
The binding energy per nucleon increases as we move from light elements to medium-mass elements like iron (\( Fe \)). Beyond iron, the binding energy per nucleon decreases. This variation suggests that fission (splitting heavy nuclei) and fusion (joining light nuclei) both release energy.
\begin{figure
\centering
\label{fig:enter-label
\end{figure
\textit{Fission and Fusion:
- \textit{Fission is the process in which a heavy nucleus (such as uranium) splits into smaller nuclei, releasing a large amount of energy.
- \textit{Fusion is the process in which light nuclei (such as hydrogen) combine to form a heavier nucleus, also releasing energy. Quick Tip: Nuclear fission and fusion processes both release energy because the binding energy per nucleon increases for nuclei with atomic mass between 1 to 60.
Calculate the conductivity of an n-type semiconductor from the following data:
Density of conduction electrons = \( 8 \times 10^{13} \, cm^{-3} \)
Density of holes = \( 5 \times 10^{12} \, cm^{-3} \)
Mobility of electrons = \( 2.3 \times 10^4 \, cm^2/V-s \)
Mobility of holes = \( 100 \, cm^2/V-s \)
OR
Explain the depletion layer and potential barrier in the formation of a p-n junction. How are both changing in the condition of forward biasing and reverse biasing?
View Solution
Conductivity of N-Type Semiconductor:
The electrical conductivity (\( \sigma \)) of a semiconductor is given by:
\[ \sigma = q \cdot (n_e \mu_e + n_h \mu_h), \]
where:
- \( q \) is the charge of an electron,
- \( n_e \) is the density of conduction electrons,
- \( n_h \) is the density of holes,
- \( \mu_e \) is the mobility of electrons,
- \( \mu_h \) is the mobility of holes.
Using the given values, the conductivity can be calculated as:
\[ \sigma = (1.6 \times 10^{-19) \cdot \left( (8 \times 10^{13}) \cdot (2.3 \times 10^4) + (5 \times 10^{12}) \cdot (100) \right). \] Quick Tip: The conductivity of a semiconductor depends on the density and mobility of both electrons and holes.
OR
Question 9:
Explain the depletion layer and potential barrier in the formation of a p-n junction. How are both changing in the condition of forward biasing and reverse biasing?
View Solution
In a p-n junction, when p-type and n-type materials are brought together, free electrons from the n-side diffuse into the p-side, and holes from the p-side diffuse into the n-side. This results in the formation of a depletion region where no free charge carriers are present, and it develops a potential barrier.
Effect of Biasing:
Forward Bias: When the junction is forward biased, the external voltage reduces the potential barrier, allowing current to flow.
Reverse Bias: In reverse bias, the potential barrier increases, and little to no current flows. Quick Tip: In forward bias, the potential barrier reduces, allowing current to flow easily, while in reverse bias, the potential barrier increases and current is blocked.













Comments