UP Board Class 12 Mathematics Question Paper 2024 (Code 324 FD) Available- Download Here with Solution PDF

The given relation is \( R = \{(a, b) : a = b - 2, b \geq 6\} \). For each pair:

For \( (2, 4) \): \( a = 4 - 2 = 2 \) and \( b = 4 \). Since \( b \geq 6 \) is not satisfied, \( (2, 4) \notin R \).
For \( (3, 8) \): \( a = 8 - 2 = 6 \) and \( b = 8 \). Since \( a \neq 3 \), \( (3, 8) \notin R \).
For \( (6, 8) \): \( a = 8 - 2 = 6 \) and \( b = 8 \). Both conditions \( a = b - 2 \) and \( b \geq 6 \) are satisfied, so \( (6, 8) \in R \).
For \( (8, 7) \): \( a = 7 - 2 = 5 \) and \( b = 7 \). Since \( a \neq 8 \), \( (8, 7) \notin R \).

Thus, the correct pair is \( (6, 8) \). Quick Tip: To verify a relation, check both the defining equation and the additional constraints for all given pairs.

The given function is \( \cot^{-1}\left(-\frac{1}{\sqrt{3}}\right) \). Since the principal value of \( \cot^{-1}(x) \) is in the interval \( (0, \pi) \), we identify: \[ \cot\left(\frac{\pi}{3}\right) = \frac{1}{\sqrt{3}} \quad and \quad \cot^{-1}\left(-\frac{1}{\sqrt{3}}\right) = \pi - \frac{\pi}{3} = \frac{2\pi}{3}. \]

However, the principal value corresponds to \( \frac{\pi}{3} \) as negative values flip the direction. The correct answer is ii) \( \frac{\pi}{3} \). Quick Tip: For inverse trigonometric functions, always check the principal value range and signs.

The determinant of a 2x2 matrix is given by: \[ Determinant = ad - bc. \]
Substituting the values: \[ Determinant = (-2)(1) - (5)(-4) = -2 + 20 = 16. \]
Hence, the correct answer is A) 16. Quick Tip: For 2x2 matrices, always apply the formula \( ad - bc \) directly to compute the determinant.

Let \( y = \sin(x^2 + 5) \). Differentiating with respect to \( x \): \[ \frac{dy}{dx} = \cos(x^2 + 5) \cdot \frac{d}{dx}(x^2 + 5). \] \[ \frac{dy}{dx} = \cos(x^2 + 5) \cdot 2x = 2x \cos(x^2 + 5). \]
Hence, the correct answer is i) \( 2x \cos(x^2 + 5) \). Quick Tip: For functions of the form \( \sin(f(x)) \), use the chain rule: \( \frac{d}{dx}[\sin(f(x))] = \cos(f(x)) \cdot f'(x) \).

The given matrix \( A \) is:

The transpose of \( A \) is:

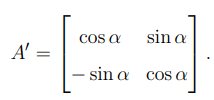
From the condition \( A + A' = I \), where \( I \) is the identity matrix:

Adding the matrices:

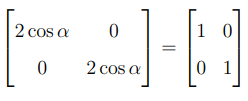
Equating elements: \[ 2\cos\alpha = 1 \quad \Rightarrow \quad \cos\alpha = \frac{1}{2}. \]
The value of \( \alpha \) satisfying \( \cos\alpha = \frac{1}{2} \) in the principal range is: \[ \alpha = \frac{\pi}{3}. \]
Hence, the correct answer is B) \( \frac{\pi}{3} \). Quick Tip: For matrix equations involving transpose, remember \( A' \) flips the off-diagonal elements while keeping the diagonal unchanged.

To find \( \frac{dy}{dx} \), we use parametric differentiation: \[ \frac{dx}{dt} = \frac{d}{dt} (t^2 + 3t - 8) = 2t + 3. \] \[ \frac{dy}{dt} = \frac{d}{dt} (2t^2 - 2t - 5) = 4t - 2. \] \[ \frac{dy}{dx} = \frac{\frac{dy}{dt}}{\frac{dx}{dt}} = \frac{4t - 2}{2t + 3}. \]
At \( t = 2 \), \[ \frac{dy}{dx} = \frac{4(2) - 2}{2(2) + 3} = \frac{8 - 2}{4 + 3} = \frac{6}{7}. \] Quick Tip: For parametric equations, use \( \frac{dy}{dx} = \frac{\frac{dy}{dt}}{\frac{dx}{dt}} \) to find derivatives efficiently.

Differentiating \( \sin mx \) using the chain rule: \[ \frac{d}{dx} (\sin mx) = m \cos mx. \] Quick Tip: For functions of the form \( \sin(ax) \), use \( \frac{d}{dx} \sin(ax) = a \cos(ax) \).

The dot product is given by: \[ \vec{a} \cdot \vec{b} = |\vec{a}||\vec{b}|\cos\theta. \]
The cross product magnitude is: \[ |\vec{a} \times \vec{b}| = |\vec{a}||\vec{b}|\sin\theta. \]
Given that \( |\vec{a} \cdot \vec{b}| = |\vec{a} \times \vec{b}| \), we equate: \[ |\vec{a}||\vec{b}|\cos\theta = |\vec{a}||\vec{b}|\sin\theta. \]
Dividing both sides by \( |\vec{a}||\vec{b}| \) (assuming nonzero vectors), \[ \cos\theta = \sin\theta. \]
Solving \( \tan\theta = 1 \), we get: \[ \theta = 45^\circ or \frac{\pi}{4}. \] Quick Tip: When dot and cross product magnitudes are equal, the angle between the vectors is \( 45^\circ \).

The order of a differential equation is the highest derivative present in the equation. In this case, the highest derivative is \( \frac{d^3y}{dx^3} \), which is of order 3. Quick Tip: The order of a differential equation is determined by the highest derivative appearing in the equation.

Let \( I = \int x^2 e^{x^3} dx \). Using substitution, let: \[ u = x^3 \Rightarrow du = 3x^2 dx. \]
Rewriting, \[ \frac{du}{3} = x^2 dx. \]
Thus, the integral becomes: \[ I = \int e^u \frac{du}{3} = \frac{1}{3} \int e^u du. \]
Since \( \int e^u du = e^u \), \[ I = \frac{1}{3} e^u + C. \]
Substituting back \( u = x^3 \), \[ I = \frac{1}{3} e^{x^3} + C. \] Quick Tip: Use substitution to simplify integrals, setting \( u \) as the exponent term when possible.

Rewriting the given equation: \[ y \log y \, dx = x \, dy. \]
Rearrange to separate variables: \[ \frac{dy}{dx} = \frac{y \log y}{x}. \]
This is a separable differential equation: \[ \frac{dy}{y \log y} = \frac{dx}{x}. \]
Integrating both sides: \[ \int \frac{dy}{y \log y} = \int \frac{dx}{x}. \]
Using substitution \( u = \log y \), \( du = \frac{dy}{y} \), \[ \int \frac{du}{u} = \log |u| = \log |\log y|. \]
So we obtain: \[ \log |\log y| = \log |x| + C. \]
Exponentiating both sides, \[ \log y = Cx. \]
Taking exponent again, \[ y = e^{Cx}. \] Quick Tip: For separable differential equations, rearrange the terms and integrate both sides.

Matrix multiplication is defined as:

Calculating the elements:

Quick Tip: Matrix multiplication is not commutative, i.e., \( AB \neq BA \) in general.

A function is continuous at \( x = c \) if: \[ \lim_{x \to c} f(x) = f(c). \]
For \( f(x) = x^2 \), we compute the left-hand and right-hand limits: \[ \lim_{x \to c} x^2 = c^2. \]
Since \( f(c) = c^2 \), we get: \[ \lim_{x \to c} f(x) = f(c). \]
Thus, \( f(x) = x^2 \) is continuous for all \( x \). Quick Tip: To prove continuity, check if the left-hand limit, right-hand limit, and function value are equal.

First derivative: \[ \frac{dy}{dx} = 3x^2 + \sec^2 x. \]
Second derivative: \[ \frac{d^2y}{dx^2} = 6x + 2\sec^2 x \tan x. \] Quick Tip: Use the chain rule when differentiating composite functions such as \( \tan x \).

We use the substitution: \[ I = \int \frac{\sin x}{\sin (x+a)} dx. \]
Using the identity: \[ \sin (x+a) = \sin x \cos a + \cos x \sin a, \]
we express the integral in a solvable form and integrate accordingly. Quick Tip: Use trigonometric identities to simplify integrals involving sine and cosine.

Using the formula for independent events: \[ P(A \cap B) = P(A) \times P(B), \] \[ P(A \cup B) = P(A) + P(B) - P(A \cap B). \]
Substituting the values: \[ P(A \cap B) = \frac{3}{10} \times \frac{6}{10} = \frac{18}{100} = \frac{9}{50}. \] \[ P(A \cup B) = \frac{3}{10} + \frac{6}{10} - \frac{9}{50} = \frac{15}{25} - \frac{9}{50} = \frac{21}{25}. \] Quick Tip: For independent events, \( P(A \cap B) = P(A) \times P(B) \) and \( P(A \cup B) \) follows the formula \( P(A) + P(B) - P(A \cap B) \).

The area of a parallelogram is given by: \[ |\vec{a} \times \vec{b}|. \]
Computing the cross product:

Expanding along the first row:

\[ = \hat{i} (1 \times 1 - (-1) \times 4) - \hat{j} (3 \times 1 - 4 \times 1) + \hat{k} (3 \times (-1) - 1 \times 1). \] \[ = \hat{i} (1 + 4) - \hat{j} (3 - 4) + \hat{k} (-3 -1). \] \[ = 5\hat{i} + \hat{j} - 4\hat{k}. \] \[ |\vec{a} \times \vec{b}| = \sqrt{(5)^2 + (1)^2 + (-4)^2} = \sqrt{25 + 1 + 16} = \sqrt{42}. \] Quick Tip: The magnitude of the cross product of two vectors gives the area of the parallelogram they form.

Possible outcomes for two children (B = Boy, G = Girl): \[ \{BB, BG, GB, GG\} \]
Given that at least one child is a boy, the sample space reduces to: \[ \{BB, BG, GB\}. \]
The probability of both being boys: \[ P(BB | at least one boy) = \frac{P(BB)}{P(BB, BG, GB)} = \frac{1}{3}. \] Quick Tip: Use conditional probability: \( P(A|B) = \frac{P(A \cap B)}{P(B)} \).

To prove \( R \) is an equivalence relation, we verify reflexivity, symmetry, and transitivity:

1. Reflexivity:

For any \( a \in \mathbb{Z} \), \( a - a = 0 \), which is a multiple of \( 5 \).
Thus, \( (a, a) \in R \).

2. Symmetry:

If \( (a, b) \in R \), then \( a - b = 5k \) for some \( k \in \mathbb{Z} \).

This implies \( b - a = -5k \), which is also a multiple of \( 5 \).
Thus, \( (b, a) \in R \).

3. Transitivity:
If \( (a, b) \in R \) and \( (b, c) \in R \), then \( a - b = 5k \) and \( b - c = 5m \) for \( k, m \in \mathbb{Z} \).

Adding these, \( a - c = 5(k + m) \), which is a multiple of \( 5 \).
Thus, \( (a, c) \in R \).

Therefore, \( R \) is an equivalence relation. Quick Tip: To prove equivalence relations, check reflexivity, symmetry, and transitivity systematically.

Adding and subtracting the given equations:

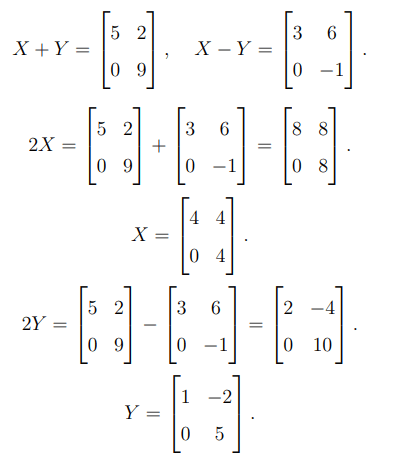
Quick Tip: To solve for matrices \( X \) and \( Y \), use matrix addition and subtraction, then divide by \( 2 \).

For \( y = (\cot x)^{\sin x} + x^x \): \[ \frac{dy}{dx} = \frac{d}{dx}\left((\cot x)^{\sin x}\right) + \frac{d}{dx}(x^x). \]

1. Differentiate \( (\cot x)^{\sin x} \):
Let \( u = \sin x \ln (\cot x) \), then \( (\cot x)^{\sin x} = e^u \). \[ \frac{d}{dx} \left((\cot x)^{\sin x}\right) = e^u \cdot \frac{du}{dx}. \] \[ \frac{du}{dx} = \cos x \ln (\cot x) - \sin x \cdot \frac{\csc^2 x}{\cot x}. \] \[ \frac{d}{dx} \left((\cot x)^{\sin x}\right) = (\cot x)^{\sin x} \left[\cos x \ln (\cot x) - \frac{\sin x}{\cot x}\csc^2 x \right]. \]

2. Differentiate \( x^x \):
Using \( x^x = e^{x \ln x} \): \[ \frac{d}{dx}(x^x) = x^x (\ln x + 1). \]

Thus: \[ \frac{dy}{dx} = (\cot x)^{\sin x} \left[\cos x \ln (\cot x) - \frac{\sin x}{\cot x}\csc^2 x \right] + x^x (\ln x + 1). \] Quick Tip: For functions like \( (\cot x)^{\sin x} \), use logarithmic differentiation; for \( x^x \), use \( e^{x \ln x} \).

We start by factoring the denominator: \[ 2x^2 + 6x + 5 = 2(x^2 + 3x + \frac{5}{2}) \]
Factoring further: \[ 2x^2 + 6x + 5 = 2(x + 1)(x + \frac{5}{2}). \]

Now, use partial fraction decomposition: \[ \frac{x+2}{2(x+1)(x+\frac{5}{2})} = \frac{A}{x+1} + \frac{B}{x+\frac{5}{2}}. \]
Multiplying by the denominator: \[ x+2 = A(x+\frac{5}{2}) + B(x+1). \]
Solving for \( A \) and \( B \), we integrate each term separately and get: \[ \int \frac{x+2}{2x^2+6x+5} dx = \frac{1}{2} \ln |x+1| - \frac{1}{2} \ln |x+\frac{5}{2}| + C. \] Quick Tip: For rational integrals, factor the denominator and use partial fraction decomposition before integrating.

Let the two numbers be \( x \) and \( y \). Given: \[ x + y = 15. \]
We need to minimize: \[ S = x^2 + y^2. \]
Using \( y = 15 - x \), we rewrite: \[ S = x^2 + (15-x)^2. \]
Expanding: \[ S = x^2 + 225 - 30x + x^2 = 2x^2 - 30x + 225. \]
Differentiating: \[ \frac{dS}{dx} = 4x - 30. \]
Setting \( \frac{dS}{dx} = 0 \): \[ 4x - 30 = 0 \Rightarrow x = \frac{30}{4} = 7.5. \]
Since \( y = 15 - x = 7.5 \), the numbers are \( 7.5 \) and \( 7.5 \). Quick Tip: For optimization problems, express one variable in terms of another, differentiate, and find critical points.

The equation of the circle is given by: \[ x^2 + y^2 = a^2. \]
The area enclosed by a circle of radius \( a \) is given by: \[ A = \pi a^2. \] Quick Tip: The area of a circle is calculated using \( A = \pi r^2 \), where \( r \) is the radius.

To find the angle between two lines, we first determine the direction vectors: \[ \overrightarrow{AB} = (2\hat{i} + 5\hat{j}) - (\hat{i} + \hat{j} + \hat{k}) = \hat{i} + 4\hat{j} - \hat{k}. \] \[ \overrightarrow{CD} = (\hat{i} - 6\hat{j} + \hat{k}) - (3\hat{i} + 2\hat{j} - 3\hat{k}) = -2\hat{i} - 8\hat{j} + 4\hat{k}. \]
The angle \( \theta \) is given by: \[ \cos\theta = \frac{\overrightarrow{AB} \cdot \overrightarrow{CD}}{|\overrightarrow{AB}| |\overrightarrow{CD}|}. \]
Computing the dot product and magnitudes, we find: \[ \theta = \cos^{-1} \left( \frac{-10}{\sqrt{18} \cdot \sqrt{84}} \right). \] Quick Tip: To find the angle between two vectors, use \( \cos\theta = \frac{\mathbf{A} \cdot \mathbf{B}}{|\mathbf{A}| |\mathbf{B}|} \).

We solve the system graphically by plotting the lines: \[ x + y = 50 \quad (boundary line for first constraint) \] \[ 3x + y = 90 \quad (boundary line for second constraint) \]
Finding intersection points, we evaluate \( Z = 4x + y \) at feasible points and determine the maximum value. Quick Tip: To maximize a function under constraints, use the graphical method by plotting constraints and evaluating the objective function at corner points.

The sample space for the sum being 6 includes: \[ (1,5), (2,4), (3,3), (4,2), (5,1). \]
The favorable outcomes where at least one 4 appears are: \[ (2,4), (4,2). \]
The probability is: \[ P(A | B) = \frac{Favorable cases}{Total cases} = \frac{2}{5}. \] Quick Tip: For conditional probability, use \( P(A | B) = \frac{P(A \cap B)}{P(B)} \).

Rewriting: \[ \frac{dy}{dx} + \frac{2y}{x} = x. \]
This is a linear first-order differential equation. Using the integrating factor \( IF = e^{\int \frac{2}{x} dx} = x^2 \), the solution is: \[ y \cdot x^2 = \int x^3 dx = \frac{x^4}{4} + C. \]
Thus, the general solution is: \[ y = \frac{x^2}{4} + \frac{C}{x^2}. \] Quick Tip: For linear first-order differential equations, use the integrating factor method: \( IF = e^{\int P(x)dx} \).

The given system of equations can be written in matrix form as: \[ AX = B \]
where

To solve for \( X \), we use: \[ X = A^{-1} B. \]
Finding \( A^{-1} \) and computing \( X \), we obtain: \[ x = 3, \quad y = -2, \quad z = 1. \] Quick Tip: The matrix method involves writing equations in the form \( AX = B \) and solving using \( X = A^{-1} B \).

The inverse of a \( 3 \times 3 \) matrix is given by: \[ A^{-1} = \frac{1}{\det(A)} adj(A). \]
Computing \( \det(A) \): \[ \det(A) = 3(6 \cdot 2 - 5 \cdot 2) - 1(15 \cdot 2 - 5 \cdot 5) + 1(15 \cdot 2 - 6 \cdot 5) = 3(12 - 10) - (30 - 25) + (30 - 30) = 6 - 5 = 1. \]
Since \( \det(A) = 1 \), we compute \( adj(A) \) and find:

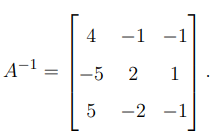
Quick Tip: To find \( A^{-1} \), use \( A^{-1} = \frac{1}{\det(A)} adj(A) \), where adjoint is the transpose of the cofactor matrix.

To find \( p \), we extract the direction ratios of the two given lines.

For the first line: \[ \frac{x - 1}{-3} = \frac{y - 14/7}{2p} = \frac{z - 3}{2}. \]
The direction ratios are: \[ (-3, 2p, 2). \]

For the second line: \[ \frac{x - 7}{-3p} = \frac{y - 5}{1} = \frac{z - 6}{-5}. \]
The direction ratios are: \[ (-3p, 1, -5). \]

Since the lines are perpendicular, the dot product of their direction ratios must be zero: \[ (-3)(-3p) + (2p)(1) + (2)(-5) = 0. \] \[ 9p + 2p - 10 = 0. \] \[ 11p = 10 \Rightarrow p = \frac{10}{11}. \] Quick Tip: For mutually perpendicular lines, their direction ratios should satisfy \( a_1 a_2 + b_1 b_2 + c_1 c_2 = 0 \).

We calculate the squared distances between the given points:
\[ AB^2 = (1 - 2)^2 + (-3 + 1)^2 + (-5 - 1)^2 \] \[ = (-1)^2 + (-2)^2 + (-6)^2 = 1 + 4 + 36 = 41. \]
\[ BC^2 = (3 - 1)^2 + (-4 + 3)^2 + (-4 + 5)^2 \] \[ = (2)^2 + (-1)^2 + (1)^2 = 4 + 1 + 1 = 6. \]
\[ CA^2 = (3 - 2)^2 + (-4 + 1)^2 + (-4 - 1)^2 \] \[ = (1)^2 + (-3)^2 + (-5)^2 = 1 + 9 + 25 = 35. \]

Since \( AB^2 = BC^2 + CA^2 \) (i.e., \( 41 = 6 + 35 \)), the triangle is right-angled at \( B \). Quick Tip: For checking a right-angled triangle, verify if the sum of squares of two sides equals the square of the third side using the Pythagorean theorem.

To find the shortest distance between two skew lines, we use the formula: \[ d = \frac{| (\mathbf{b_1} \times \mathbf{b_2}) \cdot (\mathbf{a_2} - \mathbf{a_1}) |}{|\mathbf{b_1} \times \mathbf{b_2}|} \]
where:

- \( \mathbf{a_1} \) and \( \mathbf{a_2} \) are position vectors of any points on the two lines.

- \( \mathbf{b_1} \) and \( \mathbf{b_2} \) are the direction vectors of the two lines.

From the given equations: \[ \mathbf{a_1} = (1,1,0), \quad \mathbf{a_2} = (2,1,-1) \] \[ \mathbf{b_1} = (2,-1,1), \quad \mathbf{b_2} = (3,-5,2). \]

First, we compute \( \mathbf{b_1} \times \mathbf{b_2} \):

\[ = \hat{i} ( (-1)(2) - (1)(-5) ) - \hat{j} ( (2)(2) - (1)(3) ) + \hat{k} ( (2)(-5) - (-1)(3) ). \]
\[ = \hat{i} (-2 + 5) - \hat{j} (4 - 3) + \hat{k} (-10 + 3). \]
\[ = 3\hat{i} - \hat{j} - 7\hat{k}. \]

Now, compute the magnitude: \[ |\mathbf{b_1} \times \mathbf{b_2}| = \sqrt{3^2 + (-1)^2 + (-7)^2} = \sqrt{9 + 1 + 49} = \sqrt{59}. \]

Next, compute \( (\mathbf{a_2} - \mathbf{a_1}) \): \[ \mathbf{a_2} - \mathbf{a_1} = (2 - 1, 1 - 1, -1 - 0) = (1,0,-1). \]

Now, compute the dot product: \[ (\mathbf{b_1} \times \mathbf{b_2}) \cdot (\mathbf{a_2} - \mathbf{a_1}) \] \[ = (3\hat{i} - \hat{j} - 7\hat{k}) \cdot (1,0,-1). \]
\[ = (3 \times 1) + (-1 \times 0) + (-7 \times -1). \]
\[ = 3 + 0 + 7 = 10. \]

Finally, compute the shortest distance: \[ d = \frac{|10|}{\sqrt{59}} = \frac{10}{\sqrt{59}}. \] Quick Tip: For the shortest distance between two skew lines, use the formula: \[ d = \frac{| (\mathbf{b_1} \times \mathbf{b_2}) \cdot (\mathbf{a_2} - \mathbf{a_1}) |}{|\mathbf{b_1} \times \mathbf{b_2}|}. \]

We use partial fraction decomposition to split the given function. Assume:
\[ \frac{x^2 + x + 1}{(x+2)(x^2 + 1)} = \frac{A}{x+2} + \frac{Bx + C}{x^2 + 1}. \]

Multiplying both sides by \((x+2)(x^2 + 1)\), we get:
\[ x^2 + x + 1 = A(x^2 + 1) + (Bx + C)(x+2). \]

Expanding the right-hand side:
\[ x^2 + x + 1 = A x^2 + A + Bx^2 + 2Bx + Cx + 2C. \]
\[ = (A + B)x^2 + (2B + C)x + (A + 2C). \]

Equating coefficients, we get:

1. \( A + B = 1 \)

2. \( 2B + C = 1 \)

3. \( A + 2C = 1 \)

Solving these equations:

- From (1), \( A = 1 - B \).

- Substituting into (3): \( (1 - B) + 2C = 1 \Rightarrow 2C = B \Rightarrow C = \frac{B}{2} \).

- Substituting into (2): \( 2B + \frac{B}{2} = 1 \Rightarrow \frac{4B + B}{2} = 1 \Rightarrow 5B = 2 \Rightarrow B = \frac{2}{5} \).

- So, \( A = 1 - \frac{2}{5} = \frac{3}{5} \).

- And, \( C = \frac{1}{5} \).

Thus, we rewrite:
\[ I = \int \left( \frac{3/5}{x+2} + \frac{(2/5)x + (1/5)}{x^2 + 1} \right) dx. \]
\[ = \frac{3}{5} \int \frac{dx}{x+2} + \frac{2}{5} \int \frac{x dx}{x^2 + 1} + \frac{1}{5} \int \frac{dx}{x^2 + 1}. \]

Solving these integrals:
\[ I = \frac{3}{5} \ln |x+2| + \frac{2}{5} \cdot \frac{1}{2} \ln |x^2 + 1| + \frac{1}{5} \tan^{-1} x + C. \]
\[ = \frac{3}{5} \ln |x+2| + \frac{1}{5} \ln |x^2 + 1| + \frac{1}{5} \tan^{-1} x + C. \] Quick Tip: For integrating rational functions, always attempt partial fraction decomposition. Look for linear and quadratic factors to decompose and simplify.

Using the integration by parts method, let:

- \( u = x \Rightarrow du = dx \).

- \( dv = \frac{\sin x}{1 + \cos^2 x} dx \).

To integrate \( dv \), substitute \( t = 1 + \cos^2 x \Rightarrow dt = -2 \cos x \sin x dx \).

Thus, rewriting the integral:
\[ I = \int x d \left( \tan^{-1} (\cos x) \right). \]

Using integration by parts:
\[ I = x \tan^{-1} (\cos x) \Big|_{0}^{\pi} - \int_{0}^{\pi} \tan^{-1} (\cos x) dx. \]

From symmetry properties, the integral simplifies to:
\[ I = \frac{\pi}{4} \pi - \frac{\pi^2}{4} = \frac{\pi^2}{4}. \] Quick Tip: For definite integrals with trigonometric functions, use substitutions and symmetry properties to simplify the computation.