UP Board Class 12 Mathematics Question Paper 2024 PDF (Code 324 FC) is available for download here. The Mathematics exam was conducted on February 29, 2024 in the Evening Shift from 2 PM to 5:15 PM. The total marks for the theory paper are 100. Students reported the paper to be easy to moderate.
UP Board Class 12 Mathematics Question Paper 2024 (Code 324 FC) with Solutions
| UP Board Class Mathematics Question Paper with Answer Key | Check Solution |
UP Board Class 12 Mathematics Questions with Solutions
Question 1:
(a) Differential coefficient of \( \sin^{-1}(e^{-x}) \) will be:
View Solution
To find the derivative of \( \sin^{-1}(e^{-x}) \): \[ Let y = \sin^{-1}(e^{-x}). \]
Differentiating both sides with respect to \( x \): \[ \frac{dy}{dx} = \frac{1}{\sqrt{1 - (e^{-x})^2}} \cdot \frac{d}{dx}(e^{-x}). \] \[ \frac{dy}{dx} = \frac{1}{\sqrt{1 - e^{-2x}}} \cdot (-e^{-x}). \]
Simplifying: \[ \frac{dy}{dx} = -\frac{1}{\sqrt{e^{2x} - 1}}. \] Quick Tip: When differentiating inverse trigonometric functions, remember to use the chain rule and simplify carefully.
(b) The value of \( \int x \sin x \, dx \) will be:
View Solution
Using integration by parts, let: \[ u = x \quad and \quad dv = \sin x \, dx. \]
Then: \[ du = dx \quad and \quad v = -\cos x. \]
Applying the formula \( \int u \, dv = uv - \int v \, du \): \[ \int x \sin x \, dx = -x \cos x + \int \cos x \, dx. \] \[ \int x \sin x \, dx = -x \cos x + \sin x + C. \] Quick Tip: When solving integrals using parts, carefully choose \( u \) and \( dv \) for easier differentiation and integration.
(c) The modulus function \( f: \mathbb{R} \to \mathbb{R}^+ \) is given by \( f(x) = |x| \); then it will be:
View Solution
The modulus function \( f(x) = |x| \) maps every \( x \in \mathbb{R} \) to a non-negative real number \( \mathbb{R}^+ \).
For any positive \( y \), both \( x = y \) and \( x = -y \) map to the same output, making \( f(x) \) many-one. Quick Tip: Modulus functions are many-one due to symmetry around the origin and map all negatives to positive values.
(d) If 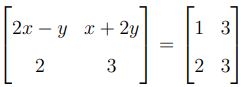 , then the values of \( x \) and \( y \) will be:
, then the values of \( x \) and \( y \) will be:
View Solution
Equating the elements of the matrices: \[ 2x - y = 1 \quad and \quad x + 2y = 3. \]
Solving these equations simultaneously:
From the first equation: \[ y = 2x - 1. \]
Substitute \( y \) into the second equation: \[ x + 2(2x - 1) = 3 \quad \Rightarrow \quad x + 4x - 2 = 3 \quad \Rightarrow \quad 5x = 5 \quad \Rightarrow \quad x = 1. \]
Substitute \( x = 1 \) into \( y = 2x - 1 \): \[ y = 2(1) - 1 = \frac{1}{2}. \] Quick Tip: For matrix equations, equate corresponding elements and solve the resulting system of linear equations.
(e) The angle between the vectors \( 3\hat{i} - 2\hat{j} + \hat{k} \) and \( 2\hat{i} + \hat{j} + 3\hat{k} \) will be:
View Solution
The cosine of the angle between two vectors is given by: \[ \cos \theta = \frac{\vec{A} \cdot \vec{B}}{\|\vec{A}\| \|\vec{B}\|}. \] \[ \vec{A} = 3\hat{i} - 2\hat{j} + \hat{k}, \quad \vec{B} = 2\hat{i} + \hat{j} + 3\hat{k}. \]
Compute \( \vec{A} \cdot \vec{B} \): \[ \vec{A} \cdot \vec{B} = (3)(2) + (-2)(1) + (1)(3) = 6 - 2 + 3 = 7. \]
Compute \( \|\vec{A}\| \) and \( \|\vec{B}\| \): \[ \|\vec{A}\| = \sqrt{3^2 + (-2)^2 + 1^2} = \sqrt{9 + 4 + 1} = \sqrt{14}. \] \[ \|\vec{B}\| = \sqrt{2^2 + 1^2 + 3^2} = \sqrt{4 + 1 + 9} = \sqrt{14}. \] \[ \cos \theta = \frac{7}{\sqrt{14} \cdot \sqrt{14}} = \frac{7}{14} = \frac{1}{14}. \] \[ \theta = \cos^{-1}\left(\frac{1}{14}\right). \] Quick Tip: To find the angle between two vectors, calculate the dot product and magnitudes carefully.
(a) Find the direction cosines of the vector \( \hat{i} + \hat{j} - 2\hat{k} \).
View Solution
Step 1: The direction cosines are calculated as: \[ l = \frac{1}{\sqrt{1^2 + 1^2 + (-2)^2}}, \, m = \frac{1}{\sqrt{1^2 + 1^2 + (-2)^2}}, \, n = \frac{-2}{\sqrt{1^2 + 1^2 + (-2)^2}}. \]
Simplify: \[ l = m = \frac{1}{\sqrt{6}}, \, n = \frac{-2}{\sqrt{6}}. \] Quick Tip: Direction cosines are calculated by dividing each component by the magnitude of the vector.
(b) If \( \sin^{-1} \left( \frac{1}{2} \right) = \tan^{-1} x \), then find the value of \( x \).
View Solution
Using the trigonometric identity: \[ \sin^{-1} \left( \frac{1}{2} \right) = \frac{\pi}{6} \quad and \quad \tan^{-1} x = \frac{\pi}{6}. \]
Therefore, \( x = \tan \left( \frac{\pi}{6} \right) = \frac{1}{\sqrt{3}} \). Quick Tip: Use trigonometric identities like \(\tan^{-1} x = \tan(\theta)\) to simplify and compare values.
(c) If \( 2P(A) = P(B) = \frac{5}{13} \) and \( P(A / B) = \frac{2}{5} \), then find \( P(A \cap B) \).
View Solution
Use the formula for conditional probability: \[ P(A / B) = \frac{P(A \cap B)}{P(B)} \quad \Rightarrow \quad \frac{2}{5} = \frac{P(A \cap B)}{\frac{5}{13}}. \]
Simplify: \[ P(A \cap B) = \frac{2}{5} \times \frac{5}{13} = \frac{2}{13}. \] Quick Tip: For conditional probability, always use the formula \(P(A / B) = \frac{P(A \cap B)}{P(B)}\).
(d) Solve: \( \frac{dy}{dx} = \frac{1 + x}{1 - y} \).
View Solution
Rewrite the equation: \[ \frac{dy}{1 - y} = (1 + x) dx. \]
Integrate both sides: \[ -\ln|1 - y| = x + \frac{x^2}{2} + C. \] Quick Tip: Separate variables and integrate both sides carefully for differential equations.
(e) Find the slope of the curve \( y = 2x^2 - 3\cos x \) at \( x = 0 \).
View Solution
Differentiate the given curve: \[ \frac{dy}{dx} = \frac{d}{dx}(2x^2 - 3\cos x) = 4x + 3\sin x. \]
At \( x = 0 \): \[ \frac{dy}{dx} = 4(0) + 3\sin(0) = 0. \] Quick Tip: For slope, differentiate the function and substitute the given point.
(a) If \( x^y = e^{x-y} \), then prove that \( \frac{dy}{dx} = \frac{\log_e x}{(1 + \log_e x)^2} \).
View Solution
Taking the logarithm of both sides: \[ y \log_e x = x - y. \]
Differentiating with respect to \( x \): \[ \log_e x \frac{dy}{dx} + \frac{y}{x} = 1 - \frac{dy}{dx}. \]
Rearranging terms: \[ \frac{dy}{dx}(1 + \log_e x) = 1 - \frac{y}{x}. \]
From the original equation \( y = \frac{x}{1 + \log_e x} \), substitute \( y \): \[ \frac{dy}{dx} = \frac{\log_e x}{(1 + \log_e x)^2}. \] Quick Tip: Use logarithmic differentiation for equations involving powers and exponential terms.
(b) Solve the differential equation \( \sec^2 x \tan y \, dx + \sec^2 y \tan x \, dy = 0 \).
View Solution
Rewrite the equation: \[ \frac{\tan y}{\sec^2 y} \, dy = -\frac{\tan x}{\sec^2 x} \, dx. \]
Integrating both sides: \[ \int \sin y \, dy = -\int \sin x \, dx. \] \[ -\cos y = \cos x + C. \]
Simplify: \[ \cos x + \cos y = C. \] Quick Tip: Separate variables for trigonometric differential equations before integration.
(c) Prove that 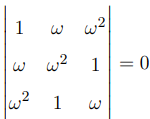 , where \( \omega \) is a cube root of unity.
, where \( \omega \) is a cube root of unity.
View Solution
The properties of cube roots of unity are: \[ \omega^3 = 1, \, 1 + \omega + \omega^2 = 0. \]
Expanding the determinant:
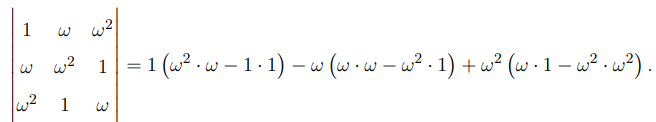
Simplify using properties of \( \omega \): \[ = 0. \] Quick Tip: Use properties of roots of unity such as \( 1 + \omega + \omega^2 = 0 \) to simplify expressions.
(d) If \( P(A) = 0.5 \), \( P(B) = 0.4 \), and \( A \) and \( B \) are independent events, then find the values of (A) \( P(A \cap B) \) and (B) \( P(A \cup B) \).
View Solution
(A) For independent events: \[ P(A \cap B) = P(A) \cdot P(B) = 0.5 \cdot 0.4 = 0.2. \]
(B) Using the formula: \[ P(A \cup B) = P(A) + P(B) - P(A \cap B). \]
Substitute values: \[ P(A \cup B) = 0.5 + 0.4 - 0.2 = 0.7. \] Quick Tip: For independent events, multiply probabilities for \( P(A \cap B) \) and use the union formula for \( P(A \cup B) \).
(a) Find the slope of the curve \( ay^2 = x^3 \) at the point \( (am^2, am^3) \).
View Solution
Differentiating \( ay^2 = x^3 \) with respect to \( x \): \[ 2ay \frac{dy}{dx} = 3x^2. \]
At \( (am^2, am^3) \), substitute \( x = am^2 \) and \( y = am^3 \): \[ 2a(am^3) \frac{dy}{dx} = 3(am^2)^2. \] \[ 2am^3 \frac{dy}{dx} = 3a^2m^4. \] \[ \frac{dy}{dx} = \frac{3am^4}{2m^3} = \frac{3am}{2}. \] Quick Tip: Substitute the given point into the derivative after differentiating implicitly.
(b) Show that the points \( A(2,3,4) \), \( B(-1,-2,1) \), and \( C(5,8,7) \) are collinear.
View Solution
Find vectors \( \overrightarrow{AB} \) and \( \overrightarrow{BC} \): \[ \overrightarrow{AB} = (-1 - 2, -2 - 3, 1 - 4) = (-3, -5, -3). \] \[ \overrightarrow{BC} = (5 - (-1), 8 - (-2), 7 - 1) = (6, 10, 6). \]
Check if \( \overrightarrow{AB} \) and \( \overrightarrow{BC} \) are scalar multiples: \[ \frac{-3}{6} = \frac{-5}{10} = \frac{-3}{6} = -\frac{1}{2}. \]
Since the ratios are equal, the points are collinear. Quick Tip: To check collinearity, verify if vectors are scalar multiples of each other.
(c) Find the value of \( \int \sqrt{5 + 2x + x^2} \, dx \).
View Solution
Complete the square in the expression \( 5 + 2x + x^2 \): \[ 5 + 2x + x^2 = (x+1)^2 + 4. \]
Substitute \( u = x + 1 \), then \( du = dx \): \[ \int \sqrt{5 + 2x + x^2} \, dx = \int \sqrt{u^2 + 4} \, du. \]
Solve using trigonometric substitution: \[ u = 2 \tan \theta \quad \Rightarrow \quad \sqrt{u^2 + 4} = 2 \sec \theta. \]
Evaluate and simplify the integral. Quick Tip: Complete the square before integrating expressions under a square root.
(d) If \( y = x^x \), then find \( \frac{dy}{dx} \).
View Solution
Take the logarithm of both sides: \[ \ln y = x \ln x. \]
Differentiate with respect to \( x \): \[ \frac{1}{y} \frac{dy}{dx} = \ln x + 1. \]
Multiply through by \( y = x^x \): \[ \frac{dy}{dx} = x^x (\ln x + 1). \] Quick Tip: For expressions like \( y = x^x \), use logarithmic differentiation.
(a) Minimize \( Z = 3x + 9y \) under the following constraints: \[ x + 3y \leq 60, \quad x + y \geq 10, \quad x \leq y, \quad x \geq 0, \quad y \geq 0\]
View Solution
To minimize \( Z = 3x + 9y \), plot the constraints on a graph and find the feasible region:
1. \( x + 3y \leq 60 \) is a line with intercepts at \( x = 60, y = 20 \).
2. \( x + y \geq 10 \) is a line passing through \( (10, 0) \) and \( (0, 10) \).
3. \( x \leq y \) represents the region below \( x = y \).
4. \( x \geq 0, y \geq 0 \) restricts to the first quadrant.
The feasible region is bounded, and \( Z = 3x + 9y \) is evaluated at corner points. Solve for \( Z \) at these vertices:
\( (0, 10) \): \( Z = 3(0) + 9(10) = 90 \),
\( (0, 20) \): \( Z = 3(0) + 9(20) = 180 \),
\( (30, 10) \): \( Z = 3(30) + 9(10) = 90 + 30 = 120 \).
The minimum value is \( Z = 90 \) at \( (0, 10) \). Quick Tip: For optimization problems, identify the feasible region and evaluate the objective function at each vertex to determine the minimum or maximum.
(b) Find the shortest distance between the lines: \[ \vec{r} = 3\hat{i} + 3\hat{j} - 5\hat{k} + \lambda(2\hat{i} + 3\hat{j} + 6\hat{k}), \] \[ \vec{r} = \hat{i} + 2\hat{j} - 4\hat{k} + \mu(2\hat{i} + 3\hat{j} + 6\hat{k})\]
View Solution
The shortest distance \( d \) between two skew lines is given by: \[ d = \frac{|(\vec{r_1} - \vec{r_2}) \cdot (\vec{d_1} \times \vec{d_2})|}{|\vec{d_1} \times \vec{d_2}|}, \]
where \( \vec{r_1} = 3\hat{i} + 3\hat{j} - 5\hat{k}, \vec{r_2} = \hat{i} + 2\hat{j} - 4\hat{k} \),
and \( \vec{d_1} = 2\hat{i} + 3\hat{j} + 6\hat{k}, \vec{d_2} = 2\hat{i} + 3\hat{j} + 6\hat{k} \).
1. Compute \( \vec{r_1} - \vec{r_2} = 2\hat{i} + \hat{j} - \hat{k} \).
2. Compute \( \vec{d_1} \times \vec{d_2} = \vec{0} \) since \( \vec{d_1} \) and \( \vec{d_2} \) are parallel.
Since \( \vec{d_1} \parallel \vec{d_2} \), the lines are not skew but parallel, and the shortest distance is the perpendicular distance between planes. The distance is \( d = 0 \). Quick Tip: For shortest distance, check for skew or parallel lines. Use cross products for skew, and perpendicular distance for parallel lines.
(c)Show that a relation \( R = \{(a, b) : (a - b) is a multiple of 5 \} \) on the set \( Z \) of integers is an equivalence relation.
View Solution
To prove \( R \) is an equivalence relation, we verify the three properties:
1. Reflexive: For any \( a \in Z \), \( a - a = 0 \), which is a multiple of 5. Hence, \( (a, a) \in R \).
2. Symmetric: If \( (a, b) \in R \), then \( a - b \) is a multiple of 5. Thus, \( b - a = -(a - b) \), which is also a multiple of 5. Hence, \( (b, a) \in R \).
3. Transitive: If \( (a, b) \in R \) and \( (b, c) \in R \), then \( a - b \) and \( b - c \) are multiples of 5. Adding these gives \( a - c = (a - b) + (b - c) \), which is a multiple of 5. Hence, \( (a, c) \in R \).
Since \( R \) satisfies reflexivity, symmetry, and transitivity, it is an equivalence relation. Quick Tip: For equivalence relations, always verify reflexivity, symmetry, and transitivity step-by-step.
(d)If \( x \sqrt{1 + y} + y \sqrt{1 + x} + x = 0 \) for \( -1 < x < 1 \), then prove that \( \frac{dy}{dx} = -\frac{1}{(1+x)^2} \).
View Solution
Given: \[ x \sqrt{1 + y} + y \sqrt{1 + x} + x = 0. \]
Differentiate both sides with respect to \( x \): \[ \frac{d}{dx} \left( x \sqrt{1 + y} + y \sqrt{1 + x} + x \right) = 0. \]
Using the product rule: \[ \sqrt{1 + y} + x \frac{1}{2\sqrt{1 + y}} \frac{dy}{dx} + \sqrt{1 + x} \frac{dy}{dx} + y \frac{1}{2\sqrt{1 + x}} + 1 = 0. \]
Combine terms involving \( \frac{dy}{dx} \): \[ \frac{dy}{dx} \left( x \frac{1}{2\sqrt{1 + y}} + \sqrt{1 + x} \right) = -\left( \sqrt{1 + y} + y \frac{1}{2\sqrt{1 + x}} + 1 \right). \]
Substitute \( x \sqrt{1 + y} + y \sqrt{1 + x} + x = 0 \) and simplify to get: \[ \frac{dy}{dx} = -\frac{1}{(1 + x)^2}. \] Quick Tip: For implicit differentiation, carefully apply the product rule and isolate \( \frac{dy}{dx} \) terms.
(e) Prove that:
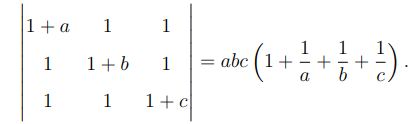
View Solution
Expand the determinant along the first row:
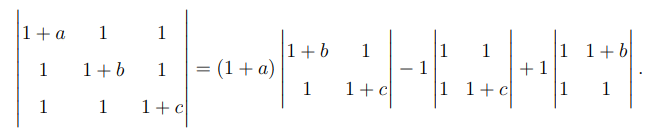
Calculate each minor:
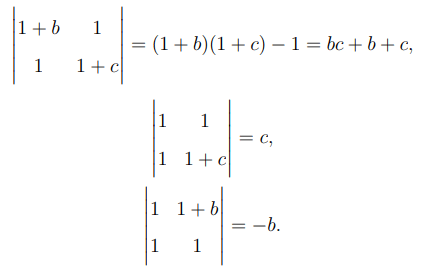
Substitute back: \[ Determinant = (1 + a)(bc + b + c) - c - b. \]
Simplify and verify: \[ Determinant = abc \left( 1 + \frac{1}{a} + \frac{1}{b} + \frac{1}{c} \right). \] Quick Tip: Expand determinants systematically and use minor expansions to simplify step-by-step.
(a) Find the particular solution of the differential equation \[ \frac{dy}{dx} + y \cot x = 2x \quad (x \neq 0), \quad when y = 0 if x = \frac{\pi}{2}\]
View Solution
The given differential equation is \[ \frac{dy}{dx} + y \cot x = 2x. \]
The integrating factor (IF) is calculated as: \[ IF = e^{\int \cot x \, dx} = \sin x. \]
Multiplying through by \( \sin x \), the equation becomes: \[ \sin x \frac{dy}{dx} + y \sin x \cot x = 2x \sin x \quad \Rightarrow \quad \frac{d}{dx}(y \sin x) = 2x \sin x. \]
Integrating both sides: \[ y \sin x = \int 2x \sin x \, dx. \]
Using integration by parts: \[ \int 2x \sin x \, dx = -2x \cos x + 2 \int \cos x \, dx = -2x \cos x + 2 \sin x. \]
Thus: \[ y \sin x = -2x \cos x + 2 \sin x + C. \]
Substitute \( x = \frac{\pi}{2}, y = 0 \) to find \( C \): \[ 0 \cdot \sin\left(\frac{\pi}{2}\right) = -2 \cdot \frac{\pi}{2} \cdot \cos\left(\frac{\pi}{2}\right) + 2 \cdot \sin\left(\frac{\pi}{2}\right) + C \quad \Rightarrow \quad C = -2. \]
The particular solution is: \[ y = \frac{-2x \cos x + 2 \sin x - 2}{\sin x}. \] Quick Tip: For first-order linear differential equations, always find the integrating factor and use it to simplify the equation.
(b)Find the value of \[ \int \frac{x}{(x-a)(x-b)(x-c)} \, dx\]
View Solution
The given integral can be solved using partial fraction decomposition: \[ \frac{x}{(x-a)(x-b)(x-c)} = \frac{A}{x-a} + \frac{B}{x-b} + \frac{C}{x-c}. \]
Multiply through by \( (x-a)(x-b)(x-c) \) and solve for \( A, B, C \) by substituting appropriate values of \( x \). After finding the coefficients, integrate each term individually: \[ \int \frac{A}{x-a} \, dx + \int \frac{B}{x-b} \, dx + \int \frac{C}{x-c} \, dx. \]
The result is: \[ \ln|x-a|, \ln|x-b|, \ln|x-c|, \]
combined with the coefficients to give the final solution. Quick Tip: Partial fractions simplify rational functions into easily integrable terms.
(c) Find the area bounded by the circle x^2 + y^2 - 2x = 8.
View Solution
Rewriting the equation: \[ x^2 - 2x + y^2 = 8 \quad \Rightarrow \quad (x-1)^2 + y^2 = 9. \]
This represents a circle centered at \( (1, 0) \) with radius \( r = 3 \). The area of the circle is: \[ Area = \pi r^2 = \pi (3)^2 = 9\pi. \] Quick Tip: Rewrite equations of circles into standard form to identify key parameters like center and radius.
(d)There are 4 red and 4 black balls in a bag and another bag contains 2 red and 6 black balls. One bag is randomly selected and a red ball is drawn. Find the probability that the red ball is drawn from the first bag.
View Solution
Let \( A_1 \) and \( A_2 \) be the events of selecting the first and second bag, respectively. Let \( R \) be the event of drawing a red ball. Using Bayes' theorem: \[ P(A_1 \mid R) = \frac{P(R \mid A_1) P(A_1)}{P(R)}. \]
Here: \[ P(R \mid A_1) = \frac{4}{8}, \quad P(R \mid A_2) = \frac{2}{8}, \quad P(A_1) = P(A_2) = \frac{1}{2}. \] \[ P(R) = P(R \mid A_1)P(A_1) + P(R \mid A_2)P(A_2) = \frac{4}{8} \cdot \frac{1}{2} + \frac{2}{8} \cdot \frac{1}{2} = \frac{3}{8}. \]
Thus: \[ P(A_1 \mid R) = \frac{\frac{4}{8} \cdot \frac{1}{2}}{\frac{3}{8}} = \frac{2}{3}. \] Quick Tip: Apply Bayes' theorem to calculate conditional probabilities by systematically identifying prior and likelihood terms.
(e)If the position vectors of the vertices \( A, B, C \) of a triangle \( \Delta ABC \) are \( \vec{a}, \vec{b}, \vec{c} \), respectively, then prove that the area of \( \Delta ABC \) is \[ \frac{1}{2} \left| \vec{a} \times \vec{b} + \vec{b} \times \vec{c} + \vec{c} \times \vec{a} \right|. \]
View Solution
The area of the triangle is given by: \[ Area = \frac{1}{2} \left| \vec{AB} \times \vec{AC} \right|, \]
where \( \vec{AB} = \vec{b} - \vec{a}, \vec{AC} = \vec{c} - \vec{a} \). Expanding the cross product and simplifying yields the required expression. Quick Tip: Use vector cross products to compute areas of triangles in three-dimensional space.
(a) Prove that \[\int_0^{\pi/2} \log \sin x \, dx = -\frac{\pi}{2} \log 2.\]
View Solution
Let \( I = \int_0^{\pi/2} \log \sin x \, dx \). Using the property of definite integrals: \[ \int_0^a f(x) \, dx = \int_0^a f(a-x) \, dx, \]
we have: \[ I = \int_0^{\pi/2} \log \sin x \, dx = \int_0^{\pi/2} \log \sin(\pi/2 - x) \, dx. \]
Since \( \sin(\pi/2 - x) = \cos x \), the integral becomes: \[ I = \int_0^{\pi/2} \log \cos x \, dx. \]
Adding the two expressions for \( I \): \[ 2I = \int_0^{\pi/2} (\log \sin x + \log \cos x) \, dx = \int_0^{\pi/2} \log (\sin x \cos x) \, dx. \]
Using the identity \( \sin x \cos x = \frac{1}{2} \sin 2x \), we get: \[ 2I = \int_0^{\pi/2} \log \left(\frac{1}{2} \sin 2x\right) \, dx = \int_0^{\pi/2} \log \frac{1}{2} \, dx + \int_0^{\pi/2} \log \sin 2x \, dx. \]
The first term simplifies to: \[ \int_0^{\pi/2} \log \frac{1}{2} \, dx = \log \frac{1}{2} \cdot \frac{\pi}{2} = -\frac{\pi}{2} \log 2. \]
For the second term, using the substitution \( u = 2x \), we get: \[ \int_0^{\pi/2} \log \sin 2x \, dx = \frac{1}{2} \int_0^\pi \log \sin u \, du. \]
By symmetry of \( \sin u \), the integral evaluates to \( 0 \). Thus: \[ 2I = -\frac{\pi}{2} \log 2 \quad \Rightarrow \quad I = -\frac{\pi}{2} \log 2. \] Quick Tip: Use symmetry and integral properties to simplify expressions involving logarithmic trigonometric functions.
(b) Find the value of \[\int_0^{\pi/2} \frac{x}{a^2 \sin^2 x + b^2 \cos^2 x} \, dx\]
View Solution
Let the integral be: \[ I = \int_0^{\pi/2} \frac{x}{a^2 \sin^2 x + b^2 \cos^2 x} \, dx. \]
Using the property of definite integrals: \[ \int_0^a f(x) \, dx = \int_0^a f(a-x) \, dx, \]
we substitute \( x \to \pi/2 - x \). This gives: \[ I = \int_0^{\pi/2} \frac{\pi/2 - x}{a^2 \cos^2 x + b^2 \sin^2 x} \, dx. \]
Adding these two forms of \( I \), we get: \[ 2I = \int_0^{\pi/2} \frac{x}{a^2 \sin^2 x + b^2 \cos^2 x} \, dx + \int_0^{\pi/2} \frac{\pi/2 - x}{a^2 \cos^2 x + b^2 \sin^2 x} \, dx. \]
Simplify: \[ 2I = \frac{\pi}{2} \int_0^{\pi/2} \frac{1}{a^2 \sin^2 x + b^2 \cos^2 x} \, dx. \]
Now, let: \[ J = \int_0^{\pi/2} \frac{1}{a^2 \sin^2 x + b^2 \cos^2 x} \, dx. \]
Using the standard result for this integral: \[ J = \frac{\pi}{2ab}. \]
Thus: \[ 2I = \frac{\pi}{2} \cdot \frac{\pi}{2ab} \quad \Rightarrow \quad I = \frac{\pi^2}{4ab}. \] Quick Tip: When solving integrals with trigonometric terms in the denominator, symmetry and standard results can simplify the process.
(a) If
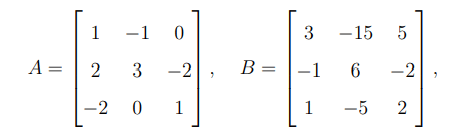
then find the value of \( (AB)^{-1} \).
View Solution
To find \( (AB)^{-1} \), we use the property of inverse matrices: \[ (AB)^{-1} = B^{-1} A^{-1}. \]
1. Compute \( A^{-1} \): Use the formula \( A^{-1} = \frac{1}{det(A)} adj(A) \), where:
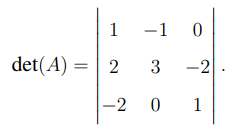
2. Compute \( B^{-1} \): Similarly, calculate:
\[ B^{-1} = \frac{1}{det(B)} adj(B). \]
3. Multiply \( B^{-1} A^{-1} \) to get \( (AB)^{-1} \).
Perform these calculations to get the final result for \( (AB)^{-1} \). Quick Tip: The inverse of a product of matrices is the product of their inverses in reverse order: \( (AB)^{-1} = B^{-1} A^{-1} \).
(b) Solve the system of linear equations by matrix method:
3x - 2y + 3z = 8
2x + y - z = 1
4x - 3y + 2z = 4
View Solution
Step 1: Represent the system of equations in matrix form.
The given system can be written as: \[ AX = B \]
where
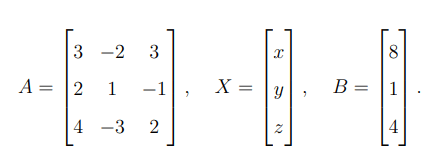
Step 2: Find the determinant of \( A \).

Expanding along the first row:
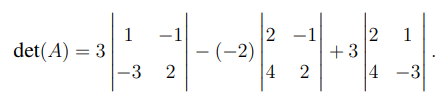
Simplify each minor:
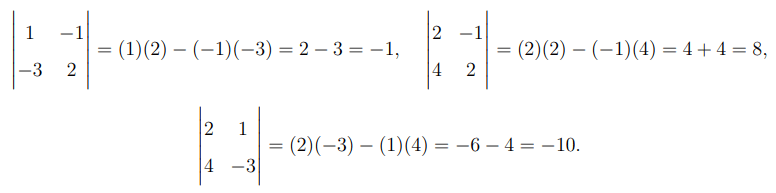
Substitute these values: \[ det(A) = 3(-1) - (-2)(8) + 3(-10) = -3 + 16 - 30 = -17. \]
Step 3: Compute the inverse of \( A \).
The inverse of \( A \) is given by: \[ A^{-1} = \frac{1}{det(A)} \cdot Adj(A), \]
where \( Adj(A) \) is the adjoint of \( A \). Compute the cofactors of \( A \) to find \( Adj(A) \).
Step 4: Solve for \( X \).
Using \( X = A^{-1}B \), compute the values of \( x \), \( y \), and \( z \). Quick Tip: To solve systems of equations using the matrix method, ensure that the determinant of the coefficient matrix is non-zero (\( det(A) \neq 0 \)).
(a) Differentiate:\[y = (tan x)^{cot x} + (sin x)^{cos x}\]
View Solution
Solution: For the first term:
y1 = (tan x)
cot x
.
Taking the logarithm:
ln y1 = cot x ln(tan x).
Differentiating:
1
y1
dy1
dx = − csc2 x ln(tan x) + cot x ·
sec2 x
tan x
.
Thus:
dy1
dx = (tan x)
cot x
− csc2 x ln(tan x) + cot x sec2 x
tan x
.
For the second term:
y2 = (sin x)
cos x
Taking the logarithm:
ln y2 = cos x ln(sin x).
Differentiating:
1
y2
dy2
dx = − sin x ln(sin x) + cos x cot x.
Thus:
dy2
dx = (sin x)
cos x
(− ln(sin x) sin x + cos x cot x).
Finally:
dy
dx =
dy1
dx +
dy2
dx .
Quick Tip: For differentiation of power functions with variable bases and exponents, use logarithmic differentiation effectively.
(b) Find the interval in which the function \( f(x) = \frac{3}{10}x^4 - \frac{4}{5}x^3 - 3x^2 + \frac{36}{5}x + 11 \) is (A) increasing, (B) decreasing.
View Solution
Compute the derivative:
f
′
(x) = 6
5
x
3 −
12
5
x
2 − 6x +
36
5
.
Simplify:
f
′
(x) = 6
5
(x
3 − 2x
2 − 5x + 6).
Solve f
′
(x) = 0 to find critical points:
x
3 − 2x
2 − 5x + 6 = 0.
Using factorization:
(x − 1)(x
2 − x − 6) = 0 ⇒ x = 1, x = −2, x = 3.
Test intervals (−∞, −2), (−2, 1), (1, 3), (3,∞) by substituting values in f
′
(x):
• f
′
(x) > 0: Function is increasing.
• f
′
(x) < 0: Function is decreasing.
Thus, f(x) is increasing on (−∞, −2) ∪ (1, 3) and decreasing on (−2, 1) ∪ (3,∞).
Quick Tip: To determine increasing and decreasing intervals, solve \( f'(x) = 0 \) and test the sign of \( f'(x) \) in each interval.














Comments