KCET 2023 Mathematics Question Paper Set D2 is available here for download. KCET 2023 Question Paper May 20 Shift 2 2:30 PM to 3:50 PM was conducted for Mathematics Paper. KCET 2023 Question Paper included 60 MCQ-based questions in total. Each candidate is awarded +1 for correct answers, however, there will be no negative marking for incorrect responses. Students got 80 minutes to attempt KCET 2023 Mathematics Question Paper.
KCET 2023 Mathematics Question Paper with Answer Key PDF Set D2
| KCET 2024 Mathematics Question Paper with Answer Key | Check Solutions |

KCET 2023 Mathematics Questions with Solutions
Question 1:
If a line makes an angle of π/3 with each X and Y axis, then the acute angle made by Z-axis is:
(A) π/3
(B) π/3
(C) π/3
(D) π/4
The length of perpendicular drawn from the point (3, −1, 11) to the line (x-5)/2 = (y-2)/3 = (z-3)/4 is:
(Α) √29
(B) √33
(C) √53
(D) √66
The equation of the plane through the points (2, 1,0), (3, 2, −2), and (3, 1, 7) is:
(A) 2x – 3y + 4z – 27 = 0
(B) 6x - 3y+2z-7=0
(C) 7x - 9y-z-5=0
(D) 3x - 2y + 6z - 27 = 0
The point of intersection of the line (x+1)/3 = (y+3)/3 = (z+2)/2 with the plane 3x + 4y + 5z = 10 is:
(A) (2, -6, -4)
(B) (2, 6, -4)
(C) (2, 6, 4)
(D) (-2, 6, -4)
If (2, 3, -1) is the foot of the perpendicular from (4, 2, 1) to a plane, then the equation of the plane is:
(A) 2x + y + 2z − 1 = 0
(B) 2x - y + 2z = 0
(C) 2x + y + 2z - 5 = 0
(D) 2x - y + 2x + 1 = 0
If |a × b|² + |a – b|² = 144 and |a| = 4, then |b| is equal to:
(A) 3
(B) 8
(C) 4
(D) 12
If a + 2b + 3c = 0 and (a × b) + (b x c) + (c × a) = λ(b × c), then the value of λ is equal to:
(A) 3
(B) 6
(C) 4
(D) 2
A bag contains 2n + 1 coins. It is known that n of these coins have heads on both sides, whereas the other n + 1 coins are fair. One coin is selected at random and tossed. If the probability that the toss results in heads is 31/42, then the value of n is:
(A) 6
(B) 8
(C) 10
(D) 5
Let A = {x, y, z, u} and B = {a,b}. A function f : A → B is selected randomly. The probability that the function is an onto function is:
(A) 2/5
(B) 7/8
(C) 3/5
(D) 1/2
The shaded region in the figure given is the solution of which of the inequalities?
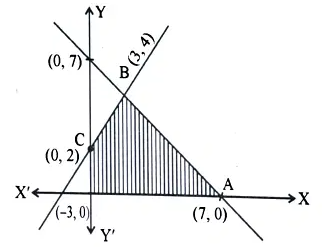
(A) x + y ≥ 7, 2x – 3y + 6 < 0, x ≥ 0, y ≥ 0
(B) x + y ≥ 7, 2x – 3y + 6 ≥ 0, x ≥ 0, y ≥ 0
(C) x + y ≤ 7, 2x – 3y + 6 < 0, x ≥ 0, y ≥ 0
(D) x + y ≤ 7, 2x – 3y + 6 ≥ 0, x ≥ 0, y ≥ 0
If A and B are events such that P(A) = 1/4, P(A/B) = 1/2 and P(B/A) = 2/3, then P(B) is:
(A) 2/3
(B) 1/3
(C) 1/4
(D) 1/5
The value of log₁₀ tan 1° + log₁₀ tan 2° + log₁₀ tan 3° + ··· + log₁₀ tan 89° is:
(A) 3
(B) 1
(C) 1
(D) 0
The value of |sin² 14° sin² 66° tan 135°| |sin² 66° tan 135° sin² 14°| is: |tan 135° sin² 14° sin² 66°|
(A) 0
(B) 1
(C) 2
(D) -1
The modulus of the complex number ((1+i)²(1+3i))/((2-6i)(2-2i)) is:
(A) 1/4
(B) 1/√2
(C) √3/4
(D) √2/3
Question 15:
Given that a, b, and x are real numbers and a < b, x < 0 then:
(A) a/x ≥ b/x
(B) a/x ≤ b/x
(C) a/x ≥ b/x
(D) a/x ≤ b/x
Ten chairs are numbered as 1 to 10. Three women and two men wish to occupy one chair each. First, the women choose the chairs marked 1 to 6, then the men choose the chairs from the remaining. The number of possible ways is:
(A) 6P3 × 4P2
(B) 6C3 × 4P2
(C) 6P3 × 4C2
(D) 6C3 × 4C2
Which of the following is an empty set?
(A) {x : x² + 1 = 0, x ∈ R}
(B) {x : x² − 9 = 0, x ∈ R}
(C) {x : x² = x + 2, x ∈ R}
(D) {x : x² − 1 = 0, x ∈ R}
If f(x) = ax + b, where a and b are integers, f(-1) = −5 and f(3) = 3, then a and b are respectively:
(A) 2, -3
(B) 0, 2
(C) 2, 3
(D) -3, -1
If (p/(q+r)), (q/(r+p)), (r/(p+q)) are in A.P., then p, q, r are:
(A) in G.P.
(B) are in A.P.
(C) are not in G.P.
(D) are not in A.P.
A line passes through (2, 2) and is perpendicular to the line 3x + y = 3. Its y-intercept is:
(A) 1/3
(B) 1
(C) 2/3
(D) 4/3
The distance between the foci of a hyperbola is 16 and its eccentricity is √2. Its equation is:
(A) x²/32 - y²/32 = 1
(B) 2x² – 3y² = 7
(C) y² – x² = 32
(D) x² – y² = 32
If limₓ→₀ (sin(2+x)-sin(2-x))/x = A cos B, then the values of A and B respectively are:
(A) 1, 2
(B) 2, 1
(C) 1, 1
(D) 2, 2
If n is even and the middle term in the expansion of (x² + (1/x))ⁿ is 924 x⁶, then n is equal to:
(A) 14
(B) 12
(C) 8
(D) 10
The nth term of the series 1 + 3/7 + 5/7² + 7/7³ +... is:
(A) (2n+1)/7ⁿ
(B) (2n-1)/7ⁿ
(C) (2n+1)/7ⁿ⁻¹
(D) (2n-1)/7ⁿ⁻¹
Let f : R → R and g : [0, ∞) → R be defined by f(x) = x² and g(x) = √x. Which one of the following is not true?
(A) (f ◦ g)(-4) = 4
(B) (f ◦ g)(2) = 2
(C) (g ◦ f)(-2) = 2
(D) (g ◦ f)(4) = 4
Let f : R → R be defined by f(x) = 3x² − 5 and g : R → R by g(x) = x/(x²+1). Then g ◦ f is:
(A) (3x²-5)/(9x⁴-6x²+26)
(B) (3x²)/(x⁴+2x²-4)
(C) (9x²+30x²-2)/(x²+1)
(D) (3x²-5)/(9x⁴-30x²+26)
Let the relation R be defined in N by aRb if 3a + 2b = 27. Then R is:
(A) {(0, 27), (1, 12), (3, 9), (5, 6), (9,3)}
(B) {(1, 12), (3, 9), (5, 6), (7, 3), (9,0)}
(C) {(2, 1), (9, 3), (6, 5), (3, 7)}
(D) {(1, 12), (3, 9), (5, 6), (7, 3)}
Let f(x) = sin 2x + cos 2x and g(x) = x² + 1, then g(f(x)) is invertible in the domain:
(A) x ∈ [-π/2, π/2]
(B) x ∈ [-π/8, π/8]
(C) x ∈ [0,1]
(D) x ∈ [-π/4, π/4]
The contrapositive of the statement "If two lines do not intersect in the same plane then they are parallel” is:
(A) If two lines are parallel then they intersect in the same plane.
(B) If two lines are not parallel then they do not intersect in the same plane.
(C) If two lines are parallel then they do not intersect in the same plane.
(D) If two lines are not parallel then they intersect in the same plane.
The mean of 100 observations is 50 and their standard deviation is 5. Then the sum of squares of all observations is:
(A) 252500
(B) 250000
(C) 255000
(D) 50000
If x(3/2) +y(1/-1) = (15/5) then the value of x and y are:
(A) x = 4, y = -3
(B) x = −4, y = −3
(C) x = 4, y = 3
(D) x = 4, y = 3
If A and B are two matrices such that AB = B and BA = A then A² + B² = ?
(A) 2AB
(B) AB
(C) 2ВА
(D) A + B
If |2-k 2| |1 3-k| is a singular matrix, then the value of 5k - k² is:
(A) 2
(B) -2
(C) 4
(D) -4
The area of a triangle with vertices (-3,0), (3,0) and (0, k) is 9 square units. The value of k is:
(A) -9
(B) 6
(C) 3
(D) 9
If |1 a a²| |1 b b²| and △₁ = |bc ca ab| |1 c c²| |a b c| then:
(A) Δ₁ = 3Δ
(B) Δ₁ ≠ Δ
(C) Δ₁ = -Δ
(D) Δ₁ = Δ
If sin⁻¹(2x/(1+x²)) + cos⁻¹((1-a²)/(1+a²)) = tan⁻¹((2a)/(1-a²)) where a, x ∈ (0, 1), then the value of x is:
(A) a/2
(B) 1+a/2
(C) 2a/(1-a²)
(D) 0
The value of cot⁻¹((√(1 - sinx) + √(1 + sinx))/(√(1 - sinx) - √(1 + sinx))) where x ∈ (0, π/4) is:
(A) π/4 - x
(B) π/4 - x/2
(C) π/2 - x/2
(D) π/2 - x
The function f(x) = cot x is discontinuous on every point of the set
(A) {x = 2nπ, n ∈ Z}
(B) {x = (2n + 1)π/2, n ∈ Z}
(C) {x = nπ/2, n ∈ Z}
(D) {x = nπ, n ∈ Z}
If the function is f(x) = 1/(x+2), then the point of discontinuity of the composite function y = f(f(x)) is:
(A) -5/2
(B) 2/5
(C) -2/5
(D) -5/2
If y = a sin x + b cos x, then y² + (dy/dx)² is:
(A) function of y
(B) function of x and y
(C) constant
(D) function of x
If f(x) = 1 + nx + n(n-1)/2 * x² + n(n-1)(n-2)/6 * x³ + ... + xⁿ then f'(1) =
(A) n(n - 1)2ⁿ⁻²
(B) n(n - 1)2ⁿ
(C) 2ⁿ⁻¹
(D) (n - 1)2ⁿ⁻¹
If A = |1 tan(α/2)| and AB = I then B = |-tan(α/2) 1|
(A) cos²(α/2) * A
(B) cos²(α/2) * I
(C) sin²(α/2) * A
(D) cos²(α/2) * Aᵀ
If u = sin⁻¹(2x/(1+x²)) and v = tan⁻¹(2x/(1-x²)), then du/dv is:
(A) 2
(B) (1-x²)/(1+x²)
(C) 1
(D) 1/2
The distance s in meters travelled by a particle in t seconds is given by s = (2t³/3) − 18t + (5/3). The acceleration when the particle comes to rest is:
(A) 10 m/sec²
(B) 12 m/sec²
(C) 18 m/sec²
(D) 3 m/sec²
A particle moves along the curve x²/16 + y²/4 = 1. When the rate of change of abscissa is 4 times that of its ordinate, then the quadrant in which the particle lies is:
(A) II or IV
(B) III or IV
(C) II or III
(D) I or III
An enemy fighter jet is flying along the curve given by y = x² + 2. A soldier is placed at (3, 2) wants to shoot down the jet when it is nearest to him. Then the nearest distance is:
(A) √6 units
(B) 2 units
(C) √5 units
(D) √3 units
Evaluate the integral ∫₂⁸ (5√(10 - x))/(5√x + 5√(10 - x)) dx
(A) 6
(B) 4
(C) 3
(D) 5
Evaluate the integral ∫√(csc x - sin x) dx
(A) 2√(sin x) + C
(B) √(sin x) + C
(C) 2/√(sin x) + C
(D) √(sin x) + C
If f(x) and g(x) are two functions with g(x) = 1/x and f(g(x)) = x³ - 1/x³, then f'(x) =
(A) 3x² + 3/x⁴
(B) x² - 1/x²
(C) 1 - 4/x³
(D) 3x² + 3
A circular plate of radius 5 cm is heated. Due to expansion, its radius increases at the rate of 0.05 cm/sec. The rate at which its area is increasing when the radius is 5.2 cm is:
(A) 27.4π cm²/sec
(B) 5.05π cm²/sec
(C) 0.52π cm²/sec
(D) 5.2π cm²/sec
Evaluate the integral ∫₋₂⁰ (x³ + 3x² + 3x + 3 + (x + 1) cos(x + 1)) dx
(A) 3
(B) 4
(C) 1
(D) 0
Evaluate the integral ∫0π (x tan x)/(sec x - csc x) dx:
(A) π/4
(B) π/8
(C) π/2
(D) π
Evaluate the integral ∫ √(5 - 2x + x²) dx
(A) x/2 √(5 - 2x + x²) + 4 log |x + 1| + √(x² - 2x + 5) + C
(B) x/2 √(5 - 2x + x²) + 2 log |x − 1| + √(5 + 2x + x²) + C
(C) x/2 √(5 - 2x + x²) + 2 log |x − 1| + √(5 - 2x + x²) + C
(D) x/2 √(5 - 2x + x²) + 2 log |x + 1| + √(x² - 2x + 5) + C
Evaluate the integral ∫ 1/(1+3 sin²x + 8 cos² x) dx
(A) 1/3 tan⁻¹((5 tan x)/3) + C
(B) 1/√45 tan⁻¹((5 tan x)/3) + C
(C) 6 tan⁻¹((2 tan x)/3) + C
(D) 1/3 tan⁻¹((2 tan x)/3) + C
If a curve passes through the point (1, 1) and at any point (x, y) on the curve, the product of the slope of its tangent and the x-coordinate of the point is equal to the y-coordinate of the point, then the curve also passes through the point:
(A) (√3, 0)
(B) (-1, 2)
(C) (√3, 0)
(D) (2, 2)
The degree of the differential equation 1 + (dy/dx)² + (d²y/dx²)² = √( (d³y/dx³)² + 1) is:
(A) 3
(B) 1
(C) 2
(D) 6
If |a + b| = |a – b|, then:
(A) a and b are parallel.
(B) a and b are coincident.
(C) a and b are inclined to each other at 60°.
(D) a and b are perpendicular.
The component of î in the direction of î + j + 2k is:
(A) 6
(B) 6/√6
(C) 1/√6
(D) √6
In the interval (0, π/4), the area lying between the curves y = tan x and y = cot x and the X-axis is:
(A) 2 log 2 sq. units
(B) 4 log 2 sq. units
(C) log 2 sq. units
(D) 3 log 2 sq. units
The area of the region bounded by the line y = x + 1, and the lines x = 3 and x = 5 is:
(A) 7/2 sq. units
(B) 11/2 sq. units
(C) 7 sq. units
(D) 10 sq. units










KCET 2023 Paper Analysis May 20
KCET 2023 paper analysis May 20 is available here. Candidates can check KCET 2023 paper analysis by clicking on the link provided below.
Also Check:
KCET Previous Year Question Paper
| KCET 2022 Question Paper | KCET 2021 Question Paper | KCET 2020 Question Paper |
| KCET 2019 Question Paper | KCET 2018 Question Paper | KCET 2017 Question Paper |




Comments