
GRE 2025 Model Paper Set 2 Question Paper with Solutions PDF is available for download. The overall test time is about 1 hour and 58 minutes. GRE has total 5 sections:
- Analytical Writing (One "Analyze an Issue" task, Alloted time 30 minutes)
- Verbal Reasoning (Two Sections, with 12 questions and 15 questions respectively)
- Quantitative Reasoning (Two Sections, with 12 questions and 15 questions respectively)
GRE 2025 Model Paper Set 2 Question Paper with Solutions PDF
| GRE 2025 Model Paper Set 2 Question Paper with Solutions PDF | Check Solutions |

A computer program can provide information in ways that force students to --- learning instead of being merely ---- of knowledge.
The form and physiology of leaves vary according to the -- in which they develop: for example, leaves display a wide range of adaptations to different degrees of light and moisture.
One theory about intelligence sees ---- as the logical structure underlying thinking and insists that since animals are mute, they must be ---- as well.
Though ---- in her personal life, Edna St. Vincent Millay was nonetheless ---- about her work, usually producing several pages of complicated rhyme in a day.
The children's ---- natures were in sharp contrast to the even-tempered dispositions of their parents.
By ---- scientific rigor with a quantitative approach, researchers in the social sciences may often have ---- their scope to those narrowly circumscribed topics that are well suited to quantitative methods.
As early as the seventeenth century, philosophers called attention to the ---- character of the issue, and their twentieth-century counterparts still approach it with ----.
TRIPOD: CAMERA::
AQUATIC: WATER::
EMOLLIENT: SUPPLENESS::
DRAW: DOODLE::
CONSPICUOUS: SEE::
IMMATURE: DEVELOPED::
PERSPICACITY: ACUTE::
PLAYFUL: BANTER::
QUARANTINE: CONTAGION::
Influenced by the view of some twentieth-century feminists that women's position within the family is one of the central factors determining women's social position, some historians have underestimated the significance of the woman suffrage movement. These historians contend that nineteenth-century suffragism was less radical and, hence, less important than, for example, the moral reform movement or domestic feminism—two nineteenth-century movements in which women struggled for more power and autonomy within the family. True, by emphasizing these struggles, such historians have broadened the conventional view of nineteenth-century feminism, but they do a historical disservice to suffragism. Nineteenth-century feminists and anti-feminist alike perceived the suffragists' demand for enfranchisement as the most radical element in women's protest, in part because suffragists were demanding power that was not based on the institution of the family, women's traditional sphere. When evaluating nineteenth-century feminism as a social force, contemporary historians should consider the perceptions of actual participants in the historical events.
Question 17:
The author asserts that the historians discussed in the passage have
The author of the passage asserts that some twentieth-century feminists have influenced some historians view of the
The author of the passage suggests that which of the following was true of nineteenth-century feminists?
The author implies that which of the following is true of the historians discussed in the passage?
In the passage, the author is primarily concerned with
It can be inferred that the author thinks engineering curricula are
Which of the following statements best illustrates the main point of lines 1-28 of the passage?
Which of the following statements would best serve as an introduction to the passage?
The author calls the predicament faced by the Historic American Engineering Record "paradoxical" (lines 36-37) most probably because
View Solution
Step 1: Understanding the Concept:
This question asks us to explain the meaning of the word "paradoxical" in the context of the passage. A paradox is a situation that seems contradictory but is nevertheless true. We need to identify the contradiction described in lines 36-43.
Step 2: Detailed Explanation:
The situation is that the "Historic American Engineering Record" needed special drawings to document the history of American engineering. One would logically expect that engineering students would be the ideal candidates for this job. However, the passage states that "the only college students with the requisite abilities were not engineering students, but rather students attending architectural schools."
The paradox is the contradiction: the students of a particular field (engineering) were not equipped to document the history of that very same field, while students from another field (architecture) were.
Option (E) captures this contradiction perfectly: "engineering students were not trained to make the type of drawings needed to record the development of their own discipline."
Let's analyze the other options:
(A) The paradox is not about the staff, but about the contrast between students of different disciplines.
(B) This is irrelevant to the specific contradiction the author points out.
(C) The comparison in the text is between engineering students and architectural students, not students vs. practicing engineers.
(D) The passage does not state that the drawings were complicated, only that they required certain "abilities."
Step 3: Final Answer:
The paradoxical situation is that the very people studying engineering were not the ones qualified to visually document it, a task that fell to students of architecture. Option (E) is the most accurate description of this irony.
Quick Tip: To understand a paradox, identify the two conflicting ideas. Here, idea 1 is "It's an engineering project." Idea 2 is "Engineering students can't do it." The paradox lies in the conflict between these two truths.
According to the passage, random failures in automatic control systems are "not merely trivial aberrations" (line 53) because
The author uses the example of the early models of high-speed railroad cars primarily to
IGNITE:
MUTATE:
FRAGMENT:
OSTENSIBLE:
PROLIXITY:
CONCERTED:
FORBEARANCE:
COSSETED:
PROBITY:
ESCHEW:
REDOUBTABLE:
Which of the following is an order in which the six magazines can be arranged, from position 1 through position 6?
If P occupies position 3, which of the following must be true?
If O and T, not necessarily in that order, occupy consecutively numbered positions, then T can be in position
Which of the following can be true?
If V occupies position 4, then T must occupy the position that is numbered exactly one lower than the position occupied by
If S and V, not necessarily in that order, occupy consecutively numbered positions, which of the following must be true?
Patel: Although enrollment in the region's high school has been decreasing for several years, enrollment at the elementary school has grown considerably. Therefore, the regional school board proposes building a new elementary school.
Quintero: Another solution would be to convert some high school classrooms temporarily into classrooms for elementary school students.
Which of the following, if true, most helps to support Quintero's alternative proposal?
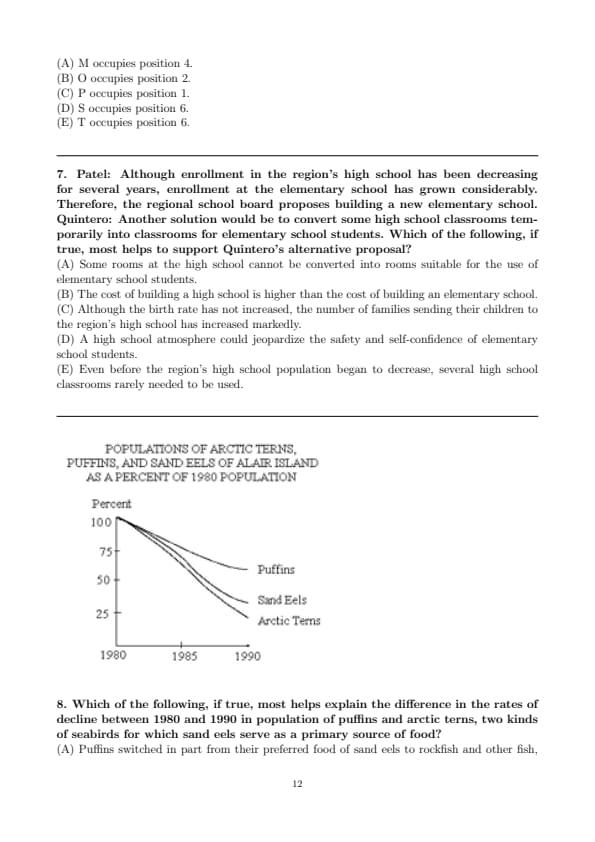
Which of the following, if true, most helps explain the difference in the rates of decline between 1980 and 1990 in population of puffins and arctic terns, two kinds of seabirds for which sand eels serve as a primary source of food?
Peter: More than ever before in Risland, college graduates with science degrees are accepting permanent jobs in other fields. That just goes to show that scientists in Risland are not being paid enough.
Lila: No, it does not. These graduates are not working in science for the simple reason that there are not enough jobs in science in Risland to employ all of these graduates.
Which of the following, if true in Risland, would most undermine the reasoning in Peter's argument?
Which of the following can be the order of lectures and lunch at the conference?
If exactly two lectures are given before lunch, they must be
If exactly three lectures, including Y and Z, are given before lunch, which of the following can be true?
If T is the sixth lecture, which of the following must be true?
If S and Z are both given after lunch, which of the following must be true?
Which of the following lectures CANNOT be given immediately before lunch?
If the lion is in enclosure 1 and the tiger is in enclosure 3, and the lion is to be moved to enclosure 7, the tiger could be in which of the following enclosures when all of the transfers have been completed?
If the tiger is in enclosure 5 and the lion is in enclosure 3, moving the tiger to which of the following enclosures requires exactly two transfers?
If the lion is in enclosure 6 and the tiger is in enclosure 7, and the lion is to be moved to enclosure 7 and the tiger to enclosure 6, then which of the following must be true?
If the lion is in enclosure 3 and the tiger is in enclosure 4, and the lion is to be moved to enclosure 5 and the tiger to enclosure 7, then exactly how many transfers must be made?
If the lion is in enclosure 1 and the tiger is in enclosure 7, and the lion is to be transferred to enclosure 3 and the tiger to enclosure 1, then which of the following CANNOT be true?
If the lion is in enclosure 1 and the tiger is in enclosure 3, and the lion is to be moved to enclosure 6 and the tiger to enclosure 5, then the second transfer could be a transfer of the
If the lion is in enclosure 3 and the tiger is in enclosure 6, and the lion is to be moved to enclosure 6 and the tiger to enclosure 3, then which of the following must be true?
Counselor: Every year a popular newsmagazine publishes a list of United States colleges, ranking them according to an overall numerical score that is a composite of ratings according to several criteria. However, the overall scores generally should not be used by students as the basis for deciding to which colleges to apply.
Which of the following, if true, most helps to justify the counselor's recommendation?
A thorough search of Edgar Allan Poe's correspondence has turned up not a single letter in which he mentions his reputed morphine addiction. On the basis of this evidence it is safe to say that Poe's reputation for having been a morphine addict is undeserved and that reports of his supposed addiction are untrue.
Which of the following is assumed by the argument above?
Adelle: The government's program to reduce the unemployment rate in the province of Carthena by encouraging job creation has failed, since the rate there has not changed appreciably since the program began a year ago.
Fran: But the unemployment rate in Carthena had been rising for three years before the program began, so the program is helping.
Which of the following, if true, most strongly counters Fran's objection to Adelle's argument?
\(x^2 - 1 = y\)
\(x = 3\)
Column A: \(y^2\)
Column B: 80
The gross receipts from the sale of t tickets, at
(17 per ticket, total
)16,660.
Column A: \(t\)
Column B: 1,000
Points T and U are on a circle with center O.
Column A: The length of segment OT
Column B: The length of segment TU
A box contains 20 marbles, all of which are solid colored; 5 of the marbles are green and 10 of the marbles are red.
Column A: The probability that a marble selected at random from the box will be green
Column B: The probability that a marble selected at random from the box will be neither red nor green
Column A: Eleven thousand plus eleven hundred plus eleven
Column B: 11,111
Column A: \(x\)
Column B: 15
The cost \(c\) of an order of \(n\) special envelopes is given by \(c = (
(0.50)n +
)15.00\).
Column A: The cost of an order of 500 special envelopes
Column B:
(260
The average (arithmetic mean) of 7, 9, and \(x\) is greater than 9.
Column A: \(x\)
Column B: 11
\(a > 0\)
Column A: \((4\sqrt{5a})^2\)
Column B: \(40a\)
Column A: \(\frac{0.27}{0.53}\)
Column B: \(\frac{0.027}{0.053}\)
Each of the numbers x, y, w, and z (not necessarily distinct) can have any of the values 2, 3, 9, or 14.
Column A: \(\frac{x}{y}\)
Column B: \(wz\)
\(a = -219\)
Column A: \(a^7 + a^5\)
Column B: \(a^8 + a^{18}\)
Column A: \(x^2 + 2x + 1\)
Column B: \(x^2\)
\(a > 0\)
Column A: d
Column B: e
w, x, y, and z are consecutive positive integers and w < x < y < z.
Column A: The remainder when \((w+x)(x+y)(y+z)\) is divided by 2
Column B: 1
A certain machine drills 30 holes in 8 minutes. At that constant rate, how many holes will 4 such machines drill in \(1 \frac{1}{3}\) hours?
Tina, Ed, and Lauren agree to share the cost of a gift and to make their contributions in proportion to their ages. Ed's age is \(\frac{1}{2}\) of Tina's age, and Lauren's age is \(\frac{1}{3}\) of Ed's age. If Lauren's share of the cost is
(2.50, what is the cost of the gift?
Three solid cubes of lead, each with edges 10 centimeters long, are melted together in a level, rectangular-shaped pan. The base of the pan has inside dimensions of 20 centimeters by 30 centimeters, and the pan is 15 centimeters deep. If the volume of the solid lead is approximately the same as the volume of the melted lead, approximately how many centimeters deep is the melted lead in the pan?
Which of the following CANNOT be the sum of two integers that have a product of 30?
In the rectangular coordinate system above, if point (a, b), shown, and the two points (4a, b) and (2a, 2b), not shown, were connected by straight lines, then the area of the resulting triangular region, in terms of a and b, would be
What was the range in the daily number of shirts sold during March?
The average (arithmetic mean) number of shirts sold per day during February was approximately what percent greater than the average number sold during January?
For which two uses of electricity was the ratio of the amounts of electricity used most nearly 3 to 1?
View Solution
Step 1: Understanding the Concept:
This question asks us to find a pair of electricity uses from the pie chart whose consumption percentages have a ratio of approximately 3 to 1. We will test the ratio for each pair given in the options.
Step 2: Key Formula or Approach:
\[ Ratio = \frac{Percentage of first use}{Percentage of second use} \]
We need this ratio to be close to 3.
Step 3: Detailed Explanation:
From the pie chart, the percentages are:
Air Conditioner: 53%
Water Heater: 20%
Large Appliances: 18%
Lights/Small Appliances: 9%
Now, let's test the ratio for each option:
(A) Water heater to lights/small appliances: \(\frac{20}{9} \approx 2.22\). Not close to 3.
(B) Large appliances to lights/small appliances: \(\frac{18}{9} = 2\). The ratio is exactly 2 to 1. Not 3 to 1.
(C) Air conditioner to water heater: \(\frac{53}{20} = 2.65\). This is somewhat close, but let's check other options.
(D) Air conditioner to lights/small appliances: \(\frac{53}{9} \approx 5.89\). Not close to 3.
(E) Air conditioner to large appliances: \(\frac{53}{18} \approx 2.94\). This value is the closest to 3.
Step 4: Final Answer:
The ratio for air conditioner and large appliances (2.94 to 1) is the most nearly 3 to 1.
Quick Tip: When a question says "most nearly," it implies you should calculate the value for all options and then choose the one that is arithmetically closest to the target number.
The electricity used by the water heater was measured separately and its cost per kilowatt-hour was one-half the cost per kilowatt-hour of the rest of the electricity used. The cost of the electricity used by the water heater was most nearly what fraction of the total cost of all the electricity used?
View Solution
Step 1: Understanding the Concept:
This is a weighted average cost problem. The cost per unit (kWh) is different for the water heater than for the other appliances. We need to calculate the total cost by considering these different rates and then find what fraction of that total cost is attributable to the water heater.
Step 2: Detailed Explanation:
1. Define variables for the cost rates.
Let \(C\) be the cost per kWh for the "rest of the electricity".
Then the cost per kWh for the water heater is \(\frac{C}{2}\).
2. Calculate the amount of electricity used for each category.
Water heater usage = 20% of total usage = 0.20 \(\times\) Total.
Rest of the usage = (53% + 18% + 9%) of total usage = 80% of total usage = 0.80 \(\times\) Total.
(Note: We don't need the 800 kWh value, as it will cancel out. We can work with percentages.)
3. Calculate the cost for each category in terms of C and Total Usage.
Cost of water heater = (Water heater usage) \(\times\) (Cost rate for water heater)
\[ = (0.20 \times Total) \times \left(\frac{C}{2}\right) = 0.10 \times Total \times C \]
Cost of the rest = (Rest of usage) \(\times\) (Cost rate for the rest)
\[ = (0.80 \times Total) \times C = 0.80 \times Total \times C \]
4. Calculate the total cost.
Total Cost = Cost of water heater + Cost of the rest
\[ = (0.10 \times Total \times C) + (0.80 \times Total \times C) = 0.90 \times Total \times C \]
5. Find the required fraction.
Fraction = \(\frac{Cost of water heater}{Total Cost}\)
\[ = \frac{0.10 \times Total \times C}{0.90 \times Total \times C} = \frac{0.10}{0.90} = \frac{1}{9} \]
Step 3: Final Answer:
The cost of the electricity used by the water heater was \(\frac{1}{9}\) of the total cost.
Quick Tip: In problems involving fractions or percentages of a total, you often don't need the actual total value. You can work with the percentages or fractions directly, as the total value will cancel out in the final ratio.
In November the Smythe household used the same total amount of electricity as in July, but the water heater used 33 percent of this total amount. By approximately what percent did the amount of electricity used by the water heater increase from July to November?
View Solution
Step 1: Understanding the Concept:
This is another percent increase problem. We need to calculate the amount of electricity (in kWh) used by the water heater in July and in November, and then find the percent increase from the July amount to the November amount.
Step 2: Key Formula or Approach:
\[ Percent Increase = \left( \frac{November Usage - July Usage}{July Usage} \right) \times 100% \]
Step 3: Detailed Explanation:
1. Calculate July water heater usage.
Total electricity in July = 800 kWh.
Water heater usage in July = 20% of 800 kWh = \(0.20 \times 800 = 160\) kWh.
2. Calculate November water heater usage.
Total electricity in November = 800 kWh (same as July).
Water heater usage in November = 33% of 800 kWh = \(0.33 \times 800 = 264\) kWh.
3. Apply the percent increase formula.
July Usage (Original Value) = 160 kWh.
November Usage (New Value) = 264 kWh.
Increase = 264 - 160 = 104 kWh.
\[ Percent Increase = \left( \frac{104}{160} \right) \times 100% \]
Simplify the fraction: \(\frac{104}{160} = \frac{52}{80} = \frac{26}{40} = \frac{13}{20}\).
\[ Percent Increase = \frac{13}{20} \times 100% = 0.65 \times 100% = 65% \]
Step 4: Final Answer:
The amount of electricity used by the water heater increased by 65% from July to November.
Quick Tip: You can also solve this problem just using the percentages, since the base (total electricity) is the same for both months. The increase is from 20% to 33%. The percent increase is \(((33-20)/20) \times 100 = (13/20) \times 100 = 65%\).
One integer will be randomly selected from the integers 11 to 60, inclusive. What is the probability that the selected integer will be a perfect square or a perfect cube?
The measures of two angles of a parallelogram differ by 52 degrees. The number of degrees in the smaller angle is
The odds in favor of winning a game can be found by computing the ratio of the probability of winning to the probability of not winning. If the probability that Pat will win a game is \(\frac{4}{9}\), what are the odds that Pat will win the game?
If a, b, c, and d are consecutive integers such that a < b < c < d, then in terms of a, the sum a + b + d =
\(2^x + 2^x =\)
Since most if not all learning occurs through ----, relating one observation to another, it would be strange indeed if the study of other cultures did not also illuminate the study of our own.
The new ---- of knowledge has created ---- people: everyone believes that his or her subject cannot and possibly should not be understood by others.
If a species of parasite is to survive, the host organisms must live long enough for the parasite to ----; if the host species becomes ----, so do its parasites.
The author argues for serious treatment of such arts as crochet and needlework, finding in too many art historians a cultural blindness ---- to their ---- textiles as a medium in which women artists predominate.
Those who fear the influence of television deliberately ---- its persuasive power, hoping that they might keep knowledge of its potential to effect social change from being widely disseminated.
Because the high seriousness of their narratives resulted in part from their metaphysics, Southern writers were praised for their ---- bent.
Far from being ----, Pat was always ---- to appear acquiescent.
CHUCKLE: LAUGHING::
PARAGRAPH: ESSAY::
STUPOR: ALERT::
PAEAN: JOY::
RENEGADE: ALLEGIANCE::
DEVOTED: ZEALOUS::
VESTIGE: REMAINDER::
EPHEMERAL: ENDURE::
MISDEMEANOR: CRIME::
It can be inferred from the passage that in species in which vigilant behavior is directed at predators, the tendency of the animals to be more vigilant in smaller groups than in larger ones would most likely be minimized if which of the following were true?
Which of the following best describes the relationship of the second paragraph to the first?
It can be inferred from the passage that the author of the passage would be most likely to agree with which of the following assertions about vigilant behavior?
The passage provides information in support of which of the following assertions?
In the passage, the author is primarily concerned with
Which of the following adjectives best describes "the concept of art imposed by the triumph of Modernism" as the author represents it in lines 25-27?
The author introduces Abstract Expressionist painters (lines 34) in order to
According to the author, the nineteenth-century defenders of photography mentioned in the passage stressed that photography was
View Solution
Step 1: Understanding the Concept:
This is a detail question asking about a specific point made in the first paragraph. We need to find what the "defenders of photography" in the 19th century asserted.
Step 2: Detailed Explanation:
The first paragraph describes the 19th-century debate. It states, "Against the charge that photography was a soulless, mechanical copying of reality, photographers asserted that it was instead a privileged way of seeing...and no less worthy an art than painting." (lines 8-11).
This phrase directly states their main argument: that photography was an art form that was just as valuable and worthy as painting.
Let's evaluate the options based on this text:
(A) This is a use of photography, but not the specific argument mentioned in the passage.
(B) While true, their defense focused on its artistic merit, not its technological aspect.
(C) "Impartially observing" is a claim made by contemporary photographers (line 15), not the 19th-century defenders.
(D) This is a direct paraphrase of "no less worthy an art than painting."
(E) The passage does not state that they claimed photography would replace other arts.
Step 3: Final Answer:
The passage explicitly states that 19th-century defenders argued photography was "no less worthy an art than painting."
Quick Tip: For "according to the author" questions, the answer is almost always directly stated in the text. Scan the relevant section of the passage for keywords from the question to locate the exact sentence that provides the answer.
According to the passage, which of the following best explains the reaction of serious contemporary photographers to the question of whether photography is an art?
According to the passage, certain serious contemporary photographers expressly make which of the following claims about their photographs?
It can be inferred from the passage that the author most probably considers serious contemporary photography to be a
PREOCCUPATION:
CHROMATIC:
PEDESTRIAN:
EQUIVOCATE:
DENUDE:
RANCOR:
OSSIFIED:
CONTROVERT:
PROTRACT:
ABRADE:
APOLOGIST:
In the rectangular coordinate system, the circle with center P is tangent to both the x- and y-axes.
Column A: The x-coordinate of P
Column B: The y-coordinate of P
Column A: \(\frac{3}{5} + \frac{2}{3}\)
Column B: 1
Column A: \(|x^2|\)
Column B: \(|x|^2\)
The square is inscribed in the circle.
Column A: The length of a diagonal of the square
Column B: The length of a diameter of the circle
\(x < y < 20\)
Column A: \(x + y\)
Column B: 35
In college M the average (arithmetic mean) number of students per course is 30 and the ratio of the number of students to the number of faculty is 20 to 1.
Column A: The total number of students in College M
Column B: 600
\(x > 0\)
Column A: \(\frac{590 + x}{800}\)
Column B: \(\frac{600 + x}{790}\)

Column A: x
Column B: 80
Integer n will be randomly selected from the integers 1 to 13, inclusive.
Column A: The probability that n will be even
Column B: The probability that n will be odd
\(p + q = 1\)
\(0 < p < q\)
Column A: \(\frac{1}{pq}\)
Column B: 1
\(2x + 3y = 29\)
\(3x + 4y = 41\)
Column A: \(x + y\)
Column B: 12

\(PQ = OQ = 5\)
Column A: The area of region OPQ
Column B: 10
Column A: \((\sqrt{5} + \sqrt{5})^2\)
Column B: 20
\(\frac{n}{4} + \frac{r}{8} = \frac{s}{8} + \frac{t}{6}\), where n, r, s, and t are positive integers.
Column A: \(2n + r\)
Column B: \(2s + t\)
In the xy-coordinate system, the point (x, y) lies on the circle with equation \(x^2 + y^2 = 1\).
Column A: \(x + y\)
Column B: 1.01
A health food store prepares a breakfast food that consists of oats, raisins, and nuts mixed in the ratio 9:2:1, respectively, by weight. If the nuts in the mixture weigh 9.2 pounds, how many pounds does the total mixture weigh?
\(3 - 2[5 - 7(3+2)] =\)
For every positive integer n greater than 1, n! is defined as the product of the first n positive integers. For example, \(4! = (1)(2)(3)(4) = 24\). What is the value of \(\frac{12!}{10!}\)?
A market survey showed that 76 percent of the visitors at a certain resort came from Pacific or southwestern states. Of these, \(\frac{2}{3}\) were from California, and 87 percent of the Californians were from southern California. Approximately what percent of the visitors at the resort were from southern California?
If \(\frac{5^4 - 1}{n}\) is an integer an n is an integer, then n could be each of the following EXCEPT
What is the ratio of the amount budgeted annually for food to the amount budgeted annually for savings?
View Solution
Step 1: Understanding the Concept:
The question asks for the ratio of the amounts budgeted for two different categories. Since the amounts are percentages of the same total budget, the ratio of the amounts will be the same as the ratio of their percentages.
Step 2: Detailed Explanation:
1. Find the percentages from the table.
Percent budgeted for Food = 20%.
Percent budgeted for Savings = 15%.
2. Form the ratio of the percentages.
Ratio of Food to Savings = 20 : 15.
3. Simplify the ratio.
To simplify the ratio, we find the greatest common divisor (GCD) of 20 and 15. The GCD is 5.
Divide both parts of the ratio by 5:
\[ \frac{20}{5} : \frac{15}{5} \]
\[ 4 : 3 \]
The simplified ratio is 4 to 3.
Step 3: Final Answer:
The ratio of the amount budgeted for food to the amount budgeted for savings is 4 to 3.
Quick Tip: When finding the ratio of two parts of the same whole, you don't need to calculate the actual values. The ratio of the percentages (or fractions) is sufficient and saves calculation time.
If a pie graph (such as the one above) were drawn to scale to represent the budget distribution into the five categories, what would be the measure of the central angle of the sector representing savings?
View Solution
Step 1: Understanding the Concept:
A pie chart represents a whole (100%) as a full circle (360°). To find the central angle for a specific category, we need to calculate that category's percentage of the total 360 degrees.
Step 2: Key Formula or Approach:
\[ Central Angle = (Percentage for Category) \times 360^\circ \]
Step 3: Detailed Explanation:
1. Find the percentage for Savings from the table.
The percentage for Savings is 15%.
2. Calculate the central angle.
We need to find 15% of 360°.
First, convert the percentage to a decimal: 15% = 0.15.
Now, multiply by 360°:
\[ Angle = 0.15 \times 360^\circ \]
We can break this down for easier mental calculation:
10% of 360° is 36°.
5% of 360° is half of 10%, which is 18°.
So, 15% of 360° = 36° + 18° = 54°.
Alternatively, using multiplication:
\[ 0.15 \times 360 = 54 \]
Step 4: Final Answer:
The measure of the central angle for the savings sector would be 54°.
Quick Tip: For pie chart calculations, it's useful to remember that 1% corresponds to 3.6°. You can simply multiply the percentage by 3.6 to find the angle. Here, \(15 \times 3.6 = 54\).
The funds distributed in 1992 for youth development were approximately
)380,000
View Solution
Step 1: Understanding the Concept:
This question requires us to calculate a specific amount of money from a pie chart by taking the given percentage of the total funds for that year.
Step 2: Detailed Explanation:
1. Identify the relevant data for 1992.
From the 1992 pie chart, the percentage for Youth Development is 15%.
The total funds distributed in 1992 were
(2.54 million, which is
)2,540,000.
2. Calculate the amount.
We need to find 15% of
(2,540,000.
Amount = \(0.15 \times 2,540,000\)
Let's perform the multiplication:
\[ 0.15 \times 254 = 38.1 \]
So, \(0.15 \times 2,540,000 = 381,000\).
Alternatively, using mental math:
10% of 2,540,000 is 254,000.
5% of 2,540,000 is half of 10%, which is 127,000.
15% = 10% + 5% = 254,000 + 127,000 =
)381,000.
3. Compare with the options.
The calculated amount,
(381,000, is approximately
)380,000.
Step 3: Final Answer:
The funds distributed for youth development in 1992 were approximately
(380,000.
Quick Tip: When the question asks for an "approximate" value, you can often round the numbers to make the calculation easier. For instance, calculate 15% of
)2.5 million: \(0.15 \times 2.5 = 0.375\) million, which is
(375,000. This value is very close to option (C).
The increase in the amount of money distributed for family support from 1992 to 1993 was closest to which of the following?
If all of the emergency assistance funds in 1993 were distributed among 40 groups, which of the following is closest to the average (arithmetic mean) amount distributed per group?
The curve above consists of three semicircles: AB, BC, and CD. The diameter of AB is 2, the diameter of BC is twice the diameter of AB, and the diameter of CD is twice the diameter of BC. What is the total length of the curve?

What is the cost, in cents, of using a certain fax machine to send n pages of a report if the total cost for sending the first k pages is r cents and the cost for sending each additional page is s cents? (Assume that n > k)
A rectangular solid has a square base and altitude of 7. If the volume of the solid is 252, then the perimeter of the square base is
In a series of races, 10 toy cars are raced, 2 cars at a time. If each car must race each of the other cars exactly twice, how many races must be held?
\((2^{10} - 2^9)(2^8 - 2^7) =\)
Soft Drink Manufacturer: Our new children's soft drink, RipeCal, is fortified with calcium. Since calcium is essential for developing healthy bones, drinking RipeCal regularly will help make children healthy.
Consumer Advocate: But RipeCal also contains large amounts of sugar, and regularly consuming large amounts of sugar is unhealthful, especially for children.
In responding to the soft drink manufacturer, the consumer advocate does which of the following?
Over a period of several months, researchers attached small lights to the backs of wetas—flightless insects native to New Zealand—enabling researchers for the first time to make comprehensive observations of the insects' nighttime activities. Thus, since wetas forage only at night, the researchers' observations will significantly improve knowledge of the normal foraging habits of wetas.
Which of the following is an assumption on which the argument depends?
Which of the following can be the week's telephone duty schedule?

If Hilda has telephone duty for exactly two days of the week, which of the following must be true?
If Hilda and Irene have telephone duty together on Monday and on Wednesday, which of the following must be true?
If George and Hilda have telephone duty together on Monday and George and Irene have telephone duty together on Friday, any of the following can be true EXCEPT:
If there is one pair of employees who have telephone duty together for three of the five days, which of the following must be true?
Any of the following can be true EXCEPT:
Question 9 is based on the following graph.
Which of the following, if true, contributes most to an explanation of the change in ice cream sales?
People whose bodies cannot produce the substance cytochrome P450 are three times as likely to develop Parkinson's disease, a disease that affects the brain, as are people whose bodies do produce this substance. Since cytochrome P450 protects the brain from toxic chemicals, toxic chemicals probably play a role in the development of Parkinson's disease.
Which of the following, if true, most strongly supports the argument?
The early universe contained only the lightest elements, hydrogen and helium. Heavier elements, such as carbon, form only in nuclear reactions in stars and are dispersed when the stars explode. A recently discovered gas cloud contained carbon several billion years ago, when the universe was no more than two billion years old.
If the statements above are true, which of the following must, on the basis of them, also be true?
Sleep deprivation is a known cause of workplace error, and many physicians frequently go without sleep for periods of 24 hours or more. However, few of these physicians have, in the course of a routine examination by a peer, been diagnosed with sleep deprivation. So there is little cause for concern that habitual sleep deprivation will cause widespread physician error.
The answer to which of the following questions would be most helpful in evaluating the argument?
Which of the following could be the order, from first through seventh, in which the performers sing?
If there are exactly four performers who are to sing after Nelson sings but before Strapp sings, Harris must be assigned to time slot
If Williams is to sing immediately after Harris sings and immediately before Trevino sings, which of the following performers could be assigned to time slot 6?
If Jones is to sing immediately before Harris sings, which of the following must be assigned to time slot 7?
If McIntyre is to sing immediately before Strapp sings, Trevino could be assigned to which of the following time slots?
If McIntyre is assigned to time slot 4, which of the following must be true?
Which of the following can be the trees planted along the side of the street that has four trees, in order of their positions beginning with position 1?
There seems to be a slight confusion in the prompt here, as the pattern shows a total of seven trees. The question "the side of the street that has four trees" might refer to the row 1-3-5-7. I will assume this is the case.
If red oaks are used, then which of the following must be true?
Among the trees left over after the planting is done there must be
View Solution
Step 1: Understanding the Concept:
This question asks what must be true about the set of unplanted trees, regardless of which valid planting arrangement is chosen. We need to consider all possible valid combinations of two tree types.
Step 2: Detailed Explanation:
There are three possible pairings of two tree types:
1. Red Oaks and Sycamores: We have 3 red oaks and 4 sycamores available, for a total of 7 trees. To plant 7 trees, we must use all of them.
- Trees left over: 0 red oaks, 0 sycamores, 4 maples.
2. Red Oaks and Maples: As determined in the previous question, it's impossible to plant 4 maples and 3 red oaks while satisfying the maple rule. So this combination is not possible.
3. Sycamores and Maples: We have 4 sycamores and 4 maples available, for a total of 8 trees. We only need to plant 7. This means we must plant some combination of sycamores and maples, and one tree will be left over.
- Can we plant 4 maples and 3 sycamores? No, it's impossible to place 4 maples.
- Can we plant 3 maples and 4 sycamores? Yes, this is possible. Let's try to place 3 maples. e.g., at positions 1, 4, 7. This is a valid placement. The other 4 spots would be sycamores.
- Trees left over: 1 maple, 0 sycamores, 3 red oaks.
- Can we plant 2 maples and 5 sycamores? We only have 4 sycamores available, so this is impossible.
- Can we plant 1 maple and 6 sycamores? Impossible, not enough sycamores.
- Can we plant 0 maples and 7 sycamores? Impossible, not enough sycamores.
Summary of Leftover Trees in all Possible Scenarios:
- Scenario 1 (Oaks + Sycamores): 4 maples are left over.
- Scenario 2 (Maples + Sycamores): 1 maple and 3 red oaks are left over.
In every single possible planting scenario, there are always maples left over. In one case there are 4, in the other there is 1. Therefore, there must be at least one maple left over.
Evaluate the options:
(A) at least one maple: True in all scenarios.
(B) at least one red oak: False in Scenario 1.
(C) at least one sycamore: False in both scenarios.
(D) at most one maple: False in Scenario 1.
(E) at most one red oak: False in Scenario 2.
Step 3: Final Answer:
In all valid planting combinations, there is always at least one maple tree left over.
Quick Tip: For "must be true" questions that don't provide a new condition, you must consider all possible valid scenarios allowed by the original rules. The correct answer is the only statement that holds true in every single one of those scenarios.
If maples are planted, the side of the street that has four trees must have
A list of the fifteen operas most frequently performed in recent times includes no works by the nineteenth-century German composer Richard Wagner. Although music producers tend to produce what audiences want, relative infrequency of performance probably does not indicate lack of popularity in Wagner's case, since Wagner's operas are notoriously expensive to perform on stage.
Which of the following, if true, most strongly supports the conclusion of the argument above?
The bodies of dwarf individuals of mammalian species are generally smaller in relation to those of nondwarf individuals than are the teeth of the dwarf individuals in relation to those of the nondwarf individuals. Fragmentary skeletal remains of an adult dwarf woolly mammoth were recently found. The teeth are three-fourths the size of the teeth of an average adult nondwarf woolly mammoth.
The statements above, if true, most strongly support which of the following?
Excluding purchases by businesses, the average amount spent on a factory-new car has risen 30 percent in the last five years. In the average household budget, the proportion spent on car purchases has remained unchanged in that period. Therefore the average household budget must have increased by 30 percent over the last five years.
Which of the following is an assumption on which the argument relies?
























































Comments