GRE 2024 Quantitative Reasoning Practice Test Set 12 Question Paper with Solutions PDF

A bakery stocks 3 cookies for every 2 cupcakes and 6 pastries for every 5 cookies. What is the ratio of cupcakes to pastries?

• (A) 5:9
• (B) 2:5
• (C) 1:3
• (D) 4:5
• (E) 4:9

Jessica bought a few pairs of socks for 50. If there had been a 20% discount, she could have bought 5 more pairs of socks for the same total price. How many pairs of socks did she buy?

• (A) 5
• (B) 2
• (C) 10
• (D) 15
• (E) 20

If \( |x-3| = 3 \), compare the two quantities:

Quantity A: \( x \)

Quantity B: 2

• (A) Quantity A is greater.
• (B) Quantity B is greater.
• (C) The two quantities are equal.
• (D) The relationship cannot be determined.

If operation \( x ¤ y = 4x - y^2 \), and \( x,y \) are positive integers, which of the following cannot produce an odd value?

• (A) \( x ¤ y^2 \)
• (B) \( x  ¤ 2y \)
• (C) \( y ¤ x \)
• (D) \( x ¤ y \)
• (E) \( x  ¤ (y+1) \)

Let \( p = 4 \times 6 \times 11 \times n \), where \( n \) is a positive integer. Compare the following:

Quantity A: Remainder when \( p \) is divided by 5

Quantity B: Remainder when \( p \) is divided by 33

• (A) Quantity A is greater.
• (B) Quantity B is greater.
• (C) The two quantities are equal.
• (D) The relationship cannot be determined.

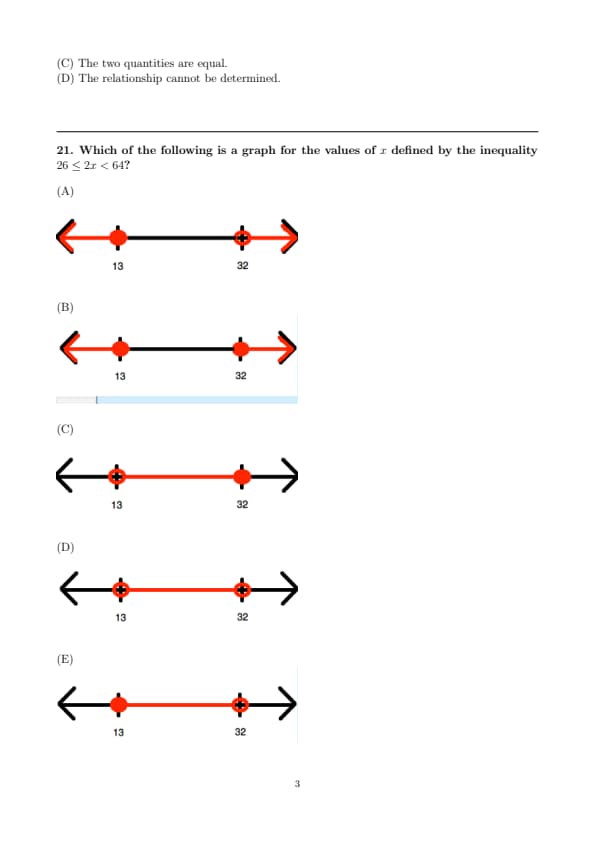
Which of the following is a graph for the values of \( x \) defined by the inequality \( 26 \leq 2x < 64 \)?

• (A)
• (B)
• (C)
• (D)
• (E)

Sam is a caterer who needs to bake 300 pies. Each pie requires 4 apples. Apples are sold in bushels, with 126 apples in each bushel. How many bushels must Sam order to ensure he has enough apples?

• (A) 11
• (B) 9
• (C) 9.5
• (D) 10
• (E) 12

What is the sum of all of the four-digit integers that can be created with the digits 1, 2, 3, and 4?

• (A) 5994
• (B) 37,891
• (C) 711,040
• (D) 482,912
• (E) 48,758

Which of the following defines any term in a linear sequence having 30 for its first term and 126 for its ninth term?

• (A) \( s_n = s_{n-1} + \frac{16}{3} \)
• (B) \( s_n = s_{n-1} + 8 \)
• (C) \( s_n = s_{n-1} + 12 \)
• (D) \( s_n = 2s_{n-1} + 4 \)
• (E) \( s_n = s_{n-1} + \frac{32}{3} \)

Robert has 22.8% of his cereal left. Choose the decimal that best represents how much of his cereal he has eaten.

• (A) 0.325
• (B) 0.228
• (C) 0.22
• (D) 0.77
• (E) 0.772

A group of five students averaged 85 points on an exam taken out of 100 total points. If the addition of two additional students raises the group average to 88 points, what is the minimum score that one of those two students can receive? Assume that 100 is the highest score for the exam.

• (A) 93
• (B) 100
• (C) None of the other answers
• (D) 95.5
• (E) 91

In a bag, there are 10 red, 15 green, and 12 blue marbles. If you draw two marbles (without replacing), what is the approximate probability of drawing two different colors?

• (A) 33.33%
• (B) 0.06%
• (C) None of the other answers
• (D) 67.57%
• (E) 25%

How many different license passwords can one make if said password must contain exactly 6 characters, two of which are distinct numbers, another of which must be an uppercase letter, and the remaining 3 can be any digit or letter (upper- or lower-case) such that there are no repetitions of any characters in the password?

• (A) 231
• (B) 456426360
• (C) 219
• (D) 619652800
• (E) 365580800

Sample Set A has 25 data points with an arithmetic mean of 50. Sample Set B has 75 data points with an arithmetic mean of 100.
Quantity A: The arithmetic mean of the 100 data points encompassing A and B.
Quantity B: 80

• (A) Quantity A is greater.
• (B) Quantity B is greater.
• (C) The two quantities are equal.
• (D) The relationship cannot be determined from the information given.

Which statement is correct assuming that \(a\) represents the range, \(b\) represents the mean, \(c\) represents the median, and \(d\) represents the mode for the number set: 8, 3, 11, 12, 3, 4, 6, 15, 1 ?

• (A) \(a < c < d < b\)
• (B) \(d < c < b < a\)
• (C) \(b = c < a < d\)
• (D) \(c < b < a < d\)
• (E) \(b < c < a = d\)