MHT CET 2024 PCM Question Paper(Available) : Download PCM Question Paper with Answers Key PDF

Question 1:

Force between two point charges q₁ and q₂ placed in vacuum at a distance r cm apart is F. Force between them when placed in a medium having dielectric K = 5 at r/5 cm apart will be:

(1) F / 25
(2) 5F
(3) F / 5
(4) 25F

Question 2:

A thin circular disc of mass M and radius R is rotating in a horizontal plane about an axis passing through its center and perpendicular to its plane with angular velocity ω. If another disc of the same dimensions but of mass M / 2 is placed gently on the first disc coaxially, then the new angular velocity of the system is:

(1) (4/5)ω
(2) (5/4)ω
(3) (2/3)ω
(4) (3/2)ω

Question 3:

Correct Bernoulli’s equation is (symbols have their usual meaning):

(1) P + mgh + (1/2)mv² = constant
(2) P + ρgh + (1/2)ρv² = constant
(3) P + ρgh + ρv² = constant
(4) P + (1/2)ρgh + (1/2)ρv² = constant

Question 4:

Two projectiles are projected at 30° and 60° with the horizontal with the same speed. The ratio of the maximum height attained by the two projectiles respectively is:

(1) 2 : √3
(2) √3 : 1
(3) 1 : 3
(4) 1 : √3

Question 5:

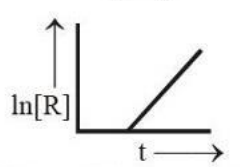
A real gas within a closed chamber at 27°C undergoes the cyclic process as shown in the figure. The gas obeys the equation PV³ = RT for the path A to B. The net work done in the complete cycle is (assuming R = 8 J/mol·K):

(1) 225 J
(2) 205 J
(3) 20 J
(4) -20 J

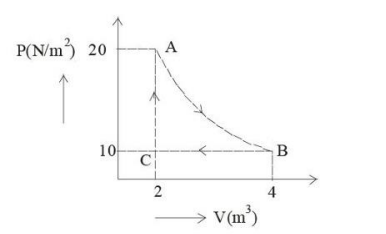
Question 7:

A monkey of mass 50 kg climbs on a rope that can withstand a tension of 350 N. If the monkey initially climbs down with an acceleration of 4 m/s² and then climbs up with an acceleration of 5 m/s², choose the correct option (g = 10 m/s²):

Question 8:

Figure shows a part of an electric circuit. The potentials at points a, b, and c are 30 V, 12 V, and 2 V, respectively. The current through the 20 Ω resistor will be:

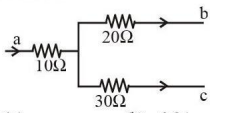
Question 9:

A current of 200 μA deflects the coil of a moving coil galvanometer through 60°. The current to cause deflection through π/10 radians is:

(1) 30 μA
(2) 120 μA
(3) 60 μA
(4) 180 μA

Question 10:

The value of acceleration due to gravity at Earth's surface is 9.8 m/s². The altitude above its surface at which the acceleration due to gravity decreases to 4.9 m/s² is close to: (Radius of Earth R = 6.4 × 10⁶ m)

(1) 2.6 × 10⁶ m
(2) 6.4 × 10⁶ m
(3) 9.0 × 10⁶ m
(4) 1.6 × 10⁶ m

Question 11:

Relative permittivity and permeability of a material are εᵣ and μᵣ, respectively. Which of the following values of these quantities are allowed for a diamagnetic material?

(1) εᵣ = 0.5, μᵣ = 1.5
(2) εᵣ = 1.5, μᵣ = 0.5
(3) εᵣ = 0.5, μᵣ = 0.5
(4) εᵣ = 1.5, μᵣ = 1.5

Question 12:

The magnetic flux through a coil perpendicular to its plane is varying according to the relation φ = 5t³ + 4t² + 2t - 5. If the resistance of the coil is 5 Ω, then the induced current through the coil at t = 2 seconds will be:

(1) 15.6 A
(2) 16.6 A
(3) 17.6 A
(4) 18.6 A

Question 13:

A solid metallic cube having a total surface area of 24 m² is uniformly heated. If its temperature is increased by 10°C, calculate the increase in the volume of the cube. (Given: α = 5.0 × 10⁻⁴ °C⁻¹)

(1) 2.4 × 10⁶ cm³
(2) 1.2 × 10⁵ cm³
(3) 6.0 × 10⁴ cm³
(4) 4.8 × 10⁵ cm³

Question 14:

Two coils are placed close to each other. The mutual inductance of the pair of coils depends upon:

(1) The rates at which currents are changing in the two coils
(2) The relative position and orientation of the two coils
(3) The materials of the wires of the coils
(4) The currents in the two coils

Question 15:

A proton, an electron, and an alpha particle have the same energies. Their de-Broglie wavelengths will be compared as:

(1) λ_e > λ_α > λ_p
(2) λ_α < λ_p < λ_e
(3) λ_p < λ_e < λ_α
(4) λ_p > λ_e > λ_α

Question 16:

An ice cube has a bubble inside. When viewed from one side, the apparent distance of the bubble is 12 cm. When viewed from the opposite side, the apparent distance of the bubble is 4 cm. If the side of the ice cube is 24 cm, the refractive index of the ice cube is:

(1) 4/3
(2) 3/2
(3) 2/3
(4) 6/5

Question 17:

The longest wavelength associated with the Paschen series is:

(Given R_H = 1.097 × 10⁷ SI unit)

(1) 1.094 × 10^-6 m
(2) 2.973 × 10^-6 m
(3) 3.646 × 10^-6 m
(4) 1.876 × 10^-6 m

Question 18:

The ratio of the mass densities of nuclei of ⁴⁰Ca and ¹⁶O is close to:

(1) 1
(2) 0.1
(3) 5
(4) 2

Question 19:

Point charge of 10 μC is placed at the origin. At what location on the X-axis should a point charge of 40 μC be placed so that the net electric field is zero at x = 2 cm on the X-axis?

(1) 6 cm
(2) 4 cm
(3) 8 cm
(4) -4 cm

Question 20:

A magnetic needle is kept in a non-uniform magnetic field. It experiences:

(1) neither a force nor a torque
(2) a torque but not a force
(3) a force but not a torque
(4) a force and a torque

Question 21:

A current-carrying rectangular loop PQRS is made of uniform wire. The length PR = QS = 5 cm and PQ = RS = 100 cm. If the ammeter current reading changes from I to 2I, the ratio of magnetic forces per unit length on the wire PQ due to wire RS in the two cases respectively F^I_PQ : F^2I_PQ is:

(1) 1:2
(2) 1:4
(3) 1:5
(4) 1:3

Question 22:

At which temperature will the r.m.s. velocity of a hydrogen molecule be equal to that of an oxygen molecule at 47°C?

(1) 80 K
(2) -73 K
(3) 4 K
(4) 20 K

Question 23:

A light-emitting diode (LED) is fabricated using GaAs semiconductor material whose band gap is 1.42 eV. The wavelength of light emitted from the LED is:

(1) 650 nm
(2) 1243 nm
(3) 875 nm
(4) 1400 nm

Question 24:

A steel wire with mass per unit length 7.0 × 10⁻³ kg/m is under a tension of 70 N. The speed of transverse waves in the wire will be:

Question 25:

Two vessels A and B are of the same size and are at the same temperature. Vessel A contains 1 g of hydrogen and vessel B contains 1 g of oxygen. P_A and P_B are the pressures of the gases in A and B respectively. Then P_A / P_B is:

(1) 8
(2) 16
(3) 32
(4) 4

Question 26:

A wire of length 1 m moving with velocity 8 m/s at right angles to a magnetic field of 2 T. The magnitude of induced emf between the ends of the wire will be:

(1) 20 V
(2) 8 V
(3) 12 V
(4) 16 V

Question 27:

Two identical particles each of mass m go around a circle of radius a under the action of their mutual gravitational attraction. The angular speed of each particle will be:

(1) √(Gm / 2a³)
(2) √(Gm / 8a³)
(3) √(Gm / 4a³)
(4) √(Gm / a³)

Question 28:

In an unbiased p-n junction, electrons diffuse from n-region to p-region because:

Question 29:

A particle is executing Simple Harmonic Motion (SHM). The ratio of potential energy and kinetic energy of the particle when its displacement is half of its amplitude will be:

(1) 1:1
(2) 2:1
(3) 1:4
(4) 1:3

Question 30:

Eight equal drops of water are falling through air with a steady speed of 10 cm/s. If the drops coalesce, the new velocity is:

(1) 10 cm/s
(2) 40 cm/s
(3) 16 cm/s
(4) 5 cm/s

Question 31:

In a coil, the current changes from -2 A to +2 A in 0.2 s and induces an emf of 0.1 V. The self-inductance of the coil is:

(1) 5 mH
(2) 1 mH
(3) 2.5 mH
(4) 4 mH

Question 32:

For a uniform rectangular sheet shown in the figure, the ratio of moments of inertia about the axes perpendicular to the sheet and passing through O (the center of mass) and O' (corner point) is:

(1) 2/3
(2) 1/4
(3) 1/8
(4) 1/2

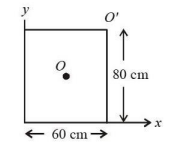
Question 33:

If n is the number density and d is the diameter of the molecule, then the average distance covered by a molecule between two successive collisions (i.e., mean free path) is represented by:

(1) 1 / √(2πnd²)
(2) √(2nπd²)
(3) 1 / (√2 nπd²)
(4) 1 / √(2n²π²d²)

Question 34:

A mixture of one mole of monoatomic gas and one mole of diatomic gas (rigid) are kept at room temperature (27°C). The ratio of specific heat of gases at constant volume respectively is:

(1) 7/5
(2) 3/2
(3) 3/5
(4) 5/3

Question 35:

In an a.c. circuit, voltage and current are given by:

V = 100 sin(100t) V and I = 100 sin(100t + π/3) mA. The average power dissipated in one cycle is:

Question 36:

The difference between threshold wavelengths for two metal surfaces A and B having work functions:

ϕ_A = 9 eV and ϕ_B = 4.5 eV is:

(Given: h c = 1242 eV·nm)

Question 37:

The logic performed by the circuit shown in the figure is equivalent to:

Question 38:

A particle performs simple harmonic motion with amplitude A. Its speed is tripled at the instant that it is at a distance (2A/3) from the equilibrium position. The new amplitude of the motion is:

Question 39:

The mass of proton, neutron, and helium nucleus are respectively 1.0073 u, 1.0087 u, 4.0015 u. The binding energy of the helium nucleus is:

Question 40:

A series LCR circuit is subjected to an AC signal of 200 V, 50 Hz. If the voltage across the inductor (L = 10 mH) is 31.4 V, then the current in this circuit is:

Question 41:

When two soap bubbles of radii a and b (b > a) coalesce, the radius of curvature of the common surface is:

Question 42:

A liquid is allowed to flow into a tube of truncated cone shape. Identify the correct statement:

Question 43:

The velocity of sound in a gas in which two wavelengths 4.08 m and 4.16 m produce 40 beats in 12 seconds will be:

Question 44:

σ is the uniform surface charge density of a thin spherical shell of radius R. The electric field at any point on the surface of the spherical shell is:

Question 45:

An electric field is given by E = (6i + 5j + 3k) N/C. The electric flux through a surface area of 30i m² lying in the YZ-plane (in SI units) is:

Question 46:

A big drop is formed by coalescing 1000 small droplets of water. The surface energy will become:

Question 47:

If M is the mass of water that rises in a capillary tube of radius r, then the mass of water which will rise in a capillary tube of radius 2r is:

Question 48:

A closed organ pipe (closed at one end) is excited to support the third overtone. It is found that air in the pipe has:

Question 49:

The electrostatic potential due to an electric dipole at a distance r varies as:

Question 50:

A battery of 6 V is connected to the circuit as shown below. The current I drawn from the battery is:

Chemistry

Question 51:

If the length of the body diagonal of a FCC unit cell is x Å, the distance between two octahedral voids in the cell in Å is:

Question 52:

Ortho-sulphobenzimide is used as:

Question 53:

The volume of a gas at NTP is 1.12 × 10⁻⁷ cm³. The number of molecules in it is:

Question 54:

The wavelength of radiation emitted, when a hydrogen atom electron falls from infinity to stationary state 1, would be: (Rydberg constant R = 1.097 × 10⁷ m⁻¹)

Question 55:

In NO₃⁻ ion, the number of bond pairs and lone pairs of electrons on the nitrogen atom are:

Question 56:

In which of the compounds does 'manganese' exhibit the highest oxidation number?

Question 57:

Alkali metals are powerful reducing agents because:

Question 58:

A balloon filled with an air sample occupies 3 L volume at 35°C. On lowering the temperature to T, the volume decreases to 2.5 L. The temperature T is:

Assume pressure constant.

Question 59:

Which one of the following is used as an eye lotion?

Question 60:

Identify ortho and para directing groups from the following:

-CHO, -NHCOCH₃, -OCH₃, -SO₃H.

Question 61:

Which one of the carbanions is the least stable?

Question 62:

In O₂⁻, O₂, and O₂²⁻ molecular species, the total number of antibonding electrons respectively are:

Question 63:

People living at high altitudes often reported a problem of feeling weak and inability to think clearly. The reason for this is:

Question 64:

Specific conductance of 0.1 M HNO₃ is 6.3 × 10⁻² ohm⁻¹ cm⁻¹. The molar conductance of the solution is:

Question 65:

The rate constant for a first-order reaction whose half-life is 480 seconds is:

Question 66:

If the activation energy for the forward reaction is 150 kJ/mol and that of the reverse reaction is 260 kJ/mol, what is the enthalpy change for the reaction?

Question 67:

For As₂S₃ sol, the most effective coagulating agent is:

Question 68:

Element not showing variable oxidation state is:

Question 64:

Specific conductance of 0.1 M HNO₃ is 6.3 × 10⁻² ohm⁻¹ cm⁻¹. The molar conductance of the solution is:

Question 65:

The rate constant for a first-order reaction whose half-life is 480 seconds is:

Question 66:

If the activation energy for the forward reaction is 150 kJ/mol and that of the reverse reaction is 260 kJ/mol, what is the enthalpy change for the reaction?

Question 67:

For As₂S₃ sol, the most effective coagulating agent is:

Question 68:

Element not showing variable oxidation state is:

Question 69:

Which of the following arrangements does not represent the correct order of the property stated against it?

Question 70:

The IUPAC name for the complex [Co(ONO)(NH₃)₅]Cl₂ is:

Question 71:

Which of the following compounds will give a racemic mixture on nucleophilic substitution by OH⁻ ion?

Question 72:

Which one of the following is not correct for an ideal solution?

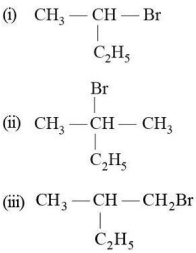
Question 73:

For the relation Δ_rG = -nF E_cell, E_cell = E^°_cell, in which of the following conditions?

Question 74:

Which one of the lanthanoids given below is the most stable in divalent form?

Question 75:

The value of the 'spin only' magnetic moment for one of the following configurations is 2.84 BM. The correct one is:

Question 76:

Chlorobenzene reacts with Mg in dry ether to give a compound (A) which further reacts with ethanol to yield:

Question 78:

Which of the following represents the correct order of acidity in the given compounds?

Question 79:

Ethyl alcohol can be prepared from Grignard reagent by the reaction of:

Question 80:

Which of the following is most acidic?

Question 81:

Nitration of the compound is carried out. This compound gives a red-orange precipitate with 2,4-DNP, undergoes Cannizzaro reaction but not aldol, then the possible product due to nitration is:

Question 82:

Which of the following reactions will not give a primary amine?

Question 83:

Which of the following compounds is most reactive towards nucleophilic addition reactions?

Question 84:

Molecules whose mirror image is non-superimposable over them are known as chiral. Which of the following molecules is chiral in nature?

Question 85:

The most reactive amine towards dilute hydrochloric acid is:

Question 86:

One of essential alpha-amino acids is:

Question 87:

Which of the following statements is true about a peptide bond (RCONHR')?

Question 88:

Which of the following is an example of chain-growth polymer?

Question 89:

Which of the following polymers is formed due to the co-polymerization of 1,3-butadiene and phenylethene?

Question 90:

For 1 molal aqueous solution of the following compounds, which one will show the highest freezing point?

Question 91:

Which of the following expressions correctly represents molar conductivity?

Question 92:

The plot that represents the zero-order reaction is:

Question 93:

In acidic medium, which of the following does not change its colour?

Question 94:

Which of the following is the life-saving mixture for an asthma patient?

Question 95:

The compounds [PtCl₂(NH₃)₄]Br₂ and [PtBr₂(NH₃)₄]Cl₂ constitute a pair of:

Question 96:

Tincture of iodine is the common name for:

Question 97:

The monomers of Buna-S rubber are:

Question 98:

The number of nearest neighbours in a BCC unit cell is:

Question 99:

The cell potential for the following cell is approximately:

M(s) | M³⁺(aq, 0.1M) || N²⁺(aq, 0.1M) | N(s)

E⁰_M³⁺/M = 0.6 V, E⁰_N²⁺/N = 0.1 V.

Question 100:

In Williamson synthesis, if tertiary alkyl halide is used, then:

Question 101:

If A = [[1, 0], [1/2, 1]], then A⁵⁰ is:

Question 102:

The range of the function f(x) = sin^-1(x - √x) is equal to:

Question 103:

If a = i + 2j - 3k and b = 2i - 3j - 5k, then:

Question 104:

If √(y/x) + 4√(x/y) = 4, then dy/dx:

Question 105:

The function f(x) = tan^-1(sin x + cos x) is an increasing function in:

Question 106:

If f(x) = |x| - |1|, then points where f(x) is not differentiable, is/are:

Question 107:

The integral ∫(π/11 to 9π/22) dx / (1 + √(tan x)) is equal to:

Question 108:

Let a = i + 2j + k, b = i - j + k, and c = i + j - k. A vector in the plane of a and b whose projection on c is 1/√3, is:

Question 109:

Let p: "I am brave," q: "I will climb Mount Everest." The symbolic form of the statement "I am neither brave nor I will climb Mount Everest" is:

Question 110:

If x ≠ 0, then

(sin(π + x) * cos(π/2 + x) * tan(3π/2 - x) * cot(2π - x)) / (sin(2π - x) * cos(2π + x) * csc(-x) * sin(3π/2 + x)) =

Question 111:

Evaluate i² + i³ + ... + i⁴⁰⁰⁰:

Question 112:

The number of all four-digit numbers which begin with 4 and end with either 0 or 5 is:

Question 113:

The number of ways of distributing 500 dissimilar boxes equally among 50 persons is:

Question 114:

Given, the function f(x) = (aˣ + a⁻ˣ) / 2 (a > 2), then f(x + y) + f(x - y) is equal to:

Question 115:

The point on the line 4x - y - 2 = 0 which is equidistant from the points (-5, 6) and (3, 2) is:

Question 116:

The equation of a circle with center (5, 4) and touching the Y-axis is:

Question 117:

Evaluate the following limit:

Question 119:

If two numbers ( p ) and ( q ) are chosen randomly from the set {1, 2, 3, 4} with replacement, what is the probability that ( p² ≥ 4q )?

Question 120:

Question 121:

Let vectors a, b, and c be non-zero such that (a × b) ⋅ c = (1/3) × |b| × |c| × |a|. If θ is the acute angle between b and c, find sin θ.

Question 122:

Find the distance of the foot of the perpendicular from (1, 2, 4) to the plane 3x + 4y + 12z + 23 = 0, given that it lies on the line (x + 2) / 4 = (y - 1) / 2 = (z + 1) / 3.

Question 123:

If one of the lines given by 6x² - xy + 4cy² = 0 is 3x + 4y = 0, find the value of c.

Question 124:

If x = a(cos θ + θ sin θ) and y = a(sin θ - θ cos θ), find d²y / dx².

Question 125:

Find the absolute maximum value of f(x) = 2x³ - 3x² - 36x + 9 on [-3, 3].

Question 126:

Define f(x) = {x² + bx + c for x < 1, x for x ≥ 1}. If f(x) is differentiable at x = 1, then b - c is equal to:

Question 127:

The Boolean expression (~(p ∧ q)) ∨ q is equivalent to:

Question 128:

If x = (1 - t²) / (1 + t²) and y = (2t) / (1 + t²), find dy/dx:

Question 129:

The tangent at point (x₁, y₁) on the curve y = x³ + 3x² + 5 passes through the origin. Find the curve where (x₁, y₁) does NOT lie:

Question 130:

Evaluate the integral of [x sin⁻¹(x)] / √(1 - x²) with respect to x:

Question 131:

The value of the integral of (x + 1) / (x(1 + xe^x)) with respect to x is:

Question 132:

The order and degree of the differential equation √(dy/dx) - 4(dy/dx) - 7x = 0 are:

Question 133:

Given vectors a = i + j + k, b = i + 3j + 5k, and c = 7i + 9j + 11k, the area of a parallelogram with diagonals a + b and b + c is:

Question 134:

If X is a random variable with P(X = -2) = P(X = -1) = P(X = 1) = P(X = 2) = 1/6 and P(X = 0) = 1/3, the mean of X is:

Question 135:

Evaluate the integral of e^x (2 + sin(2x)) / (1 + cos(2x)) with respect to x:

Question 136:

The solution of the differential equation y² dx + (x² - xy + y²) dy = 0 is:

Question 137:

Two lines given by the vector equations r₁ = (2i - 3j + 7k) + λ(2i + pj + 5k) and r₂ = (i + 2j + 3k) + μ(3i - pj + pk) are perpendicular for all λ and μ. The value of p is:

Question 138:

Evaluate sin(tan⁻¹(4/5) + tan⁻¹(4/3) + tan⁻¹(1/9) - tan⁻¹(1/7)):

Question 139:

Let f(x) = (2 - √(x + 4)) / sin(2x), x ≠ 0. For f(x) to be continuous at x = 0, f(0) must be defined as:

Question 140:

Evaluate the integral ∫ from 0 to π/4 of (cos²(x) / (cos²(x) + 4sin²(x))) dx:

Question 141:

The area of the region described by {(x, y) | x² + y² ≤ 1 and y² ≤ 1 - x} is:

Question 142:

Two players A and B alternately throw a coin and a die. The first to throw both a head and a 6 wins. If A starts, the probability that B wins is:

Question 143:

Consider the system of equations: kx + y + z = 1, x + ky + z = k, x + y + kz = k². Find |k| if the system has no solution:

Question 144:

If f(x) is differentiable at x = 1, and limit as h approaches 0 of (1/h)f(1 + h) = 5, then f'(1) is:

Question 145:

The area of the region {(x, y): 0 ≤ y ≤ x² + 1, 0 ≤ y ≤ x + 1, 0 ≤ x ≤ 2} is:

Question 146:

The solution of the differential equation √(1 - y²) dx + x dy - sin⁻¹(y) dy = 0 is:

Question 147:

Let X be a discrete random variable representing the number rolled on a biased die. The probability distribution of X is:

X = {1, 2, 3, 4, 5, 6}

P(X = x) = {0.1, 0.15, 0.3, 0.25, k, k}

The variance of X is:

Question 148:

If the vector equation of the line (x - 2)/2 = (2y - 5)/-3 = z + 1 is rewritten as:

r = (2i + 5/2j - k) + λ(2i - 3/2j + pk)

Then p is equal to:

Question 149:

Which of the following is correct?

Question 150:

A spherical iron ball with a radius of 10 cm is coated with a layer of ice of uniform thickness that melts at a rate of 50 cm³/min. When the thickness of the ice is 15 cm, the rate at which the thickness of the ice decreases is: