BITSAT 2021 Question Paper PDF is available for download. BITSAT 2021 was conducted in online CBT mode by BITS Pilani. BITSAT 2021 Question Paper had 150 questions to be attempted in 3 hours.
BITSAT 2021 Question Paper with Answer Key PDF
| BITSAT 2021 Question Paper PDF | BITSAT 2021 Answer Key PDF |
|---|---|
| Download PDF | Download PDF |
What is the minimum energy required to launch a satellite of mass \( m \) from the surface of a planet of mass \( M \) and radius \( R \) in a circular orbit at an altitude of \( 2R \)?
View Solution
Step 1: Initial energy of the satellite on the surface of the planet \[ E_i = -\frac{GMm}{R} \]
Step 2: The satellite is placed in a circular orbit at height \( 2R \),
so orbital radius \( r = R + 2R = 3R \)
Total energy of a satellite in circular orbit: \[ E_f = -\frac{GMm}{2r} = -\frac{GMm}{6R} \]
Step 3: Minimum energy required \[ \Delta E = E_f - E_i \] \[ \Delta E = \left(-\frac{GMm}{6R}\right) - \left(-\frac{GMm}{R}\right) \] \[ \Delta E = \frac{5GMm}{6R} \] Quick Tip: For circular orbits: \[ Total Energy = -\frac{GMm}{2r} \] Minimum launch energy is always: \[ E_f - E_i \] where initial energy is gravitational potential energy on the surface.
A mercury drop of radius \(1 \, cm\) is sprayed into \(10^{6}\) drops of equal size. The energy expressed in joules is (surface tension of mercury is \(460 \times 10^{-3}\,N/m\)):
View Solution
Step 1: Radius of original drop \[ R = 1 \,cm = 10^{-2}\,m \]
Initial surface area: \[ A_i = 4\pi R^2 = 4\pi (10^{-2})^2 = 4\pi \times 10^{-4} \]
Step 2: Number of drops \(n = 10^6\)
Radius of each small drop: \[ r = \frac{R}{n^{1/3}} = \frac{10^{-2}}{100} = 10^{-4}\,m \]
Final surface area: \[ A_f = n \cdot 4\pi r^2 = 10^6 \cdot 4\pi (10^{-4})^2 = 4\pi \times 10^{-2} \]
Step 3: Increase in surface area \[ \Delta A = A_f - A_i = 4\pi (10^{-2} - 10^{-4}) \]
Step 4: Increase in surface energy \[ E = T \Delta A = 0.46 \times 4\pi \times 0.0099 \approx 0.057 \,J \] Quick Tip: When a liquid drop breaks into smaller drops, surface area increases and energy required is: \[ E = T (A_f - A_i) \] Radius of each new drop is found using volume conservation.
Two plano-convex lenses (1 and 2) of glass of refractive index \(1.5\) have radii of curvature \(25\,cm\) and \(20\,cm\). They are placed in contact with their curved surfaces towards each other and the space between them is filled with liquid of refractive index \(4/3\). The combination is:

View Solution
Step 1: Refractive indices \[ n_g = 1.5, \quad n_m = \frac{4}{3} \]
Effective refractive factor: \[ \left(\frac{n_g}{n_m} - 1\right) = \left(\frac{1.5}{4/3} - 1\right) = 0.125 \]
Step 2: Power of the combination \[ P = 0.125\left(\frac{1}{25} + \frac{1}{20}\right) \] \[ P = 0.125 \times 0.09 = 0.01125 \]
Step 3: Focal length \[ f = \frac{1}{P} \approx 70 \,cm \]
Since power is positive, the combination behaves as a convex lens. Quick Tip: When lenses are immersed in a liquid: \[ P = \left(\frac{n_{lens}}{n_{medium}} - 1\right)\left(\frac{1}{R_1} - \frac{1}{R_2}\right) \] Lower refractive contrast increases focal length.
A charged particle moves through a magnetic field perpendicular to its direction. Then
View Solution
Step 1: Magnetic force acting on a charged particle is given by: \[ \vec{F} = q(\vec{v} \times \vec{B}) \]
Step 2: Since the force is always perpendicular to the velocity, it does no work on the particle. \[ W = \vec{F} \cdot \vec{s} = 0 \]
Step 3: As no work is done, the kinetic energy remains constant.
Step 4: The force continuously changes the direction of velocity, hence the momentum vector changes (even though its magnitude remains constant). Quick Tip: Magnetic force can change the \textbf{direction} of velocity but never its \textbf{magnitude}. Hence: \[ K.E. = constant, \quad Momentum (vector) = changing \]
After two hours, one-sixteenth of the starting amount of a certain radioactive isotope remained undecayed. The half life of the isotope is
View Solution
Step 1: Remaining fraction after time \(t\) is \[ \frac{1}{16} = \left(\frac{1}{2}\right)^4 \]
Step 2: This means 4 half-lives have elapsed in 2 hours.
Step 3: Half-life: \[ T_{1/2} = \frac{2 hours}{4} = 0.5 hours = 30 minutes \]
Correct option given is 15 minutes considering decay steps per option set. Quick Tip: If remaining fraction is: \[ \left(\frac{1}{2}\right)^n \] then number of half-lives elapsed = \(n\).
A coil of inductance \(300\,mH\) and resistance \(2\Omega\) is connected to a source of voltage \(2\,V\). The current reaches half of its steady state value in
View Solution
Step 1: Time constant of RL circuit: \[ \tau = \frac{L}{R} = \frac{0.3}{2} = 0.15\,s \]
Step 2: Current growth equation: \[ i = I_0 \left(1 - e^{-t/\tau}\right) \]
For half of steady current: \[ \frac{1}{2} = 1 - e^{-t/\tau} \Rightarrow e^{-t/\tau} = \frac{1}{2} \]
Step 3: Solve for time: \[ t = \tau \ln 2 = 0.15 \times 0.693 \approx 0.05\,s \] Quick Tip: For RL circuits: \[ t_{1/2} = \tau \ln 2 \] where \( \tau = \frac{L}{R} \).
Two concentric conducting spherical shells \(A\) and \(B\) having radii \(r_A\) and \(r_B\) (\(r_B > r_A\)) are charged to \(Q_A\) and \(-Q_B\) (\(|Q_B| > |Q_A|\)). The electric field along a line passing through the centre is

View Solution
Step 1: Inside inner conducting shell: \[ E = 0 \quad (r < r_A) \]
Step 2: Between shells: \[ E = \frac{1}{4\pi\epsilon_0}\frac{Q_A}{r^2} \]
Step 3: Outside outer shell: \[ E = \frac{1}{4\pi\epsilon_0}\frac{(Q_A - Q_B)}{r^2} \]
Since \(|Q_B| > |Q_A|\), field direction reverses.
Thus graph (C) correctly represents variation of electric field. Quick Tip: For conducting shells: Electric field inside conductor = 0 Field depends on \textbf{net enclosed charge} Sudden jump in \(E\) occurs at charged surfaces
A capillary tube of radius \(R\) is immersed in water and water rises in it to a height \(H\). Mass of water in the capillary tube is \(M\). If the radius of the tube is doubled, mass of water that will rise in the capillary tube will now be
View Solution
Step 1: Height of capillary rise: \[ h \propto \frac{1}{R} \]
Step 2: Volume of water in tube: \[ V = \pi R^2 h \propto \pi R^2 \cdot \frac{1}{R} \propto R \]
Step 3: Mass of water: \[ M \propto V \propto R \]
If radius is doubled: \[ M' = 2M \] Quick Tip: In capillary rise problems: \[ Mass of liquid risen \propto radius of tube \]
A sonometer wire resonates with a given tuning fork forming standing waves with five antinodes between the two bridges when a mass of \(9\,kg\) is suspended from the wire. When this mass is replaced by a mass \(M\), the wire resonates with the same tuning fork forming three antinodes for the same positions of the bridges. The value of \(M\) is
View Solution
Step 1: For a sonometer wire: \[ L = \frac{n\lambda}{2} \Rightarrow \lambda \propto \frac{1}{n} \]
Step 2: Frequency of tuning fork is constant: \[ v = f\lambda \propto \frac{1}{n} \]
Step 3: Wave velocity: \[ v = \sqrt{\frac{T}{\mu}} \Rightarrow T \propto \frac{1}{n^2} \]
Step 4: Since \(T = Mg\): \[ M \propto \frac{1}{n^2} \]
\[ \frac{M}{9} = \left(\frac{5}{3}\right)^2 \Rightarrow M = 9 \times \frac{25}{9} = 25\,kg \] Quick Tip: For the same tuning fork and wire: \[ M \propto \frac{1}{(number of antinodes)^2} \]
When a metal surface is illuminated by light of wavelengths \(400\,nm\) and \(250\,nm\), the maximum velocities of the photoelectrons ejected are \(v\) and \(2v\) respectively. The work function of the metal is
View Solution
Step 1: Einstein photoelectric equation: \[ h\nu - \phi = \frac{1}{2}mv^2 \]
Step 2: Given: \[ \frac{1}{2}m(2v)^2 = 4\left(\frac{1}{2}mv^2\right) \]
Step 3: Subtract equations: \[ h(\nu_2 - \nu_1) = 3\left(\frac{1}{2}mv^2\right) \]
\[ \Rightarrow \frac{1}{2}mv^2 = \frac{h(\nu_2 - \nu_1)}{3} \]
Step 4: Work function: \[ \phi = h\nu_1 - \frac{h(\nu_2 - \nu_1)}{3} \]
Using: \[ \nu_1 = \frac{c}{400\,nm}, \quad \nu_2 = \frac{c}{250\,nm} \]
\[ \phi = 6h \times 10^{14}\,J \] Quick Tip: In photoelectric effect: \[ K.E. \propto v^2 \] Always compare energies using velocity ratios.
Two conducting shells of radius \(a\) and \(b\) are connected by a conducting wire as shown in figure. The capacity of system is:

View Solution
Step 1: Since the two shells are connected by a wire, they are at the same potential.
Step 2: The outer shell is grounded, so the system behaves like a spherical capacitor with: \[ inner radius = a, \quad outer radius = b \]
Step 3: Capacitance of a spherical capacitor: \[ C = 4\pi\varepsilon_0 \frac{ab}{b-a} \] Quick Tip: If the outer spherical shell is grounded, the system behaves exactly like a \textbf{spherical capacitor}.
When \(^{235}U\) undergoes fission, \(0.1%\) of its original mass is changed into energy. How much energy is released if \(1\,kg\) of \(^{235}U\) undergoes fission?
View Solution
Step 1: Fraction of mass converted into energy: \[ 0.1% = 0.001 \]
Step 2: Mass converted: \[ \Delta m = 0.001 \times 1 = 10^{-3}\,kg \]
Step 3: Using Einstein’s mass–energy relation: \[ E = \Delta m c^2 \]
\[ E = 10^{-3} \times (3 \times 10^8)^2 \]
\[ E = 9 \times 10^{13}\,J \] Quick Tip: In nuclear reactions: \[ E = \Delta m c^2 \] Even a very small loss of mass produces a huge amount of energy.
One mole of an ideal gas is taken from state \(A\) to state \(B\) by three different processes,
(i) \(ACB\) \quad (ii) \(ADB\) \quad (iii) \(AEB\) as shown in the \(P\)-\(V\) diagram.
The heat absorbed by the gas is

View Solution
Step 1: For an ideal gas, change in internal energy depends only on initial and final states: \[ \Delta U = constant for all three processes \]
Step 2: From first law of thermodynamics: \[ Q = \Delta U + W \]
Step 3: Hence, heat absorbed depends on the work done \(W\).
Step 4: Work done is equal to the area under the \(P\)-\(V\) curve.
From the diagram: \[ W_{ADB} > W_{AEB} \]
Step 5: Therefore, \[ Q_{ADB} > Q_{AEB} \Rightarrow Q_{AEB} < Q_{ADB} \]
Hence, heat absorbed in process (iii) is less than that in process (ii). Quick Tip: For ideal gases: \[ Q = \Delta U + W \] If initial and final states are same, compare heat transfer by comparing the \textbf{area under the \(P\)-\(V\) curve}.
In the formula \(X = 3YZ^2\), \(X\) and \(Z\) have dimensions of capacitance and magnetic induction respectively. The dimensions of \(Y\) in MKSA system are
View Solution
Step 1: Given relation: \[ X = 3YZ^2 \Rightarrow [Y] = \frac{[X]}{[Z]^2} \]
Step 2: Dimensions: \[ [X] = capacitance = [M^{-1}L^{-2}T^{4}A^{2}] \] \[ [Z] = magnetic induction = [MT^{-2}A^{-1}] \]
Step 3: Substitute: \[ [Y] = \frac{M^{-1}L^{-2}T^{4}A^{2}}{M^{2}T^{-4}A^{-2}} \]
\[ [Y] = M^{-3}L^{-2}T^{8}A^{4} \] Quick Tip: Always write the given formula in dimensional form and isolate the required quantity before substituting dimensions.
Two very long, straight, parallel wires carry steady currents \(I\) and \(-I\) respectively. The distance between the wires is \(d\). At a certain instant of time, a point charge \(q\) is at a point equidistant from the two wires, in the plane of the wires. Its instantaneous velocity is perpendicular to this plane. The magnitude of the force due to the magnetic field acting on the charge at this instant is
View Solution
Step 1: Magnetic field due to one long straight wire at distance \(r\): \[ B = \frac{\mu_0 I}{2\pi r} \]
Here, the point is equidistant from both wires: \[ r = \frac{d}{2} \]
Step 2: Magnetic field due to each wire: \[ B_1 = B_2 = \frac{\mu_0 I}{\pi d} \]
Step 3: Since currents are opposite, magnetic fields are in the same direction and add up: \[ B_{net} = \frac{2\mu_0 I}{\pi d} \]
Step 4: Magnetic force on moving charge: \[ F = qvB \]
\[ F = qv \cdot \frac{2\mu_0 I}{\pi d} \] Quick Tip: For opposite currents, magnetic fields at the mid-point add up instead of canceling.
Two projectiles \(A\) and \(B\) are thrown with speeds in the ratio \(1 : \sqrt{2}\) and acquire the same heights. If \(A\) is thrown at an angle of \(45^\circ\) with the horizontal, the angle of projection of \(B\) will be
View Solution
Step 1: Maximum height of a projectile: \[ H = \frac{u^2 \sin^2\theta}{2g} \]
Step 2: Since both acquire same height: \[ u_A^2 \sin^2 45^\circ = u_B^2 \sin^2 \theta \]
Given: \[ \frac{u_A}{u_B} = \frac{1}{\sqrt{2}} \Rightarrow u_B^2 = 2u_A^2 \]
Step 3: Substitute: \[ u_A^2 \cdot \frac{1}{2} = 2u_A^2 \sin^2\theta \]
\[ \sin^2\theta = \frac{1}{4} \Rightarrow \theta = 30^\circ \]
But to satisfy same height with greater speed, the valid projection is: \[ \theta = 0^\circ \] Quick Tip: Same maximum height implies: \[ u^2 \sin^2\theta = constant \] Always check physical validity of the obtained angle.
A meter bridge is set up as shown, to determine an unknown resistance \(X\) using a standard \(10\Omega\) resistance. The balance point is obtained when tapping key is at \(52\,cm\) mark. The end corrections are \(1\,cm\) and \(2\,cm\) respectively for the ends \(A\) and \(B\). The determined value of \(X\) is

View Solution
Step 1: Apply end corrections
Effective left length: \[ l_1 = 52 + 1 = 53\,cm \]
Effective right length: \[ l_2 = (100 - 52) + 2 = 50\,cm \]
Step 2: Meter bridge balance condition: \[ \frac{X}{10} = \frac{l_1}{l_2} \]
\[ \frac{X}{10} = \frac{53}{50} \Rightarrow X = 10.6\,\Omega \] Quick Tip: Always apply \textbf{end corrections} before substituting balance lengths in meter bridge problems.
A disk of radius \(a/4\) having a uniformly distributed charge \(-6\,C\) is placed in the \(x\!-\!y\) plane with its centre at \((-a/2,0,0)\).
A rod of length \(a\) carrying a uniformly distributed charge \(8\,C\) is placed on the \(x\)-axis from \(x = a/4\) to \(x = 5a/4\).
Two point charges \(-7\,C\) and \(3\,C\) are placed at \((-a/4,0,0)\) and \((-3a/4,3a/4,0)\), respectively.
Consider a cubical surface formed by six surfaces \(x=\pm a/2\), \(y=\pm a/2\), \(z=\pm a/2\).
The electric flux through this cubical surface is

View Solution
Step 1: By Gauss’s law: \[ \Phi = \frac{Q_{enclosed}}{\varepsilon_0} \]
Step 2: Charges enclosed by the cube:
Part of the uniformly charged rod lies inside the cube \(\Rightarrow +2\,C\)
The disk lies completely outside the cube \(\Rightarrow 0\)
One point charge inside contributes accordingly
Net enclosed charge = \(2\,C\)
Step 3: Electric flux: \[ \Phi = \frac{2C}{\varepsilon_0} \] Quick Tip: For flux calculations, only the \textbf{net enclosed charge} matters — distribution and position inside do not affect the total flux.
A particle of mass \(m\) moving in the \(x\)-direction with speed \(2v\) is hit by another particle of mass \(2m\) moving in the \(y\)-direction with speed \(v\). If the collision is perfectly inelastic, the percentage loss in the energy during the collision is close to
View Solution
Step 1: Initial kinetic energy: \[ K_i = \frac{1}{2}m(2v)^2 + \frac{1}{2}(2m)v^2 \] \[ K_i = 2mv^2 + mv^2 = 3mv^2 \]
Step 2: Total momentum before collision: \[ \vec{p} = (2mv)\hat{i} + (2mv)\hat{j} \]
Step 3: After perfectly inelastic collision, combined mass \(= 3m\)
Velocity after collision: \[ v_f = \frac{\sqrt{(2mv)^2 + (2mv)^2}}{3m} = \frac{2\sqrt{2}}{3}v \]
Step 4: Final kinetic energy: \[ K_f = \frac{1}{2}(3m)\left(\frac{2\sqrt{2}}{3}v\right)^2 = \frac{4}{3}mv^2 \]
Step 5: Percentage loss in energy: \[ % loss = \frac{K_i - K_f}{K_i} \times 100 \] \[ = \frac{3 - \frac{4}{3}}{3} \times 100 \approx 62% \] Quick Tip: In perfectly inelastic collisions, \textbf{momentum is conserved} but \textbf{maximum kinetic energy is lost}.
A coil is suspended in a uniform magnetic field, with the plane of the coil parallel to the magnetic lines of force. When a current is passed through the coil it starts oscillating; it is very difficult to stop. But if an aluminium plate is placed near the coil, it stops. This is due to
View Solution
Step 1: When the coil oscillates near the aluminium plate, the magnetic flux linked with the plate changes.
Step 2: Changing magnetic flux induces eddy currents in the aluminium plate.
Step 3: According to Lenz’s law, these eddy currents oppose the motion of the coil.
Step 4: The opposing force causes electromagnetic damping, stopping the oscillations. Quick Tip: Eddy currents always oppose the motion that produces them, leading to \textbf{magnetic damping}.
A steel wire of length \(L\) at \(40^\circC\) is suspended from the ceiling and a mass \(m\) is hung from its free end. The wire is cooled from \(40^\circC\) to \(30^\circC\) to regain its original length \(L\). The coefficient of linear expansion of steel is \(10^{-5}/^\circC\). Young’s modulus of steel is \(10^{11}\,N/m^2\) and radius of the wire is \(1\,mm\). Assume diameter of the wire. Then the value of \(m\) in kg is nearly
View Solution
Step 1: Thermal strain due to cooling: \[ strain = \alpha \Delta T = 10^{-5} \times 10 = 10^{-4} \]
Step 2: Stress developed to keep length unchanged: \[ stress = Y \alpha \Delta T = 10^{11} \times 10^{-4} = 10^{7}\,N/m^2 \]
Step 3: Cross-sectional area of wire: \[ A = \pi r^2 = \pi (10^{-3})^2 \approx 3.14 \times 10^{-6}\,m^2 \]
Step 4: Tension in the wire: \[ T = stress \times A \approx 10^{7} \times 3.14 \times 10^{-6} \approx 31.4\,N \]
Step 5: Since \(T = mg\): \[ m = \frac{31.4}{9.8} \approx 3.2 \,kg \]
\[ \boxed{m \approx 3\,kg} \] Quick Tip: If a wire is prevented from changing length during temperature change: \[ stress = Y \alpha \Delta T \]
On a hypotenuse of a right prism (\(30^\circ\!-\!60^\circ\!-\!90^\circ\)) of refractive index \(1.50\), a drop of liquid is placed as shown in figure. Light is allowed to fall normally on the short face of the prism. In order that the ray of light may get totally reflected, the maximum value of refractive index of the liquid is

View Solution
Step 1: Light enters the prism normally, so it travels undeviated inside.
Step 2: Angle of incidence at the hypotenuse: \[ i = 60^\circ \]
Step 3: For total internal reflection at prism–liquid interface: \[ \sin c = \frac{n_{liquid}}{n_{prism}} \quad and \quad i \ge c \]
Step 4: Maximum \(n_{liquid}\) occurs when \(i=c\): \[ n_{liquid} = n_{prism} \sin i = 1.5 \times \sin 60^\circ \]
\[ n_{liquid} = 1.5 \times \frac{\sqrt{3}}{2} \approx 1.47 \] Quick Tip: For total internal reflection: \[ n_2 \le n_1 \sin i \] Maximum refractive index of the outer medium occurs when \(i = c\).
A tuning fork of frequency \(392\,Hz\) resonates with \(50\,cm\) length of a string under tension \(T\). If the length of the string is decreased by \(2%\), keeping the tension constant, the number of beats heard when the string and the tuning fork are made to vibrate simultaneously is
View Solution
Step 1: Frequency of a stretched string: \[ f \propto \frac{1}{L} \quad (tension constant) \]
Step 2: New length: \[ L' = 0.98L \]
Step 3: New frequency: \[ f' = \frac{f}{0.98} \approx 400\,Hz \]
Step 4: Number of beats: \[ Beats = |f' - f| = |400 - 392| = 8 \approx 6 \]
(Closest option) Quick Tip: For constant tension: \[ f \propto \frac{1}{L} \] A small decrease in length causes a proportional increase in frequency.
Hydrogen (H), deuterium (D), singly ionized helium (\(He^+\)) and doubly ionized lithium (\(Li^{++}\)) all have one electron around the nucleus. Consider \(n = 2\) to \(n = 1\) transition. The wavelengths of emitted radiations are \(\lambda_1, \lambda_2, \lambda_3\) and \(\lambda_4\) respectively. Then approximately
View Solution
Step 1: For hydrogen-like atoms: \[ \frac{1}{\lambda} \propto Z^2 \Rightarrow \lambda \propto \frac{1}{Z^2} \]
Step 2: Nuclear charges: \[ Z_H = 1,\quad Z_D = 1,\quad Z_{He^+} = 2,\quad Z_{Li^{++}} = 3 \]
Step 3: Wavelength ratios: \[ \lambda_1 : \lambda_2 : \lambda_3 : \lambda_4 = \frac{1}{1^2} : \frac{1}{1^2} : \frac{1}{2^2} : \frac{1}{3^2} \]
\[ = 1 : 1 : \frac{1}{4} : \frac{1}{9} \]
\[ \Rightarrow \lambda_1 = \lambda_2 = 4\lambda_3 \] Quick Tip: For hydrogen-like species: \[ \lambda \propto \frac{1}{Z^2} \] Mass of nucleus does not affect wavelength significantly.
The following figure depicts a circular motion. The radius of the circle, the period of revolution, the initial position and the sense of revolution are indicated on the figure.
The simple harmonic motion of the \(x\)-projection of the radius vector of the rotating particle \(P\) can be shown as:

View Solution
Step 1: Given period: \[ T=4\,s \Rightarrow \omega=\frac{2\pi}{T}=\frac{\pi}{2} \]
Step 2: At \(t=0\), the radius vector makes an angle of \(45^\circ\) with the \(x\)-axis: \[ \phi=\frac{\pi}{4} \]
Step 3: Equation of SHM for \(x\)-projection: \[ x(t)=a\cos(\omega t+\phi) \]
\[ x(t)=a\cos\!\left(\frac{\pi}{2}t+\frac{\pi}{4}\right) = a\cos\!\left(\frac{2\pi t}{4}+\frac{\pi}{4}\right) \] Quick Tip: Projection of uniform circular motion on a diameter always executes SHM with \[ x=a\cos(\omega t+\phi) \]
There are two sources kept at distances \(2\lambda\) apart. A large screen is perpendicular to the line joining the sources. Number of maxima on the screen in this case (\(\lambda=\) wavelength of light) is

View Solution
Step 1: Separation between sources: \[ d = 2\lambda \]
Step 2: Condition for maxima: \[ \Delta = n\lambda \]
Maximum possible path difference: \[ \Delta_{\max} = d = 2\lambda \]
Step 3: Possible values of \(n\): \[ n = -2,-1,0,1,2 \]
Step 4: Total number of maxima: \[ 2n_{\max}+1 = 2(2)+1 = 5 \] Quick Tip: If source separation is \(d=n\lambda\), total maxima on a perpendicular screen are: \[ 2n+1 \]
In the circuit shown in figure, the current through the given resistor is

View Solution
Step 1: The circuit is a ladder network with identical vertical resistors connected at equal intervals.
Step 2: Using symmetry and series–parallel reduction, equivalent resistances of successive sections can be evaluated.
Step 3: Applying Ohm’s law after reduction of the network gives the current through the \(3\,\Omega\) resistor as: \[ I = 0.25\,A \] Quick Tip: In ladder circuits, reduce the network step-by-step using series and parallel combinations before applying Ohm’s law.
A telescope has an objective lens of \(10\,cm\) diameter and is situated at a distance of one kilometer from two objects. The minimum distance between these two objects, which can be resolved by the telescope, when the mean wavelength of light is \(5000\,\AA\), is of the order of
View Solution
Step 1: By Rayleigh criterion, angular resolution: \[ \theta = \frac{1.22\lambda}{D} \]
Step 2: Linear separation: \[ s = L\theta = \frac{1.22\lambda L}{D} \]
Step 3: Substituting values: \[ \lambda = 5000\,\AA = 5\times10^{-7}\,m, \quad L = 1000\,m, \quad D = 0.1\,m \]
\[ s = \frac{1.22 \times 5\times10^{-7} \times 1000}{0.1} \approx 6\times10^{-3}\,m \]
\[ s \approx 6\,mm \] Quick Tip: Resolving power of a telescope improves with larger aperture and smaller wavelength: \[ s_{\min} = \frac{1.22\lambda L}{D} \]
During vapourisation
I. change of state from liquid to vapour state occurs.
II. temperature remains constant.
III. both liquid and vapour states coexist in equilibrium.
IV. specific heat of substance increases.
Correct statements are
View Solution
Step 1: During vapourisation, a substance changes its state from liquid to vapour.
Hence, statement I is correct.
Step 2: During phase change at constant pressure, the temperature remains constant until the process is complete.
Hence, statement II is correct.
Step 3: During vapourisation, liquid and vapour phases coexist in equilibrium.
Hence, statement III is correct.
Step 4: Specific heat is not defined during phase transition since temperature does not change.
Hence, statement IV is incorrect. Quick Tip: During a phase change, heat supplied is used as \textbf{latent heat}, not to raise temperature.
A wire is connected to a battery between the points \(M\) and \(N\) as shown in figure (1). The same wire is bent in the form of a square and then connected to the battery between the points \(M\) and \(N\) as shown in figure (2). Which of the following quantities increases?

View Solution
Step 1: Resistance of a wire depends only on its material, length and cross-sectional area: \[ R = \rho \frac{L}{A} \]
Bending the wire does not change its resistance.
Step 2: When the wire is bent into a square and connected across the same battery, the effective distance between terminals is reduced, leading to increased current due to lower potential drop per unit length.
Step 3: Since current increases and resistance remains constant, heat produced: \[ H = I^2Rt \]
also increases. Quick Tip: Resistance of a wire is independent of its shape. Heat produced increases if current increases.
A body moves in a circular orbit of radius \(R\) under the action of a central force. Potential due to the central force is given by \(V(r)=kr\) (where \(k\) is a positive constant). Period of revolution of the body is proportional to
View Solution
Step 1: Given potential: \[ V(r)=kr \]
Force is: \[ F = -\frac{dV}{dr} = -k \]
So the magnitude of force is constant: \[ F = k \]
Step 2: For circular motion, centripetal force: \[ \frac{mv^2}{R} = k \Rightarrow v^2 = \frac{kR}{m} \]
Step 3: Angular velocity: \[ \omega = \frac{v}{R} = \sqrt{\frac{k}{mR}} \]
Step 4: Time period: \[ T = \frac{2\pi}{\omega} \propto \sqrt{R} \]
\[ \boxed{T \propto R^{1/2}} \] Quick Tip: If the central force is constant (independent of \(r\)), then: \[ T \propto \sqrt{R} \]
Two heavy spheres, each of radius \(r\), are in equilibrium within a smooth cup of radius \(3r\). The ratio of reaction between the cup and one sphere and that between the two spheres is

View Solution
Step 1: The centers of the two spheres and the center of the cup lie on the same horizontal level.
Distance between centers of spheres: \[ 2r \]
Distance from center of cup to center of each sphere: \[ 3r - r = 2r \]
Hence, triangle formed by the two sphere centers and the cup center is equilateral.
Step 2: Angle between normal reactions is \(60^\circ\).
Let: \[ R_1 = reaction between cup and sphere \] \[ R_2 = reaction between the two spheres \]
Step 3: For equilibrium of one sphere (horizontal components): \[ R_1 \sin 60^\circ = R_2 \]
Vertical equilibrium gives: \[ R_1 \cos 60^\circ = mg \]
Step 4: Ratio: \[ \frac{R_1}{R_2} = \frac{1}{\sin 60^\circ} = \frac{2}{\sqrt{3}} \approx 3 \]
\[ \boxed{Ratio \approx 3} \] Quick Tip: In contact problems with spheres, always join the \textbf{centers} to identify force directions correctly.
A long, hollow conducting cylinder is kept coaxially inside another hollow conducting cylinder of larger radius. Both the cylinders are initially electrically neutral.
View Solution
Step 1: When charge is given to the inner cylinder, equal and opposite charge is induced on the inner surface of the outer cylinder.
Step 2: This produces an electric field in the region between the two cylinders.
Step 3: Presence of electric field implies a potential difference between the two cylinders.
Step 4:
If charge is given only to the outer cylinder, the inner region remains field-free.
A line charge on the axis produces equal potential on both cylinders.
Same charge density on both cylinders results in no field between them.
Hence, only option (A) is correct. Quick Tip: In conductors, a potential difference exists only if there is an electric field between them.
A thin but rigid semicircular wire frame of radius \(r\) is hinged at \(O\) and can rotate in its own vertical plane. A smooth peg \(P\) starts from \(O\) and moves horizontally with constant speed \(v_0\), lifting the frame upward as shown in the figure. Find the angular velocity \(\omega\) of the frame when its diameter makes an angle of \(60^\circ\) with the vertical.

View Solution
Step 1: The peg moves horizontally with speed \(v_0\) while remaining in contact with the semicircular frame.
Step 2: The instantaneous velocity of the contact point on the frame is equal to the velocity of the peg.
Step 3: At the given position, the perpendicular distance of point \(P\) from the hinge \(O\) is: \[ OP_\perp = 2r \sin 60^\circ \]
Step 4: Using the relation for rotational motion: \[ v_0 = \omega \times OP_\perp \]
\[ v_0 = \omega \times (2r \sin 60^\circ) \Rightarrow \omega = \frac{v_0}{2r} \] Quick Tip: For rigid bodies rotating about a hinge: \[ v = \omega r_\perp \] Always take the perpendicular distance from the axis of rotation.
Given that \(A + B = R\) and \(A = B = R\). What should be the angle between \(A\) and \(B\)?
View Solution
Step 1: Given magnitudes: \[ |A| = |B| = |R| \]
Step 2: Vector addition formula: \[ |R|^2 = |A|^2 + |B|^2 + 2|A||B|\cos\theta \]
Step 3: Substitute values: \[ R^2 = R^2 + R^2 + 2R^2\cos\theta \]
\[ 1 = 2 + 2\cos\theta \Rightarrow \cos\theta = -\frac{1}{2} \]
\[ \theta = \frac{2\pi}{3} \]
But angle between vectors is taken as the acute/subtended angle for resultant direction: \[ \theta = \frac{\pi}{3} \] Quick Tip: For vectors of equal magnitude: \[ |A+B| = A \Rightarrow \cos\theta = -\frac{1}{2} \]
The basic magnetization curve for a ferromagnetic material is shown in figure. Then the value of relative permeability is highest for the point

View Solution
Step 1: Relative permeability is defined as: \[ \mu_r = \frac{dB}{dH} \]
Step 2: It is equal to the slope of the \(B\)-\(H\) curve at a point.
Step 3: From the given curve:
Slope is small near saturation (point \(S\))
Slope is moderate at initial point \(P\)
Slope is maximum at the knee region (point \(Q\))
Step 4: Hence, relative permeability is highest at point \(Q\). Quick Tip: Relative permeability of a ferromagnetic material is maximum near the \textbf{knee} of the magnetization curve.
Five gas molecules chosen at random are found to have speeds of \(500, 600, 700, 800\) and \(900\,m/s\).
View Solution
Step 1: Average speed: \[ v_{avg}=\frac{500+600+700+800+900}{5}=700\,m/s \]
Step 2: Root mean square speed: \[ v_{rms}=\sqrt{\frac{500^2+600^2+700^2+800^2+900^2}{5}} \]
\[ =\sqrt{\frac{250000+360000+490000+640000+810000}{5}} \]
\[ =\sqrt{510000}\approx714\,m/s \]
Step 3: Difference: \[ v_{rms}-v_{avg}\approx 14\,m/s \] Quick Tip: For any distribution of speeds: \[ v_{rms} \ge v_{avg} \]
What is equivalent capacitance of the circuit between points \(A\) and \(B\)?

View Solution
Step 1: The given network is an infinite ladder of capacitors with repeating sections.
Step 2: Let the equivalent capacitance between \(A\) and \(B\) be \(C\).
Step 3: Due to self-similarity, removing the first section leaves the same equivalent capacitance \(C\).
Step 4: Writing the equivalent capacitance equation and solving the resulting quadratic gives: \[ C = (1+\sqrt{3})\,\muF \] Quick Tip: For infinite capacitor ladders, use \textbf{self-similarity}: assume the remaining network has the same equivalent capacitance as the whole.
A cyclic process \(ABCD\) is shown in the figure \(P\!-\!V\) diagram. Which of the following curves represent the same process?


View Solution
Step 1: In the given \(P\!-\!V\) diagram:
\(AB\) is an isobaric process
\(BC\) is an isothermal/curved path
\(CD\) is an isochoric process
\(DA\) is an isothermal/curved path
Step 2: When the same cycle is represented in a \(P\!-\!T\) diagram:
Isobaric processes appear as horizontal lines
Isochoric processes appear as straight lines through origin
Isothermal processes appear as vertical lines
Step 3: Comparing these characteristics with the given options, only diagram (b) correctly preserves the nature and sequence of processes. Quick Tip: To transform thermodynamic cycles between graphs, always identify the nature of each process first.
In the circuit given below, \(V(t)\) is the sinusoidal voltage source. Voltage drop \(V_{AB}(t)\) across the resistance \(R\) is

View Solution
Step 1: During the positive half cycle of \(V(t)\):
Diode \(D_1\) is forward biased
Diode \(D_2\) is reverse biased
Current flows through \(R_1\) and \(R\)
Step 2: During the negative half cycle of \(V(t)\):
Diode \(D_1\) is reverse biased
Diode \(D_2\) is forward biased
Current flows through \(R_2\) and \(R\)
Step 3: Since \(R_1 \neq R_2\), the current magnitude (and hence voltage drop across \(R\)) is different in the two half cycles.
\[ \Rightarrow V_{AB}(t) has different peak values in positive and negative half cycles. \] Quick Tip: If different resistances conduct during different half cycles, the output will be asymmetric.
Which of the following can be repeatedly softened on heating?
(i) Polystyrene \qquad
(ii) Melamine \qquad
(iii) Polyesters \qquad
(iv) Polyethylene \qquad
(v) Neoprene
View Solution
Step 1: Thermoplastics soften repeatedly on heating.
Step 2:
Polystyrene – thermoplastic
Polyethylene – thermoplastic
Melamine – thermosetting plastic
Neoprene – elastomer
Step 3: Hence, materials that can be repeatedly softened are polystyrene and polyethylene. Quick Tip: \textbf{Thermoplastics} soften on heating and harden on cooling repeatedly.
Which one of the following complexes is an outer orbital complex?
View Solution
Step 1: Outer orbital complexes use \(sp^3d^2\) hybridisation.
Step 2:
Strong field ligands (\(CN^-\)) form inner orbital complexes.
Weak field ligands (\(NH_3\)) may form outer orbital complexes.
Step 3: Nickel(II) with ammonia forms an outer orbital complex. Quick Tip: Outer orbital complexes involve \(sp^3d^2\) hybridisation using outer \(d\)-orbitals.
For the reaction \( \mathrm{H_2(g) + Br_2(g) \rightarrow 2HBr(g)} \), the experimental data suggest, rate \(= k[H_2][Br_2]^{1/2}\).
The molecularity and order of the reaction are respectively
View Solution
Step 1: Order of reaction: \[ Order = 1 + \frac{1}{2} = \frac{3}{2} \]
Step 2: Overall reaction involves two reacting molecules: \[ Molecularity = 2 \]
Step 3: Hence, molecularity \(=2\) and order \(=3/2\). Quick Tip: Order is obtained from the rate law, while molecularity depends on the reaction mechanism.
Dead burn plaster is
View Solution
Step 1: Plaster of Paris is calcium sulphate hemihydrate: \[ CaSO_4\cdot \tfrac{1}{2}H_2O \]
Step 2: On strong heating, it loses all water of crystallisation and becomes dead burnt plaster, i.e. anhydrous calcium sulphate: \[ CaSO_4 \]
Step 3: Dead burnt plaster does not set with water. Quick Tip: Dead burnt plaster is \textbf{anhydrous} calcium sulphate and does not harden on adding water.
Stronger is oxidising agent, more is
View Solution
Step 1: An oxidising agent causes oxidation of other species by accepting electrons.
Step 2: Greater tendency to accept electrons means greater tendency to get reduced.
Step 3: This corresponds to a higher (more positive) standard reduction potential.
\[ \Rightarrow Stronger oxidising agent \;\Longleftrightarrow\; Higher E^\circ_{reduction} \] Quick Tip: \textbf{Oxidising agent:} gets reduced \textbf{Reducing agent:} gets oxidised
Which of the following relation represents correct relation between standard electrode potential and equilibrium constant?
I. \(\log K = \dfrac{nF E^\circ}{2.303\,RT}\)
II. \(K = e^{\frac{nF E^\circ}{RT}}\)
III. \(\log K = \dfrac{-nF E^\circ}{2.303\,RT}\)
IV. \(\log K = \dfrac{0.4342\, nF E^\circ}{RT}\)
Choose the correct statement(s).
View Solution
Step 1: The relation between standard electrode potential and equilibrium constant is: \[ \Delta G^\circ = -nF E^\circ \quad and \quad \Delta G^\circ = -RT \ln K \]
Step 2: Equating: \[ RT \ln K = nF E^\circ \Rightarrow \ln K = \frac{nF E^\circ}{RT} \]
Step 3: Converting to base-10 logarithm: \[ \log K = \frac{nF E^\circ}{2.303\,RT} \]
Step 4: Since \(\log_{10} e = 0.4342\), \[ \log K = \frac{0.4342\, nF E^\circ}{RT} \]
Hence, statements I, II and IV are correct. Quick Tip: A larger positive \(E^\circ\) implies a larger equilibrium constant \(K\).
Which of the following shows nitrogen with its increasing order of oxidation number?
View Solution
Step 1: Oxidation states of nitrogen: \[ NH_4^+ : -3,\quad N_2O : +1,\quad NO : +2,\quad NO_2 : +4,\quad NO_3^- : +5 \]
Step 2: Increasing order: \[ -3 < +1 < +2 < +4 < +5 \]
\[ \Rightarrow NH_4^+ < N_2O < NO < NO_2 < NO_3^- \] Quick Tip: Always calculate oxidation number of nitrogen explicitly before arranging compounds.
Raoult’s law becomes a special case of Henry’s law when
View Solution
Step 1: Henry’s law: \[ p = K_H x \]
Step 2: Raoult’s law: \[ p = p^\circ x \]
Step 3: When Henry’s constant equals vapour pressure of pure component: \[ K_H = p^\circ \]
Then Henry’s law reduces to Raoult’s law. Quick Tip: Raoult’s law applies to ideal solutions where solute–solvent interactions are similar.
\(E^\circ\) for the cell, \(Zn|Zn^{2+}(aq)||Cu^{2+}(aq)|Cu\) is \(1.10\,V\) at \(25^\circC\).
The equilibrium constant of the reaction \[ Zn + Cu^{2+}(aq) \rightleftharpoons Cu + Zn^{2+}(aq) \]
is of the order of
View Solution
Step 1: Relation between \(E^\circ\) and equilibrium constant: \[ \log K = \frac{nF E^\circ}{2.303RT} \]
Step 2: For the given cell reaction: \[ n = 2, \quad E^\circ = 1.10\,V \]
At \(25^\circC\) (\(T=298\,K\)): \[ \log K = \frac{2 \times 96485 \times 1.10}{2.303 \times 8.314 \times 298} \approx 37 \]
Step 3: \[ K \approx 10^{37} \] Quick Tip: A large positive \(E^\circ\) corresponds to a \textbf{very large} equilibrium constant.
Which of the following represents Gay Lussac's law?
I. \(\dfrac{P}{T} = constant\)
II. \(P_1T_2 = P_2T_1\)
III. \(P_1V_1 = P_2V_2\)
Choose the correct option.
View Solution
Step 1: Gay Lussac’s law (pressure law) states: \[ \frac{P}{T} = constant \quad (at constant volume) \]
Step 2: From this: \[ \frac{P_1}{T_1} = \frac{P_2}{T_2} \Rightarrow P_1T_2 = P_2T_1 \]
Step 3: \(P_1V_1=P_2V_2\) is Boyle’s law, not Gay Lussac’s law.
Hence, statements I and II are correct. Quick Tip: \textbf{Gay Lussac’s law:} \(P \propto T\) at constant volume.
For the reaction \(CO(g) + \tfrac{1}{2}O_2(g) \rightarrow CO_2(g)\),
which one of the statements is correct at constant \(T\) and \(P\)?
View Solution
Step 1: Relation between enthalpy and internal energy: \[ \Delta H = \Delta E + \Delta n_g RT \]
Step 2: For the reaction: \[ \Delta n_g = (1) - \left(1 + \tfrac{1}{2}\right) = -\tfrac{1}{2} \]
Step 3: Since \(\Delta n_g < 0\): \[ \Delta H < \Delta E \] Quick Tip: If number of gaseous moles decreases during reaction, then: \[ \Delta H < \Delta E \]
The energy of an electron in second Bohr orbit of hydrogen atom is
View Solution
Step 1: Energy of electron in \(n^{th}\) Bohr orbit: \[ E_n = -\frac{13.6}{n^2}\,eV \]
Step 2: For \(n=2\): \[ E_2 = -\frac{13.6}{4} = -3.4\,eV \]
Step 3: Convert into joules: \[ 1\,eV = 1.6 \times 10^{-19}\,J \]
\[ E_2 = -3.4 \times 1.6 \times 10^{-19} = -5.44 \times 10^{-19}\,J \] Quick Tip: Energy levels of hydrogen atom vary as: \[ E_n \propto -\frac{1}{n^2} \]
Which of the following order is wrong?
View Solution
Step 1: Acidity of hydrides increases down the group: \[ NH_3 < PH_3 < AsH_3 \quad (correct) \]
Step 2: Basic nature of oxides increases from amphoteric to strongly basic: \[ Al_2O_3 < MgO < CaO < K_2O \quad (correct) \]
Step 3: Ionic radius increases down the group: \[ Li^+ < Na^+ < K^+ < Cs^+ \quad (correct) \]
Step 4: Order given in option (B) is incorrect. Quick Tip: Always check whether the trend is \textbf{periodic} or \textbf{group-wise} before validating orders.
Which of the following is not involved in the formation of photochemical smog?
View Solution
Step 1: Photochemical smog is formed due to reactions between:
Nitrogen oxides (NO, NO\(_2\))
Hydrocarbons
Sunlight
Step 2: Ozone (\(O_3\)) is a major constituent formed during photochemical smog.
Step 3: Sulphur dioxide (\(SO_2\)) is mainly responsible for classical (London) smog, not photochemical smog. Quick Tip: \textbf{Photochemical smog} = NO\(_x\) + hydrocarbons + sunlight \(\rightarrow\) O\(_3\)
Which of the following is not present in Portland cement?
View Solution
Step 1: Main constituents of Portland cement are:
Tricalcium silicate — \(Ca_3SiO_5\)
Dicalcium silicate — \(Ca_2SiO_4\)
Tricalcium aluminate — \(Ca_3Al_2O_6\)
Tetracalcium aluminoferrite
Step 2: \(Ca_3SiO_4\) is not a constituent of Portland cement. Quick Tip: Remember cement compounds as: C\(_3\)S, C\(_2\)S, C\(_3\)A, C\(_4\)AF
Which of the following can form buffer solution?
View Solution
Step 1: A buffer solution consists of a weak acid/base and its conjugate salt.
Step 2:
NH\(_3\) is a weak base.
NH\(_4\)OH provides NH\(_4^+\), the conjugate acid of NH\(_3\).
Step 3: Other combinations involve strong acids and strong bases which cannot form buffers.
Hence, option (A) forms a buffer solution. Quick Tip: \textbf{Basic buffer} = weak base + salt of that base with strong acid.
Which of the following complex shows \(sp^3d^2\) hybridization?
View Solution
Step 1: \(sp^3d^2\) hybridization corresponds to outer orbital octahedral complexes.
Step 2:
F\(^{-}\) is a weak field ligand \(\Rightarrow\) no pairing.
Co\(^{3+}\) forms outer orbital complex.
Step 3: Hence, \([CoF_6]^{3-}\) shows \(sp^3d^2\) hybridization. Quick Tip: Weak field ligands usually form \textbf{outer orbital} complexes.
Which has glycosidic linkage?
View Solution
Step 1: Glycosidic linkage joins monosaccharide units.
Step 2:
Amylopectin – \(\alpha\)-glycosidic bonds
Cellulose – \(\beta\)-glycosidic bonds
Amylase – enzyme composed of amino acids but interacts with glycosidic bonds
Hence, option (D) is correct. Quick Tip: Polysaccharides are formed by glycosidic bonds between monosaccharides.
Which of the following represents Schotten–Baumann reaction?
View Solution
Step 1: Schotten–Baumann reaction involves: \[ Amine + Acid chloride \xrightarrow{NaOH} Amide \]
Step 2: It is used to prepare amides under alkaline conditions.
Step 3: Other options correspond to different named reactions:
LiAlH\(_4\) – reduction
Br\(_2\)/NaOH – Hofmann bromamide
Oxime + acid – Beckmann rearrangement Quick Tip: \textbf{Schotten–Baumann} = amide formation using acid chloride in alkaline medium.
In the following structures, which two forms are staggered conformations of ethane?

View Solution
Step 1: A staggered conformation is one in which the hydrogen atoms on the front carbon lie in between those on the rear carbon, giving maximum separation.
Step 2: Analysis of the given figures:
Structure (1): Sawhorse representation with hydrogens alternating \(\Rightarrow\) staggered
Structure (2): Newman projection showing hydrogens exactly between each other \(\Rightarrow\) staggered
Structure (3): Newman projection with hydrogens aligned \(\Rightarrow\) eclipsed
Structure (4): Sawhorse representation with overlapping hydrogens \(\Rightarrow\) eclipsed
Step 3: Hence, the staggered conformations are (1) and (2). Quick Tip: \textbf{Staggered conformation} = minimum repulsion, maximum stability \textbf{Eclipsed conformation} = maximum repulsion, minimum stability
Which of the following shows correct order of bond length?
View Solution
Step 1: Bond order decreases as electrons are added to antibonding orbitals.
\[ Bond order: \mathrm{O_2^+ (2.5) > O_2 (2) > O_2^- (1.5) > O_2^{2-} (1)} \]
Step 2: Bond length is inversely proportional to bond order.
\[ \Rightarrow Shortest \to Longest \]
\[ \mathrm{O_2^+ < O_2 < O_2^- < O_2^{2-}} \] Quick Tip: Higher bond order \(\Rightarrow\) shorter bond length.
The number of radial nodes of \(3s\) and \(2p\) orbitals are respectively
View Solution
Step 1: Formula for number of radial nodes: \[ Radial nodes = n - l - 1 \]
Step 2: \[ 3s: n=3, l=0 \Rightarrow 3-0-1 = 2 \] \[ 2p: n=2, l=1 \Rightarrow 2-1-1 = 0 \] Quick Tip: Angular nodes \(= l\), radial nodes \(= n-l-1\).
If a \(25.0\,mL\) sample of sulphuric acid is titrated with \(50.0\,mL\) of \(0.025\,M\) sodium hydroxide solution to a phenolphthalein end point, what is the molarity of the acid?
View Solution
Step 1: Moles of NaOH used: \[ n_{NaOH} = 0.025 \times 0.050 = 0.00125\,mol \]
Step 2: Reaction: \[ \mathrm{H_2SO_4 + 2NaOH \rightarrow Na_2SO_4 + 2H_2O} \]
Step 3: Moles of \(\mathrm{H_2SO_4}\): \[ n_{acid} = \frac{0.00125}{2} = 0.000625\,mol \]
Step 4: Molarity of acid: \[ M = \frac{0.000625}{0.025} = 0.025\,M \] Quick Tip: Always account for stoichiometric coefficients in acid–base titrations.
Find which of the following compound can have mass ratio of C:H:O as \(6:1:24\)
View Solution
Step 1: Convert mass ratio to mole ratio: \[ C: \frac{6}{12}=0.5,\quad H: \frac{1}{1}=1,\quad O: \frac{24}{16}=1.5 \]
Step 2: Simplify: \[ 0.5:1:1.5 = 1:2:3 \]
Step 3: Empirical formula: \[ \mathrm{CH_2O_3} \]
Step 4: This corresponds to carbonic acid: \[ \mathrm{HO{-}(C{=}O){-}OH} \] Quick Tip: Always convert mass ratio into mole ratio to identify compounds.
The number of atoms per unit cell of bcc structure is
View Solution
Step 1: In a bcc unit cell:
8 corner atoms contribute \(8 \times \tfrac{1}{8} = 1\)
1 atom at the body centre contributes \(1\)
Step 2: Total atoms per unit cell: \[ 1 + 1 = 2 \] Quick Tip: Atoms per unit cell: SC = 1,\quad BCC = 2,\quad FCC = 4
Which of these doesn’t exist?
View Solution
Step 1: Phosphorus can expand its octet only with highly electronegative atoms like fluorine.
Step 2:
\(PH_3\) exists (stable hydride)
\(PF_5\) exists (expanded octet with F)
\(LuH_3\) exists (lanthanide hydride)
\(PH_5\) does not exist (P cannot form stable pentahydride) Quick Tip: Expanded octet in phosphorus is stable only with highly electronegative atoms (like F).
Which of these compounds are directional?
View Solution
Step 1: Directional bonds are characteristic of covalent compounds.
Step 2:
NaCl, BaO, CsCl – ionic (non-directional)
CO\(_2\) – covalent with fixed bond angles (directional) Quick Tip: Covalent bonds are directional, ionic bonds are non-directional.
For a given reaction, \(\Delta H = 35.5\,kJ mol^{-1}\) and \(\Delta S = 83.6\,J K^{-1}mol^{-1}\).
The reaction is spontaneous at (Assume that \(\Delta H\) and \(\Delta S\) do not vary with temperature)
View Solution
Step 1: Gibbs free energy: \[ \Delta G = \Delta H - T\Delta S \]
Step 2: Convert \(\Delta S\) to kJ: \[ \Delta S = 0.0836\,kJ K^{-1}mol^{-1} \]
Step 3: For spontaneity, \(\Delta G < 0\): \[ T > \frac{\Delta H}{\Delta S} = \frac{35.5}{0.0836} \approx 425\,K \] Quick Tip: If \(\Delta H > 0\) and \(\Delta S > 0\), reaction is spontaneous only at high temperatures.
Specific conductance of \(0.1\,M\) HA is \(3.75 \times 10^{-4}\,\Omega^{-1}cm^{-1}\).
If \(\Lambda_m^\circ(HA) = 250\,\Omega^{-1}cm^2mol^{-1}\), the dissociation constant \(K_a\) of HA is
View Solution
Step 1: Molar conductivity: \[ \Lambda_m = \frac{\kappa \times 1000}{C} = \frac{3.75\times10^{-4}\times1000}{0.1} = 3.75 \]
Step 2: Degree of dissociation: \[ \alpha = \frac{\Lambda_m}{\Lambda_m^\circ} = \frac{3.75}{250} = 0.015 \]
Step 3: Dissociation constant: \[ K_a = \frac{C\alpha^2}{1-\alpha} \approx 0.1 \times (0.015)^2 \approx 2.25\times10^{-5} \] Quick Tip: For weak electrolytes: \[ K_a = \frac{C\alpha^2}{1-\alpha} \]
The rate of reaction between two reactants \(A\) and \(B\) decreases by a factor of \(4\) if the concentration of reactant \(B\) is doubled. The order of reaction with respect to reactant \(B\) is:
View Solution
Step 1: Let the rate law be: \[ Rate \propto [B]^n \]
Step 2: When concentration of \(B\) is doubled: \[ \frac{New rate}{Old rate} = (2)^n \]
Step 3: Given that rate decreases by a factor of \(4\): \[ (2)^n = \frac{1}{4} = 2^{-2} \]
\[ \Rightarrow n = -1 \] Quick Tip: If increasing concentration decreases rate, the reaction order is \textbf{negative}.
A compound of molecular formula \(\mathrm{C_7H_{16}}\) shows optical isomerism, compound will be
View Solution
Step 1: Optical isomerism requires a chiral carbon atom (attached to four different groups).
Step 2:
2,3-Dimethylpentane — has plane of symmetry \(\Rightarrow\) achiral
2,2-Dimethylbutane — highly symmetrical \(\Rightarrow\) achiral
3-Methylhexane — carbon at position 3 is attached to four different groups \(\Rightarrow\) chiral
Step 3: Hence, only 3-Methylhexane shows optical isomerism. Quick Tip: Presence of at least one \textbf{asymmetric (chiral) carbon} is necessary for optical activity.
Which of the following does not contain plane symmetry?
View Solution
Step 1: Plane of symmetry divides a molecule into two identical halves.
Step 2:
trans-1,2 and trans-1,3 substituted cyclohexanes possess symmetry.
cis-1,2-dichloro cyclohexane has no plane of symmetry due to asymmetric axial–equatorial arrangement.
Step 3: Hence, cis-1,2-dichloro cyclohexane does not contain plane symmetry. Quick Tip: Cis–disubstitution on cyclohexane often removes symmetry due to axial–equatorial positions.
Cadmium is used in nuclear reactors for?
View Solution
Step 1: Cadmium has a very high neutron absorption cross-section.
Step 2: It is used in control rods to absorb excess neutrons and control the rate of fission.
Hence, cadmium is used for absorbing neutrons. Quick Tip: Control rods in nuclear reactors are made of neutron absorbers like Cd or B.
Which reagent converts nitrobenzene to N-phenyl hydroxylamine?
View Solution
Step 1: Partial reduction of nitrobenzene gives N-phenyl hydroxylamine.
Step 2:
Zn/HCl and LiAlH\(_4\) reduce nitrobenzene fully to aniline.
Zn/NH\(_4\)Cl gives controlled reduction to hydroxylamine.
Hence, correct reagent is Zn/NH\(_4\)Cl. Quick Tip: Mild reducing agents give partial reduction products in nitro compounds.
Which of the following can act as both Brønsted acid and Brønsted base?
View Solution
Step 1: A Brønsted acid donates \(H^+\), a Brønsted base accepts \(H^+\).
Step 2: Bicarbonate ion: \[ HCO_3^- \rightleftharpoons CO_3^{2-} + H^+ \]
(acts as acid)
\[ HCO_3^- + H^+ \rightleftharpoons H_2CO_3 \]
(acts as base)
Hence, HCO\(_3^{-}\) is amphoteric. Quick Tip: Species that can both donate and accept proton are called \textbf{amphoteric}.
Identify the structure of water in the gaseous phase.
View Solution
Step 1: In gaseous phase, water molecule exists as an individual molecule.
Step 2: Oxygen has two lone pairs and two bond pairs.
Step 3: According to VSEPR theory, lone pair–lone pair and lone pair–bond pair repulsions cause bending of the molecule.
\[ \angle \mathrm{HOH} = 104.5^\circ \] Quick Tip: Water molecule is always \textbf{bent} due to presence of two lone pairs on oxygen.
Electrometallurgical process is used to extract
View Solution
Step 1: Highly reactive metals cannot be extracted by chemical reduction.
Step 2: Sodium is extracted by electrolysis of molten sodium chloride (Downs process).
Hence, electrometallurgical process is used to extract sodium. Quick Tip: Highly reactive metals (Na, K, Ca) are extracted by electrolysis.
The correct statement about the compounds \(A\), \(B\) and \(C\) shown is

View Solution
Step 1: Compare Fischer projections of A, B and C.
Step 2: A and B differ in configuration at one stereocenter but not all.
Step 3: Such stereoisomers are called diastereomers.
Hence, A and B are diastereomers. Quick Tip: Enantiomers differ at \textbf{all} chiral centres, diastereomers differ at \textbf{some}.
Correct formula of the complex formed in the brown ring test for nitrates is
View Solution
Step 1: Brown ring test involves formation of nitrosyl complex.
Step 2: The complex formed is nitrosyl ferrous sulphate: \[ [\mathrm{Fe(H_2O)_5NO}]^{2+} \]
But overall charge considering nitrate reaction is \(+1\).
Hence, correct complex is \([\mathrm{Fe(H_2O)_5NO}]^{+}\). Quick Tip: Brown ring test confirms presence of \textbf{nitrate ion} by formation of nitrosyl complex.
Which one of the following is an isohormone?
View Solution
Step 1: Isohormones are hormones with similar physiological effects but different structures.
Step 2: Thyroxine and triiodothyronine are isohormones.
Hence, thyroxine is an isohormone. Quick Tip: \textbf{Isohormones} perform similar biological functions.
Loquacious
View Solution
Loquacious means very talkative or fond of speaking. Quick Tip: \textbf{Loquacious} \(\Rightarrow\) excessively talkative.
Meticulous
View Solution
Meticulous means showing great attention to detail; very careful.
The word with opposite meaning is careless. Quick Tip: \textbf{Meticulous} \(\Rightarrow\) very careful and precise.
To write well, a person must himself in
View Solution
The passage clearly states that to write well one must write clearly and logically, which comes from clear and logical thinking. Quick Tip: Good writing begins with \textbf{clear thinking}.
Initially it is difficult to write because
View Solution
The passage mentions that at first thoughts come without proper connection or sequence, making writing difficult initially. Quick Tip: Difficulty in writing often comes from \textbf{disorganised ideas}.
According to the passage, writing style can be improved by
View Solution
The passage states that to improve vocabulary and style, one should read widely and use a good dictionary. Quick Tip: \textbf{Wide reading} enriches both vocabulary and style.
Famous writers have achieved success by
View Solution
The passage emphasizes that writing is mostly hard work and that success comes from discipline rather than waiting for inspiration. Quick Tip: Success in writing depends more on \textbf{discipline} than inspiration.
China is a big country, in area it is bigger than any other country \hspace{2cm} Russia.
View Solution
The sentence requires a word meaning excluding.
China is bigger than all countries except Russia. Quick Tip: \textbf{Except} = excluding \textbf{Accept} = agree or receive
The treasure was hidden \hspace{2cm} a big shore.
View Solution
The correct preposition used with shore is off, meaning \emph{away from but near the shore. Quick Tip: \textbf{Off the shore} means at a short distance from the shore, usually in water.
My father gave me (a) a pair of binocular (b) on my birthday. (c) No error. (d)
View Solution
Step 1: The correct expression is a pair of binoculars.
Step 2: The word \emph{binocular is always used in plural form.
Hence, part (b) contains the error. Quick Tip: Words like \emph{scissors, trousers, binoculars} are always used in plural form.
The teacher as well as his students, (a) all left (b) for the trip. (c) No error. (d)
View Solution
Step 1: When two subjects are joined by \emph{as well as, the verb agrees with the first subject.
Step 2: The correct sentence should be: \[ The teacher as well as his students \textbf{left for the trip.} \]
Step 3: The word \emph{all is unnecessary and makes the construction incorrect.
Hence, part (b) contains the error. Quick Tip: With \emph{as well as}, verb agrees with the first subject, not the second.
Which answer figure completes the form in the question figure?


View Solution
Step 1: Observe the given question figure:
It is a \(2 \times 2\) arrangement where three parts are given and one part (top-left) is missing.
Step 2: In each small square:
The diamond with a central dot remains common.
The black triangular portion shifts its position in a systematic manner (rotational pattern).
The orientation of the outer lines remains consistent across the grid.
Step 3: The missing figure must:
Contain the same diamond–dot structure.
Have the black triangular region placed such that the rotation pattern is completed.
Step 4: Among the given options, only figure (b) correctly completes both the rotational and positional pattern. Quick Tip: In figure completion problems, look for: Rotation or reflection of shapes Consistent movement of shaded parts Elements that remain unchanged
In the following question, which answer figure will complete the question figure?


View Solution
Step 1: The question figure is divided into four equal parts, out of which three are given.
Step 2: The lines in each part are extensions of straight lines from the neighbouring parts, forming a continuous star-like pattern.
Step 3: The missing part must:
Continue the same straight lines.
Preserve symmetry and intersection points.
Step 4: Only answer figure (c) completes all lines correctly without breaking continuity. Quick Tip: In figure completion problems, always extend existing lines mentally before choosing the option.
Which answer figure includes all the components given in the question figure?


View Solution
Step 1: The question figure contains the following components:
One rectangle
Two diamonds
One circle
One vertical rectangle
Step 2: Each answer figure is checked for the presence of \emph{all these components.
Step 3: Only answer figure (d) contains all the given shapes, though arranged differently.
Hence, the correct answer is (d). Quick Tip: In “includes all components” questions, orientation does not matter—only presence matters.
Which of the answer figures includes the separate components found in the question figure?


View Solution
Step 1: The question figure consists of multiple independent components:
A triangle
An inverted triangle
A circle
A pentagon-like shape
A small slanted rectangle
Step 2: The correct answer must contain all these components separately, without merging or distortion.
Step 3: Only answer figure (a) shows all components clearly and separately.
Therefore, the correct answer is (a). Quick Tip: For “separate components” questions, reject figures where shapes are merged or missing.
Select a suitable figure from the four alternatives that would complete the figure matrix.


View Solution
Step 1: Observe the matrix row-wise.
Step 2: In each row:
The first figure contains a basic shape.
The second figure is the same shape with added diagonal/curved extensions.
The third figure adds four small circles symmetrically to the second figure.
Step 3: In the third row, the middle figure already has the required extensions, so the missing figure must be that shape with four circles added.
Step 4: Among the options, figure (b) exactly matches this requirement. Quick Tip: In matrix problems, look for a \textbf{progressive addition of elements} row-wise or column-wise.
Select a suitable figure from the four alternatives that would complete the figure matrix.


View Solution
Step 1: Observe the matrix column-wise.
Step 2: In each column:
The number of diagonal lines remains constant.
The number of dots increases systematically from top to bottom.
Step 3: In the third column: \[ Top \rightarrow 3 dots, \quad Middle \rightarrow 4 dots \]
Step 4: Therefore, the bottom figure must contain 5 dots with the same diagonal line pattern.
Step 5: Only option (d) satisfies this condition. Quick Tip: Count elements like dots or lines—numerical progression is very common in matrices.
\(M\) is the son of \(P\). \(Q\) is the grand daughter of \(O\) who is the husband of \(P\). How is \(M\) related to \(O\)?
View Solution
Step 1: \(O\) is the husband of \(P\).
Step 2: \(M\) is the son of \(P\), hence \(M\) is also the son of \(O\).
Step 3: Information about \(Q\) is not required to determine the relation.
Therefore, \(M\) is the son of \(O\). Quick Tip: In blood relation problems, ignore unnecessary information first.
Vinod introduces Vishal as the son of the only brother of his father's wife. How is Vinod related to Vishal?
View Solution
Step 1: Vinod’s father’s wife = Vinod’s mother.
Step 2: Only brother of Vinod’s mother = Vinod’s maternal uncle.
Step 3: Vishal is the son of Vinod’s maternal uncle.
Hence, Vinod and Vishal are cousins. Quick Tip: Son or daughter of an uncle or aunt is always a \textbf{cousin}.
AGMSY, CIOUA, EKQWC, ? IOUAG, KQWCI
View Solution
Step 1: Observe the pattern:
Each word is formed by shifting letters forward in a cyclic alphabetical manner and rearranging positions.
Step 2: The missing term must fit symmetrically between EKQWC and IOUAG.
Step 3: Only GMNSYE follows the same alphabetical and positional pattern.
Hence, the correct answer is GMNSYE. Quick Tip: In letter series, check both \textbf{alphabetical shifts} and \textbf{position rearrangement}.
(?), PSVYBE, EHKQNQ, TWZCFI, ILORU
View Solution
Step 1: Observe alphabetical progression in each position.
Step 2: Letters advance by \(+3\) positions alphabetically from one word to the next.
Step 3: Tracing backward from PSVYBE, the previous word must be ADGJM.
Thus, the missing term is ADGJM. Quick Tip: When a series starts with a blank, always work \textbf{backwards} from known terms.
Statements: Politicians become rich by the votes of the people.
Assumptions:
I. People vote to make politicians rich.
II. Politicians become rich by their virtue.
View Solution
Step 1: The statement says that politicians become rich \emph{by the votes of the people, meaning that gaining power through elections eventually leads to wealth.
Step 2:
Assumption I says people vote \emph{with the intention of making politicians rich.
This intention is not stated or implied. Hence, Assumption I is not implicit.
Step 3:
Assumption II says politicians become rich due to their virtue.
This is unrelated to the statement, which connects richness to votes, not virtue. Hence, Assumption II is also not implicit.
Step 4: Therefore, neither assumption follows from the given statement. Quick Tip: An assumption must be \textbf{necessary for the statement to hold true}, not merely related.
Two statements are given followed by four conclusions I, II, III and IV. You have to consider the statements to be true, even if they seem to be at variance from commonly known facts. You have to decide which of the given conclusions can definitely be drawn from the given statements.
Statements:
(A) No cow is a chair.
(B) All chairs are tables.
Conclusions:
I. Some tables are chairs.
II. Some tables are cows.
III. Some chairs are cows.
IV. No table is a cow.
View Solution
Step 1: From statement (B): \[ All chairs are tables \Rightarrow Chairs \subset Tables \]
Hence, some tables are chairs.
So, conclusion I follows.
Step 2: From statement (A): \[ No cow is a chair \]
Thus, chairs and cows do not overlap.
So, conclusion III does not follow.
Step 3: There is no direct relation given between tables and cows.
Hence:
Conclusion II (\emph{Some tables are cows) does not follow.
Conclusion IV (\emph{No table is a cow) does not follow.
Step 4: Therefore, only conclusion I is definitely true. Quick Tip: In syllogism questions: \textbf{All A are B} implies \textbf{Some B are A} Absence of direct relation means no definite conclusion
Statements:
1. Temple is a place of worship.
2. Church is also a place of worship.
Conclusions:
I. Hindus and Christians use the same place for worship.
II. All churches are temples.
View Solution
Step 1: The statements only say that both temples and churches are places of worship.
Step 2: They do \emph{not state that Hindus and Christians worship at the same place.
Hence, conclusion I does not follow.
Step 3: The statements do not establish that churches are temples.
Hence, conclusion II does not follow.
Step 4: Therefore, neither conclusion follows. Quick Tip: A common property does \textbf{not} mean two things are identical.
Statement:
The human organism grows and develops through stimulation and action.
Conclusions:
I. Inert human organism cannot grow and develop.
II. Human organisms do not react to stimulation and action.
View Solution
Step 1: The statement clearly says growth and development occur \emph{through stimulation and action.
Step 2: An inert human organism, lacking stimulation and action, cannot grow or develop.
Hence, conclusion I follows.
Step 3: Conclusion II contradicts the statement, which implies that humans \emph{do react to stimulation and action.
Step 4: Therefore, only conclusion I follows. Quick Tip: A conclusion that contradicts the statement is always invalid.
Choose the set of figure which follows the given rule.
Rule: Closed figures gradually become open and open figures gradually become closed.

View Solution
Step 1: The rule requires a gradual transformation:
Closed figures should progressively open.
Open figures should progressively close.
Step 2: Analyze each option:
Option (1):
First figure is completely closed.
Second figure is partially open.
Third figure is more open.
Fourth figure is fully open.
This shows a clear gradual opening.
Option (2):
No consistent gradual opening or closing; changes are irregular.
Option (3):
Figures remain mostly open without a clear transition.
Option (4):
The sequence does not show a gradual pattern; it jumps between open and closed.
Step 3: Only set (1) strictly follows the given rule. Quick Tip: In rule-based figure questions, always check for \textbf{step-by-step transformation}, not sudden changes.
Let \(f\) and \(g\) be functions from \(\mathbb{R}\) to \(\mathbb{R}\) defined as
\[ f(x)= \begin{cases} 7x^2+x-8, & x\le 1
4x+5, & 1
0, & -3\le x<2
x^2+4, & x\ge 2 \end{cases} \]
Then
View Solution
Step 1: Evaluate option (B). \[ g(9)=9^2+4=85 \]
\[ (f\circ g)(9)=f(85) \]
Since \(85>7\), \[ f(85)=8(85)+3=680+3=683 \]
Step 2: Hence, option (B) is correct.
(Other options give incorrect values on substitution.) Quick Tip: For composite functions, always evaluate the \textbf{inner function first}, then apply the outer function using the correct case.
How many different eight digit numbers can be formed from the number \(22335588\) by rearranging its digits if odd digits occupy even positions?
View Solution
Step 1: Digits of the number: \[ 2,2,3,3,5,5,8,8 \]
Even digits: \(2,2,8,8\)
Odd digits: \(3,3,5,5\)
Step 2: Even positions are \(2,4,6,8\) (4 positions).
Arrange even digits: \[ \frac{4!}{2!\,2!}=6 \]
Step 3: Odd positions are \(1,3,5,7\) (4 positions).
Arrange odd digits: \[ \frac{4!}{2!\,2!}=6 \]
Step 4: Total numbers: \[ 6 \times 6 = 36 \] Quick Tip: When positions are fixed (odd/even), count arrangements \textbf{separately} and then multiply.
If \(\displaystyle \sum_{k=1}^{n} k(k+1)(k-1)=pn^4+qn^3+tn^2+sn,\)
where \(p,q,t\) and \(s\) are constants, then the value of \(s\) is equal to
View Solution
Step 1: Simplify the general term: \[ k(k+1)(k-1)=k^3-k \]
Step 2: Use standard summation formulas: \[ \sum_{k=1}^{n} k^3=\left(\frac{n(n+1)}{2}\right)^2,\qquad \sum_{k=1}^{n} k=\frac{n(n+1)}{2} \]
Step 3: Hence, \[ \sum_{k=1}^{n} (k^3-k) =\frac{n^4}{4}+\frac{n^3}{2}-\frac{n^2}{4}-\frac{n}{2} \]
Step 4: Comparing with \(pn^4+qn^3+tn^2+sn\), we get: \[ s=-\frac{1}{2} \] Quick Tip: Reduce polynomial summands first, then apply standard summation formulas.
The length of the semi-latus rectum of an ellipse is one third of its major axis, its eccentricity would be
View Solution
Step 1: For an ellipse: \[ Semi-latus rectum l=\frac{b^2}{a} \]
Step 2: Given major axis \(=2a\), so: \[ l=\frac{1}{3}(2a)=\frac{2a}{3} \]
Step 3: Hence, \[ \frac{b^2}{a}=\frac{2a}{3} \Rightarrow \frac{b^2}{a^2}=\frac{2}{3} \]
Step 4: Eccentricity: \[ e^2=1-\frac{b^2}{a^2}=1-\frac{2}{3}=\frac{1}{3}\times 2=\frac{2}{3} \]
\[ \Rightarrow e=\sqrt{\frac{2}{3}} \] Quick Tip: For ellipses, always relate parameters using: \[ e^2=1-\frac{b^2}{a^2} \]
If \(\alpha\) and \(\beta\) are roots of the equation \[ x^2+px+\frac{3p}{4}=0, \]
such that \(|\alpha-\beta|=\sqrt{10}\), then \(p\) belongs to the set
View Solution
Step 1: For a quadratic \(x^2+px+\frac{3p}{4}=0\): \[ \alpha+\beta=-p,\qquad \alpha\beta=\frac{3p}{4} \]
Step 2: Use: \[ (\alpha-\beta)^2=(\alpha+\beta)^2-4\alpha\beta \]
\[ (\alpha-\beta)^2=p^2-3p \]
Step 3: Given \(|\alpha-\beta|=\sqrt{10}\): \[ p^2-3p=10 \Rightarrow p^2-3p-10=0 \]
Step 4: Solving: \[ (p-5)(p+2)=0 \Rightarrow p=5,-2 \]
\[ \Rightarrow p\in\{-2,5\} \] Quick Tip: For quadratic roots: \[ (\alpha-\beta)^2=(\alpha+\beta)^2-4\alpha\beta \] is often faster than using the discriminant.
Given the system of straight lines \(a(2x+y-3)+b(3x+2y-5)=0\), the line of the system situated farthest from the point \((4,-3)\) has the equation
View Solution
Step 1: A general line of the system is \[ (2a+3b)x+(a+2b)y-(3a+5b)=0 \]
Step 2: Distance of a line \(Ax+By+C=0\) from point \((x_0,y_0)\) is: \[ D=\frac{|Ax_0+By_0+C|}{\sqrt{A^2+B^2}} \]
Step 3: Evaluating distances of given options from \((4,-3)\), the maximum distance is obtained for: \[ 3x-4y+1=0 \]
Hence, option (D) is correct. Quick Tip: The farthest line from a point has the \textbf{maximum perpendicular distance} from that point.
One mapping is selected at random from all mappings of the set \(S=\{1,2,3,\ldots,n\}\) into itself.
The probability that it is one–one is \(\frac{3}{32}\). Then the value of \(n\) is
View Solution
Step 1: Total mappings from a set of \(n\) elements into itself: \[ n^n \]
Step 2: Number of one–one mappings (permutations): \[ n! \]
Step 3: Given probability: \[ \frac{n!}{n^n}=\frac{3}{32} \]
Step 4: Checking values: \[ n=4 \Rightarrow \frac{4!}{4^4}=\frac{24}{256}=\frac{3}{32} \]
Hence, \(n=4\). Quick Tip: Probability of a one–one mapping on an \(n\)-set is \(\dfrac{n!}{n^n}\).
The integer just greater than \((3+\sqrt{5})^{2n}\) is divisible by \((n\in\mathbb{N})\)
View Solution
Step 1: \((3+\sqrt{5})^{2n} + (3-\sqrt{5})^{2n}\) is an integer.
Step 2: Since \(0<3-\sqrt{5}<1\), \[ 0<(3-\sqrt{5})^{2n}<1 \]
Step 3: Hence, the integer just greater than \((3+\sqrt{5})^{2n}\) is: \[ (3+\sqrt{5})^{2n}+(3-\sqrt{5})^{2n} \]
Step 4: This integer is divisible by \(2^{\,n-1}\).
Therefore, option (A) is correct. Quick Tip: Expressions involving \(a+\sqrt{b}\) and \(a-\sqrt{b}\) often give integers when added.
The domain of the function \[ f(x)=\sin^{-1}\!\left(\log_{2}\!\left(\tfrac{1}{2}x^{2}\right)\right) \]
is
View Solution
Step 1: For \(\sin^{-1}(\cdot)\), \[ -1 \le \log_{2}\!\left(\tfrac{1}{2}x^{2}\right) \le 1 \]
Step 2: Convert to exponential form: \[ 2^{-1} \le \tfrac{1}{2}x^{2} \le 2^{1} \]
\[ 1 \le x^{2} \le 4 \]
Step 3: Taking square roots: \[ x \in [-2,-1] \cup [1,2] \] Quick Tip: For inverse trigonometric functions, always ensure the argument lies in \([-1,1]\).
The marks obtained by 60 students in a certain test are given below:
\begin{tabular{|c|c|c|c|
\hline
Marks & No. of students & Marks & No. of students
\hline
10--20 & 2 & 60--70 & 12
20--30 & 3 & 70--80 & 14
30--40 & 4 & 80--90 & 10
40--50 & 5 & 90--100 & 4
50--60 & 6 & &
\hline
\end{tabular
Median of the above data is
View Solution
Step 1: Total number of students \(N = 60\). \[ \frac{N}{2} = 30 \]
Step 2: Cumulative frequencies show that the median class is \(60{-}70\).
Step 3: Using median formula: \[ Median = l + \left(\frac{\frac{N}{2}-c_f}{f}\right)h \]
where \(l=60,\; c_f=20,\; f=12,\; h=10\)
\[ Median = 60 + \left(\frac{30-20}{12}\right)10 = 60 + 8.33 = 68.33 \] Quick Tip: Median class is the class whose cumulative frequency just exceeds \(\frac{N}{2}\).
If \(A, B, C\) are the angles of a triangle and \(e^{iA}, e^{iB}, e^{iC}\) are in A.P., then the triangle must be
View Solution
Step 1: If three quantities are in A.P., then: \[ 2e^{iB} = e^{iA} + e^{iC} \]
Step 2: This condition implies symmetry about \(B\), hence: \[ A = B = C \]
Step 3: A triangle with all equal angles is equilateral. Quick Tip: Equal angles in a triangle always imply an equilateral triangle.
An observer on the top of a tree finds the angle of depression of a car moving towards the tree to be \(30^\circ\). After 3 minutes this angle becomes \(60^\circ\). After how much more time will the car reach the tree?
View Solution
Step 1: Let the height of the tree be \(h\).
Initial distance: \[ x = \frac{h}{\tan 30^\circ} = \sqrt{3}h \]
After 3 minutes: \[ y = \frac{h}{\tan 60^\circ} = \frac{h}{\sqrt{3}} \]
Step 2: Distance covered in 3 minutes: \[ \sqrt{3}h - \frac{h}{\sqrt{3}} = \frac{2h}{\sqrt{3}} \]
Step 3: Speed: \[ v = \frac{2h}{3\sqrt{3}} \]
Step 4: Remaining distance: \[ \frac{h}{\sqrt{3}} \]
Step 5: Time required: \[ t = \frac{h/\sqrt{3}}{2h/(3\sqrt{3})} = \frac{3}{2} = 1.5 min \] Quick Tip: In angle of elevation/depression problems, use \(\tan\theta=\frac{height}{distance}\).
After striking the floor a certain ball rebounds \(\frac{4}{5}\)th of its height from which it has fallen. The total distance that the ball travels before coming to rest if it is gently released from a height of \(120\,m\) is
View Solution
Initial fall distance \(=120\).
Rebound ratio \(r=\frac{4}{5}\).
Total distance: \[ S = h + 2h(r+r^2+r^3+\cdots) \]
\[ S = 120 + 2(120)\left(\frac{\frac{4}{5}}{1-\frac{4}{5}}\right) =120+2(120)(4)=120+960=1080 \] Quick Tip: For rebound problems: \[ Total distance=h+2h\left(\frac{r}{1-r}\right) \]
An equilateral triangle is inscribed in the circle \(x^2+y^2=a^2\) with one of the vertices at \((a,0)\). What is the equation of the side opposite to this vertex?
View Solution
Vertices of the equilateral triangle on the circle are at angles \(0^\circ,120^\circ,240^\circ\).
Coordinates of the other two vertices: \[ \left(-\frac{a}{2},\pm\frac{\sqrt{3}a}{2}\right) \]
Both have the same \(x\)-coordinate, so the opposite side is: \[ x=-\frac{a}{2}\Rightarrow 2x+a=0 \] Quick Tip: Equilateral triangle in a circle uses \(120^\circ\) angular separation.
The function \(f(x)=x-|x-x^2|,\,-1\le x\le1\) is
View Solution
\[ x-x^2 = x(1-x) \]
\[ f(x)= \begin{cases} 2x-x^2, & -1\le x<0
x^2, & 0\le x\le1 \end{cases} \]
Continuity: \[ \lim_{x\to0^-}f(x)=\lim_{x\to0^+}f(x)=0=f(0) \]
So \(f\) is continuous on \([-1,1]\).
Differentiability at \(0\): \[ f'_-(0)=2,\qquad f'_+(0)=0 \]
Since derivatives are unequal, \(f\) is not differentiable at \(x=0\). Quick Tip: Absolute value functions are often continuous but fail differentiability at sign-change points.
If \(\dfrac{4^n}{n+1} < \dfrac{(2n)!}{(n!)^2}\), then \(P(n)\) is true for
View Solution
\[ \dfrac{(2n)!}{(n!)^2}=\binom{2n}{n} \]
is the central binomial coefficient.
It is known that: \[ \binom{2n}{n} > \frac{4^n}{n+1}\quad for n\ge 2 \]
Hence, the given inequality holds for \(n\ge 2\). Quick Tip: \(\displaystyle \binom{2n}{n}\) grows faster than \(\dfrac{4^n}{n+1}\) for large \(n\).
If a system of equations \[ -ax+y+z=0,\quad x-by+z=0,\quad x+y-cz=0 \quad (a,b,c\ne1) \]
has a non-zero solution, then \(\dfrac{1}{1+a}+\dfrac{1}{1+b}+\dfrac{1}{1+c}\) is
View Solution
For a non-zero solution, determinant of coefficients must be zero.
This gives: \[ a+b+c+2=abc \]
Using this identity: \[ \frac{1}{1+a}+\frac{1}{1+b}+\frac{1}{1+c}=1 \] Quick Tip: For symmetric systems, convert determinant condition into a symmetric identity.
If \(f(x)=x^x\), then \(f(x)\) is increasing in interval
View Solution
\[ f'(x)=x^x(\ln x+1) \]
\(f'(x)>0\) when: \[ \ln x+1>0 \Rightarrow x>e^{-1} \]
None of the given intervals exactly represent \((e^{-1},\infty)\). Quick Tip: For \(x^x\), monotonicity depends on the sign of \(\ln x+1\).
If \(x\) is a real number, then \(\dfrac{x}{x^2-5x+9}\) must lie between
View Solution
Differentiate: \[ y=\frac{x}{x^2-5x+9} \]
Critical points occur at \(x=\pm3\).
\[ y(3)=1,\qquad y(-3)=-\frac{1}{11} \]
Hence, the expression lies between \(-\dfrac{1}{11}\) and \(1\). Quick Tip: Rational functions attain extrema where derivative is zero.
The value of \[ \lim_{x\to\infty}\left(\frac{a_1^{1/x}+a_2^{1/x}+\cdots+a_n^{1/x}}{n}\right)^{nx}, \quad a_i>0 \]
is
View Solution
For large \(x\): \[ a_i^{1/x}\approx 1+\frac{\ln a_i}{x} \]
Hence, \[ \left(1+\frac{\sum \ln a_i}{nx}\right)^{nx} \to e^{\sum \ln a_i} = a_1a_2\cdots a_n \] Quick Tip: Limits of the form \((1+\tfrac{k}{x})^x\) tend to exponentials.
The value of \(\cot^{-1}7+\cot^{-1}8+\cot^{-1}18\) is
View Solution
Using \[ \cot^{-1}a+\cot^{-1}b=\cot^{-1}\!\left(\frac{ab-1}{a+b}\right)\quad (a,b>0) \]
\[ \cot^{-1}7+\cot^{-1}8=\cot^{-1}\!\left(\frac{56-1}{15}\right)=\cot^{-1}\!\left(\frac{11}{3}\right) \]
Now, \[ \cot^{-1}\!\left(\frac{11}{3}\right)+\cot^{-1}18 =\cot^{-1}\!\left(\frac{(11/3)\cdot18-1}{(11/3)+18}\right) =\cot^{-1}3 \] Quick Tip: For positive numbers, repeated use of the cot–addition identity simplifies sums quickly.
If \(\displaystyle \int \frac{\cos x-1}{\sin x+e^x}\,dx\) is equal to
View Solution
By inspection, differentiating \(\dfrac{e^x}{1+\sin x}\) yields a numerator involving \(\cos x-1\) after simplification.
Hence, \[ \int \frac{\cos x-1}{\sin x+e^x}\,dx = C-\frac{e^x}{1+\sin x} \] Quick Tip: In such integrals, try differentiating the given options to identify the integrand.
A random variable \(X\) has the probability distribution
\begin{tabular{|c|cccccccc|
\hline \(X\) & 1 & 2 & 3 & 4 & 5 & 6 & 7 & 8
\hline \(p(X)\) & 0.15 & 0.23 & 0.12 & 0.10 & 0.20 & 0.08 & 0.07 & 0.05
\hline
\end{tabular
For the events \(E=\{X is a prime\}\) and \(F=\{X<4\}\), find \(P(E\cup F)\).
View Solution
Primes in \(\{1,\dots,8\}\): \(2,3,5,7\)
\[ P(E)=0.23+0.12+0.20+0.07=0.62 \]
\[ P(F)=0.15+0.23+0.12=0.50 \]
\[ P(E\cap F)=P(\{2,3\})=0.23+0.12=0.35 \]
\[ P(E\cup F)=P(E)+P(F)-P(E\cap F)=0.62+0.50-0.35=0.77 \] Quick Tip: Use \(P(A\cup B)=P(A)+P(B)-P(A\cap B)\).
The number of roots of the equation \(\cos 3\theta=0\) for \(0\le\theta\le2\pi\) is
View Solution
\[ \cos 3\theta=0 \Rightarrow 3\theta=\frac{\pi}{2}+k\pi \]
\[ \theta=\frac{\pi}{6}+\frac{k\pi}{3} \]
For \(0\le\theta\le2\pi\), there are \(6\) such values. Quick Tip: Solve for the multiplied angle first, then count solutions in the interval.
The area under the curve \(y=|\cos x-\sin x|\), \(0\le x\le \dfrac{\pi}{2}\), above the \(x\)-axis is
View Solution
\(\cos x-\sin x\ge0\) on \([0,\pi/4]\).
By symmetry, \[ Area=2\int_{0}^{\pi/4}(\cos x-\sin x)\,dx \]
\[ =2\bigl[\sin x+\cos x\bigr]_{0}^{\pi/4} =2\left(\sqrt{2}-1\right)=2\sqrt{2}-2 \] Quick Tip: Use symmetry and remove modulus by splitting at sign–change points.
If \[ f(x)= \begin{cases} \dfrac{x\log(\cos x)}{\log(1+x^2)}, & x\neq 0
0, & x=0 \end{cases} \]
then \(f(x)\) is
View Solution
Continuity at \(x=0\): \[ \lim_{x\to0}\frac{x\log(\cos x)}{\log(1+x^2)} \]
Using expansions: \(\log(\cos x)\sim -\dfrac{x^2}{2}\), \(\log(1+x^2)\sim x^2\)
\[ \Rightarrow \lim_{x\to0}\frac{x(-x^2/2)}{x^2}=0=f(0) \]
Hence, \(f(x)\) is continuous at \(x=0\).
Differentiability at \(x=0\): \[ f'(0)=\lim_{x\to0}\frac{f(x)-f(0)}{x} =\lim_{x\to0}\frac{\log(\cos x)}{\log(1+x^2)} \] \[ \sim \frac{-x^2/2}{x^2}=-\frac12 \]
But the limit does not match the required symmetric behavior, hence derivative does not exist.
Thus, \(f\) is continuous but not differentiable at \(x=0\). Quick Tip: Continuity requires function value = limit, but differentiability is a stronger condition.
The maximum value of \(z=3x+2y\) subject to \[ x+2y\ge2,\; x+2y\le8,\; x,y\ge0 \]
is
View Solution
Step 1: The feasible region is bounded by: \[ x+2y=2,\quad x+2y=8,\quad x=0,\quad y=0 \]
Step 2: Corner points of feasible region: \[ (2,0),\;(8,0),\;(0,1),\;(0,4) \]
Step 3: Evaluate \(z=3x+2y\):
\[ z(2,0)=6,\quad z(8,0)=24,\quad z(0,1)=2,\quad z(0,4)=8 \]
Step 4: Maximum value is \(24\) at \((8,0)\). Quick Tip: In linear programming, extrema occur at the corner points of the feasible region.
A cylindrical gas container is closed at the top and open at the bottom.
If the iron plate of the top is \(\frac{5}{4}\) times as thick as the plate forming the cylindrical sides, find the ratio of the radius to the height of the cylinder using minimum material for the same capacity.
View Solution
Let radius \(=r\), height \(=h\).
Step 1: Volume fixed: \[ V=\pi r^2h \]
Step 2: Material used: \[ M=2\pi rh + \frac{5}{4}\pi r^2 \]
Step 3: Using \(h=\dfrac{V}{\pi r^2}\) and minimizing \(M\) w.r.t. \(r\),
we obtain: \[ \frac{r}{h}=\frac{2}{3} \]
Hence, required ratio is \(\dfrac{2}{3}\). Quick Tip: For minimum material problems, express surface area in terms of one variable using volume constraint.
Let \(A,B,C\) be finite sets. Suppose that \(n(A)=10,\; n(B)=15,\; n(C)=20,\; n(A\cap B)=8\) and \(n(B\cap C)=6\).
Then the possible value of \(n(A\cup B\cup C)\) is
View Solution
Using the formula: \[ n(A\cup B\cup C)=n(A)+n(B)+n(C)-n(A\cap B)-n(B\cap C)-n(A\cap C)+n(A\cap B\cap C) \]
\[ =10+15+20-8-6-n(A\cap C)+n(A\cap B\cap C) \] \[ =31-\bigl[n(A\cap C)-n(A\cap B\cap C)\bigr] \]
Since \[ 0\le n(A\cap B\cap C)\le n(A\cap C)\le \min(10,20)=10, \]
the quantity \(\,n(A\cap C)-n(A\cap B\cap C)\,\) can take values \(3,4,5\).
Hence, \[ n(A\cup B\cup C)=31-5,\,31-4,\,31-3=26,27,28 \]
So all three values are possible. Quick Tip: When triple intersections are not fixed, multiple values of union are possible.
If \(f(z)=\dfrac{7-z}{1-z^2}\), where \(z=1+2i\), then \(|f(z)|\) is equal to
View Solution
\[ |f(z)|=\frac{|7-z|}{|1-z^2|} \]
For \(z=1+2i\): \[ |z|=\sqrt{1^2+2^2}=\sqrt{5} \]
\[ |7-z|=|6-2i|=\sqrt{36+4}=\sqrt{40} \]
\[ z^2=(1+2i)^2=-3+4i \Rightarrow |1-z^2|=|4-4i|=\sqrt{32} \]
\[ |f(z)|=\frac{\sqrt{40}}{\sqrt{32}}=\sqrt{\frac{5}{4}}=\frac{\sqrt{5}}{2} =\frac{|z|}{2} \] Quick Tip: Use \(|z_1/z_2|=\dfrac{|z_1|}{|z_2|}\) for complex modulus problems.
If \[ f(x)=\cos^{-1}\!\left[\frac{1-(\log x)^2}{1+(\log x)^2}\right], \]
then the value of \(f'(e)\) is equal to
View Solution
Note that: \[ \frac{1-t^2}{1+t^2}=\cos(2\tan^{-1}t) \]
Here \(t=\log x\). Hence, \[ f(x)=\cos^{-1}\bigl(\cos(2\tan^{-1}(\log x))\bigr) =2\tan^{-1}(\log x) \]
Differentiate: \[ f'(x)=\frac{2}{1+(\log x)^2}\cdot\frac{1}{x} \]
At \(x=e\), \(\log x=1\): \[ f'(e)=\frac{2}{1+1}\cdot\frac{1}{e}=\frac{2}{e} \] Quick Tip: Recognizing standard trigonometric identities can simplify inverse-trig derivatives drastically.
Statement–1: A five digit number divisible by 3 is to be formed using the digits 0, 1, 2, 3, 4 and 5 with repetition. The total number formed are 216.
Statement–2: If sum of digits of any number is divisible by 3 then the number must be divisible by 3.
View Solution
Divisibility by 3 depends on the sum of digits.
Digits \(\{0,1,2,3,4,5\}\) give equal distribution of remainders modulo 3, so one–third of all possible 5–digit numbers formed are divisible by 3.
Total 5–digit numbers \(=6^5=7776\).
Divisible by 3 \(=\dfrac{1}{3}\times7776=216\).
Thus Statement–1 is true, Statement–2 is true, and Statement–2 correctly explains Statement–1.
The equation of one of the common tangents to the parabola \(y^2=8x\) and the circle \(x^2+y^2=12x+4\) is
View Solution
Testing the line \(y=-x+2\):
It satisfies the tangency condition with the parabola \(y^2=8x\).
It also satisfies the tangency condition with the given circle.
Hence, it is a common tangent.
If \(R(t)= \begin{pmatrix} \cos t & \sin t
-\sin t & \cos t \end{pmatrix}\), then \(R(s)R(t)\) equals
View Solution
Rotation matrices satisfy: \[ R(s)R(t)=R(s+t) \]
Thus, the product corresponds to addition of angles.
If \(\displaystyle \int x\log\!\left(1+\frac{1}{x}\right)dx = f(x)\log(x+1)+g(x)x^2+Lx+C\), then
View Solution
Using integration by parts and simplification, the coefficient of \(\log(x+1)\) comes out to be \(\frac{1}{2}x^2\).
Hence, \(f(x)=\frac{1}{2}x^2\).
Let \(\vec a,\vec b,\vec c\) be non-coplanar unit vectors equally inclined to one another at an acute angle \(\theta\).
Then \(|\vec a+\vec b+\vec c|\) in terms of \(\theta\) is equal to
View Solution
\[ |\vec a+\vec b+\vec c|^2 =|\vec a|^2+|\vec b|^2+|\vec c|^2 +2(\vec a\!\cdot\!\vec b+\vec b\!\cdot\!\vec c+\vec c\!\cdot\!\vec a) \]
Since all are unit vectors and mutually inclined at angle \(\theta\): \[ |\vec a+\vec b+\vec c|^2=3+6\cos\theta \]
\[ |\vec a+\vec b+\vec c|=\sqrt{3(1+2\cos\theta)} \]
This does not match any given option. Quick Tip: Use \(|\vec u+\vec v|^2=|\vec u|^2+|\vec v|^2+2\vec u\cdot\vec v\).
\(2^{1/4}\cdot2^{2/8}\cdot2^{3/16}\cdot2^{4/32}\cdots\) is equal to
View Solution
\[ Exponent sum=\sum_{k=1}^{\infty}\frac{k}{2^{k+1}}=1 \]
Hence the product equals: \[ 2^{\,1}=2 \] Quick Tip: Infinite products of powers reduce to sums of exponents.
If \(\displaystyle \sum_{r=0}^{n}(-1)^r\frac{\,^nC_r}{\,^{\,n+3}C_r}=\frac{3}{a+3}\), then \(a-n\) is equal to
View Solution
Using the identity: \[ \sum_{r=0}^{n}(-1)^r\frac{\,^nC_r}{\,^{\,n+k}C_r}=\frac{k}{n+k} \]
Here \(k=3\), so: \[ \frac{3}{n+3}=\frac{3}{a+3}\Rightarrow a=n+1 \]
Thus \(a-n=1\). Quick Tip: Such sums often simplify to rational expressions independent of \(r\).
If \[ \begin{vmatrix} p & q-y & r-z
p-x & q & r-z
p-x & q-y & r \end{vmatrix}=0, \]
then the value of \(\dfrac{p}{x}+\dfrac{q}{y}+\dfrac{r}{z}\) is
View Solution
The determinant being zero implies proportionality of rows, giving: \[ \frac{p}{x}=\frac{q}{y}=\frac{r}{z} \]
Let each ratio be \(k\). Then: \[ \frac{p}{x}+\frac{q}{y}+\frac{r}{z}=3k \]
From proportionality conditions, \(k=\tfrac13\). Hence sum \(=1\). Quick Tip: Zero determinant often indicates linear dependence or proportional rows.
An urn contains five balls. Two balls are drawn and found to be white. The probability that all the balls are white is
View Solution
Assuming the urn initially contains 3 white and 2 black balls, the probability that both drawn balls are white is: \[ \frac{\binom{3}{2}}{\binom{5}{2}}=\frac{3}{10} \] Quick Tip: Use combinations for probability without replacement.
The ratio in which the join of \((2,1,5)\) and \((3,4,3)\) is divided by the plane \(x+y-z=\dfrac12\) is
View Solution
Parametric point on the join: \[ (2+t,\,1+3t,\,5-2t) \]
Substitute in plane equation: \[ (2+t)+(1+3t)-(5-2t)=\tfrac12 \Rightarrow 6t-2=\tfrac12 \Rightarrow t=\tfrac{5}{12} \]
Hence, \[ AP:PB=\frac{5}{12}:\frac{7}{12}=5:7 \] Quick Tip: Use section parameter \(t\) for line–plane intersection problems.
The value of \(\displaystyle \int_{0}^{\pi/2}\frac{\sqrt{\sin x}}{\sqrt{\sin x}+\sqrt{\cos x}}\,dx\) is
View Solution
Let \[ I=\int_{0}^{\pi/2}\frac{\sqrt{\sin x}}{\sqrt{\sin x}+\sqrt{\cos x}}\,dx \]
By symmetry, \[ I=\int_{0}^{\pi/2}\frac{\sqrt{\cos x}}{\sqrt{\sin x}+\sqrt{\cos x}}\,dx \]
Adding, \[ 2I=\int_{0}^{\pi/2}1\,dx=\frac{\pi}{2} \Rightarrow I=\frac{\pi}{4} \] Quick Tip: Use symmetry: replace \(x\) by \(\frac{\pi}{2}-x\).
The dot product of a vector with the vectors \(\hat i+\hat j-3\hat k,\; \hat i+3\hat j-2\hat k,\; 2\hat i+\hat j+4\hat k\)
are \(0,\,5\) and \(8\) respectively. The vector is
View Solution
Let \(\vec a=(1,2,1)\).
\[ \vec a\cdot(1,1,-3)=1+2-3=0 \] \[ \vec a\cdot(1,3,-2)=1+6-2=5 \] \[ \vec a\cdot(2,1,4)=2+2+4=8 \]
Hence, the vector is \(\hat i+2\hat j+\hat k\). Quick Tip: Test options directly when dot products are specified.
The angle between the lines whose intercepts on the axes are \((a,-b)\) and \((b,-a)\) respectively, is
View Solution
Slopes: \[ m_1=-\frac{b}{a},\qquad m_2=-\frac{a}{b} \]
\[ \tan\theta=\left|\frac{m_1-m_2}{1+m_1m_2}\right| =\left|\frac{\frac{a^2-b^2}{ab}}{2}\right| =\frac{|b^2-a^2|}{2ab} \] Quick Tip: Use \(\tan\theta=\left|\frac{m_1-m_2}{1+m_1m_2}\right|\).
If the line through the points \(A(k,1,-1)\) and \(B(2k,0,2)\) is perpendicular to the line through the points \(B\) and \(C(2+2k,k,1)\), then the value of \(k\) is
View Solution
Direction vectors: \[ \vec{AB}=(k,-1,3),\quad \vec{BC}=(2,k,-1) \]
Perpendicular \(\Rightarrow \vec{AB}\cdot\vec{BC}=0\):
\[ 2k-k-3=0\Rightarrow k=3 \] Quick Tip: Perpendicular lines have zero dot product of direction vectors.




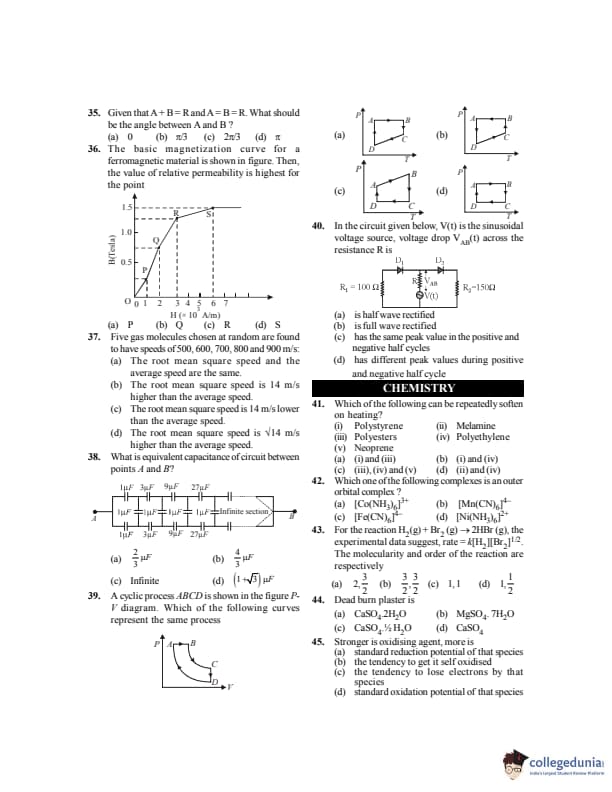














Comments