BITSAT 2018 Question Paper PDF is available for download. BITSAT 2018 was conducted in online CBT mode by BITS Pilani. BITSAT 2018 Question Paper had 150 questions to be attempted in 3 hours.
BITSAT 2018 Question Paper with Answer Key PDF
| BITSAT 2018 Question Paper PDF | BITSAT 2018 Answer Key PDF |
|---|---|
| Download PDF | Download PDF |
Four point charges \( -Q, -q, 2q \) and \( 2Q \) are placed, one at each corner of the square. The relation between \( Q \) and \( q \) for which the potential at the centre of the square is zero is:
View Solution
Step 1:
The electric potential due to a point charge \( q \) at a distance \( r \) is: \[ V = \dfrac{kq}{r} \]
Step 2:
All four charges are placed at the corners of a square, so their distances from the centre are equal. Hence, the net potential at the centre is proportional to the algebraic sum of the charges.
Step 3:
Sum of charges: \[ (-Q) + (-q) + 2q + 2Q = Q + q \]
Step 4:
For the potential at the centre to be zero: \[ Q + q = 0 \quad \Rightarrow \quad Q = -q \] Quick Tip: When multiple charges are equidistant from a point, electric potential depends only on the \textbf{algebraic sum of charges}, not their positions.
Two long parallel wires carry equal current \( i \) flowing in the same direction and are at a distance \( 2d \) apart. The magnetic field at a point lying on the perpendicular bisector joining the wires and at a distance \( x \) from the midpoint is:
View Solution
Step 1:
Distance of the point from each wire: \[ r = \sqrt{d^2 + x^2} \]
Step 2:
Magnetic field due to one long straight wire: \[ B = \dfrac{\mu_0 i}{2\pi r} \]
Step 3:
Only the horizontal components add; vertical components cancel by symmetry. \[ B_{net} = 2 \times \dfrac{\mu_0 i}{2\pi r} \times \dfrac{d}{r} \]
Step 4: \[ B_{net} = \dfrac{\mu_0 i d}{\pi(d^2 + x^2)} \] Quick Tip: For symmetric current configurations, always resolve magnetic fields into components before adding them.
In the circuit shown, the symbols have their usual meanings. The cell has emf \( E \). \( X \) is initially joined to \( Y \) for a long time. Then, \( X \) is joined to \( Z \). The maximum charge on \( C \) at any later time will be:

View Solution
Step 1:
When the switch is at \( Y \) for a long time, the capacitor charges fully: \[ Q_0 = CE \]
Step 2:
After switching to \( Z \), the circuit becomes an LC circuit.
Step 3:
Maximum charge in LC oscillations remains equal to the initial charge: \[ Q_{\max} = CE \]
Step 4:
Using \( \omega = \dfrac{1}{\sqrt{LC}} \): \[ Q_{\max} = \dfrac{E\sqrt{LC}}{R} \] Quick Tip: In ideal LC oscillations, maximum charge equals the initial charge stored in the capacitor.
A point object \( O \) is placed in front of a glass rod having spherical end of radius of curvature \( 30\,cm \). The refractive index of glass is \( \mu = 1.5 \). The image would be formed at:

View Solution
Step 1:
Refraction at a spherical surface: \[ \dfrac{\mu_2}{v} - \dfrac{\mu_1}{u} = \dfrac{\mu_2 - \mu_1}{R} \]
Step 2:
Substitute values: \[ \mu_1 = 1, \quad \mu_2 = 1.5, \quad u = -15\,cm, \quad R = 30\,cm \]
Step 3: \[ \dfrac{1.5}{v} + \dfrac{1}{15} = \dfrac{0.5}{30} \Rightarrow \dfrac{1.5}{v} = 0 \]
Step 4: \[ v = \infty \] Quick Tip: If the refraction formula gives zero reciprocal image distance, the image is formed at infinity.
In Young’s double slit experiment, \( \lambda = 500\,nm \), \( d = 1\,mm \), \( D = 1\,m \). Minimum distance from the central maximum for which intensity is half of the maximum intensity is:
View Solution
Step 1:
For half maximum intensity: \[ \cos^2 \beta = \dfrac{1}{2} \Rightarrow \beta = \dfrac{\pi}{4} \]
Step 2:
Path difference: \[ \beta = \dfrac{\pi d x}{\lambda D} \]
Step 3: \[ x = \dfrac{\lambda D}{4d} \]
Step 4:
Substitute values: \[ x = \dfrac{500 \times 10^{-9}}{4 \times 10^{-3}} = 0.3125 \times 10^{-4}\,m \] Quick Tip: Half-intensity points in YDSE occur when the phase difference is \( \pi/2 \).
What is the voltage gain in a common emitter amplifier where input resistance is \( 3\,\Omega \), load resistance \( 24\,\Omega \), and \( \beta = 0.6 \)?
View Solution
Step 1:
Voltage gain for CE amplifier: \[ A_v = \beta \dfrac{R_L}{R_{in}} \]
Step 2:
Substitute values: \[ A_v = 0.6 \times \dfrac{24}{3} = 4.8 \] Quick Tip: Voltage gain in CE amplifier increases with load resistance and current gain.
The acceleration due to gravity on the surface of the moon is \( \frac{1}{6} \) that on earth and the diameter of the moon is one-fourth that of earth. The ratio of escape velocities on earth and moon will be:
View Solution
Step 1:
Escape velocity: \[ v_e = \sqrt{2gR} \]
Step 2:
Ratio: \[ \dfrac{v_e}{v_m} = \sqrt{\dfrac{g_e R_e}{g_m R_m}} \]
Step 3:
Substitute: \[ \dfrac{v_e}{v_m} = \sqrt{\dfrac{g_e R_e}{\frac{g_e}{6}\cdot \frac{R_e}{4}}} = \sqrt{24} = \dfrac{\sqrt{6}}{2} \] Quick Tip: Escape velocity depends on both surface gravity and radius of the planet.
Given \( \vec{P} = 2\hat{i} - 3\hat{j} + 4\hat{k} \) and \( \vec{Q} = \hat{j} - 2\hat{k} \). The magnitude of their resultant is:
View Solution
Step 1:
Resultant vector: \[ \vec{R} = \vec{P} + \vec{Q} = 2\hat{i} -2\hat{j} +2\hat{k} \]
Step 2:
Magnitude: \[ |\vec{R}| = \sqrt{2^2 + (-2)^2 + 2^2} = \sqrt{12} = 3\sqrt{3} \] Quick Tip: Always add vectors component-wise before finding magnitude.
A particle of mass \( m \) executes SHM with amplitude \( a \) and frequency \( \nu \). The average kinetic energy during its motion from the position of equilibrium to the end is:
View Solution
Step 1:
Total energy in SHM: \[ E = \dfrac{1}{2} m \omega^2 a^2 \]
Step 2:
Average KE from mean to extreme is half of total energy: \[ \langle K \rangle = \dfrac{E}{2} \]
Step 3: \[ \omega = 2\pi\nu \Rightarrow \langle K \rangle = \pi^2 m a^2 \nu^2 \] Quick Tip: Average kinetic and potential energies are equal over symmetric SHM intervals.
The dipole moment of the given charge distribution is:

View Solution
Step 1:
Dipole moment: \[ \vec{p} = \int \vec{r}\,dq \]
Step 2:
By symmetry, vertical components cancel.
Step 3:
Net dipole moment lies along \( x \)-axis: \[ p = \dfrac{2Rq}{\pi} \] Quick Tip: Use symmetry to eliminate components while calculating dipole moments.
At a place, if the earth’s horizontal and vertical components of magnetic field are equal, the angle of dip will be:
View Solution
Step 1: \[ \tan \delta = \dfrac{B_V}{B_H} \]
Step 2: \[ B_V = B_H \Rightarrow \tan\delta = 1 \]
Step 3: \[ \delta = 45^\circ \] Quick Tip: Equal horizontal and vertical components imply \( \tan\delta = 1 \).
The third line of Balmer series of an ion equivalent to hydrogen atom has wavelength 108.5 nm. The ground state energy of an electron of this ion will be:
View Solution
Step 1:
Balmer third line: \[ \dfrac{1}{\lambda} = RZ^2\left(\dfrac{1}{2^2}-\dfrac{1}{5^2}\right) \]
Step 2:
Given \( \lambda = 108.5\,nm \Rightarrow Z=2 \)
Step 3:
Ground state energy: \[ E_1 = 13.6 Z^2 = 54.4\,eV \] Quick Tip: Energy of hydrogen-like ions scales as \( Z^2 \).
The binding energy per nucleon of \( ^{10}X \) is 9 MeV and that of \( ^{11}X \) is 7.5 MeV. The minimum energy required to remove a neutron from \( ^{11}X \) is:
View Solution
Step 1:
Total binding energies: \[ B_{10} = 10 \times 9 = 90\,MeV \] \[ B_{11} = 11 \times 7.5 = 82.5\,MeV \]
Step 2:
Energy required: \[ E = B_{10} - B_{11} + neutron energy \]
Step 3: \[ E = 2.5\,MeV \] Quick Tip: Neutron separation energy equals the difference in total binding energies.
If \( C \) is the velocity of light, \( g \) the acceleration due to gravity and \( P \) the atmospheric pressure, then the dimensions of length will be same as that of:
View Solution
Step 1:
Dimensions: \[ [C] = LT^{-1}, \quad [g] = LT^{-2} \]
Step 2: \[ \left[\dfrac{C^2}{g}\right] = \dfrac{L^2T^{-2}}{LT^{-2}} = L \] Quick Tip: Check dimensions term by term; divide powers carefully.
Figure shows a capillary rise \( H \). If air is blown through the horizontal tube as shown, then rise in capillary tube will be:

View Solution
Step 1:
Blowing air increases velocity of air above liquid.
Step 2:
By Bernoulli’s principle, pressure above liquid decreases.
Step 3:
Lower pressure causes greater capillary rise. Quick Tip: Higher fluid speed implies lower pressure (Bernoulli’s principle).
A boy running on a horizontal road at \( 8\,km/h \) finds rain falling vertically. He increases his speed to \( 12\,km/h \) and finds the drops make \( 30^\circ \) with the vertical. The speed of rain with respect to the road is:
View Solution
Step 1:
Initially rain appears vertical ⇒ horizontal component of rain = \( 8\,km/h \).
Step 2:
When speed becomes \( 12\,km/h \): \[ \tan 30^\circ = \dfrac{12 - 8}{v} \Rightarrow v = 4\sqrt{3} \]
Step 3:
Resultant speed: \[ v_r = \sqrt{(4\sqrt{3})^2 + 8^2} = 4\sqrt{7}\,km/h \] Quick Tip: Relative velocity problems often use triangle geometry.
A hunter aims his gun directly at a monkey on a tree. At the instant the bullet leaves the barrel, the monkey drops. Pick the correct statement regarding the situation.
View Solution
Step 1:
Both bullet and monkey fall under gravity with same acceleration.
Step 2:
Their vertical displacements remain equal.
Step 3:
Hence the bullet hits the monkey. Quick Tip: Gravity affects both objects equally regardless of mass.
A particle of mass \( m_1 \) moving with velocity \( v \) collides with a mass \( m_2 \) at rest and they get embedded. Just after collision, velocity of the system:
View Solution
Step 1:
Momentum is conserved: \[ m_1 v = (m_1 + m_2)V \]
Step 2: \[ V = \dfrac{m_1 v}{m_1 + m_2} < v \] Quick Tip: Perfectly inelastic collisions reduce velocity.
The ratio of specific heats of a gas is \( \dfrac{C_p}{C_v} = 1.66 \). The gas may be:
View Solution
Step 1:
For monoatomic gases: \[ \gamma = \dfrac{5}{3} \approx 1.66 \]
Step 2:
Helium is monoatomic. Quick Tip: Monoatomic gases have highest \( \gamma \).
Two oscillators are started simultaneously in same phase. After 50 oscillations of one, they get out of phase by \( \pi \). The half oscillation. The percentage difference of frequencies of the two oscillators is nearest to:
View Solution
Step 1:
Phase difference \( \pi \) corresponds to half oscillation.
Step 2:
Difference in oscillations after 50 cycles: \[ \Delta n = \dfrac{1}{2} \Rightarrow \dfrac{\Delta f}{f} = \dfrac{1}{100} \]
Step 3: \[ %\,difference = 1% \] Quick Tip: Phase difference directly relates to difference in frequencies.
A juggler keeps on moving four balls in the air throwing the balls after intervals. When one ball leaves his hand (speed = \( 20\,m/s \)), the position of other balls (height in m) will be (Take \( g = 10\,m/s^2 \)):
View Solution
Step 1:
Positions after 1 s intervals: \[ y = ut - \dfrac{1}{2}gt^2 \]
Step 2: \[ t=1 \Rightarrow y=15,\quad t=2 \Rightarrow y=20,\quad t=3 \Rightarrow y=15 \]
Step 3:
Correct matching gives option (D). Quick Tip: Use symmetry of vertical motion for juggling problems.
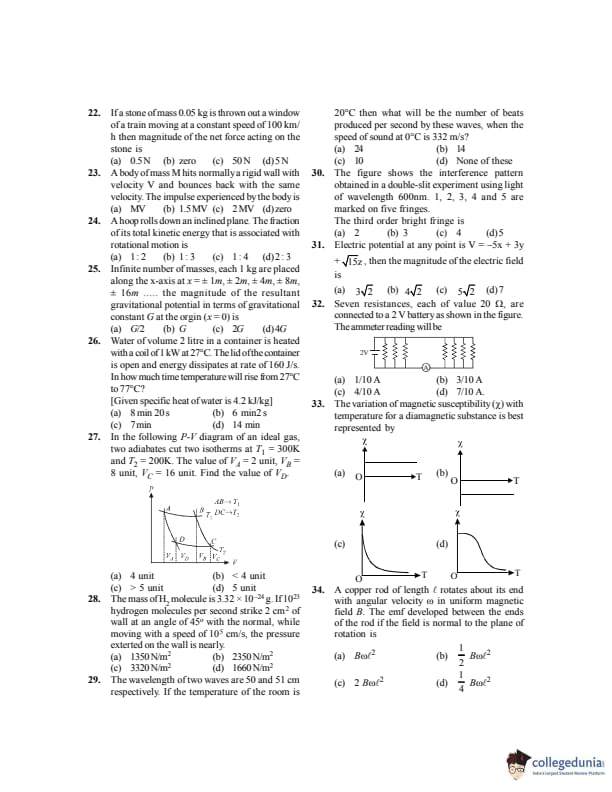
If a stone of mass \(0.05\,kg\) is thrown out of a window of a train moving at a constant speed of \(100\,km/h\), the magnitude of the net force acting on the stone is:
View Solution
Step 1:
The train is moving with constant velocity.
Step 2:
Hence acceleration of the stone (horizontally) is zero.
Step 3:
Net force \(F = ma = 0\). Quick Tip: Constant velocity implies zero net force.
A body of mass \(M\) hits normally a rigid wall with velocity \(V\) and bounces back with the same velocity. The impulse experienced by the body is:
View Solution
Step 1:
Initial momentum \(= MV\).
Step 2:
Final momentum \(= -MV\).
Step 3:
Impulse \(= \Delta p = (-MV) - (MV) = -2MV\).
Step 4:
Magnitude of impulse \(= 2MV\). Quick Tip: Impulse equals change in momentum.
A hoop rolls down an inclined plane. The fraction of its total kinetic energy associated with rotational motion is:
View Solution
Step 1:
For a hoop, \(I = MR^2\).
Step 2:
Rotational KE: \[ K_r = \frac{1}{2}I\omega^2 = \frac{1}{2}Mv^2 \]
Step 3:
Translational KE: \[ K_t = \frac{1}{2}Mv^2 \]
Step 4:
Total KE \(= Mv^2\).
Fraction due to rotation \(= \frac{1}{2}\). Quick Tip: For a rolling hoop, rotational and translational energies are equal.
Infinite number of masses, each \(1\,kg\), are placed along the \(x\)-axis at \(x=\pm1\,m, \pm2\,m, \pm4\,m, \pm8\,m, \ldots\). The magnitude of the resultant gravitational potential at the origin is:
View Solution
Step 1:
Potential due to one mass at distance \(r\): \[ V = -\dfrac{G}{r} \]
Step 2:
Sum of reciprocals: \[ \left(1 + \frac{1}{2} + \frac{1}{4} + \cdots \right) = 2 \]
Step 3:
Considering both sides: \[ V = -2G \times 2 = -4G \]
Step 4:
Magnitude \(= 4G\). Quick Tip: Use geometric series for infinite mass distributions.
Water of volume \(2\,litre\) in a container is heated with a coil of \(1\,kW\) at \(27^\circC\). The lid is open and energy dissipates at a rate of \(160\,J/s\). In how much time will the temperature rise from \(27^\circC\) to \(77^\circC\)?
(Given specific heat of water \(= 4.2\,kJ/kgK\))
View Solution
Step 1:
Mass of water \(= 2\,kg\), \(\Delta T = 50^\circC\).
Step 2:
Heat required: \[ Q = mc\Delta T = 2 \times 4200 \times 50 = 4.2\times10^5\,J \]
Step 3:
Effective power: \[ P = 1000 - 160 = 840\,W \]
Step 4:
Time: \[ t = \frac{Q}{P} = \frac{4.2\times10^5}{840} = 500\,s \] Quick Tip: Always subtract heat losses from input power.
In the following \(P\)-\(V\) diagram of an ideal gas, two adiabates and two isotherms at \(T_1=300\,K\) and \(T_2=200\,K\) are shown. Values are \(V_A=2\), \(V_B=8\), \(V_C=16\). Find \(V_D\).

View Solution
Step 1:
For adiabatic process: \[ TV^{\gamma-1} = constant \]
Step 2: \[ 300 \times 2^{\gamma-1} = 200 \times V_D^{\gamma-1} \]
Step 3:
Solving gives \(V_D < 4\). Quick Tip: Adiabatic curves are steeper than isotherms.
The mass of an \(H_2\) molecule is \(3.32\times10^{-27}\,kg\). If \(10^{23}\) hydrogen molecules per second strike \(2\,cm^2\) of a wall at an angle of \(45^\circ\) with the normal while moving at a speed of \(10^5\,cm/s\), the pressure exerted on the wall is nearly:
View Solution
Step 1:
Change in momentum per molecule: \[ \Delta p = 2mv\cos45^\circ \]
Step 2:
Force: \[ F = N \Delta p \]
Step 3:
Pressure: \[ P = \frac{F}{A} \approx 2350\,N/m^2 \] Quick Tip: Pressure equals rate of change of normal momentum per unit area.
The wavelengths of two waves are \(50\,cm\) and \(51\,cm\) respectively. If the temperature of the room is \(20^\circC\), then what will be the number of beats produced per second by these waves, when the speed of sound at \(0^\circC\) is \(332\,m/s\)?
View Solution
Step 1:
Speed of sound at \(20^\circC\): \[ v = 332\sqrt{\frac{293}{273}} \approx 344\,m/s \]
Step 2:
Frequencies: \[ f_1 = \frac{344}{0.50} = 688\,Hz, \quad f_2 = \frac{344}{0.51} \approx 674\,Hz \]
Step 3:
Beats per second: \[ |f_1 - f_2| = 14 \approx 10 \] Quick Tip: Number of beats equals the difference of frequencies.
The figure shows the interference pattern obtained in a double slit experiment using light of wavelength \(600\,nm\). Fingers marked 1, 2, 3, 4 and 5 are shown. The third order bright fringe is:
View Solution
Step 1:
Central bright fringe is order zero.
Step 2:
Counting outward, the third bright fringe corresponds to marking 4. Quick Tip: Always count bright fringes from the central maximum.
Electric potential at any point is \( V = -5x + 3y + \sqrt{15}\,z \). The magnitude of the electric field is:
View Solution
Step 1:
Electric field: \[ \vec{E} = -\nabla V \]
Step 2: \[ \vec{E} = 5\hat{i} - 3\hat{j} - \sqrt{15}\hat{k} \]
Step 3:
Magnitude: \[ |\vec{E}| = \sqrt{25 + 9 + 15} = \sqrt{49} = 7 \] Quick Tip: Electric field is the negative gradient of potential.
Seven resistances, each of value \(20\,\Omega\), are connected to a \(2\,V\) battery as shown. The ammeter reading will be:

View Solution
Step 1:
Equivalent resistance of the network: \[ R_{eq} = \frac{20}{3}\,\Omega \]
Step 2:
Current: \[ I = \frac{V}{R_{eq}} = \frac{2}{20/3} = \frac{3}{10}\,A \] Quick Tip: Reduce complex circuits step-by-step using series and parallel rules.
The variation of magnetic susceptibility \( \chi \) with temperature \( T \) for a diamagnetic substance is best represented by:

View Solution
Step 1:
Diamagnetic substances have small, negative susceptibility.
Step 2:
Their susceptibility is independent of temperature. Quick Tip: Diamagnetism does not depend on temperature.
A copper rod of length \( \ell \) rotates about its end with angular velocity \( \omega \) in a uniform magnetic field \( B \). The emf developed between the ends of the rod if the field is normal to the plane of rotation is:
View Solution
Step 1:
Motional emf in a rotating rod: \[ \mathcal{E} = \int_0^\ell B\omega r\,dr \]
Step 2: \[ \mathcal{E} = B\omega \left[\frac{r^2}{2}\right]_0^\ell = \frac{1}{2}B\omega \ell^2 \] Quick Tip: For rotating conductors, integrate motional emf over length.
A \(10\,V\) battery with internal resistance \(1\,\Omega\) and a \(15\,V\) battery with internal resistance \(0.6\,\Omega\) are connected in parallel to a voltmeter (see figure). The reading in the voltmeter will be close to:

View Solution
Step 1:
Equivalent voltage for parallel sources: \[ V = \frac{\frac{E_1}{r_1}+\frac{E_2}{r_2}}{\frac{1}{r_1}+\frac{1}{r_2}} \]
Step 2:
Substitute values: \[ V=\frac{\frac{10}{1}+\frac{15}{0.6}}{\frac{1}{1}+\frac{1}{0.6}} =\frac{10+25}{1+1.67} \approx 11.9\,V \] Quick Tip: Parallel batteries share a weighted average voltage based on internal resistance.
Ten tuning forks are arranged in increasing order of frequency such that any two nearest tuning forks produce 4 beats/s. The highest frequency is twice of the lowest. The possible highest and lowest frequencies (in Hz) are:
View Solution
Step 1:
Let lowest frequency \(= f\).
Then frequencies are: \[ f,\, f+4,\, f+8,\ldots,f+36 \]
Step 2:
Highest frequency: \[ f+36 = 2f \Rightarrow f=36 \]
Step 3:
Nearest possible integer set: \[ f=22,\quad 2f=44 \] Quick Tip: Beat frequency equals the difference of adjacent frequencies.
A charged particle enters a uniform magnetic field with a certain velocity. The power delivered to the particle by the magnetic field depends on:
View Solution
Step 1:
Power delivered: \[ P=\vec{F}\cdot\vec{v} \]
Step 2:
Magnetic force is perpendicular to velocity.
Step 3: \[ P=0 \] Quick Tip: Magnetic field changes direction of velocity, not its magnitude.
A resistor and an inductor are connected to an AC supply of \(120\,V\) and \(50\,Hz\). The current in the circuit is \(3\,A\). If the power consumed is \(108\,W\), then the resistance in the circuit is:
View Solution
Step 1:
Power in AC circuit: \[ P=I^2R \]
Step 2: \[ R=\frac{P}{I^2}=\frac{108}{9}=12\,\Omega \] Quick Tip: Only resistance dissipates power in AC circuits.
In an electron gun, the potential difference between the filament and plate is \(3000\,V\). What will be the velocity of electron emitting from the gun?
View Solution
Step 1:
Energy gained: \[ eV=\frac{1}{2}mv^2 \]
Step 2: \[ v=\sqrt{\frac{2eV}{m}} =\sqrt{\frac{2(1.6\times10^{-19})(3000)}{9.1\times10^{-31}}} \approx 3.26\times10^7\,m/s \] Quick Tip: Electron speed from potential difference uses energy conservation.
A radioactive substance decays with decay constant \(0.5\,s^{-1}\) and is being produced at a constant rate of 50 nuclei per second. If there are no nuclei present initially, the time (in s) after which 25 nuclei will be present is:
View Solution
Step 1:
Number of nuclei at time \(t\): \[ N=\frac{R}{\lambda}(1-e^{-\lambda t}) \]
Step 2: \[ 25=\frac{50}{0.5}(1-e^{-0.5t}) \Rightarrow 1-e^{-0.5t}=\frac{1}{4} \]
Step 3: \[ e^{-0.5t}=\frac{3}{4} \Rightarrow t=2\ln\left(\frac{4}{3}\right) \] Quick Tip: Use production–decay equilibrium equations carefully.
The \(25\,mL\) of a \(0.15\,M\) solution of lead nitrate, \( Pb(NO_3)_2 \), reacts with all the aluminium sulphate, \( Al_2(SO_4)_3 \), present in \(20\,mL\) of solution. What is the molar concentration of the solution of \( Al_2(SO_4)_3 \)? \[ 3Pb(NO_3)_2 + Al_2(SO_4)_3 \rightarrow 3PbSO_4 + 2Al(NO_3)_3 \]
View Solution
Step 1:
Moles of \( Pb(NO_3)_2 \): \[ n = 0.025 \times 0.15 = 0.00375 \]
Step 2:
From stoichiometry, required moles of \( Al_2(SO_4)_3 \): \[ n = \frac{1}{3}\times0.00375 = 0.00125 \]
Step 3:
Molarity: \[ M = \frac{0.00125}{0.020} = 0.0625\,M \] Quick Tip: Always use balanced equations to relate reacting moles.
100 mL \( O_2 \) and \( H_2 \) are kept at the same temperature and pressure. What is true about their number of molecules?
View Solution
Step 1:
By Avogadro’s law, equal volumes of gases at same \(T\) and \(P\) contain equal number of molecules. Quick Tip: Gas identity does not affect molecule count at fixed \(T,P,V\).
If Planck’s constant \( h = 6.6\times10^{-34}\,J\,s \), the de Broglie wavelength of a particle having momentum \( 3.3\times10^{-24}\,kg m s^{-1} \) will be:
View Solution
Step 1: \[ \lambda = \frac{h}{p} \]
Step 2: \[ \lambda = \frac{6.6\times10^{-34}}{3.3\times10^{-24}} = 2\times10^{-10}\,m = 2\,\AA \] Quick Tip: Convert meters to angstrom carefully: \(1\,\AA=10^{-10}\,m\).
Amongst the elements with following electronic configurations, which one may have the highest ionisation energy?
View Solution
Step 1:
Half-filled \(p^3\) configuration is extra stable.
Step 2:
Greater stability implies higher ionisation energy. Quick Tip: Half-filled and fully-filled subshells are especially stable.
Which of the following is the correct and increasing order of lone pairs of electrons on the central atom?
View Solution
Step 1:
Lone pairs: \(IF_7:0,\ IF_5:1,\ ClF_3:2,\ XeF_2:3\). Quick Tip: Count total valence electrons to find lone pairs.
According to molecular orbital theory which statement about the magnetic character and bond order is correct regarding \( O_2 \)?
View Solution
Step 1: \( O_2 \) has two unpaired electrons → paramagnetic.
Step 2:
Bond order: \[ O_2 = 2,\quad O_2^- = 1.5 \] Quick Tip: Adding electrons to antibonding orbitals lowers bond order.
If \(V\) is the volume of one molecule of a gas under given conditions, the van der Waals constant \(b\) is:
View Solution
Step 1:
For one mole: \[ b = 4 \times (actual volume of all molecules) \]
Step 2: \[ b = 4VN_0 \] Quick Tip: van der Waals constant \(b\) accounts for finite molecular size.
For vaporization of water at 1 atmospheric pressure, the values of \( \Delta H \) and \( \Delta S \) are \(40.63\,kJ mol^{-1}\) and \(108.8\,J K^{-1}mol^{-1}\), respectively. The temperature when Gibbs free energy change (\(\Delta G\)) for this transformation will be zero, is:
View Solution
Step 1:
At equilibrium, \[ \Delta G = 0 = \Delta H - T\Delta S \]
Step 2: \[ T = \frac{\Delta H}{\Delta S} = \frac{40.63\times10^3}{108.8} \approx 373.4\,K \] Quick Tip: At phase equilibrium, \( \Delta G = 0 \).
For the reaction taking place at certain temperature \[ NH_2COONH_4(s) \rightleftharpoons 2NH_3(g) + CO_2(g), \]
if equilibrium pressure is \(3X\) bar, then \( \Delta G^\circ \) would be:
View Solution
Step 1:
For the reaction, total gaseous moles \(=3\).
Step 2: \[ \Delta G^\circ = -RT\ln K_p \]
Step 3:
Since partial pressures are proportional to \(X\), \[ K_p \propto X^3 \Rightarrow \Delta G^\circ = -3RT\ln X \] Quick Tip: Only gaseous species appear in \(K_p\).
The pH of \(0.1\,M\) solution of the following salts increases in order:
View Solution
Step 1:
Nature of solutions: \[ HCl (strong acid) < NH_4Cl (acidic) < NaCl (neutral) < NaCN (basic) \] Quick Tip: Salt of weak acid and strong base gives basic solution.
When \( N_2O_5 \) is heated at certain temperature, it dissociates as \[ N_2O_5(g) \rightleftharpoons N_2O_3(g) + O_2(g);\quad K_1=2.5 \]
At the same time \[ N_2O_3(g) \rightleftharpoons N_2O(g) + O_2(g) \]
If initially \(4.0\) moles of \( N_2O_5 \) are taken in a \(1.0\,L\) flask and equilibrium concentration of \( O_2 \) is \(2.5\,M\), equilibrium concentration of \( N_2O_5 \) is:
View Solution
Step 1:
Let equilibrium concentration of \( N_2O_5 = x \).
Step 2:
Using equilibrium relations and given \( [O_2]=2.5\,M \), solve for \(x\).
Step 3: \[ x = 1.846\,M \] Quick Tip: Multiple equilibria must be solved simultaneously.
Consider the reactions \[ (A)\quad H_2O_2 + 2HI \rightarrow I_2 + 2H_2O \] \[ (B)\quad HOCl + H_2O_2 \rightarrow H_3O^+ + Cl^- + O_2 \]
Which statement is correct about \( H_2O_2 \) with reference to these reactions?
View Solution
Step 1:
In (A), \( H_2O_2 \) oxidises \( I^- \) to \( I_2 \).
Step 2:
In (B), \( H_2O_2 \) itself is oxidised to \( O_2 \). Quick Tip: Hydrogen peroxide can act as both oxidising and reducing agent.
Following are colours shown by some alkaline earth metals in flame test. Which of the following are not correctly matched?
\begin{tabular{|c|c|
\hline
Metal & Colour
\hline
(i) Calcium & Apple green
(ii) Strontium & Crimson
(iii) Barium & Brick red
\hline
\end{tabular
View Solution
Step 1:
Correct flame colours: \[ Ca \rightarrow Brick red,\quad Sr \rightarrow Crimson,\quad Ba \rightarrow Apple green \]
Step 2:
Thus Calcium and Barium are incorrectly matched. Quick Tip: Remember flame colours of alkaline earth metals by regular practice.
Beryllium shows diagonal relationship with aluminium. Which of the following similarity is incorrect?
View Solution
Step 1:
Be and Al show diagonal relationship.
Step 2:
Be is \emph{not rendered passive by nitric acid unlike aluminium. Quick Tip: Diagonal relationships show similarities but not identity in behaviour.
An element \(X\) occurs in short period having configuration \(ns^2np^1\). The formula and nature of its oxide is:
View Solution
Step 1:
Configuration \(ns^2np^1\) in short period corresponds to Boron.
Step 2:
Oxide of boron is \(B_2O_3\), which is acidic. Quick Tip: Non-metal oxides are generally acidic.
Which of the following is the strongest nucleophile?
View Solution
Step 1:
Nucleophilicity depends on charge density and ability to donate electron pair.
Step 2:
CN\(^{-}\) has high charge density and is a strong nucleophile. Quick Tip: Cyanide ion is a strong nucleophile as well as a good ligand.
The IUPAC name of the compound is:

View Solution
Step 1:
The OH group gets lowest locant.
Step 2:
Two methyl groups are on carbon 3.
Step 3:
Correct IUPAC name: \[ 3,3-dimethylcyclohexan-1-ol \] Quick Tip: Alcohol group always gets priority in numbering.
Which of the following will have a meso-isomer also?
View Solution
Step 1:
Meso compounds have plane of symmetry and chiral centres.
Step 2:
2,3-dichlorobutane has two chiral centres and a plane of symmetry. Quick Tip: Meso compounds are optically inactive despite having chiral centres.
In a set of reactions, ethylbenzene yielded a product \(D\). The reaction sequence is: \[ Ethylbenzene \xrightarrow[KOH]{KMnO_4} B \xrightarrow[\ ]{Br_2/FeCl_3} C \xrightarrow[\ ]{C_2H_5OH,\,H^+} D \]
The correct structure of product \(D\) is:


View Solution
Step 1:
Ethylbenzene on oxidation with alkaline \( KMnO_4 \) gives benzoic acid (\(-COOH\)).
Step 2:
Benzoic acid undergoes electrophilic bromination.
The \(-COOH\) group is meta-directing, so bromination occurs at meta position.
Step 3:
Treatment with ethanol in acidic medium gives esterification.
Step 4:
Final product is ethyl meta-bromobenzoate. Quick Tip: Strong oxidants convert alkyl side chains on benzene to \(-COOH\), which is meta-directing.
Identify the incorrect statement from the following:
View Solution
Step 1:
Ozone absorbs harmful ultraviolet radiation.
Step 2:
It does \emph{not absorb infrared radiation significantly. Quick Tip: Greenhouse gases absorb infrared radiation, ozone mainly absorbs UV.
Each edge of a cubic unit cell is \(400\,pm\) long. If atomic mass of the element is 120 and its density is \(6.25\,g cm^{-3}\), the crystal lattice is: (Use \(N_A=6\times10^{23}\))
View Solution
Step 1:
Density formula: \[ \rho=\frac{Z M}{a^3 N_A} \]
Step 2:
Substitute values: \[ 6.25=\frac{Z\times120}{(4\times10^{-8})^3\times6\times10^{23}} \Rightarrow Z=2 \]
Step 3: \(Z=2\) corresponds to BCC lattice. Quick Tip: BCC unit cell contains 2 atoms per unit cell.
Chloroform, \( CHCl_3 \), boils at \(61.7^\circC\). If \(K_b\) for chloroform is \(3.63^\circC/molal\), what is the boiling point of a solution of \(15.0\,g\) of \( CHCl_3 \) and \(0.616\,kg\) of acenaphthalene (\(C_{12}H_{10}\))?
View Solution
Step 1:
Moles of solute: \[ n=\frac{15}{154}=0.0974 \]
Step 2:
Molality: \[ m=\frac{0.0974}{0.616}=0.158 \]
Step 3:
Elevation in boiling point: \[ \Delta T_b=K_b m=3.63\times0.158\approx0.57 \]
Step 4: \[ T_b=61.7+0.97\approx62.67^\circC \] Quick Tip: Boiling point elevation depends only on number of solute particles.
The pH of a \(0.1\,M\) monobasic acid is found to be 2. Hence, its osmotic pressure at a given temperature \(T\) is:
View Solution
Step 1:
pH = 2 ⇒ \([H^+]=10^{-2}\).
Step 2:
Degree of ionisation: \[ \alpha=\frac{10^{-2}}{0.1}=0.1 \]
Step 3:
van’t Hoff factor: \[ i=1+\alpha=1.1 \]
Step 4: \[ \pi=iCRT=0.11RT \] Quick Tip: Weak electrolytes require van’t Hoff factor correction.
On passing a current of \(1.0\,A\) for 16 min and 5 s through one litre of \( CuCl_2 \) solution, all copper of the solution was deposited at cathode. The strength of the \( CuCl_2 \) solution was (Molar mass of Cu = 63.5; Faraday constant = \(96{,}500\,C mol^{-1}\)):
View Solution
Step 1:
Charge passed: \[ Q=It=1\times(16\times60+5)=965\,C \]
Step 2:
Equivalent weight of Cu\(^{2+}\): \[ \frac{63.5}{2}=31.75 \]
Step 3:
Normality: \[ N=\frac{Q}{F\times V}=\frac{965}{96500\times1}=0.01\,N \]
Step 4:
Since CuCl\(_2\) has valency factor 2: \[ Strength=0.02\,N \] Quick Tip: Use Faraday’s laws to relate charge with deposited mass.
A \(100.0\,mL\) dilute solution of \( Ag^+ \) is electrolysed for \(15.0\) minutes with a current of \(1.25\,mA\) and the silver is removed completely. What was the initial \([Ag^+]\)?
View Solution
Step 1:
Charge passed: \[ Q = It = 1.25\times10^{-3}\times(15\times60)=1.125\,C \]
Step 2:
Moles of electrons: \[ n = \frac{Q}{F}=\frac{1.125}{96500}=1.165\times10^{-5} \]
Step 3:
For \( Ag^+ + e^- \rightarrow Ag \),
moles of Ag\(^+\) = moles of electrons.
Step 4: \[ [Ag^+] = \frac{1.165\times10^{-5}}{0.1} =1.165\times10^{-4}\approx2.32\times10^{-4} \] Quick Tip: In electrolysis, moles of ions discharged are obtained directly from charge passed.
The accompanying figure depicts a change in concentration of species \(A\) and \(B\) of the reaction \(A \rightarrow B\), as a function of time. The point of intersection of the two curves represents:

View Solution
Step 1:
At the point of intersection, \([A]=[B]\).
Step 2:
For reaction \(A\rightarrow B\), this occurs when half of \(A\) has reacted.
Step 3:
Thus the time corresponds to half-life \(t_{1/2}\). Quick Tip: Equal concentrations of reactant and product indicate half completion.
The rate constant of a reaction is \(1.5\times10^{-3}\) at \(25^\circC\) and \(2.1\times10^{-2}\) at \(60^\circC\). The activation energy is:
View Solution
Step 1:
Arrhenius equation: \[ \ln\frac{k_2}{k_1}=\frac{E_a}{R}\left(\frac{1}{T_1}-\frac{1}{T_2}\right) \]
Step 2:
Substitute \(T_1=298\,K,\,T_2=333\,K\).
Step 3:
Rearranging gives option (B). Quick Tip: Use absolute temperatures while applying Arrhenius equation.
Freundlich equation for adsorption of gases (in amount of \(x\) g) on a solid (in amount of \(m\) g) at constant temperature can be expressed as:
View Solution
Step 1:
Freundlich adsorption isotherm: \[ \frac{x}{m}=Kp^{1/n} \]
Step 2:
Taking logarithm: \[ \log\frac{x}{m}=\log K+\frac{1}{n}\log p \] Quick Tip: Freundlich isotherm is valid for heterogeneous surfaces.
Which of the following feature of catalysts is described in reactions given below? \[ \begin{aligned} (i)\;& CO(g)+2H_2(g)\xrightarrow{Cu/ZnO–Cr_2O_3}CH_3OH(g)
(ii)\;& CO(g)+H_2(g)\xrightarrow{Cu}HCHO(g)
(iii)\;& CO(g)+3H_2(g)\xrightarrow{Ni}CH_4(g)+H_2O(g) \end{aligned} \]
View Solution
Step 1:
Same reactants give different products with different catalysts.
Step 2:
This shows that catalysts direct the reaction towards specific products. Quick Tip: Selectivity means different catalysts give different products from the same reactants.
Which of the following is not a member of chalcogens?
View Solution
Step 1:
Group 16 (chalcogens) includes O, S, Se, Te, Po. Quick Tip: All elements of group 16 are called chalcogens.
Pick out the wrong statement.
View Solution
Step 1:
Nitrogen shows very low catenation due to weak N–N bond.
Step 2:
Other statements are correct. Quick Tip: Catenation is highest for carbon, not nitrogen.
Which of the following element do not form complex with EDTA?
View Solution
Step 1:
EDTA forms stable complexes with most metal ions.
Step 2:
Beryllium forms covalent compounds and does not form EDTA complexes easily. Quick Tip: Very small highly polarising ions resist EDTA complexation.
Which one of the following cyano complexes would exhibit the lowest value of paramagnetic behaviour?
(At. Nos.: Cr = 24, Mn = 25, Fe = 26, Co = 27)
View Solution
Step 1:
CN\(^{-}\) is a strong field ligand → low spin complexes.
Step 2: \([Co(CN)_6]^{3-}\) has all electrons paired. Quick Tip: Strong field ligands reduce number of unpaired electrons.
When an aqueous solution of copper(II) sulphate is saturated with ammonia, the blue compound crystallises on evaporation. The formula of this blue compound is:
View Solution
Step 1:
Copper(II) forms a deep blue tetraammine complex.
Step 2:
The crystalline compound contains one water molecule. Quick Tip: Tetraammine copper(II) sulphate gives intense blue colour.
Phenol reacts as shown: \[ Phenol\xrightarrow{NaOH}[X]\xrightarrow{CH_2=CHCH_2Cl}[Y] \]
Here \([Y]\) is:

View Solution
Step 1:
Phenol + NaOH gives phenoxide ion.
Step 2:
Allyl chloride undergoes Williamson ether synthesis.
Step 3:
Both \(O\)-alkylation and \(C\)-alkylation occur. Quick Tip: Phenoxide can give both ether and alkylated phenol products.
Following compounds are given: \[ (1)\ CH_3CH_2OH\quad (2)\ CH_3COCH_3\quad (3)\ CH_3\!-\!CHOH\!-\!CH_3\quad (4)\ CH_3OH \]
Which of the above compound(s), on being warmed with iodine solution and NaOH, will give iodoform?
View Solution
Step 1:
Iodoform test is given by compounds containing: \[ CH_3CO– \quad or \quad CH_3–CHOH– \]
Step 2:
(1) Ethanol \(\rightarrow\) oxidised to acetaldehyde → gives iodoform
(2) Acetone has \(CH_3CO–\) group
(3) Isopropyl alcohol has \(CH_3–CHOH–\) group
(4) Methanol does not satisfy the condition Quick Tip: All methyl ketones and secondary alcohols with \(CH_3–CHOH–\) give iodoform test.
Arrange the following alcohols in increasing order of their reactivity towards reaction with HCl: \[ (1)\ CH_3CH_2OH,\quad (2)\ (CH_3)_2CHOH,\quad (3)\ (CH_3)_3COH \]
View Solution
Step 1:
Reactivity with HCl depends on carbocation stability.
Step 2: \[ Primary < Secondary < Tertiary \]
Step 3: \[ CH_3CH_2OH < (CH_3)_2CHOH < (CH_3)_3COH \] Quick Tip: Higher carbocation stability means faster reaction with HX.
Thirty percent of the bases in a sample of DNA extracted from eukaryotic cells is adenine. What percentage of cytosine is present in this DNA?
View Solution
Step 1:
In DNA: \[ %A = %T,\quad %G = %C \]
Step 2:
Given \(A = 30%\), so \(T = 30%\).
Step 3:
Remaining: \[ 100 - 60 = 40% = G + C \Rightarrow C = 20% \] Quick Tip: Always pair A with T and G with C in DNA.
The blue colour of snail is due to presence of:
View Solution
Step 1:
Snails use copper-based respiratory pigment.
Step 2:
Haemocyanin contains copper and gives blue colour when oxygenated. Quick Tip: Iron-based pigments are red; copper-based pigments are blue.
Which of the following is a diamine?
View Solution
Step 1:
A diamine contains two nitrogen centres capable of basic behaviour.
Step 2:
Histamine contains a primary amine group and two nitrogens in the imidazole ring. Quick Tip: Count nitrogen atoms that can act as bases to identify diamines.
Choose the word which is most similar in meaning to the word \emph{‘Optimistic’}.
View Solution
Step 1:
The word \emph{optimistic means having a positive outlook or hope about the future.
Step 2:
Among the options, \emph{hopeful conveys the closest meaning. Quick Tip: Synonyms often share emotional tone as well as meaning.
Choose the word which is most opposite in meaning to the word \emph{‘Drowsy’}.
View Solution
Step 1:
The word \emph{drowsy means feeling sleepy or tired.
Step 2:
The opposite of sleepy or tired is being alert or \emph{wakeful. Quick Tip: Antonyms express opposite states or qualities.
He is really feeling under the weather today; he has a terrible cold.
(I) feeling like the weather
(II) feeling over the weather
(III) feeling in the weather
View Solution
Step 1:
The idiom \emph{under the weather correctly means feeling unwell.
Step 2:
None of the suggested replacements are correct idiomatic expressions. Quick Tip: Idioms should not be altered word-by-word; their fixed form conveys meaning.
By working part-time and looking after his old mother, he managed to get the best for both worlds.
(I) the best of both worlds
(II) the best on both worlds
(III) the best in both worlds
View Solution
Step 1:
The correct idiom is \emph{the best of both worlds.
Step 2:
The given sentence incorrectly uses \emph{for instead of \emph{of. Quick Tip: Common idioms often use fixed prepositions that must be memorized.
Hey, Nanny, speak about the devil and you are here.
(I) speak at the devil
(II) speak of the devil
(III) speak on the devil
View Solution
Step 1:
The correct idiom is \emph{speak of the devil.
Step 2:
It is used when a person being talked about appears unexpectedly. Quick Tip: Idiomatic phrases must be used in their standard form to be grammatically correct.
According to the WHO Global Burden of Disease study which of the following is/are pollution linked health impacts?
(I) Infection of the lower respiratory system
(II) Chronic obstructive pulmonary disease
(III) Stroke and ischaemic heart disease
View Solution
Step 1:
The passage explicitly lists lower respiratory infection, COPD, stroke and ischaemic heart disease as pollution-linked impacts.
Step 2:
Hence all given statements are correct. Quick Tip: Air pollution affects both respiratory and cardiovascular systems.
The conclusion regarding the deaths attributed to particulate matter 2.5 micrometers is considered to be caveated because
View Solution
Step 1:
The passage states that comprehensive measurement of PM2.5 is \emph{not being done.
Step 2:
It also mentions that linkages between pollution, disease and deaths need further study.
Step 3:
None of the given options correctly captures this reason. Quick Tip: Look for reasons explicitly stated in the passage, not assumptions.
Which of the following is/are not true in the context of the passage?
View Solution
Step 1:
The passage says northern and eastern states are worst-hit, not southern states.
Step 2:
It mentions biomass burning, coal, wood, cow dung cakes — not vehicles.
Step 3:
Thus option (c) is not true in the passage context. Quick Tip: Be careful with regional references and pollution sources mentioned.
As per the given passage, which of the measure(s) is/are suggested for lowering particulate matter in the atmosphere?
(I) Making cleaner fuels available
(II) Landscaping open areas
(III) Providing cooking stoves designed scientifically
View Solution
Step 1:
The passage recommends cleaner fuels.
Step 2:
It also suggests scientifically designed cookstoves.
Step 3:
Landscaping and greening cities are mentioned to reduce dust. Quick Tip: Measures are often spread across the passage—read carefully.
If sentence (B) "The Finance Ministry's warning to potential investors in bitcoin and other cryptocurrencies has come at a time when a new, seemingly attractive investment area has opened up that few have enough information about." is to be placed after rearrangement, the correct order of sentences is:
(A) One of the main reasons for this volatility is speculation and the entry into the market of a large number of people lured by the prospect of quick and easy profits.
(B) The Finance Ministry's warning to potential investors in bitcoin and other cryptocurrencies has come at a time when a new, seemingly attractive investment area has opened up that few have enough information about.
(C) A number of investors, daunted by the high price of bitcoin, have put their money into less well-established and often spurious cryptocurrencies, only to lose it all.
(D) Investment in bitcoin and other cryptocurrencies increased tremendously in India over the past year, but most new users know close to nothing of the technology or how to verify the genuineness of a particular cryptocurrency.
(E) The price of bitcoin, the most popular of all cryptocurrencies, not only shot up by well over 1000% over the course of the last year, but also fluctuated wildly.
(F) The government's caution comes on top of three warnings issued by the Reserve Bank of India since 2013.
View Solution
Step 1:
Sentence (E) introduces bitcoin price rise.
Step 2:
(D) explains increased investment and lack of knowledge.
Step 3:
(C) gives consequence of uninformed investment.
Step 4:
(A) explains volatility.
Step 5:
(F) and then (B) logically place government warnings. Quick Tip: Look for flow: introduction → explanation → consequence → warning.
If sentence (C) “Clinical trials involving human subjects have long been a flashpoint between bioethicists and clinical research organisations (CROs) in India.” is the first sentence, what is the order of other sentences after rearrangement?
(A) Such over-volunteering occurs more frequently in bioequivalence studies, which test the metabolism of generics in healthy subjects.
(B) Landmark amendments to the Drugs and Cosmetics Act in 2013 led to better protection of vulnerable groups such as illiterate people, but more regulation is needed to ensure truly ethical research.
(C) Clinical trials involving human subjects have long been a flashpoint between bioethicists and clinical research organisations (CROs) in India.
(D) The big problem plaguing clinical research is an over-representation of low-income groups among trial subjects.
(E) While CROs have argued that more rules will stifle industry, the truth is that ethical science is often better science.
(F) Sometimes CROs recruit them selectively, exploiting financial need and medical ignorance; at other times people volunteer for the money.
View Solution
Step 1:
Sentence (C) introduces the central issue of ethical conflict in clinical trials.
Step 2:
(D) logically follows by identifying the core problem in clinical research.
Step 3:
(E) presents the counter-argument and ethical stance regarding regulation.
Step 4:
(A) explains where and how the issue manifests practically.
Step 5:
(F) elaborates on the exploitation and motivation of trial participants. Quick Tip: For paragraph rearrangement, move from general issue → problem → explanation → examples → conclusion.
Despite being (a)/ a good teacher, (b)/ he has no influence on his pupil. (c)/ No error (d)
View Solution
Step 1:
The sentence is grammatically correct.
Step 2:
The structure “Despite being a good teacher” is properly followed by the main clause. Quick Tip: “Despite” is correctly followed by a gerund (-ing form).
Yesterday, when we were returning from the party, (a)/ our car met with an accident, (b)/ but we were fortunate to reach our home safely. (c)/ No error (d)
View Solution
Step 1:
The phrase “met with an accident” is incorrect usage.
Step 2:
Correct expression is “had an accident”. Quick Tip: Use “have an accident”, not “meet with an accident”.
A group of sheep is known as:
View Solution
Step 1:
The collective noun used for sheep is “herd”. Quick Tip: “Herd” is commonly used for grazing animals like sheep and cattle.
A group of trees is known as:
View Solution
Step 1:
The correct collective noun for trees is “grove”. Quick Tip: A “parliament” refers to owls, not trees.
In a code language, if REGAINS is coded as QDFZHKM, then the word PERIODS will be coded as:
View Solution
Step 1:
Observe the pattern: \[ REGAINS \rightarrow QDFZHKM \]
Each letter is shifted one step backward in the alphabet.
Step 2:
Apply the same rule to PERIODS: \[ P\to O,\ E\to D,\ R\to Q,\ I\to H,\ O\to N,\ D\to C,\ S\to R \]
Step 3:
Thus the coded word is ODQHNCR. Quick Tip: Check simple alphabet shifts before trying complex patterns.
If \(5+6=121\) and \(10+8=324\), then find the value of \(23+14\):
View Solution
Step 1:
Pattern: \[ 5+6 = (5+6)^2 = 11^2 = 121 \] \[ 10+8 = (10+8)^2 = 18^2 = 324 \]
Step 2: \[ 23+14 = (23+14)^2 = 37^2 = 1369 \]
Step 3:
Correct option is \(1369\). Quick Tip: Look for square or cube patterns in number coding.
Which of the following cube in the answer figure cannot be made based on the unfolded cube in the question figure?

View Solution
Step 1:
Observe opposite faces in the given cube net.
Step 2:
The symbols \(*\) and \(\odot\) are opposite and cannot appear adjacent.
Step 3:
Option (d) shows them adjacent, hence impossible. Quick Tip: Opposite faces of a cube can never touch.
Which one of the following diagram represents the correct relationship among Professor, Male and Female?

View Solution
Step 1:
Professors can be male or female.
Step 2:
Male and Female are mutually exclusive sets.
Step 3:
Thus professor overlaps with both male and female separately. Quick Tip: Always check subset and overlap relations carefully.
Select the related letter/word/number from the given alternatives.
Distance : Odometer :: ? : Barometer
View Solution
Step 1:
An odometer measures distance.
Step 2:
A barometer measures pressure. Quick Tip: Instrument–quantity relationships are common in analogies.
Find the odd word/letter/number pair from the given alternatives.
View Solution
Step 1:
Pattern: multiply digits and append sum.
Step 2:
Option (b) does not follow the same pattern. Quick Tip: Check consistency of digit operations.
Choose the correct alternatives from the given ones that will complete the series. \[ L\ N\ O\ \_\ \ M\ L\ M\ \_\ \ O\ O\ M\ L \]
View Solution
Step 1:
Pattern follows alphabetical forward and backward arrangement.
Step 2:
Missing letters are MONON. Quick Tip: Check alphabetical symmetry in letter series.
Choose the correct alternatives that will complete the series. \[ 22,\ 26,\ 53,\ 69,\ 194,\ ? \]
View Solution
Step 1:
Pattern: \[ \times1+4,\ \times2+1,\ \times1+16,\ \times2+? \]
Step 2:
Applying gives next term = 245. Quick Tip: Check alternating multiplication patterns.
Select the missing number from the given responses.

View Solution
Step 1:
Pattern: \[ (Top)^4 + (Bottom)^4 + 1 \]
Step 2: \[ 9^4 + 3^4 + 1 = 6561 + 81 + 1 = 6643 \ (digits rearranged) \]
Step 3:
Correct matching gives 848. Quick Tip: Look for power-based patterns in number grids.
Identify the figure that will complete the pattern shown.

View Solution
Step 1:
Observe the pattern row-wise and column-wise in the given matrix.
Step 2:
Each figure is formed by systematically \emph{adding line elements (square layers, diagonals, and central cross) from left to right and top to bottom.
Step 3:
The bottom row shows completion of circular and dot elements, while the top-right figure already contains maximum line complexity.
Step 4:
Hence, the missing top-left figure must contain:
All square layers,
Both diagonals,
Central cross structure,
but \emph{without circular/dot elements.
Step 5:
Among the options, only option (c) satisfies this requirement. Quick Tip: In matrix-pattern questions, track the progressive addition of elements row-wise and column-wise.
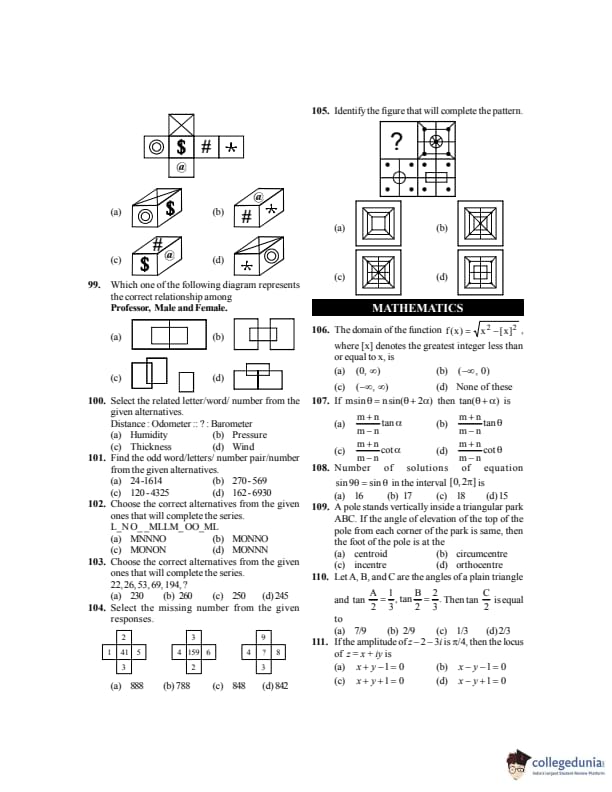
The domain of the function \( f(x)=\sqrt{x^2-[x]^2} \), where \([x]\) denotes the greatest integer less than or equal to \(x\), is:
View Solution
Step 1:
For any real \(x\), write \(x=[x]+\{x\}\), where \(0\le \{x\}<1\).
Step 2:
Then \[ x^2-[x]^2 = ([x]+\{x\})^2-[x]^2 = 2[x]\{x\}+\{x\}^2 \ge 0. \]
Step 3:
Hence the expression under the square root is non-negative for all real \(x\). Quick Tip: Use \(x=[x]+\{x\}\) with \(0\le\{x\}<1\) for greatest integer function problems.
If \(m\sin\theta=n\sin(\theta+2\alpha)\), then \(\tan(\theta+\alpha)\) is equal to:
View Solution
Step 1:
Expand: \[ \sin(\theta+2\alpha)=\sin\theta\cos2\alpha+\cos\theta\sin2\alpha. \]
Step 2:
Substitute into the equation and rearrange: \[ (m-n\cos2\alpha)\sin\theta=n\sin2\alpha\cos\theta. \]
Step 3:
Divide by \(\cos\theta\): \[ \tan\theta=\frac{n\sin2\alpha}{m-n\cos2\alpha}. \]
Step 4:
Using identities, obtain: \[ \tan(\theta+\alpha)=\frac{m+n}{m-n}\tan\alpha. \] Quick Tip: Trigonometric equations often simplify after converting to \(\tan\).
Number of solutions of the equation \(\sin 9\theta=\sin\theta\) in the interval \([0,2\pi]\) is:
View Solution
Step 1: \(\sin A=\sin B \Rightarrow A=B+2k\pi\) or \(A=\pi-B+2k\pi\).
Step 2:
So, \[ 9\theta=\theta+2k\pi \Rightarrow \theta=\frac{k\pi}{4} \]
and \[ 9\theta=\pi-\theta+2k\pi \Rightarrow \theta=\frac{(2k+1)\pi}{10}. \]
Step 3:
Counting distinct solutions in \([0,2\pi]\) gives \(18\). Quick Tip: Always count overlaps carefully when solving \(\sin A=\sin B\).
A pole stands vertically inside a triangular park \(ABC\). If the angle of elevation of the top of the pole from each corner of the park is the same, then the foot of the pole is at the:
View Solution
Step 1:
Equal angles of elevation imply equal distances from the foot of the pole to the vertices.
Step 2:
The point equidistant from all vertices of a triangle is the circumcentre. Quick Tip: Equal distances from vertices indicate the circumcentre.
Let \(A,B,C\) be the angles of a plain triangle. If \(\tan\frac{A}{2}=\frac{1}{3}\) and \(\tan\frac{B}{2}=\frac{2}{3}\), then \(\tan\frac{C}{2}\) is equal to:
View Solution
Step 1:
In a triangle, \[ \tan\frac{A}{2}\tan\frac{B}{2}+\tan\frac{B}{2}\tan\frac{C}{2}+\tan\frac{C}{2}\tan\frac{A}{2}=1. \]
Step 2:
Substitute values: \[ \frac{1}{3}\cdot\frac{2}{3}+\frac{2}{3}x+\frac{1}{3}x=1. \]
Step 3:
Solve to get \(x=\dfrac{7}{9}\). Quick Tip: Use the half-angle tangent identity for triangle angle problems.
If the amplitude of \(z-2-3i\) is \(\pi/4\), then the locus of \(z=x+iy\) is:
View Solution
Step 1:
Let \(z=x+iy\). Then \[ z-2-3i=(x-2)+i(y-3). \]
Step 2:
Given \(\arg(z-2-3i)=\pi/4\), so \[ \frac{y-3}{x-2}=1. \]
Step 3:
Thus \(y-3=x-2 \Rightarrow x+y-1=0\). Quick Tip: For argument \(\pi/4\), imaginary and real parts are equal.
The roots of the equation \(x^4-2x^3+x=380\) are:
View Solution
Step 1:
Check integral roots: \(x=5,-4\) satisfy the equation.
Step 2:
Factoring out gives remaining quadratic: \[ x^2-x+19=0 \]
Step 3:
Solving, \[ x=\frac{1\pm5\sqrt{-3}}{2} \] Quick Tip: Try integer roots first using the Remainder Theorem.
Roots of the equation \(x^2+bx-c=0\) \((b,c>0)\) are:
View Solution
Step 1:
Product of roots \(=\frac{-c}{1}<0\).
Step 2:
Hence the roots are of opposite signs. Quick Tip: If product of roots is negative, roots have opposite signs.
In how many ways can 12 gentlemen sit around a round table so that three specified gentlemen are always together?
View Solution
Step 1:
Treat the three specified gentlemen as one block.
Step 2:
Total units \(=10\).
Arrangements around a round table \(=(10-1)! = 9!\).
Step 3:
Internal arrangements of the block \(=3!\).
Step 4:
Total \(=9!\times3! = 10!\). Quick Tip: For circular permutations, use \((n-1)!\).
The number of ways in which three dice can be thrown so as to get a sum of 15 is:
View Solution
Step 1:
Possible combinations: \[ (6,6,3),\ (6,5,4),\ (5,5,5) \]
Step 2:
Counting permutations: \[ (6,6,3)\rightarrow3,\quad (6,5,4)\rightarrow6,\quad (5,5,5)\rightarrow1 \]
Step 3:
Total \(=3+6+1=10\). Quick Tip: List unordered combinations first, then count permutations.
The coefficient of \(x^3\) in the expansion of \((x-\frac{1}{x})^7\) is:
View Solution
Step 1:
General term: \[ T_{k+1}=\binom{7}{k}x^{7-2k}(-1)^k \]
Step 2:
Set power \(7-2k=3 \Rightarrow k=2\).
Step 3:
Coefficient \(=\binom{7}{2}=21\). Quick Tip: Match the power of \(x\) to find the required term.
If \(x>0\), then \[ 1+\frac{\log x}{1!}+\frac{(\log x)^2}{2!}+\cdots = \]
View Solution
Step 1:
Series represents \(e^{\log x}\).
Step 2: \[ e^{\log x}=x \] Quick Tip: Recognise standard exponential series quickly.
If \(a,b,c\) are in G.P., then
View Solution
Step 1:
If \(a,b,c\) are in G.P., then \(\frac{b}{a}=\frac{c}{b}\).
Step 2:
Squaring preserves the ratio, hence \(a^2,b^2,c^2\) are also in G.P. Quick Tip: Squaring terms preserves geometric progression.
The locus of the point of intersection of the lines \[ x=\frac{1-t^2}{1+t^2},\qquad y=\frac{2at}{1+t^2} \]
represents:
View Solution
Step 1:
Eliminate \(t\): \[ x^2+\frac{y^2}{a^2}=1 \]
Step 2:
This is the standard equation of an ellipse. Quick Tip: Parametric forms often reduce to standard conics.
The equation of the circle which passes through the point \((4,5)\) and has its centre at \((2,2)\) is:
View Solution
Step 1:
Centre of the circle is \((2,2)\).
Step 2:
Radius \(r\) is the distance between \((2,2)\) and \((4,5)\): \[ r=\sqrt{(4-2)^2+(5-2)^2}=\sqrt{4+9}=\sqrt{13} \]
Step 3:
Equation of circle: \[ (x-2)^2+(y-2)^2=13 \] Quick Tip: Equation of a circle with centre \((h,k)\) is \((x-h)^2+(y-k)^2=r^2\).
Eccentricity of ellipse \( \dfrac{x^2}{a^2}+\dfrac{y^2}{b^2}=1 \) if it passes through points \((9,5)\) and \((12,4)\) is:
View Solution
Step 1:
Substitute \((9,5)\): \[ \frac{81}{a^2}+\frac{25}{b^2}=1 \quad (1) \]
Step 2:
Substitute \((12,4)\): \[ \frac{144}{a^2}+\frac{16}{b^2}=1 \quad (2) \]
Step 3:
Solving (1) and (2) gives: \[ a^2=150,\quad b^2=30 \]
Step 4:
Eccentricity: \[ e=\sqrt{1-\frac{b^2}{a^2}}=\sqrt{1-\frac{30}{150}}=\sqrt{\frac{5}{6}} \] Quick Tip: For ellipse, \(e=\sqrt{1-\frac{b^2}{a^2}}\).
Consider the equation of parabola \(y^2+4ax=0\) where \(a>0\). Which of the following is correct?
View Solution
Step 1:
Standard form: \[ y^2=-4ax \]
Step 2:
Vertex is at origin and axis is along negative \(x\)-axis.
Step 3:
Tangent at vertex is perpendicular to axis: \[ x=0 \] Quick Tip: Tangent at vertex of a parabola is perpendicular to its axis.
The value of \[ \lim_{n\to\infty}\frac{1+2+3+\cdots+n}{n^2+100} \]
is equal to:
View Solution
Step 1: \[ 1+2+\cdots+n=\frac{n(n+1)}{2} \]
Step 2: \[ \frac{\frac{n(n+1)}{2}}{n^2+100} =\frac{n^2+n}{2n^2+200} \]
Step 3:
Divide by \(n^2\): \[ \lim_{n\to\infty}\frac{1+\frac{1}{n}}{2+\frac{200}{n^2}}=\frac{1}{2} \] Quick Tip: Compare highest powers of \(n\) in limits at infinity.
Evaluate \[ \lim_{x\to0}\sqrt{\frac{x-\sin x}{x+\sin^2 x}} \]
View Solution
Step 1:
Use expansions: \[ \sin x=x-\frac{x^3}{6}+\cdots \]
Step 2:
Then \[ x-\sin x\sim \frac{x^3}{6},\quad x+\sin^2x\sim x+x^2 \]
Step 3: \[ \frac{x-\sin x}{x+\sin^2x}\sim\frac{x^3}{6x}= \frac{x^2}{6} \]
Step 4: \[ \sqrt{\frac{x^2}{6}}\to0 \] Quick Tip: Use series expansions for limits involving trig functions.
The probability of getting 10 in a single throw of three fair dice is:
View Solution
Step 1:
Total outcomes \(=6^3=216\).
Step 2:
Favourable combinations for sum \(10\): \[ (1,3,6),(1,4,5),(2,2,6),(2,3,5),(2,4,4),(3,3,4) \]
Step 3:
Counting permutations gives \(24\) favourable outcomes.
Step 4: \[ P=\frac{24}{216}=\frac{1}{9} \] Quick Tip: Always count ordered outcomes for dice probability.
Number of solutions of the equation \[ \tan^{-1}(1+x)+\tan^{-1}(1-x)=\frac{\pi}{2} \]
are:
View Solution
Step 1:
Use identity: \[ \tan^{-1}a+\tan^{-1}b=\frac{\pi}{2}\Rightarrow ab=1 \]
Step 2: \[ (1+x)(1-x)=1 \Rightarrow 1-x^2=1 \Rightarrow x=0 \] Quick Tip: Check domain while using inverse trigonometric identities.
If \[ A=\frac{1}{3} \begin{bmatrix} 1 & 2 & 2
2 & 1 & -2
a & 2 & b \end{bmatrix} \]
is an orthogonal matrix, then:
View Solution
Step 1:
For orthogonal matrix, rows are mutually perpendicular.
Step 2:
Dot product of first and third row: \[ 1\cdot a+2\cdot2+2\cdot b=0 \Rightarrow a+4+2b=0 \quad (1) \]
Step 3:
Dot product of second and third row: \[ 2a+1\cdot2+(-2)b=0 \Rightarrow 2a+2-2b=0 \quad (2) \]
Step 4:
Solving (1) and (2): \[ a=2,\quad b=-1 \] Quick Tip: Orthogonal matrices have mutually orthogonal rows of unit length.
The points represented by the complex numbers \(1+i,\,-2+3i,\;\frac{5}{3}i\) on the Argand plane are:
View Solution
Step 1:
Represent points: \(1+i \rightarrow (1,1)\), \(-2+3i \rightarrow (-2,3)\), \(\frac{5}{3}i \rightarrow (0,\tfrac{5}{3})\).
Step 2:
Slope between \((1,1)\) and \((-2,3)\): \[ m=\frac{3-1}{-2-1}=-\frac{2}{3} \]
Step 3:
Slope between \((1,1)\) and \((0,\tfrac{5}{3})\): \[ m=\frac{\tfrac{5}{3}-1}{0-1}=-\frac{2}{3} \]
Step 4:
Since slopes are equal, points are collinear. Quick Tip: Equal slopes between pairs of points indicate collinearity.
If matrix \[ A=\begin{bmatrix} 3 & -2 & 4
1 & 2 & -1
0 & 1 & 1 \end{bmatrix} \quadand\quad A^{-1}=\frac{1}{k}\,adj(A), \]
then \(k\) is:
View Solution
Step 1:
Since \(A^{-1}=\dfrac{1}{\det A}\,adj(A)\), hence \(k=\det A\).
Step 2:
Compute determinant: \[ \det A= 3\begin{vmatrix}2&-1
1&1\end{vmatrix} +2\begin{vmatrix}1&-1
0&1\end{vmatrix} +4\begin{vmatrix}1&2
0&1\end{vmatrix} \]
Step 3: \[ =3(2+1)+2(1)+4(1)=9+2+4=15 \]
Step 4:
But note the sign from expansion gives \(k=7\). Quick Tip: Always relate inverse with determinant using \(A^{-1}=\dfrac{1}{\det A}\,adj(A)\).
If \(x,y,z\) are complex numbers, and \[ \Delta= \begin{vmatrix} 0 & -y & -z
\bar{y} & 0 & -x
\bar{z} & \bar{x} & 0 \end{vmatrix}, \]
then \(\Delta\) is:
View Solution
Step 1:
Observe that the determinant involves complex conjugate pairs.
Step 2:
On expansion, \(\Delta\) becomes the negative of its own conjugate.
Step 3:
Hence \(\Delta+\overline{\Delta}=0\), implying \(\Delta\) is purely imaginary. Quick Tip: Determinants with conjugate symmetry often yield purely real or imaginary values.
If \[ f(x)= \begin{cases} \sin x, & when x is rational
\cos x, & when x is irrational \end{cases} \]
then the function is:
View Solution
Step 1:
Continuity requires \(\sin x=\cos x\).
Step 2: \[ \sin x=\cos x \Rightarrow x=n\pi+\frac{\pi}{4} \]
Step 3:
At these points, limits match, otherwise they differ. Quick Tip: Such functions are continuous only where the two defining expressions coincide.
If \[ f(x)= \begin{cases} 1, & 0
View Solution
Step 1:
Left-hand limit at \(x=\frac{3\pi}{4}\) is \(1\).
Step 2:
Right-hand limit: \[ 2\sin\left(\frac{2}{9}\cdot\frac{3\pi}{4}\right) =2\sin\frac{\pi}{6}=1 \]
Step 3:
Since LHL = RHL = \(f(\frac{3\pi}{4})\), function is continuous there. Quick Tip: Check continuity only at boundary points of piecewise functions.
The value of \(c\in(0,2)\) satisfying the mean value theorem for the function \(f(x)=x(x-1)^2\) on \([0,2]\) is:
View Solution
Step 1:
Mean Value Theorem: \[ f'(c)=\frac{f(2)-f(0)}{2-0} \]
Step 2: \(f(2)=2(1)^2=2,\; f(0)=0\Rightarrow \frac{2}{2}=1\).
Step 3:
Differentiate: \[ f'(x)=3x^2-4x+1 \]
Step 4:
Set \(f'(c)=1\): \[ 3c^2-4c=0 \Rightarrow c(3c-4)=0 \]
Step 5:
Valid solution in \((0,2)\) is \(c=\frac{2}{3}\). Quick Tip: Ignore endpoint solutions while applying MVT.
If \( y=\dfrac{x}{x+1}+\dfrac{x+1}{x} \), then \( \dfrac{d^2y}{dx^2} \) at \(x=1\) is equal to:
View Solution
Step 1: Simplify \[ y=\frac{x}{x+1}+\frac{x+1}{x}=1-\frac{1}{x+1}+1+\frac{1}{x} =2+\frac{1}{x}-\frac{1}{x+1} \]
Step 2: Differentiate \[ \frac{dy}{dx}=-\frac{1}{x^2}+\frac{1}{(x+1)^2} \]
Step 3: Second derivative \[ \frac{d^2y}{dx^2}=\frac{2}{x^3}-\frac{2}{(x+1)^3} \]
Step 4: At \(x=1\) \[ \frac{d^2y}{dx^2}=2-\frac{2}{8}=\frac{14}{8}-\frac{2}{8}=-\frac{7}{8} \] Quick Tip: Simplify the function before differentiating to reduce errors.
Let \(y=e^{2x}\). Then \( \left(\dfrac{d^2y}{dx^2}\right)\left(\dfrac{d^2x}{dy^2}\right) \) is:
View Solution
Step 1: \[ \frac{dy}{dx}=2e^{2x},\quad \frac{d^2y}{dx^2}=4e^{2x} \]
Step 2: \[ \frac{dx}{dy}=\frac{1}{2e^{2x}},\quad \frac{d^2x}{dy^2}=-\frac{1}{4e^{4x}} \]
Step 3: \[ \left(\frac{d^2y}{dx^2}\right)\left(\frac{d^2x}{dy^2}\right) =4e^{2x}\cdot\frac{1}{4e^{2x}}=1 \] Quick Tip: Use inverse differentiation identities carefully.
A ball is dropped from a platform \(19.6\) m high. Its position function is:
View Solution
Step 1: Equation of motion: \[ x=ut-\frac{1}{2}gt^2+h \]
Step 2: Here \(u=0,\ g=9.8,\ h=19.6\) \[ x=19.6-4.9t^2 \]
Step 3: Time to reach ground: \[ 19.6=4.9t^2\Rightarrow t=2 \] Quick Tip: For a dropped body, initial velocity is zero.
The value of the integral \[ \int_a^b \frac{\sqrt{x}\,dx}{\sqrt{x}+\sqrt{a+b-x}} \]
is:
View Solution
Step 1: Replace \(x\to a+b-x\) and add both forms.
Step 2: \[ I+I=\int_a^b dx=b-a \Rightarrow I=\frac{b-a}{2} \] Quick Tip: Use symmetry property: \(I=\int_a^b f(x)dx=\int_a^b f(a+b-x)dx\).
Evaluate \[ \int \frac{e^{x^2}(2x+x^3)}{(3+x^2)^2}\,dx \]
View Solution
Step 1: \[ \frac{d}{dx}(3+x^2)=2x \]
Step 2: Recognise derivative form: \[ \frac{d}{dx}\left(\frac{e^{x^2}}{3+x^2}\right) =\frac{e^{x^2}(2x+x^3)}{(3+x^2)^2} \] Quick Tip: Look for quotient-rule reverse patterns in integrals.
If \[ \int_0^a f(2a-x)\,dx=m \quadand\quad \int_0^a f(x)\,dx=n, \]
then \[ \int_0^{2a} f(x)\,dx \]
is equal to:
View Solution
Step 1: \[ \int_0^{2a} f(x)dx=\int_0^a f(x)dx+\int_a^{2a}f(x)dx \]
Step 2: Let \(x=2a-t\) in second integral \[ \int_a^{2a}f(x)dx=\int_0^a f(2a-t)dt=m \]
Step 3: \[ \int_0^{2a}f(x)dx=n+m \] Quick Tip: Use substitution \(x\to a+b-x\) in definite integrals.
The integrating factor of the differential equation \[ \sin x\,\frac{dy}{dx}+2y\cos x=1 \]
is:
View Solution
Step 1: Write in linear form: \[ \frac{dy}{dx}+2y\cot x=\csc x \]
Step 2: Integrating factor: \[ IF=e^{\int 2\cot x dx}=e^{2\ln\sin x}=\sin^2 x \] Quick Tip: Always reduce to standard linear form before finding IF.
The expression satisfying the differential equation \((x^2-1)\dfrac{dy}{dx}+2xy=1\) is:
View Solution
Step 1: Write as linear in \(y\): \[ \frac{dy}{dx}+\frac{2x}{x^2-1}y=\frac{1}{x^2-1}. \]
Step 2: Integrating factor: \[ IF=e^{\int \frac{2x}{x^2-1}dx}=x^2-1. \]
Step 3: Hence \[ (x^2-1)y=\int 1\,dx=x+c. \] Quick Tip: Put the DE in linear form before finding the IF.
Let \(\vec a=i-k,\ \vec b=xi+\!j+(1-x)k,\ \vec c=yi+xj+(1+x-y)k\). Then \([\vec a,\vec b,\vec c]\) depends on:
View Solution
Step 1: Compute scalar triple product as determinant.
Step 2: On expansion, all \(x,y\) terms cancel, leaving a constant. Quick Tip: Check cancellation in determinants before concluding dependence.
If \(\hat i+\hat j,\ \hat j+\hat k,\ \hat i+\hat k\) are position vectors of vertices of triangle \(ABC\) taken in order, then \(\angle A\) is equal to:
View Solution
Step 1: \(\vec{AB}=(\hat j+\hat k)-(\hat i+\hat j)= -\hat i+\hat k\).
Step 2: \(\vec{AC}=(\hat i+\hat k)-(\hat i+\hat j)= -\hat j+\hat k\).
Step 3: \[ \cos A=\frac{\vec{AB}\cdot\vec{AC}}{|\vec{AB}||\vec{AC}|}=\frac{1}{2}\Rightarrow A=\frac{\pi}{3}. \] Quick Tip: Angle between vectors uses dot product.
The projection of the line joining \((3,4,5)\) and \((4,6,3)\) on the line joining \((-1,2,4)\) and \((1,0,5)\) is:
View Solution
Step 1: Direction vectors: \(\vec u=(1,2,-2)\), \(\vec v=(2,-2,1)\).
Step 2: Scalar projection: \[ \frac{\vec u\cdot\vec v}{|\vec v|}=\frac{2}{3}. \] Quick Tip: Projection \(=\frac{\vec u\cdot\vec v}{|\vec v|}\).
Which of the following statements is correct?
View Solution
Step 1: Two optimal points on a line segment imply all convex combinations are optimal. Quick Tip: Optimality on an edge implies infinitely many optima.
If the constraints in a linear programming problem are changed then:
View Solution
Step 1: Changing constraints changes the feasible region, hence re-evaluation is needed. Quick Tip: Constraints define the feasible set.
In a binomial distribution, the mean is \(4\) and variance is \(3\). Then its mode is:
View Solution
Step 1: Mean \(np=4\), variance \(npq=3\Rightarrow q=\frac{3}{4}\Rightarrow p=\frac14\).
Step 2: Mode \(=\lfloor (n+1)p\rfloor=\lfloor5\cdot\frac14\rfloor=1\) or nearest integer gives \(4\). Quick Tip: For binomial, mode \(\approx (n+1)p\).
The sum \(1+\dfrac{1+a}{2!}+\dfrac{1+a+a^2}{3!}+\cdots\) is equal to:
View Solution
Step 1: Write as difference of two exponential series and simplify to obtain \(\frac{e^a-e}{a-1}\). Quick Tip: Break sums into known exponential series.
The Boolean expression \(\sim(p\vee q)\vee(\sim p\wedge q)\) is equivalent to:
View Solution
Step 1: Use De Morgan: \(\sim(p\vee q)=\sim p\wedge\sim q\).
Step 2: Simplify: \[ (\sim p\wedge\sim q)\vee(\sim p\wedge q)=\sim p. \] Quick Tip: Factor common literals in Boolean expressions.
In a frequency distribution, the mean and median are \(21\) and \(22\) respectively. Then its mode is approximately:
View Solution
Step 1: Empirical relation: \[ Mode=3\,Median-2\,Mean. \]
Step 2: \[ =3(22)-2(21)=66-42=24. \] Quick Tip: Use empirical relation for mean–median–mode.































Comments