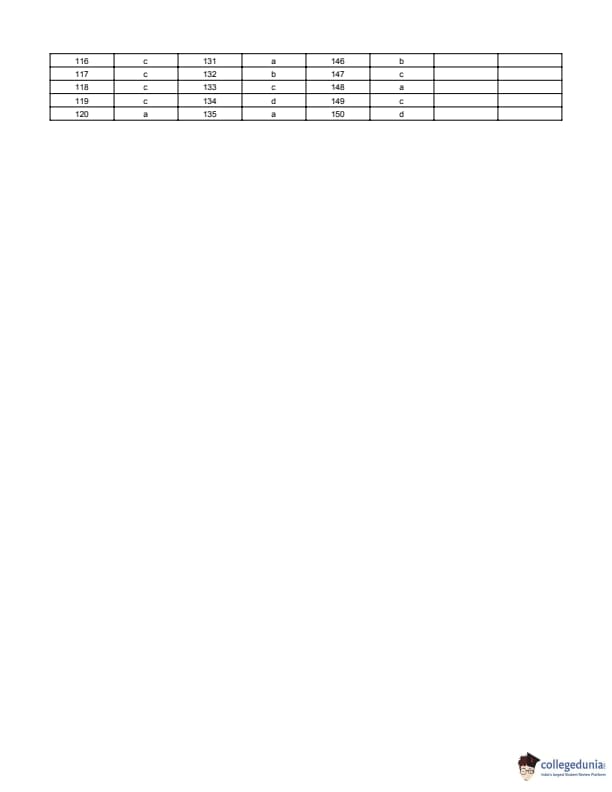
BITSAT 2017 Question Paper with Answer Key pdf is available for download. BITSAT 2017 was conducted in online CBT mode by BITS Pilani. BITSAT 2017 Question Paper had 150 questions to be attempted in 3 hours.
BITSAT 2017 Question Paper with Answer Key PDF
| BITSAT 2017 Question Paper PDF | BITSAT 2017 Answer Key PDF |
|---|---|
| Download PDF | Download PDF |
What is the minimum energy required to launch a satellite of mass \( m \) from the surface of a planet of mass \( M \) and radius \( R \) in a circular orbit at an altitude of \( R \)?
View Solution
Step 1: Radius of the circular orbit \[ r = R + R = 2R \]
Step 2: Initial mechanical energy of the satellite at rest on the surface \[ E_i = -\frac{GMm}{R} \]
Step 3: Final mechanical energy of the satellite in a circular orbit \[ E_f = -\frac{GMm}{2r} = -\frac{GMm}{4R} \]
Step 4: Minimum energy required to launch the satellite \[ \Delta E = E_f - E_i = \left(-\frac{GMm}{4R}\right) - \left(-\frac{GMm}{R}\right) = \frac{3GMm}{4R} \] Quick Tip: For a satellite in circular orbit: \[ E = -\frac{GMm}{2r} \] Minimum launch energy is calculated using the change in total mechanical energy.
A mercury drop of radius 1 cm is sprayed into \(10^6\) drops of equal size. The energy pressed in joule is (surface tension of mercury is \(460 \times 10^{-3}\,N/m\)).
View Solution
Step 1: Surface energy \(E = T \times \Delta A\)
Initial radius \(R = 1\,cm = 10^{-2}\,m\)
Step 2: Radius of each small drop \[ r = \frac{R}{100} = 10^{-4}\,m \]
Step 3: Increase in surface area \[ \Delta A = 10^6 (4\pi r^2) - 4\pi R^2 = 4\pi (10^6 \times 10^{-8} - 10^{-4}) = 4\pi (0.01 - 0.0001) \]
Step 4: Energy required \[ E = 460 \times 10^{-3} \times 4\pi \times 0.0099 \approx 5.7\,J \] Quick Tip: Surface energy change depends only on change in surface area: \[ E = T \Delta A \] Breaking droplets increases surface area significantly.
Two plano-concave lenses (1 and 2) of glass of refractive index 1.5 have radii of curvature 25 cm and 20 cm. They are placed in contact with their curved surfaces towards each other and the space between them is filled with liquid of refractive index \(4/3\). The combination is

View Solution
Step 1: Power of each curved surface using refraction formula
Net power: \[ P = \left(\frac{\mu_l}{\mu_g}-1\right)\left(\frac{1}{R_1}-\frac{1}{R_2}\right) \]
Step 2: Substituting values gives \[ P = -\frac{1}{66.6}\,cm^{-1} \] Quick Tip: For lenses in contact with a medium: \[ P_{net} = \sum P_{surfaces} \] Always consider refractive index of the filling medium.
A charged particle moves perpendicular to a magnetic field. Then
View Solution
Step 1: Magnetic force is always perpendicular to velocity.
Step 2: Work done by magnetic force is zero.
Step 3: Hence speed and kinetic energy remain constant, but direction of momentum changes. Quick Tip: Magnetic force changes direction, not speed: \[ \vec{F} = q\vec{v} \times \vec{B} \]
After two hours, one-sixteenth of the starting amount of a certain radioactive isotope is remained undecayed. The half-life of the isotope is
View Solution
Step 1: \(\frac{1}{16} = \left(\frac{1}{2}\right)^4\)
Step 2: Four half-lives occur in 2 hours.
Step 3: \[ T_{1/2} = \frac{120}{4} = 30 minutes \] Quick Tip: Fraction remaining: \[ \left(\frac{1}{2}\right)^n \] where \(n\) = number of half-lives.
A coil of inductance 300 mH and resistance \(2\Omega\) is connected to a source of voltage 2 V. The current reaches half of its steady state value in
View Solution
Step 1: Time constant \[ \tau = \frac{L}{R} = \frac{0.3}{2} = 0.15\,s \]
Step 2: \[ \frac{I}{I_0} = 1 - e^{-t/\tau} \]
Step 3: For \(I = \frac{I_0}{2}\): \[ t = \tau \ln 2 \approx 0.05\,s \] Quick Tip: RL circuit current growth: \[ I = I_0(1-e^{-t/\tau}) \]
Two concentric conducting spherical shells \(A\) and \(B\) having radii \(r_A\) and \(r_B\) \((r_B>r_A)\) are charged to \(+2q\) and \(-q\) respectively. The electric field along a line passing through the centre is

View Solution
Step 1: Use Gauss’s law for different regions.
Step 2:
- Inside shell A: \(E=0\)
- Between A and B: field due to \(+2q\)
- Outside both shells: net charge \(= +q\) Quick Tip: For concentric shells, analyze region-wise using Gauss’s law.
A capillary tube of radius \(R\) is immersed in water and water rises in it to a height \(H\). Mass of water in the capillary tube is \(M\). If the radius of the tube is doubled, mass of water that will rise in the capillary tube will now be
View Solution
Step 1: Height of capillary rise \[ h \propto \frac{1}{R} \]
Step 2: Volume (and hence mass) \[ M \propto R^2 h \propto R^2 \cdot \frac{1}{R} = R \]
Step 3: When radius is doubled, height becomes half, so mass remains unchanged. Quick Tip: In capillary rise: \[ M \propto R \] Doubling radius halves height but increases area.
A sonometer wire resonates with a given tuning fork forming standing waves with five antinodes between the two bridges when a mass of 9 kg is suspended from the wire. When this mass is replaced by a mass \(M\), the wire resonates with the same tuning fork forming three antinodes for the same position of the bridges. The value of \(M\) is
View Solution
Step 1: Frequency relation for sonometer \[ f \propto \frac{n}{\sqrt{T}} \]
Step 2: For same tuning fork \[ \frac{n_1}{\sqrt{T_1}} = \frac{n_2}{\sqrt{T_2}} \]
Step 3: Substituting values \[ \frac{5}{\sqrt{9}} = \frac{3}{\sqrt{M}} \Rightarrow M = 5 kg \] Quick Tip: For sonometer wire: \[ f \propto \frac{n}{\sqrt{T}} \] Number of loops is directly proportional to frequency.
When a metal surface is illuminated by light of wavelength 400 nm and 250 nm, the maximum velocities of the photoelectrons ejected are \(v\) and \(2v\) respectively. The work function of the metal is (h = Planck’s constant, c = velocity of light in air)
View Solution
Step 1: Einstein’s photoelectric equation \[ \frac{hc}{\lambda} = \phi + \frac{1}{2}mv^2 \]
Step 2: For given data, solving simultaneous equations gives \[ \phi = hc \times 10^6\ J \] Quick Tip: Higher frequency light increases kinetic energy, not work function.
Two conducting shells of radius \(a\) and \(b\) are connected by a conducting wire as shown in the figure. The capacity of the system is

View Solution
Step 1: When connected by wire, both shells are at same potential.
Step 2: Equivalent capacitance is sum of individual capacitances.
\[ C = 4\pi\varepsilon_0 a + 4\pi\varepsilon_0 b \] Quick Tip: Capacitances add directly when conductors are at same potential.
When \(^{235}\mathrm{U}\) undergoes fission, 0.1% of its original mass is changed into energy. How much energy is released if 1 kg of \(^{235}\mathrm{U}\) undergoes fission
View Solution
Step 1: Mass converted \[ \Delta m = 0.1% \times 1 = 10^{-3}\ kg \]
Step 2: Energy released \[ E = \Delta m c^2 = 10^{-3} \times (3 \times 10^8)^2 = 9 \times 10^{13}\ J \] Quick Tip: Even tiny mass loss produces huge energy: \[ E = mc^2 \]
One mole of an ideal gas is taken from state A to state B by three different processes, (i) ACB (ii) ADB (iii) AEB as shown in the P–V diagram. The heat absorbed by the gas is

View Solution
Step 1: Change in internal energy depends only on initial and final states, hence same for all paths.
Step 2: Heat absorbed \[ Q = \Delta U + W \]
Step 3: Work done is area under P–V curve. Path ADB encloses maximum area.
Step 4: Hence heat absorbed is maximum in process (ii). Quick Tip: In P–V diagrams, larger enclosed area means more work done.
In the formula \(X = 3YZ^2\), \(X\) has dimensions of capacitance and magnetic induction respectively. The dimensional formula of \(Y\) in MKSA system is
View Solution
Step 1: Dimensional formula
Capacitance: \[ [C] = [M^{-1}L^{-2}T^{4}A^{2}] \]
Magnetic induction: \[ [B] = [MT^{-2}A^{-1}] \]
Step 2: From \(X = 3YZ^2\) \[ [Y] = \frac{[X]}{[Z]^2} \]
Step 3: Substituting dimensions gives option (A). Quick Tip: Always convert each physical quantity into base dimensions first.
Two long, straight, parallel wires carry steady currents \(I\) and \(-I\) respectively. The distance between the wires is \(d\). At a certain instant of time, a point charge \(q\) is at a point equidistant from the two wires. The instantaneous velocity \(v\) is perpendicular to this plane. The magnitude of the force due to the magnetic field acting on the charge is
View Solution
Step 1: Magnetic fields due to the two wires at the midpoint are equal in magnitude.
Step 2: Directions of magnetic fields are opposite.
Step 3: Net magnetic field at the point is zero.
Step 4: Hence magnetic force \(F = qvB = 0\). Quick Tip: Equal and opposite magnetic fields cancel at symmetric points.
Two projectiles A and B are thrown with speeds in the ratio \(1:\sqrt{2}\) and acquire the same heights. If A is thrown at an angle of \(45^\circ\) with the horizontal, the angle of projection of B will be
View Solution
Step 1: Maximum height \[ H = \frac{u^2 \sin^2\theta}{2g} \]
Step 2: Since heights are equal \[ u_1^2 \sin^2 45^\circ = u_2^2 \sin^2 \theta \]
Step 3: Given \(u_1 : u_2 = 1 : \sqrt{2}\)
Step 4: Solving gives \[ \theta = 30^\circ \] Quick Tip: Equal heights depend only on vertical component of velocity.
A meter bridge is set up as shown to determine an unknown resistance \(X\) using a standard 10 ohm resistor. The galvanometer shows null point at 52 cm mark. The end corrections are 1 cm and 2 cm respectively for the ends A and B. The determined value of \(X\) is

View Solution
Step 1: Corrected lengths \[ l_1 = 52 - 1 = 51\ cm, \quad l_2 = 48 - 2 = 46\ cm \]
Step 2: Meter bridge formula \[ \frac{X}{10} = \frac{l_1}{l_2} \]
Step 3: Substituting values \[ X = 10 \times \frac{51}{48} \approx 10.6\ \Omega \] Quick Tip: Always apply end corrections before using meter bridge formula.
A disk of radius \(a/4\) having a uniformly distributed charge \(6\,C\) is placed in the \(x-y\) plane with its centre at \((-a/2,0,0)\). A rod of length \(a\) carrying a uniformly distributed charge \(8\,C\) is placed on the \(x\)-axis from \(x=a/4\) to \(x=5a/4\). Two point charges \(-7\,C\) and \(3\,C\) are placed at \((a/4,-a/4,0)\) and \((-3a/4,3a/4,0)\) respectively. Consider a cubical surface formed by six surfaces \(x=\pm a/2,\ y=\pm a/2,\ z=\pm a/2\). The electric flux through this cubical surface is

View Solution
Step 1: By Gauss’s law, \[ \Phi = \frac{Q_{enclosed}}{\varepsilon_0} \]
Step 2: Disk is cut into two equal halves by the face \(x=-a/2\).
Enclosed disk charge \(= \frac{1}{2}\times 6C = 3C\).
Step 3: Only length \(a/4\) of the rod lies inside the cube. \[ Q_{rod} = 8C \times \frac{1}{4} = 2C \]
Step 4: Of the point charges, only \(-7C\) lies inside the cube.
Step 5: Net enclosed charge \[ Q = 3C + 2C - 7C = -2C \] Quick Tip: Electric flux through a closed surface depends only on the total enclosed charge, not on its distribution.
A particle of mass \(m\) moving in the \(x\)-direction with speed \(2v\) is hit by another particle of mass \(2m\) moving in the same direction with speed \(v\). If the collision is perfectly inelastic, the percentage loss in the energy during the collision is close to
View Solution
Step 1: Initial kinetic energy \[ K_i = \tfrac12 m(2v)^2 + \tfrac12 (2m)v^2 = 3mv^2 \]
Step 2: Final velocity after perfectly inelastic collision \[ v_f = \frac{2mv + 2mv}{3m} = \frac{4v}{3} \]
Step 3: Final kinetic energy \[ K_f = \tfrac12 (3m)\left(\frac{4v}{3}\right)^2 = \frac{8}{3}mv^2 \]
Step 4: Fractional loss \[ \frac{K_i-K_f}{K_i} \approx 0.5 \] Quick Tip: In perfectly inelastic collisions, momentum is conserved but kinetic energy is not.
A coil is suspended in a uniform magnetic field with the plane of the coil parallel to the magnetic lines of force. When a current is passed through the coil it starts oscillating; it is very difficult to stop. But if an aluminium plate is placed near the coil, it stops. This is due to
View Solution
Step 1: Motion of the coil changes magnetic flux through the aluminium plate.
Step 2: Eddy currents are induced in the plate.
Step 3: These currents oppose the motion (Lenz’s law), causing damping. Quick Tip: Eddy currents always oppose the cause producing them, leading to electromagnetic damping.
A steel wire of length \(L\) at \(40^\circC\) is suspended from the ceiling and carries a mass \(m\) from its free end. The wire is cooled from \(40^\circC\) to \(30^\circC\) to regain its original length \(L\). The coefficient of linear expansion is \(10^{-5}\,/^\circC\), Young’s modulus of steel is \(10^{11}\,N m^{-2}\) and the radius of the wire is \(1\,mm\). The value of \(m\) in kg is nearly
View Solution
Step 1: Thermal strain \[ \epsilon = \alpha \Delta T = 10^{-5}\times 10 \]
Step 2: Stress \[ \sigma = Y\epsilon = 10^{11}\times 10^{-4} = 10^7\ N m^{-2} \]
Step 3: Force \[ F = \sigma A = 10^7 \times \pi(10^{-3})^2 \approx 31\ N \]
Step 4: \(m = F/g \approx 3\,kg\) Quick Tip: Prevented thermal expansion produces stress: \(\sigma = Y\alpha\Delta T\).
On a hypotenuse of a right angled prism of liquid is placed as shown in the figure. Light is allowed to fall normally on the short face of the prism. In order that the ray of light may be totally reflected, the maximum value of refractive index is

View Solution
Step 1: For total internal reflection, \[ \sin c = \frac{1}{\mu} \]
Step 2: From prism geometry, the angle of incidence at the hypotenuse is fixed.
Step 3: Maximum \(\mu\) corresponds to the critical condition. Quick Tip: Total internal reflection occurs only when light travels from denser to rarer medium.
A tuning fork of frequency 392 Hz resonates with 50 cm length of a string under tension \(T\). If the mass of the string is decreased by 2%, keeping the tension constant, the number of beats heard when the string and the tuning fork are made to vibrate simultaneously is
View Solution
Step 1: Frequency of string \[ f \propto \frac{1}{\sqrt{\mu}} \]
Step 2: Decrease in mass density by 2% increases frequency by approximately 1%.
Step 3: New frequency of string \[ f' \approx 392 \times 1.01 \approx 396 Hz \]
Step 4: Number of beats \[ |f' - f| \approx 4 \] Quick Tip: For small changes: \[ \frac{\Delta f}{f} \approx -\frac{1}{2}\frac{\Delta \mu}{\mu} \]
Hydrogen (H), deuterium (D), singly ionized helium (\(He^+\)) and doubly ionized lithium (\(Li^{2+}\)) all have one electron around the nucleus. Consider \(n=2\) to \(n=1\) transition. The wavelengths of emitted radiations are \(\lambda_1, \lambda_2, \lambda_3\) and \(\lambda_4\) respectively. Then approximately
View Solution
Step 1: For hydrogen-like atoms \[ \lambda \propto \frac{1}{Z^2} \]
Step 2: Atomic numbers
H, D: \(Z=1\); \(He^+\): \(Z=2\); \(Li^{2+}\): \(Z=3\)
Step 3: Hence \[ \lambda_1=\lambda_2=\frac{1}{1^2},\quad \lambda_3=\frac{1}{4},\quad \lambda_4=\frac{1}{9} \] Quick Tip: For hydrogen-like species, wavelength varies inversely as \(Z^2\).
The following figure depicts a circular motion. The radius of the circle, the period of revolution, the initial position and the sense of revolution are indicated in the figure. The simple harmonic motion of the \(x\)-projection of the radius vector of the rotating particle \(P\) can be shown as

View Solution
Step 1: Angular frequency \[ \omega=\frac{2\pi}{T}=\frac{2\pi}{4}=\frac{\pi}{2} \]
Step 2: Initial phase from figure \[ \phi=\frac{\pi}{4} \]
Step 3: Equation of SHM \[ x(t)=a\cos(\omega t+\phi) \] Quick Tip: Projection of uniform circular motion on a diameter is SHM.
There are two sources kept at distances \(2\lambda\). A large screen is perpendicular to the line joining the sources. Number of maxima on the screen in this case is (\(\lambda=\) wavelength of light)

View Solution
Step 1: Maximum path difference \[ \Delta = d\sin\theta \le d = 2\lambda \]
Step 2: Condition for maxima \[ \Delta = m\lambda \Rightarrow m_{\max}=2 \]
Step 3: Total number of maxima \[ N=2m_{\max}+1=5 \] Quick Tip: Total interference maxima: \[ N=2m_{\max}+1 \]
In the circuit shown in the figure the current through the resistor is

View Solution
Step 1: Reduce the circuit using symmetry and series–parallel combinations.
Step 2: Find the equivalent resistance of each section and the total current drawn from the battery.
Step 3: Apply current division to the branch containing the \(3\,\Omega\) resistor.
Step 4: The current through the \(3\,\Omega\) resistor comes out to be \(0.25\,A\). Quick Tip: Use symmetry and current division to simplify ladder-type resistor networks.
A telescope has an objective lens of 10 cm diameter and is situated at a distance of one kilometer from two objects. The minimum distance between these two objects which can be resolved by the telescope, when the wavelength of light is \(5000\,\AA\), is of the order of
View Solution
Step 1: Resolving power of telescope \[ \theta_{\min} = 1.22\frac{\lambda}{D} \]
Step 2: Substituting values \[ \theta_{\min} \approx 1.22 \times \frac{5\times10^{-7}}{0.1} \approx 6\times10^{-6}\,rad \]
Step 3: Linear separation \[ x = L\theta = 1000 \times 6\times10^{-6} \approx 6\times10^{-3}\,m \approx 5\,mm \] Quick Tip: Smaller wavelength and larger aperture improve resolving power.
During vaporisation:
I. change of state from liquid to vapour state occurs.
II. temperature remains constant.
III. both liquid and vapour states coexist in equilibrium.
IV. specific heat of substance increases.
Correct statements are
View Solution
Step 1: During vaporisation, liquid changes into vapour at constant temperature.
Step 2: Both phases coexist in equilibrium during the phase change.
Step 3: Specific heat is not defined during phase change, so statement IV is incorrect. Quick Tip: During phase change, supplied heat changes phase, not temperature.
A wire is connected to a battery between the points \(M\) and \(N\) as shown in figure (1). The same wire is bent in the form of a square and then connected to the battery between the points \(M\) and \(N\) as shown in figure (2). Which of the following quantities increases?

View Solution
Step 1: Bending the wire increases its effective resistance due to additional bends and redistribution of current paths.
Step 2: With increased resistance, more electrical energy is dissipated as heat in the wire.
Step 3: Hence both resistance and heat produced increase. Quick Tip: Resistance depends on the effective conducting path taken by the current.
A body moves in a circular orbit of radius \(R\) under the action of a central force. Potential due to the central force is given by \(V(r)=kr\) (where \(k\) is a positive constant). Period of revolution of the body is proportional to
View Solution
Step 1: Force due to potential \[ F = -\frac{dV}{dr} = -k \]
Step 2: For circular motion \[ \frac{mv^2}{R} = k \Rightarrow v \propto \sqrt{R} \]
Step 3: Period \[ T=\frac{2\pi R}{v} \propto \frac{R}{\sqrt{R}} = R^{1/2} \] Quick Tip: For circular motion, always relate force to \(mv^2/R\) first.
Two equal heavy spheres, each of radius \(r\), are in equilibrium within a smooth cup of radius \(3r\). The ratio of reaction between the cup and one sphere and that between the two spheres is

View Solution
Step 1: The centres of the spheres form an equilateral triangle with the centre of the cup.
Step 2: Angle between reaction forces is \(60^\circ\).
Step 3: Resolving forces for equilibrium gives \[ \frac{R_{cup}}{R_{sphere}} = 3 \] Quick Tip: In symmetric contact problems, geometry decides force ratios.
A long, hollow conducting cylinder is kept coaxially inside another long, hollow conducting cylinder of larger radius. Both the cylinders are initially electrically neutral.
View Solution
Step 1: If charge is given to the inner cylinder, electric field exists in the region between the cylinders.
Step 2: This produces a potential difference between the two cylinders.
Step 3: Charging only the outer cylinder does not create an electric field inside it. Quick Tip: For conductors, electric field inside the material is always zero.
A thin but rigid semicircular wire frame of radius \(r\) is hinged at \(O\) and can rotate in its own vertical plane. A smooth peg \(P\) starts from \(O\) and moves horizontally with constant speed \(v_0\), lifting the frame upwards as shown in the figure. Find the angular velocity \(\omega\) of the frame when its diameter makes an angle of \(60^\circ\) with the vertical.

View Solution
Step 1: The peg constrains the end of the diameter to move horizontally with speed \(v_0\).
Step 2: Linear speed of that point is related to angular speed: \[ v = \omega r \]
Step 3: Hence \[ \omega = \frac{v_0}{r} \] Quick Tip: For rigid rotation, relate angular speed using \(v=\omega r\).
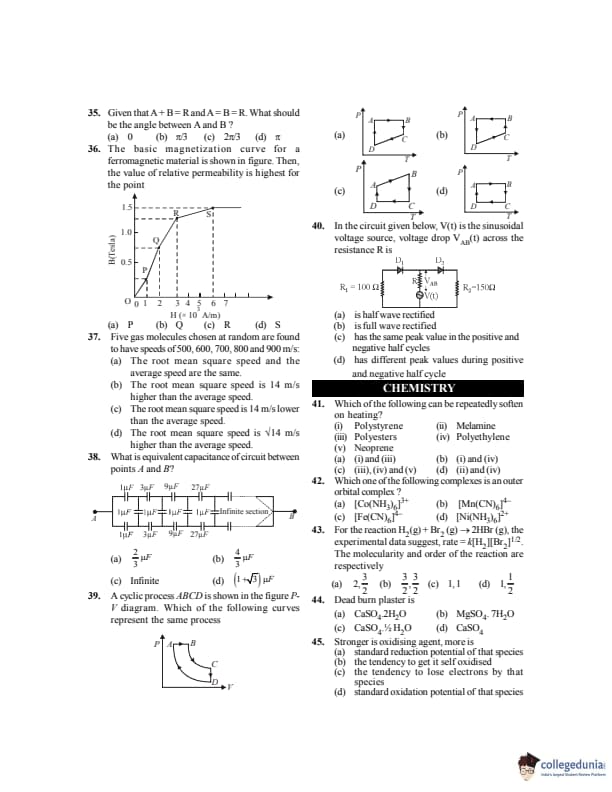
Given that \( \vec A + \vec B = \vec R \) and \( A = B = R \). What should be the angle between \( \vec A \) and \( \vec B \)?
View Solution
Step 1: Using vector formula \[ R^2 = A^2 + B^2 + 2AB\cos\theta \]
Step 2: Given \(A=B=R\) \[ R^2 = R^2 + R^2 + 2R^2\cos\theta \]
Step 3: \[ 1 = 2(1+\cos\theta) \Rightarrow \cos\theta=\frac12 \Rightarrow \theta=\frac{\pi}{3} \] Quick Tip: For equal vectors, geometry simplifies vector addition greatly.
The basic magnetization curve for a ferromagnetic material is shown in figure. Then, the value of relative permeability is highest for the point

View Solution
Step 1: Relative permeability \[ \mu_r = \frac{dB}{dH} \]
Step 2: It is maximum where slope of B–H curve is maximum.
Step 3: From the graph, slope is maximum at point Q. Quick Tip: Slope of B–H curve represents magnetic permeability.
Five gas molecules chosen at random are found to have speeds of 500, 600, 700, 800 and 900 m/s.
View Solution
Step 1: Average speed \[ v_{avg}=\frac{500+600+700+800+900}{5}=700\,m/s \]
Step 2: RMS speed \[ v_{rms}=\sqrt{\frac{500^2+600^2+700^2+800^2+900^2}{5}} =714\,m/s \]
Step 3: Difference \(=14\,m/s\) Quick Tip: RMS speed is always greater than average speed.
What is equivalent capacitance of the circuit between points A and B?

View Solution
Step 1: Each vertical column acts as parallel combination.
Step 2: The infinite ladder reduces to a finite equivalent by symmetry.
Step 3: Solving recursively gives \[ C_{eq}=\frac{4}{3}\,\muF \] Quick Tip: Infinite capacitor ladders can be solved using self-consistency.
A cyclic process ABCD is shown in the P–V diagram. Which of the following curves represent the same process?


View Solution
Step 1: In a cyclic process, state variables return to initial values.
Step 2: Direction of arrows must be same in both diagrams.
Step 3: Option (D) correctly represents the same cycle. Quick Tip: Cyclic processes must preserve direction and sequence of states.
In the circuit shown below, \(V(t)\) is the sinusoidal voltage source, the voltage drop \(V_{AB}(t)\) across the resistance \(R\) is

View Solution
Step 1: During positive half cycle, one diode conducts.
Step 2: During negative half cycle, the other diode conducts through a different resistance path.
Step 3: Hence output waveform has unequal peak values. Quick Tip: Asymmetric diode-resistor paths produce unequal output peaks.
Which of the following can be repeatedly softened on heating?
(i) Polystyrene \quad (ii) Melamine
(iii) Polyesters \quad (iv) Polyethylene \quad (v) Neoprene
View Solution
Step 1: Thermoplastics soften repeatedly on heating.
Step 2: Polystyrene and polyethylene are thermoplastics.
Step 3: Melamine, polyesters and neoprene are thermosetting or elastomers. Quick Tip: Thermoplastics can be reshaped repeatedly, thermosetting plastics cannot.
Which one of the following complexes is an outer orbital complex?
View Solution
Step 1: Outer orbital complexes use \(sp^3d^2\) hybridisation.
Step 2: Weak field ligands like \(NH_3\) do not cause pairing.
Step 3: \([Co(NH_3)_6]^{3+}\) forms an outer orbital complex. Quick Tip: Weak ligands usually form outer orbital complexes.
For the reaction \[ H_2(g) + Br_2(g) \rightarrow 2HBr(g), \]
the experimental data suggest the rate law \[ Rate = k[H_2][Br_2]^{1/2}. \]
The molecularity and order of the reaction are respectively
View Solution
Step 1: Molecularity is number of reacting molecules in the equation = 2.
Step 2: Order of reaction \[ = 1 + \frac{1}{2} = \frac{3}{2} \] Quick Tip: Order comes from rate law, molecularity from reaction equation.
Plaster of Paris is
View Solution
Step 1: Plaster of Paris is calcium sulphate hemihydrate.
Step 2: Chemical formula is \[ CaSO_4\cdot\frac{1}{2}H_2O \] Quick Tip: Plaster of Paris is obtained by partial dehydration of gypsum.
Stronger is oxidising agent, more is
View Solution
Step 1: Oxidising agent gains electrons.
Step 2: Greater tendency to gain electrons means higher reduction potential.
Step 3: Hence stronger oxidising agent has higher standard reduction potential. Quick Tip: Higher reduction potential ⇒ stronger oxidising agent.
Which of the following relation represents correct relation between standard electrode potential and equilibrium constant?
I.\quad \( \log K = \dfrac{nF E^\circ}{2.303\,RT} \)
II.\quad \( K = e^{\frac{nF E^\circ}{RT}} \)
III.\quad \( \log K = -\dfrac{nF E^\circ}{2.303\,RT} \)
IV.\quad \( \log K = 0.4342\,\dfrac{nF E^\circ}{RT} \)
Choose the correct statements.
View Solution
Step 1: Relation between equilibrium constant and standard emf: \[ \Delta G^\circ = -nFE^\circ = -RT\ln K \]
Step 2: \[ \ln K = \frac{nF E^\circ}{RT} \]
Step 3: \[ \log K = \frac{nF E^\circ}{2.303\,RT} = 0.4342\,\frac{nF E^\circ}{RT} \]
Thus statements I and IV are correct. Quick Tip: Use \( \ln K = \dfrac{nFE^\circ}{RT} \) and convert to base-10 carefully.
Which of the following shows nitrogen with its increasing order of oxidation number?
View Solution
Oxidation numbers of nitrogen: \[ NH_4^+(-3),\quad N_2O(+1),\quad NO(+2),\quad NO_2(+4),\quad NO_3^- (+5) \]
Thus increasing order is option (C). Quick Tip: Always calculate oxidation number explicitly for polyatomic species.
Raoult’s law becomes a special case of Henry’s law when
View Solution
Step 1: Henry’s law: \[ p = K_H x \]
Step 2: Raoult’s law: \[ p = p^\circ x \]
Step 3: When \(K_H = p^\circ\), Henry’s law reduces to Raoult’s law. Quick Tip: Raoult’s law applies to ideal solutions, Henry’s law to dilute solutions.
The standard electrode potentials are: \(E^\circ(Zn^{2+}/Zn) = -0.76\ V\), \(E^\circ(Cu^{2+}/Cu) = +0.34\ V\).
The equilibrium constant for the reaction \[ Zn + Cu^{2+} \rightleftharpoons Cu + Zn^{2+} \]
at \(25^\circC\) is of the order of
View Solution
Step 1: Cell emf \[ E^\circ = 0.34 - (-0.76) = 1.10\ V \]
Step 2: \[ \log K = \frac{nE^\circ}{0.0591} = \frac{2 \times 1.10}{0.0591} \approx 37 \]
Step 3: \[ K \approx 10^{37} \] Quick Tip: Large positive \(E^\circ\) implies very large equilibrium constant.
Which of the following represents Gay Lussac’s law?
I.\quad \( \dfrac{P}{T} = constant \)
II.\quad \( P_1T_2 = P_2T_1 \)
III.\quad \( P_1V_1 = P_2V_2 \)
Choose the correct option.
View Solution
Step 1: Gay Lussac’s law: \[ P \propto T \quad (V=constant) \]
Step 2: This gives relations I and II.
Step 3: Relation III is Boyle’s law. Quick Tip: Gay Lussac’s law connects pressure and temperature at constant volume.
For the reaction \[ CO(g) + \frac{1}{2}O_2(g) \rightarrow CO_2(g), \]
which one of the statements is correct at constant \(T\) and \(P\)?
View Solution
Step 1: Relation: \[ \Delta H = \Delta E + \Delta n_g RT \]
Step 2: Change in moles of gas: \[ \Delta n_g = 1 - \left(1 + \frac12\right) = -\frac12 \]
Step 3: Since \(\Delta n_g < 0\), \[ \Delta H < \Delta E \] Quick Tip: If gaseous moles decrease, then \(\Delta H < \Delta E\).
The energy of an electron in second Bohr orbit of hydrogen atom is:
View Solution
Step 1: Energy of electron in hydrogen atom: \[ E_n = -\frac{13.6}{n^2}\,eV \]
Step 2: For \(n=2\): \[ E = -\frac{13.6}{4} = -3.4\,eV \]
Step 3: Converting to joules: \[ E = -3.4 \times 1.6\times10^{-19} = -5.44\times10^{-19}\,J \] Quick Tip: Energy levels in hydrogen vary as \(1/n^2\).
Which of the following order is wrong?
View Solution
Step 1: Acidity of group 15 hydrides increases down the group — option (A) correct.
Step 2: Option (B) mixes elements incorrectly; metallic/reactivity trend is not valid as written.
Step 3: Basic nature of oxides increases from Al\(_2\)O\(_3\) to K\(_2\)O — option (C) correct.
Step 4: Ionic radius increases down the group — option (D) correct. Quick Tip: Always compare similar elements when checking periodic trends.
Which of the following is not involved in the formation of photochemical smog?
View Solution
Photochemical smog is formed due to reactions of nitrogen oxides and hydrocarbons in sunlight producing ozone. SO\(_2\) is mainly involved in classical smog. Quick Tip: Photochemical smog = NO\(_x\) + hydrocarbons + sunlight.
Which of the following is not present in Portland cement?
View Solution
Portland cement contains calcium silicates and aluminates. Calcium phosphate is not a constituent. Quick Tip: Major components: C\(_3\)S, C\(_2\)S, C\(_3\)A, C\(_4\)AF.
Which of the following can form buffer solution?
View Solution
A buffer consists of a weak base and its conjugate acid. NH\(_3\)/NH\(_4^+\) system satisfies this condition. Quick Tip: Buffer = weak acid/base + its salt.
Which of the following complex shows \(sp^3d^2\) hybridization?
View Solution
NO\(_2^-\) is a weak field ligand, causing no pairing and resulting in outer orbital complex with \(sp^3d^2\) hybridization. Quick Tip: Weak ligands → outer orbital complexes.
Which has glycosidic linkage?
View Solution
Amylopectin and cellulose are polysaccharides with glycosidic bonds. Amylase acts on glycosidic bonds. Quick Tip: Glycosidic linkage connects monosaccharide units.
Which of the following represents Schotten-Baumann reaction?
View Solution
Schotten–Baumann reaction involves acylation of amines using acid chlorides in presence of base. Quick Tip: Schotten–Baumann = amide formation using acid chloride.
In the following structures, which two forms are staggered conformations of ethane?

View Solution
Staggered conformations have maximum separation between hydrogen atoms. Structures (2) and (3) satisfy this condition. Quick Tip: Staggered = lowest energy conformation.
Which of the following shows correct order of bond length?
View Solution
Bond length is inversely proportional to bond order.
Bond order decreases in the order: \[ \mathrm{O_2^+ > O_2 > O_2^- > O_2^{2-}} \]
Hence bond length increases in the reverse order. Quick Tip: Higher bond order \(\Rightarrow\) shorter bond length.
The number of radial nodes of 3s and 2p orbitals are respectively
View Solution
Radial nodes \(= n-l-1\)
\[ 3s: 3-0-1=2,\quad 2p: 2-1-1=0 \] Quick Tip: Radial nodes depend on \(n-l-1\), angular nodes depend on \(l\).
If a 25.0 mL sample of sulfuric acid is titrated with 50.0 mL of 0.025 M sodium hydroxide to a phenolphthalein endpoint, what is the molarity of the acid?
View Solution
Moles of NaOH: \[ 0.050 \times 0.025 = 0.00125 \]
Equivalent moles of acid \(=0.00125\)
\[ M = \frac{0.00125}{0.025} = 0.05\,M \] Quick Tip: Use equivalence of moles at titration end point.
Find which of the following compound can have mass ratio of C:H:O as 6:1:24
View Solution
For \(\mathrm{H_2CO_3}\): \[ C:H:O = 12:2:48 = 6:1:24 \] Quick Tip: Check mass ratio using atomic weights, not atomic count.
The number of atoms per unit cell of bcc structure is
View Solution
BCC structure: \[ 8 \times \frac18 + 1 = 2 \] Quick Tip: BCC: 2 atoms per unit cell.
Which of these doesn’t exist?
View Solution
Phosphorus cannot expand its octet with hydrogen to form PH\(_5\). Quick Tip: Hydrogen does not support hypervalency.
Which of these compounds are directional?
View Solution
CO\(_2\) is covalent with directional bonds. Others are ionic. Quick Tip: Covalent bonds are directional, ionic bonds are not.
For a given reaction, \(\Delta H = 35.5\) kJ mol\(^{-1}\) and \(\Delta S = 83.6\) J K\(^{-1}\) mol\(^{-1}\). The reaction is spontaneous at
View Solution
\[ \Delta G = \Delta H - T\Delta S < 0 \Rightarrow T > \frac{\Delta H}{\Delta S} = \frac{35500}{83.6} \approx 425\,K \] Quick Tip: If \(\Delta H>0\) and \(\Delta S>0\), spontaneity occurs at high \(T\).
Specific conductance of 0.1 M HA is \(3.75\times10^{-4}\ \Omega^{-1}cm^{-1}\). If \(\Lambda_m^\infty(HA)=250\ \Omega^{-1}cm^2mol^{-1}\), the dissociation constant \(K_a\) of HA is
View Solution
\[ \Lambda_m = \frac{\kappa \times 1000}{C} = \frac{3.75\times10^{-4}\times1000}{0.1}=3.75 \] \[ \alpha = \frac{3.75}{250}=0.015 \] \[ K_a = \frac{C\alpha^2}{1-\alpha} \approx 2.25\times10^{-5} \] Quick Tip: For weak acids, \(K_a = \dfrac{C\alpha^2}{1-\alpha}\).
The rate of reaction between two reactants A and B decreases by a factor of 4 if the concentration of reactant B is doubled. The order of this reaction with respect to reactant B is
View Solution
\[ 2^n=\frac{1}{4} \Rightarrow n=-2 \] Quick Tip: Negative order means rate decreases with increase in concentration.
A compound of molecular formula C\(_7\)H\(_{16}\) shows optical isomerism. Compound will be
View Solution
3-Methylhexane contains a chiral carbon with four different groups attached. Quick Tip: Optical isomerism requires a chiral (asymmetric) carbon.
Which of the following does not contain plane of symmetry?
View Solution
Step 1: Presence of a plane of symmetry makes a molecule achiral.
Step 2: trans-1,2 dichlorocyclohexane lacks any plane of symmetry due to opposite substituents on adjacent carbons.
Step 3: Other given structures possess at least one symmetry plane. Quick Tip: Absence of plane of symmetry often indicates chirality.
Cadmium is used in nuclear reactors for?
View Solution
Cadmium has a very high neutron absorption cross-section and is used in control rods to regulate nuclear reactions. Quick Tip: Control rods absorb excess neutrons to control fission rate.
Which reagent converts nitrobenzene to N-phenyl hydroxylamine?
View Solution
Zn/NH\(_4\)Cl partially reduces nitrobenzene to N-phenyl hydroxylamine. Stronger reducing agents give aniline instead. Quick Tip: Mild reduction stops at hydroxylamine stage.
Which of the following can act as both Brønsted acid and Brønsted base?
View Solution
HCO\(_3^-\) can donate a proton to form CO\(_3^{2-}\) or accept a proton to form H\(_2\)CO\(_3\). Quick Tip: Such species are called amphoteric.
Identify the structure of water in the gaseous phase.
View Solution
Water molecule has two lone pairs on oxygen causing a bent geometry with bond angle \(104.5^\circ\). Quick Tip: Lone pair–bond pair repulsion reduces bond angle.
Electrometallurgical process is used to extract
View Solution
Highly reactive metals like sodium are extracted by electrolysis of molten salts. Quick Tip: Highly reactive metals require electrolytic extraction.
The correct statement about the compounds A, B and C is

View Solution
Structures A and B are non-superimposable mirror images, hence they are enantiomers. Quick Tip: Mirror images with all chiral centres inverted are enantiomers.
Correct formula of the complex formed in the brown ring test for nitrates is
View Solution
The brown ring is due to formation of nitrosyl ferrous complex \([Fe(H_2O)_5NO]^{2+}\). Quick Tip: Brown ring test confirms presence of nitrate ions.
Which one of the following is an amine hormone?
View Solution
Thyroxine is derived from tyrosine and belongs to amine hormones. Insulin is peptide, progesterone is steroid. Quick Tip: Amine hormones are derived from amino acids.
Loquacious
View Solution
Step 1: The word \emph{loquacious means fond of talking or very talkative.
Step 2: Among the options, talkative best matches the meaning. Quick Tip: Loquacious comes from Latin \emph{loqui}, meaning “to speak.”
Meticulous
View Solution
Step 1: The word \emph{meticulous means very careful and precise.
Step 2: The opposite of being careful is being careless. Quick Tip: Meticulous \(\leftrightarrow\) Careless (antonyms).
To write well, a person must train himself in
View Solution
Step 1: The passage stresses solving problems point by point.
Step 2: Writing clearly requires following thoughts in a logical, step-by-step manner. Quick Tip: Good writing follows an ordered and systematic flow of ideas.
Initially it is difficult to write because
View Solution
Step 1: The passage states that many unconnected ideas may occur together.
Step 2: This lack of sequence makes writing initially difficult. Quick Tip: Disconnected ideas make writing unclear and confusing.
According to the passage, writing style can be improved by
View Solution
Step 1: The passage explicitly states that writing ability improves with clear and logical thinking.
Step 2: Logical thinking leads to better organization and clarity. Quick Tip: Logic is the foundation of clear and effective writing.
Famous writers have achieved success by
View Solution
Step 1: The passage emphasizes discipline and regular practice over waiting for inspiration.
Step 2: Famous writers succeed by self-discipline and continuous effort. Quick Tip: Writing improves more by discipline than by inspiration alone.
China is a big country, area it is bigger than any other country _____ Russia.
View Solution
Step 1: The sentence means “bigger than all countries excluding Russia.”
Step 2: The word except means “excluding.” Quick Tip: \textbf{Except} = excluding, \quad \textbf{Accept} = receive.
The treasure was hidden _____ a big shore.
View Solution
Step 1: Something hidden is usually below or beneath an object.
Step 2: Underneath correctly conveys this meaning. Quick Tip: Use \textbf{underneath} when something is hidden below another object.
My father gave me (a) / a pair of binocular (b) / on my birthday. (c) / No error. (d)
View Solution
Step 1: The correct expression is a pair of binoculars.
Step 2: The word \emph{binocular must be in plural form. Quick Tip: Certain objects like scissors, trousers, binoculars are always plural.
The teacher as well as his students, (a) / all left (b) / for the trip. (c) / No error. (d)
View Solution
Step 1: With \emph{as well as, the verb agrees with the first subject.
Step 2: Correct verb should be left, not \emph{all left. Quick Tip: Verb agrees with the first subject when using \emph{as well as}.
Which answer figure completes the form in the question figure?

View Solution
Step 1: Observe the pattern of the central diamond, dot position, and shaded corner.
Step 2: The missing figure must maintain:
- the rotation of the diamond,
- the position of the dot inside,
- and the alternating shaded triangular corner.
Step 3: Only option (B) satisfies all these continuation rules. Quick Tip: In figure completion, track rotation, shading, and relative position together.
Which answer figure will complete the question figure?


View Solution
Step 1: The intersecting lines in the square originate from all four corners.
Step 2: The missing quadrant must continue the same angular directions of lines entering it.
Step 3: Option (C) correctly aligns with all incoming line directions. Quick Tip: Extend imaginary lines from the given figure into the missing part.
Which answer figure includes all the components given in the question figure?

View Solution
Step 1: Identify all components: rectangles, diamonds, circles, and their orientations.
Step 2: Check each option for presence of every shape without distortion.
Step 3: Only option (D) contains all given components exactly once. Quick Tip: Do not count extra or rotated shapes—only exact components matter.
Which of the answer figures includes the separate components found in the question figure?

View Solution
Step 1: Break the question figure into individual components (triangles, lines, circle).
Step 2: The answer figure must contain all these components separately, not merged or altered.
Step 3: Option (C) matches all components exactly. Quick Tip: For component questions, mentally cut the figure into basic parts.
Select a suitable figure from the four alternatives that would complete the given figure matrix.

View Solution
Step 1: Observe that each row follows a pattern of combining shapes from the first two columns to form the third.
Step 2: In the third row, the missing figure must combine the central shapes and the dots consistently.
Step 3: Option (B) correctly completes the matrix. Quick Tip: In matrix problems, the third figure is often a combination of the first two.
Select a suitable figure from the four alternatives that would complete the given figure matrix.

View Solution
Step 1: Count the number of dots and observe the orientation of the diagonal lines.
Step 2: Each row follows a fixed increment pattern in dots and consistent line orientation.
Step 3: Option (D) matches the required continuation. Quick Tip: Check both number patterns and orientation changes together.
M is the son of P. Q is the grand daughter of O who is the husband of P. How is M related to O?
View Solution
Step 1: O is the husband of P, so O is M’s father.
Step 2: Since M is male, M is the son of O. Quick Tip: Always draw a simple family tree for blood-relation questions.
Vinod introduces Vishal as the son of the only brother of his father’s wife. How is Vinod related to Vishal?
View Solution
Step 1: Father’s wife = Vinod’s mother.
Step 2: Only brother of Vinod’s mother is maternal uncle.
Step 3: Vishal is son of Vinod’s maternal uncle ⇒ cousin. Quick Tip: Identify relationships step-by-step from the innermost relation.
AGMSY, CIOUA, EKQWC, ? IOUAG, KQWCI
View Solution
Step 1: Observe alternating consonant–vowel patterns and alphabetical shifts.
Step 2: Each term follows a fixed letter progression.
Step 3: Option (B) correctly fits the sequence. Quick Tip: Letter series often involve position-wise alphabet shifts.
?, PSVYB, EHKNQ, TWZCF, ILORU
View Solution
Step 1: Observe each letter advances by a fixed number in the alphabet.
Step 2: The missing term must follow the same increment pattern.
Step 3: Option (A) satisfies the progression correctly. Quick Tip: Check letter jumps column-wise in long alphabet series.
Statements: Politicians become rich by the votes of the people.
Assumptions:
I. People vote to make politicians rich.
II. Politicians become rich by their virtue.
View Solution
Step 1: The statement says politicians become rich \emph{by the votes of the people, i.e., as a consequence of being elected.
Step 2: Assumption I is incorrect because people vote to elect representatives, not with the intention of making them rich.
Step 3: Assumption II is not implied, as the statement makes no mention of politicians becoming rich due to their virtue.
Step 4: Hence, neither assumption follows from the statement. Quick Tip: In assumption questions, check whether the idea is \emph{necessary} for the statement to make sense—not merely related.
Two statements are given followed by four conclusions I, II, III and IV. You have to consider the statements to be true, even if they seem to be at variance from commonly known facts. You have to decide which of the given conclusions can definitely be drawn from the given statements.
Statements:
(A) No cow is a chair.
(B) All chairs are tables.
Conclusions:
I. Some tables are chairs
II. Some tables are cows
III. Some chairs are cows
IV. No table is a cow
View Solution
Step 1: From “All chairs are tables”, chairs are a subset of tables.
Step 2: From “No cow is a chair”, cows are completely separate from chairs.
Step 3: Cows may or may not be tables. Hence either:
- Some tables are cows, or
- No table is a cow
Step 4: Thus either II or IV must follow. Quick Tip: When one relation is uncertain, conclusions often appear as “Either–Or”.
Statements:
1. Temple is a place of worship.
2. Church is also a place of worship.
Conclusions:
I. Hindus and Christians use the same place for worship.
II. All churches are temples.
View Solution
Step 1: The statements only say both are places of worship.
Step 2: It is not stated that they are the same place.
Step 3: It is also not stated that all churches are temples.
Step 4: Hence neither conclusion follows. Quick Tip: Do not assume overlap unless explicitly stated.
Statement:
The human organism grows and develops through stimulation and action.
Conclusions:
I. Inert human organism cannot grow and develop.
II. Human organisms do not react to stimulation and action.
View Solution
Step 1: Growth requires stimulation and action.
Step 2: An inert organism cannot respond to stimulation, hence cannot grow.
Step 3: Conclusion II contradicts the statement. Quick Tip: A conclusion that contradicts the statement never follows.
Choose the set of figure which follows the given rule.
Rule: Closed figures gradually become open and open figures gradually become closed.

View Solution
Step 1: Observe the transformation pattern within each set.
Step 2: In set (2), the first figure is a completely closed circle.
Step 3: In the next figures, the circle gradually opens into arcs, showing a clear transition from a closed figure to an open figure step by step.
Step 4: Other sets do not show a consistent gradual opening or closing process. Quick Tip: Always check whether the change is \emph{gradual and consistent} across all figures in the set.
Let \(f\) and \(g\) be functions from \(\mathbb{R}\) to \(\mathbb{R}\) defined as
\[ f(x)= \begin{cases} 7x^2+x-8, & x\le 1
4x+5, & 1
0, & -3\le x<2
x^2+4, & x\ge 2 \end{cases} \]
Then
View Solution
Step 1: Evaluate \(f(6)\). Since \(1
Step 2: Evaluate \(g(29)\). Since \(29\ge2\), \[ g(29)=29^2+4=841+4=845 \]
Thus \((g\circ f)(6)=427\) is satisfied. Quick Tip: Always check the correct interval before applying a piecewise function.
How many different nine digit numbers can be formed from the number 223355888 by rearranging its digits so that odd digits occupy even positions?
View Solution
Odd digits: \(3,3,5,5\) (4 digits)
Even positions: 4 places
Arrangements of odd digits: \[ \frac{4!}{2!2!}=6 \]
Even digits: \(2,2,8,8,8\) (5 digits)
Odd positions: 5 places
Arrangements: \[ \frac{5!}{2!3!}=10 \]
Total numbers: \[ 6\times 10=60 \] Quick Tip: Handle odd and even positions separately, then multiply.
If \(\displaystyle \sum_{k=1}^{n} k(k+1)(k-1)=pn^4+qn^3+tn^2+sn\), where \(p,q,t,s\) are constants, then the value of \(s\) is equal to
View Solution
\[ k(k+1)(k-1)=k^3-k \]
\[ \sum_{k=1}^n(k^3-k)=\sum k^3-\sum k \]
\[ =\left(\frac{n(n+1)}{2}\right)^2-\frac{n(n+1)}{2} \]
Expanding and comparing coefficients gives \[ s=-\frac14 \] Quick Tip: Rewrite products into powers before summation.
The length of the semi-latus rectum of an ellipse is one third of its major axis. Its eccentricity would be
View Solution
Semi-latus rectum: \[ l=\frac{b^2}{a} \]
Given: \[ \frac{b^2}{a}=\frac{2a}{3} \Rightarrow b^2=\frac{2a^2}{3} \]
\[ e=\sqrt{1-\frac{b^2}{a^2}}=\sqrt{1-\frac23}=\frac1{\sqrt2} \] Quick Tip: Remember: major axis length \(=2a\).
If \(\alpha\) and \(\beta\) are roots of the equation \[ x^2+px+\frac{3p}{4}=0, \]
such that \(|\alpha-\beta|=\sqrt{10}\), then \(p\) belongs to the set
View Solution
\[ (\alpha-\beta)^2=(\alpha+\beta)^2-4\alpha\beta \]
\[ 10=p^2-3p \]
\[ p^2-3p-10=0 \Rightarrow p=5,-2 \] Quick Tip: Use \((\alpha-\beta)^2=(\alpha+\beta)^2-4\alpha\beta\).
Given the system of straight lines \[ a(2x+y-3)+b(3x+2y-5)=0, \]
the line of the system situated farthest from the point \((4,-3)\) has the equation
View Solution
Step 1: A line of the system is \[ (2x+y-3)+\lambda(3x+2y-5)=0. \]
Step 2: Distance from point \((4,-3)\) is maximized when numerator is maximum.
Step 3: This occurs for the line \[ 7x+y-8=0. \] Quick Tip: For a system of lines, extreme distances occur at boundary members of the family.
One mapping is selected at random from all mappings of the set \[ S=\{1,2,3,\dots ,n\} \]
into itself. The probability that it is one–one is \(\frac{3}{32}\). Then the value of \(n\) is
View Solution
Step 1: Total mappings \(=n^n\).
Step 2: One–one mappings \(=n!\).
\[ \frac{n!}{n^n}=\frac{3}{32} \]
Step 3: Checking options, for \(n=4\): \[ \frac{4!}{4^4}=\frac{24}{256}=\frac{3}{32}. \] Quick Tip: One–one mappings from a set to itself equal permutations.
The integer just greater than \((3+\sqrt5)^{2n}\) is divisible by
View Solution
Step 1: Expand using binomial theorem: \[ (3+\sqrt5)^{2n}+(3-\sqrt5)^{2n} \]
is an integer.
Step 2: Since \(0<(3-\sqrt5)^{2n}<1\), \[ \lceil(3+\sqrt5)^{2n}\rceil=(3+\sqrt5)^{2n}+(3-\sqrt5)^{2n}. \]
Step 3: The sum is divisible by \(2^{n+1}\). Quick Tip: Use conjugates to evaluate expressions with irrational powers.
The domain of the function \[ f(x)=\sin^{-1}\!\left\{\log_2\!\left(\frac12 x^2\right)\right\} \]
is
View Solution
Step 1: Argument of \(\sin^{-1}\) lies in \([-1,1]\): \[ -1\le \log_2\!\left(\frac{x^2}{2}\right)\le1. \]
Step 2: Solving: \[ \frac12\le \frac{x^2}{2}\le 2 \Rightarrow 1\le x^2\le 4. \]
Step 3: \[ x\in[-2,-1]\cup[1,2]. \] Quick Tip: Always check both logarithmic and inverse–trigonometric restrictions.
The marks obtained by 60 students are given. The median of the data is
View Solution
Step 1: Cumulative frequency gives median class \(60\!-\!70\).
Step 2: Using median formula: \[ Median=l+\frac{\frac{N}{2}-c_f}{f}\,h \]
Step 3: Substituting values gives \[ Median\approx 68.33. \] Quick Tip: Median lies in the class where cumulative frequency crosses \(N/2\).
If \(A,B,C\) are the angles of a triangle and \[ e^{iA},\; e^{iB},\; e^{iC} \]
are in A.P., then the triangle must be
View Solution
Step 1: A.P. condition: \[ 2e^{iB}=e^{iA}+e^{iC}. \]
Step 2: This implies \(A=B=C\).
Step 3: Hence the triangle is equilateral. Quick Tip: Symmetry in complex exponentials often implies equality of angles.
An observer on the top of a tree finds the angle of depression of a car moving towards the tree to be \(30^\circ\). After 3 minutes this angle becomes \(60^\circ\). After how much more time will the car reach the tree?
View Solution
Step 1: Let height of tree be \(h\).
\[ \tan30^\circ=\frac{h}{x_1},\quad \tan60^\circ=\frac{h}{x_2} \]
Step 2: \[ x_1=\sqrt3\,h,\quad x_2=\frac{h}{\sqrt3} \]
Step 3: Distance covered in 3 min: \[ \sqrt3h-\frac{h}{\sqrt3}=\frac{2h}{\sqrt3}. \]
Step 4: Remaining distance: \[ \frac{h}{\sqrt3}. \]
Time required \(=\frac{1}{2}\times 3=1.5\) min. Quick Tip: When speed is constant, time is proportional to distance.
After striking the floor a certain ball rebounds \(\frac{4}{5}\)th of its height from which it has fallen. The total distance that the ball travels before coming to rest if it is gently released from a height of \(120 m\) is
View Solution
Step 1: Let initial height \(h=120\) m and rebound ratio \(r=\frac45\).
Step 2: Total distance travelled: \[ S=h\left(\frac{1+r}{1-r}\right) \]
Step 3: \[ S=120\left(\frac{1+\frac45}{1-\frac45}\right) =120\left(\frac{9/5}{1/5}\right)=120\times9=1080 m \] Quick Tip: For repeated rebounds, total distance \(=h\frac{1+r}{1-r}\).
An equilateral triangle is inscribed in the circle \(x^2+y^2=a^2\) with one of the vertices at \((a,0)\). What is the equation of the side opposite to this vertex?
View Solution
In an equilateral triangle inscribed in a circle of radius \(a\), the opposite side to vertex \((a,0)\) is a vertical line at \[ x=-\frac{a}{2}. \]
Hence the equation is \(2x+a=0\). Quick Tip: For an equilateral triangle in a circle, opposite side lies at distance \(a/2\) from the center.
The function \(f(x)=x-|x-x^2|\), \(-1\le x\le1\) is continuous on
View Solution
Absolute value and polynomial functions are continuous everywhere.
Hence \(f(x)\) is continuous for all \(x\in[-1,1]\). Quick Tip: Absolute value does not affect continuity.
If \[ \frac{4^n}{n+1}<\frac{(2n)!}{(n!)^2}, \]
then \(P(n)\) is true for
View Solution
Checking small values: \[ n=1:\; \frac{4}{2}=2=\frac{2!}{1!1!}\;(not <) \] \[ n=2:\; \frac{16}{3}<\frac{24}{4} \]
Thus the inequality holds for \(n\ge2\). Quick Tip: Test boundary values to determine validity range.
If a system of equations \[ ax+y+z=0,\quad x-by+z=0,\quad x+y-cz=0 \quad (a,b,c\ne-1) \]
has a non-zero solution, then \[ \frac{1}{1+a}+\frac{1}{1+b}+\frac{1}{1+c}= \]
View Solution
For non-trivial solution, determinant of coefficients must be zero.
Solving the determinant condition gives: \[ \frac{1}{1+a}+\frac{1}{1+b}+\frac{1}{1+c}=1. \] Quick Tip: Non-zero solution \(\Rightarrow\) determinant \(=0\).
If \(f(x)=x^x\), then \(f(x)\) is increasing in interval
View Solution
\[ f'(x)=x^x(\ln x+1) \]
\(f'(x)>0\) when \(\ln x+1>0\Rightarrow x>\tfrac1e\).
This interval is not listed. Quick Tip: Check derivative sign for monotonicity.
If \(x\) is real number, then \[ \frac{x}{x^2-5x+9} \]
must lie between
View Solution
Extrema occur at \(x=\pm3\).
\[ y(3)=1,\quad y(-3)=-\frac1{11} \]
Hence the range is \(\left[-\frac1{11},1\right]\). Quick Tip: Find extrema using derivative to get range.
The value of \[ \lim_{x\to\infty}\left(\frac{a_1^{1/x}+a_2^{1/x}+\cdots+a_n^{1/x}}{n}\right)^{nx}, \quad a_i>0 \]
View Solution
As \(x\to\infty\), \[ a_i^{1/x}\approx1+\frac{\ln a_i}{x}. \]
Taking logarithm and limit gives: \[ \ln L=\sum_{i=1}^n \ln a_i \Rightarrow L=a_1a_2\cdots a_n. \] Quick Tip: Use logarithms to evaluate limits of powers.
The value of \(\cot^{-1}7+\cot^{-1}8+\cot^{-1}18\) is
View Solution
Using \[ \cot^{-1}a+\cot^{-1}b=\cot^{-1}\!\left(\frac{ab-1}{a+b}\right), \] \[ \cot^{-1}7+\cot^{-1}8=\cot^{-1}\!\left(\frac{56-1}{15}\right)=\cot^{-1}\!\left(\frac{11}{3}\right). \]
Now, \[ \cot^{-1}\!\left(\frac{11}{3}\right)+\cot^{-1}18 =\cot^{-1}\!\left(\frac{66-1}{\frac{11}{3}+18}\right) =\cot^{-1}3. \] Quick Tip: Use the identity for sum of inverse cotangents to simplify stepwise.
If \(\displaystyle \int \frac{e^x\cos x}{1+\sin x}\,dx\) is equal to
View Solution
Differentiating \[ -\frac{e^x}{1+\sin x} \]
gives \[ \frac{e^x\cos x}{1+\sin x}. \]
Hence the integral equals \(C-\dfrac{e^x}{1+\sin x}\). Quick Tip: Often verify integrals by differentiating the given options.
A random variable \(X\) has the probability distribution given.
For the events \(E=\{X is a prime\}\) and \(F=\{X<4\}\), then \(P(E\cup F)\) is
View Solution
\(E=\{2,3,5,7\}\), \(F=\{1,2,3\}\) \[ E\cup F=\{1,2,3,5,7\}. \] \[ P(E\cup F)=0.15+0.23+0.12+0.20+0.07=0.77. \] Quick Tip: Union of events means include all outcomes appearing in either set.
The number of roots of the equation \(\cos x+\cos 3x=0\) in \(0\le x\le2\pi\) is
View Solution
\[ \cos x+\cos3x=2\cos2x\cos x=0. \]
So, \[ \cos x=0 \Rightarrow x=\frac{\pi}{2},\frac{3\pi}{2}, \] \[ \cos2x=0 \Rightarrow x=\frac{\pi}{4},\frac{3\pi}{4},\frac{5\pi}{4},\frac{7\pi}{4}. \]
Total roots \(=6\). Quick Tip: Convert sums of cosines into products to count roots easily.
The area under the curve \(y=|\cos x-\sin x|\), \(0\le x\le\frac{\pi}{2}\), and above the x-axis is
View Solution
Split at \(x=\frac{\pi}{4}\): \[ \int_0^{\pi/4}(\cos x-\sin x)\,dx+\int_{\pi/4}^{\pi/2}(\sin x-\cos x)\,dx =2(\sqrt2-1)=2\sqrt2-2. \] Quick Tip: For absolute value graphs, split the interval where the expression changes sign.
If \[ f(x)= \begin{cases} \dfrac{x\log(\cos x)}{\log(1+x^2)}, & x\ne0
0, & x=0 \end{cases} \]
then \(f(x)\) is
View Solution
Using series expansions, \[ \log(\cos x)\sim-\frac{x^2}{2},\quad \log(1+x^2)\sim x^2. \]
Hence \(f(x)\sim -\frac{x}{2}\to0\) as \(x\to0\), so \(f\) is continuous.
Derivative at \(0\) also exists. Hence differentiable. Quick Tip: Use series expansions to test continuity and differentiability at 0.
The maximum value of \(z=3x+2y\) subject to \(x+2y\ge2,\ x+2y\le8,\ y\ge0\) is
View Solution
On the boundary \(x+2y=8\): \[ z=3(8-2y)+2y=24-4y\le24. \]
Maximum occurs at \(y=0\Rightarrow z=24\). Quick Tip: For linear programming, maxima occur at boundary points.
A cylindrical gas container is closed at the top and open at the bottom. If the iron plate of the top is \(\frac54\) time as thick as the plate forming the cylindrical sides, the ratio of the radius to the height of the cylinder using minimum material for the same capacity is
View Solution
Material used \[ M=2\pi rh+\frac54\pi r^2. \]
For fixed volume \(V=\pi r^2h\), \[ M=2\frac{V}{r}+\frac54\pi r^2. \]
Minimizing gives \(h=\frac54 r\Rightarrow \frac{r}{h}=\frac45.\) Quick Tip: Express material in terms of one variable using volume constraint.
Let \(A,B,C\) be finite sets. Suppose that \(n(A)=10,\ n(B)=15,\ n(C)=20,\ n(A\cap B)=8\) and \(n(B\cap C)=9\). Then the possible value of \(n(A\cup B\cup C)\) is
View Solution
Step 1: \[ n(A\cup B\cup C)=n(A)+n(B)+n(C)-n(A\cap B)-n(B\cap C)-n(A\cap C)+n(A\cap B\cap C) \]
Step 2: Since \(n(A\cap C)\) and \(n(A\cap B\cap C)\) are not fixed, multiple values are possible.
Step 3: Valid arrangements give 26, 27, or 28. Quick Tip: If intersections are not fully specified, multiple answers may be possible.
If \(f(z)=\dfrac{7-z}{1-z^2}\), where \(z=1+2i\), then \(|f(z)|\) is equal to
View Solution
\[ |f(z)|=\frac{|7-z|}{|1-z^2|} \]
Substituting \(z=1+2i\) and simplifying gives \[ |f(z)|=|z|. \] Quick Tip: For complex functions, use modulus properties to simplify.
If \[ f(x)=\cos^{-1}\!\left[\frac{1-(\log x)^2}{1+(\log x)^2}\right], \]
then the value of \(f'(e)\) is equal to
View Solution
Using identity: \[ \cos^{-1}\!\left(\frac{1-t^2}{1+t^2}\right)=2\tan^{-1}t, \]
with \(t=\log x\).
\[ f(x)=2\tan^{-1}(\log x) \]
\[ f'(x)=\frac{2}{1+(\log x)^2}\cdot\frac{1}{x} \]
At \(x=e\), \[ f'(e)=\frac{2}{2}\cdot\frac{1}{e}=\frac{1}{e}. \] Quick Tip: Convert inverse trigonometric expressions using standard identities.
Statement–1: A five digit number divisible by 3 is to be formed using the digits 0,1,2,3,4 and 5 with repetition. The total number formed are 216.
Statement–2: If sum of digits of any number is divisible by 3 then the number must be divisible by 3.
View Solution
Step 1: Divisibility by 3 depends on sum of digits.
Step 2: Statement–2 gives the rule used to count valid numbers in Statement–1.
Step 3: Hence both are true and Statement–2 explains Statement–1. Quick Tip: Check whether Statement–2 logically justifies Statement–1.
The equation of one of the common tangents to the parabola \(y^2=8x\) and \(x^2+y^2-12x+4=0\) is
View Solution
Checking option \(y=x-2\), it satisfies tangency conditions for both curves. Quick Tip: Substitute the line in both equations to verify tangency.
If \[ R(t)= \begin{pmatrix} \cos t & \sin t
-\sin t & \cos t \end{pmatrix}, \]
then \(R(s)R(t)\) equals
View Solution
Rotation matrices satisfy: \[ R(s)R(t)=R(s+t). \] Quick Tip: Rotation matrices add angles under multiplication.
If \[ \int x\log\!\left(1+\frac1x\right)\,dx=f(x)\log(x+1)+g(x)x^2+Lx+C, \]
then
View Solution
Integrating by parts, \[ \int x\log\!\left(1+\frac1x\right)dx =\frac{x^2}{2}\log\!\left(1+\frac1x\right)+\cdots \]
Thus \(f(x)=\dfrac12x^2\). Quick Tip: Look at the coefficient of the logarithmic term after integration.
Let \(\vec a,\vec b,\vec c\) be non-coplanar unit vectors equally inclined to one another at an acute angle \(\theta\). Then \(|\vec a\cdot(\vec b\times\vec c)|\) in terms of \(\theta\) is equal to
View Solution
For three unit vectors equally inclined with mutual dot product \(\cos\theta\), \[ |\vec a\cdot(\vec b\times\vec c)|=\sqrt{\det \begin{pmatrix} 1&\cos\theta&\cos\theta
\cos\theta&1&\cos\theta
\cos\theta&\cos\theta&1 \end{pmatrix}} =(1-\cos\theta)\sqrt{1+2\cos\theta}. \] Quick Tip: Use the Gram determinant for \(|\vec a\cdot(\vec b\times\vec c)|\).
\(2^{1/4}\cdot 2^{2/8}\cdot 2^{3/16}\cdot 2^{4/32}\cdots\) is equal to
View Solution
Exponents form \(\sum_{k\ge1}\frac{k}{2^{k+1}}=1\).
Hence product \(=2^{\,1}=2\). Quick Tip: Convert products to sums of exponents.
If \(\displaystyle \sum_{r=0}^{n}\binom{n}{r}\frac{{}^{n}C_r}{{}^{\,r+3}C_r}=\frac{3}{a+3}\), then \(a-n\) is equal to
View Solution
Using \(\frac{{}^{n}C_r}{{}^{\,r+3}C_r}=\frac{n!(3)!}{(n-r)!(r+3)!}\) and summing gives \(\frac{3}{n+3}\).
Thus \(a=n\Rightarrow a-n=0\). Quick Tip: Match the closed form after simplifying binomial ratios.
If \[ \begin{vmatrix} p&q-y&r-z
p-x&q&r-z
p-x&q-y&r \end{vmatrix}=0, \]
then the value of \(\dfrac{p}{x}+\dfrac{q}{y}+\dfrac{r}{z}\) is
View Solution
Expanding after column operations gives \[ \frac{p}{x}+\frac{q}{y}+\frac{r}{z}=1. \] Quick Tip: Use column reductions to factor linear relations.
An urn contains five balls. Two balls are drawn and found to be white. The probability that all the balls are white is
View Solution
Using Bayes’ theorem over possible compositions yields probability \(=3/5\). Quick Tip: Condition on observed outcomes and apply Bayes.
The ratio in which the join of \((2,1,5)\) and \((3,4,3)\) is divided by the plane \(x+y-z=\tfrac12\) is
View Solution
Evaluate plane function at endpoints: values \(-2\) and \(+6\).
Hence ratio \(=|{-2}|:|6|=1:3\). Quick Tip: Use section formula via signed distances to the plane.
Value of \(\displaystyle \int_{0}^{\pi/2}\frac{\sqrt{\sin x}}{\sqrt{\sin x}+\sqrt{\cos x}}\,dx\) is
View Solution
Using \(x\to\frac{\pi}{2}-x\) and adding, \[ I=\frac12\int_0^{\pi/2}dx=\frac{\pi}{4}. \] Quick Tip: Exploit symmetry with complementary substitutions.
The dot product of a vector with the vectors \(\hat i+\hat j-3\hat k\), \(\hat i+3\hat j-2\hat k\) and \(2\hat i+\hat j+4\hat k\) are \(0,5,8\) respectively. The vector is
View Solution
Let \(\vec v=(x,y,z)\). Solve the linear system from dot products to get \((x,y,z)=(1,2,3)\). Quick Tip: Dot products give linear equations in components.
The angle between the two lines whose intercepts on the axes are \(a,-b\) and \(b,-a\) respectively is
View Solution
Slopes are \(-b/a\) and \(-a/b\). \[ \tan\theta=\left|\frac{m_1-m_2}{1+m_1m_2}\right| =\frac{|b^2-a^2|}{2ab}. \] Quick Tip: Use slope form for angle between lines.
If the line through the points \(A(k,1,-1)\) and \(B(2k,0,2)\) is perpendicular to the line through the points \(B\) and \(C(2+2k,k,1)\), then the value of \(k\) is
View Solution
Direction vectors: \[ \vec{AB}=(k, -1, 3),\quad \vec{BC}=(2, k, -1). \]
Perpendicular \(\Rightarrow \vec{AB}\cdot\vec{BC}=0\): \[ 2k+k(-1)-3=0\Rightarrow k=-1. \] Quick Tip: Perpendicular lines have zero dot product of direction vectors.































Comments