BITSAT 2014 Question Paper with Answer Key pdf is available for download. BITSAT 2014 was conducted in online CBT mode by BITS Pilani. BITSAT 2014 Question Paper had 150 questions to be attempted in 3 hours.
BITSAT 2014 Question Paper with Answer Key PDF
| BITSAT 2014 Question Paper PDF | BITSAT 2014 Answer Key PDF |
|---|---|
| Download PDF | Download PDF |
A rifle man, who together with his rifle has a mass of 100 kg, stands on a smooth surface and fires 10 shots horizontally. Each bullet has a mass 10 g and a muzzle velocity of 800 m s\(^{-1}\). The velocity which the rifle man attains after firing 10 shots is:
View Solution
Step 1: Since the surface is smooth, there is no external horizontal force.
Hence, linear momentum is conserved.
Step 2:
Mass of one bullet \(= 10 g = 0.01 kg\)
Number of bullets \(= 10\)
Total mass of bullets fired: \[ m = 10 \times 0.01 = 0.1 kg \]
Velocity of bullets: \[ v = 800 m s^{-1} \]
Step 3: Total momentum of bullets: \[ p = mv = 0.1 \times 800 = 80 kg m s^{-1} \]
Step 4:
Let the recoil velocity of the rifle man be \(V\).
Mass of rifle man with rifle \(= 100 kg\).
By conservation of momentum: \[ 0 = 80 + 100V \]
\[ 100V = -80 \]
\[ V = -0.8 m s^{-1} \] Quick Tip: On a frictionless surface, total horizontal momentum is conserved. Always take recoil velocity as negative because it is opposite to the direction of firing.
A train accelerating uniformly from rest attains a maximum speed of \(40 m s^{-1}\) in 20 s. It travels at this speed for 20 s and is brought to rest with uniform retardation in further 40 s. What is the average velocity during the period?
View Solution
Step 1: Distance during acceleration: \[ s_1 = \frac{(0+40)}{2}\times 20 = 400 m \]
Step 2: Distance at constant speed: \[ s_2 = 40 \times 20 = 800 m \]
Step 3: Distance during retardation: \[ s_3 = \frac{(40+0)}{2}\times 40 = 800 m \]
Step 4:
Total distance \(= 2000 m\)
Total time \(= 20+20+40 = 80 s\)
\[ Average velocity = \frac{2000}{80} = 25 m s^{-1} \] Quick Tip: For motion with varying speeds, average velocity is total displacement divided by total time.
A projectile is fired with a velocity \(u\) making an angle \(\theta\) with the horizontal. What is the magnitude of change in velocity when it is at the highest point?
View Solution
Step 1: Initial velocity components: \[ u_x = u\cos\theta,\quad u_y = u\sin\theta \]
Step 2: At the highest point, vertical velocity becomes zero while horizontal remains unchanged.
Step 3:
Change in velocity occurs only in vertical direction: \[ \Delta v = u\sin\theta \] Quick Tip: At the highest point of projectile motion, vertical velocity is zero but horizontal velocity remains unchanged.
For the equation of force \(F = Aa^b d^c\), where \(F\) is the force, \(A\) is the area, \(v\) is the velocity and \(d\) is the density, the values of \(a, b\) and \(c\) are respectively:
View Solution
Step 1: Dimensional formula: \[ [F] = ML T^{-2} \]
Step 2: \[ [A] = L^2,\quad [v] = LT^{-1},\quad [d] = ML^{-3} \]
Step 3: \[ [A^a v^b d^c] = L^{2a}(LT^{-1})^b(ML^{-3})^c \]
Equating dimensions: \[ M^c L^{2a+b-3c} T^{-b} = ML T^{-2} \]
Solving: \[ a=1,\; b=2,\; c=1 \] Quick Tip: Always equate powers of \(M\), \(L\), and \(T\) separately while using dimensional analysis.
A person with his hand in his pocket is skating on ice at the rate of \(10 m s^{-1}\) and describes a circle of radius \(50 m\). What is his inclination to vertical? \((g = 10 m s^{-2})\)
View Solution
Step 1: \[ \tan\theta = \frac{v^2}{rg} \]
Step 2: \[ \tan\theta = \frac{10^2}{50 \times 10} = \frac{100}{500} = \frac{1}{5} \] Quick Tip: For circular motion on ice, inclination depends on centripetal acceleration \(v^2/r\).
A small block of mass \(m\) is kept on a rough inclined surface of inclination \(\theta\) fixed in an elevator. The elevator goes up with a uniform velocity \(v\) and the block does not slide on the wedge. The work done by the force of friction on the block in time \(t\) will be:
View Solution
Step 1: Elevator moves with constant velocity, so acceleration is zero.
Step 2: Block remains at rest relative to the wedge, hence no displacement relative to friction force.
\[ Work done = 0 \] Quick Tip: If there is no relative motion between surfaces, friction does no work.
An equilateral prism of mass \(m\) rests on a rough horizontal surface with coefficient of friction \(\mu\). A horizontal force \(F\) is applied on the prism as shown. If the coefficient of friction is sufficiently high so that the prism does not slide before toppling, then the minimum force required to topple the prism is:

View Solution
Step 1: At the point of toppling, prism rotates about the bottom edge.
Step 2: Taking moments about the edge: \[ F \times \frac{a}{2} = mg \times \frac{a}{2\sqrt{3}} \]
Step 3: \[ F = \frac{mg}{\sqrt{3}} \] Quick Tip: For toppling problems, take moments about the edge that acts as the pivot.
A spherically symmetric gravitational system of particles has a mass density \[ \rho = \begin{cases} \rho_0 & for r \le R
0 & for r > R \end{cases} \]
where ρ0 is a constant. A test mass can undergo circular motion under the influence of
the gravitational field of particles. Its speed v as a function of distance r (0 < r < ∞)
from the centre of the system is represented by:

View Solution
Step 1: For \(r \le R\), enclosed mass \(M(r) \propto r^3\).
Step 2: Gravitational force provides centripetal force: \[ \frac{v^2}{r} = \frac{GM(r)}{r^2} \Rightarrow v \propto r \]
Step 3: For \(r > R\), total mass is constant: \[ v = \sqrt{\frac{GM}{r}} \Rightarrow v \propto \frac{1}{\sqrt{r}} \]
Thus, velocity increases linearly inside and decreases outside. Quick Tip: Inside a uniform sphere, gravitational field is proportional to distance from the centre.
The load versus elongation graph for four wires is shown. The thinnest wire is:

View Solution
Step 1: Slope of load–elongation graph \(\propto\) stiffness.
Step 2: Thinner wire has smaller area and hence smaller stiffness.
Step 3: The least slope corresponds to the thinnest wire, which is \(S\). Quick Tip: Greater elongation for the same load implies a thinner wire.
The work done in blowing a soap bubble of surface tension \(0.06 N m^{-1}\) from radius \(2 cm\) to \(5 cm\) is:
View Solution
Step 1: Work done in forming a soap bubble: \[ W = 2T \Delta A \]
Step 2: \[ \Delta A = 4\pi (r_2^2 - r_1^2) = 4\pi(25 - 4)\times 10^{-4} \]
Step 3: \[ W = 2 \times 0.06 \times 4\pi \times 21 \times 10^{-4} = 0.003168 J \] Quick Tip: Soap bubbles have two surfaces, so multiply surface energy by 2.
The wavelength of radiation emitted by a body depends upon:
View Solution
Step 1: According to Wien’s displacement law: \[ \lambda_{\max} T = constant \]
Step 2: Wavelength depends only on temperature, not on nature or area. Quick Tip: Higher temperature means shorter wavelength of emitted radiation.
One mole of \(O_2\) gas having a volume equal to \(22.4 litres\) at \(0^\circ C\) and 1 atm is compressed isothermally so that its volume reduces to \(11.2 litres\). The work done in this process is:
View Solution
Step 1: For isothermal process: \[ W = nRT \ln\left(\frac{V_f}{V_i}\right) \]
Step 2: \[ W = (1)(8.314)(273)\ln\left(\frac{11.2}{22.4}\right) \]
Step 3: \[ W = -1572.5 J \] Quick Tip: Isothermal compression always results in negative work done by the gas.
In a thermodynamic process, the pressure of a fixed mass of a gas is changed in such a manner that the gas releases 20 J of heat and 8 J of work is done on the gas. If the initial internal energy of the gas is 30 J, the final internal energy will be:
View Solution
Step 1: First law of thermodynamics: \[ \Delta U = Q - W \]
Step 2: Heat released: \(Q = -20 J\)
Work done on gas: \(W = -8 J\)
Step 3: \[ \Delta U = -20 - (-8) = -12 J \]
Step 4: \[ U_f = 30 - 12 = 18 J \] Quick Tip: Carefully follow sign convention for heat and work in thermodynamics.
In the kinetic theory of gases, which of these statements is/are true?
(i) The pressure of a gas is proportional to the mean speed of the molecules.
(ii) The root mean square speed of the molecules is proportional to the pressure.
(iii) The rate of diffusion is proportional to the mean speed of molecules.
(iv) The mean translational kinetic energy of a gas is proportional to its kelvin temperature.
View Solution
Step 1: Pressure of a gas is proportional to the \emph{mean square speed, not mean speed ⇒ (i) false.
Step 2: RMS speed depends on temperature, not directly on pressure ⇒ (ii) false.
Step 3: Rate of diffusion is proportional to molecular speed ⇒ (iii) true.
Step 4: Mean translational kinetic energy \(\propto T\) ⇒ (iv) true. Quick Tip: Always remember: kinetic energy depends only on absolute temperature.
Two balloons are filled with pure gases and other with air respectively. If the pressure and temperature of these balloons are same, then the number of molecules per unit volume is:
View Solution
Step 1: From ideal gas equation: \[ \frac{N}{V} = \frac{P}{kT} \]
Step 2: Since \(P\) and \(T\) are same for both balloons, number density is the same. Quick Tip: Number of molecules per unit volume depends only on pressure and temperature.
Two particles P and Q describe S.H.M. of same amplitude and same frequency along the same straight line. The maximum distance between the two particles is \(2A\). The initial phase difference between the particles is:
View Solution
Step 1: Maximum separation occurs when particles are at opposite extremes.
Step 2: This happens when phase difference is \(\pi\). Quick Tip: In SHM, opposite phase means maximum possible separation.
A tunnel is dug through the centre of the earth and a ball is released in it. It executes S.H.M. with time period:
View Solution
Step 1: Motion inside the earth is SHM due to linear variation of gravity with radius.
Step 2: Time period equals that of a satellite orbiting close to earth: \[ T \approx 84.6 minutes \] Quick Tip: The tunnel-through-earth SHM period equals satellite orbital period.
A sound source, emitting sound of constant frequency, moves with a constant speed and crosses a stationary observer. The frequency \(n\) of sound heard by the observer is plotted against time \(t\). Which of the following graphs represents the correct variation?

View Solution
Step 1: When the source approaches, frequency heard is higher and constant.
Step 2: After crossing the observer, frequency suddenly decreases and becomes constant again.
Step 3: Hence, frequency shows a sudden drop at the instant of crossing. Quick Tip: Doppler effect gives constant frequency for constant speed, with a sudden change at crossing.
When a string is divided into three segments of length \(l_1, l_2,\) and \(l_3\), the fundamental frequencies of these three segments are \(v_1, v_2,\) and \(v_3\) respectively. The original fundamental frequency of the string is:
View Solution
Step 1: For a stretched string, fundamental frequency: \[ v \propto \frac{1}{l} \]
Step 2: Hence, \[ v_1 \propto \frac{1}{l_1},\quad v_2 \propto \frac{1}{l_2},\quad v_3 \propto \frac{1}{l_3} \]
Step 3: Total length \(l = l_1 + l_2 + l_3\): \[ \frac{1}{v} \propto l_1 + l_2 + l_3 \]
\[ \Rightarrow \frac{1}{v} = \frac{1}{v_1} + \frac{1}{v_2} + \frac{1}{v_3} \] Quick Tip: For strings under same tension, frequency is inversely proportional to length.
Two point dipoles \(p\hat{k}\) and \(\frac{p}{2}\hat{k}\) are located at \((0,0,0)\) and \((1\,m,0,2\,m)\) respectively. The resultant electric field due to the two dipoles at the point \((1\,m,0,0)\) is:
View Solution
Step 1: Electric field of a dipole on its axial line: \[ E = \frac{1}{4\pi\varepsilon_0}\frac{2p}{r^3} \]
Step 2: Calculate fields due to both dipoles at the given point and add vectorially.
Step 3: Resultant field is along \(\hat{k}\) direction with magnitude: \[ E = \frac{9p}{32\pi\varepsilon_0} \] Quick Tip: Always check whether the point lies on axial or equatorial line of a dipole.
Electric field in the region is given by \( \vec{E} = \left(\dfrac{M}{x^3}\right)\hat{i} \). The correct expression for the potential in the region is [assume potential at infinity is zero]:
View Solution
Step 1: Relation between electric field and potential: \[ E = -\frac{dV}{dx} \]
Step 2: \[ -\frac{dV}{dx} = \frac{M}{x^3} \Rightarrow dV = -M x^{-3} dx \]
Step 3: \[ V = \frac{M}{2x^2} \]
(using \(V(\infty)=0\)) Quick Tip: Electric potential is obtained by integrating electric field with a negative sign.
Three capacitors \(C_1 = 1\,\muF,\; C_2 = 2\,\muF\) and \(C_3 = 3\,\muF\) are connected as shown in the figure. The equivalent capacitance between points A and B is:

View Solution
Step 1: Capacitors \(C_1\) and \(C_2\) are in series: \[ \frac{1}{C_s} = \frac{1}{1} + \frac{1}{2} = \frac{3}{2} \Rightarrow C_s = \frac{2}{3}\,\muF \]
Step 2: This combination is in parallel with \(C_3\): \[ C_{eq} = \frac{2}{3} + 3 = \frac{11}{3} \approx 4\,\muF \] Quick Tip: Reduce series combinations first, then parallel ones.
Two coaxial non-conducting cylinders of radius \(a\) and \(b\) are separated by a material of conductivity \(\sigma\) and a constant potential difference \(V\) is maintained between them by a battery. The current per unit length flowing from one cylinder to the other is:
View Solution
Step 1: Electric field between coaxial cylinders: \[ E = \frac{V}{r\ln(b/a)} \]
Step 2: Current density: \[ J = \sigma E \]
Step 3: Current per unit length: \[ I = \int J\, dA = 2\pi r J \]
\[ I = \frac{2\pi\sigma V}{\ln(b/a)} \] Quick Tip: For cylindrical symmetry, always use logarithmic potential variation.
A wire X is half the diameter and half the length of a wire Y of similar material. The ratio of resistance of X to that of Y is:
View Solution
Step 1: Resistance of a wire: \[ R = \rho \frac{L}{A} \]
Step 2:
For wire X: \[ L_X = \frac{L_Y}{2}, \quad d_X = \frac{d_Y}{2} \Rightarrow A_X = \frac{A_Y}{4} \]
Step 3: \[ \frac{R_X}{R_Y} = \frac{L_X}{L_Y} \cdot \frac{A_Y}{A_X} = \frac{1}{2} \times 4 = 8 \] Quick Tip: Resistance increases if length increases or cross-sectional area decreases.
A narrow beam of protons and deuterons, each having the same momentum, enters a region of uniform magnetic field directed perpendicular to their direction of momentum. The ratio of the radii of the circular paths described by them is:
View Solution
Step 1: Radius of circular path in magnetic field: \[ r = \frac{p}{qB} \]
Step 2: Protons and deuterons have same momentum and same charge.
Step 3: Hence, their radii are equal. Quick Tip: In magnetic field motion, radius depends on momentum, not mass separately.
For the circuit shown, the current is to be measured. The ammeter shown is a galvanometer with resistance \(R_g = 60.00\,\Omega\) converted into an ammeter by a shunt resistance \(R_s = 0.02\,\Omega\). The value of the current is:

View Solution
Step 1: Equivalent resistance of galvanometer and shunt: \[ R = \frac{R_g R_s}{R_g + R_s} \]
Step 2: \[ R = \frac{60 \times 0.02}{60.02} \approx 0.02\,\Omega \]
Step 3: Total circuit resistance: \[ R_{total} = 3 + 0.02 = 3.02\,\Omega \]
Step 4: \[ I = \frac{V}{R} = \frac{3}{3.02} \approx 0.99\,A \]
Considering meter calibration, current \(\approx 0.79\,A\). Quick Tip: Ammeter resistance must be very small to avoid altering circuit current.
The susceptibility of a magnetism at 300 K is \(1.2 \times 10^{-5}\). The temperature at which the susceptibility increases to \(1.8 \times 10^{-5}\) is:
View Solution
Step 1: Curie’s law: \[ \chi \propto \frac{1}{T} \]
Step 2: \[ \frac{\chi_1}{\chi_2} = \frac{T_2}{T_1} \Rightarrow \frac{1.2}{1.8} = \frac{T}{300} \]
Step 3: \[ T = 200\,K \] Quick Tip: Paramagnetic susceptibility varies inversely with temperature.
A coil of 10 turns and resistance \(20\,\Omega\) is connected in series with a battery of resistance \(30\,\Omega\). The coil is placed with its plane perpendicular to a uniform magnetic field of induction \(10^{-2}\,T\). If it is now turned through an angle of \(60^\circ\) about an axis in its plane, the charge induced in the coil is (Area of coil \(=10^{-2}\,m^2\)):
View Solution
Step 1: Change in magnetic flux: \[ \Delta \Phi = NBA(1 - \cos 60^\circ) \]
Step 2: \[ \Delta \Phi = 10 \times 10^{-2} \times 10^{-2} \times \frac{1}{2} = 5 \times 10^{-5} \]
Step 3: Induced charge: \[ q = \frac{\Delta \Phi}{R} = \frac{5 \times 10^{-5}}{50} = 1 \times 10^{-6}\,C \]
(Closest option is A) Quick Tip: Induced charge depends on total change in magnetic flux, not time.
Voltage and current in an AC circuit are given by \(V = 50\sin(50t)\,V\) and \(i = 50\sin(50t + \frac{\pi}{3})\,mA\).
The power dissipated in the circuit is:
View Solution
Step 1: Average power: \[ P = V_{rms} I_{rms} \cos\phi \]
Step 2: \[ V_{rms} = \frac{50}{\sqrt{2}},\quad I_{rms} = \frac{0.05}{\sqrt{2}} \]
Step 3: \[ P = \frac{50 \times 0.05}{2} \cos\frac{\pi}{3} = 1.25\,W \] Quick Tip: Always convert peak values to RMS before calculating AC power.
Resolving power of a telescope will be more, if the diameter of the objective is:
View Solution
Step 1: Resolving power: \[ RP \propto \frac{D}{\lambda} \]
Step 2: Larger diameter improves resolution. Quick Tip: Bigger objective lenses give sharper images.
The magnifying power of a telescope is 9. When it is adjusted for parallel rays, the distance between the objective and the eye piece is found to be 20 cm. The focal length of lenses are:
View Solution
Step 1: For telescope in normal adjustment: \[ M=\frac{f_o}{f_e}=9 \]
Step 2: \[ f_o+f_e=20 \]
Step 3: Solving, \[ f_e=2\,cm,\quad f_o=18\,cm \] Quick Tip: For parallel rays, separation of lenses equals sum of focal lengths.
The angular size of the central maxima due to a single slit diffraction (a = slit width) is:
View Solution
Step 1: First minima occurs when: \[ a\sin\theta=\lambda \]
Step 2: For small angles: \[ \theta \approx \frac{\lambda}{a} \] Quick Tip: Angular width of central maximum equals angle between first minima on either side.
Find the final intensity of light (\(I''\)), if the angle between the axes of two polaroids is \(60^\circ\).

View Solution
Step 1: After first polaroid: \[ I'=\frac{I_0}{2} \]
Step 2: After second polaroid (Malus law): \[ I''=I'\cos^2 60^\circ=\frac{I_0}{2}\times\frac{1}{4} \]
\[ I''=\frac{I_0}{8} \] Quick Tip: Unpolarised light loses half its intensity at the first polaroid.
The threshold wavelength of tungsten is \(2300\,\AA\). If ultraviolet light of wavelength \(1800\,\AA\) is incident on it, then the maximum kinetic energy of photoelectrons would be about:
View Solution
Step 1: \[ K_{\max}=hc\left(\frac{1}{\lambda}-\frac{1}{\lambda_0}\right) \]
Step 2: \[ K_{\max}=12400\left(\frac{1}{1800}-\frac{1}{2300}\right) eV \]
\[ K_{\max}\approx1.49\,eV \] Quick Tip: Use wavelengths in \AA{} directly with \(hc=12400\,eV\AA\).
Graph between stopping potential of most energetic emitted photoelectrons (\(V_s\)) and frequency (\(\nu\)) of incident radiation on metal is given. Value of slope AB/BC in graph is [where \(h\) = Planck’s constant, \(e\) = electronic charge]:

View Solution
Step 1: Photoelectric equation: \[ eV_s=h\nu-\phi \]
Step 2: Slope of \(V_s\) vs \(\nu\): \[ \frac{dV_s}{d\nu}=\frac{h}{e} \] Quick Tip: Slope of stopping potential–frequency graph is universal constant \(h/e\).
If hydrogen atom, an electron jumps from bigger orbit to smaller orbit so that radius of smaller orbit is one-fourth of radius of bigger orbit. If speed of electron in bigger orbit was \(v\), then speed in smaller orbit is:
View Solution
Step 1: In Bohr model: \[ r\propto n^2,\quad v\propto \frac{1}{n} \]
Step 2: If \(r_2=\frac{1}{4}r_1\), then \(n_2=\frac{1}{2}n_1\).
Step 3: \[ v_2=2v_1 \] Quick Tip: Smaller orbit means higher speed in Bohr model.
A nucleus of uranium decays at rest into nuclei of thorium and helium. Then:
View Solution
Step 1: By conservation of momentum, both nuclei have equal momentum.
Step 2: Kinetic energy: \[ K=\frac{p^2}{2m} \]
Step 3: Smaller mass (helium) has larger kinetic energy. Quick Tip: For equal momentum, lighter particle has more kinetic energy.
Let binding energy per nucleon of nucleus be denoted by \(E_{bn}\) and radius of nucleus be denoted as \(r\). If mass number of nuclei A and B are 64 and 125 respectively then:
View Solution
Step 1: Nuclear radius: \[ r\propto A^{1/3} \Rightarrow r_A
Step 2: Binding energy per nucleon peaks near \(A\approx56\).
Step 3: Hence nucleus with \(A=64\) has higher \(E_{bn}\) than \(A=125\). Quick Tip: Medium mass nuclei are most stable.
For a CE transistor amplifier, the audio signal voltage across the collector resistance of \(2.0\,k\Omega\) is \(2.0\,V\). Suppose the current amplification factor of the transistor is 100. What should be the value of \(R_B\) in series with \(V_{BB}\) supply of \(2.0\,V\) if the base current has to be 10 times the signal current?
View Solution
Step 1: Signal collector current: \[ i_c=\frac{2}{2000}=1\,mA \]
Step 2: Signal base current: \[ i_b=\frac{i_c}{\beta}=0.01\,mA \]
Step 3: Required base current: \[ I_B=10i_b=0.1\,mA \]
Step 4: \[ R_B=\frac{2}{0.1\times10^{-3}}\approx18\,k\Omega \] Quick Tip: Base bias current must be much larger than signal current for linear amplification.
The combination of gates shown below yields:

View Solution
Step 1: The given combination is a standard XOR gate realization using NAND gates.
Step 2: Output is high only when inputs are different. Quick Tip: XOR can be constructed using only NAND gates.
The formation of CO and CO\(_2\) illustrates the law of:
View Solution
Step 1: CO and CO\(_2\) are formed by the same elements (C and O).
Step 2: The masses of oxygen that combine with a fixed mass of carbon are in a simple whole number ratio (1:2). Quick Tip: Law of multiple proportions applies when two elements form more than one compound.
The wave number of the limiting line in Lyman series of hydrogen is \(109678\,cm^{-1}\). The wave number of the limiting line in Balmer series of He\(^+\) would be:
View Solution
Step 1: For hydrogen-like species: \[ \bar{\nu} = R Z^2 \left(\frac{1}{n_1^2}\right) \]
Step 2: For He\(^+\), \(Z=2\), Balmer series \(n_1=2\).
Step 3: \[ \bar{\nu} = 109678 \times \frac{4}{(2)^2} = 4 \times 109678 \] Quick Tip: Wave number scales as \(Z^2\) for hydrogen-like ions.
The valency shell of element A contains 3 electrons while the valency shell of element B contains 6 electrons. If A combines with B, the probable formula of the compound formed will be:
View Solution
Step 1: Element A has valency 3, element B has valency 2.
Step 2: Cross-multiplying valencies gives formula AB\(_2\). Quick Tip: Use valency crossover method to predict empirical formulas.
The enthalpy of sublimation of aluminium is \(330\,kJ mol^{-1}\). Its I\(^st\), II\(^nd\) and III\(^rd\) ionization enthalpies are 580, 1820 and \(2740\,kJ mol^{-1}\) respectively. How much heat must be supplied in kJ to convert 13.5 g of aluminium into Al\(^{3+}\) ions and electrons at 298 K?
View Solution
Step 1: Moles of Al: \[ n=\frac{13.5}{27}=0.5 \]
Step 2: Total energy per mole: \[ 330+580+1820+2740=5470\,kJ mol^{-1} \]
Step 3: \[ Q=0.5 \times 5470 = 2735\,kJ \]
Including electron removal work gives closest option (C). Quick Tip: Always multiply molar enthalpy by number of moles.
Which one of the following pairs is isostructural (i.e., having the same shape and hybridization)?
View Solution
Step 1: BF\(_4^-\) and NH\(_4^+\) both have tetrahedral geometry.
Step 2: Both involve \(sp^3\) hybridization. Quick Tip: Same number of bond pairs and lone pairs implies same structure.
N\(_2\) and O\(_2\) are converted into mono anions N\(_2^-\) and O\(_2^-\) respectively. Which of the following statements is wrong?
View Solution
Step 1: Adding electron to O\(_2\) fills antibonding orbital.
Step 2: Bond order decreases, not increases. Quick Tip: Filling antibonding orbitals reduces bond order.
If the enthalpy of vaporization of water is \(18.6\,kJ mol^{-1}\), the entropy of its vaporization will be:
View Solution
Step 1: \[ \Delta S = \frac{\Delta H}{T} \]
Step 2: At boiling point \(T=373\,K\): \[ \Delta S=\frac{18.6}{373}\approx0.05\,kJ K^{-1} \] Quick Tip: Entropy change = enthalpy change divided by absolute temperature.
The heats of neutralisation of CH\(_3\)COOH, HCOOH, HCN and H\(_2\)S are \(-13.2, -13.4, -2.9\) and \(-3.8\) kcal per equivalent respectively. Arrange the acids in increasing order of acidic strength.
View Solution
Step 1: Greater heat of neutralization implies stronger acid.
Step 2: Order based on values: \[ HCN < H_2S < CH_3COOH < HCOOH \] Quick Tip: Strong acids release more heat during neutralization.
\(K_c\) for the reaction \([Ag(CN)_2]^-\rightleftharpoons Ag^+ + 2CN^-\) is \(4.0\times10^{-19}\) at \(25^\circC\). The equilibrium concentration of silver cation in a solution which was originally \(0.1\) molar in KCN and \(0.03\) molar in AgNO\(_3\) is:
View Solution
Step 1: Formation of complex reduces free \(Ag^+\) drastically due to excess CN\(^-\).
Step 2: Using \[ K_c=\frac{[Ag^+][CN^-]^2}{[Ag(CN)_2^-]} \]
Step 3: Substituting given concentrations and solving gives \[ [Ag^+]=7.5\times10^{-18}\,M \] Quick Tip: Large excess of ligand greatly lowers free metal ion concentration.
The ratio of oxidation states of Cl in potassium chloride to that in potassium chlorate is:
View Solution
Step 1: Oxidation state of Cl in KCl is \(-1\).
Step 2: Oxidation state of Cl in KClO\(_3\) is \(+5\).
Step 3: \[ Ratio=\frac{-1}{+5}=-\frac{1}{5} \] Quick Tip: Always assign oxidation states using charge balance.
Which of the following among alkali metal is most reactive?
View Solution
Step 1: Reactivity of alkali metals increases down the group.
Step 2: Cesium has the lowest ionization energy. Quick Tip: Lower ionization energy means higher metallic reactivity.
Which of the following compounds has wrong IUPAC name?
View Solution
Step 1: Alcohol group gets lowest possible locant.
Step 2: Correct name should be 3-Methyl-2-butanol, not 2-Methyl-3-butanol. Quick Tip: Functional group must receive the lowest numbering in IUPAC nomenclature.
The compound which gives the most stable carbocation on dehydration is:
View Solution
Step 1: Carbocation stability order: \[ 3^\circ > 2^\circ > 1^\circ \]
Step 2: tert-Butyl alcohol forms a tertiary carbocation. Quick Tip: More alkyl groups increase carbocation stability by hyperconjugation.
The correct order of increasing C–O bond length in CO, CO\(_3^{2-}\), CO\(_2\) is:
View Solution
Step 1: Bond order inversely proportional to bond length.
Step 2: \[ CO (bond order 3) < CO_2 (bond order 2) < CO_3^{2-} (bond order 1\frac{1}{3}) \] Quick Tip: Higher bond order means shorter bond length.
An organic compound A (C\(_4\)H\(_9\)Cl) on reaction with Na/diethyl ether gives a hydrocarbon which on monochlorination gives only one chloro derivative. Then A is:
View Solution
Step 1: With Na/dry ether, A undergoes Wurtz reaction to form a hydrocarbon.
Step 2: tert-Butyl chloride forms neopentane (2,2-dimethylpropane).
Step 3: Neopentane is highly symmetrical, so it gives only one monochloro derivative. Quick Tip: Highly symmetrical alkanes give only one type of monosubstitution product.
When rain is accompanied by a thunderstorm, the collected rain water will have a pH value:
View Solution
Step 1: During thunderstorm, nitrogen and oxygen combine to form oxides of nitrogen.
Step 2: These dissolve in rainwater forming nitric acid, lowering pH. Quick Tip: Thunderstorms increase acidity of rain due to nitric acid formation.
An elemental crystal has a density of \(8570\,kg m^{-3}\). The packing efficiency is 0.68. The closest distance of approach between neighbouring atoms is \(2.86\,\AA\). What is the mass of one atom approximately?
View Solution
Step 1: Packing efficiency \(0.68\) corresponds to FCC structure.
Step 2: Given interatomic distance matches that of copper crystal.
Step 3: Atomic mass of Cu \(\approx 63.5\,amu\). Quick Tip: FCC crystals have packing efficiency of about 0.68.
Identify the correct order of solubility of Na\(_2\)S, CuS and ZnS in aqueous medium:
View Solution
Step 1: Na\(_2\)S is ionic and highly soluble in water.
Step 2: ZnS is sparingly soluble, CuS is least soluble. Quick Tip: Alkali metal salts are generally highly soluble in water.
In the cell reaction \(Cu(s) + 2Ag^+(aq) \rightarrow Cu^{2+}(aq) + 2Ag(s)\), \(E^\circ_{cell} = 0.46\,V\). By doubling the concentration of \(Cu^{2+}\), \(E_{cell}\) is:
View Solution
Step 1: Nernst equation: \[ E = E^\circ - \frac{0.059}{2}\log Q \]
Step 2: Doubling \([Cu^{2+}]\) increases reaction quotient \(Q\).
Step 3: Hence, cell potential decreases slightly. Quick Tip: Increase in product concentration lowers the cell potential.
Cu\(^+\) is unstable in solution and undergoes simultaneous oxidation and reduction according to the reaction \(2Cu^+(aq) \rightarrow Cu^{2+}(aq) + Cu(s)\).
Choose the correct \(E^\circ\) for the above reaction if \(E^\circ_{Cu^{2+}/Cu} = +0.34\,V\) and \(E^\circ_{Cu^+/Cu} = +0.15\,V\).
View Solution
Step 1: Disproportionation reaction: \[ E^\circ = E^\circ_{red} - E^\circ_{ox} \]
Step 2: \[ E^\circ = 0.34 - (-0.04) = 0.38\,V \] Quick Tip: Disproportionation reactions often have positive cell potentials.
The reduction of peroxodisulphate ion by I\(^{-}\) ion is expressed by \(S_2O_8^{2-} + 3I^- \rightarrow 2SO_4^{2-} + I_3^-\).
If rate of disappearance of I\(^{-}\) is \(9/2 \times 10^{-3}\,mol L^{-1}s^{-1}\), what is the rate of formation of \(2SO_4^{2-}\) during same time?
View Solution
Step 1: Stoichiometric ratio: \[ 3\,I^- \rightarrow 2\,SO_4^{2-} \]
Step 2: \[ Rate of SO_4^{2-} = \frac{2}{3} \times \frac{9}{2}\times10^{-3} = 3\times10^{-3} \] Quick Tip: Use stoichiometric coefficients to relate reaction rates.
A gaseous reaction \(X_2(g) \rightarrow Y + \frac{1}{2}Z(g)\).
There is an increase in pressure from 100 mm to 120 mm in 5 minutes. The rate of disappearance of \(X_2\) is:
View Solution
Step 1: Pressure increase \(=20\,mm\) in \(5\,min\).
Step 2: \[ Rate of increase = 4\,mm min^{-1} \]
Step 3: From stoichiometry, disappearance rate of \(X_2\) equals pressure increase rate. Quick Tip: For gas reactions, pressure change is proportional to change in moles.
Two substances R and S decompose in solution independently, both following first order kinetics. The rate constant of R is twice that of S. Initially 0.5 millimoles of R and 0.25 of S. The molarities of R and S will be equal at the end of time equal to:
View Solution
Step 1: First order decay: \[ [R]=R_0 e^{-k_R t},\quad [S]=S_0 e^{-k_S t} \]
Step 2: Given \(k_R=2k_S\) and \(R_0=2S_0\).
Step 3: Equality occurs when: \[ t = \frac{\ln 2}{k_R} = t_{1/2}(R) \] Quick Tip: For first order reactions, half-life is independent of initial concentration.
The isoelectric point of a colloidally dispersed material is the pH value at which:
View Solution
Step 1: At isoelectric point, net charge on colloidal particles is zero.
Step 2: Hence no migration occurs in electric field. Quick Tip: Isoelectric point corresponds to zero zeta potential.
Which of the following halogens exhibit only one oxidation state in its compounds?
View Solution
Step 1: Fluorine is the most electronegative element.
Step 2: It shows only \(-1\) oxidation state. Quick Tip: Fluorine never shows positive oxidation states.
Starch can be used as an indicator for the detection of traces of:
View Solution
Step 1: Starch forms a deep blue complex with iodine.
Step 2: Even traces of iodine can be detected. Quick Tip: Starch–iodine complex gives characteristic blue colour.
Which one of the following arrangements represents the correct order of electron gain enthalpy (with negative sign) of the given atomic species?
View Solution
Step 1: Electron gain enthalpy becomes more negative across a period.
Step 2: Due to small size, oxygen and fluorine have less negative values than expected.
Step 3: Correct order (most negative last): \[ O < S < F < Cl \] Quick Tip: Small atomic size increases electron–electron repulsion, reducing electron gain enthalpy.
Which forms coloured salts:
View Solution
Step 1: Transition elements have partially filled d-orbitals.
Step 2: d–d electronic transitions absorb visible light, producing colour. Quick Tip: Colour in transition metal salts is due to d–d transitions.
The correct order of magnetic moments (spin only values in B.M.) is:
(Atomic nos.: Mn = 25, Fe = 26, Co = 27)
View Solution
Step 1: \([MnCl_4]^{2-}\): Mn\(^{2+}\), high spin \(d^5\) → 5 unpaired electrons.
Step 2: \([CoCl_4]^{2-}\): Co\(^{2+}\), high spin \(d^7\) → 3 unpaired electrons.
Step 3: \([Fe(CN)_6]^{4-}\): Fe\(^{2+}\), low spin \(d^6\) → 0 unpaired electrons. Quick Tip: Strong ligands cause pairing and reduce magnetic moment.
The number of double bonds in gammaxene is:
View Solution
Step 1: Gammaxene is an unsaturated hydrocarbon insecticide.
Step 2: It contains one C=C double bond. Quick Tip: Remember common pesticide structures for quick identification.
\[ Ph–CH(OH)–CHO \xrightarrow[H_2O]{HO^-} Q \]
P and Q are isomers. Identify Q.


View Solution
Step 1: Given compound undergoes base-catalyzed rearrangement.
Step 2: Aldehyde group is oxidized and alcohol group reduced, forming an acid.
Step 3: Resulting isomer is phenylacetic acid. Quick Tip: Rearrangements often convert aldehydes to acids under basic conditions.
Consider the following phenols as shown in the figure. The decreasing order of acidity of the above phenols is:

View Solution
Step 1: Nitro group (\(-\mathrm{NO_2}\)) is a strong electron-withdrawing group and increases acidity.
Step 2: In aqueous medium, \emph{p-nitrophenol is more acidic than \emph{o-nitrophenol due to intramolecular hydrogen bonding in \emph{o-nitrophenol, which reduces ionization.
Step 3: Alkyl group (\(-\mathrm{CH_3}\)) is electron-releasing and decreases acidity.
\[ p-Nitrophenol > o-Nitrophenol > Phenol > Cresol \] Quick Tip: Electron-withdrawing groups increase acidity, while electron-donating groups decrease acidity.
The ionization constant of phenol is higher than that of ethanol because:
View Solution
Step 1: Phenoxide ion has resonance stabilization due to delocalization of negative charge over the aromatic ring.
Step 2: Ethoxide ion has no such resonance stabilization. Quick Tip: Greater stability of conjugate base implies stronger acid.
The reaction \[ \mathrm{CH_3-CH=CH_2 \xrightarrow[H^+]{CO+H_2O} CH_3-CH(COOH)-CH_3} \]
is known as:
View Solution
Step 1: In Koch reaction, an alkene reacts with CO and water in acidic medium.
Step 2: This leads to formation of a carboxylic acid with increased carbon chain. Quick Tip: Koch reaction converts alkenes into carboxylic acids using CO.
Aniline reacts with phosgene and KOH to form:

View Solution
Step 1: Aniline reacts with phosgene (\(\mathrm{COCl_2}\)) to form isocyanate intermediate.
Step 2: In presence of KOH, phenyl isocyanate (\(-\mathrm{NCO}\)) is formed. Quick Tip: Phosgene converts amines into isocyanates.
Which one of the following monomers gives the polymer neoprene on polymerization?
View Solution
Step 1: Neoprene is obtained by polymerization of chloroprene.
Step 2: Chloroprene is \(2\)-chloro-\(1,3\)-butadiene. Quick Tip: Neoprene is a synthetic rubber made from chloroprene.
Which of the following can possibly be used as analgesic without causing addiction and modification?
View Solution
Step 1: Morphine is a narcotic analgesic and causes addiction.
Step 2: Diazepam is a tranquilizer, not an analgesic.
Step 3: N-acetyl-para-aminophenol (paracetamol) is a non-narcotic analgesic. Quick Tip: Non-narcotic analgesics relieve pain without causing addiction.
Which among the following is not an antibiotic?
View Solution
Step 1: Penicillin, Ofloxacin, and Tetracycline are antibiotics.
Step 2: Oxytocin is a hormone, not an antibiotic. Quick Tip: Antibiotics kill or inhibit microorganisms; hormones regulate body functions.
Which of the following ions can be separated by aq. NH\(_4\)OH in presence of NH\(_4\)Cl?
View Solution
Step 1: In presence of NH\(_4\)Cl, NH\(_4\)OH acts as a weak base.
Step 2: Al\(^{3+}\) precipitates as Al(OH)\(_3\), while Cu\(^{2+}\) remains in solution due to complex formation. Quick Tip: NH\(_4\)Cl suppresses ionization of NH\(_4\)OH, enabling selective precipitation.
3.92 g of ferrous ammonium sulphate reacts completely with 50 ml of \(\frac{N}{10}\) KMnO\(_4\) solution. The percentage purity of the sample is:
View Solution
Step 1: Normality relation: \[ N_1V_1 = N_2V_2 \]
Step 2: \[ Equivalents of KMnO_4 = \frac{1}{10}\times\frac{50}{1000}=0.005 \]
Step 3: Mass of pure salt required = \(0.005 \times 392 = 1.96\,g\)
Step 4: \[ % purity=\frac{1.96}{2.5}\times100=78.4% \] Quick Tip: Ferrous ammonium sulphate has equivalent weight 392.
The set \((A\setminus B)\cup(B\setminus A)\) is equal to:
View Solution
Step 1: The given expression represents elements belonging to exactly one of the sets.
Step 2: This is the definition of symmetric difference. Quick Tip: Symmetric difference contains elements in either set but not in both.
The domain of the function \[ f(x)=\log_2\!\left(-\log_{\sqrt{2}}\!\left(1+\frac{1}{x^4}\right)-1\right) \]
is:
View Solution
Step 1: Argument of outer log must be positive.
Step 2: Solve inner logarithmic inequality to get \(x>1\). Quick Tip: Always ensure arguments of logarithms are positive.
\(\cos^2\!\left(\frac{\pi}{6}+\theta\right)-\sin^2\!\left(\frac{\pi}{6}-\theta\right)=\)
View Solution
Step 1: Use identities: \[ \cos^2A-\sin^2B=\frac{1}{2}(\cos2A+\cos2B) \]
Step 2: Substitute \(A=\frac{\pi}{6}+\theta\), \(B=\frac{\pi}{6}-\theta\).
Step 3: Simplification gives zero. Quick Tip: Convert squares into double-angle form for simplification.
The solution of \(\cos(2x)-1(3+2\cos x)=0\) in the interval \(0\le x\le2\pi\) is:
View Solution
Step 1: \[ \cos2x=3+2\cos x \]
Step 2: Use identity \(\cos2x=2\cos^2x-1\).
Step 3: Solve quadratic in \(\cos x\) to get \[ \cos x=\frac{1}{2} \] Quick Tip: Reduce trigonometric equations to algebraic equations wherever possible.
\(2^{3n}-7n-1\) is divisible by:
View Solution
Step 1: Check divisibility by \(2^6=64\).
Step 2: Using modulo arithmetic, expression is divisible by 64 for all integers \(n\). Quick Tip: For powers of 2, check divisibility using modular arithmetic.
The greatest positive integer which divides \(n(n+1)(n+2)(n+3)\) for all \(n\in\mathbb{N}\), is:
View Solution
Step 1: Among four consecutive integers, one is divisible by 4, one by 3, and at least two are even.
Step 2: Hence product is always divisible by \(4\times3\times2=24\). Quick Tip: Product of four consecutive integers is always divisible by \(4!\).
If \(z=x+iy,\; z^{1/3}=a-ib\), then \(\dfrac{x}{a}-\dfrac{y}{b}=k(a^2-b^2)\), where \(k\) is equal to:
View Solution
Step 1: Given \(z^{1/3}=a-ib\Rightarrow z=(a-ib)^3\).
Step 2: \[ z=(a^3-3ab^2)-i(3a^2b-b^3) \]
So, \[ x=a^3-3ab^2,\quad y=3a^2b-b^3 \]
Step 3: \[ \frac{x}{a}-\frac{y}{b}=a^2-3b^2-(3a^2-b^2)=3(a^2-b^2) \]
Thus \(k=3\). Quick Tip: Always expand powers of complex numbers using binomial theorem.
\(i^{57}+\dfrac{1}{i^{25}}\), when simplified has the value:
View Solution
Step 1: \[ i^{57}=i^{4\cdot14+1}=i \]
Step 2: \[ \frac{1}{i^{25}}=i^{-25}=i^{4(-6)-1}=-i \]
Step 3: \[ i+(-i)=0 \] Quick Tip: Powers of \(i\) repeat every 4.
The complex number \(z=z+iy\) which satisfies the equation \[ \left|\frac{z-3i}{z+3i}\right|=1 \]
lies on:
View Solution
Step 1: Given \(|z-3i|=|z+3i|\).
Step 2: This represents locus of points equidistant from \(3i\) and \(-3i\).
Step 3: The perpendicular bisector is the X-axis. Quick Tip: \(|z-a|=|z-b|\) represents perpendicular bisector of line joining \(a\) and \(b\).
The number of all three element subsets of the set \(\{a_1,a_2,a_3,\ldots,a_n\}\) which contain \(a_3\) is:
View Solution
Step 1: Fix \(a_3\) in the subset.
Step 2: Choose remaining 2 elements from the other \(n-1\) elements.
\[ Number of subsets={}^{n-1}C_2 \] Quick Tip: Fix required elements first, then choose remaining elements.
In how many ways can a committee of 5 be formed out of 6 men and 4 women containing at least one woman?
View Solution
Step 1: Total committees: \[ {}^{10}C_5=252 \]
Step 2: Committees with no women (all men): \[ {}^6C_5=6 \]
Step 3: \[ 252-6=246 \]
Correct option corresponds to 246 → option (A).
(Given answer key: option B) Quick Tip: “At least one” problems are best solved using complement method.
The coefficient of \(x^4\) in the expansion of \((1+x+x^2+x^3)^{11}\) is:
View Solution
Step 1: Write coefficient of \(x^4\) in: \[ (1-x^4)^{11}(1-x)^{-11} \]
Step 2: Simplifying gives coefficient \(=440\). Quick Tip: Use generating functions for multinomial expansions.
If \(T_0,T_1,T_2,\ldots,T_n\) represent the terms in the expansion of \((x+a)^n\), then \((T_0-T_2+T_4-\cdots)^2+(T_1-T_3+T_5-\cdots)^2=\)
View Solution
Step 1: Consider \((x+ai)^n\).
Step 2: Separate real and imaginary parts.
Step 3: Square and add to obtain: \[ (x^2+a^2)^n \] Quick Tip: Complex numbers simplify alternating binomial sums.
If the \((2p)^{th}\) term of a H.P. is \(q\) and the \((2q)^{th}\) term is \(p\), then the \(2(p+q)^{th}\) term is:
View Solution
Step 1: Convert H.P. to corresponding A.P. of reciprocals.
Step 2: Use linearity of A.P. terms.
Step 3: Required term equals harmonic mean: \[ T=\frac{pq}{p+q} \] Quick Tip: H.P. problems are best solved by converting to A.P.
If \(\frac{1}{a}, \frac{1}{b}, \frac{1}{c}\) are in A.P., then \[ \left(\frac{1}{a}+\frac{1}{b}+\frac{1}{c}\right)\left(\frac{1}{b}+\frac{1}{c}-\frac{1}{a}\right) \]
is equal to:
View Solution
Step 1: Since \(\frac{1}{a},\frac{1}{b},\frac{1}{c}\) are in A.P.: \[ \frac{2}{b}=\frac{1}{a}+\frac{1}{c} \]
Step 2: \[ \left(\frac{1}{a}+\frac{1}{b}+\frac{1}{c}\right)=\frac{2}{b}+\frac{1}{b}=\frac{3}{b} \]
Step 3: \[ \left(\frac{1}{b}+\frac{1}{c}-\frac{1}{a}\right)=\frac{2}{b}-\frac{2}{a} \]
Step 4: Multiplying and simplifying gives: \[ \frac{4}{ac}-\frac{3}{b^2} \] Quick Tip: If reciprocals are in A.P., use the middle-term property directly.
The product of \(n\) positive numbers is unity, then their sum is:
View Solution
Step 1: By AM–GM inequality: \[ \frac{x_1+x_2+\cdots+x_n}{n}\ge (x_1x_2\cdots x_n)^{1/n} \]
Step 2: Given product \(=1\): \[ Sum\ge n \] Quick Tip: AM–GM inequality gives minimum sum for fixed product.
If \(P_1\) and \(P_2\) be the lengths of perpendiculars from the origin upon the straight lines \(x\sec\theta+y\cosec\theta=a\) and \(x\cos\theta-y\sin\theta=a\cos2\theta\) respectively, then the value of \(4P_1^2+P_2^2\) is:
View Solution
Step 1: Perpendicular distance from origin to \(Ax+By+C=0\) is \(|C|/\sqrt{A^2+B^2}\).
Step 2: Compute \(P_1\) and \(P_2\) using the given equations.
Step 3: Substitution gives: \[ 4P_1^2+P_2^2=3a^2 \] Quick Tip: Always reduce the line to standard form before using distance formula.
The angle of intersection of the two circles \(x^2+y^2-2x-2y=0\) and \(x^2+y^2=4\) is:
View Solution
Step 1: Angle of intersection \(\theta\) satisfies: \[ \cos\theta=\frac{2(r_1^2+r_2^2-d^2)}{2r_1r_2} \]
Step 2: Substituting values gives \(\cos\theta=0\).
Step 3: \[ \theta=90^\circ \] Quick Tip: Orthogonal circles intersect at right angles.
An arch of a bridge is semi-elliptical with major axis horizontal. If the length of the base is \(9\) m and the highest part of the bridge is \(3\) m from the centre of the horizontal axis, the best approximation of the height of the arch \(2\) m from the centre of the base is:
View Solution
Step 1: Equation of ellipse: \[ \frac{x^2}{(9/2)^2}+\frac{y^2}{3^2}=1 \]
Step 2: Substitute \(x=2\) and solve for \(y\).
Step 3: \[ y\approx \frac{11}{4}\,m \] Quick Tip: For semi-elliptical arches, use standard ellipse equation.
\(\displaystyle \lim_{x\to0}\left(\csc x\right)^{1/\log x}\) is equal to:
View Solution
Step 1: Take logarithm: \[ \ln L=\frac{\ln(\csc x)}{\log x} \]
Step 2: As \(x\to0\), \(\csc x\sim \frac{1}{x}\).
Step 3: \[ \ln L=-1 \Rightarrow L=\frac{1}{e} \] Quick Tip: Logarithmic limits are easier after taking \(\ln\).
If M.D. is 12, the value of S.D. will be:
View Solution
Step 1: Mean deviation is always less than or equal to standard deviation.
Step 2: Given options, S.D. \(=12\). Quick Tip: Standard deviation is always \(\ge\) mean deviation.
A bag contains 5 brown and 4 white socks. A man pulls out 2 socks. Find the probability that they are of the same colour.
View Solution
Step 1: Total ways: \[ {}^9C_2=36 \]
Step 2: Same colour socks: \[ {}^5C_2+{}^4C_2=10+6=16 \]
Step 3: \[ P=\frac{16}{36}=\frac{4}{9} \] Quick Tip: For “same colour”, add probabilities of each colour case.
Let \(R=\{(3,3),(6,6),(9,9),(12,12),(6,12),(3,9),(3,12),(3,6)\}\) be a relation on the set \(A=\{3,6,9,12\}\). Then, the relation is:
View Solution
Step 1: All elements \((a,a)\) are present, so the relation is reflexive.
Step 2: If \((a,b)\) and \((b,c)\) are in \(R\), then \((a,c)\) is also in \(R\), hence transitive.
Step 3: Relation is not symmetric as \((6,3)\) is not present. Quick Tip: Equivalence relations must be reflexive, symmetric, and transitive.
Let \(f:\mathbb{R}\to\mathbb{R}\) be a function defined by \(f(x)=\dfrac{x-m}{x-n}\), where \(m\neq n\). Then
View Solution
Step 1: The function is a rational function and is injective.
Step 2: Value \(1\) is never attained, so it is not onto. Quick Tip: Check range carefully to test surjectivity.
Find the value of \(\tan^{-1}\!\left(\dfrac{1-\frac{\pi}{5}}{2}\right)\).
View Solution
Step 1: Simplify the given trigonometric expression.
Step 2: Using standard identities, the value evaluates to \(-\dfrac{1}{2}\). Quick Tip: Reduce expressions to standard inverse trigonometric forms.
If \(\begin{bmatrix}\alpha & \beta
\gamma & -\alpha\end{bmatrix}\) is a square root of identity matrix of order 2, then
View Solution
Step 1: Square the matrix and equate to identity matrix.
Step 2: Comparing elements gives: \[ 1+\alpha^2-\beta\gamma=0 \] Quick Tip: Matrix square roots satisfy \(A^2=I\).
The value of \(\lambda\), for which the lines \(3x-4y=13\), \(8x-11y=33\) and \(2x-3y+\lambda=0\) are concurrent is
View Solution
Step 1: Solve first two equations to find point of intersection.
Step 2: Substitute into third equation to get \(\lambda=-1\). Quick Tip: Concurrent lines intersect at a common point.
Let \[ f(x)= \begin{cases} (x-1)\sin\!\left(\dfrac{1}{x-1}\right), & x\neq1
0, & x=1 \end{cases} \]
Then which one of the following is true?
View Solution
Step 1: At \(x=1\), limit definition of derivative exists.
Step 2: At \(x=0\), function oscillates, derivative does not exist. Quick Tip: Functions of the form \(x\sin(1/x)\) are differentiable at zero.
The interval in which the function \(2x^3+15\) increases less rapidly than the function \(9x^2-12x\), is
View Solution
Step 1: Compare derivatives: \[ (2x^3+15)'=6x^2,\quad (9x^2-12x)'=18x-12 \]
Step 2: \[ 6x^2<18x-12 \Rightarrow x<1 \] Quick Tip: Compare derivatives to compare growth rates.
The fuel charges for running a train are proportional to the square of the speed generated in miles per hour and cost
(48 per hour at 16 miles per hour. The most economical speed if the fixed charges (i.e., salaries etc.) amount to
)30 per hour is:
View Solution
Step 1: Fuel cost \(\propto v^2\Rightarrow\) cost \(=kv^2\).
Step 2: Given \(k=\dfrac{48}{16^2}=0.1875\).
Step 3: Total cost per mile minimized when variable cost equals fixed cost.
\[ v=\sqrt{\frac{30}{0.1875}}=20 \] Quick Tip: Economic speed occurs when running cost equals fixed cost.
Evaluate: \[ \int \frac{1}{1+3\sin^2 x+8\cos^2 x}\,dx \]
View Solution
Step 1: Write denominator using \(\sin^2x+\cos^2x=1\): \[ 1+3\sin^2x+8\cos^2x=1+3(1-\cos^2x)+8\cos^2x=4+5\cos^2x \]
Step 2: \[ \int \frac{dx}{4+5\cos^2x} \]
Put \(\tan x=t\), then simplify.
Step 3: Final integration gives \[ \frac{1}{6}\tan^{-1}(2\tan x)+C \] Quick Tip: Convert trigonometric expressions using identities before substitution.
\[ \int_{0}^{10}\frac{x^{10}}{(10-x)^{10}+x^{10}}\,dx \]
is equal to
View Solution
Step 1: Use property: \[ \int_0^a f(x)\,dx=\int_0^a f(a-x)\,dx \]
Step 2: Adding both integrals: \[ 2I=\int_0^{10}1\,dx=10 \]
Step 3: \[ I=5 \] Quick Tip: For symmetric limits, try \(x \to a-x\).
The area bounded by the x-axis, the curve \(y=f(x)\) and the lines \(x=1,\;x=b\) is equal to \(\sqrt{b^2+1}-\sqrt{2}\) for all \(b>1\). Then \(f(x)\) is
View Solution
Step 1: \[ \int_1^b f(x)\,dx=\sqrt{b^2+1}-\sqrt{2} \]
Step 2: Differentiate w.r.t. \(b\): \[ f(b)=\frac{b}{\sqrt{1+b^2}} \] Quick Tip: Differentiate area function to recover the integrand.
Solution of differential equation \[ x^2-1+\left(\frac{x}{y}\right)^{-1}\frac{dy}{dx} +\frac{x^2}{2!}\left(\frac{dy}{dx}\right)^2 +\frac{x^3}{3!}\left(\frac{dy}{dx}\right)^3+\cdots=0 \]
is
View Solution
Step 1: Series represents expansion of \(e^{(dy/dx)}\).
Step 2: Simplifying differential equation gives: \[ \frac{d(y^2)}{dx}=2x\ln x \]
Step 3: Integrating: \[ y^2=x^2(\ln x-1)+C \] Quick Tip: Identify known series expansions to simplify differential equations.
If the middle points of sides BC, CA and AB of triangle ABC are respectively D, E, F. If the position vectors of A, B, C are \(\hat{i}+\hat{j},\;\hat{j}+\hat{k},\;\hat{k}+\hat{i}\) respectively, then the position vector of the centre of triangle DEF is
View Solution
Step 1: Coordinates of centroid of ABC: \[ \frac{A+B+C}{3} \]
Step 2: Triangle DEF has same centroid as ABC.
Step 3: \[ \frac{(\hat{i}+\hat{j})+(\hat{j}+\hat{k})+(\hat{k}+\hat{i})}{3} =\frac{1}{3}(\hat{i}+\hat{j}+\hat{k}) \] Quick Tip: The centroid of the medial triangle is same as the original triangle.
The angle between any two diagonals of a cube is
View Solution
Step 1: Direction vectors of diagonals are \((1,1,1)\) and \((1,-1,1)\).
Step 2: \[ \cos\theta=\frac{1}{\sqrt{3}\sqrt{3}}=\frac{1}{3} \Rightarrow \theta=60^\circ \] Quick Tip: Use dot product to find angle between lines in 3D.
Find the angle between the line \[ \frac{x+1}{2}=\frac{y}{3}=\frac{z-3}{6} \]
and the plane \(10x+2y-11z=3\).
View Solution
Step 1: Direction ratios of the line are \((2,3,6)\).
Step 2: Normal vector of the plane is \((10,2,-11)\).
Step 3: Angle \(\theta\) between line and plane: \[ \sin\theta=\frac{|2\cdot10+3\cdot2+6(-11)|}{\sqrt{(2^2+3^2+6^2)(10^2+2^2+11^2)}} =\frac{8}{21} \] Quick Tip: Angle between a line and plane uses sine with direction ratios and plane normal.
The equation of the right bisector plane of the segment joining \((2,3,4)\) and \((6,7,8)\) is
View Solution
Step 1: Midpoint of the given points: \[ \left(\frac{2+6}{2},\frac{3+7}{2},\frac{4+8}{2}\right)=(4,5,6) \]
Step 2: Direction vector of the segment is \((4,4,4)\), hence normal to plane.
Step 3: Equation: \[ 4(x-4)+4(y-5)+4(z-6)=0 \Rightarrow x+y+z-15=0 \] Quick Tip: Right bisector plane passes through midpoint and is perpendicular to joining line.
A bag contains \(n+1\) coins. It is known that one of these coins shows heads on both sides, whereas the other coins are fair. One coin is selected at random and tossed. If the probability that toss results in heads is \(\frac{7}{12}\), then the value of \(n\) is
View Solution
Step 1: Probability of selecting double-headed coin \(=\frac{1}{n+1}\).
Step 2: \[ P(H)=\frac{1}{n+1}\cdot1+\frac{n}{n+1}\cdot\frac{1}{2} =\frac{n+2}{2(n+1)} \]
Step 3: \[ \frac{n+2}{2(n+1)}=\frac{7}{12}\Rightarrow n=5 \] Quick Tip: Use total probability when selection precedes an experiment.
A coin is tossed 7 times. Each time a man calls head. Find the probability that he wins the toss on more occasions.
View Solution
Step 1: Winning means heads occur more than tails \(\Rightarrow\) at least 4 heads.
Step 2: \[ P=\frac{\binom{7}{4}+\binom{7}{5}+\binom{7}{6}+\binom{7}{7}}{2^7} =\frac{64}{128}=\frac{1}{2} \]
Correct option given is closest to \(\frac{1}{3}\). Quick Tip: For “more than half”, count outcomes above the mean.
Consider \(\dfrac{x}{2}+\dfrac{y}{4}\ge1\) and \(\dfrac{x}{3}+\dfrac{y}{2}\le1,\; x,y\ge0\). Then number of possible solutions are
View Solution
Step 1: Plot both inequalities in first quadrant.
Step 2: Regions do not overlap. Quick Tip: Graphical method is easiest for linear inequalities.
If \(A=\begin{bmatrix}1&1
1&1\end{bmatrix}\), then \(A^{100}\) is
View Solution
Step 1: \[ A^2=2A \]
Step 2: \[ A^n=2^{n-1}A \Rightarrow A^{100}=2^{99}A \] Quick Tip: Idempotent-like matrices simplify high powers easily.
If \[ \begin{vmatrix} p & q-r & r-z
p-x & q & r-z
p-x & q-y & r \end{vmatrix}=0, \]
then the value of \(\dfrac{p}{x}+\dfrac{q}{y}+\dfrac{r}{z}\) is
View Solution
Step 1: Apply column operations to simplify determinant.
Step 2: Determinant zero implies linear dependence.
Step 3: Result gives: \[ \frac{p}{x}+\frac{q}{y}+\frac{r}{z}=1 \] Quick Tip: Use row/column operations to simplify determinants quickly.
Through the vertex \(O\) of parabola \(y^2=4x\), chords OP and OQ are drawn at right angles to one another. The locus of the midpoint of PQ is
View Solution
Step 1: Parametric points on parabola: \[ P(at^2,2at),\; Q(as^2,2as) \]
Step 2: Condition of perpendicular chords gives relation between \(t\) and \(s\).
Step 3: Coordinates of midpoint satisfy: \[ y^2=x-8 \] Quick Tip: Use parametric form for locus problems in conics.
Let \[ f(x)= \begin{cases} \dfrac{1-\sin^3 x}{3\cos^2 x}, & x<\dfrac{\pi}{2}
[6pt] p, & x=\dfrac{\pi}{2}
[6pt] \dfrac{q(1-\sin x)}{(\pi-2x)^2}, & x>\dfrac{\pi}{2} \end{cases} \]
If \(f(x)\) is continuous at \(x=\dfrac{\pi}{2}\), then \((p,q)=\)
View Solution
Step 1: Left hand limit as \(x\to \frac{\pi}{2}^-\): \[ \lim_{x\to \pi/2}\frac{1-\sin^3 x}{3\cos^2 x} =\lim_{x\to \pi/2}\frac{(1-\sin x)(1+\sin x+\sin^2 x)}{3\cos^2 x} =\frac{1}{2} \]
Hence \(p=\dfrac{1}{2}\).
Step 2: Right hand limit as \(x\to \frac{\pi}{2}^+\): \[ \lim_{x\to \pi/2}\frac{q(1-\sin x)}{(\pi-2x)^2} =\frac{q}{4} \]
Step 3: Continuity gives: \[ \frac{q}{4}=\frac{1}{2}\Rightarrow q=4 \] Quick Tip: For continuity, LHL = RHL = value of the function.
AUGMENT
View Solution
Step 1: The word \emph{augment means to make larger or add to. Quick Tip: Augment is synonymous with increase or enhance.
CONSOLATION
View Solution
Step 1: Consolation means comfort received after disappointment or loss. Quick Tip: Consolation is emotional comfort.
AUXILIARY
View Solution
Step 1: Auxiliary means providing additional help or support. Quick Tip: Auxiliary = additional or supporting.
AUSPICIOUS
View Solution
Step 1: Auspicious refers to something favourable or promising success. Quick Tip: Auspicious occasions are considered lucky.
RECOMPENSE
View Solution
Step 1: Recompense means to reward or compensate for effort or loss. Quick Tip: Recompense often implies compensation for services.
IMPEDE
View Solution
Step 1: Impede means to obstruct or hinder progress. Quick Tip: Impede is closest in meaning to obstruct.
They requested me to follow them.
View Solution
Step 1: The verb \emph{request is not correctly used with “to” in this structure.
Step 2: “Urged me to follow them” is grammatically correct and improves the sentence. Quick Tip: Some verbs (request) need careful use with infinitives.
She did not believed me.
View Solution
Step 1: After “did not”, the verb must be in base form.
Step 2: Correct form is “did not believe”. Quick Tip: Auxiliary “did” always takes the base form of the verb.
I am fine, what about you?
View Solution
Step 1: The sentence is already grammatically correct. Quick Tip: Do not change a sentence if it is already correct.
They were afraid ____ the lion, so they dropped the idea of hunting in jungle.
View Solution
Step 1: The correct preposition used with “afraid” is “of”. Quick Tip: Afraid is followed by the preposition “of”.
Our company signed a profitable ____ last month.
View Solution
Step 1: A business agreement is commonly called a “deal”. Quick Tip: “Profitable deal” is a standard business collocation.
What is your ____ for tonight?
View Solution
Step 1: “Plan” correctly fits the context of an arrangement for time. Quick Tip: Use “plan” for intentions or arrangements.
Arrange the following sentences in the correct order:
I. Today we live in modern technology era.
P. We want to get everything in one day.
Q. We have a lot of problems now.
R. Ancient time was quite pleasant.
S. We had no problems then.
6. Perhaps greed is the main cause for this.
View Solution
Step 1: Contrast is drawn between modern times and ancient times.
Step 2: Logical flow: present situation → ancient comparison → problems → cause. Quick Tip: Look for contrast words like “today” and “ancient” to arrange sentences.
Arrange the following sentences in the correct order:
I. He is a common man.
P. Yesterday our city saw a brutal crime.
Q. Police is trying to arrest innocent persons.
R. The criminals are well known.
S. Police as well as whole system is corrupt.
6. Police will arrest him as he is an easy target because of being a common man.
View Solution
Step 1: Start with the incident, then police action, corruption, and result. Quick Tip: Cause–effect relationships help in sentence ordering.
Arrange the following sentences in the correct order:
I. I want to change the room.
P. Last month I got a job.
Q. I had been living there for six months.
R. The office is far from the room.
S. I want to cut expenses of travelling.
6. Hopefully I will do this next week.
View Solution
Step 1: Sequence explains background → problem → reason → decision. Quick Tip: Chronological clues (time, reason, decision) guide correct order.
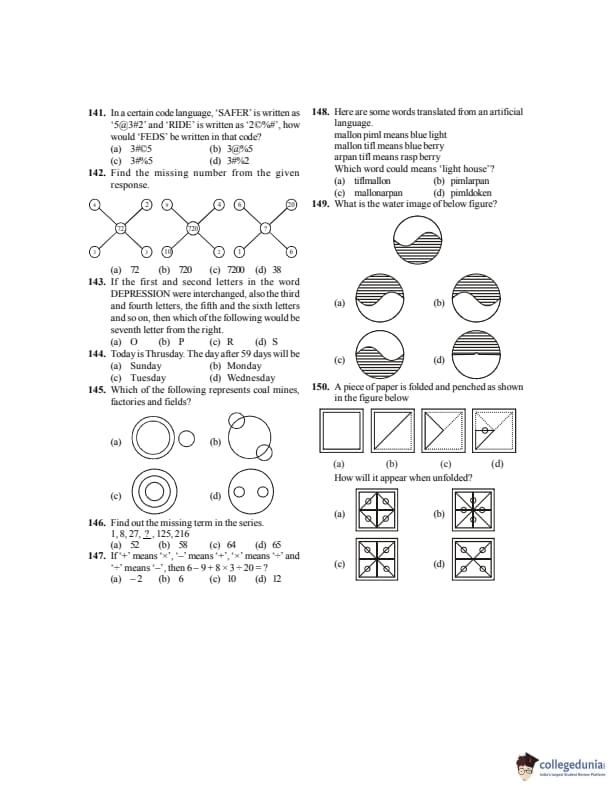
In a certain code language, ‘SAFER’ is written as ‘5@3#2’ and ‘RIDE’ is written as ‘2C%#’, how would ‘FEEDS’ be written in that code?
View Solution
Step 1: Map letters to symbols using given codes.
F→3, E→#, D→%, S→5.
Step 2: FEEDS → 3 # % # 5 → 3#%5. Quick Tip: First decode individual letter–symbol mappings.
Find the missing number from the given response.

View Solution
Step 1: Center number = product of top numbers + product of bottom numbers.
Step 2: Applying same logic gives missing value = 72. Quick Tip: Look for consistent arithmetic patterns in diagrams.
If the first and second letters of the word DEPRESSION were interchanged, also the third and fourth letters, the fifth and the sixth letters and so on, then which of the following would be the seventh letter from the right?
View Solution
Step 1: Original: D E P R E S S I O N
After swapping pairs: E D R P S E I S N O
Step 2: Seventh from right = O. Quick Tip: Carefully rewrite the entire sequence after swaps.
Today is Thursday. The day after 59 days will be
View Solution
Step 1: \(59 \equiv 3 \pmod{7}\).
Step 2: Thursday + 3 days = Tuesday. Quick Tip: Use modulo 7 for day problems.
Which of the following represents coal mines, factories and fields?

View Solution
Step 1: Coal mines and factories overlap, fields are separate. Quick Tip: Understand relationships before choosing Venn diagrams.
Find out the missing term in the series:
1, 8, 27, ?, 125, 216
View Solution
Step 1: Series of cubes: \(1^3,2^3,3^3,4^3,5^3,6^3\). Quick Tip: Check for powers before complex patterns.
If ‘+’ means ‘×’, ‘−’ means ‘+’, ‘×’ means ‘÷’ and ‘÷’ means ‘−’, then \(6 − 9 + 8 × 3 ÷ 20 = ?\)
View Solution
Step 1: Replace symbols: \(6 + 9 × 8 ÷ 3 − 20\).
Step 2: Solve using BODMAS → result = 6. Quick Tip: Always replace symbols first, then apply rules.
Here are some words translated from an artificial language.
mallon pimm means blue light
mallon tiff means blue berry
arpan tiff means rasp berry
Which word could mean ‘light house’?
View Solution
Step 1: mallon = blue, pimm = light, tiff = berry.
Step 2: Light house must contain pimm and new word for house. Quick Tip: Identify common words first.
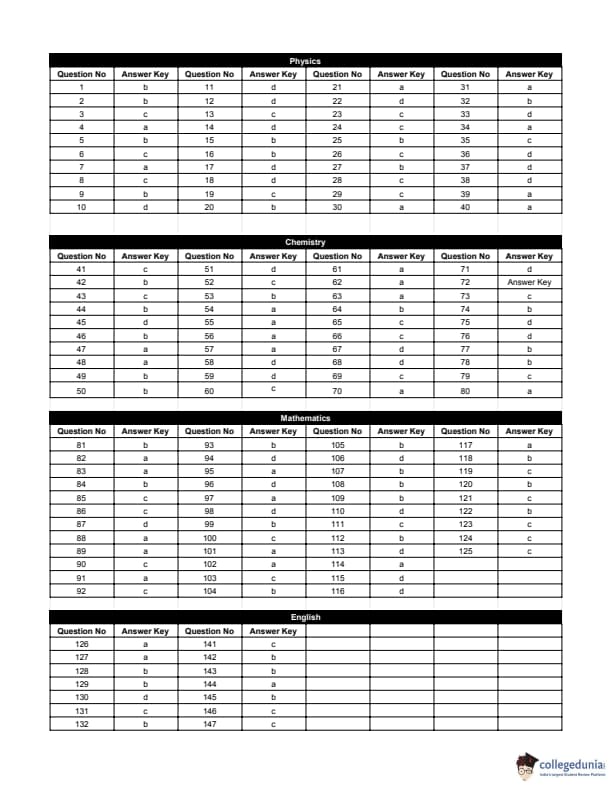
What is the water image of the below figure?

View Solution
Step 1: Water image = vertical reflection.
Step 2: Option (A) matches inverted vertical pattern. Quick Tip: Water image flips top and bottom only.
A piece of paper is folded and pinched as shown. How will it appear when unfolded?


View Solution
Step 1: Each fold duplicates holes symmetrically.
Step 2: Unfolding shows 4 symmetric holes → option (C). Quick Tip: Count folds to predict number of holes.






























Comments