Jasmine Grover Content Strategy Manager
Content Strategy Manager
Mechanical properties of solids are the characteristics of a solid which define its resistance, deformation, strength etc. The mechanical properties of solids are studied to understand such characteristics which further helps in the efficient designing of products and machinery for the market. This study also helps engineers and technicians prevent accidents from happening. Some mechanical properties include plasticity, stress, elasticity, strain, young’s modulus etc. These characteristics help in determining a suitable solid for a given specific work.
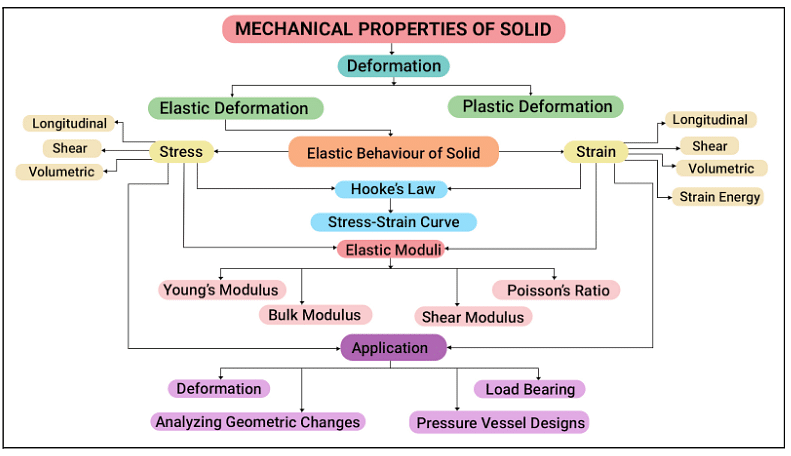
Mechanical Properties of Solids
Very Short Answer Questions (1 Marks Questions)
Ques. Why is the stretching of a coil spring determined by its shear modulus?
Ans. When a coil spring is stretched, neither does its length nor its volume change, the only change that occurs is in its shape. Therefore, the stretching of the coil spring is determined only by shear modulus.
Ques. What is elastic fatigue?
Ans. It is the loss in strength of a material caused when the material is subjected to repeated alternating strains.
Ques. Define tensor physical quantities. Give an example.
Ans. They are defined as the physical quantities having different values in different directions e.g. stress.
Ques. Why do machine parts get jammed in winter?
Ans. At low temperatures, the viscosity of lubricants increases.
Ques. The shearing force is proportional to the shear strain for the solids that have an elastic modulus of rigidity. On what factor does it depend in the case of fluids?
Ans. Rate of Shear Strain.
Ques. How the use of a parachute helps a person who is jumping from an aeroplane?
Ans. The calculated viscous force on the parachute is large so, its terminal velocity becomes comparably small. Thus, the person hits the ground with this small velocity and does not get injured.
Ques. Why are railway tracks laid on large-sized wooden sleepers?
Ans. Large-sized wooden sleepers spread force due to the weight of the train on a larger area and hence reduce the pressure considerably which in turn prevents the yielding of the ground under the weight of the train.
Read More: Relation Between Viscosity and Density
Short Answer Questions (2 Marks Questions)
Ques. Define longitudinal strain.
Ans. It is defined to be the ratio of change in length to the original length of an object when it gets deformed by an external force i.e. Longitudinal strain = l /L= change in length/ original length
Ques. Define volumetric strain.
Ans. It is defined as the ratio of change in volume per unit of the original volume of the body when deformed by an external force change in volume AV i.e. Volumetric strain = change in volume/ original volume =ΔV/V
Ques. Define longitudinal or tensile stress.
Ans. It is defined as the restoring force developed per unit area of cross-section of a body when the length of the body increases in the direction of the deforming force.
Read More: Stress
Ques. What are the factors due to which three states of matter differ from one another?
Ans. Three states of matter differ from each other due to the following two factors:
(a) The different amounts of tester atomic and intermolecular forces.
(b) The degree of haphazard thermal motion of the atoms and molecules of a substance depends upon the temperature.
Ques. When we stretch a wire, we have to perform work. Why? What happens to the energy given to the wire in this process?
Ans. In a normal or ordinary situation/circumstances, the atoms of a solid are at the locations of minimum potential energy. When we intentionally stretch a wire, the work has to be done against interatomic forces. This work is stored in the wire in the form of elastic potential energy for the time being.
Ques. Why are the bridges declared unsafe after long use?
Ans. A bridge during its use undertakes alternative strains a large number of times each day, depending upon the movement of vehicles on it. When a bridge is used for a long time it exhausts its elastic strength, due to which the number of strains in the bridge for given stress will become hefty and ultimately the bridge may collapse. Thus, to avoid this, the bridges are stated unsafe after long use.
Ques. Give reasons why the springs are made of steel and not of copper.
Ans. Spring should have a large restoring force which is set up in it on being deformed, which in turn depends upon the elasticity of the material of the spring. Since Young’s modulus of elasticity of steel is more than that of copper, hence steel is preferred in making such springs.
Read More: Interaction of Forces & Effects of Force Interaction
Long Answer Questions (3 Marks Questions)
Ques. Read the following two statements below carefully and state if it is true or false with reasons.
(a) The Young’s modulus of rubber is greater than that of steel;
(b) The stretching of a coil is determined by its shear modulus.
Ans. (a) False (b) True
(a) For given stress, the strain in rubber is more than it is in steel.
Young’s modulus, Y = \(\frac{Stress}{Strain}\)
For constant stress: Y ∝ =
\(\frac{1}{Strain}\)Therefore, it can be said that Young’s modulus for rubber is less than it is for steel.
(b) Shear modulus is known to be the ratio of the applied stress to the change in the shape of a body. The stretching of a coil changes its shape. Therefore, it is clear that the shear modulus of elasticity is involved in this process.
Ques. In the following stress-strain curve, which has

- Greater young’s Modulus
- More Ductility
- More Tensile strength
Ans. 1. Since young’s Modulus is given by the slope of the stress-strain graph. Since the slope of A is more than that of B, hence it has a greater young’s Modulus.
- Ductility is defined as the extent of plastic deformation and it is greater for A.
- Tensile strength is termed the direct measure of stress required, from by graph, it is greater for A.
Ques. Two friends Mohan and Dinesh arc discussing elasticity. Mohan said that steel is more elastic than rubber. Dinesh was surprised and asked his teacher about it.
(i) What value is displayed by Dinesh?
(ii) How does his teacher explain it?
Ans. (i) The values displayed by Dinesh are Curiosity and Interest in learning.
(ii) Let the two pieces of wire, one of steal and the other of rubber have an equal length (L) and equal area of cross-section (A). Each piece must be stretched by equal force (F).
Then, Young’s modulus of steel and rubber are:
∴ Ys = \(\frac{F.L}{AI_s}\) and \( Yr = \frac{F.L}{AI_r}\)
i.e \(\frac{Ys}{Yr} = \frac{I_r}{I_s}\) (on dividing)
Since, Ir > Is
∴ \(\frac{Y_s}{Y_r} > 1\) ⇒ Ys > Yr
Hence, Steal is more elastic than rubber.
Ques. Given that the potential energy is minimum at r = ro = 0.74AO, Will the force be attractive or repulsive at r = 0.5AO; 1.9AO and α?
Ans. Since potential energy is minimum at rO = 0.74AO, therefore interatomic force between two atoms is zero for rO = 0.74AO
- At r = 0.5 AO (Which is less than rO), the force is repulsive
- At r = 1.9AO (Which is greater than ro), the force is attractive
- At r = α, the force is zero.
Read More: Strain Energy
Very Long Answer Questions (5 Marks Questions)
Ques. (a) What are the factors affecting elasticity?
(b) Define Poisson’s ratio.
(c) Define breaking load
Ans. (a) The following factors affect the elasticity of a material:
- Effect of hammering and rolling on a material: It causes a decrease in the plasticity of the material due to the break-up of crystal grains into smaller units and thus, the elasticity of the material increases.
- Effect of Annealing on a material: Annealing results in an increase in the plasticity of the material due to, the formation of large crystal grains. Henceforth, the elasticity of the material decreases.
- Effect of the presence of impurities on a material: The effect of the presence of impurities in a material can be both ways i.e. it can increase as well as decrease the elasticity of the material. The type of effect depends upon the nature of the impurity present in the material.
- Effect of temperature on a material: The increase in the temperature of the material in most cases causes a decrease in the elasticity of the material. The elasticity does not change with the change in temperature.
(b) Poisson’s Ratio (σ): Within elastic limits, it is defined; as the ratio of lateral strain (β) to the linear strain i.e. σ = βα
(c) Breaking Load: It is defined as the product of the breaking stress and area of cross-section of the given object. It is also called the maximum load a body (cable/ wire) can support or hold i.e. it is given as breaking load = Breaking stress × area of cross-section. It should be noted that breaking stress is always constant for the given material.
Ques. The length of a metallic wire is L1 when tension is T1 and L2 when tension is T2. Find the original length of the wire.
Ans. Let L, A be the length and area of the cross-section of the wire.
Let us consider l to be the extension produced on applying a force F
Now, using the relation, Y = \(\frac{Stress}{Strain}\), we get
Y = \(\frac{F/A}{I/L}\) = \(\frac{FL}{AI}\) ……...(1)
where Y = Young’s modulus.Then,
Y = \(\frac{T_1L}{A(L_1 - L)}\) …..(2)
and when F = T2, and I = L2 – L,
Then, Y = \(\frac{T_2L}{A(L_2 - L)}\) …….(3)
∴ From (2) and (3), we get
\(\frac{T_1L}{A(L_1 - L)} = \frac{T_2L}{A(L_2 - L)}\)
or T1(L2 – L) = T2 (L1 – L)
or (T2 – T)L = T2L1 – T1L2
or L = \(\frac{T_2L_1 - T_1L_2}{T_2 - T_1}\)
Read More: Derivation Relation Between Elastic Constants
Ques. The length of metal is l1, when the tension in it is T1 and is l2 when the tension is l2. Find the original length of wire?
Ans. Let l = original length of material wire
A = original length of metal wire.
Change in length in the first case = (l1 – l)
Change in length in the second case = (l2 – l)
Now, Young Modulus is given as =
\(\frac{ Normal Stress}{Longitudinal Strain}\)Y = \(\frac{T/A}{\Delta I / I}\)
Y = Young’s Modulus
T = Tension
A = Area
∆l = Change in length
l = Original Length
∴ Y = \(\frac{T_1}{A} X \frac{I}{(I_1 - I)}\) for first case
Y = \(\frac{T_2}{A} X \frac{I}{(I_2 - I)}\)for second case
Since Young’s Modulus remains the same,
So,

T1 (I2 – I) = T2 (I1 – I)
T1I2 – T1I = T2I1 – T2I
I (T2 – T1) = T2I1 – T1I2
l = \(\frac{T_2I_1 - T_1I_2}{T_2 - T_1}\)
Read Also:





Comments