Mechanical Properties of Fluid is an important topic in the Physics section in WBJEE exam. Practising this topic will increase your score overall and make your conceptual grip on WBJEE exam stronger.
This article gives you a full set of WBJEE PYQs for Mechanical Properties of Fluid with explanations for effective preparation. Practice of WBJEE Physics PYQs including Mechanical Properties of Fluid questions regularly will improve accuracy, speed, and confidence in the WBJEE 2026 exam.
Also Read

WBJEE PYQs for Mechanical Properties of Fluid with Solutions
1.
A small spherical body of radius r and density ? moves with the terminal velocity v in a fluid of coefficient of viscosity $\eta$ and density $\sigma$. What will be the net force on the body ?- $\frac{4\pi}{3}r^{3} \left(\rho-\sigma\right) g$
- $6\pi\eta rv$
- Zero
- Infinity
2.
A body floats in water with $40\%$ of its volume outside water. When the same body floats in an oil, $60\%$ of its volume remains outside oil. The relative density of oil is- $0.9$
- $1.0$
- $1.2$
- $1.5$
3.
A $20\,cm$ long capillary tube is dipped vertically in water and the liquid rises upto $10\, cm$. If the entire system is kept in a freely falling platform, the length of water column in the tube will be- 5 cm
- 10 cm
- 15 cm
- 20 cm
4.
As shown in the figure, a liquid is at the same levels in two arms of a U-tube of uniform cross-section when at rest. If the U-tube moves with an acceleration 'f' towards the right,the difference in liquid heights between the two arms of the U-tube will be,(acceleration due to gravity=g)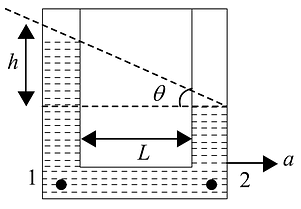
- \(\frac{f}{g}a\)
- \(\frac{g}{f}a\)
- a
- 0
5.
A small metal sphere of radius $a$ is falling with a velocity $v$ through a vertical column of a viscous liquid. If the coefficient of viscosity of the liquid is $\eta$ then the sphere encounters an opposing force of- $6\pi\eta a^{2}v$
- $\frac{6\eta v}{\pi a}$
- $6\pi\eta av$
- $\frac{\pi\eta v}{6a^{3}}$
6.
Water is flowing in streamline motion through a horizontal tube. The pressure at a point in the tube is $p$ where the velocity of flow is $v$. At another point, where the pressure is $p/2$, the velocity of flow is [density of water = $?$]- $ \sqrt{v^{2}+\frac{p}{\rho}}$
- $ \sqrt{v^{2}-\frac{p}{\rho}}$
- $ \sqrt{v^{2}+\frac{2p}{\rho}}$
- $ \sqrt{v^{2}-\frac{2p}{\rho}}$
7.
To determine the composition of a bimetallic alloy, a sample is first weighed in air and then in water. These weights are found to be $w_1$ and $w_2$ respectively. If the densities of the two constituent metals are $\rho_1$ and $\rho_2$ respectively, then the weight of the first metal in the sample is (where $\rho_w$ is the density of water)- $\frac{\rho_{1}}{\rho_{w}\left(\rho_{2}-\rho_{1}\right)}\left[w_{1}\left(\rho_{2}-\rho_{w}\right)-w_{2}\rho_{2}\right]$
- $\frac{\rho_{1}}{\rho_{w}\left(\rho_{2}+\rho_{1}\right)}\left[w_{1}\left(\rho_{2}-\rho_{w}\right)+w_{2}\rho_{2}\right]$
- $\frac{\rho_{1}}{\rho_{w}\left(\rho_{2}-\rho_{1}\right)}\left[w_{1}\left(\rho_{2}+\rho_{w}\right)-w_{2}\rho_{1}\right]$
- $\frac{\rho_{1}}{\rho_{w}\left(\rho_{2}-\rho_{1}\right)}\left[w_{1}\left(\rho_{1}+\rho_{w}\right)-w_{2}\rho_{1}\right]$
8.
A hollow sphere of external radius $R$ and thickness $t (<< R)$ is made of a metal of density $\rho$, sphere will float in water if- $t \le \frac{R}{\rho}$
- $t \le \frac{R}{3\rho}$
- $t \le \frac{R}{2\rho}$
- $t \ge \frac{R}{2\rho}$
9.
A uniform capillary tube of length $l$ and inner radius $r$ with its upper end sealed is submerged vertically into water. The outside pressure is $p_0$ and surface tension of water is $\gamma$. When a length $x$ of the capillary is submerged into water, it is found that water levels inside and outside the capillary coincide. The value of $x$ is- $\frac{l}{\left(l+\frac{p_{o}r}{4\gamma}\right)}$
- $l\left(l-\frac{p_{o}r}{4\gamma}\right)$
- $l\left(l-\frac{p_{o}r}{2\gamma}\right)$
- $\frac{l}{\left(l+\frac{p_{o}r}{2\gamma }\right)}$
10.
As shown in the figure, a pump is designed as a horizontal cylinder with a piston having area A and an outer orifice having an area 'a'. The piston moves with a constant velocity under the action of force F. If the density of the liquid is ρ, then the speed of liquid emerging from the orifice is(assume A>>a)
- \(\sqrt{\frac{F}{\rho A}}\)
- \(\frac{a}{A}\sqrt{\frac{F}{\rho A}}\)
- \(\sqrt{\frac{2F}{\rho A}}\)
- \(\frac{A}{a}\sqrt{\frac{2F}{\rho A}}\)
11.
Water is flowing through a very narrow tube. The velocity of water below which the flow remains a streamline flow is known as- Relative velocity
- Terminal velocity
- Critical velocity
- Particle velocity
12.
Two solid spheres of same metal but of mass $M$ and $8\,M$ fall simultaneously on a viscous liquid and their terminal velocities are $v$ and $nv$, then value of $n$ is- 16
- 8
- 4
- 2
13.
A body when fully immersed in a liquid of specific gravity $1.2\, $ weighs $44\,gwt$. The same body when fully immersed in water weighs $50\, gwt$. The mass of the body is- 36 g
- 48 g
- 64 g
- 80 g
14.
An object weights $m_1$, in a liquid of density $d_1$ and that in liquid of density $d_2\,$ is $\, m_2.$ The density $d$ of the object is- $d = \frac{m_2 d_2 - m_1 d_1}{m_2 - m_1}$
- $d = \frac{m_1 d_1 - m_2 d_2}{m_2 - m_1}$
- $d = \frac{m_2 d_1 - m_1 d_2}{m_1 - m_2}$
- $d = \frac{m_1 d_2 - m_2 d_1}{m_1 - m_2}$
15.
What will be the approximate terminal velocity of a rain drop of diameter $ 1.8 ? 10^{-3}\, m$, when density of rain water $\approx 10^3\, kgm^{-3}$ and the co-efficient of viscosity of air $\approx 1.8 ? 10^{-5}\, Nsm^{-2}$ ? (Neglect buoyancy of air).- $49\, ms^{-1}$
- $98\, ms^{-1}$
- $392 \,ms^{-1} $
- $980 \,ms^{-1} $





Comments