Jasmine Grover Content Strategy Manager
Content Strategy Manager
Uniform Circular Motion is a motion where the acceleration and angular speed of a particle moving in a circle remains constant. Circular motion is described as the movement of an object in a circular path while spinning. It can further be divided into two types: uniform and non-uniform circular motion.
- When the position of a body constantly varies with reference to a stationary object, the object is said to be in motion.
- All moving bodies change their position over time.
- Uniform Circular Motion is when a body moves in a circular path at a constant speed.
- Due to the continual change in the direction of motion, the velocity of a body travelling at a constant speed in a circle is not uniform.
Key Terms: Uniform Circular Motion, Speed, Circular Path, Velocity, Acceleration, Centripetal Force
What is Uniform Circular Motion?
[Click Here for Sample Questions]
The motion of a body going at a constant speed along a circular path is known as uniform circular motion. The velocity varies while the speed of the body in uniform circular motion remains constant.
- If a particle is travelling in a circle, it must be experiencing some acceleration, causing it to rotate around the centre.
- As this acceleration is always perpendicular to a particle's velocity, it only alters the direction of velocity rather than the magnitude, which is why the motion is circular and uniform.
- The force acting towards the centre is termed centripetal force, and the acceleration is called centripetal acceleration (or radial acceleration).
- The moving object is accelerated by a centripetal force in the direction of the centre of rotation because the object's velocity vector is in a continually changing direction.
- According to Newton's laws of motion, the object would move in a straight line without this acceleration.
- When a rigid body rotates around a fixed axis that is not negligibly small compared to the path's radius, each of the body's particles describes a uniform circular motion with the same angular velocity, but with velocity and acceleration varied with the axis' location.
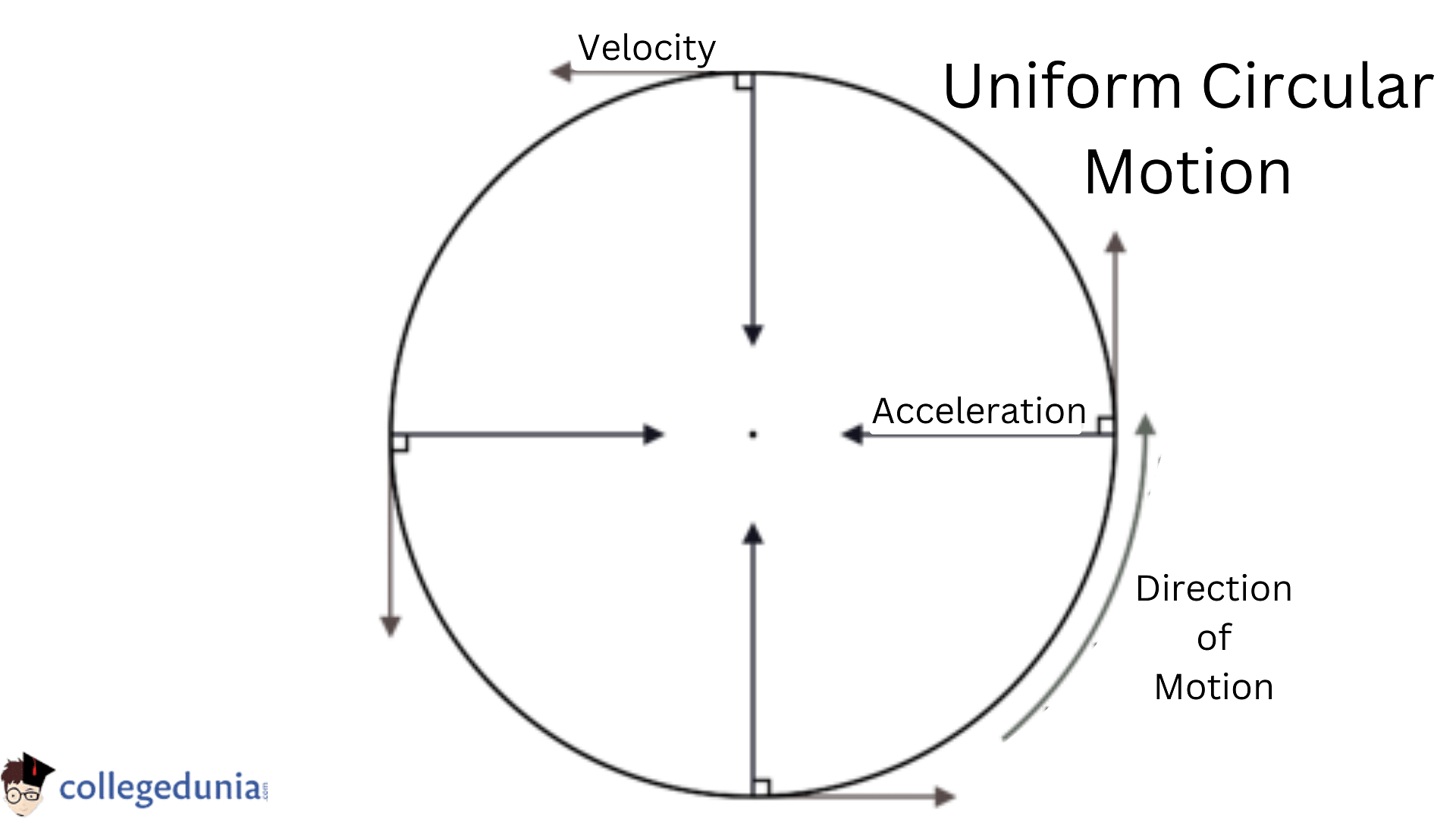
Uniform Circular Motion
| Uniform Circular Motion – Related Topics | ||
|---|---|---|
| Resolution of vectors | Displacement vector | Tangential Acceleration Formula |
Uniform Circular Motion Formula
[Click Here for Previous Year Questions]
If the circular path's radius is R and the magnitude of the object's velocity is V. The object's radial acceleration will then be:
arad= \(\frac{v^2}{R}\)
This radial acceleration, once again, will always be perpendicular to the velocity direction. The SI unit for it is m2s-2.
- The radial acceleration can alternatively be calculated using the motion's period, i.e. T.
- T is taken as the length of time it takes to complete a rotation. It is measured in seconds.
- The velocity of an item traveling in uniform circular motion is equal to the circumference C of the circle divided by the period of time if the magnitude of the velocity is v. Thus,
\(V = \frac{C}{T}\)
- The circumference of the circle can be calculated as the radius R multiplied by pi.
- As a result, C = 2ΠR
- As a result, the velocity will be constant throughout the motion.
\(V = \frac{2{\pi}R}{T}\)
- Using this value in the radial acceleration equation, we get,
arad =\(\frac{4 \Pi^2 R}{T^2}\)
NoteLet us take a stone that is tethered to a thread rotating in a clockwise motion at a constant speed. When the stone reaches any point A, its motion is directed eastward. If the stone is released while it is at point A, it flies east. The speed of the stone is directed south when it reaches point B. When released from that point, the stone flies off in the south direction. Therefore, when a body moves in a circular path, the direction of speed at any 2 points is the same. When the body’s direction changes, the velocity does not remain constant. Hence, even though the speed of the body is constant, a circular motion is accelerated. The force required to cause an object to move in a circular path is known as centripetal force. |
Also Read: Motion in a Straight Line
Characteristics of Uniform Circular Motion
[Click Here for Sample Questions]
In the case of uniform circular motion, the acceleration is:
ar = v2r = ω2r
If m is the mass of the particle,
F = ma
mv2r = mω2r
If a particle is travelling in a uniform circular motion, then:
- It moves at a constant speed.
- Velocity is constantly changing at each constant, v = R.
- No tangential acceleration is present.
- Its centripetal acceleration (radial) is ω2R.
- v = ωr
There is some tangential acceleration in a non-uniform circular motion, which causes the particle's speed to increase or decrease. The resulting acceleration is referred to as the vector sum of the tangential and radial accelerations.
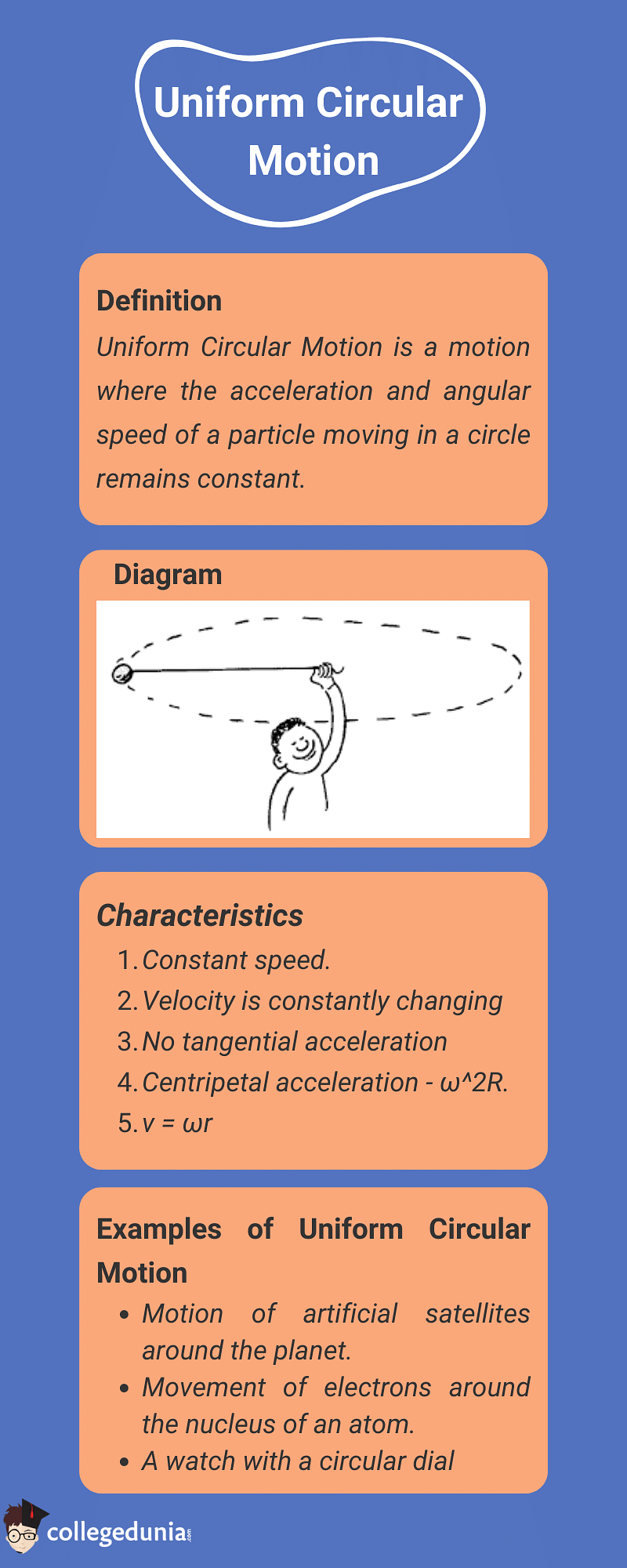
Examples of Uniform Circular Motion
[Click Here for Previous Year Questions]
The examples of uniform circular motion are as follows –
- The motion of artificial satellites around the planet exemplifies uniform circular motion, which is kept in a circular orbit around the planet by the gravitational attraction of the earth.
- The moon revolves around Earth in a circular motion.
- The movement of electrons around the nucleus of an atom is a uniform circular motion.
- The rotation of the windmill blades.
- A watch with a circular dial has a uniform circular motion at the tip of the second hand.
Uniform circular motion, therefore, occurs when a body moves in a circular path at a consistent speed.

Uniform Circular Motion of a satellite around a planet
| Motion in a Straight Line – Related Topics | ||
|---|---|---|
| Projectile Motion Formula | Resultant Vector Formula | Relation between Torque and speed |
| Horizontal Motion | Velocity Vectors | Trajectory Formula |
Things to Remember
- A circular motion is defined as a body movement that follows a circular route.
- The motion of a body going at a constant speed along a circular path is known as uniform circular motion.
- When a body moves in a circle at a constant speed, the work it does is zero. This implies that the centripetal force does no work.
- The moving object is accelerated by a centripetal force in the direction of the centre of rotation because the object's velocity vector is in a continually changing direction.
- The frictional force between the tires and the ground provides the essential centripetal force for turning cars on the roads.
- The motion of artificial satellites around the planet exemplifies uniform circular motion.
Sample Questions
Ques. Define Uniform Circular Motion. (2 marks)
Ans. A circular motion is defined as a body movement that follows a circular route. The motion of a body going at a constant speed along a circular path is known as uniform circular motion. The velocity varies, but the speed remains constant.
Ques. What is the name of the gadget that is used to measure rotational speed? (1 marks)
Ans. A tachometer is a gadget that is used to measure rotational speed.
Ques. When a particle is moving at a constant angular velocity, which property is conserved? (2 marks)
Ans. The energy of a particle is preserved when it moves at a constant angular velocity. This is since, in a uniform circular motion, kinetic energy remains constant while the particle's momentum varies as velocity changes.
Ques. What happens to a particle's velocity vector if it moves in a circle at equal angles and at the same time? (1 marks)
Ans. The direction of a particle's velocity vector will change. This is because it is always pointed in the direction of the circle's tangent.
Ques. Describe characteristics of a uniform circular motion. (3 marks)
Ans. If a particle is traveling in a circular motion, then:
1) It moves at a constant speed.
2) Velocity is constantly changing.
3) No tangential acceleration is present.
Ques. State some examples of uniform circular motion. (3 marks)
Ans. The following are examples of uniform circular motion:
- The motion of artificial satellites around the planet exemplifies uniform circular motion.
- The movement of electrons around the nucleus of an atom.
- The rotation of the windmill blades.
Ques. Write the formula of radial acceleration. (1 marks)
Ans.The formula of radial acceleration is arad=4π2R/T2
Ques. Define centripetal force. (1 mark)
Ans. A force that acts on a body traveling in a circular route and is directed towards the body's center of rotation is centripetal force.
Ques. A cyclist travels at a pace of 10 meters per second around a circular circuit with a radius of 50 meters. (3 marks)
(a) Determine the cyclist's rate of acceleration?
(b) Given a combined mass of 120 kg for the cyclist and the bicycle, what is the net force acting on them?
Ans. (a) An element with constant speed travel around a circular path producing a radially inward acceleration known as centripetal acceleration, whose magnitude is as follows
ac = v2/r
= 102/50
= 2 m/s2
(b) Centripetal force is the net force that exerts on an object to maintain it going down a circular track. Its magnitude may be calculated using Newton's second law, as shown below.
Fnet=mac
=120×2
=240N
Ques. At a constant speed of 2160 km/h, a jet plane maneuvers in a circular path with a radius of 5km. In g's, what is the plane's acceleration? (5 marks)
Ans. The only acceleration is due to centripetal acceleration because this is a circular motion problem with constant speed.
Because we'll be comparing this acceleration to gravitational acceleration, g = 9.8m/s2, it's best to convert all quantities to SI units first.
In SI units, 2160 km/h is equivalent to
2160 x (10/36) = 600 m/s2
ac= v2/r
= 6002/5000
= 72 m/s2
We should divide it by g to compare it to gravity.
\(\frac{a_c}{g} = \frac{72}{9.8} \)= 7.35g
Read More:








Comments