Derivation of Centripetal Acceleration: Definition, Equation and Derivation

Centripetal acceleration is the acceleration that is produced when a body moves in a circular path. The velocity of the body continuously changes its direction when the object is in circular motion. Due to this change in velocity, an acceleration is produced which is known as Centripetal acceleration.

• Centripetal acceleration always acts radially toward the center of the circular path.
• The force causing this acceleration is known as Centripetal force.
• Centripetal acceleration is given by the magnitude of the square of the velocity of the body divided by the radius of the circular path.
• The SI unit of centripetal acceleration is meter-per-second square (m/s²).

Key Terms: Centripetal Force, Centripetal Acceleration, Centripetal Acceleration Formula, Circular motion, Linear velocity, Motion, Angular acceleration.

---

Centripetal Acceleration

[Click Here for Sample Questions]

Centripetal acceleration refers to the acceleration that is produced when the body is in a circular motion. If the body is not in circular motion then no centripetal acceleration is produced.

• Centripetal acceleration is always directed toward the center of the circular in which the body is moving and it is perpendicular to the direction of tangential velocity.
• Since the circular motion of a body is due to the centripetal force which acts radially towards the center of the circular path, therefore the acceleration caused due to this force is known as centripetal acceleration.

Read more: Uniform Circular Motion

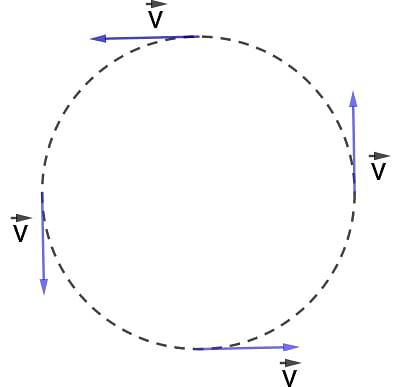
Centripetal Acceleration

The video below explains this:

Centripetal Acceleration Detailed Video Explanation:

The formula for centripetal acceleration is given by

a_c = v²/r

Where

• a_c = centripetal acceleration
• v = tangential velocity or linear velocity
• r = radius of the circular path

Read more: Types of Friction

When an object moves in a circular path it has three different types of acceleration: Angular acceleration, Tangential acceleration, and Centripetal acceleration

• Angular acceleration is an angular quantity, whereas Centripetal and Tangential acceleration are linear quantities.
• The major difference between centripetal acceleration and tangential acceleration is that centripetal acceleration is produced due to the change in the direction of the tangential velocity, while tangential acceleration is produced due to the change in the magnitude of tangential velocity.

Centripetal Force

Read more: Centripetal and Centrifugal force

---

Derivation of Centripetal Acceleration

[Click Here for Sample Questions]

Consider a body of mass m moving in a circular path of radius r with velocity v, as shown in the figure.

Centripetal force F_c helps the body to move in a circular path and is directed toward the center of the circle. This force acting on the body of mass m produced an acceleration known as centripetal acceleration a_c and is given by

F_c = ma_c

Also, centripetal acceleration is given by the rate of change of linear velocity with time.

a_c = Δv/Δt   ...(i)

From the ΔPQR, we have

\(\vec {PQ}+\vec {QS} = \vec {SP}\)

-v₁ + v₂ = Δv

Δv = v₂ – v₁

Now triangle PQR and AOB are similar, therefore

\(\frac {\Delta v}{AB}=\frac {v}{r}\)

Also, we have

AB = arc AB = vΔt

\(\Rightarrow \frac {\Delta v}{v\Delta t}=\frac {v}{r}\)

\(\Rightarrow \frac {\Delta v}{\Delta t}=\frac {v^2}{r}\)

Substituting the above equation in equation (i), we get

\(a_c=\frac {v^2}{r}\)

This is the derivation for the formula of centripetal acceleration. 

Also check: 

---

Solved Examples

Ques. A rock tied to a string is moving at a fixed speed of 20.0 m/s in a circle having a radius of 6.0 m. Evaluate the approximate magnitude of the centripetal acceleration of the rock.

Ans. Given,

• the velocity of the rock tied to the string, v = 20 m/s
• the radius of the circular path, r = 6 m

From the formula of centripetal acceleration,

a_c = v² / r

a_c = (20)²/ 6 = 66.67 m/s²

Therefore, centripetal acceleration is 66.67 m/s²

Ques. A 23 kg girl is riding a merry-go-round with a radius of 4 m. What is the centripetal force on the girl if her velocity is 5 m/s?

Ans. Given,

• mass of the girl, m = 23 kg
• the radius of the circular path, r = 4 m
• the tangential velocity of the girl, v = 5 m/s

The centripetal force acting on the girl is given by

F_c = mv²/r

⇒ F_c = (23 × 5²) / 4 = 143.75 N

---

Things to Remember

• Acceleration refers to a change in speed or velocity, both in magnitude and direction or in any of them.
• In the case of uniform circular motion, the direction of velocity changes continuously. As a result, even though the speed is constant, a related acceleration is always there.
• Centripetal acceleration is the property of motion of an object moving through a circular path. It refers to an object which moves in a circle with an acceleration vector pointing toward the circle's center.
• Centripetal force is the net force that causes an object's centripetal acceleration in a circular motion. The centripetal force is directed toward the center, which is perpendicular to the body's motion.
• When an object moves in a circular motion, the following equation can be used to calculate its speed: a_c = v²/r