Collegedunia Team Content Curator
Content Curator
Torque is a force that causes an object to rotate about its axis. It is also called the moment of force. In physics, speed is the distance covered per unit time. When an object is rotating, its speed is called angular velocity. Angular velocity is the measure of the number of rotations per unit time by an object.
Key Takeaways: Torque, Moment of Force, Angular Velocity, Angular Acceleration, Static Torque, Dynamic Torque, Orbital Angular Velocity, Spin Angular Velocity, Right-hand thumb rule
What is Torque?
Torque is the force that provides angular acceleration to a rotating body. It is the angular equivalent of linear force. When an object is rotating around its axis, there must be a force acting upon it in order to keep it rotating.
Torque is a vector quantity. It is denoted by the symbol τ.The SI unit of torque is Newton-metre.
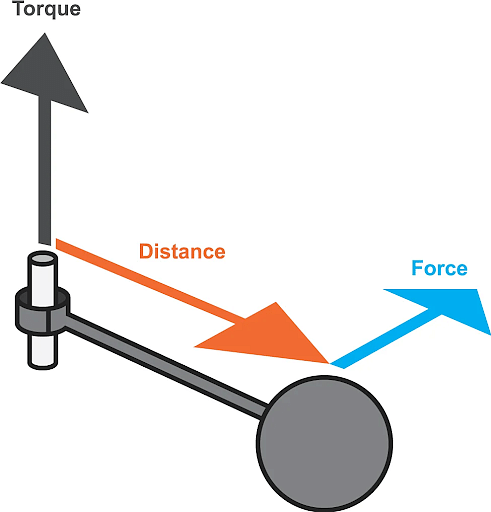
Torque
Torque is of two types:
- Static Torque: The torque which does not produce angular acceleration is called Static Torque.
- Dynamic Torque: The torque which produces angular acceleration is called Dynamic Torque.
Torque depends upon the following factors:
- The magnitude of the force.
- Distance between the point where force is applied and the rotation axis.
- The orientation of force with respect to the displacement from the point of force.
Read Also:
| Angular Momentum | Angular Displacement | Relative Speed |
| Moment of Inertia | Rolling Motion | Radius of Gyration |
| Third Law of Motion | Centre of Mass | Couple |
How is Torque Calculated?
The torque is given by the formula,
τ = F . r sinθ
Where,
F → Force
r → Length of the moment arm
θ → Angle between force and moment arm
The direction of the torque can be found with the help of the right-hand thumb rule.
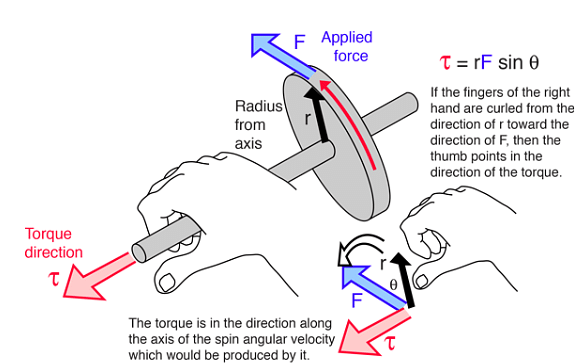
Right-hand thumb rule
What is Angular Velocity?
Angular velocity is the rate at which an object rotates around its axis. It is a vector quantity. It is denoted by ω . The SI unit of angular velocity is radians per second.
Angular Velocity is of two types:
- Orbital Angular Velocity: It is the rotational motion of an object around an axis present outside the body of the object.
- Spin Angular Velocity: It is the motion of an object around an axis that lies within the body of the object.
When an object rotates in a clockwise direction, its angular velocity is positive and if the body rotates in an anti-clockwise direction, its angular velocity is negative.
Relation between Torque and Angular Velocity
Linear distance is given by
Linear distance = radius × angular velocity × time
Linear distance = r × ω × t
And, torque = force × radius
τ = f × r
So,
f = τ / r
Now,
Power = Force × Linear distance / Time
P = ( τ /r ) × r × ω × t / t
P = τ × ω
τ = P / ω
Torque = Power / Angular Velocity
Thus, Torque is inversely proportional to the angular velocity.
Applications of Torque
There are many real-life applications of torque. Some of them are listed below:
- Opening and closing of doors also work on the principle of torque. The doorknob is put at a long distance from the hinges so that torque for opening the door can be applied easily.
- Using a wrench to tighten or loosen a nut around a bolt is an example of applying torque.

Application of Torque
- The steering wheel of a car is smaller than those of 18-wheelers because the force required for a car is less than an 18-wheeler. So, the radius is increased for the steering wheel of 18-wheelers so that torque can be applied easily.
Things to Remember
- Torque is a force that causes an object to rotate about its axis. Torque is also called moment of force.
- Torque is a vector quantity. It is of two types namely, Static and Dynamic.
- Angular velocity is the rate at which an object rotates about its axis. It is a vector quantity.
- Angular velocity is of two types Orbital angular velocity and spin angular velocity.
- Torque is given by, τ = F . r sinθ
- The direction of the torque is determined by the right-hand thumb rule.
- Torque is inversely proportional to the angular velocity.
Read More:
Sample Questions
Ques. A bolt connecting the main and rear frame of a mountain bike requires a torque of 15 N-m to tighten. If you are capable of applying 40N of force to a wrench in any given direction, what is the minimum length of the wrench that will result in the required torque? (2 marks)
Ans. The minimum length of the wrench will assume that the maximum force is applied at an angle of 90°.
So,
τ = F . r
where,
r = length of the wrench)
r = τ / F
r = 15 / 40 = 0.375m.
Ques. A uniform rod of length 50cm and mass 0.2kg is placed on a fulcrum at a distance of 40cm from the left end of the rod. At what distance from the left end of the rod should a 0.6kg mass be hung to balance the rod? (3 marks)
Ans. For the rod to balance, the clockwise and counter-clockwise torque must be equal. If we assume fulcrum as the pivot point, the counterclockwise torque is because of the rod's weight. If we use pivot as the reference point, then the centre of the rod is 15cm from the reference.
τccw = r × F = 0.15m × 10m/s2 × 0.2kg = 0.3 Nm
This is equal to clockwise torque due to additional mass, a distance r to the right of the pivot.
τcw = r × F = r × (10m/s2) × 0.6kg = 0.3Nm
r = 0.3 / 10 × 0.6
r = 0.05m
So, r is 0.05m to the right of the pivot, so 40+5 cm from the end of the rod.
Ques. Two students are balancing on a 10m seesaw. The seesaw is designed so that each side of the seesaw is 5m long. The student on the left weighs 60kg and is standing three metres away from the centre. The student on the right weighs 45kg. The seesaw is parallel to the ground. Assume the board that makes the seesaw is massless. What distance from the centre should the student on the right be if they want the seesaw to stay parallel to the ground? (3 marks)
Ans. τ = F r sinθ
Since both the students will exert a downward force perpendicular to the length of seesaw, so sinθ = 1. Here, force is the force of gravity and r is the distance from the centre of the seesaw.
F = mg = m (10m/s2)
For a seesaw to remain parallel (not move), torque must be zero. For this, the torque of the student at left must be equal to the torque of the student at right.
∴ F1r1 = F2r2
60kg × 10m/s2 × 3m = 45kg × 10m/s2 × r2
r2 = 4m
Ques. A 3m beam of negligible weight is balancing in equilibrium with a fulcrum placed 1m from its left end. If a force of 50N is applied to its right end, how much force would need to be applied to the left end? (5 marks)
Ans. This is an example of rotational equilibrium involving torque.
τ = Fdsinθ
Where,
θ = angle between the force vector and the object in equilibrium
d = distance from the fulcrum to the point of the force vector
To achieve equilibrium, torques must be equal
F1d1sinθ1 = F2d2sinθ2
Since the forces are applied perpendicular to the beam, sinθ = 1.
The distance of the fulcrum from the left end is 1m and its distance from the right is 2m.
F1d1 = F2d2
50 × 2 = y × 1
y = 50 × 2 / 1 = 100N
Since the 50N force is twice as far from the fulcrum as the force that must be applied on the left side, it must be half as strong as the force on the left. The force on the left can be found to be 100N.
Ques. One side of a seesaw carries a 21kg mass four metres from the fulcrum and a 25.5kg mass two metres from the fulcrum. To balance the seesaw, what mass should be placed nine metres from the fulcrum on the side opposite the first two masses? (3 marks)
Ans. For the seesaw to be balanced, the system must be in rotational equilibrium. For this to occur, torque must be the same on both sides.
τ = Fd = mgd
For net torque to be zero, the total torque must be equal on both sides.
τ1 + τ2 = τ3
m1gd1 + m2gd2 = m3gd3
21 × g × 4 + 25.5 × g × 2 = m3 × g × 9
The acceleration due to gravity cancels from each term.
84 + 51 = m3 × 9
135 = m3 × 9
m3 = 15 kg
Read More:
Ques. An attraction at a science museum helps teach students about the power of torque. There is a long metal beam that has one pivot point. At one end of the bar hangs a full sedan, and on the other end is a rope at which students can pull down, raising the car off the ground. The beam is 40 metres long and the pivot point is 5 metres from one end. A car of mass 500kg hangs from the short end of the beam. Neglecting the mass of the beam, what is the minimum mass of a student who can hang from the rope and begin to raise the car off the ground? (3 marks)
Ans. Torque applied by the car:
τ = mgd
τ = 500 × 10 × 5 = 25,000J
We can now use this to find the mass of student that will create the same amount of torque while hanging from the rope;
25,000J = mgd = m × 10 × 35
m = 71.4 kg
Ques. There is a 100kg weight 3m to the left of the centre of a seesaw. What distance from the centre on the right side of the seesaw should Bob sit so that the seesaw is balanced? Bob's mass is 60kg. (3 marks)
Ans. τ = Frsinθ
Here, θ is zero because Bob and the weight are sitting directly on the top of the seesaw; all of their weight is projected directly downward. Therefore, the torque that the weight applies is;
τweight = 3 × (100 × 10) = 3000N
In order for the seesaw to balance, the torque applied by Bob must be equal to 3000N.
3000N = r × (60 × 10)
r = 5m
Ques. Define Centre of Mass. (2 marks)
Ans. For a system of particles, the centre of mass is defined as that point where the entire mass of the system is imagined to be concentrated, for consideration of its translational motion.
If all the external forces acting on the body/system of bodies were to be applied at the centre of mass, the state of rest/ motion of the body/system of bodies shall remain unaffected.
Ques. A child sits stationary at one end of a long trolley moving uniformly with a speed V on a smooth horizontal floor. If the child gets up and runs about on the trolley in any manner, what is the speed of the CM of the (trolley + child) system? (2 marks)
Ans. When the child gets up and runs about on the trolley, the speed of the centre of mass of the trolley and child remains unchanged irrespective of the manner of movement of the child. It is because here child and trolley constitute one single system and forces involved are purely internal forces. As there is no external force, there is no change in momentum of the system and velocity remains unchanged.
Ques. Torques of equal magnitude are applied to a hollow cylinder and a solid sphere, both having the same mass and radius. The cylinder is free to rotate about its standard axis of symmetry, and the sphere is free to rotate about an axis passing through its centre. Which of the two will acquire a greater angular speed after a given time? (3 marks)
Ans. Let M be the mass and R the radius of the hollow cylinder, and also of the solid sphere. Their moments of inertia about the respective axes are I1 = MR² and I2 = 2/5 MR²
Let τ be the magnitude of the torque applied to the cylinder and the sphere, producing angular accelerations α1and α2 respectively. Then τ = I1 α1 = I2 α2
The angular acceleration produced in the sphere is larger. Hence, the sphere will acquire a larger angular speed after a given time.
Ques. A solid cylinder of mass 20 kg rotates about its axis with angular speed 100 rad s?¹. The radius of the cylinder is 0.25 m. What is the kinetic energy associated with the rotation of the cylinder? What is the magnitude of angular momentum of the cylinder about its axis? (3 marks)
Ans. M = 20 kg
Angular speed, w = 100 rad s-¹; R = 0.25 m
Moment of inertia of the cylinder about its axis =1/2 MR² = 1/2 x 20 (0.25)² kg m² = 0.625 kg m²
Rotational kinetic energy,
Er = 1/2 Iw² = 1/2 x 0.625 x (100)² J = 3125 J
Angular momentum,
L = Iw = 0.625 x 100 Js= 62.5 Js.
Ques. (a) Find the moment of inertia of a sphere about a tangent to the sphere, given the moment of inertia of the sphere about any of its diameters to be 2 MR2/5, where M is the mass of the sphere and R is the radius of the sphere.
(b) Given the moment of inertia of a disc of mass M and radius R about any of its diameters to 1 be 1/4 MR2, find the moment of inertia about an axis normal to the disc passing through a point on its edge. (3 marks)
Ans. (a) Moment of inertia of sphere about any diameter = 2/5 MR²
Applying theorem of parallel axes, Moment of inertia of a sphere about a tangent to the sphere = 2/5 MR² +M(R)² =7/5 MR²
(b) We are given, the moment of inertia of the disc about any of its diameters = 1/4 MR²
(i) Using the theorem of perpendicular axes, moment of inertia of the disc about an axis passing through its centre and normal to the disc = 2 x 1/4 MR² = 1/2 MR².
(ii) Using theorem axes, moment of inertia of the disc passing through a point on its edge and normal to the dies = 1/2 MR² + MR² = 3/2 MR²





Comments