Collegedunia Team Content Curator
Content Curator
In this article, we have listed some important questions for CBSE class 10 real numbers. These questions will help the students to practice and score well in the CBSE class 10th maths exam. This article has covered all the important topics with a detailed explanation.
Class 10th real numbers concepts include real numbers, operation on real numbers, properties of real numbers, number line, and the law of exponents for real numbers. Also, few advanced concepts of real numbers are included. Similarly, the topic which is listed in the questions has covered the full syllabus that aims to develop problem-solving skills and confidence among students regarding their exams.
| Table of Contents |
Keyterms: Number, Number system, Number line, Rational and irrational numbers, Multiplication
Read Also:- Real Numbers Formula
Explanation
[Click Here for Sample Questions]
Real Numbers
The combination of rational and irrational numbers, in the numbers system, is referred to as Real Numbers. The arithmetic operations are based on these numbers. Real numbers are also represented on the number line. Here is a detailed explanation about the real numbers, along with the examples.
Definition
Real Numbers is a set of both Rational and Irrational numbers. However, the numbers can be both positive and negative and they are denoted by the symbol “R”. all the decimals, natural numbers, and fractions belong to this category. Below is the classification of real numerals, these classifications of numbers are also called set of real numbers. Here are some examples, 8.99, 5/2, π(3.14), 22, -13, √3, etc.
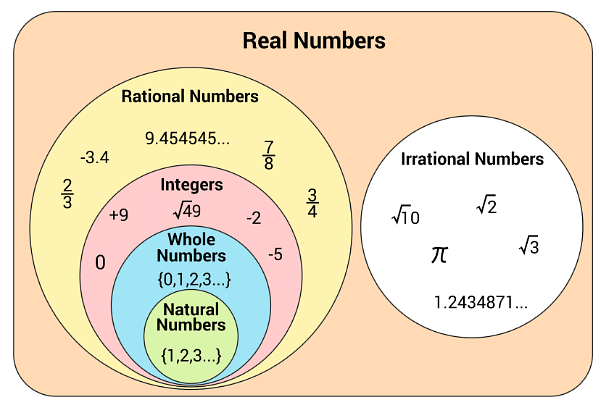
Real Numbers
Real Numbers Chart
Here is a chart representation of all types of real numbers:
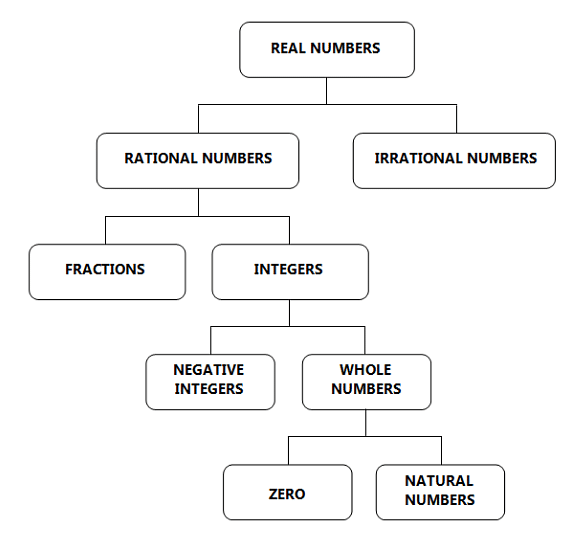
Real Numbers Chart
Properties of Real Numbers
[Click Here for Sample Questions]
Real numbers have four main properties. The properties are associative property, distributive property, communicative property, and identity property. Suppose there are three real numbers “m,n, and r”, then these properties can be explained using m,n, and r as mentioned below:
- Communicative Property
The general form of communicative property is m+n= n+m for addition and m.n= n.m for multiplication purposes.
- Associative Property
The general form of associative property is m+(n+r) = (m+n) +r for addition (mn)r= m(nr) for multiplication purpose.
- Distributive Property
The general form of distributive property is m(n+r) =mn + mr and (m+n)r =mr + nr.
- Identity Property
The general form of Identity property is m + 0 = m. (0 is the additive identity) for addition and m × 1 = 1 × m = m. (1 is the multiplicative identity) for multiplication.
Also Read:
Important Questions
Ques 1: HCF (306, 657) = 9, what will be the LCM of (306, 567) (2 marks)
Solution: we already know that,
HCF * LCM is equalled to the Product of the two given numbers
Therefore,
9 * LCM = 306 * 657
LCM = (306 × 657)/9 = 22338
Hence, LCM(306,657) = 22338
Ques 2: By using Euclid’s division lemma show that the square of any positive integer is either of form 3m or 3m + 1 for some integer m. (3 marks)
Solution: Let x be the positive integer and y = 3.
A per the Euclid’s division algorithm;
for some integer q ≥ 0 and r = 0, 1, 2 as r ≥ 0 and r < 3)x = ( 3q + r )
Therefore,
for, x = 3q, 3q + 1 & 3q + 2
Based on the given question, if we take the square on both the sides, we get;
x2 = (3q)2 = 9q2 = 3.3q2
Let 3q2 = m
Therefore,
x2 = 3m ………………….(1)
x2 = (3q + 1)2
= (3q)2 + 12 + 2 × 3q × 1
= 9q2 + 1 + 6q
= 3(3q2 + 2q) + 1
By Substitute, 3q2+2q = m, we get,
x2 = 3m + 1 ……………………………. (2)
x2 = (3q + 2)2
= (3q)2 + 22 + 2 × 3q × 2
= 9q2 + 4 + 12q
= 3(3q2 + 4q + 1) + 1
Commute, 3q2 + 4q + 1 = m, to get,
x2 = 3m + 1…………………………… (3)
Therefore, equations 1, 2, and 3, show that the square of every positive integer is either of form 3m or 3m + 1 for some integer m.
Ques 3: Show that 3 + 2√5 is an irrational number. (2 marks)
Solution: suppose, 3 + 2√5 be a rational number.
Hence, the co-primes x and y of the given rational number where (y ≠ 0) is such that:
3 + 2√5 = x/y
Rearranging, we get,
2√5 = (x/y) – 3
√5 = 1/2[(x/y) – 3]
As x and y are integers, therefore, 1/2[(x/y) – 3] is a rational number.
Similarly, √5 is also a rational number. But this proves the fact that √5 is irrational.
Thus, as per our assumption that 3 + 2√5 is a rational number is wrong.
Hence, 3 + 2√5 is irrational.
Ques 4: Demonstrate each number as a product of its prime factors:
(a) 140
(b) 156
(c) 3825
(d) 5005
(e) 7429 (2 marks)
Solution:
- 140
By taking the division of a number by prime numbers method, we will get the product of prime factors of 140. Therefore, 140 = 2 × 2 × 5 × 7 × 1 = 22 × 5 × 7
- 156
By taking the division of a number by prime numbers method, we will get the product of prime factors of 156. Hence, 156 = 2 × 2 × 13 × 3 = 22 × 13 × 3
- 3825
By taking the division of a number by prime numbers method, we will get the product of prime factors of 3825. Therefore, 3825 = 3 × 3 × 5 × 5 × 17 = 32 × 52 × 17
- 5005
By taking the division of a number by prime numbers method, we will get the product of prime factors of 5005. Hence, 5005 = 5 × 7 × 11 × 13 = 5 × 7 × 11 × 13
- 7429
By taking the division of a number by prime numbers method, we will get the product of prime factors of 7429. Therefore, 7429 = 17 × 19 × 23 = 17 × 19 × 23
Ques 5: Check whether 6n can end with the digit 0 for any natural number n. (2 marks)
Solution: Suppose, the number 6n ends with the digit zero (0), then it will be divisible by 5, as we know any number with a unit place as 0 or 5 is divisible by 5.
Prime factorization of 6n = (2 × 3)n
Hence, the prime factorization of 6n doesn’t include prime number 5.
Therefore, you get that, for every natural number n, 6n is not divisible by 5, and in conclusion, it shows that 6n cannot end with the digit 0 for any natural number n.
Ques 6: Without explaining the long division, state whether the following rational numbers will have a non-terminating repeating decimal expansion or terminating decimal expansion.
(a) 13/3125
(b) 17/8
(c) 64/455 (2 marks)
Solution: Note= As we know, if the denominator has only factors of 2 and 5 or in the form of 2m × 5n then it has a terminating decimal expansion.
And suppose, If the denominator has factors other than 2 and 5 then it has a non-terminating repeating decimal expansion.
- 13/3125
Factorizing the denominator, we get,
3125 = 5 × 5 × 5 × 5 × 5 = 55
Or
= 20 × 55
Since the denominator is of form 2m × 5n then, 13/3125 has a terminating decimal expansion.
- 17/8
Factorizing the denominator, we get,
8 = 2× 2 × 2 = 23
Or
= = 23 × 50
Since the denominator is of form 2m × 5n then, 17/8 has a terminating decimal expansion.
- 64/455
Factorizing the denominator, we get,
455 = 5 × 7 × 13
Since the denominator is not in the form of 2m × 5n, therefore 64/455 has a non-terminating repeating decimal expansion.
Ques 7: Show whether the following real numbers with decimal expansion are rational or not. If they are rational, and of the form, p/q what will be the prime factors of q?
(a) 43.123456789
(b) 0.120120012000120000... (2 marks)
Solution:
- 43.123456789
This number has a terminating decimal expansion, it is a rational number in the form of p/q and q has factors of 2 and 5 only.
- 0.120120012000120000. . .
This number has a non-terminating and non-repeating decimal expansion, it is an irrational number.
Ques: Is Zero an Imaginary or a Real Number? (2 marks)
Ans: Zero is included in both imaginary and real numbers. We already know that imaginary numbers are considered as the square root of non-positive real numbers. However, zero is also a non-positive number, in conclusion, it comes under the category of imaginary numbers. On the other hand, 0 is considered as a rational number and defined in the number line that’s why it is a real number.
Ques: What is the exact definition of HCF? (1 mark)
Ans: HCF- Highest Common Factor of two positive integers called a and b.
Ques: What is exactly a Lemma and Algorithm? (1 mark)
Ans: Lemma is considered as a proven statement that is used for proving other statements. On the other hand, the algorithm is defined as a series of well-defined steps that are used for solving or proving the problem.
Also Read:



Comments