Collegedunia Team Content Curator
Content Curator
Midpoint Formula also helps us in finding the exact coordinate of an endpoint if the coordinates of another endpoint and coordinates of the midpoint are given. Midpoint generally means a point on a plane or line segment which is at an equal distance from both the end points. In clear terms, it divides the segment in equal halves or bisects it.
| Table of Content |
Keyterms: Midpoint, Centroid, Line segment, Traingle, Endpoint, Circles, Ellipses, Hyperbolas, Quadrilateral, General polygons, Number
Also, read: Section Formula in Coordinate Geometry
What is Midpoint?
[Click Here for Sample Questions]
The term ‘midpoint’s origin of the word dates back to the early 14th century and means the absolute ‘center’ of something. It is the point midway between the endpoints. It can also be called as the centroid of the line segment, as well as the endpoints.
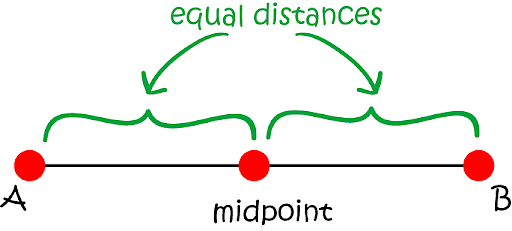
What is Midpoint?
The video below explains this:
Coordinate Geometry Detailed Video Explanation:
Also, read: Medians of a triangle
Midpoint Theorem
[Click Here for Sample Questions]
The midpoint theorem states that "The line segment in a triangle joining the midpoint of two sides of the triangle is said to be parallel to its third side and is also half of the length of the third side."
The midpoint theorem came to be invented by Rene Descartes, the popular mathematician of all time. It was a basic geometrical idea at first in Rene’s mind, which represented an ordered pair of numbers. This was later made into a method so as to help combine arithmetic and geometry. Apart from the cartesian plane, the midpoint has great uses in geometrical figures like triangles, circles, ellipses, hyperbolas, quadrilaterals and general polygons.
Proof of Midpoint Theorem
Consider the triangle PQR, as shown in the figure,

Proof of Midpoint Theorem
Let E and D be the midpoints of the sides PR and PQ. Then the line DE is said to be parallel to the side QR, whereas the side DE is half of the side QR, that is,
DE Δ QR
DE = Half of QR or (½ * QR)
Now if we consider the figure below, we can see that it is an extended version of the figure above.
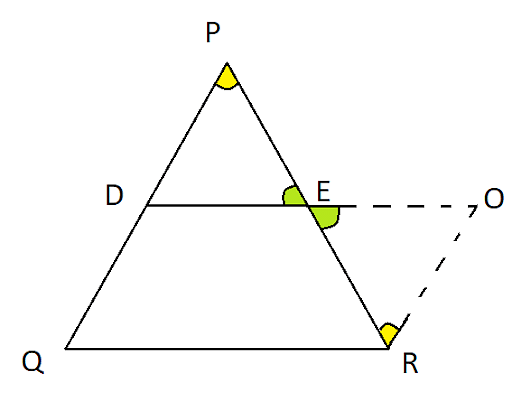
Proof of Midpoint Theorem
Construction- Extend the line segment DE and produce it to O such that, EO = DE.
In triangle PDE and EOR,
ER = AP —– (given)
∠REO = ∠PED (vertically opposite angles)
∠DPE = ∠ERO (alternate angles)
By ASA congruence criterion,
Δ PDE ≅ Δ EOR
Therefore,
∠ROE = ∠PDE {by c.p.c.t.}
∠ORE= ∠DPE {by c.p.c.t.}
and RO = PD {by c.p.c.t.}
∠ROE and ∠PDE are the alternate interior angles.
Assume OR and PQ as two lines which are intersected by the transversal DO.
In a similar way, ∠ORE and ∠DPE are the alternate interior angles.
Let us again assume that OR and PQ are the two lines which are intersected by the transversal PR.
Therefore, OR ΔPQ
So, OR Δ DQ
and OR = DQ {since DQ = DP, it is proved that OR = PD}
Thus, ODQR forms a parallelogram.
By the properties of a parallelogram, we can write
QR Δ DO
and QR = DO
DE Δ QR
and DE = (½ * QR)
Hence, the midpoint theorem is proved.
Also Read:
Midpoint Formula
[Click Here for Sample Questions]
In order to find the midpoint of a cartesian plane, in a graph, we use the midpoint theorem which will help us find out the coordinates.
Let’s suppose that a line connects two points (2,6) and (4,2), then the coordinates of the midpoint of the line joining these two points are, [(2+4)/2, (6+2)/2] which gives us (3,4).

Midpoint Formula
Suppose the endpoints of a line are given as (x1, y2) and (x2, y2), then,
Midpoint formula is,
| (x, y) = (\(\frac{x_1 +x_2}{2} , \frac{y_1 + y_2}{2}\)) |
Here, x1 and x2 are coordinates of the x axis whereas y1 and y2 are the coordinates of the y axis.
Now, suppose we want to find the midpoint of a plane of a three dimensional space,
For example find the midpoint of (x,y,z)
Midpoint formula is,
| (x,y,z) = (\(\frac{x_1 +x_2}{2} , \frac{y_1 + y_2}{2}, \frac{z_1 + z_2}{2}\)) |
The coordinates will be (x1,y1,z1) and (x2,y2,z2).
Also Read:
| Related Articles | ||
|---|---|---|
| Two-Dimensional Coordinate Geometry | Coordinate Geometry MCQs | Coordinate Geometry Important Questions |
| Quadrant | Centroid | Ordinate |
| Triangles | Polar Coordinates | Geometry Formula |
Things to Remember
- The Midpoint theorem was invented by Rene Descartes, a popular mathematician of that time. The theorem states that " The line segment in a triangle joining the midpoint of two sides of the triangle is said to be parallel to its third side and is also half of the length of the third side."
- Midpoint is a point on the line segment which is equidistant from both of the end points. It is referred to as the exact center of something, and is considered as the centroid of both the segment as well as the endpoints. It bisects the endpoints in equal halves.
- The concept of midpoint is used in circles, quadrilaterals, ellipses, triangles and general polygons as well. Apart from coordinate geometry, certain applications of midpoint theorem are also used in Economics to find the coefficient of elasticity. It helps to find out how quantity supplied and quantity demanded changes.
- The midpoint of the diameter of a circle is the center of that same circle. The midpoint of a segment connecting the vertices of a hyperbola, is the center of the hyperbola itself. A regular polygon has an inscribed circle within itself which is tangent to each side of the polygon at its midpoint.
- The key characteristic of this midpoint equation is that it calculates the percentage changes based on the difference between the beginning and the ending values. The importance of midpoint and its application are highly essential for calculations in architecture, studying market conditions like demand and supply elasticity.
Sample Questions
Ques. What is the use of midpoint in everyday life? (2 Marks)
Ans. Midpoint theorem is basically used to find specific information regarding the length of the sides of the triangle. It states that the segment joining two sides of a triangle at the midpoint of those sides is parallel to the third side and is the length of the third side. Besides this, it is also used in architecture, in finding the position of elasticity in economics and other fields.
Ques. How do you solve a problem such that the point (0,2) is the midpoint of (2,-3) and at what point? (3 Marks)
Ans. The first point is (2,-3). Let us assume that the other coordinate is (m,n).
Now,
(x,y) = \([\frac{x_1 +x_2}{2} , \frac{y_1 + y_2}{2}]\)
Putting known values, we get : (0,2)= [(2+m)/2, (−3+n)/2] i.e. (2+m)/2 = 0 And (−3+n)/2 = 2
Solving we get
m= -2 and n=7
Thus the second point will have coordinate (-2,7)
Ques. Find the coordinates of the centre of the circle. The endpoints of the diameter are given as (5, 2), (3, 4) (3 Marks)
Ans. Given coordinates of endpoints are:
(5, 2) = (x1, y1)
(3, 4) = (x2, y2)
Coordinates of the centre of a circle =\([\frac{x_1 +x_2}{2} , \frac{y_1 + y_2}{2}]\)
= [(5 + 3)/2, (2 + 4)/2]
= (8/2, 6/2)
= (4, 3)
Ques. The midpoint of line segment AB is (4, -5). If the coordinates of point A are (4, 3), what are the coordinates of B? (3 Marks)
Ans. Given (x1,x2) = (4,-5)
(x2,y2) = (4,9)
We know that according to the formula we can find the midpoint (x,y):
(x,y) = \([\frac{x_1 +x_2}{2} , \frac{y_1 + y_2}{2}]\)
(x,y) = [(4+4)/2, (-5+9)/2]
(x,y) = (4,2)
Ques. The following coordinates represent the vertices of a box. What is the coordinate of the centre of the box? (1,1),(1,9),(9,9),(9,1) (4 Marks)
Ans. To solve this, we need to choose two points that lie diagonally across from each other.
Let's use (1,1) and (1,9)
Now, we can substitute
M =\([\frac{x_1 +x_2}{2} , \frac{y_1 + y_2}{2}]\) = [(1+1)/2, (1+9)/2]
M = (1,5)
Then we have (9,9) and (9,1)
M =\([\frac{x_1 +x_2}{2} , \frac{y_1 + y_2}{2}]\)= [(9+9)/2, (9+1)/2]
M = (9,5)
Now we have (1,5) and (9,5)M =\([\frac{x_1 +x_2}{2} , \frac{y_1 + y_2}{2}]\)
M = [(1+9)/2, (5+5)/2]
M = (5,5)
Ques. M(3, 8) is the midpoint of the line AB. A has the coordinates (-2, 3), what are the coordinates of B? (4 Marks)
Ans. Let us consider the coordinates of B be (x,y)
We know that according to the formula we can find the midpoint (x,y):
(x,y) = \([\frac{x_1 +x_2}{2} , \frac{y_1 + y_2}{2}]\)
[(-2+x)/2, (3+y)/2] = (3,8)
(-2+x)/2 = 3
Therefore, x = 8
Similarly,
(3+y)/2 = 8
Therefore, y = 13
Hence, Coordinates of B = (8, 13)
Do Check Out:





Comments