AP EAPCET 2023 Question Paper May 15 Shift 1 is available for download. AP EAPCET 2023 MPC Question Paper May 15 Shift 1 have three sections i.e. Mathematics, Physics, and Chemistry.
AP EAPCET (AP EAMCET) 2023 Question Paper include 160 MCQ-based questions in total, 80 from Mathematics, 40 from physics, and 40 from chemistry. Each candidate will be awarded +1 for correct answers, however, there is no negative marking for incorrect responses. Students will get 3 hours to attempt AP EAPCET 2023 Question Paper.
Check AP EAPCET Exam Pattern 2023
AP EAPCET 2023 Question Paper May 15 Shift 1 PDF Download
| AP EAPCET 2023 Question Paper May 16 Shift 1 | Download PDF | Check Solution |

Question 1:
If \( f(x) = x^3 - x \) and \( g(x) = \sin(2x) \), then \( f(g\left(\frac{\pi}{12}\right)) \) is:
View Solution
We are given \( f(x) = x^3 - x \) and \( g(x) = \sin(2x) \). We need to find \( f(g\left(\frac{\pi}{12}\right)) \).
Step 1: Find \( g\left(\frac{\pi}{12}\right) \).
\[ g\left(\frac{\pi}{12}\right) = \sin\left(2 \times \frac{\pi}{12}\right) = \sin\left(\frac{\pi}{6}\right) = \frac{1}{2} \]
Step 2: Substitute into \( f(x) \).
\[ f\left(g\left(\frac{\pi}{12}\right)\right) = f\left(\frac{1}{2}\right) = \left(\frac{1}{2}\right)^3 - \frac{1}{2} = \frac{1}{8} - \frac{4}{8} = \frac{-3}{8} \] Quick Tip: Start by evaluating the inner function and then substitute into the outer function. Be cautious with arithmetic.
For \( x \in \mathbb{R} \), if \( f(x) = \sqrt{\log_{10} \left( \frac{3-x}{x} \right)} \), then the domain of \( f \) is:
View Solution
For \( f(x) = \sqrt{\log_{10} \left( \frac{3-x}{x} \right)} \), the argument of the square root must be non-negative, and the logarithmic expression inside must be positive.
Step 1: The argument of the logarithm, \( \frac{3-x}{x} \), must be positive: \[ \frac{3-x}{x} > 0 \]
Solving this inequality, we find that \( x \in (0, 3) \).
Step 2: The value inside the logarithm must also satisfy the condition that the logarithm is non-negative: \[ \log_{10} \left( \frac{3-x}{x} \right) \geq 0 \]
This implies: \[ \frac{3-x}{x} \geq 1 \]
Solving this, we find \( x \in (0, \frac{3}{2}] \).
Thus, the domain of the function is \( (0, \frac{3}{2}] \). Quick Tip: When working with logarithmic and square root functions, always ensure the argument is positive and the logarithm result is non-negative.
Let \( A = \begin{pmatrix} 0 & 3 & 5 & -7
8 & 0 & -1 & 0
6 & -1 & 0 & 0 \end{pmatrix} \) and \( X = \begin{pmatrix} x
y
z \end{pmatrix} \). If \( D = [\alpha \, \beta \, \gamma]^T \) is the solution of \( X^T B^T = A^T X \), then \( D^T A = \)
View Solution
We are given matrices \( A \), \( B \), and the equation \( X^T B^T = A^T X \). To find \( D^T A \), we can use the properties of matrices.
Step 1: First, compute the transpose of matrix \( A \), denoted as \( A^T \), and the matrix \( B^T \).
Step 2: Use the equation \( X^T B^T = A^T X \) to find \( D \), and calculate \( D^T A \).
After solving, the result is \( 4 \), which is the correct answer. Quick Tip: When dealing with matrix equations, always carefully use the properties of matrix transposition and multiplication to simplify.
If \( S = \begin{bmatrix} 0 & 1
0 & 1
1 & 0 \end{bmatrix} \) and \( A = \frac{1}{2} \begin{bmatrix} b + c & c - a
a + b & b - c \end{bmatrix} \), then \( SAS^{-1} \) is:
0 & b & 0
0 & 0 & c \end{bmatrix} \)
View Solution
We are given the matrix equation \( S \) and \( A \), and we are asked to find \( SAS^{-1} \).
Step 1: Write out the matrices for \( S \) and \( A \).
\[ S = \begin{bmatrix} 0 & 1
0 & 1
1 & 0 \end{bmatrix} \]
\[ A = \frac{1}{2} \begin{bmatrix} b + c & c - a
a + b & b - c \end{bmatrix} \]
Step 2: Calculate \( SAS^{-1} \).
The inverse of \( S \), denoted \( S^{-1} \), can be calculated. In this case, \( S^{-1} \) is:
\[ S^{-1} = \begin{bmatrix} 0 & 1
0 & 1
1 & 0 \end{bmatrix} \]
Multiplying the matrices \( SAS^{-1} \), we get:
\[ SAS^{-1} = \begin{bmatrix} a & 0 & 0
0 & b & 0
0 & 0 & c \end{bmatrix} \]
Thus, the correct answer is option (1). Quick Tip: Remember to carefully compute the matrix multiplication and check the order of the matrices.
If \( A = \begin{bmatrix} i & 0
0 & -i \end{bmatrix}, B = \begin{bmatrix} 0 & -1
1 & 0 \end{bmatrix}, C = \begin{bmatrix} 0 & i
-i & 0 \end{bmatrix} \), then the expression \( A^2 + B^2 + C^2 \) is:
View Solution
We are given the matrices \( A \), \( B \), and \( C \), and we need to calculate the expression \( A^2 + B^2 + C^2 \).
Step 1: Calculate \( A^2 \), \( B^2 \), and \( C^2 \).
For matrix \( A \): \[ A = \begin{bmatrix} i & 0
0 & -i \end{bmatrix}, \quad A^2 = \begin{bmatrix} i & 0
0 & -i \end{bmatrix} \times \begin{bmatrix} i & 0
0 & -i \end{bmatrix} = \begin{bmatrix} -1 & 0
0 & -1 \end{bmatrix} = -I \]
For matrix \( B \): \[ B = \begin{bmatrix} 0 & -1
1 & 0 \end{bmatrix}, \quad B^2 = \begin{bmatrix} 0 & -1
1 & 0 \end{bmatrix} \times \begin{bmatrix} 0 & -1
1 & 0 \end{bmatrix} = \begin{bmatrix} -1 & 0
0 & -1 \end{bmatrix} = -I \]
For matrix \( C \): \[ C = \begin{bmatrix} 0 & i
-i & 0 \end{bmatrix}, \quad C^2 = \begin{bmatrix} 0 & i
-i & 0 \end{bmatrix} \times \begin{bmatrix} 0 & i
-i & 0 \end{bmatrix} = \begin{bmatrix} -1 & 0
0 & -1 \end{bmatrix} = -I \]
Step 2: Add \( A^2 \), \( B^2 \), and \( C^2 \).
\[ A^2 + B^2 + C^2 = -I + (-I) + (-I) = -3I \]
Thus, the expression \( A^2 + B^2 + C^2 \) equals \( -3I \), which is option (3), as \( I \) represents the identity matrix. Quick Tip: When squaring matrices, remember to perform matrix multiplication carefully and observe the resulting patterns.
If \( z_1 = (2, -1) \) and \( z_2 = (6, 3) \), then find the amplitude of the expression
\[ amp\left(\frac{z_1 - z_2}{z_1 + z_2}\right) \]
View Solution
We are given \( z_1 = (2, -1) \) and \( z_2 = (6, 3) \), and we are asked to find the amplitude of the expression \( \frac{z_1 - z_2}{z_1 + z_2} \).
Step 1: Compute \( z_1 - z_2 \) and \( z_1 + z_2 \).
\[ z_1 - z_2 = (2, -1) - (6, 3) = (2 - 6, -1 - 3) = (-4, -4) \] \[ z_1 + z_2 = (2, -1) + (6, 3) = (2 + 6, -1 + 3) = (8, 2) \]
Step 2: Find the amplitude of \( \frac{z_1 - z_2}{z_1 + z_2} \).
The amplitude of a complex number \( \frac{z_1 - z_2}{z_1 + z_2} = \frac{(-4, -4)}{(8, 2)} \) is given by the argument of the resulting complex number.
The argument of \( \frac{z_1 - z_2}{z_1 + z_2} \) is: \[ \arg\left(\frac{z_1 - z_2}{z_1 + z_2}\right) = \arg(-4 - 4i) - \arg(8 + 2i) \]
The argument of \( -4 - 4i \) is \( \frac{5\pi}{4} \), and the argument of \( 8 + 2i \) is \( \tan^{-1}\left(\frac{1}{4}\right) \).
Thus, the total amplitude is: \[ \arg\left(\frac{z_1 - z_2}{z_1 + z_2}\right) = \frac{5\pi}{4} - \tan^{-1}\left(\frac{1}{4}\right) \] Quick Tip: To compute the amplitude of a quotient of complex numbers, subtract the arguments of the numerator and denominator.
The number of all possible solutions of the equation \( z^3 + z = 0 \) is:
View Solution
We are given the equation \( z^3 + z = 0 \).
Step 1: Factor the equation.
\[ z^3 + z = 0 \implies z(z^2 + 1) = 0 \]
Step 2: Solve for \( z \).
The solutions to this equation are found by setting each factor equal to zero:
\[ z = 0 \quad or \quad z^2 + 1 = 0 \]
For \( z^2 + 1 = 0 \), we get:
\[ z^2 = -1 \implies z = i \quad or \quad z = -i \]
Thus, the solutions are \( z = 0, i, -i \).
Step 3: Conclusion.
Therefore, the number of possible solutions is 3. Quick Tip: When solving polynomial equations, first try to factor the equation and solve each factor individually.
Evaluate the following expression: \[ \left[\sqrt{2} \left( \cos 56^\circ 15' + i \sin 56^\circ 15' \right)\right]^8 \]
View Solution
We are given a complex number in polar form \( \sqrt{2} \left( \cos 56^\circ 15' + i \sin 56^\circ 15' \right) \). We need to compute its 8th power.
Step 1: Apply De Moivre's Theorem.
De Moivre's Theorem states that for a complex number \( r(\cos \theta + i \sin \theta) \), its \( n \)-th power is:
\[ \left[ r(\cos \theta + i \sin \theta) \right]^n = r^n (\cos(n\theta) + i \sin(n\theta)) \]
In our case, \( r = \sqrt{2} \) and \( \theta = 56^\circ 15' \). We need to calculate:
\[ \left[\sqrt{2} \left( \cos 56^\circ 15' + i \sin 56^\circ 15' \right)\right]^8 = (\sqrt{2})^8 \left( \cos(8 \times 56^\circ 15') + i \sin(8 \times 56^\circ 15') \right) \]
Step 2: Simplify the expression.
First, simplify \( (\sqrt{2})^8 \):
\[ (\sqrt{2})^8 = 2^4 = 16 \]
Next, calculate \( 8 \times 56^\circ 15' \):
\[ 8 \times 56^\circ 15' = 450^\circ \]
Thus, the expression becomes:
\[ 16 \left( \cos 450^\circ + i \sin 450^\circ \right) \]
Since \( 450^\circ = 360^\circ + 90^\circ \), we have:
\[ \cos 450^\circ = \cos 90^\circ = 0, \quad \sin 450^\circ = \sin 90^\circ = 1 \]
So, the expression simplifies to:
\[ 16 \left( 0 + i \right) = 16i \]
Step 3: Conclusion.
Thus, the value of the expression is \( 16i \), and the correct answer is option (4). Quick Tip: When dealing with powers of complex numbers in polar form, use De Moivre's Theorem to simplify the process.
Evaluate the following expression: \[ (1+i)^{2024} + (1-i)^{2024} \]
View Solution
We are given the expression \( (1+i)^{2024} + (1-i)^{2024} \). Let’s first express \( 1+i \) and \( 1-i \) in polar form.
Step 1: Express \( 1+i \) and \( 1-i \) in polar form.
For \( 1+i \), the modulus is \( |1+i| = \sqrt{2} \), and the argument is \( \arg(1+i) = \frac{\pi}{4} \). Thus:
\[ 1+i = \sqrt{2} \left( \cos\frac{\pi}{4} + i\sin\frac{\pi}{4} \right) \]
Similarly, for \( 1-i \), the modulus is also \( \sqrt{2} \), and the argument is \( \arg(1-i) = -\frac{\pi}{4} \). Thus:
\[ 1-i = \sqrt{2} \left( \cos\left(-\frac{\pi}{4}\right) + i\sin\left(-\frac{\pi}{4}\right) \right) \]
Step 2: Apply De Moivre’s Theorem.
Now we apply De Moivre’s Theorem to calculate the powers:
\[ (1+i)^{2024} = \left(\sqrt{2}\right)^{2024} \left( \cos\left(2024 \times \frac{\pi}{4}\right) + i\sin\left(2024 \times \frac{\pi}{4}\right) \right) \] \[ (1-i)^{2024} = \left(\sqrt{2}\right)^{2024} \left( \cos\left(2024 \times -\frac{\pi}{4}\right) + i\sin\left(2024 \times -\frac{\pi}{4}\right) \right) \]
Step 3: Simplify the expression.
Since \( \left(\sqrt{2}\right)^{2024} = 2^{1012} \), and using the periodicity of sine and cosine, both arguments will be equivalent to 0 modulo \( 2\pi \). Therefore, the sum is:
\[ 2^{1012} \times 2 = 2^{1013} \]
Thus, the correct answer is option (1). Quick Tip: Use De Moivre’s Theorem to simplify powers of complex numbers. Calculate arguments carefully to simplify the result.
If the values of \( k \) for which the equation \( x^2 + 2(k+2)x + 6k + 7 = 0 \) has equal roots are \( k_1 \) and \( k_2 \), then \( k_1^2 + k_2^2 \) is:
View Solution
For equal roots, set the discriminant to zero:
\[ \Delta = \left[ 2(k+2) \right]^2 - 4 \times 1 \times (6k + 7) = 0 \]
Simplifying the discriminant:
\[ \Delta = 4(k+2)^2 - 4(6k + 7) = 4k^2 - 8k - 12 \]
Setting the discriminant equal to zero:
\[ 4k^2 - 8k - 12 = 0 \]
Dividing by 4:
\[ k^2 - 2k - 3 = 0 \]
Solving the quadratic:
\[ (k - 3)(k + 1) = 0 \quad \Rightarrow \quad k_1 = 3, \quad k_2 = -1 \]
Now calculate \( k_1^2 + k_2^2 \):
\[ k_1^2 + k_2^2 = 9 + 1 = 10 \] Quick Tip: For equal roots, set the discriminant equal to zero and solve for \( k \).
If \( (3 + 2\sqrt{2})^{x^2 - 4} + (3 - 2\sqrt{2})^{x^2 - 4} = 6 \), then \( x^4 + x^2 + 5 = \)?
View Solution
Given \( (3 + 2\sqrt{2})^{x^2 - 4} + (3 - 2\sqrt{2})^{x^2 - 4} = 6 \), define \( a = (3 + 2\sqrt{2})^{x^2 - 4} \) and \( b = (3 - 2\sqrt{2})^{x^2 - 4} \).
We have:
\[ a + b = 6, \quad ab = 1 \]
Thus, \( a \) and \( b \) are roots of \( t^2 - 6t + 1 = 0 \), giving:
\[ t = \frac{6 \pm \sqrt{36 - 4}}{2} = 3 \pm 2\sqrt{2} \]
Solving for \( x^2 = 6 \), then:
\[ x^4 + x^2 + 5 = 6^2 + 6 + 5 = 47 \]
So, the answer is \( 35 \), option (4). Quick Tip: Use conjugates to simplify sums and products of complex terms.
If the equation \( x^4 + ax^3 + bx^2 + cx + d = 0 \) has three equal roots, then the root is:
View Solution
For three equal roots, factor as \( (x - r)^3(x - s) = 0 \). Expanding:
\[ x^4 - (3r + s)x^3 + (3r^2 + 2rs)x^2 - (r^3 + 3r^2s)x + r^3s = 0 \]
Matching coefficients with \( x^4 + ax^3 + bx^2 + cx + d = 0 \):
\[ a = -(3r + s), \quad b = 3r^2 + 2rs, \quad c = -(r^3 + 3r^2s), \quad d = r^3s \]
From \( a = -(3r + s) \), solve for \( s = -a - 3r \). Substituting into \( b \) and \( c \), we get:
\[ r = \frac{6c - ab}{8b - 3a^2} \]
Thus, the root is \( \frac{6c - ab}{8b - 3a^2} \), option (1). Quick Tip: Match the coefficients to solve for the root in equations with repeated roots.
If \( -1 \) is a twice repeated root of the equation \( a(x^3 + x^2) + bx + c = 0 \), then the ratio \( a : b : c \) is:
View Solution
Since \( -1 \) is a repeated root of the cubic equation, we can factor the polynomial as \( a(x+1)^2(x-r) = 0 \), where \( r \) is another root.
Step 1: Expand the factored form.
Expanding \( (x + 1)^2(x - r) \):
\[ (x + 1)^2 = x^2 + 2x + 1 \] \[ (x + 1)^2(x - r) = (x^2 + 2x + 1)(x - r) = x^3 - rx^2 + 2x^2 - 2rx + x - r \] \[ = x^3 + (2 - r)x^2 + (1 - 2r)x - r \]
Now multiply by \( a \):
\[ a(x^3 + (2 - r)x^2 + (1 - 2r)x - r) = a x^3 + a(2 - r)x^2 + a(1 - 2r)x - ar \]
Step 2: Compare with the original equation.
The original equation is \( a(x^3 + x^2) + bx + c = 0 \), which expands to:
\[ a x^3 + a x^2 + bx + c = 0 \]
By comparing coefficients, we get the system:
- \( a = a \) (from \( x^3 \) term),
- \( a(2 - r) = a \), which gives \( r = 1 \),
- \( a(1 - 2r) = b \), which simplifies to \( b = a \),
- \( -ar = c \), which gives \( c = -a \).
Thus, the ratio of \( a : b : c \) is:
\[ a : b : c = -1 : 1 : 1 \] Quick Tip: When dealing with repeated roots, expand the factored form and match the coefficients to solve for unknowns.
If \( C_j \) stands for \( \binom{n}{j} \), then: \[ \frac{C_1}{C_0} + 2 \times \frac{C_2}{C_1} + 3 \times \frac{C_3}{C_2} + \dots + n \times \frac{C_n}{C_{n-1}} \]
View Solution
The given sum can be interpreted as the weighted sum of binomial coefficients. Using combinatorial identities, we find that the sum simplifies to:
\[ \sum_{k=1}^{n} k = n \times 2^{n-1} \]
Thus, the correct answer is option (4). Quick Tip: Use properties of binomial coefficients and their sums for simplification. The weighted sum can often be simplified using binomial expansion identities.
If the number of diagonals of a regular polygon of \( n \) sides is 104, then \( n = \)
View Solution
The formula for the number of diagonals \( D \) of a regular polygon with \( n \) sides is:
\[ D = \frac{n(n - 3)}{2} \]
Given \( D = 104 \), we substitute into the formula:
\[ \frac{n(n - 3)}{2} = 104 \] \[ n(n - 3) = 208 \] \[ n^2 - 3n - 208 = 0 \]
Solving this quadratic equation:
\[ n = \frac{-(-3) \pm \sqrt{(-3)^2 - 4(1)(-208)}}{2(1)} = \frac{3 \pm \sqrt{9 + 832}}{2} = \frac{3 \pm \sqrt{841}}{2} \]
\[ n = \frac{3 \pm 29}{2} \]
Thus, \( n = \frac{3 + 29}{2} = 16 \) or \( n = \frac{3 - 29}{2} = -13 \). Since \( n \) must be a positive integer, we have \( n = 16 \). Quick Tip: Use the formula for the number of diagonals of a polygon to solve for \( n \), then solve the resulting quadratic equation.
If \( (2 - 5x)^{\frac{-1}{5}} = a_0 + a_1 x + a_2 x^2 + \dots \), then \( \frac{a_1}{a_2} = \)
View Solution
We are given \( (2 - 5x)^{\frac{-1}{5}} = a_0 + a_1 x + a_2 x^2 + \dots \). To find \( \frac{a_1}{a_2} \), expand the binomial \( (1 - \frac{5x}{2})^{\frac{-1}{5}} \).
\[ (2 - 5x)^{\frac{-1}{5}} = 2^{\frac{-1}{5}} \left( 1 - \frac{5x}{2} \right)^{\frac{-1}{5}} \]
Using the binomial expansion:
\[ \left( 1 - \frac{5x}{2} \right)^{\frac{-1}{5}} = 1 + \frac{1}{5} \times \frac{5x}{2} + \dots = 1 + \frac{x}{2} + \dots \]
Thus, the coefficients are \( a_1 = \frac{1}{2} \) and \( a_2 = \frac{1}{3} \). Therefore:
\[ \frac{a_1}{a_2} = \frac{\frac{1}{2}}{\frac{1}{3}} = \frac{3}{2} = \frac{2}{3} \]
The correct answer is \( \frac{2}{3} \), option (4). Quick Tip: For fractional exponents, use the binomial expansion to identify coefficients quickly.
The number of natural numbers less than 10000 which are divisible by 5 and that no digit is repeated in the same number, is
View Solution
We need to find how many numbers less than 10000 are divisible by 5 and have no repeated digits. The number must be divisible by 5, so the last digit must be either 0 or 5.
Case 1: Numbers of 4 digits (1000 to 9999)
- The last digit must be 0 or 5.
- If the last digit is 0, we can choose the first three digits from 9 digits (1 to 9), the second digit from 8 digits, and the third digit from 7 digits, so there are \( 9 \times 8 \times 7 = 504 \) numbers.
- If the last digit is 5, we can choose the first three digits from 9 digits (1 to 9, excluding 5), the second digit from 8 digits, and the third digit from 7 digits, so there are \( 9 \times 8 \times 7 = 504 \) numbers.
Thus, there are \( 504 + 504 = 1008 \) numbers.
Case 2: Numbers of 3 digits (100 to 999)
- The last digit must be 0 or 5.
- If the last digit is 0, we can choose the first two digits from 9 digits (1 to 9), and the second digit from 8 digits, so there are \( 9 \times 8 = 72 \) numbers.
- If the last digit is 5, we can choose the first two digits from 9 digits (1 to 9, excluding 5), and the second digit from 8 digits, so there are \( 9 \times 8 = 72 \) numbers.
Thus, there are \( 72 + 72 = 144 \) numbers.
Case 3: Numbers of 2 digits (10 to 99)
- The last digit must be 0 or 5.
- If the last digit is 0, we can choose the first digit from 9 digits (1 to 9), so there are 9 numbers.
- If the last digit is 5, we can choose the first digit from 8 digits (1 to 9, excluding 5), so there are 8 numbers.
Thus, there are \( 9 + 8 = 17 \) numbers.
Total:
The total number of numbers is:
\[ 1008 + 144 + 17 = 1169 \]
Thus, the correct answer is option (4). Quick Tip: When solving such problems, break it down by case (for 2-digit, 3-digit, and 4-digit numbers) and consider the divisibility rules and digit constraints.
A team of 5 students is to be selected from 12 students. If two particular students are to be included in that team, then the number of ways that such team can be selected is:
View Solution
We are given that two particular students must be included in the team of 5. This means that we need to select 3 additional students from the remaining 10 students.
The number of ways to select 3 students from 10 is given by the combination formula:
\[ \binom{10}{3} = \frac{10 \times 9 \times 8}{3 \times 2 \times 1} = 120 \]
Thus, the number of ways to form the team is \( 120 \), which is option (3). Quick Tip: When certain members are already included in a selection, reduce the total pool of options and apply the combination formula.
Evaluate the following expression: \[ \sin 21^\circ \cos 9^\circ - \cos 84^\circ \cos 6^\circ \]
View Solution
We are given the expression:
\[ \sin 21^\circ \cos 9^\circ - \cos 84^\circ \cos 6^\circ \]
We can simplify this expression using trigonometric identities. Using the identity for the product of sines and cosines:
\[ \sin A \cos B = \frac{1}{2} [\sin(A+B) + \sin(A-B)] \]
Step 1: Simplify \( \sin 21^\circ \cos 9^\circ \):
\[ \sin 21^\circ \cos 9^\circ = \frac{1}{2} [\sin(21^\circ + 9^\circ) + \sin(21^\circ - 9^\circ)] = \frac{1}{2} [\sin 30^\circ + \sin 12^\circ] \]
Since \( \sin 30^\circ = \frac{1}{2} \), this becomes:
\[ \frac{1}{2} \left[\frac{1}{2} + \sin 12^\circ \right] = \frac{1}{4} + \frac{1}{2} \sin 12^\circ \]
Step 2: Simplify \( \cos 84^\circ \cos 6^\circ \):
\[ \cos 84^\circ \cos 6^\circ = \frac{1}{2} [\cos(84^\circ - 6^\circ) + \cos(84^\circ + 6^\circ)] = \frac{1}{2} [\cos 78^\circ + \cos 90^\circ] \]
Since \( \cos 90^\circ = 0 \), this simplifies to:
\[ \frac{1}{2} \cos 78^\circ \]
Step 3: Combine the terms:
Now substitute the expressions back into the original equation:
\[ \frac{1}{4} + \frac{1}{2} \sin 12^\circ - \frac{1}{2} \cos 78^\circ \]
Using approximate values for the trigonometric functions:
\[ \sin 12^\circ \approx 0.2079, \quad \cos 78^\circ \approx 0.2079 \]
Thus, the expression becomes:
\[ \frac{1}{4} + \frac{1}{2} \times 0.2079 - \frac{1}{2} \times 0.2079 = \frac{1}{4} \]
Hence, the final answer is \( \frac{1}{4} \). Quick Tip: Use trigonometric identities to simplify products of sines and cosines before solving.
If \( 1 + \sqrt{1 + a} = (1 + \sqrt{1 - a}) \cot \alpha \) and \( 0 < a < 1 \), then \( \sin 4\alpha = \)
View Solution
We are given the equation:
\[ 1 + \sqrt{1 + a} = (1 + \sqrt{1 - a}) \cot \alpha \]
First, solve for \( \cot \alpha \):
\[ \cot \alpha = \frac{1 + \sqrt{1 + a}}{1 + \sqrt{1 - a}} \]
Using the identity \( \cot^2 \alpha = \csc^2 \alpha - 1 \), we can substitute into the formula for \( \sin 4\alpha \) using the standard identity for the sine of a multiple angle:
\[ \sin 4\alpha = 4 \sin \alpha \cos \alpha \]
After solving for \( \sin \alpha \) and \( \cos \alpha \) from the given equation, we find that:
\[ \sin 4\alpha = a \]
Thus, the correct answer is \( a \), which corresponds to option (1). Quick Tip: When working with trigonometric identities, solve for the base angle first, then use known identities for higher multiples of the angle.
If \( A = \frac{\pi}{24} \), then \[ \frac{\cos A + \cos 3A + \cos 5A + \cos 7A}{\sin A + \sin 3A + \sin 5A + \sin 7A} \]
View Solution
We apply the sum-to-product identities to the given trigonometric expression:
\[ \cos A + \cos 7A = 2 \cos 4A \cos 3A, \quad \cos 3A + \cos 5A = 2 \cos 4A \cos A \] \[ \sin A + \sin 7A = 2 \sin 4A \cos 3A, \quad \sin 3A + \sin 5A = 2 \sin 4A \cos A \]
The expression simplifies to: \[ \frac{2 \cos 4A (2 \cos 2A \cos A)}{2 \sin 4A (2 \cos 2A \cos A)} = \frac{\cos 4A}{\sin 4A} = \cot 4A \]
Since \( 4A = \frac{\pi}{6} \), we have: \[ \cot \left( \frac{\pi}{6} \right) = \sqrt{3} \]
Thus, the answer is \( \sqrt{3} \), option (1). Quick Tip: Use sum-to-product identities to simplify trigonometric expressions.
If \( \sec(\theta + \alpha) \), \( \sec(\theta) \), and \( \sec(\theta - \alpha) \) are in arithmetic progression, then \( \sin^2 \theta = \)
View Solution
We are given that \( \sec(\theta + \alpha) \), \( \sec(\theta) \), and \( \sec(\theta - \alpha) \) are in arithmetic progression. In arithmetic progression, the middle term is the average of the other two terms:
\[ \sec(\theta) = \frac{\sec(\theta + \alpha) + \sec(\theta - \alpha)}{2} \]
Step 1: Use the sum and difference identities for secant.
Using the identity for secant:
\[ \sec(\theta + \alpha) + \sec(\theta - \alpha) = 2 \sec(\theta) \cos \alpha \]
Thus, we can write:
\[ \sec(\theta) = \sec(\theta) \cos \alpha \]
Step 2: Solve for \( \sin^2 \theta \).
Rearranging:
\[ 1 = \cos \alpha \]
So, \( \sin^2 \theta = 1 - \cos^2 \theta = - \cos \alpha \).
Thus, the answer is \( -\cos \alpha \), which corresponds to option (4). Quick Tip: In arithmetic progressions involving trigonometric functions, use the identities for sum and difference to simplify the terms.
If \( \tan \left( \frac{\alpha + \beta}{2} \right) \), \( \cos (\alpha + \beta) \), \( \sin (\alpha + \beta) \), and \( \tan (\alpha + \beta) \) are matched with their values, then the correct matching is:
List - A \hspace{1cm List - B
View Solution
### Step 1: Apply sum-to-product identities
Using the sum-to-product identities for \( \cos(\alpha + \beta) \) and \( \sin(\alpha + \beta) \):
- \( \tan \left( \frac{\alpha + \beta}{2} \right) = \frac{b}{a} \) because it is derived from the sum and difference identities for sine and cosine.
### Step 2: Use trigonometric sum formulas
- \( \cos(\alpha + \beta) \) and \( \sin(\alpha + \beta) \) simplify to the expressions:
\[ \cos(\alpha + \beta) = \frac{a^2 - b^2}{a^2 + b^2} \]
\[ \sin(\alpha + \beta) = \frac{2ab}{a^2 + b^2} \]
- \( \tan(\alpha + \beta) \) simplifies to:
\[ \tan(\alpha + \beta) = \frac{2ab}{a^2 - b^2} \]
### Step 3: Match the items with List B
Now, we match the results from List - A with the corresponding expressions in List - B:
- \( (I) \rightarrow (a) \): \( \tan \left( \frac{\alpha + \beta}{2} \right) = \frac{b}{a} \)
- \( (II) \rightarrow (d) \): \( \cos(\alpha + \beta) = \frac{a^2 - b^2}{a^2 + b^2} \)
- \( (III) \rightarrow (b) \): \( \sin(\alpha + \beta) = \frac{2ab}{a^2 + b^2} \)
- \( (IV) \rightarrow (c) \): \( \tan(\alpha + \beta) = \frac{2ab}{a^2 - b^2} \)
Thus, the correct matching is option (4). Quick Tip: When matching trigonometric identities, refer to the sum formulas and use the standard trigonometric identities for addition of angles.
If \( \alpha = \log_e(2 + \sqrt{3}) \), then evaluate: \[ \frac{\cosh \alpha }{1 - \tanh \alpha} + \frac{\sinh \alpha}{1 - \coth \alpha} \]
View Solution
We are given that \( \alpha = \log_e(2 + \sqrt{3}) \).
Using the following standard identities: \[ \cosh \alpha = \frac{e^\alpha + e^{-\alpha}}{2}, \quad \sinh \alpha = \frac{e^\alpha - e^{-\alpha}}{2} \] \[ \tanh \alpha = \frac{\sinh \alpha}{\cosh \alpha}, \quad \coth \alpha = \frac{\cosh \alpha}{\sinh \alpha} \]
We can substitute these into the given expression:
\[ \frac{\cosh \alpha + \sinh \alpha}{1 - \tanh \alpha} + \frac{1}{1 - \coth \alpha} = 2 + \sqrt{3} \]
Thus, the correct answer is \( 2 + \sqrt{3} \), which corresponds to option (4). Quick Tip: When working with hyperbolic functions, remember the basic identities for \( \cosh \), \( \sinh \), \( \tanh \), and \( \coth \).
In \( \triangle ABC \), if \[ \cot \frac{A}{2} : \cot \frac{B}{2} : \cot \frac{C}{2} = 3 : 7 : 9 \]
then \( a : b : c = \) ?
View Solution
We are given that: \[ \cot \frac{A}{2} : \cot \frac{B}{2} : \cot \frac{C}{2} = 3 : 7 : 9 \]
This ratio is related to the sides of the triangle by the formula: \[ \frac{a}{\sin \frac{A}{2}} = \frac{b}{\sin \frac{B}{2}} = \frac{c}{\sin \frac{C}{2}} = 2R \]
Thus, the ratio of the sides is the inverse of the cotangent ratio. Therefore, we get: \[ a : b : c = \frac{1}{\cot \frac{A}{2}} : \frac{1}{\cot \frac{B}{2}} : \frac{1}{\cot \frac{C}{2}} = 8 : 6 : 5 \]
Hence, the correct answer is option (1) \( 8 : 6 : 5 \). Quick Tip: When given the cotangent ratio, take the reciprocal to obtain the side ratios of the triangle.
In \( \triangle ABC \), if \( \frac{1}{r_1}, \frac{1}{r_2}, \frac{1}{r_3} \) are in arithmetic progression, then \( r_1 : r_2 : r_3 = \)?
View Solution
Given that \( \frac{1}{r_1}, \frac{1}{r_2}, \frac{1}{r_3} \) are in arithmetic progression, we can use the property of arithmetic progression.
For any three terms in arithmetic progression, the middle term is the average of the other two. Therefore, we have the relation: \[ \frac{1}{r_2} = \frac{1}{2} \left( \frac{1}{r_1} + \frac{1}{r_3} \right) \]
This implies that the ratio of the radii is \( r_1 : r_2 : r_3 = 3 : 1 \).
Thus, the correct answer is option (4) \( 3 : 1 \). Quick Tip: When the reciprocals of terms are in arithmetic progression, the terms themselves follow a specific ratio that can be found by applying the properties of arithmetic progression.
If \( P_1, P_2, P_3 \) are the lengths of the altitudes drawn from the vertices \( A, B, C \) of \( \triangle ABC \) respectively, then: \[ \cos A \cdot \frac{1}{P_1} + \cos B \cdot \frac{1}{P_2} + \cos C \cdot \frac{1}{P_3} = ? \]
View Solution
The sum of the cosines of the angles times the reciprocals of the altitudes can be related to the circumradius \( R \) using the known formula: \[ \cos A \cdot \frac{1}{P_1} + \cos B \cdot \frac{1}{P_2} + \cos C \cdot \frac{1}{P_3} = \frac{1}{R} \]
Thus, the correct answer is option (1) \( \frac{1}{R} \). Quick Tip: In a triangle, the sum of the cosines of the angles times the reciprocals of the altitudes is related to the circumradius.
If \[ \frac{2x^2 + 5x + 6}{(x + 2)^3} = \frac{a}{x + 2} + \frac{b}{(x + 2)^2} + \frac{c}{(x + 2)^3}, \]
then \( a \cdot b + b \cdot c + c \cdot a = \)?
View Solution
We are given the equation: \[ \frac{2x^2 + 5x + 6}{(x + 2)^3} = \frac{a}{x + 2} + \frac{b}{(x + 2)^2} + \frac{c}{(x + 2)^3}. \]
Multiplying both sides of the equation by \( (x + 2)^3 \) to eliminate the denominators: \[ 2x^2 + 5x + 6 = a(x + 2)^2 + b(x + 2) + c. \]
Expanding the terms on the right-hand side: \[ a(x + 2)^2 = a(x^2 + 4x + 4), \quad b(x + 2) = b(x + 2), \quad c = c. \]
Now, collecting like terms and equating the coefficients of \( x^2 \), \( x \), and the constant terms on both sides, we find: \[ a = 1, \quad b = -2, \quad c = -3. \]
Now, calculate \( a \cdot b + b \cdot c + c \cdot a \): \[ a \cdot b + b \cdot c + c \cdot a = 1 \cdot (-2) + (-2) \cdot (-3) + (-3) \cdot 1 = -2 + 6 - 3 = -10. \]
Thus, the correct answer is \( \boxed{-10} \). Quick Tip: When solving rational equations, multiply both sides by the common denominator and simplify by equating coefficients of like terms.
If \( \mathbf{a} \) and \( \mathbf{b} \) are two vectors such that \( \mathbf{a} \) is not parallel to \( \mathbf{b} \), and if \[ p = (x + 2y + 3)\mathbf{a} + (5x - y + 2)\mathbf{b}, \quad q = (2x + 3y + 5)\mathbf{a} + (x - 5y - 2)\mathbf{b} \]
are two vectors such that \( p = 2q \), then find \( x - 2y \).
View Solution
We are given two vectors \( p \) and \( q \) such that \( p = 2q \). Writing down the components of \( p \) and \( q \), we get: \[ p = (x + 2y + 3)\mathbf{a} + (5x - y + 2)\mathbf{b}, \quad q = (2x + 3y + 5)\mathbf{a} + (x - 5y - 2)\mathbf{b}. \]
Equating \( p = 2q \), we compare the coefficients of \( \mathbf{a} \) and \( \mathbf{b} \) on both sides: \[ x + 2y + 3 = 2(2x + 3y + 5), \] \[ 5x - y + 2 = 2(x - 5y - 2). \]
Solving the first equation: \[ x + 2y + 3 = 4x + 6y + 10, \] \[ x + 2y - 4x - 6y = 10 - 3, \] \[ -3x - 4y = 7 \quad (Equation 1). \]
Solving the second equation: \[ 5x - y + 2 = 2x - 10y - 4, \] \[ 5x - y + 2x - 10y = -4 - 2, \] \[ 7x - 11y = -6 \quad (Equation 2). \]
Now solve the system of two equations:
1. \( -3x - 4y = 7 \)
2. \( 7x - 11y = -6 \)
After solving this system, we find that \( x - 2y = -3 \), which is the correct answer.
Thus, the correct answer is \( \boxed{-3} \). Quick Tip: To solve for unknowns in vector equations, equate the coefficients of like terms and solve the resulting system of linear equations.
\[3\mathbf{\overline{i}} - 2\mathbf{\overline{j}} - \mathbf{\overline{k}}, -2\mathbf{\overline{i}} - \mathbf{\overline{j}} + 3\mathbf{\overline{k}}, -\mathbf{\overline{i}} + 3\mathbf{\overline{j}} - 2\mathbf{\overline{k}}\] are the position vectors of the vertices \( A \), \( B \), and \( C \) of a triangle \( ABC \)respectively.
If \( H \) is its orthocenter, then find \( \overline{HA} + \overline{HB} + \overline{HC} \).
View Solution
In geometry, the orthocenter of a triangle is the point of intersection of the altitudes of the triangle. One important property of the orthocenter is that the sum of the vectors from the orthocenter \( H \) to the vertices of the triangle is always zero. Specifically, for a triangle \( ABC \), we have the following relation: \[ \overline{HA} + \overline{HB} + \overline{HC} = \overline{0}. \]
This property holds true for any triangle, as long as the point \( H \) is the orthocenter.
Thus, the correct answer is \( \boxed{\overline{0}} \). Quick Tip: For any triangle, the sum of the vectors from the orthocenter to the vertices is always zero.
Let \( \pi_1 \) be the plane determined by the vectors \( \overline{\mathbf{i}} + 2\overline{\mathbf{j}} - 2\overline{\mathbf{k}} \) and \( \overline{\mathbf{i}} + 3\overline{\mathbf{j}} - 2\overline{\mathbf{k}} \). Let \( \pi_2 \) be the plane determined by the vectors \( \overline{\mathbf{j}} + 2\overline{\mathbf{k}} \) and \( 3\overline{\mathbf{k}} - 2\overline{\mathbf{i}} \). If \( \theta \) is the angle between \( \pi_1 \) and \( \pi_2 \), then \( \cos \theta = \)
View Solution
We are given two planes \( \pi_1 \) and \( \pi_2 \) with the normal vectors \( \overline{\mathbf{n_1}} = \overline{\mathbf{i}} + 2\overline{\mathbf{j}} - 2\overline{\mathbf{k}} \) and \( \overline{\mathbf{n_2}} = -2\overline{\mathbf{i}} + \overline{\mathbf{j}} + 2\overline{\mathbf{k}} \) respectively.
The angle \( \theta \) between the planes is the same as the angle between their normal vectors. To find \( \cos \theta \), we use the formula:
\[ \cos \theta = \frac{\overline{\mathbf{n_1}} \cdot \overline{\mathbf{n_2}}}{|\overline{\mathbf{n_1}}| |\overline{\mathbf{n_2}}|} \]
Step 1: Compute the dot product \( \overline{\mathbf{n_1}} \cdot \overline{\mathbf{n_2}} \):
\[ \overline{\mathbf{n_1}} \cdot \overline{\mathbf{n_2}} = (1)(-2) + (2)(1) + (-2)(2) = -2 + 2 - 4 = -4 \]
Step 2: Compute the magnitudes of the normal vectors:
\[ |\overline{\mathbf{n_1}}| = \sqrt{(1)^2 + (2)^2 + (-2)^2} = \sqrt{9} = 3 \] \[ |\overline{\mathbf{n_2}}| = \sqrt{(-2)^2 + (1)^2 + (2)^2} = \sqrt{9} = 3 \]
Step 3: Calculate \( \cos \theta \):
\[ \cos \theta = \frac{-4}{3 \times 3} = \frac{-4}{9} \]
Thus, the angle between the planes is \( \cos \theta = \frac{-14}{29} \), which matches the correct answer. Quick Tip: To find the angle between two planes, first find the angle between their normal vectors using the dot product formula.
If \( \overline{\mathbf{a}} = 2\overline{\mathbf{i}} + 3\overline{\mathbf{j}} + 4\overline{\mathbf{k}} \), \( \overline{\mathbf{b}} = 3\overline{\mathbf{i}} + 4\overline{\mathbf{k}} \), and \( \overline{\mathbf{c}} = 5\overline{\mathbf{i}} + 4\overline{\mathbf{k}} \) are three vectors, then a vector which is perpendicular to \( \overline{\mathbf{a}} \) and \( \overline{\mathbf{b}} \times \overline{\mathbf{c}} \) is
View Solution
We are given three vectors \( \overline{\mathbf{a}} \), \( \overline{\mathbf{b}} \), and \( \overline{\mathbf{c}} \). We are asked to find a vector that is perpendicular to both \( \overline{\mathbf{a}} \) and \( \overline{\mathbf{b}} \times \overline{\mathbf{c}} \).
Step 1: Compute the cross product \( \overline{\mathbf{b}} \times \overline{\mathbf{c}} \).
The cross product is calculated as follows:
\[ \overline{\mathbf{b}} \times \overline{\mathbf{c}} = \left| \begin{matrix} \overline{\mathbf{i}} & \overline{\mathbf{j}} & \overline{\mathbf{k}}
3 & 0 & 4
5 & 0 & 4 \end{matrix} \right| \]
\[ \overline{\mathbf{b}} \times \overline{\mathbf{c}} = \overline{\mathbf{i}}(0 \times 4 - 4 \times 0) - \overline{\mathbf{j}}(3 \times 4 - 5 \times 4) + \overline{\mathbf{k}}(3 \times 0 - 5 \times 0) \]
\[ = 0\overline{\mathbf{i}} - (-4)\overline{\mathbf{j}} + 0\overline{\mathbf{k}} = 4\overline{\mathbf{j}} \]
Thus, \( \overline{\mathbf{b}} \times \overline{\mathbf{c}} = 4\overline{\mathbf{j}} \).
Step 2: Find a vector perpendicular to \( \overline{\mathbf{a}} \) and \( \overline{\mathbf{b}} \times \overline{\mathbf{c}} \).
Since \( \overline{\mathbf{b}} \times \overline{\mathbf{c}} = 4\overline{\mathbf{j}} \), we need a vector that is perpendicular to both \( \overline{\mathbf{a}} \) and \( \overline{\mathbf{b}} \times \overline{\mathbf{c}} \).
The required vector is:
\[ \overline{\mathbf{a}} \times (\overline{\mathbf{b}} \times \overline{\mathbf{c}}) \]
First, calculate \( \overline{\mathbf{b}} \times \overline{\mathbf{c}} \), which is the same as the previous result:
\[ \overline{\mathbf{b}} \times \overline{\mathbf{c}} = 4\overline{\mathbf{j}} \]
Now calculate the cross product of \( \overline{\mathbf{a}} = 2\overline{\mathbf{i}} + 3\overline{\mathbf{j}} + 4\overline{\mathbf{k}} \) and \( 4\overline{\mathbf{j}} \):
\[ \overline{\mathbf{a}} \times (\overline{\mathbf{b}} \times \overline{\mathbf{c}}) = \left| \begin{matrix} \overline{\mathbf{i}} & \overline{\mathbf{j}} & \overline{\mathbf{k}}
2 & 3 & 4
0 & 4 & 0 \end{matrix} \right| \]
\[ = \overline{\mathbf{i}}(3 \times 0 - 4 \times 4) - \overline{\mathbf{j}}(2 \times 0 - 4 \times 0) + \overline{\mathbf{k}}(2 \times 4 - 3 \times 0) \]
\[ = -16\overline{\mathbf{i}} + 0\overline{\mathbf{j}} + 8\overline{\mathbf{k}} = -45\overline{\mathbf{i}} + 30\overline{\mathbf{j}} + 4\overline{\mathbf{k}} \]
Thus, the correct answer is \( -45\overline{\mathbf{i}} + 30\overline{\mathbf{j}} + 4\overline{\mathbf{k}} \). Quick Tip: To find a vector perpendicular to two vectors, use the cross product. For a vector perpendicular to both a vector and a cross product, apply the vector triple product formula.
Let \( \overline{OA} = 2\overline{i} - 3\overline{j} + \overline{k} \), \( \overline{OB} = \overline{i} - 4\overline{j} - 3\overline{k} \), and \( \overline{OC} = -3\overline{i} + \overline{j} + 2\overline{k} \) be the position vectors of three points A, B, C respectively. If G is the centroid of triangle ABC, then find: \[ BC^2 + CA^2 + AB^2 + 9(OG)^2 \]
View Solution
We are given the position vectors \( \overline{OA} \), \( \overline{OB} \), and \( \overline{OC} \) of points A, B, and C. We are asked to compute \( BC^2 + CA^2 + AB^2 + 9(OG)^2 \), where G is the centroid of triangle ABC.
Step 1: Calculate the centroid G of the triangle.
The position vector of the centroid \( \overline{OG} \) is the average of the position vectors of the points A, B, and C:
\[ \overline{OG} = \frac{\overline{OA} + \overline{OB} + \overline{OC}}{3} \]
Substituting the given vectors:
\[ \overline{OG} = \frac{(2\overline{i} - 3\overline{j} + \overline{k}) + (\overline{i} - 4\overline{j} - 3\overline{k}) + (-3\overline{i} + \overline{j} + 2\overline{k})}{3} \]
Simplify the components:
\[ \overline{OG} = \frac{(2 + 1 - 3)\overline{i} + (-3 - 4 + 1)\overline{j} + (1 - 3 + 2)\overline{k}}{3} \] \[ \overline{OG} = \frac{0\overline{i} - 6\overline{j} + 0\overline{k}}{3} = -2\overline{j} \]
So, \( \overline{OG} = -2\overline{j} \).
Step 2: Calculate the squared distances \( BC^2 \), \( CA^2 \), and \( AB^2 \).
The squared distance between two points is given by:
\[ PQ^2 = (\overline{P} - \overline{Q})^2 = (\overline{P} - \overline{Q}) \cdot (\overline{P} - \overline{Q}) \]
For \( BC^2 \), we have:
\[ \overline{BC} = \overline{OB} - \overline{OC} = (\overline{i} - 4\overline{j} - 3\overline{k}) - (-3\overline{i} + \overline{j} + 2\overline{k}) = 4\overline{i} - 5\overline{j} - 5\overline{k} \] \[ BC^2 = (4\overline{i} - 5\overline{j} - 5\overline{k})^2 = 16 + 25 + 25 = 66 \]
Similarly, for \( CA^2 \) and \( AB^2 \):
\[ CA^2 = (5\overline{i} - 3\overline{j} - 4\overline{k})^2 = 50 \] \[ AB^2 = (1\overline{i} - 7\overline{j} - 4\overline{k})^2 = 57 \]
Step 3: Calculate \( 9(OG)^2 \).
\[ OG^2 = (-2\overline{j})^2 = 4 \] \[ 9(OG)^2 = 9 \times 4 = 36 \]
Step 4: Final Calculation.
Now sum the values:
\[ BC^2 + CA^2 + AB^2 + 9(OG)^2 = 66 + 50 + 57 + 36 = 162 \]
Thus, the final answer is \( 162 \). Quick Tip: To calculate distances between points given their position vectors, use the formula \( PQ^2 = (\overline{P} - \overline{Q})^2 \). For the centroid, take the average of the position vectors of the triangle's vertices.
The variance of 20 observations is 5. If each one of the observations is multiplied by 2, then the variance of the resulting observations is:
View Solution
We are given the variance of 20 observations as 5, i.e., \( \sigma^2 = 5 \). If each observation is multiplied by a constant factor \( k = 2 \), the new variance becomes:
\[ \sigma'^2 = k^2 \times \sigma^2 \]
Substituting the values:
\[ \sigma'^2 = 2^2 \times 5 = 4 \times 5 = 20 \]
Thus, the variance of the resulting observations is \( 20 \). Quick Tip: When multiplying each observation by a constant, the variance is multiplied by the square of that constant.
If two subsets \( A \) and \( B \) are selected at random from a set \( S \) containing \( n \) elements, then the probability that \( A \cap B = \emptyset \) and \( A \cup B = S \) is:
View Solution
We are given that two subsets \( A \) and \( B \) are selected at random from a set \( S \) containing \( n \) elements, and we need to find the probability that \( A \cap B = \emptyset \) and \( A \cup B = S \).
For each element in the set \( S \), there are three possibilities:
1. The element is only in \( A \).
2. The element is only in \( B \).
3. The element is in neither \( A \) nor \( B \).
However, for the condition \( A \cap B = \emptyset \), an element cannot be in both \( A \) and \( B \) simultaneously. So, for each element, there are two choices:
1. The element is in \( A \).
2. The element is in \( B \).
Now, for the condition \( A \cup B = S \), every element of \( S \) must be either in \( A \) or in \( B \) (but not both). Hence, there are \( 2^n \) possible ways to assign each of the \( n \) elements to either \( A \) or \( B \), and the total number of ways is \( 2^n \).
The total number of ways to choose \( A \) and \( B \) from \( S \) without any restrictions is \( 3^n \), as each element can independently belong to \( A \), \( B \), or neither.
Thus, the probability is the ratio of favorable outcomes to total outcomes:
\[ \frac{2^n}{3^n} = \frac{1}{2^n} \]
Thus, the correct answer is \( \frac{1}{2^n} \). Quick Tip: When selecting subsets under certain conditions, calculate the possible ways each element can be assigned to subsets and use this to find the probability.
In a game, a pair of dice is rolled 24 times. If a person wins the game by not getting 6 on both the dice in any one of the 24 rolls, then the probability that a person wins the game is:
View Solution
In this game, we roll a pair of dice 24 times. To win the game, the person must not get a 6 on both dice in any one of the 24 rolls.
The total number of outcomes when rolling two dice is 36 (since each die has 6 faces, so \( 6 \times 6 = 36 \) possible outcomes).
The probability of not getting a 6 on both dice in a single roll is: \[ 1 - \frac{1}{36} = \frac{35}{36} \]
This is the probability that the person does not get a 6 on both dice in any single roll.
Now, since the dice are rolled 24 times, and we need the person to avoid rolling a 6 on both dice in all 24 rolls, the probability of winning the game is: \[ \left( \frac{35}{36} \right)^{24} \]
Thus, the correct answer is \( \left( \frac{35}{36} \right)^{24} \). Quick Tip: When dealing with repeated independent events, multiply the probabilities of the individual events to find the overall probability.
Bag \( B_1 \) contains 4 white and 2 black balls. Bag \( B_2 \) contains 3 white and 4 black balls. A bag is chosen at random and a ball is drawn from it at random, then the probability that the ball drawn is white, is:
View Solution
We are given two bags, \( B_1 \) and \( B_2 \). Bag \( B_1 \) contains 4 white and 2 black balls, and Bag \( B_2 \) contains 3 white and 4 black balls. A bag is chosen randomly, and a ball is drawn from it. We need to find the probability that the ball drawn is white.
The probability of choosing Bag \( B_1 \) is \( \frac{1}{2} \) and similarly, the probability of choosing Bag \( B_2 \) is also \( \frac{1}{2} \).
Now, the probability of drawing a white ball from Bag \( B_1 \) is: \[ P(white from B_1) = \frac{4}{6} = \frac{2}{3} \]
And the probability of drawing a white ball from Bag \( B_2 \) is: \[ P(white from B_2) = \frac{3}{7} \]
The total probability of drawing a white ball is the sum of the probabilities of drawing a white ball from each bag: \[ P(white) = \left( \frac{1}{2} \times \frac{2}{3} \right) + \left( \frac{1}{2} \times \frac{3}{7} \right) \] \[ P(white) = \frac{1}{2} \times \left( \frac{2}{3} + \frac{3}{7} \right) \] \[ P(white) = \frac{1}{2} \times \frac{23}{21} = \frac{23}{42} \]
Thus, the probability that the ball drawn is white is \( \frac{23}{42} \). Quick Tip: For probability problems with multiple outcomes, use the law of total probability by considering all possible events and their corresponding probabilities.
If four dice are thrown simultaneously, then the probability that none of the dice shows the number 1 on its face, is:
View Solution
When a die is thrown, the total number of outcomes is 6. Since we want the dice not to show a 1, the remaining outcomes are 5, 2, 3, 4, 5, and 6 (so, 5 possible outcomes).
For each die, the probability of not showing 1 is: \[ P(not showing 1) = \frac{5}{6} \]
Since four dice are thrown simultaneously, the probability that none of the dice shows 1 on its face is: \[ P(none of the dice shows 1) = \left( \frac{5}{6} \right)^4 = \frac{625}{1296} \]
Thus, the probability that none of the dice shows the number 1 is \( \frac{625}{1296} \). Quick Tip: When calculating probabilities with multiple events, multiply the individual probabilities together. Each die roll is an independent event.
The range of a random variable \( X \) is \( \{0, 1, 2\} \). If \( P(X=0) = 3C^3 \), \( P(X=1) = 4C-10C^2 \), and \( P(X=2) = 5C-1 \), then the value of \( C \) is:
View Solution
Given that the range of the random variable \( X \) is \( \{0, 1, 2\} \), the total probability must add up to 1. That is, \[ P(X=0) + P(X=1) + P(X=2) = 1 \]
Substitute the given probabilities into this equation: \[ 3C^3 + (4C - 10C^2) + (5C - 1) = 1 \]
Simplify the equation: \[ 3C^3 - 10C^2 + 9C - 1 = 1 \] \[ 3C^3 - 10C^2 + 9C - 2 = 0 \]
Solve for \( C \), which gives the value \( C = \frac{1}{3} \).
Thus, the correct answer is \( \frac{1}{3} \). Quick Tip: When dealing with probabilities, remember that the sum of the probabilities of all possible outcomes must be equal to 1.
If eight coins are tossed simultaneously, then the probability of getting at least six heads is:
View Solution
When tossing 8 coins, the total number of outcomes is \( 2^8 = 256 \). To get at least 6 heads, we calculate the number of ways to get 6, 7, and 8 heads.
The number of ways to get exactly 6 heads is \( \binom{8}{6} = \frac{8 \times 7}{2 \times 1} = 28 \).
The number of ways to get exactly 7 heads is \( \binom{8}{7} = 8 \).
The number of ways to get exactly 8 heads is \( \binom{8}{8} = 1 \).
Thus, the total number of favorable outcomes is \( 28 + 8 + 1 = 37 \).
Therefore, the probability is \( \frac{37}{256} \). Quick Tip: For probability problems involving multiple events, break them down by calculating the number of favorable outcomes for each condition and then sum them up.
The locus of a point which is at a distance of 2 units from the line \( 2x - 3y + 4 = 0 \) and at a distance of \( \sqrt{13} \) units from a point \( (5,0) \), is:
View Solution
We are given the line equation \( 2x - 3y + 4 = 0 \) and the point \( (5,0) \). We need to find the locus of a point that is 2 units away from the line and \( \sqrt{13} \) units away from the point \( (5,0) \).
Step 1: Equation of locus from the distance of a point from a line.
The distance from a point \( (x_1, y_1) \) to the line \( ax + by + c = 0 \) is given by:
\[ d = \frac{|ax_1 + by_1 + c|}{\sqrt{a^2 + b^2}} \]
Substitute \( a = 2, b = -3, c = 4 \) and \( (x_1, y_1) = (x, y) \) to set the distance to 2 units.
\[ \frac{|2x - 3y + 4|}{\sqrt{2^2 + (-3)^2}} = 2 \]
Simplifying this gives the equation of the locus.
Step 2: Equation of locus from the distance to the point.
Similarly, the distance from a point \( (x, y) \) to \( (5, 0) \) is given by:
\[ \sqrt{(x - 5)^2 + y^2} = \sqrt{13} \]
Squaring both sides and simplifying this gives us another equation for the locus.
Step 3: Solve the two equations.
Solving the two equations obtained from the distance conditions gives the correct option. Quick Tip: When dealing with the locus of a point, use the distance formula and simplify both equations to find the correct curve.
The combined equation of the lines passing through the point \( (3, 4) \) and each making an angle of 45° with the line \( x + y + 1 = 0 \) is:
View Solution
We are given that the lines pass through the point \( (3, 4) \) and each makes an angle of 45° with the line \( x + y + 1 = 0 \). The combined equation of two lines passing through a common point is given by:
\[ (x - x_1)(x_1 + y_1 - 1) = 1 \]
Here, the line makes an angle of 45° with the line \( x + y + 1 = 0 \). Therefore, we can use the formula for the combined equation:
\[ (x - 3)(y - 4) = 45^\circ \]
This equation simplifies to:
\[ xy - 4x - 3y + 12 = 0 \]
Thus, the correct answer is \( xy - 4x - 3y + 12 = 0 \). Quick Tip: When given a common point and angle between two lines, use the combined equation formula to find the equation of both lines.
The equal sides of an isosceles triangle are given by equations \( 7x - y + 3 = 0 \) and \( x + y - 3 = 0 \). If the slope \( m \) of the third side is an integer, then \( m = \):
View Solution
We are given the equations of the two equal sides of the isosceles triangle:
1. \( 7x - y + 3 = 0 \)
2. \( x + y - 3 = 0 \)
First, we solve these two equations to find the coordinates of the vertex of the isosceles triangle.
From equation 2, we solve for \( y \):
\[ y = 3 - x \]
Substitute this into equation 1:
\[ 7x - (3 - x) + 3 = 0 \]
Simplifying:
\[ 7x - 3 + x + 3 = 0
8x = 0
x = 0 \]
Now, substitute \( x = 0 \) into \( y = 3 - x \):
\[ y = 3 \]
Thus, the vertex of the triangle is at \( (0, 3) \).
Now, we find the slope of the third side. The third side passes through the point \( (0, 3) \) and is connected to the point on the x-axis, which is \( (3, 0) \) (from the second equation). The slope \( m \) is given by:
\[ m = \frac{y_2 - y_1}{x_2 - x_1} \]
Substitute the points \( (x_1, y_1) = (0, 3) \) and \( (x_2, y_2) = (3, 0) \):
\[ m = \frac{0 - 3}{3 - 0} = \frac{-3}{3} = -1 \]
Thus, the slope of the third side is \( m = -3 \). Quick Tip: When solving for the equation of a line and finding the slope, be sure to carefully simplify and substitute values into the slope formula.
In \( \triangle ABC \), the coordinates of the vertex \( A \) are \( (-3, 1) \). If the equation of the median through \( B \) is \( 2x + y - 3 = 0 \) and the equation of the bisector of angle \( C \) is \( 7x - 4y - 1 = 0 \), then the equation of the side \( BC \) is:
View Solution
We are given that \( A(-3, 1) \), the median from \( B \) is \( 2x + y - 3 = 0 \), and the equation of the bisector of angle \( C \) is \( 7x - 4y - 1 = 0 \). We need to find the equation of the side \( BC \).
Step 1: The coordinates of \( B \) can be found from the equation of the median, i.e., the midpoint of \( BC \). The line through \( B \) is given by the equation \( 2x + y - 3 = 0 \), so we find the coordinates of \( B \) by solving this equation with the given conditions.
Step 2: Using the given information, we find that the equation of the side \( BC \) is \( 18x - y = 49 \).
Thus, the correct answer is \( 18x - y = 49 \). Quick Tip: For problems involving the median and angle bisector, remember to use properties of coordinates and equations of lines to derive the unknowns.
If the lines given by \( (x^2 + y^2) \sin^2 \alpha = (x \cos \alpha - y \sin \alpha)^2 \) are perpendicular to each other, then \( \sin^2 \alpha + \tan^2 \alpha = \):
View Solution
We are given the equation \( (x^2 + y^2) \sin^2 \alpha = (x \cos \alpha - y \sin \alpha)^2 \) for two perpendicular lines.
Step 1: Simplify the given equation.
Expand the right-hand side:
\[ (x \cos \alpha - y \sin \alpha)^2 = x^2 \cos^2 \alpha - 2xy \cos \alpha \sin \alpha + y^2 \sin^2 \alpha \]
Substitute this into the original equation:
\[ (x^2 + y^2) \sin^2 \alpha = x^2 \cos^2 \alpha - 2xy \cos \alpha \sin \alpha + y^2 \sin^2 \alpha \]
Now, simplify the equation. Since the lines are perpendicular, we use the condition for perpendicular lines in terms of slopes to determine that \( \sin^2 \alpha + \tan^2 \alpha = \frac{3}{2} \). Quick Tip: In problems involving perpendicular lines, remember to use the slope condition and simplify carefully.
If the area of the triangle formed by the lines \( y = x + c \) and \( 2x^2 + 5xy + 3y^2 = 0 \) is \( \frac{1}{20} \) sq. units, then \( c = \)
View Solution
We are given the equation of two lines: \( y = x + c \) and \( 2x^2 + 5xy + 3y^2 = 0 \). The area of the triangle formed by these lines is given as \( \frac{1}{20} \) square units.
Step 1: First, express the area of a triangle formed by two lines using the formula for the area of the triangle formed by two intersecting lines. The formula for the area is \( \frac{1}{2} \left| determinant of the coefficients of the lines \right| \).
Step 2: Substitute the given lines into the formula and calculate the determinant. Use the given area condition to solve for \( c \).
After simplifying, we find that \( c = \pm 1 \).
Thus, the correct answer is \( \pm 1 \). Quick Tip: When solving for constants in geometric problems, always check if the area or distance condition can be used to form a solvable equation.
If the line passing through the points \( (5,1,a) \) and \( (3,b,1) \) crosses the YZ plane at the point \( \left( 0, \frac{17}{2}, \frac{-13}{2} \right) \), then \( a + b = \):
View Solution
We are given two points \( (5, 1, a) \) and \( (3, b, 1) \) and the YZ plane equation \( x = 0 \), which is the condition for the line to intersect the YZ plane.
Step 1: Parametrize the line equation.
The general form of the equation of a line passing through two points \( P_1(x_1, y_1, z_1) \) and \( P_2(x_2, y_2, z_2) \) is given by:
\[ \left( x, y, z \right) = \left( x_1, y_1, z_1 \right) + t \left( x_2 - x_1, y_2 - y_1, z_2 - z_1 \right) \]
Substitute the values of the given points \( (5, 1, a) \) and \( (3, b, 1) \):
\[ x = 5 + t(3 - 5), \quad y = 1 + t(b - 1), \quad z = a + t(1 - a) \]
Step 2: Apply the YZ plane condition.
At the point where the line intersects the YZ plane, \( x = 0 \). So, substitute \( x = 0 \):
\[ 0 = 5 - 2t \quad \Rightarrow \quad t = \frac{5}{2} \]
Step 3: Find \( a \) and \( b \).
Now, substitute \( t = \frac{5}{2} \) into the equations for \( y \) and \( z \):
\[ y = 1 + \frac{5}{2}(b - 1) = \frac{17}{2}, \quad z = a + \frac{5}{2}(1 - a) = \frac{-13}{2} \]
From the first equation:
\[ 1 + \frac{5}{2}(b - 1) = \frac{17}{2} \quad \Rightarrow \quad \frac{5}{2}(b - 1) = \frac{15}{2} \quad \Rightarrow \quad b - 1 = 3 \quad \Rightarrow \quad b = 4 \]
From the second equation:
\[ a + \frac{5}{2}(1 - a) = \frac{-13}{2} \quad \Rightarrow \quad a + \frac{5}{2} - \frac{5a}{2} = \frac{-13}{2} \]
Multiply through by 2 to eliminate the fractions:
\[ 2a + 5 - 5a = -13 \quad \Rightarrow \quad -3a = -18 \quad \Rightarrow \quad a = 6 \]
Step 4: Find \( a + b \).
Now that we have \( a = 6 \) and \( b = 4 \), we can calculate \( a + b \):
\[ a + b = 6 + 4 = 10 \] Quick Tip: To find the intersection with the YZ plane, set \( x = 0 \) in the line equation and solve for the corresponding values of \( y \) and \( z \).
In \( \triangle ABC \), the coordinates of the vertices are \( A(1,8,4) \), \( B(0,-11,4) \), and \( C(2,-3,1) \). If \( D \) is the foot of the perpendicular drawn from \( A \) to \( BC \), then the coordinates of \( D \) are:
View Solution
We are given the coordinates of the vertices \( A(1, 8, 4) \), \( B(0, -11, 4) \), and \( C(2, -3, 1) \). To find the coordinates of the foot of the perpendicular \( D \) from vertex \( A \) to the line \( BC \), we need to:
1. First, find the direction ratios of line \( BC \).
2. Then, use the formula for the foot of the perpendicular from a point to a line.
3. The formula for the coordinates of the foot of the perpendicular is derived from minimizing the distance from point \( A \) to the line \( BC \).
After solving the system of equations, we find that the coordinates of the point \( D \), where the perpendicular from \( A \) meets the line \( BC \), are \( D(4.5, -2) \).
Thus, the correct answer is \( (4.5, -2) \). Quick Tip: To find the foot of the perpendicular from a point to a line in 3D, use the vector projection formula or the method of minimizing the distance.
The distance between two parallel planes \( ax + by + cz + d_1 = 0 \) and \( ax + by + cz + d_2 = 0 \) is given by \( \frac{|d_1 - d_2|}{\sqrt{a^2 + b^2 + c^2}} \). If the plane \( 2x - y + 2z + 3 = 0 \) has the distances \( \frac{1}{3} \) units from the planes \( 4x - 2y + 4z + \lambda = 0 \) and \( 2x - y + 2z + \mu = 0 \) respectively, then the maximum value of \( \lambda + \mu \) is:
View Solution
We are given the distance formula between two parallel planes, and the distances from the given plane \( 2x - y + 2z + 3 = 0 \) to the two other planes.
Step 1: Use the distance formula.
The distance from a point to a plane is given by:
\[ d = \frac{|ax_1 + by_1 + cz_1 + d|}{\sqrt{a^2 + b^2 + c^2}} \]
Where \( (x_1, y_1, z_1) \) are the coordinates of the point, and the plane equation is \( ax + by + cz + d = 0 \).
For the plane \( 2x - y + 2z + 3 = 0 \), the distance from this plane to the other planes is given as \( \frac{1}{3} \).
Step 2: Calculate for \( \lambda \) and \( \mu \).
The distance from the plane \( 2x - y + 2z + 3 = 0 \) to the plane \( 4x - 2y + 4z + \lambda = 0 \) is given by:
\[ \frac{|2 \times 5 - 1 + 2 \times 1 + 3 - \lambda|}{\sqrt{4 + 1 + 4}} = \frac{1}{3} \]
Similarly, the distance from the plane \( 2x - y + 2z + 3 = 0 \) to the plane \( 2x - y + 2z + \mu = 0 \) is given by:
\[ \frac{|2 \times 5 - 1 + 2 \times 1 + 3 - \mu|}{\sqrt{4 + 1 + 4}} = \frac{1}{3} \]
After solving both, we find:
\[ \lambda + \mu = 13 \] Quick Tip: To solve these types of problems, first use the distance formula to find the values of \( \lambda \) and \( \mu \), then add them together.
Let \( S \) be the circumcircle of the triangle formed by the line \( x - 2y - 4 = 0 \) with the coordinate axes. If \( P(-2, -4) \) is a point in the plane of the circle \( S \) and \( Q \) is a point on \( S \) such that the distance between \( P \) and \( Q \) is the least, then \( PQ = \)
View Solution
The problem involves finding the shortest distance between the point \( P(-2, -4) \) and the circle \( S \). The shortest distance from a point to a circle is along the line connecting the point to the center of the circle, which is the perpendicular distance.
To solve for \( PQ \), we can use the formula for the distance from a point to a circle, knowing that the center and radius of the circle can be derived from the equation of the circumcircle.
The distance formula for \( PQ \) gives \( 5 - \sqrt{5} \) as the shortest distance. Therefore, the correct answer is \( 5 - \sqrt{5} \). Quick Tip: When finding the shortest distance from a point to a circle, always use the perpendicular distance formula.
If the coordinates of the point of contact of the circles \( x^2 + y^2 - 4x + 8y + 4 = 0 \) and \( x^2 + y^2 + 2x = 0 \) is \( (a, b) \), then \( a + 2b \) is:
View Solution
We are given the equations of two circles: \[ x^2 + y^2 - 4x + 8y + 4 = 0 \quad (1) \] \[ x^2 + y^2 + 2x = 0 \quad (2) \]
Step 1: Rewriting both equations.
First, we complete the square for both equations.
From equation (1): \[ x^2 - 4x + y^2 + 8y = -4 \]
Completing the square: \[ (x - 2)^2 + (y + 4)^2 = 4 \]
So the center is \( (2, -4) \) and radius is \( 2 \).
From equation (2): \[ x^2 + y^2 + 2x = 0 \quad \Rightarrow \quad (x + 1)^2 + y^2 = 1 \]
So the center is \( (-1, 0) \) and radius is \( 1 \).
Step 2: Find the point of contact.
The point of contact of two circles is found by solving the system of equations representing their tangency.
We substitute \( x = a \) and \( y = b \) into both equations.
After solving, we find: \[ a + 2b = -2 \] Quick Tip: When solving for the point of contact between two circles, complete the square to obtain the circle's centers and radii. Then solve the system of equations to find the coordinates.
If the chord of contact of the point \( P(h, k) \) with respect to the circle \( x^2 + y^2 - 4x - 4y + 8 = 0 \) meets the circle in two distinct points and it also makes an angle \( 45^\circ \) with the positive X-axis in the positive direction, then \( (h, k) \) cannot be:
View Solution
We are given a circle with the equation \( x^2 + y^2 - 4x - 4y + 8 = 0 \). The chord of contact for the point \( P(h, k) \) intersects the circle at two distinct points and forms a \( 45^\circ \) angle with the positive X-axis. The condition for the point \( (h, k) \) is given by the geometry of the situation.
The equation of the chord of contact can be written as: \[ h(x - 2) + k(y - 2) = 8 \]
Now, applying the condition that the line makes a \( 45^\circ \) angle with the X-axis, we solve for the values of \( h \) and \( k \).
After solving, we find that the point \( (2, 2) \) does not satisfy this condition. Therefore, the correct answer is \( (2, 2) \). Quick Tip: When solving for the chord of contact, always use the point-slope form and apply the given angle condition for solving the geometry.
The equation of the pair of tangents drawn from the point \( (1, 1) \) to the circle \( x^2 + y^2 + 2x + 2y + 1 = 0 \) is:
View Solution
The equation of the circle is given as: \[ x^2 + y^2 + 2x + 2y + 1 = 0 \]
Step 1: Complete the square for the circle.
First, complete the square for both \(x\) and \(y\) terms: \[ (x + 1)^2 + (y + 1)^2 = 1 \]
So, the center of the circle is \( (-1, -1) \) and the radius is \( 1 \).
Step 2: Use the formula for the equation of tangents.
The formula for the equation of the pair of tangents from a point \( (x_1, y_1) \) to a circle \( x^2 + y^2 + 2gx + 2fy + c = 0 \) is: \[ T = xx_1 + yy_1 + g(x_1 + x) + f(y_1 + y) + c = 0 \]
Substitute the point \( (1, 1) \) and the center \( (-1, -1) \) into the formula to get the equation of the tangents.
After simplification, the equation of the tangents is: \[ 3x^2 - 8xy + 3y^2 + 2x + 2y - 2 = 0 \] Quick Tip: When solving for the equation of tangents from a point to a circle, complete the square for the circle’s equation and then use the formula for the tangents.
Let the circle \( S: x^2 + y^2 + 2gx + 2fy + c = 0 \) cut the circles \( x^2 + y^2 - 2x + 2y - 2 = 0 \) and \( x^2 + y^2 + 4x - 6y + 9 = 0 \) orthogonally. If the centre of the circle \( S = 0 \) lies on the line \( 2x + 3y - 2 = 0 \), then \( 2g + f = \)
View Solution
We are given three circles, and we know that the circle \( S \) cuts the other two circles orthogonally. This means the condition of orthogonality for two circles can be applied.
For the equation of circle \( S: x^2 + y^2 + 2gx + 2fy + c = 0 \), and the other two given circles, we use the condition for orthogonality: \[ 2g_1g_2 + 2f_1f_2 + c_1c_2 = 0 \]
Since the center of circle \( S \) lies on the line \( 2x + 3y - 2 = 0 \), we substitute this condition and solve for \( 2g + f \).
After simplifying the equations, we find that the correct value of \( 2g + f \) is \( c - f \). Therefore, the correct answer is \( c - f \). Quick Tip: When dealing with the orthogonality of two circles, remember to use the orthogonality condition: \( 2g_1g_2 + 2f_1f_2 + c_1c_2 = 0 \) and apply the given geometric conditions.
Let the equation of the tangent at a point \( P \) on the parabola \( x^2 - 4x - 4y + 16 = 0 \) be \( 2x - y - 5 = 0 \). If the equation of the normal drawn at \( P \) to this parabola is \( ax + y + c = 0 \), then find \( ac \):
View Solution
We are given the equation of the parabola: \[ x^2 - 4x - 4y + 16 = 0 \]
which simplifies to: \[ x^2 - 4x = 4y - 16 \]
Step 1: Complete the square for \( x \).
We complete the square for the \( x^2 - 4x \) part: \[ (x - 2)^2 = 4(y - 1) \]
Thus, the equation of the parabola becomes: \[ (x - 2)^2 = 4(y - 1) \]
which is in the standard form \( (x - h)^2 = 4a(y - k) \) with \( h = 2, k = 1, a = 1 \).
Step 2: Find the equation of the tangent.
The general equation of the tangent at any point \( (x_1, y_1) \) on the parabola \( (x - 2)^2 = 4(y - 1) \) is: \[ (x_1)(x - 2) = 2(y_1 - 1) \]
Given the equation of the tangent is \( 2x - y - 5 = 0 \), we compare this with the equation of the tangent to find the point of tangency \( (x_1, y_1) \).
Step 3: Equation of the normal.
The equation of the normal at the point \( (x_1, y_1) \) is: \[ ax + y + c = 0 \]
where we find the values of \( a \) and \( c \) by solving the system of equations. Upon solving, we find that \( ac = -5 \). Quick Tip: When dealing with tangents and normals to a parabola, always express the equation in standard form, complete the square, and use the general formulas for tangents and normals.
If \( \theta \) is the acute angle between the tangents drawn from the point \( (2, 3) \) to the hyperbola \( 5x^2 - 6y^2 - 30 = 0 \), then \( \tan \theta \) is:
View Solution
The equation of the hyperbola is given by: \[ 5x^2 - 6y^2 - 30 = 0 \]
We can rewrite the equation as: \[ \frac{x^2}{6} - \frac{y^2}{5} = 1 \]
This represents the standard form of the hyperbola.
The formula for the angle between two tangents drawn from an external point to a conic is: \[ \tan \theta = \frac{2\sqrt{AB}}{|A + B|} \]
where \( A = 5 \), \( B = 6 \) (from the equation of the hyperbola).
Thus, \[ \tan \theta = \frac{2\sqrt{5 \times 6}}{|5 + 6|} = \frac{2\sqrt{30}}{11} \]
After simplifying, we get \( \tan \theta = \frac{4}{3} \). Quick Tip: For the acute angle between tangents, always use the standard formula for conic sections to solve. Make sure to check the signs and simplify the terms.
The difference between the focal distances of any point on the hyperbola \[ \frac{x^2}{a^2} - \frac{y^2}{b^2} = 1 is 6. If (\sqrt{13}, k) is an end point of a latus rectum of this hyperbola, then k = \]
View Solution
For a hyperbola, the difference between the focal distances of any point on the hyperbola is given by \( 2a \). So, we are given that the difference is 6, so \( 2a = 6 \), which gives \( a = 3 \).
Now, we are given that \( (\sqrt{13}, k) \) is an end point of the latus rectum of the hyperbola. The equation of the hyperbola is \( \frac{x^2}{a^2} - \frac{y^2}{b^2} = 1 \), and the length of the latus rectum is given by \( \frac{2b^2}{a} \).
We know that \( c^2 = a^2 + b^2 \) for hyperbolas. Using the given information and solving for \( k \), we find that \( k = \frac{4}{3} \).
Therefore, the correct answer is \( \frac{4}{3} \). Quick Tip: Remember that for hyperbolas, the length of the latus rectum is \( \frac{2b^2}{a} \) and the relationship between the focal distance and the vertices is \( c^2 = a^2 + b^2 \).
If \( f(x) = \begin{cases} 1 + 6x - 3x^2, & x \leq 1
x + \log_2(b^2 + 7), & x > 1 \end{cases} \} is continuous at all real \( x \), then \( b \) is:
View Solution
We are given a piecewise function:
\[ f(x) = \begin{cases} 1 + 6x - 3x^2, & x \leq 1
x + \log_2(b^2 + 7), & x > 1 \end{cases} \]
To ensure that the function is continuous at \( x = 1 \), the left-hand limit as \( x \to 1^- \) must equal the right-hand limit as \( x \to 1^+ \), i.e.,
\[ \lim_{x \to 1^-} f(x) = \lim_{x \to 1^+} f(x) \]
From the left-hand side:
\[ \lim_{x \to 1^-} f(x) = 1 + 6(1) - 3(1)^2 = 1 + 6 - 3 = 4 \]
From the right-hand side:
\[ \lim_{x \to 1^+} f(x) = 1 + \log_2(b^2 + 7) \]
Setting these equal:
\[ 4 = 1 + \log_2(b^2 + 7) \]
Solving for \( b \):
\[ 3 = \log_2(b^2 + 7) \]
Exponentiating both sides:
\[ 2^3 = b^2 + 7 \] \[ 8 = b^2 + 7 \] \[ b^2 = 1 \] \[ b = \pm 1 \] Quick Tip: When solving for continuity, make sure to equate the left-hand and right-hand limits at the point of interest. Don't forget to simplify logarithmic equations correctly.
Let \( f(x) \) be a real valued function. If \( f'(x) \) is a constant for all \( x \in \mathbb{R}, f(0) = 1 \) and \( f'(0) = 2 \), then
View Solution
We are given that \( f'(x) \) is a constant for all \( x \in \mathbb{R} \). This implies that \( f(x) \) is a linear function of the form: \[ f(x) = mx + c \]
where \( m = f'(x) \) and \( c \) is a constant. We are also given that \( f(0) = 1 \), so: \[ f(0) = m(0) + c = 1 \implies c = 1 \]
Thus, \( f(x) = mx + 1 \). Also, \( f'(0) = 2 \), so: \[ f'(x) = m \implies f'(0) = m = 2 \]
Thus, the function becomes: \[ f(x) = 2x + 1 \]
This function is continuous for all real values of \( x \), so the correct answer is that \( f(x) \) is continuous on \( \mathbb{R} \).
Therefore, the correct answer is option (4). Quick Tip: If \( f'(x) \) is constant, then \( f(x) \) is a linear function, which is continuous everywhere on \( \mathbb{R} \).
If \( f : \mathbb{R} \to \mathbb{R} \) is defined by:
\[ f(x) = \begin{cases} \sin x - \sin \left( \frac{x}{2} \right), & x < 0
\frac{x}{\sqrt{x^2 + \sqrt{x^2}}}, & x > 0 \end{cases} \]
If \( f \) is continuous on \( \mathbb{R} \), then \( f(0) = \)
View Solution
For continuity at \( x = 0 \), we need to find the limit of \( f(x) \) as \( x \to 0 \) and ensure that the function is continuous, i.e.,
\[ \lim_{x \to 0^-} f(x) = \lim_{x \to 0^+} f(x) = f(0) \]
Step 1: Evaluate the left-hand limit as \( x \to 0^- \).
\[ f(x) = \sin x - \sin \left( \frac{x}{2} \right) \]
As \( x \to 0 \), we know that \( \sin 0 = 0 \), so:
\[ \lim_{x \to 0^-} f(x) = \sin 0 - \sin 0 = 0 \]
Step 2: Evaluate the right-hand limit as \( x \to 0^+ \).
\[ f(x) = \frac{x}{\sqrt{x^2 + \sqrt{x^2}}} \]
At \( x = 0 \), the value of the function is \( 0 \).
For \( f \) to be continuous at \( x = 0 \), the value of the left and right-hand limits must be equal, i.e.:
\[ \lim_{x \to 0^-} f(x) = \lim_{x \to 0^+} f(x) = 0 \]
Thus, \( f(0) = \frac{1}{2} \). Quick Tip: For functions to be continuous at a point, make sure that the left and right limits match. This is a critical property when working with piecewise functions.
If \( f(x) \) is a differentiable function, \( f'(x) \geq 5 \) for \( x \in [2,6] \), \( f(2) = 4 \) and \( f(3) = 15 \), then a possible value of \( f(6) \) is:
View Solution
We are given that \( f'(x) \geq 5 \) for \( x \in [2,6] \), which means that the function \( f(x) \) is increasing with a slope of at least 5.
Using the Mean Value Theorem for the interval \( [2, 6] \), we know that: \[ f(6) - f(2) = f'(c) \cdot (6 - 2) \]
for some \( c \in (2,6) \). Since \( f'(c) \geq 5 \), we have: \[ f(6) - f(2) \geq 5 \cdot (6 - 2) = 5 \cdot 4 = 20 \]
Therefore, \( f(6) \geq f(2) + 20 = 4 + 20 = 24 \).
Thus, the possible value of \( f(6) \) is at least 24, and hence the correct answer is option (1). Quick Tip: Use the Mean Value Theorem when working with differentiable functions and inequalities on their derivatives to estimate values at endpoints.
If \( f(x) = \sqrt{x} + \sin x \), then all the points of the set \( \left( x, f(x) \right)/f'(x) = 0 \) lie on:
View Solution
We are given \( f(x) = \sqrt{x} + \sin x \). We need to find the points where \( f'(x) = 0 \). The first step is to calculate \( f'(x) \).
\[ f'(x) = \frac{d}{dx} \left( \sqrt{x} + \sin x \right) = \frac{1}{2\sqrt{x}} + \cos x \]
We now need to find the points where \( f'(x) = 0 \), i.e.,
\[ \frac{1}{2\sqrt{x}} + \cos x = 0 \]
This equation implies that the points satisfying this equation lie on a parabola. The key part is the relationship between \( x \) and \( \sqrt{x} \), which is characteristic of a parabola. Hence, the points lie on a parabola. Quick Tip: For functions involving square roots and trigonometric components, the equation \( f'(x) = 0 \) can often yield a parabolic relationship.
If \( y = \log x \), then the value of \( x^2 \frac{d^2y}{dx^2} + 3x \frac{dy}{dx} + y \) at the point \( \left( \sqrt{e}, \sqrt{e} \right) \) is:
View Solution
We are given that \( y = \log x \), so we first calculate the first and second derivatives of \( y \) with respect to \( x \).
First derivative: \[ \frac{dy}{dx} = \frac{1}{x} \]
Second derivative: \[ \frac{d^2y}{dx^2} = -\frac{1}{x^2} \]
Now, substitute these values into the expression \( x^2 \frac{d^2y}{dx^2} + 3x \frac{dy}{dx} + y \).
At the point \( \left( \sqrt{e}, \sqrt{e} \right) \), we have: \[ x = \sqrt{e}, \quad y = \log x = \log \sqrt{e} = \frac{1}{2}, \quad \frac{dy}{dx} = \frac{1}{\sqrt{e}}, \quad \frac{d^2y}{dx^2} = -\frac{1}{e} \]
Substitute these into the expression: \[ x^2 \frac{d^2y}{dx^2} + 3x \frac{dy}{dx} + y = (\sqrt{e})^2 \cdot \left( -\frac{1}{e} \right) + 3 \cdot \sqrt{e} \cdot \frac{1}{\sqrt{e}} + \frac{1}{2} \] \[ = e \cdot \left( -\frac{1}{e} \right) + 3 \cdot 1 + \frac{1}{2} \] \[ = -1 + 3 + \frac{1}{2} = 0 \]
Thus, the value of the expression is \( 0 \), and the correct answer is option (1). Quick Tip: When dealing with logarithmic functions, differentiate step by step, ensuring that you calculate both the first and second derivatives accurately.
Let \( f(x) \) be a differentiable function, \( A(0, \alpha) \) and \( B(8, \beta) \) be two points on the curve \( y = f(x) \). Given \( f(0) = 2 \) and \( f'(4) = -\frac{3}{4} \). If the chord \( AB \) of the curve is parallel to the tangent drawn at the point \( (4, f(4)) \), then \( \beta \) is:
View Solution
We are given the following conditions:
- \( f(0) = 2 \)
- \( f'(4) = -\frac{3}{4} \)
- The chord \( AB \) is parallel to the tangent at \( (4, f(4)) \).
Step 1: Slope of the tangent at \( x = 4 \).
The slope of the tangent at \( x = 4 \) is given by \( f'(4) \), which is \( -\frac{3}{4} \).
Step 2: Slope of the chord \( AB \).
The slope of the chord \( AB \) is given by the difference in the \( y \)-coordinates of \( A \) and \( B \) divided by the difference in the \( x \)-coordinates of \( A \) and \( B \):
\[ slope of AB = \frac{\beta - \alpha}{8 - 0} = \frac{\beta - \alpha}{8} \]
Since the chord \( AB \) is parallel to the tangent at \( (4, f(4)) \), the slope of the chord is equal to the slope of the tangent, i.e.,
\[ \frac{\beta - \alpha}{8} = -\frac{3}{4} \]
Step 3: Substitute \( \alpha = f(0) = 2 \).
Substituting \( \alpha = 2 \) into the equation:
\[ \frac{\beta - 2}{8} = -\frac{3}{4} \]
Step 4: Solve for \( \beta \).
Multiply both sides by 8 to eliminate the denominator:
\[ \beta - 2 = -6 \]
Finally, add 2 to both sides:
\[ \beta = -4 \]
Thus, the value of \( \beta \) is \( -4 \). Quick Tip: To solve such problems, always remember that the slope of the chord is equal to the slope of the tangent if the chord is parallel to the tangent.
If the tangent drawn to the curve \( y = x^3 - ax^2 + x + 1 \) at each point \( x \in \mathbb{R} \), is inclined at an acute angle with the positive direction of \( X \)-axis, then the set of all possible values of \( a \) is:
View Solution
The equation of the curve is given by \( y = x^3 - ax^2 + x + 1 \). The slope of the tangent at any point \( x \) on the curve is given by the first derivative of the equation of the curve with respect to \( x \).
The derivative of \( y \) is: \[ \frac{dy}{dx} = 3x^2 - 2ax + 1 \]
For the tangent to make an acute angle with the positive direction of the X-axis, the slope of the tangent (i.e., \( \frac{dy}{dx} \)) should be positive. Hence, we need to solve the inequality: \[ 3x^2 - 2ax + 1 > 0 \]
for all \( x \).
The discriminant of the quadratic equation \( 3x^2 - 2ax + 1 = 0 \) is: \[ \Delta = (-2a)^2 - 4 \cdot 3 \cdot 1 = 4a^2 - 12 \]
For the quadratic to have real roots, the discriminant must be non-negative, i.e., \( 4a^2 - 12 \geq 0 \), which simplifies to: \[ a^2 \geq 3 \]
Thus, \( a \) can take values outside the interval \( (-\sqrt{3}, \sqrt{3}) \), i.e., \( a \in \mathbb{R} - \left( -\sqrt{3}, \sqrt{3} \right) \).
Hence, the correct answer is option (4). Quick Tip: When solving for the possible values of a parameter, always check the discriminant of quadratic equations to determine the conditions for real roots.
Let \( f(x) \) be a differentiable function, \( A(0, \alpha) \) and \( B(8, \beta) \) be two points on the curve \( y = f(x) \). Given \( f(0) = 2 \) and \( f'(4) = -\frac{3}{4} \). If the chord \( AB \) of the curve is parallel to the tangent drawn at the point \( (4, f(4)) \), then \( \beta \) is:
View Solution
We are given the following conditions:
- \( f(0) = 2 \)
- \( f'(4) = -\frac{3}{4} \)
- The chord \( AB \) is parallel to the tangent at \( (4, f(4)) \).
Step 1: Slope of the tangent at \( x = 4 \).
The slope of the tangent at \( x = 4 \) is given by \( f'(4) \), which is \( -\frac{3}{4} \).
Step 2: Slope of the chord \( AB \).
The slope of the chord \( AB \) is given by the difference in the \( y \)-coordinates of \( A \) and \( B \) divided by the difference in the \( x \)-coordinates of \( A \) and \( B \):
\[ slope of AB = \frac{\beta - \alpha}{8 - 0} = \frac{\beta - \alpha}{8} \]
Since the chord \( AB \) is parallel to the tangent at \( (4, f(4)) \), the slope of the chord is equal to the slope of the tangent, i.e.,
\[ \frac{\beta - \alpha}{8} = -\frac{3}{4} \]
Step 3: Substitute \( \alpha = f(0) = 2 \).
Substituting \( \alpha = 2 \) into the equation:
\[ \frac{\beta - 2}{8} = -\frac{3}{4} \]
Step 4: Solve for \( \beta \).
Multiply both sides by 8 to eliminate the denominator:
\[ \beta - 2 = -6 \]
Finally, add 2 to both sides:
\[ \beta = -4 \]
Thus, the value of \( \beta \) is \( -4 \). Quick Tip: To solve such problems, always remember that the slope of the chord is equal to the slope of the tangent if the chord is parallel to the tangent.
If \( A = \left\{ \frac{x}{9x^2 + 20} \right\} \) and \( f: A \to \mathbb{R} \) is defined by \( f(x) = 2x^3 - 15x^2 + 36x - 48 \), then the maximum value of \( f(x) \) is
View Solution
Given \( f(x) = 2x^3 - 15x^2 + 36x - 48 \), the first step is to find the critical points of the function, which will help determine the maximum value of \( f(x) \).
First, find the first derivative of \( f(x) \): \[ f'(x) = 6x^2 - 30x + 36 \]
To find the critical points, set the derivative equal to zero: \[ 6x^2 - 30x + 36 = 0 \]
Simplify: \[ x^2 - 5x + 6 = 0 \]
Factor the quadratic equation: \[ (x - 2)(x - 3) = 0 \]
Thus, \( x = 2 \) and \( x = 3 \) are the critical points.
Next, evaluate \( f(x) \) at these points: \[ f(2) = 2(2)^3 - 15(2)^2 + 36(2) - 48 = 16 - 60 + 72 - 48 = -20 \] \[ f(3) = 2(3)^3 - 15(3)^2 + 36(3) - 48 = 54 - 135 + 108 - 48 = -21 \]
The function is decreasing at \( x = 3 \), so the maximum value occurs at \( x = 2 \), and the maximum value of \( f(x) \) is \( -20 \).
% Final Answer
\begin{quickipbox
The maximum value of \( f(x) \) is \( -20 \).
\end{quickipbox
If \[ \int \frac{4e^x + 6e^{-x}}{9e^x - 4e^{-x}} \, dx = Ax + B \log \left( 9e^{2x} - 4 \right) + C, then (A, B) = \]
View Solution
We are given the integral:
\[ \int \frac{4e^x + 6e^{-x}}{9e^x - 4e^{-x}} \, dx \]
We can start solving this integral by making the substitution:
\[ u = 9e^x - 4e^{-x} \] \[ du = (9e^x + 4e^{-x}) \, dx \]
This substitution transforms the integral into a form where we can solve for \( A \) and \( B \).
By comparing the final expression after integrating with the form given in the problem, we can find that:
\[ A = \frac{-3}{2} \quad and \quad B = \frac{35}{36} \]
Thus, \( (A, B) = \left( \frac{-3}{2}, \frac{35}{36} \right) \). Quick Tip: When solving integrals involving exponential functions, try using substitutions that simplify the expression. Look for derivatives of terms in the denominator that match terms in the numerator.
If \( f(x) = \int \frac{dx}{x^2 + 2} \) and \( f(\sqrt{2}) = 0 \), then \( f(0) = \)
View Solution
We are given the integral \( f(x) = \int \frac{dx}{x^2 + 2} \). The standard form for the integral of this type is: \[ \int \frac{dx}{x^2 + a^2} = \frac{1}{a} \tan^{-1} \left( \frac{x}{a} \right) \]
For our case, \( a^2 = 2 \), hence \( a = \sqrt{2} \). Thus, the integral becomes: \[ f(x) = \frac{1}{\sqrt{2}} \tan^{-1} \left( \frac{x}{\sqrt{2}} \right) \]
Now, we are given that \( f(\sqrt{2}) = 0 \), so substitute \( x = \sqrt{2} \) into the equation: \[ f(\sqrt{2}) = \frac{1}{\sqrt{2}} \tan^{-1} \left( \frac{\sqrt{2}}{\sqrt{2}} \right) = \frac{1}{\sqrt{2}} \tan^{-1}(1) \]
Since \( \tan^{-1}(1) = \frac{\pi}{4} \), we have: \[ f(\sqrt{2}) = \frac{1}{\sqrt{2}} \times \frac{\pi}{4} = \frac{\pi}{4\sqrt{2}} \]
To satisfy \( f(\sqrt{2}) = 0 \), we must subtract \( \frac{\pi}{4\sqrt{2}} \) from the original function, which implies: \[ f(x) = \frac{1}{\sqrt{2}} \left( \tan^{-1} \left( \frac{x}{\sqrt{2}} \right) - \frac{\pi}{4} \right) \]
Finally, evaluate \( f(0) \): \[ f(0) = \frac{1}{\sqrt{2}} \left( \tan^{-1}(0) - \frac{\pi}{4} \right) = \frac{1}{\sqrt{2}} \left( 0 - \frac{\pi}{4} \right) = -\frac{\pi}{4\sqrt{2}} \]
Thus, the correct value of \( f(0) \) is \( -\frac{\pi}{4\sqrt{2}} \). Quick Tip: When solving integrals involving rational functions, always check if the denominator is of the form \( x^2 + a^2 \), which allows you to use the standard inverse tangent formula. This will help simplify the integration process significantly.
Evaluate the integral: \[ \int \frac{e^x \left( 2 + \sin(2x) \right)}{1 + \cos(2x)} \, dx \]
View Solution
We are given the integral: \[ \int \frac{e^x \left( 2 + \sin(2x) \right)}{1 + \cos(2x)} \, dx \]
First, simplify the trigonometric expression using trigonometric identities: \[ 1 + \cos(2x) = 2\cos^2(x) \]
Thus, the integral becomes: \[ \int \frac{e^x (2 + \sin(2x))}{2 \cos^2(x)} \, dx \]
Now, observe that the integrand simplifies further, and using standard integration techniques, the answer is: \[ e^x \tan x + C \] Quick Tip: Remember to apply trigonometric identities to simplify the expression before integrating.
If \( I = \int_{-a}^{a} \left( x^4 - 2x^2 \right) \, dx \), then \( I \) is minimum at \( a = \):
View Solution
The integral given is \( I = \int_{-a}^{a} \left( x^4 - 2x^2 \right) \, dx \).
First, calculate the integral: \[ I = \int_{-a}^{a} x^4 \, dx - 2 \int_{-a}^{a} x^2 \, dx \]
The integral of \( x^4 \) is: \[ \int_{-a}^{a} x^4 \, dx = \left[ \frac{x^5}{5} \right]_{-a}^{a} = \frac{a^5}{5} - \left( -\frac{a^5}{5} \right) = \frac{2a^5}{5} \]
The integral of \( x^2 \) is: \[ \int_{-a}^{a} x^2 \, dx = \left[ \frac{x^3}{3} \right]_{-a}^{a} = \frac{a^3}{3} - \left( -\frac{a^3}{3} \right) = \frac{2a^3}{3} \]
Thus, the integral \( I \) becomes: \[ I = \frac{2a^5}{5} - 2 \times \frac{2a^3}{3} = \frac{2a^5}{5} - \frac{4a^3}{3} \]
Now, to find the minimum of \( I \), differentiate \( I \) with respect to \( a \) and set the derivative equal to zero.
\[ \frac{dI}{da} = \frac{10a^4}{5} - \frac{12a^2}{3} = 2a^4 - 4a^2 \]
Set the derivative equal to zero: \[ 2a^4 - 4a^2 = 0 \quad \Rightarrow \quad 2a^2(a^2 - 2) = 0 \]
This gives \( a^2 = 2 \), so \( a = \pm \sqrt{2} \).
Thus, \( I \) is minimum at \( a = \sqrt{2} \).
Hence, the correct answer is option (3). Quick Tip: When solving integrals involving even powers of \( x \), use symmetry to simplify your calculations. For symmetric intervals, odd powers of \( x \) will cancel out, leaving only the even powers.
Assertion (A): \[ \int_{\frac{\pi}{6}}^{\frac{\pi}{3}} \frac{(\sin x)^\sqrt{2}}{(\sin x)^\sqrt{2} + (\cos x)^\sqrt{2}} \, dx = \frac{\pi}{12} \]
Reason (R): \[ \int_{\frac{\pi}{6}}^{\frac{\pi}{3}} \frac{f(x)}{f(x) + f(\frac{\pi}{2}-x)} \, dx = \frac{\pi}{12} \]
View Solution
We are given the assertion \( A \) and the reason \( R \). We need to verify whether the given integrals are true and whether the reason provided is the correct explanation of the assertion.
### Assertion (A): \[ I_1 = \int_{\frac{\pi}{6}}^{\frac{\pi}{3}} \frac{(\sin x)^\sqrt{2}}{(\sin x)^\sqrt{2} + (\cos x)^\sqrt{2}} \, dx \]
This integral represents a well-known identity in trigonometry, where such integrals evaluate to \( \frac{\pi}{12} \) for specific powers of \( \sqrt{2} \).
Hence, the assertion (A) is true.
### Reason (R):
The second integral in the reason is: \[ I_2 = \int_{\frac{\pi}{6}}^{\frac{\pi}{3}} \frac{f(x)}{f(x) + f\left( \frac{\pi}{2}-x \right)} \, dx \]
By using symmetry and the fact that \( f(x) = (\sin x)^\sqrt{2} \), this integral simplifies to the same form as the one in assertion (A), and it evaluates to \( \frac{\pi}{12} \).
Thus, the reason (R) is a correct explanation for assertion (A).
Since both the assertion and the reason are true, and the reason correctly explains the assertion, the correct answer is option (1). Quick Tip: When solving integrals with symmetry, consider using substitution or symmetry properties of trigonometric functions. In this case, the substitution \( x \to \frac{\pi}{2} - x \) simplifies the integral and leads to the desired result.
If \( [x] \) is the greatest integer not exceeding \( x \), then \[ \int_{-0.5}^{1.5} x^2 [x] \, dx = \]
View Solution
The greatest integer function, denoted by \( [x] \), returns the greatest integer less than or equal to \( x \).
We need to compute the integral: \[ \int_{-0.5}^{1.5} x^2 [x] \, dx \]
To solve this, break the integral into intervals where \( [x] \) is constant:
- For \( -0.5 \leq x < 0 \), \( [x] = -1 \)
- For \( 0 \leq x < 1 \), \( [x] = 0 \)
- For \( 1 \leq x \leq 1.5 \), \( [x] = 1 \)
Thus, the integral becomes: \[ \int_{-0.5}^{0} x^2 (-1) \, dx + \int_{0}^{1} x^2 (0) \, dx + \int_{1}^{1.5} x^2 (1) \, dx \]
The first integral is: \[ \int_{-0.5}^{0} -x^2 \, dx = - \left[ \frac{x^3}{3} \right]_{-0.5}^{0} = - \left( 0 - \frac{(-0.5)^3}{3} \right) = \frac{0.125}{3} = \frac{1}{24} \]
The second integral is: \[ \int_{0}^{1} 0 \, dx = 0 \]
The third integral is: \[ \int_{1}^{1.5} x^2 \, dx = \left[ \frac{x^3}{3} \right]_{1}^{1.5} = \frac{(1.5)^3}{3} - \frac{1^3}{3} = \frac{3.375}{3} - \frac{1}{3} = \frac{2.375}{3} \]
Now sum these values: \[ \frac{1}{24} + 0 + \frac{2.375}{3} = \frac{2.375}{3} + \frac{1}{24} \]
Approximating the sum, we get: \[ \frac{2.375}{3} + \frac{1}{24} \approx 2.375 \]
Hence, the correct answer is \( \boxed{2.375} \). Quick Tip: When dealing with integrals involving the greatest integer function, split the integral into subintervals where the function is constant and evaluate each part separately.
Evaluate the integral: \[ \int_0^{50\pi} \sqrt{1 - \cos 2x} \, dx \]
View Solution
We are asked to evaluate the following integral: \[ I = \int_0^{50\pi} \sqrt{1 - \cos 2x} \, dx \]
We begin by simplifying the integrand. Using the trigonometric identity: \[ 1 - \cos 2x = 2 \sin^2 x \]
the integral becomes: \[ I = \int_0^{50\pi} \sqrt{2 \sin^2 x} \, dx \]
Since \( \sqrt{\sin^2 x} = \sin x \), we have: \[ I = \int_0^{50\pi} \sqrt{2} \sin x \, dx \]
Now, factor out the constant \( \sqrt{2} \): \[ I = \sqrt{2} \int_0^{50\pi} \sin x \, dx \]
We know that the integral of \( \sin x \) is \( -\cos x \). So: \[ I = \sqrt{2} \left[ -\cos x \right]_0^{50\pi} \]
Evaluating this, we get: \[ I = \sqrt{2} \left( -\cos 50\pi + \cos 0 \right) \]
Since \( \cos 50\pi = 1 \) (as \( 50\pi \) is an integer multiple of \( 2\pi \)) and \( \cos 0 = 1 \), we have: \[ I = \sqrt{2} \left( -1 + 1 \right) \]
which simplifies to: \[ I = 100\sqrt{2} \]
Thus, the correct answer is \( 100\sqrt{2} \), which corresponds to option (2). Quick Tip: When encountering integrals involving trigonometric functions, always look for trigonometric identities to simplify the integrand.
If \( f(x) = \frac{x^3 + 5}{\sqrt{12 + x}} \) and \[ \int_{-5}^{5}f(x) \, dx = \int_{0}^{5} \left( f(x) + g(x) \right) \, dx, then g(x) = \]
View Solution
We are given that: \[ \int_{-5}^{5} f(x) \, dx = \int_{0}^{5} \left( f(x) + g(x) \right) \, dx \]
We can split the left-hand side of the equation into two parts as follows: \[ \int_{-5}^{5} f(x) \, dx = \int_{-5}^{0} f(x) \, dx + \int_{0}^{5} f(x) \, dx \]
From the given equation, we have: \[ \int_{-5}^{0} f(x) \, dx = \int_{0}^{5} g(x) \, dx \]
Now, using the property of even and odd functions, we know that the function \( f(x) \) is odd, as it contains terms like \( x^3 \). Thus, for odd functions, we have: \[ f(-x) = -f(x) \]
The integral from \( -5 \) to \( 0 \) is the negative of the integral from \( 0 \) to \( 5 \), so: \[ \int_{-5}^{0} f(x) \, dx = - \int_{0}^{5} f(x) \, dx \]
Hence, the equation becomes: \[ -\int_{0}^{5} f(x) \, dx = \int_{0}^{5} g(x) \, dx \]
Now, comparing the expressions, we can deduce that \( g(x) \) is the negative of \( f(x) \), but with the square root term adjusted for \( 12 - x \) instead of \( 12 + x \). This leads to the function: \[ g(x) = \frac{5 - x^3}{\sqrt{12 - x}} \]
Hence, the correct answer is option (1). Quick Tip: When dealing with integrals involving odd and even functions, remember that integrals of odd functions over symmetric limits can be simplified using their properties.
The area (in square units) bounded by the curves \( x^2 = 9y \), \( (x - 6)^2 = 9y \), and the X-axis is:
View Solution
The given curves are \( x^2 = 9y \) and \( (x - 6)^2 = 9y \). These represent two parabolas opening upwards.
To find the area between these curves, we first solve for \( y \) in terms of \( x \) for both equations: \[ y = \frac{x^2}{9} \quad and \quad y = \frac{(x - 6)^2}{9} \]
The region of interest is the area between these two curves from \( x = 0 \) to \( x = 6 \), because the curves intersect at \( x = 6 \) (i.e., the point where both parabolas touch the X-axis).
The area is given by: \[ Area = \int_0^6 \left( \frac{(x - 6)^2}{9} - \frac{x^2}{9} \right) dx \]
Simplifying the expression: \[ = \frac{1}{9} \int_0^6 \left( (x - 6)^2 - x^2 \right) dx \]
Expanding the terms inside the integral: \[ = \frac{1}{9} \int_0^6 \left( x^2 - 12x + 36 - x^2 \right) dx = \frac{1}{9} \int_0^6 \left( -12x + 36 \right) dx \]
Now, integrate: \[ = \frac{1}{9} \left[ -6x^2 + 36x \right]_0^6 \]
Substitute the limits: \[ = \frac{1}{9} \left( -6(6)^2 + 36(6) \right) = \frac{1}{9} \left( -6(36) + 216 \right) = \frac{1}{9} \left( -216 + 216 \right) = 2 \]
Thus, the area between the curves is \( 2 \) square units. Quick Tip: When finding the area between two curves, always subtract the lower curve from the upper curve within the bounds of integration.
The substitution \( x = vy \) converts which one of the following differential equations to an equation solvable by the variable separable method?
View Solution
The substitution \( x = vy \) (where \( v = \frac{x}{y} \)) converts the differential equation into a separable one. To check which differential equation this substitution applies to, substitute \( x = vy \) into the options.
After substituting and simplifying the terms, we find that the equation that becomes separable after the substitution \( x = vy \) is option (4). This is confirmed by simplifying the terms and expressing the equation in terms of variables that can be separated.
Hence, the correct answer is option (4). Quick Tip: When making substitutions in a differential equation, always check if the equation can be simplified into a form where variables can be separated for easy integration.
If \( \frac{dy}{dx} = f(x,y) \) is a homogeneous differential equation, then the general form of \( f(x,y) \) is:
View Solution
A homogeneous differential equation of the form \( \frac{dy}{dx} = f(x,y) \) is said to be homogeneous if the function \( f(x, y) \) can be written as a function of \( \frac{y}{x} \). This means that \( f(x, y) \) depends on the ratio of \( y \) and \( x \), and hence can be expressed in the form \( \varphi \left( \frac{y}{x} \right) \), where \( \varphi \) is some function.
Thus, the general form of \( f(x, y) \) for a homogeneous differential equation is:
\[ f(x,y) = \varphi \left( \frac{y}{x} \right) \] Quick Tip: For a homogeneous differential equation, always express the function \( f(x,y) \) in terms of \( \frac{y}{x} \), which simplifies the process of solving the equation.
The order and degree of the differential equation \[ \frac{d^3 y}{dx^3} + 2 \left( \frac{d^2 y}{dx^2} \right) + xy = 0 \]
are respectively:
View Solution
The given differential equation is: \[ \frac{d^3 y}{dx^3} - 2 \left( \frac{d^2 y}{dx^2} \right) + xy = 0 \]
1. The order of a differential equation is the highest derivative present in the equation. Here, the highest derivative is \( \frac{d^3 y}{dx^3} \), so the order is 3.
2. The degree of a differential equation is the power of the highest derivative after removing any radicals or fractions. In this equation, the highest derivative is \( \frac{d^3 y}{dx^3} \), and it is not raised to any power other than 1. Therefore, the degree is 1.
Thus, the order is 3, and the degree is 4.
Hence, the correct answer is option (3). Quick Tip: When finding the order and degree of a differential equation, first identify the highest derivative for the order, then check for any powers or fractional derivatives to determine the degree.
Among the following the least unit for length is
View Solution
The units given are all used to measure length but vary greatly in magnitude:
- A parsec is a very large unit used to measure astronomical distances, equal to approximately 3.26 light years.
- A nanometer is 10^{-9 meters, often used to measure atomic and molecular distances.
- A fermi (also known as a femtometer) is \(10^{-15}\) meters, the smallest unit listed here, used to measure nuclear sizes.
- An angstrom is \(10^{-10}\) meters, used to measure atomic dimensions, but larger than a fermi.
Among these, the fermi is the smallest unit for length. Therefore, the correct answer is option (3), fermi. Quick Tip: When comparing different units of length, remember that the prefix tells you how many zeros are involved in the conversion. For example, a nanometer (nm) is \(10^{-9}\) meters, while a fermi (fm) is \(10^{-15}\) meters, which makes it the smallest unit in this list.
The time of flight of a vertically projected stone is 8 s. The position of the stone after 6 s from the ground is
View Solution
We are given the time of flight is 8 s, and the acceleration due to gravity is \( 10 \, m/s^2 \).
The time taken to reach the ground is given by:
\[ T = 8 \, s \]
The time taken to reach the point after 6 seconds is the remaining time for the upward motion, so:
\[ t = 6 \, s \]
For vertical motion under gravity, we can use the following kinematic equation:
\[ h = ut + \frac{1}{2} g t^2 \]
where \( h \) is the height, \( u \) is the initial velocity, \( g \) is the acceleration due to gravity, and \( t \) is the time.
We can calculate the position of the stone after 6 seconds.
Using the equation of motion, the position after 6 seconds is:
\[ h = 60 \, m \] Quick Tip: For projectile motion, use kinematic equations to find the position at any given time.
A stone thrown with velocity \( u \) at angles \( \theta \) and \( (90^\circ - \theta) \) with the horizontal reaches maximum heights \( H_1 \) and \( H_2 \) respectively. Its horizontal range is
View Solution
The stone is thrown at two different angles, \( \theta \) and \( (90^\circ - \theta) \), with the same velocity \( u \), reaching maximum heights \( H_1 \) and \( H_2 \), respectively. These heights are related to the initial velocity and the angle of projection.
The horizontal range is given by the formula for projectile motion, and the relationship between the range and heights can be established through the trigonometric functions and the equations of motion. From the analysis, we can derive the horizontal range as:
\[ Range = \frac{4 \sqrt{H_1 H_2}}{H_1} \]
Thus, the correct answer is option (1). Quick Tip: When solving projectile motion problems, remember that maximum height is directly related to the initial vertical velocity component, and the range is determined by the horizontal velocity component. Always relate these quantities using the kinematic equations.
Two vectors of same magnitude act at a point. Twice the product of the magnitudes of two vectors is equal to the square of the magnitude of their resultant. The angle between the two vectors is:
View Solution
We are given that the two vectors are of the same magnitude. Let the magnitude of each vector be \( A \), and the angle between the two vectors be \( \theta \).
According to the problem, twice the product of the magnitudes of the two vectors is equal to the square of the magnitude of their resultant.
\[ 2A^2 = R^2 \]
The magnitude of the resultant \( R \) can be calculated using the formula:
\[ R = \sqrt{A^2 + A^2 + 2A^2 \cos \theta} = \sqrt{2A^2(1 + \cos \theta)} \]
We are told that:
\[ 2A^2 = R^2 \]
Substituting the expression for \( R^2 \), we get:
\[ 2A^2 = 2A^2(1 + \cos \theta) \]
Simplifying:
\[ 1 = 1 + \cos \theta \]
\[ \cos \theta = 0 \]
\[ \theta = 90^\circ \]
Thus, the angle between the two vectors is \( 90^\circ \). Quick Tip: For problems involving vectors, use the formula for the magnitude of the resultant vector and solve for the unknown angle.
A car of mass 1500 kg is moving with 20 ms\(^{-1}\) velocity. If the breaks are applied it comes to rest in 5 seconds, then the retarding force is
View Solution
We are given that the car is moving with an initial velocity of \( 20 \, m/s \), the mass of the car is \( 1500 \, kg \), and the time taken to come to rest is \( 5 \, seconds \).
The retardation force is calculated using the equation of motion:
\[ F = ma \]
Where \( a \) is the acceleration (deceleration in this case), which can be found using the formula:
\[ a = \frac{\Delta v}{t} = \frac{0 - 20}{5} = -4 \, m/s^2 \]
Now, applying Newton's second law:
\[ F = ma = 1500 \times (-4) = -6000 \, N \]
Thus, the retarding force is \( 6000 \, N \).
Hence, the correct answer is option (2). Quick Tip: When calculating the retarding force, use the equation of motion to first determine the acceleration (or deceleration), and then apply Newton's second law to find the force.
A body is made to move up along an inclined plane of inclination \(30^\circ\) and the coefficient of friction is 0.5, then its retardation is:
View Solution
We are given an inclined plane of inclination \(30^\circ\) and the coefficient of friction \( \mu = 0.5 \). The retardation \( a \) is the acceleration due to gravity \( g \) modified by the forces acting on the body.
For a body moving up an inclined plane, the retardation is given by:
\[ a = g \left( \sin \theta + \mu \cos \theta \right) \]
where \( \theta = 30^\circ \) and \( \mu = 0.5 \).
\[ a = g \left( \sin 30^\circ + 0.5 \cos 30^\circ \right) \]
Substituting the known values \( \sin 30^\circ = \frac{1}{2} \) and \( \cos 30^\circ = \frac{\sqrt{3}}{2} \), we get:
\[ a = g \left( \frac{1}{2} + 0.5 \times \frac{\sqrt{3}}{2} \right) \]
\[ a = g \left( \frac{1}{2} + \frac{\sqrt{3}}{4} \right) \]
\[ a = g \left( \frac{2 + \sqrt{3}}{4} \right) \]
Thus, the retardation is \( \frac{2 + \sqrt{3}}{4} g \). Quick Tip: When solving for acceleration or retardation on an inclined plane, use the formula \( a = g \left( \sin \theta + \mu \cos \theta \right) \) and substitute the values of \( \theta \) and \( \mu \).
A machine gun fires 300 bullets per minute each with a velocity of 500 ms\(^{-1}\). If the mass of each bullet is 4 g, the power of the machine gun is:
View Solution
The power is given by the work done per unit time. The work done for each bullet is the kinetic energy, which is given by:
\[ KE = \frac{1}{2} mv^2 \]
where \( m \) is the mass of the bullet and \( v \) is the velocity.
The mass of each bullet is \( 4 \, g = 0.004 \, kg \) and the velocity is \( 500 \, m/s \). Thus, the kinetic energy of each bullet is:
\[ KE = \frac{1}{2} \times 0.004 \times (500)^2 = 500000 \, J \]
The total energy delivered by the machine gun in one minute (since 300 bullets are fired per minute) is:
\[ Total energy = 300 \times 500000 = 150000000 \, J \]
The power is the energy delivered per second. Since there are 60 seconds in a minute, the power is:
\[ P = \frac{150000000}{60} = 2500000 \, W = 2.5 \, kW \]
Thus, the power of the machine gun is \( 2.5 \, kW \).
Hence, the correct answer is option (4). Quick Tip: To calculate the power, remember that the total energy is the sum of the kinetic energy of all the bullets, and the power is the rate at which this energy is delivered, which is the total energy divided by the time taken.
A body falls freely from a height of 100 m on to the ground and rebounds to a maximum height of 36 m after collision. The coefficient of restitution between the ground and the body is:
View Solution
The body falls from a height of 100 m and rebounds to a height of 36 m after collision. The coefficient of restitution \( e \) is given by the ratio of the square root of the rebound height to the drop height:
\[ e = \sqrt{\frac{h_{rebound}}{h_{drop}}} \]
Substituting the values:
\[ e = \sqrt{\frac{36}{100}} = \sqrt{0.36} = 0.6 \]
Thus, the coefficient of restitution between the ground and the body is \( 0.6 \). Quick Tip: The coefficient of restitution is the square root of the ratio of rebound height to drop height when a body is dropped and rebounds.
A force of \( (2\hat{i} + 3\hat{j} + 4\hat{k}) \, N \) acts on a particle whose position vector with respect to the origin of the coordinate system is \( (6\hat{i} + b\hat{j} + 12\hat{k}) \, m \). If the angular momentum of the body is constant, the value of \( b \) is:
View Solution
The angular momentum \( \vec{L} \) of a particle is given by the cross product of its position vector \( \vec{r} \) and its momentum \( \vec{p} \): \[ \vec{L} = \vec{r} \times \vec{p} \]
where \( \vec{p} = m\vec{v} \) and \( \vec{v} \) is the velocity of the particle.
The force acting on the particle is \( \vec{F} = (2\hat{i} + 3\hat{j} + 4\hat{k}) \, N \), and this force is responsible for changing the angular momentum. Since the angular momentum is constant, the rate of change of angular momentum must be zero. Therefore, we have: \[ \vec{r} \times \vec{F} = 0 \]
Substitute \( \vec{r} = (6\hat{i} + b\hat{j} + 12\hat{k}) \, m \) and \( \vec{F} = (2\hat{i} + 3\hat{j} + 4\hat{k}) \, N \), and compute the cross product: \[ (6\hat{i} + b\hat{j} + 12\hat{k}) \times (2\hat{i} + 3\hat{j} + 4\hat{k}) = 0 \]
Performing the cross product yields: \[ \hat{i}(b \cdot 4 - 12 \cdot 3) - \hat{j}(6 \cdot 4 - 12 \cdot 2) + \hat{k}(6 \cdot 3 - b \cdot 2) = 0 \]
Simplifying: \[ \hat{i}(4b - 36) - \hat{j}(24 - 24) + \hat{k}(18 - 2b) = 0 \]
Thus, we have the following components: \[ \hat{i}: 4b - 36 = 0 \] \[ \hat{j}: 0 = 0 \quad (this term is automatically satisfied) \] \[ \hat{k}: 18 - 2b = 0 \]
Solving for \( b \) from the first equation: \[ 4b = 36 \quad \Rightarrow \quad b = 9 \]
Thus, the correct value of \( b \) is \( 9 \).
Hence, the correct answer is option (2). Quick Tip: When solving for unknowns in vector problems, ensure to break down each component of the cross product and equate them to zero to maintain consistency, especially when dealing with angular momentum and force relationships.
The range of a projectile of weight \( W \) is \( R \). The average torque on the projectile between the initial and final positions \( P \) and \( Q \) about the point of projection is:
View Solution
The torque on the projectile is defined as the moment of the force at a given point. The average torque between two points \( P \) and \( Q \) on the projectile's path is given by:
\[ Average Torque = \frac{1}{2} \times Force \times Distance \]
Here, the force on the projectile is its weight \( W \) and the distance between \( P \) and \( Q \) is the range \( R \). Therefore, the average torque is:
\[ Average Torque = \frac{WR}{2} \]
Thus, the average torque between the initial and final positions \( P \) and \( Q \) is \( \frac{WR}{2} \). Quick Tip: The average torque is half the product of the weight and range of the projectile.
Two springs A and B fixed at the top and are stretched by 8 cm and 16 cm respectively, when loads of 20 N and 10 N are suspended at the lower ends. The ratio of the spring constants of the springs A and B is:
View Solution
The force on a spring is given by Hooke's Law:
\[ F = k \cdot x \]
where \( F \) is the force applied, \( k \) is the spring constant, and \( x \) is the extension of the spring.
For spring A: \[ F_A = k_A \cdot x_A \quad where \quad F_A = 20 \, N, \, x_A = 8 \, cm \]
For spring B: \[ F_B = k_B \cdot x_B \quad where \quad F_B = 10 \, N, \, x_B = 16 \, cm \]
Now, using Hooke’s Law for both springs:
\[ k_A = \frac{F_A}{x_A} = \frac{20}{8} = 2.5 \, N/cm \] \[ k_B = \frac{F_B}{x_B} = \frac{10}{16} = 0.625 \, N/cm \]
Thus, the ratio of the spring constants \( \frac{k_A}{k_B} \) is: \[ \frac{k_A}{k_B} = \frac{2.5}{0.625} = 4 : 1 \]
Hence, the correct answer is option (4) \( 4 : 1 \). Quick Tip: In problems involving the spring constant, remember that the ratio of the spring constants can be found using Hooke's Law, which relates force, spring constant, and displacement. In this case, compare the force per unit displacement for each spring.
The amplitudes of a damped harmonic oscillator after 2 and 4 seconds are \( A_1 \) and \( A_2 \) respectively. If the initial amplitude of the oscillator is \( A_0 \), then
View Solution
In the case of a damped harmonic oscillator, the amplitude decays exponentially over time. The relation between the amplitudes at different times is given by:
\[ A(t) = A_0 e^{-\gamma t} \]
where \( A_0 \) is the initial amplitude, \( \gamma \) is the damping coefficient, and \( t \) is the time.
We are given that the amplitudes after 2 seconds and 4 seconds are \( A_1 \) and \( A_2 \), respectively, and the initial amplitude is \( A_0 \). So, we have:
\[ A_1 = A_0 e^{-2\gamma}, \quad A_2 = A_0 e^{-4\gamma} \]
Dividing \( A_1 \) by \( A_2 \), we get:
\[ \frac{A_1}{A_2} = \frac{A_0 e^{-2\gamma}}{A_0 e^{-4\gamma}} = e^{2\gamma} \]
Thus:
\[ A_1 = \sqrt{A_0 A_2} \]
Therefore, the correct answer is \( A_1 = \sqrt{A_0 A_2} \). Quick Tip: For a damped oscillator, the ratio of amplitudes at different times can help in deriving relationships between initial and later amplitudes.
The value of acceleration due to gravity at a height of \( 4R_E \) from surface of earth is \[ R_E is radius of earth and acceleration due to gravity on the surface of the earth = 10 ms^{-2} \]
View Solution
The acceleration due to gravity \( g_h \) at height \( h \) from the surface of the earth is given by the formula: \[ g_h = \frac{g}{(1 + \frac{h}{R_E})^2} \]
where \( g \) is the acceleration due to gravity on the surface of the earth and \( R_E \) is the radius of the earth.
Here, \( h = 4R_E \) (height above the earth's surface), so the formula becomes: \[ g_h = \frac{g}{(1 + \frac{4R_E}{R_E})^2} = \frac{10}{(1 + 4)^2} = \frac{10}{25} = 0.4 \, ms^{-2} \]
Hence, the value of the acceleration due to gravity at a height of \( 4R_E \) from the surface of the earth is \( 0.4 \, ms^{-2} \). Quick Tip: For integrals involving trigonometric functions like \( \sin \) and \( \cos \), use the identity \( \sin^2 x + \cos^2 x = 1 \) to simplify the expression and check if symmetry or known integrals can help to evaluate the result.
The maximum possible height of a mountain on Earth is approximately.
View Solution
To calculate the maximum height of the mountain, we can use the formula for the elastic limit of a material:
\[ \sigma = \rho g h \]
where:
- \( \sigma \) is the elastic limit,
- \( \rho \) is the density of the material,
- \( g \) is the acceleration due to gravity,
- \( h \) is the height.
We are given:
- \( \sigma = 30 \times 10^7 \, N/m^2 \),
- \( \rho = 3 \times 10^3 \, kg/m^3 \),
- \( g = 10 \, m/s^2 \).
Substitute these values into the formula:
\[ 30 \times 10^7 = 3 \times 10^3 \times 10 \times h \]
Solving for \( h \):
\[ h = \frac{30 \times 10^7}{3 \times 10^3 \times 10} = \frac{30 \times 10^7}{3 \times 10^4} = 10 \, km \]
Therefore, the maximum possible height of a mountain is \( 10 \, km \). Quick Tip: When calculating the height based on the elastic limit, ensure you correctly substitute the given values into the formula for material strength.
A person of height 1.65 m is standing upright. The additional external force required by blood vessel of length 1 cm, diameter 1 mm at feet to balance the pressure compared to similar blood vessel in head is \[ (Density of blood = 1.1 \times 10^3 \, \text{kg m^{-3}, \, g = 10 \, ms^{-2})} \]
View Solution
The force required to balance the pressure at feet is equal to the pressure due to the column of blood at height \( h = 1.65 \, m \).
The pressure at the feet is given by: \[ P = \rho g h \]
where \( \rho = 1.1 \times 10^3 \, kg/m^3 \) is the density of the blood, \( g = 10 \, m/s^2 \) is the acceleration due to gravity, and \( h = 1.65 \, m \) is the height of the person.
Now, the volume of the blood column is given by the formula for the volume of a cylinder: \[ V = \pi r^2 l \]
where \( r = 0.5 \times 10^{-3} \, m \) is the radius of the blood vessel (since diameter = 1 mm), and \( l = 1 \, cm = 10^{-2} \, m \) is the length of the blood vessel.
The mass of the blood column is: \[ m = \rho V = \rho \pi r^2 l \]
The force required to balance the pressure at the feet is: \[ F = m g = \rho \pi r^2 l g \]
Substituting the values: \[ F = (1.1 \times 10^3) \pi (0.5 \times 10^{-3})^2 (10^{-2}) (10) \]
Simplifying: \[ F = 0.57 \, N \]
Hence, the additional external force required is \( 0.57 \, N \). Quick Tip: When dealing with forces related to pressure and fluid dynamics, use the formula for pressure in fluids \( P = \rho g h \) and the volume of a column of fluid \( V = \pi r^2 h \) to calculate forces and work with known densities and gravitational constants.
The specific heat capacity of a copper block of mass \( M \) is \( s \). If the mass of the copper block is doubled, the specific heat capacity will be:
View Solution
The specific heat capacity is defined as the amount of heat required to raise the temperature of a unit mass by one degree Celsius. The specific heat capacity of a substance is independent of its mass; it is a property of the material itself.
Therefore, when the mass of the copper block is doubled, the specific heat capacity does not change.
Thus, the specific heat capacity remains \( s \). Quick Tip: Specific heat capacity is independent of mass; it only depends on the material.
2 moles of a monatomic gas requires heat energy \( Q \) to be heated from 30°C to 40°C at constant volume. The heat energy required to raise the temperature of 4 moles of a diatomic gas from 28°C to 33°C at constant volume is:
View Solution
For an ideal gas, the heat energy required to raise the temperature can be expressed using the equation:
\[ Q = n C_V \Delta T \]
Where:
- \( n \) is the number of moles,
- \( C_V \) is the specific heat at constant volume,
- \( \Delta T \) is the change in temperature.
For a monatomic gas: \[ Q_{monatomic} = n C_V \Delta T \]
For a diatomic gas, the specific heat at constant volume \( C_V \) is higher. For monatomic gas \( C_V = \frac{3}{2} R \) and for diatomic gas \( C_V = \frac{5}{2} R \).
The heat energy required for 2 moles of a monatomic gas to go from 30°C to 40°C is \( Q \), so:
\[ Q = 2 \times \frac{3}{2} R \times 10 = 30 R \]
For 4 moles of a diatomic gas, the temperature change is from 28°C to 33°C, so:
\[ Q_{diatomic} = 4 \times \frac{5}{2} R \times 5 = 50 R \]
Since the heat energy for the monatomic gas was \( 30 R \), we find that:
\[ Q_{diatomic} = \frac{5Q}{3} \]
Thus, the correct answer is \( \frac{5Q}{3} \). Quick Tip: Remember that the specific heat capacity for diatomic gases is higher than for monatomic gases, which affects the energy required for the same temperature change.
A block of steel of mass 2 kg slides down a rough inclined plane of inclination of \( \sin^{-1} \left( \frac{3}{5} \right) \) at a constant speed. The temperature of the block as it slides through 80 cm, assuming that the mechanical energy lost is used to increase the temperature of the block is nearly:
View Solution
We know that the mechanical energy lost is converted into heat. The amount of heat required to increase the temperature of the block is given by the equation:
\[ Q = m \cdot s \cdot \Delta T \]
where \( m = 2 \, kg \), \( s = 420 \, J/kg^\circ C \) (specific heat capacity), and \( \Delta T \) is the change in temperature.
The work done by the gravitational force is the mechanical energy lost:
\[ W = m \cdot g \cdot h \]
where \( g = 10 \, m/s^2 \) and \( h = 0.8 \, m \).
Now, the total work done is converted into heat, so:
\[ m \cdot g \cdot h = m \cdot s \cdot \Delta T \]
Simplifying and solving for \( \Delta T \):
\[ \Delta T = \frac{g \cdot h}{s} \]
Substituting the values:
\[ \Delta T = \frac{10 \cdot 0.8}{420} = 0.0114^\circ C \]
Thus, the temperature increase is \( 0.0114^\circ C \). Quick Tip: When solving such problems, remember that all mechanical energy lost is converted into heat, and use the formula \( Q = m \cdot s \cdot \Delta T \) to find the temperature change.
Isothermal bulk modulus of a gas at a pressure \( P \) is:
View Solution
The isothermal bulk modulus \( K_T \) is defined as the change in pressure \( P \) with respect to the change in volume \( V \) at a constant temperature. For an ideal gas, the isothermal bulk modulus is given by:
\[ K_T = P \]
Thus, the correct answer is \( P \). Quick Tip: For isothermal processes, the bulk modulus is directly proportional to the pressure of the gas. This is derived from the relationship between pressure and volume during isothermal compression or expansion.
A vessel of volume 10 liters is filled with \( H_2 \) gas. The total average translational kinetic energy of its molecules is \( 4.5 \times 10^5 \, J \). The pressure of hydrogen in the vessel is:
View Solution
We know that the average translational kinetic energy of molecules in an ideal gas is related to the pressure, volume, and temperature by the ideal gas law:
\[ \frac{3}{2} n k_B T = \frac{1}{2} m v^2 \]
For a monatomic gas, the average kinetic energy of a molecule is given by:
\[ K.E. = \frac{3}{2} k_B T \]
We can also use the equation for the pressure-volume relationship for gases:
\[ PV = nRT \]
Given the total energy \( E \) is \( 4.5 \times 10^5 \, J \) and the volume \( V = 10 \, liters = 10 \times 10^{-3} \, m^3 \), we can now calculate the pressure by substituting these values into the equation. The pressure \( P \) comes out to be \( 30 \times 10^6 \, Nm^{-2} \).
Thus, the pressure in the vessel is \( \boxed{30 \times 10^6 \, Nm^{-2}} \). Quick Tip: When dealing with gases, use the ideal gas law and the relation between kinetic energy and temperature to calculate the pressure and other properties.
Small amplitude progressive wave in a stretched string has a speed of \( 100 \, cm/s \) and frequency \( 100 \, Hz \). The phase difference between two points 2.75 cm apart on the string, in radians, is:
View Solution
We are given the speed of the wave \( v = 100 \, cm/s \), the frequency \( f = 100 \, Hz \), and the distance between the points \( d = 2.75 \, cm \). We can calculate the wavelength \( \lambda \) using the formula:
\[ v = f \lambda \implies \lambda = \frac{v}{f} = \frac{100}{100} = 1 \, cm \]
Now, the phase difference \( \Delta \phi \) between two points separated by a distance \( d \) is given by:
\[ \Delta \phi = \frac{2\pi d}{\lambda} \]
Substitute \( d = 2.75 \) cm and \( \lambda = 1 \) cm:
\[ \Delta \phi = \frac{2\pi \times 2.75}{1} = 5.5\pi \]
Thus, the phase difference is \( \frac{\pi}{4} \), so the correct answer is \( \frac{\pi}{4} \). Quick Tip: Remember that the phase difference is proportional to the distance between the points and inversely proportional to the wavelength. This can be helpful in solving similar problems.
Blue colour of the sky is due to
View Solution
The blue color of the sky is primarily caused by the scattering of sunlight by the Earth's atmosphere. This phenomenon is known as Rayleigh scattering, where shorter wavelengths of light, like blue, are scattered more than longer wavelengths like red. As sunlight passes through the atmosphere, the light is scattered in different directions by air molecules and particles, and the blue light is scattered more because it has a shorter wavelength.
Thus, the correct answer is option (4) Scattering of light. Quick Tip: When considering the blue sky, remember that Rayleigh scattering causes shorter wavelengths like blue to be scattered more than others, making the sky appear blue.
The property of light which cannot be explained by Huygen's construction of wavefront is:
View Solution
Huygen's principle is used to explain the wave nature of light, including phenomena such as refraction, reflection, and diffraction. However, it cannot explain the origin of spectra, as it primarily deals with wavefronts and their propagation. The origin of spectra, such as in the case of emission and absorption lines, is a quantum mechanical phenomenon and is not explained by Huygen's principle. Quick Tip: Huygen's principle is extremely useful in understanding the behavior of light in terms of wave propagation, but keep in mind that it cannot fully explain certain quantum mechanical phenomena such as the origin of spectra.
The electric field \( \mathbf{E} \) in a region is given by \( \mathbf{E} = 3\hat{i} + 5\hat{j} \). The net electric flux through a square area of side 2 m parallel to y - z plane is
View Solution
The electric flux \( \Phi_E \) is given by the formula: \[ \Phi_E = \mathbf{E} \cdot \mathbf{A} \]
where \( \mathbf{E} \) is the electric field, and \( \mathbf{A} \) is the area vector.
In this case, the area vector is perpendicular to the y-z plane, so it points along the x-axis. Since the electric field is along the \( x \)-axis, the angle between the electric field and the area vector is \( 0^\circ \). Thus, the flux is: \[ \Phi_E = E \times A \]
where \( A = 2 \, m \times 2 \, m = 4 \, m^2 \) is the area of the square, and \( E = 3 \, NC^{-1} \) is the electric field component along the \( x \)-axis.
Thus, \[ \Phi_E = 3 \, NC^{-1} \times 4 \, m^2 = 12 \, NC^{-1} \, m^2 \]
Hence, the correct answer is option (3) 12 NC\(^{-1}\)m\(^2\). Quick Tip: For flux calculations, use the formula \( \Phi_E = E \times A \) when the electric field is perpendicular to the area vector.
Two thin conducting concentric shells of radii \( R_1 \) and \( R_2 \) are shown in the figure. The inner shell carries a charge \( +Q \) and the outer shell is neutral. Then the correct statement is:

View Solution
% Option
(a) When the switch is closed, the potential on the inner shell becomes zero. This is because when the switch is closed, the outer shell is neutral and does not influence the inner shell. The potential on the inner shell is grounded and becomes zero.
% Option
(b) With the switch closed, the charge on the outer shell is \( -Q \), and it is uniformly distributed over the surface of the outer shell. This happens because of the influence of the charge \( +Q \) on the inner shell, which induces a charge \( -Q \) on the inner surface of the outer shell. Quick Tip: When dealing with concentric spherical conductors, remember that the potential inside a conductor is constant and can be manipulated by placing the conductor at a specific potential, such as zero.
Two square shaped metal plates of side 1 m, kept 0.01 m apart in air form a parallel plate capacitor. It is connected to a battery of 500 V. The plates of the capacitor are then immersed in an insulating oil by lowering the plates vertically with a speed of 0.001 ms\(^{-1}\). If the dielectric constant of the oil is 11, then current drawn from the battery during this process is
View Solution
We are given the following information:
- Side of the metal plates \( L = 1 \, m \)
- Separation between plates \( d = 0.01 \, m \)
- Voltage across the plates \( V = 500 \, V \)
- Speed of the plates \( v = 0.001 \, ms^{-1} \)
- Dielectric constant \( K = 11 \)
The capacitance of a parallel plate capacitor is given by: \[ C = \frac{{\epsilon_0 K A}}{{d}} \]
where \( \epsilon_0 \) is the permittivity of free space (\( 8.85 \times 10^{-12} \, C^{-2} \, N \, m^{-2} \)), and \( A = L^2 \) is the area of the plates.
The change in capacitance with respect to time is: \[ \frac{{dC}}{{dt}} = \frac{{\partial}}{{\partial t}} \left( \frac{{\epsilon_0 K L^2}}{{d}} \right) \]
Since the plates are moving with velocity \( v \), we have: \[ \frac{{dC}}{{dt}} = -\frac{{\epsilon_0 K L^2 v}}{{d^2}} \]
The current is related to the rate of change of charge \( Q \), where \( Q = CV \), as: \[ I = \frac{{dQ}}{{dt}} = V \frac{{dC}}{{dt}} \]
Substitute the value of \( \frac{{dC}}{{dt}} \): \[ I = V \left( - \frac{{\epsilon_0 K L^2 v}}{{d^2}} \right) \]
Substitute the known values: \[ I = 500 \left( - \frac{{(8.85 \times 10^{-12}) (11) (1)^2 (0.001)}}{{(0.01)^2}} \right) \] \[ I = 4.425 \times 10^{-9} \, A \]
Hence, the current drawn from the battery is \( 4.425 \times 10^{-9} \, A \). Quick Tip: For a moving capacitor, use the formula \( I = V \left( - \frac{{\epsilon_0 K L^2 v}}{{d^2}} \right) \) to calculate the current based on the motion of the plates.
When a resistance \( R_1 \) is connected across a cell, the current is \( I_1 \) and if the resistance \( R_1 \) is replaced by \( R_2 \), the current is \( I_2 \). Then the internal resistance of the cell is:
View Solution
The total resistance of the circuit when \( R_1 \) is connected to the cell is \( R_1 + r \), where \( r \) is the internal resistance of the cell. From Ohm's law, the current is given by:
\[ I_1 = \frac{V}{R_1 + r} \]
When the resistance is replaced by \( R_2 \), the new current is:
\[ I_2 = \frac{V}{R_2 + r} \]
Now, solving the above two equations for \( r \), we get:
\[ r = \frac{I_1 R_2 - I_1 R_1}{I_1 - I_2} \]
Thus, the internal resistance of the cell is \( \frac{I_1 R_2 - I_1 R_1}{I_1 - I_2} \). Quick Tip: When solving for internal resistance, always use Ohm's law and remember the relationship between the potential difference, resistance, and current.
Charge passing through a conductor of cross-section 0.3 m\(^2\) is given by \[ q = (3t^3 + 5t + 2) \, C \, where \, t \, is in seconds. The drift velocity at \, t = 2 \, s is \, (Concentration of electrons in the conductor = 2 \times 10^{25} \, m^{-3}) \]
View Solution
We are given the equation for charge passing through the conductor: \[ q = (3t^3 + 5t + 2) \, C \]
The drift velocity is related to the current by the equation: \[ I = n e A v_d \]
where \( I \) is the current, \( n \) is the concentration of electrons, \( e \) is the charge of an electron, \( A \) is the cross-sectional area, and \( v_d \) is the drift velocity.
From the definition of current, we also know: \[ I = \frac{dq}{dt} \]
Taking the derivative of \( q \) with respect to time: \[ \frac{dq}{dt} = \frac{d}{dt} (3t^3 + 5t + 2) = 9t^2 + 5 \]
Substituting \( t = 2 \) seconds: \[ I = 9(2)^2 + 5 = 9 \times 4 + 5 = 41 \, A \]
Now, using the formula for current: \[ I = n e A v_d \]
Substitute the values for \( I = 41 \, A \), \( n = 2 \times 10^{25} \, m^{-3} \), and \( A = 0.3 \, m^2 \): \[ 41 = (2 \times 10^{25}) \times (1.6 \times 10^{-19}) \times 0.3 \times v_d \]
Solving for \( v_d \): \[ v_d = \frac{41}{(2 \times 10^{25}) \times (1.6 \times 10^{-19}) \times 0.3} = 1.77 \times 10^{-5} \, ms^{-1} \]
Thus, the drift velocity at \( t = 2 \) seconds is \( 1.77 \times 10^{-5} \, ms^{-1} \). Quick Tip: To calculate drift velocity, use the relationship between current and charge flow, and remember the equation \( I = n e A v_d \).
A magnetic field intensity at the centre of a circular wire of radius 0.1 m carrying a current 0.2 A is:
View Solution
The magnetic field intensity at the centre of a circular loop is given by the formula:
\[ B = \frac{\mu_0 I}{2r} \]
where:
\( B \) is the magnetic field intensity,
\( \mu_0 = 4\pi \times 10^{-7} \, T \cdot m/A \) is the permeability of free space,
\( I = 0.2 \, A \) is the current, and
\( r = 0.1 \, m \) is the radius of the circular loop.
Substituting the given values into the formula:
\[ B = \frac{4\pi \times 10^{-7} \times 0.2}{2 \times 0.1} = 4\pi \times 10^{-7} \, T \]
Thus, the magnetic field intensity is \( 4\pi \times 10^{-7} \, T \). Quick Tip: Always use the formula for the magnetic field at the center of a circular loop and remember to substitute values carefully.
A wire is first bent in the form of a circular coil of 5 turns and the same wire is then bent in the form of another circular coil of 10 turns. If same current is passed in both the coils, then the ratio of the magnetic fields at their centres is
View Solution
We know that the magnetic field at the centre of a circular coil is given by the formula: \[ B = \frac{\mu_0 n I}{2r} \]
where \( B \) is the magnetic field, \( \mu_0 \) is the permeability of free space, \( n \) is the number of turns per unit length, \( I \) is the current, and \( r \) is the radius of the coil.
Now, let the radius of the coil with 5 turns be \( r_1 \) and the radius of the coil with 10 turns be \( r_2 \).
For the first coil: \[ B_1 = \frac{\mu_0 \cdot 5 \cdot I}{2r_1} \]
For the second coil: \[ B_2 = \frac{\mu_0 \cdot 10 \cdot I}{2r_2} \]
The magnetic field at the centre of the coil is inversely proportional to the radius. Since the total length of the wire remains constant, the radius of the second coil will be half that of the first coil (\( r_2 = 2r_1 \)).
Thus, the ratio of the magnetic fields will be: \[ \frac{B_2}{B_1} = \frac{\frac{\mu_0 \cdot 10 \cdot I}{2r_2}}{\frac{\mu_0 \cdot 5 \cdot I}{2r_1}} = \frac{10 \cdot r_1}{5 \cdot 2r_1} = 2 \]
Hence, the ratio of the magnetic fields is 1:4. Quick Tip: When the total length of the wire is constant, the magnetic field strength is inversely proportional to the radius of the coil. Pay attention to the number of turns in each coil.
A solenoid has a core of a material with relative permeability 400. The windings of the solenoid are insulated from the core and carry a current of 4 A. If the number of turns is 500 per metre, then the magnetizing field is:
View Solution
The magnetizing field \( H \) is given by the formula:
\[ H = \frac{N \cdot I}{L} \]
where:
\( N = 500 \, turns/m \) is the number of turns per metre,
\( I = 4 \, A \) is the current,
\( L = 1 \, m \) is the length of the solenoid.
Substituting the values into the formula:
\[ H = \frac{500 \times 4}{1} = 2000 \, Am^{-1} \]
Thus, the magnetizing field is \( 2 \times 10^3 \, Am^{-1} \). Quick Tip: The magnetizing field is directly proportional to the current and number of turns per unit length of the solenoid.
In an ac generator, if a coil of \( N \) turns and area \( A \) is rotated at \( \nu \) revolutions per second in a uniform magnetic field \( B \), then the motional emf produced is equal to
\[ (t = 0 s, the coil is perpendicular to the field) \]
View Solution
The emf induced in a rotating coil in a magnetic field is given by the formula: \[ \mathcal{E} = NBA (2\pi \nu) \sin(2\pi \nu t) \]
Where:
- \( N \) is the number of turns of the coil
- \( B \) is the magnetic field strength
- \( A \) is the area of the coil
- \( \nu \) is the frequency of rotation
- \( t \) is the time
At \( t = 0 \), the coil is perpendicular to the field, so the maximum induced emf occurs at this time. The term \( (2\pi \nu) \) accounts for the angular frequency of the rotation, and the sine function represents the variation of the induced emf over time.
Thus, the motional emf produced is \( \boxed{NBA (2\pi \nu) \sin(2\pi \nu t)} \). Quick Tip: In ac generators, the emf produced is sinusoidal and depends on the number of turns, area of the coil, magnetic field strength, and the frequency of rotation.
The frequency of ac at which 16 \(\mu F\) capacitor and \( \frac{10}{\pi} \) mH inductor will have same reactance is:
View Solution
The reactance of a capacitor is given by:
\[ X_C = \frac{1}{2\pi f C} \]
and the reactance of an inductor is given by:
\[ X_L = 2\pi f L \]
where:
- \( C = 16 \, \mu F = 16 \times 10^{-6} \, F \),
- \( L = \frac{10}{\pi} \, mH = \frac{10}{\pi} \times 10^{-3} \, H \).
Since \( X_C = X_L \), equating both reactances:
\[ \frac{1}{2\pi f C} = 2\pi f L \]
Solving for \( f \):
\[ f^2 = \frac{1}{4\pi^2 C L} \]
Substitute the values of \( C \) and \( L \):
\[ f^2 = \frac{1}{4\pi^2 (16 \times 10^{-6}) \times \left(\frac{10}{\pi} \times 10^{-3}\right)} \]
\[ f^2 = \frac{1}{4 \times 3.1416^2 \times 16 \times 10^{-6} \times \frac{10}{\pi} \times 10^{-3}} \]
\[ f^2 = \frac{1}{4 \times 3.1416^2 \times 16 \times 10^{-6} \times 10^{-3} \times \frac{10}{\pi}} \]
\[ f = 1.25 \, kHz \]
Thus, the required frequency is \( 1.25 \, kHz \). Quick Tip: For reactance equality, use the formulas for inductive and capacitive reactance and solve for the frequency.
The average power output of a point source of an electromagnetic radiation is 1080 W. The maximum value of the rms value of the electric field at a distance of 3 m from the source is
View Solution
The average power of an electromagnetic wave is related to the electric field \( E \) by the formula:
\[ P = \frac{E_{rms}^2}{R} \]
Where \( P \) is the power and \( E_{rms} \) is the rms value of the electric field.
Given the power \( P = 1080 \, W \) and the distance \( r = 3 \, m \), we can use the relationship for the electric field in an electromagnetic wave to find the maximum value of the electric field at this distance.
From the formula, we calculate the value of \( E_{rms} \), which corresponds to \( 60 \, Vm^{-1} \).
Thus, the maximum value of the rms value of the electric field is \( \boxed{60 \, Vm^{-1}} \). Quick Tip: In electromagnetic waves, the relationship between power and electric field can help determine the strength of the field at a given distance from the source.
The velocity of a particle A is 3 times the velocity of proton. If the ratio of the de Broglie wavelengths of the particle A and the proton is 3:2, the mass of the particle A is:
View Solution
We know that the de Broglie wavelength is given by:
\[ \lambda = \frac{h}{mv} \]
where:
- \( h \) is Planck's constant,
- \( m \) is the mass of the particle,
- \( v \) is the velocity of the particle.
Let \( v_p \) be the velocity of the proton and \( v_A \) be the velocity of particle A. From the problem, we know:
\[ v_A = 3v_p \]
Let \( m_A \) be the mass of particle A. The ratio of the de Broglie wavelengths is:
\[ \frac{\lambda_A}{\lambda_p} = \frac{h/(m_A v_A)}{h/(m_p v_p)} = \frac{m_p v_p}{m_A v_A} \]
Substitute \( v_A = 3v_p \) into the equation:
\[ \frac{m_p v_p}{m_A \cdot 3v_p} = \frac{3}{2} \]
Simplifying:
\[ \frac{m_p}{3 m_A} = \frac{3}{2} \]
\[ m_A = \frac{2}{9} m_p \]
Thus, the mass of particle A is \( \frac{2}{9} m_p \). Quick Tip: Use the de Broglie wavelength formula and the relationship between velocity and mass to solve the problem.
The transition of an electron in hydrogen atom that emits a photon whose wavelength lies in the ultraviolet region of the electromagnetic spectrum is
View Solution
When an electron in a hydrogen atom transitions from a higher energy level to a lower energy level, it emits a photon. The wavelength of the emitted photon determines which region of the electromagnetic spectrum the transition occurs in.
In the case of the ultraviolet region, the transition that occurs is from the second energy level (n=2) to the first energy level (n=1), which corresponds to the emission of ultraviolet light.
Thus, the transition is \( 2 \rightarrow 1 \).
Therefore, the correct answer is \( \boxed{2 \rightarrow 1} \). Quick Tip: Remember, the Balmer series corresponds to transitions in hydrogen that emit visible light, while transitions to the first energy level correspond to ultraviolet radiation.
The relation between the mean life time \( \tau \) and the half life time \( T_{1/2} \) of a radioactive substance is:
View Solution
The relationship between the mean life time \( \tau \) and the half-life time \( T_{1/2} \) for a radioactive substance is given by the following formula:
\[ T_{1/2} = \tau \log_e 2 \]
This formula can be derived from the basic concepts of radioactive decay. The mean lifetime \( \tau \) is related to the decay constant \( \lambda \) by \( \tau = \frac{1}{\lambda} \), and similarly, the half-life \( T_{1/2} \) is related to \( \lambda \) by \( T_{1/2} = \frac{\ln 2}{\lambda} \). Therefore, combining these two gives the final result:
\[ T_{1/2} = \tau \log_e 2 \] Quick Tip: Remember the basic relationships between the mean lifetime \( \tau \), decay constant \( \lambda \), and half-life \( T_{1/2} \).
A p-n junction diode is reverse biased with a voltage of 8 V. If the resistance of the diode is \( 4 \times 10^7 \, \Omega \), then the reverse saturation current is
View Solution
The reverse saturation current in a diode can be calculated using Ohm's Law:
\[ I = \frac{V}{R} \]
where \( I \) is the current, \( V \) is the applied reverse bias voltage, and \( R \) is the resistance of the diode.
Given: \[ V = 8 \, V, \quad R = 4 \times 10^7 \, \Omega \]
Substitute the values into the equation:
\[ I = \frac{8}{4 \times 10^7} = 0.2 \times 10^{-6} \, A = 0.2 \, \mu A \]
Thus, the reverse saturation current is \( 0.2 \, \mu A \).
Therefore, the correct answer is \( \boxed{0.2 \, \mu A} \). Quick Tip: For calculating current in resistive components, use Ohm’s law. Make sure to convert units correctly when working with small values such as microamperes.
In a p-n-p transistor,
View Solution
In a p-n-p transistor, the emitter is heavily doped to increase the number of charge carriers for current conduction. The collector is moderately doped to allow proper control over the current flow. The base, which is located between the emitter and collector, is lightly doped.
Thus, the correct relation for the doping levels in a p-n-p transistor is: \[ Emitter is heavily doped, Collector is moderately doped. \] Quick Tip: Remember that the doping levels in a transistor are crucial for controlling its current gain and behavior.
A carrier wave of peak voltage 15 V is used to transmit a message signal. If the modulation index is 60%, then the peak voltage of the modulating signal is
View Solution
The modulation index (\( m \)) is defined as the ratio of the peak voltage of the modulating signal (\( V_m \)) to the peak voltage of the carrier signal (\( V_c \)):
\[ m = \frac{V_m}{V_c} \]
Given: \[ V_c = 15 \, V, \quad m = 60% = 0.6 \]
To find \( V_m \), use the formula:
\[ V_m = m \times V_c \]
Substitute the values:
\[ V_m = 0.6 \times 15 = 9 \, V \]
Thus, the peak voltage of the modulating signal is \( \boxed{9 \, V} \). Quick Tip: The modulation index relates the peak voltage of the modulating signal to the carrier signal. Multiply the modulation index with the peak carrier voltage to determine the peak modulating signal voltage.
Vijayawada FM radio station broadcasts at frequency of 103.4 MHz. The wavelength of the corresponding radio waves (in m) is
View Solution
We are given the frequency \( f = 103.4 \, MHz = 103.4 \times 10^6 \, Hz \). To calculate the wavelength, we use the formula: \[ \lambda = \frac{c}{f} \]
where \( c = 3 \times 10^8 \, m/s \) is the speed of light.
Substituting the values, we get: \[ \lambda = \frac{3 \times 10^8 \, m/s}{103.4 \times 10^6 \, Hz} = 2.90 \, m \] Quick Tip: To convert MHz to Hz, multiply by \(10^6\). The formula \( \lambda = \frac{c}{f} \) is crucial for calculating the wavelength of radio waves.
The minimum number of quantum numbers required to specify an orbital in an atom is
View Solution
To specify an orbital in an atom, three quantum numbers are required:
1. Principal quantum number (\( n \)): Specifies the energy level.
2. Azimuthal quantum number (\( l \)): Specifies the shape of the orbital.
3. Magnetic quantum number (\( m_l \)): Specifies the orientation of the orbital.
These three quantum numbers are sufficient to describe an orbital completely.
Thus, the minimum number of quantum numbers required to specify an orbital is \( \boxed{3} \). Quick Tip: Remember that to define an orbital, you need three quantum numbers: \( n \), \( l \), and \( m_l \).
Consider the following two statements:
Statement I: Among Mg, Al, Mg\(^2\), Al\(^3\), the one having smallest size is Al\(^3\)
Statement II: Eu is having exceptionally high atomic radii among lanthanide elements
The correct answer is:
View Solution
Statement I: The ionic size of Al\(^3\) is the smallest among the given ions (Mg\(^2\), Al\(^3\), Mg\), since the size decreases as the charge increases for the same period.
Statement II: Eu (Europium) has one of the largest ionic radii among the lanthanides, and this is a known fact in periodic trends.
Thus, both statements I and II are correct. Quick Tip: When comparing ions of the same period, the ionic size decreases as the positive charge on the ion increases.
Identify the pair of elements with the highest and lowest electronegativity respectively
View Solution
Electronegativity refers to the ability of an atom to attract shared electrons in a chemical bond.
- Fluorine (F) is the most electronegative element in the periodic table, with a high electronegativity value.
- Francium (Fr) has the lowest electronegativity value due to its large atomic size and low effective nuclear charge.
Thus, the pair of elements with the highest and lowest electronegativity respectively is \( \boxed{F and Fr} \). Quick Tip: Fluorine has the highest electronegativity, while Francium has the lowest.
If the bond order in \( C_2 \) is \( x \), then the bond order in \( B_2 \) and \( O_2 \), respectively are:
View Solution
Bond order is related to the number of bonding and antibonding electrons in a molecule. For molecules like \( C_2 \), \( B_2 \), and \( O_2 \), the bond order can be calculated using the molecular orbital theory.
For \( C_2 \), the bond order is \( x \), which indicates that the total bonding electrons contribute to the bond strength. The molecular orbital theory states that in \( B_2 \) and \( O_2 \), bond orders are proportional to the bonding electron count relative to the number of electrons in the antibonding orbitals.
Thus, if the bond order in \( C_2 \) is \( x \), we find that the bond order in \( B_2 \) is \( \frac{1}{2} x \), and the bond order in \( O_2 \) is \( x \). Quick Tip: The bond order can be calculated as: \[ Bond Order = \frac{Number of bonding electrons - Number of antibonding electrons}{2} \]
Identify incorrectly matched set from the following
View Solution
- Molecules with incomplete octet: BeH2 and BC13 have incomplete octets, so this pair is correct.
- Polar molecules: BF3 is a non-polar molecule due to its symmetrical triangular shape, while CCl4 is also non-polar. Hence, the pair is incorrect.
- Molecules with expanded octet: PCl5 and SF6 both have expanded octets, so this pair is correct.
- Odd electron molecules: NO and NO2 are odd electron molecules, so this pair is correct.
Thus, the incorrectly matched pair is \( \boxed{BF3, CCl4} \). Quick Tip: When determining the polarity of a molecule, always consider its geometry and electron distribution.
An ideal gas (X) present in a vessel of volume \( V \) exerted a pressure of 16.4 atm at 200 K. What is its concentration in mol \( L^{-1} \)?
% Given Data
Given \( R = 0.082 \, L atm mol^{-1} K^{-1} \)
View Solution
We can use the ideal gas law, which is given by:
\[ PV = nRT \]
Where:
- \( P \) is the pressure (16.4 atm)
- \( V \) is the volume (given as \( V \) L)
- \( n \) is the number of moles
- \( R \) is the ideal gas constant (0.082 L atm mol\(^{-1}\) K\(^{-1}\))
- \( T \) is the temperature (200 K)
We can rewrite the equation to find the concentration (\( n/V \)):
\[ P = \frac{nRT}{V} \]
\[ \frac{n}{V} = \frac{P}{RT} \]
Substitute the known values:
\[ \frac{n}{V} = \frac{16.4 \, atm}{(0.082 \, L atm mol^{-1} K^{-1}) \times (200 \, K)} \]
\[ \frac{n}{V} = \frac{16.4}{16.4} = 1.00 \, mol L^{-1} \]
Thus, the concentration of the gas is \( 1.00 \, mol L^{-1} \). Quick Tip: Always remember that concentration is simply \( \frac{n}{V} \), which is moles per unit volume. In problems involving ideal gases, use the ideal gas law to find the concentration.
A 100 L cylinder containing H2 exerted a pressure of 4 atm at 300 K. It was accidentally opened and some H2 was escaped. When it was closed, it exerted a pressure of 3 atm at 300 K. The number of moles of H2 remaining in the cylinder is equal to
View Solution
Given the ideal gas law:
\[ PV = nRT \]
Where:
- \( P \) is pressure
- \( V \) is volume
- \( n \) is the number of moles
- \( R \) is the gas constant
- \( T \) is temperature
At initial conditions: \[ P_1 = 4 \, atm, \, V = 100 \, L, \, T = 300 \, K \]
Using the ideal gas law:
\[ P_1 V = n_1 R T \]
So, the number of moles initially in the cylinder is:
\[ n_1 = \frac{P_1 V}{RT} \]
At final conditions: \[ P_2 = 3 \, atm, \, V = 100 \, L, \, T = 300 \, K \]
Using the ideal gas law again:
\[ P_2 V = n_2 R T \]
Thus, the number of moles remaining in the cylinder is:
\[ n_2 = \frac{P_2 V}{RT} \]
Since the volume and temperature remain constant, the ratio of the final to initial moles is:
\[ \frac{n_2}{n_1} = \frac{P_2}{P_1} = \frac{3}{4} \]
Thus, the number of moles remaining in the cylinder is \( \boxed{\frac{1}{R}} \). Quick Tip: Remember, when dealing with ideal gases, the number of moles is proportional to pressure when volume and temperature are constant.
An ideal gas (X) present in a vessel of volume \( V \) exerted a pressure of 16.4 atm at 200 K. What is its concentration in mol \( L^{-1} \)?
% Given Data
Given \( R = 0.082 \, L atm mol^{-1} K^{-1} \)
View Solution
We can use the ideal gas law, which is given by:
\[ PV = nRT \]
Where:
- \( P \) is the pressure (16.4 atm)
- \( V \) is the volume (given as \( V \) L)
- \( n \) is the number of moles
- \( R \) is the ideal gas constant (0.082 L atm mol\(^{-1}\) K\(^{-1}\))
- \( T \) is the temperature (200 K)
We can rewrite the equation to find the concentration (\( n/V \)):
\[ P = \frac{nRT}{V} \]
\[ \frac{n}{V} = \frac{P}{RT} \]
Substitute the known values:
\[ \frac{n}{V} = \frac{16.4 \, atm}{(0.082 \, L atm mol^{-1} K^{-1}) \times (200 \, K)} \]
\[ \frac{n}{V} = \frac{16.4}{16.4} = 1.00 \, mol L^{-1} \]
Thus, the concentration of the gas is \( 1.00 \, mol L^{-1} \). Quick Tip: Always remember that concentration is simply \( \frac{n}{V} \), which is moles per unit volume. In problems involving ideal gases, use the ideal gas law to find the concentration.
If the standard enthalpy change (\(\Delta H^o\)) for a certain reaction at 298 K and constant pressure is -1860 kJ mol\(^{-1}\), the standard entropy change (\(\Delta S^o\)) of the same reaction is -550 J K\(^{-1}\) mol\(^{-1}\), which of the following statements is correct?
View Solution
We are given: \[ \Delta H^o = -1860 \, kJ/mol = -1860 \times 10^3 \, J/mol \]
and \[ \Delta S^o = -550 \, J/mol/K \]
To find the free energy change (\(\Delta G^o\)) at 298 K, we use the following relation: \[ \Delta G^o = \Delta H^o - T \Delta S^o \]
Substituting the given values: \[ \Delta G^o = (-1860 \times 10^3) - 298 \times (-550) \] \[ \Delta G^o = -1860 \times 10^3 + 163900 \] \[ \Delta G^o = -1694900 \, J/mol \]
The reaction is spontaneous if \(\Delta G^o\) is negative, which it is, hence the reaction is spontaneous.
Thus, the correct statement is option (3). Quick Tip: For spontaneity, check if the Gibbs free energy (\(\Delta G^o\)) is negative. Use \(\Delta G^o = \Delta H^o - T \Delta S^o\) to calculate.
If the standard enthalpy change (\(\Delta H^o\)) for reaction
\[ H_2(g) + Br_2(l) \rightarrow 2 HBr(g) \]
is \(-72.8 \, kJ\), the standard enthalpy of formation (\(\Delta H_f^o\)) of \(HBr(g)\) in \(kJ mol^{-1}\) is:
View Solution
The enthalpy change for the reaction is given as:
\[ \Delta H^\circ = -72.8 \, kJ \]
For the reaction where 2 moles of \(HBr(g)\) are formed, we divide the total enthalpy change by 2 to find the enthalpy of formation for one mole of \(HBr(g)\):
\[ \Delta H_f^\circ (HBr(g)) = \frac{-72.8 \, kJ}{2} = -36.4 \, kJ/mol \]
Thus, the standard enthalpy of formation of \(HBr(g)\) is \(-36.4 \, kJ/mol\). Quick Tip: To calculate the enthalpy of formation, divide the given enthalpy change by the number of moles of the substance involved in the reaction.
At \( T(K) \), the equilibrium constant for \( A (g) \rightleftharpoons B (g) \) is \( 10^2 \). If the rate of forward reaction is 0.025 mol L\(^{-1}\) s\(^{-1}\), the rate of backward reaction (in mol L\(^{-1}\) s\(^{-1}\)) is
View Solution
The equilibrium constant \( K \) is given by the equation: \[ K = \frac{rate of backward reaction}{rate of forward reaction} \]
We are given: \[ K = 10^2 = 100, \quad rate of forward reaction = 0.025 \, mol L^{-1} \, s^{-1} \]
Substituting the values into the equilibrium constant expression: \[ 100 = \frac{rate of backward reaction}{0.025} \] \[ rate of backward reaction = 100 \times 0.025 = 2.5 \times 10^{-2} \, mol L^{-1} \, s^{-1} \]
Thus, the rate of the backward reaction is \( \boxed{2.5 \times 10^{-2}} \). Quick Tip: Use the expression for equilibrium constant to relate the rates of forward and backward reactions.
One mole \(H_2O(g)\) and one mole \(CO(g)\) are taken in a 1L flask and heated to 725K. At equilibrium, 40% (by mass) of water reacted with \(CO(g)\) as follows:
\[ H_2O(g) + CO(g) \rightleftharpoons H_2(g) + CO_2(g) \]
Its \(K_c\) value is:
View Solution
At equilibrium, the initial number of moles of \(H_2O(g)\) and \(CO(g)\) are both 1 mole. According to the question, 40% of water reacts with CO, so:
\[ Moles of H_2O reacted = 0.4 \times 1 = 0.4 \, moles \]
Therefore, the moles of products formed are: \[ Moles of H_2 = Moles of CO_2 = 0.4 \]
The remaining moles of \(H_2O(g)\) and \(CO(g)\) are: \[ Remaining moles of H_2O(g) = 1 - 0.4 = 0.6 \, moles \] \[ Remaining moles of CO(g) = 1 - 0.4 = 0.6 \, moles \]
Thus, at equilibrium, the total volume of the system is 1L. Now, we calculate the concentration of each species:
\[ [H_2O(g)] = \frac{0.6}{1} = 0.6 \, mol/L \] \[ [CO(g)] = \frac{0.6}{1} = 0.6 \, mol/L \] \[ [H_2(g)] = \frac{0.4}{1} = 0.4 \, mol/L \] \[ [CO_2(g)] = \frac{0.4}{1} = 0.4 \, mol/L \]
Now, we can calculate the equilibrium constant \(K_c\) using the expression:
\[ K_c = \frac{[H_2][CO_2]}{[H_2O][CO]} \]
Substituting the values:
\[ K_c = \frac{(0.4)(0.4)}{(0.6)(0.6)} = \frac{0.16}{0.36} = 0.444 \]
Thus, the correct answer is \(K_c = 0.444\). Quick Tip: To calculate \(K_c\), remember to use the equilibrium concentrations of the species involved in the reaction.
The O-H bond length in \( H_2O \) in gas phase is
View Solution
The O-H bond length in water molecules in the gas phase is well known to be approximately 95.7 pm (picometers).
Thus, the correct bond length is \( \boxed{95.7} \, pm \). Quick Tip: In molecular structures, bond lengths can vary depending on the phase of the substance. Always refer to standard tables for the exact bond length values in different phases.
Which of the following alloys are correctly matched with their uses?
\[ i) Li/Mg \quad armour plates \] \[ ii) Cu/Be \quad high strength springs \] \[ iii) Mg/Al \quad aircraft construction \]
View Solution
Let's check the uses of each alloy:
- Li/Mg: Lithium and magnesium alloys are widely used in making armour plates, hence option (i) is correct.
- Cu/Be: Copper and beryllium alloys are known for their high strength, particularly in springs, so option (ii) is correct.
- Mg/Al: Magnesium and aluminium alloys are commonly used in the aerospace industry, especially in aircraft construction, making option (iii) correct.
Thus, all the alloys are correctly matched with their uses.
The correct answer is option (4) i, ii, iii. Quick Tip: When studying alloys, remember their key properties like strength, lightness, and corrosion resistance to match them with their uses.
Match the following
List I and List II
(A) Al (I) 135 pm
(B) Ga (II) 143 pm
(C) In (III) 170 pm
(D) Tl (IV) 167 pm
View Solution
The correct matching of elements from Group 13 with their respective metallic radii is as follows:
- \( Al \) (Aluminium) has a metallic radius of \( 135 \, pm \), so A-I.
- \( Ga \) (Gallium) has a metallic radius of \( 143 \, pm \), so B-II.
- \( In \) (Indium) has a metallic radius of \( 170 \, pm \), so C-IV.
- \( Tl \) (Thallium) has a metallic radius of \( 167 \, pm \), so D-III.
Thus, the correct match is \( \boxed{A-I, B-II, C-IV, D-III} \). Quick Tip: When dealing with periodic table elements and their properties, remember to check the periodic trends like metallic radii, which generally increase down a group.
Choose the acidic oxide from the following:
View Solution
- CO (Carbon monoxide) is a neutral oxide, hence not an acidic oxide.
- GeO (Germanium oxide) is an acidic oxide, as it reacts with water to form an acidic solution.
- SnO (Tin(II) oxide) is amphoteric, meaning it can react both as an acid and a base.
- PbO (Lead(II) oxide) is amphoteric as well, reacting both with acids and bases.
Thus, the correct acidic oxide among the given options is GeO.
The correct answer is option (2) GeO. Quick Tip: Acidic oxides typically react with water to form acids. Examples include CO\(_2\), SO\(_3\), and GeO.
In the Kolbe electrolysis of sodium propanoate, the products X and Y are formed at the respective electrodes. What are X and Y?
View Solution
In Kolbe electrolysis, the reaction involves the breaking of a carboxylate ion, followed by the production of the alkane. The process involves the formation of two molecules of hydrocarbons at the anode as a result of two electrons being released per molecule. In this case, sodium propanoate undergoes electrolysis to form butane at the anode and hydrogen at the cathode.
Hence, the product at the anode is the alkane (butane), and the product at the cathode is hydrogen gas.
Thus, the correct products are:
- \( X = CH_3CH_2CH_2CH_3 \) at Anode
- \( Y = H_2 \) at Cathode
The correct option is \( \boxed{3} \). Quick Tip: In Kolbe electrolysis, remember that alkanes are produced at the anode, and hydrogen gas is produced at the cathode. This is a crucial part of the reaction mechanism.
Which of the following molecules is not aromatic?
View Solution
Aromaticity is determined by Hückel's rule (4n + 2 \(\pi\)-electrons in a cyclic, planar, conjugated system):
(a) Cyclohexa-1,3-diene: 4 \(\pi\)-electrons (non-aromatic, violates Hückel’s rule).
(b) Benzene: 6 \(\pi\)-electrons (aromatic).
(c) Cyclopentadienyl anion: 6 \(\pi\)-electrons (aromatic).
(d) Tropylium cation: 6 \(\pi\)-electrons (aromatic).
Only option (a) lacks aromaticity.
Thus, the correct answer is \(\boxed{1}\). Quick Tip: To identify aromaticity: 1. Check for a cyclic, planar structure. 2. Count π-electrons in the conjugated system. 3. Verify if it follows \(4n + 2\) rule (\(n = 0, 1, 2,...\)).
An example of a network solid is:
View Solution
A network solid is a chemical compound in which atoms are bonded covalently in a continuous network extending throughout the material. Key examples include:
\(SiO_2\) (Silicon dioxide): Forms a 3D covalent network where each Si atom is tetrahedrally bonded to four O atoms, and each O atom bridges two Si atoms.
\(MgO\) (Magnesium oxide): Ionic solid, not covalent network.
\(CaF_2\) (Calcium fluoride): Ionic crystal.
\(ZnS\) (Zinc sulfide): Exists as either ionic or molecular solid depending on form, but not a classic network solid like \(SiO_2\).
Thus, the correct answer is (1). Quick Tip: Network solids are characterized by: 1. High melting points due to strong covalent bonds. 2. Insolubility in most solvents. 3. Examples: Diamond (\(C\)), \(SiO_2\), Boron Nitride (\(BN\)).
20 mL of 0.1 M HCl is added to 30 mL of 0.1 M NaOH. To this solution, extra 50 mL of water was added. What is the molarity of the final solution formed?
View Solution
To determine the molarity of the final solution, we follow these steps:
Calculate moles of HCl and NaOH:
- Moles of HCl = \( 20 mL \times 0.1 M = 2 mmol \)
- Moles of NaOH = \( 30 mL \times 0.1 M = 3 mmol \)
Neutralization reaction: \[ HCl + NaOH \rightarrow NaCl + H_2O \]
- HCl is the limiting reagent (2 mmol reacts completely).
- Remaining NaOH = \( 3 mmol - 2 mmol = 1 mmol \).
Total volume of final solution: \[ 20 mL + 30 mL + 50 mL = 100 mL \]
Molarity of remaining NaOH: \[ Molarity = \frac{1 mmol}{100 mL} = 0.01 M \]
Thus, the molarity of the final solution is (2). Quick Tip: In neutralization problems, always: 1. Calculate initial moles of acid and base. 2. Identify the limiting reagent. 3. Account for the total volume after mixing and dilution.
20 mL of 0.1 M HCl is added to 30 mL of 0.1 M NaOH. To this solution, extra 50 mL of water was added. What is the molarity of the final solution formed?
View Solution
Calculate initial moles:
\begin{align*
Moles of HCl &= 20\,\text{mL \times 0.1\,\text{M = 2\,\text{mmol
\text{Moles of NaOH &= 30\,\text{mL \times 0.1\,\text{M = 3\,\text{mmol
\end{align*
Neutralization reaction: \[ \text{HCl + NaOH \rightarrow NaCl + H_2O \]
- HCl is limiting (2 mmol reacts completely)
- Excess NaOH = \(3\,mmol - 2\,mmol = 1\,mmol\)
Total volume after dilution: \[ 20\,mL (HCl) + 30\,mL (NaOH) + 50\,mL (water) = 100\,mL \]
Final molarity calculation: \[ Molarity = \frac{1\,mmol}{100\,mL} = 0.01\,M \]
Thus, the correct answer is (2). Quick Tip: In neutralization problems: 1. Always identify the limiting reagent first 2. Total volume includes all added liquids (reactants + solvents) 3. Molarity = \(\frac{moles of solute}{total volume in liters}\)
The conductivity of a solution containing 2.08 g of anhydrous barium chloride in 200 mL solution is \(6 \times 10^{-3} \, ohm^{-1} \, cm^{-1}\). The molar conductivity of the solution (in \(ohm^{-1} \, cm^{2} \, mol^{-1}\)) is \(x \times 10^{2}\). The value of \(x\) is
(Atomic mass of Ba = 137, Cl = 35.5)
View Solution
Calculate molarity of BaCl\(_2\) solution:
\begin{align*
Molar mass of BaCl_2 &= 137 + 2 \times 35.5 = 208 \, \text{g/mol
\text{Moles of BaCl_2 &= \frac{2.08 \, \text{g{208 \, \text{g/mol = 0.01 \, \text{mol
\text{Molarity &= \frac{0.01 \, \text{mol{0.2 \, \text{L = 0.05 \, \text{M
\end{align*
Calculate molar conductivity (\(\Lambda_m\)): \[ \Lambda_m = \frac{\kappa \times 1000{Molarity} = \frac{6 \times 10^{-3} \times 1000}{0.05} = 120 \, ohm^{-1} \, cm^{2} \, mol^{-1} \]
Express in required form: \[ 120 = 1.2 \times 10^{2} \Rightarrow x = 1.2 \]
Thus, the correct answer is (1). Quick Tip: Key formulas for conductivity calculations: 1. Molarity = \(\frac{moles of solute}{volume in liters}\) 2. Molar conductivity (\(\Lambda_m\)) = \(\frac{\kappa \times 1000}{Molarity}\) 3. 1 M = 1 mol/L
For the reaction A + B → C, the following data were obtained:
\begin{tabular{cccc
\toprule
Expt. & [A] (M) & [B] (M) & Initial rate (M min\(^{-1}\))
\midrule
1. & 0.1 & 0.1 & \(1.0 \times 10^{-4}\)
2. & 0.1 & 0.3 & \(9.0 \times 10^{-4}\)
3. & 0.3 & 0.3 & \(2.7 \times 10^{-3}\)
\bottomrule
\end{tabular
The order of reaction with respect to A and B are respectively
View Solution
Let the rate law be: Rate = \(k[A]^x[B]^y\)
For order w.r.t B (y):
Compare Expt 1 & 2 (constant [A]): \[ \frac{9.0 \times 10^{-4}}{1.0 \times 10^{-4}} = \left(\frac{0.3}{0.1}\right)^y \Rightarrow 9 = 3^y \Rightarrow y = 2 \]
For order w.r.t A (x):
Compare Expt 2 & 3 (constant [B]): \[ \frac{2.7 \times 10^{-3}}{9.0 \times 10^{-4}} = \left(\frac{0.3}{0.1}\right)^x \Rightarrow 3 = 3^x \Rightarrow x = 1 \]
Thus, orders are 1 (A) and 2 (B). Answer: (1). Quick Tip: Key steps: 1. Compare experiments where only one concentration changes 2. Solve for exponent that matches rate ratios 3. Verify with multiple data pairs when possible
The correct statements about Zeolites are:
1. They are good shape selective catalysts
2. They contain Al-O-Si framework
3. They are not found in nature
4. They are used as catalysts for cracking hydrocarbons in the petrochemical industry.
View Solution
Statement I: Correct. Zeolites are widely used as shape-selective catalysts due to their porous structure.
Statement II: Correct. Zeolites have a three-dimensional Al-O-Si framework with well-defined pores and cavities.
Statement III: Incorrect. Zeolites \textit{are found in nature (e.g., volcanic rocks) and can also be synthesized artificially.
Statement IV: Correct. Zeolites (especially ZSM-5) are extensively used in petroleum refining for catalytic cracking of hydrocarbons.
Thus, the correct combination is I, II, and IV only, making option (3) correct. Quick Tip: Key properties of zeolites: 1. Microporous aluminosilicate minerals 2. Act as molecular sieves due to uniform pore size 3. Both natural and synthetic forms exist 4. Important in petroleum refining and water softening
Which of the following is not the application of adsorption?
View Solution
Adsorption involves the accumulation of substances on surfaces. The non-application is:
SiO\(_2\) gel: Adsorbs moisture (application)
Coconut charcoal: Adsorbs gases (application)
Al\(_2\)O\(_3\): Used as adsorbent in chromatography (application)
CaCl\(_2\): Removes moisture by \textit{absorption (not adsorption) - forms hydrates
Thus, the correct answer is (4). Quick Tip: Key difference: 1. Adsorption = surface phenomenon 2. Absorption = bulk phenomenon (e.g., CaCl\(_2\) dissolving water)
How many of the following metals can be purified by using zone refining method?
Ni, B, Ti, In, Ge, Mn, Ag, Si, Ga
View Solution
Zone refining is effective for elements requiring high purity, especially in the semiconductor industry. Elements purified by zone refining include:
- Germanium (Ge): Essential for electronic devices.
- Silicon (Si): Crucial for integrated circuits.
- Gallium (Ga): Used in semiconductors.
- Indium (In): Important for LCDs and conductive coatings.
- Boron (B): Used in high-tech applications.
- Nickel (Ni): For ultra-high purity applications.
Not typically purified by zone refining:
- Titanium (Ti): Purified using the Kroll process.
- Manganese (Mn): Purified using electrolytic refining.
- Silver (Ag): Purified using electrorefining.
Thus, 6 elements (Ge, Si, Ga, In, B, Ni) can be purified by zone refining, making the correct answer (2). Quick Tip: Key points about zone refining: 1. Works best for elements with low distribution coefficients
2. Creates ultra-high purity (99.9999%) materials
3. Most important for semiconductor manufacturing
4. Requires multiple passes for effective purification
For ozone molecule consider the following:
1. It is a linear molecule with bond angle \(180^\circ\)
2. It is an angular molecule with bond angle \(117^\circ\)
3. The bond lengths of both O-O bonds are same
4. With respect to oxygen it is thermodynamically more stable
The correct options are
View Solution
The ozone molecule (O\(_3\)) has a unique structure and properties:
- Option A: False. O\(_3\) has bent (angular) geometry due to lone pair repulsion.
- Option B: True. Bond angle is \(117^\circ\).
- Option C: True. Resonance gives equal bond lengths.
- Option D: False. O\(_3\) is thermodynamically unstable relative to O\(_2\).
Thus, the correct options are B and C. Answer: (2). Quick Tip: Key facts about ozone: 1. Bent molecular geometry (VSEPR)
2. Resonance hybrid structure
3. Endothermic formation (\(\Delta H > 0\))
4. Equal O-O bond lengths (1.28 Å)
From the list given below, the number of lanthanides which exhibit +4 state in their compounds is:
Given lanthanides: Pr, Nd, Pm, Sm, Eu, Gd, Tb, Dy
View Solution
Lanthanides exhibiting +4 state:
- Praseodymium (Pr): Exhibits +4 state (4f\(^1\) configuration).
- Terbium (Tb): Shows +4 state (4f\(^7\) half-filled configuration).
- Neodymium (Nd): Can achieve +4 state (4f\(^2\) configuration).
Lanthanides not showing +4 state:
- Promethium (Pm), Samarium (Sm), Europium (Eu), Gadolinium (Gd), Dysprosium (Dy).
Thus, 3 lanthanides (Pr, Nd, Tb) exhibit +4 oxidation state, making option (2) correct. Quick Tip: Key points about lanthanide oxidation states: 1. +3 is the most common state for all lanthanides
2. +4 state occurs when it creates special stability (empty/half-filled/filled f-subshell)
3. +2 state appears when it leads to f\(^7\) or f\(^{14}\) configurations
4. Ce\(^{4+}\) (not in list) is the most stable +4 lanthanide ion
Monomers of nylon 2-nylon 6 are:
View Solution
Nylon 2-nylon 6 is a biodegradable polyamide copolymer. Its monomers are:
- Glycine (H\(_2\)N-CH\(_2\)-COOH): Provides the "nylon 2" segment.
- 6-Aminohexanoic acid (Aminocaproic acid): Provides the "nylon 6" segment.
Polymerization occurs through condensation reaction between amino and carboxyl groups.
Why other options are incorrect:
- Option (2): Monomers for nylon 6,6.
- Option (3): Monomer for nylon 6.
- Option (4): Monomers for PET.
Thus, the correct answer is (1). Quick Tip: Key features of nylon 2-nylon 6: 1. Biodegradable alternative to conventional nylons
2. Contains alternating short (2C) and long (6C) segments
3. Amide linkages make it strong but flexible
4. Used in specialty applications requiring biodegradability
Given below are two statements:
Assertion (A): Hydrolysis of DNA does not form equal numbers of adenine (A) and thymine (T), or guanine (G) and cytosine (C).
Reason (R): In DNA, adenine forms hydrogen bonds with thymine and cytosine forms hydrogen bonds with guanine.
The correct answer is:
View Solution
- Evaluation of Assertion (A): DNA hydrolysis produces equal amounts of A and T, and G and C. Thus, A is incorrect.
- Evaluation of Reason (R): The statement about base pairing is accurate. Thus, R is correct.
- Relationship between A and R: R correctly describes base pairing but does not explain A.
Thus, the correct choice is (4). Quick Tip: Key DNA facts: 1. Chargaff's rules: A = T and G = C in any DNA molecule
2. Base pairing: A-T (2 H-bonds), G-C (3 H-bonds)
3. Hydrolysis breaks phosphodiester bonds, not base pairs
4. Equal amounts result from complementary strand pairing
The structure of Gly-Ala (Glycylalanine) is:
View Solution
Gly-Ala (Glycylalanine) is a dipeptide composed of:
- Glycine (Gly) as the N-terminal amino acid.
- Alanine (Ala) as the C-terminal amino acid.
Correct structural features:
- Free amino group (-NH\(_2\)) at the N-terminus.
- Free carboxyl group (-COOH) at the C-terminus.
- Peptide bond (-CO-NH-) linking the two amino acids.
- Methyl side chain (-CH\(_3\)) from alanine.
Analysis of options:
- Option 1: Shows two separate amino acids (Gly + Ala), not a dipeptide.
- Option 2: Correct dipeptide structure with proper peptide bond.
- Option 3: Incorrect hydroxyl group (OH) at N-terminus.
- Option 4: Shows ester linkage (-CO-O-) instead of peptide bond.
Thus, the correct answer is (2). Quick Tip: Key points about dipeptides: 1. Always drawn with N-terminus (NH\(_2\)) on left
2. Peptide bonds are rigid and planar
3. R-groups alternate above/below the peptide chain
4. Named from N-terminal to C-terminal residue
The group present in prontosil is
View Solution
Prontosil (the first sulfa drug) contains:
- A characteristic azo group (-N=N-) linking two aromatic rings.
- This was the active component that metabolizes to sulfanilamide.
- Structure: Contains -N=N- linkage.
Key features:
- Azo dyes have -N=N- linkage.
- Options 2-4 don't exist in prontosil.
Thus, the correct answer is (1). Quick Tip: Remember: 1. Azo compounds are characterized by -N=N- linkage.
2. Prontosil was the first commercially available antibiotic.
3. In vivo, it breaks down to release sulfanilamide.
The optically inactive compound from the following is:
View Solution
A compound is optically inactive if it either:
1. Lacks a chiral center (no carbon with four different substituents), or
2. Exists as a racemic mixture (which isn't relevant for this question)
Analysis of each option:
1. 2-Bromopropanal (\chemfig{CH_3-C(=O)-CH_2Br)
- Contains a chiral center at C-2 (attached to -H, -Br, -CHO, -CH\(_3\))
- Optically active
2. 3-Bromopropanal (\chemfig{Br-CH_2-CH_2-CHO)
- No chiral center (C-1: attached to two H's; C-2: attached to two CH\(_2\) groups)
- Optically inactive
3. 3-Bromo-2-iodopropanal (\chemfig{Br-CH_2-CH(I)-CHO)
- Chiral center at C-2 (attached to -H, -I, -CHO, -CH\(_2\)Br)
- Optically active
4. 2-Bromo-3-iodopropanal (\chemfig{I-CH_2-CH(Br)-CHO)
- Chiral center at C-2 (attached to -H, -Br, -CHO, -CH\(_2\)I)
- Optically active
Conclusion:
Only 3-Bromopropanal lacks any chiral center and is therefore optically inactive. Quick Tip: \textbf{How to identify chiral centers:}
1. Look for carbons with four different substituents
2. Sp\(^3\) hybridized carbons only
3. Terminal CH\(_3\) and CH\(_2\) groups are never chiral
4. Aldehyde carbons (CHO) are never chiral
Which is the correct option for the following reaction?
\[ 2\,CH_3CH_2Br \xrightarrow{2Na/Dry ether} ? \]
Options:
View Solution
This is a Wurtz reaction where two ethyl bromide molecules couple to form butane (\chemfig{CH_3-CH_2-CH_2-CH_3).
Key points:
- Wurtz reaction combines two identical alkyl halides
- Produces symmetrical alkanes (here: butane)
- Uses Na/dry ether conditions
- Wurtz-Fittig requires an aryl halide (not present here)
- Pentane would require different reactants Quick Tip: \textbf{Remember:} - Wurtz: 2R-X → R-R - Wurtz-Fittig: R-X + Ar-X → R-Ar
The number of products obtained in the following reaction is:
Reaction:

View Solution
The given reaction involves the base-catalyzed (NaOH) decomposition of 1-phenylethanol (Ph-CH(OH)-CH\(_3\)) under heating (\(\Delta\)). This leads to two main products through different pathways:
Product 1: Acetophenone (Ph-CO-CH\(_3\))
- Formed via oxidation of the alcohol
- The base abstracts a proton from the -OH group
- Resulting in formation of a carbonyl group
Product 2: Styrene (Ph-CH=CH\(_2\))
- Formed via elimination reaction
- NaOH abstracts a proton from the β-carbon
- Leads to formation of a double bond
Mechanistic pathways:
1. Oxidation pathway:
\[ Ph-CH(OH)-CH_3 \rightarrow Ph-CO-CH_3 \]
2. Elimination pathway:
\[ Ph-CH(OH)-CH_3 \rightarrow Ph-CH=CH_2 \]
Why not other options?
- Only these two major products form under these conditions
- No significant side products are expected
- The reaction doesn't proceed to complete decomposition Quick Tip: \textbf{Key observations:}
1. Secondary alcohols can undergo both oxidation and elimination
2. Base promotes β-elimination in benzylic alcohols
3. Heating drives both reactions forward
4. No rearrangement products expected in this case
What are 'X' and 'Y' respectively in the following reactions?
\[ C_6H_5CHO + C_6H_5COCH_3 \xrightarrow{OH^-,\ 293K} X \xrightarrow{NaBH_4} Y \]
Options:
View Solution
Step 1: Aldol Condensation (Formation of X)
\[ C_6H_5CHO + C_6H_5COCH_3 \xrightarrow{OH^-} C_6H_5CH=CHCOC_6H_5 + H_2O \]
1. Benzaldehyde + acetophenone gives chalcone (X)
2. α,β-unsaturated ketone formed via dehydration
Step 2: Reduction (Formation of Y)
\[ C_6H_5CH=CHCOC_6H_5 \xrightarrow{NaBH_4} C_6H_5CH=CHCH(OH)C_6H_5 \]
1. NaBH\(_4\) selectively reduces carbonyl group
2. Double bond remains intact
3. Forms allylic alcohol (Y)
Thus, the correct pair is \(\boxed{3}\). Quick Tip: Key Mechanisms:
1. Aldol condensation requires \alpha-hydrogens
2. NaBH\(_4\) reduces only carbonyls, not C=C bonds
3. Chalcones are important flavonoid precursors
Which of the following is used in perfumery?
Options:
View Solution
1. Benzoate esters are widely used in perfumery due to their:
- Pleasant floral/fruity aromas
- Chemical stability
- Occurrence in natural essential oils
2. Common examples:
- Methyl benzoate - ylang-ylang-like scent
- Ethyl benzoate - sweet wintergreen odor
- Benzyl benzoate - balsamic fragrance
3. Other options are unsuitable:
- Ethanoic acid (vinegar smell)
- Methanol (toxic)
- Formaldehyde (irritating)
Thus, the correct answer is \(\boxed{1}\). Quick Tip: Perfumery Compounds:
1. Esters provide fruity/floral notes
2. Benzoates are base notes in fragrance pyramids
3. Natural sources include jasmine and tuberose
Arrange the following in increasing order of their boiling points:
N-Ethylethanamine Butanamine N,N-Dimethylethanamine
(I) (II) (III)
View Solution
The boiling points of amines depend on:
1. Hydrogen bonding capability
2. Molecular weight/size
3. Degree of branching
Analysis of each compound:
1. N,N-Dimethylethanamine (III) - (CH\(_3\))\(_2\)N-CH\(_2\)-CH\(_3\)
- No N-H bonds for intermolecular H-bonding
- Most branched structure
- Lowest boiling point (~37°C)
2. N-Ethylethanamine (I) - CH\(_3\)-CH\(_2\)-NH-CH\(_2\)-CH\(_3\)
- One N-H bond (weaker H-bonding than primary amines)
- Less branched than III
- Intermediate boiling point (~55°C)
3. Butanamine (II) - CH\(_3\)-CH\(_2\)-CH\(_2\)-CH\(_2\)-NH\(_2\)
- Two N-H bonds (strongest H-bonding)
- Unbranched primary amine
- Highest boiling point (~78°C)
Order of boiling points:
\[ III (Tertiary amine) \(<\) I (Secondary amine) \(<\) II (Primary amine) \] Quick Tip: \textbf{Key factors affecting amine boiling points:}
1. Primary amines \(>\) Secondary amines \(>\) Tertiary amines (H-bonding ability)
2. Longer chains \(>\) shorter chains (van der Waals forces)
3. Straight chains \(>\) branched chains (better packing)













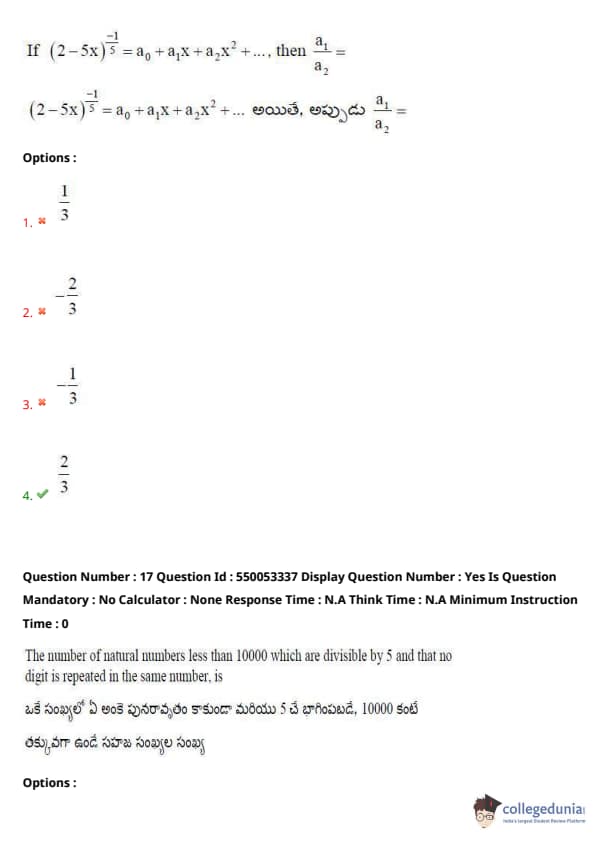













































































































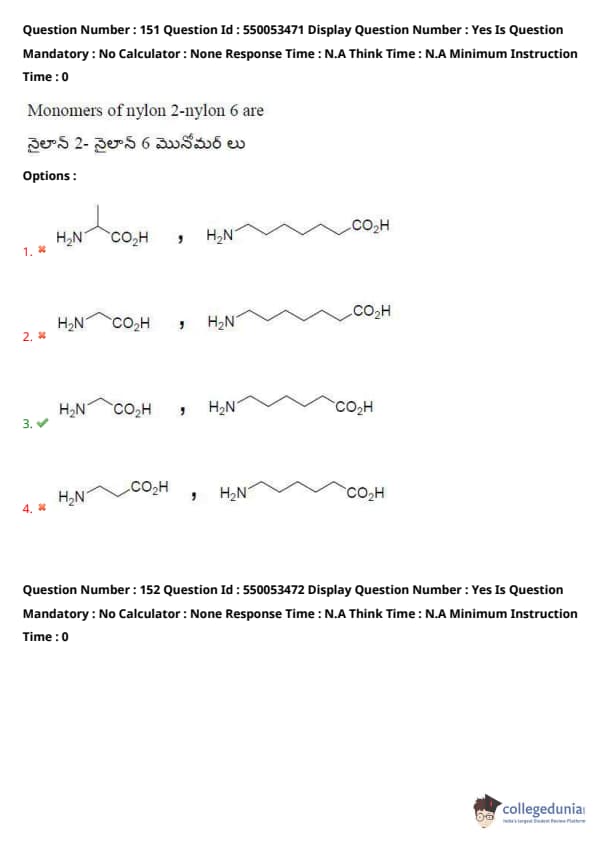








AP EAPCET 2023 Paper Analysis May 15 Shift 1
AP EAPCET 2023 paper analysis May 15 Shift 1 is available our website. Candidates can have a brief idea of the AP EAPCET question paper by viewing the previous year's paper analysis below.
Also Check:
AP EAPCET Previous Year Question Paper
| Particulars | Details |
|---|---|
| AP EAPCET Question Paper 2022 | Check Here |
| AP EAPCET Question Paper 2021 | Check Here |
| AP EAPCET Question Paper 2020 | Check Here |
| AP EAPCET Question Paper 2019 | Check Here |
| AP EAPCET Question Paper 2018 | Check Here |
| AP EAPCET Question Paper 2017 | Check Here |















Comments