Muskan Shafi Education Content Expert
Education Content Expert
Kinetic Theory of Gases is a classical model of the thermodynamic behavior of gases, with which many principal concepts of thermodynamics were established. The kinetic theory of gases describes a gas as a large number of identical submicroscopic particles, all of which are in constant, random, rapid motion. Their size is assumed to be much smaller than the average distance between the particles. The particles undergo random elastic collisions between themselves and with the enclosing walls of the container.
Kinetic Theory of Gases was found by British scientist James Clerk Maxwell and Austrian physicist Ludwig Boltzmann in the 19th century. The basic version of the model describes the ideal gas and considers no other interactions between the particles.
Read More: NCERT Solutions for Class 11 Physics Kinetic Theory
| Table of Content |
Key Terms: Kinetic Theory of Gases, Ideal Gas, Boltzmann Constant, Kinetic Energy, Root Mean Square Speed, Diffusion, Specific Heat
Kinetic Theory of Gases Assumptions
[Click Here for Sample Questions]
The application of the kinetic theory of gases to ideal gases is based on the following assumptions:
- Size of Gas Particles: The gas comprises very small particles. The size is so small that the sum of the volume of individual gas molecules is negligible when we compare it to the volume of the container in which the gas is stored. This can be alternatively stated as the average distance between the gas particles is quite large as compared to their size and the time elapsed between collisions of particles and the wall of the container is negligible between successive collisions.
- Elastic Collisions: The fast-moving particles continuously collide with each other and also with the walls of the container. All of these collisions are perfectly elastic collisions. This indicates that all the particles are perfect hard spheres.
- Negligible Interactions: The interaction between the gas molecules are negligible, except for when they collide which means they do not exert any force on each other.
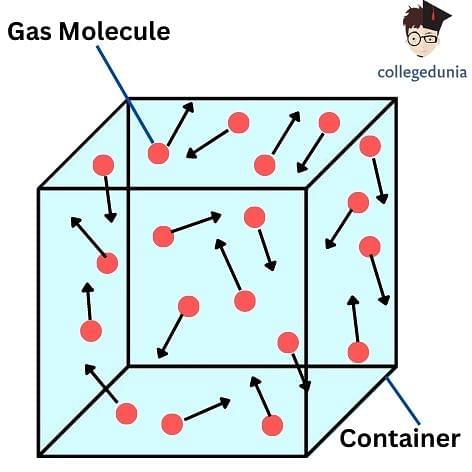
Kinetic Theory of Gas
- Thermodynamic Limit: The number of particles is so large that a statistical treatment of the problem is well defined. This assumption is often referred to as thermodynamic limit.
- Uniform Molecular Density: There is no concentration of the molecules inside the container, which means that the molecular density is constant inside the container.
- Mean Free Path and Linear Motion: A molecule moves along a straight line between two successive collisions and the average straight distance covered between two successive collisions is called the mean free path of the molecules.
Read More:
| Chapter-Related Topics | ||
|---|---|---|
| Kinetic Molecular Theory of Gases | Behaviour of Gas Molecules | Kinetic Interpretation of Temperature |
| Maxwell Boltzmann Distribution | Gas Pressure Formula | Ideal Gases Law |
Important Kinetic Theory of Gas Formulas
[Click Here for Previous Year Questions]
The important formulas for the Kinetic Theory of gases are listed below:
(1) Total Translational Kinetic Energy of Gas
Kinetic Energy = (3/2) x nRT
Where
- n = Number of moles of gas.
- R = Universal gas constant.
- T = Absolute temperature.
(2) Boltzmann Constant
kB = nR/N
Where
- kB = Boltzmann’s constant.
- R = universal gas constant.
- n = the number of moles.
- N = the number of particles in one mole (Avogadro Number = 6.022 x 1023)
Read More: Value of Boltzmann Constant
(3) Average Speed (V)
V=(v1+v2+v3+…..+vn)/n
V = √(8RT/πM) = √(8kT/m)
(4) Mean Square Speed
V2= (v12+v22 +…….vn2)/n
(5) Root Mean Square Speed
Vrms = √(3RT/M) = √(3kT/m)
Vrms = √(3P/ρ)
Therefore, Vrms is directly proportional to √T, 1/√M and 1/√ρ.
(6) Maxwell Distribution Law
Vrms > V> Vmp
- Vrms is the Root Mean Square (RMS) speed.
- V is the Mean speed.
- Vmp is the most probable speed.

Maxwell Distribution Law
(7) Pressure of Ideal Gas
p = ⅓ ρv2rms
Here, ρ is the density of molecules.
(8) Equipartition of Energy
K = ½ kBT (for each degree of freedom)
K = (f/2) (kBT for molecules with f degrees of freedom)
- kB is Boltzmann’s constant.
- T is the temperature of the gas.
Read More: Law of Equipartition of Energy
(9) Internal Energy
For n moles of an ideal gas:
U = (f/2)nRT
(10) Temperature and Kinetic Energy
(1/2) mv2 = (1/2) mVrms2 = 3/2kT (per molecule)
- Kinetic Energy per molecule = 3/2kT
- Kinetic Energy per mole = 3/2RT
- Kinetic Energy per gm = 3/2(R/M)
- Kinetic energy per unit volume = 1/2ρv2=3/2P
(11) Dalton’s Law of Partial Pressures
Dalton’s law of partial pressures is a gas law which states that the total pressure exerted by a mixture of gases is equal to the sum of the partial pressures exerted by each individual gas in the mixture.
P (total) = P1 + P2 + P3 + P4 + …… + Pn
(12) Graham’s Law of Diffusion
Graham’s law states that the rate of diffusion or of effusion of a gas is inversely proportional to the square root of its molecular weight.
D1/D2 =√(M2/M1)
D1/D2 =√(ρ2/ρ1)
(13) Van der Wall’s Gas Equation
(P + a/V2) (V – b) = RT ( for one mole)
Where a/V2 is the correction in pressure caused by the attraction between the molecules and b is the correction in volume due to finite size of the molecules.
For n moles of gas the equation becomes: (P+a (n/V)2)(V – nb) = nRT
(14) Specific Heats of Gas
Cv is the specific heat at constant volume:
- Cv = (dE/dT)v = d/dT(1/2fRT) = 1/2fR
- Cv = (1/2)fR
- Cv = 3/2R (for monoatomic gas)
- Cv = 5/2R (for diatomic gas)
Cp is the specific heat at constant pressure:
- Cp = Cv + R =((1/2)f + 1)R
- Cp = 5/2R (for monoatomic gas)
- Cp = 7/2R (for diatomic gas)
(15) Mixture of Non reacting Gases
- Mole Fraction n = n1 + n2
- Equivalent Molecular Weight = (n1M1+ n2M2)/(n1 + n2 )
Equivalent Specific Heat Cv = (n1 Cv1 + n2 Cv2)/(n1+n2)
Cp = (n1 Cp1 + n2 Cp2)/(n1 + n2)
Final Temperature = T = (n1T1 + n2T2) / (n1 + n2)
Read More:
Things to Remember
- Kinetic Theory of Gases is a scientific model that explains the physical behavior of gases as the motion of the molecular particles that compose the gas.
- Kinetic Theory of Gases was found by scientist James Clerk Maxwell and physicist Ludwig Boltzmann in the 19th century.
- Particles present in the container move very rapidly and collide with each other and with the walls of the container. These collisions are elastic collisions.
- A gas molecule moves in a straight path between successive collisions and the average distance that it travels between these collisions is termed the Mean free path.
- Dalton’s law of partial pressures is a gas law that states that the total pressure exerted by a mixture of gases is equal to the sum of the partial pressures exerted by each individual gas in the mixture.
- Degrees of freedom are the number of independent variables required to define the state of a system.
Previous Years’ Questions (PYQs)
- According to the kinetic theory of gases… (JEE Advanced 2011)
- According to kinetic theory of gases, molecules of a gas behave like…
- The kinetic theory of gases gives the formula…
- According to the kinetic theory of gases, in an ideal gas… (AIEEE 2003)
- According to kinetic theory of gases, for a diatomic molecule… (JEE Advanced 1991)
- The average kinetic energy of gas molecules at… (AIIMS 1999)
- The root mean square velocity of the molecules in a sample… (Haryana PMT 2011)
- When the universal gas constant (R) is divided by…
- The internal energy of one mole of ideal gas is… (BHU 1995)
- Two perfect gases at absolute temperatures T1 and…
- A real gas behaves as an ideal gas… (JIPMER 2014)
- The temperature of one mole of an ideal gas increases… (COMEDK UGET 2012)
Sample Questions
Ques. An ideal gas A is there. The initial temperature is 27°C. The temperature of the gas is increased to 927°C. Find the ratio of final Vrms to the initial Vrms (3 Marks)
Ans. Vrms = √3RT/M
So, it is proportional to Temperature,
Now T1 = 27°C = 300K
T2 = 927°C = 1200K
So initial Vrms = k√300
Final Vrms = k√1200
Ratio of final to initial = 2:1
Ques. The velocities of the molecules are v, 2v, 3v, 4v & 5v. The rms speed will be
a. 11v
b. v(11)1/2
c. v
d. 3.3v (3 Marks)
Ans. v(11)1/2
Vrms = ( ∑ V2 / N )1/2
= [( V2 + 4V2 + 9V2 + 16V2 + 25V2 )/5]1/2
= v (11)1/2
Ques. The specific heats, CP and CV of gas of diatomic molecules, A, is given (in units of J mol–1 K–1) by 29 and 22, respectively. Another gas of diatomic molecules, B, has the corresponding values 30 and 21. If these all are treated as ideal gases, then
(a) A has a vibrational mode but B has none.
(b) A has one vibrational mode and B has two.
(c) A is rigid but B has a vibrational mode.
(d) Both A and B have a vibrational mode each. (3 Marks)
Ans. (a) A has a vibrational mode but B has none.
Here, Cp and Cv of A are 29 and 22; Cp and Cv of B are 30 and 21.
γ = Cp/Cv = 1 + 2/f
For A, Cp/Cv = 1 + 2/f ⇒ f=6
Molecules A has 2 rotational, 3 translational, and 1 vibrational degree of freedom
For B, Cp/Cv = 1 + 2/f ⇒ f=5
Which means that B has 3 translational and 2 rotational degrees of freedom.
Ques. A gaseous mixture consists of 16 g of helium and 16 g of oxygen. The ratio CP /CV of the mixture is
(a) 1.4
(b) 1.54
(c) 1.59
(d) 1.62 (3 Marks)
Ans. (d) 1.62
For 16g of helium, n1 = 16/4 = 4
For 16g of oxygen, n2 = 16/32 = ½
For a mixture of gases
Cv = (n1Cv1 + n2Cv2) / (n1 + n2) where Cv = (f/2) R
Cp = (n1Cp1 + n2Cp2) / (n1 + n2) where Cp = ([f/2] + 1) R
For helium, f = 3, n1 = 4
For oxygen, f =5, n2 = ½
Cp/Cv = ((4* 5/2R) + ( ½* 7/2R)) / (4*3/2R) + (½* 5/2R) = 1.62
Ques. If a vessel contains 1 mole of 02 gas (molar mass 32 ) at temperature T. The pressure of the gas is P. What is the pressure if an identical vessel contains 1 mole of Hit at a temperature of 2T? (3 Marks)
Ans. According to the ideal gas equation:
PV = nRT
- P = pressure
- V =volume
- n = No. of molecule per unit volume
- R=Universal Gas Constant
- T = Temperature
So we get, PVT = nR or PVT = constant
Hence P1 V1 T1 = P2 V2 T2 →(1)
Now, in response to the query,
P1=P, T1=T
V1=V, T2=2T
Using above equations in equation (1)
P2=P1 V1/T1 * T2/V2
P2=PV/T * 2T/V
P2=2P
As a result, the pressure is doubled.
Ques. At very low pressure and high temperature, the real gas behaves like an ideal gas. Why? (3 Marks)
Ans. An ideal gas has a molecule volume of zero and no intermolecular forces.
- At extremely low pressures, the amount of gas is so huge that the volume of a molecule is insignificant in comparison to the volume of gas.
- As the kinetic energy of molecules is very high at very high temperatures, thus, the effect of intermolecular forces can be ignored.
As a result, at low pressure, real gases behave like ideal gas.
Ques. What is the Mean free path? (1 Mark)
Ans. The average distance that a molecule travels between collisions is defined as the mean free path.
Ques. What are the assumptions of the kinetic theory of gas? (3 Marks)
Ans. The following are the assumptions of the kinetic theory of gases:
A gas is made up of a vast number of molecules that should all be elastic spheres and identical.
The molecules of a gas are in a constant state of rapid and possess unpredictable mobility.
Gas molecules are extremely small in comparison to the distance between them.
There is no attraction or repulsion between the molecules of a gas.
The collision of molecules with one another and with the vessel's walls are perfectly elastic.
Ques. How to derive Boyle's law using the kinetic theory of gases? (3 Marks)
Ans. Boyle's law states that the volume of a given quantity of gas is inversely proportional to the pressure P, i.e. PV = Constant, with the temperature constant,
The pressure exerted by a gas is stated by the kinetic theory of gases:
- P= Pressure
- V = Volume
- V¯= Average Velocity
- m = Mass of 1 molecule
- N= No. of molecules
M = mN (Mass of gas)
P = mNV¯2 / 3V
PV = 1/3 MV2
Ques. What does Dalton’s law of partial pressures state? (1 Mark)
Ans. Dalton’s law of partial pressures is a gas law. According to the law, the total pressure exerted by a mixture of gases is equal to the sum of the partial pressures exerted by each individual gas in the mixture.
Check-Out:




Comments