Collegedunia Team Content Curator
Content Curator
Distance-time graph, in a given time period, helps to show how far an object has travelled. It can be expressed as a simple line graph which represents the distance versus time findings on the graph.
- Distance, in this case, is plotted on the Y-axis
- Time, in this case, is plotted on the X-axis
It is important when studying the motion of bodies. A distance-time graph can be obtained if the distance and time for the motion of a body are plotted on a rectangular graph, thus corresponding to the motion of that body.
- In case it is a straight line, then the motion is uniform.
- In case it has been provided, its speed can be estimated by means graph’s slope.
- The slope of the straight-line graph is the same, despite the chosen interval.
- It indicates that the speed of an object under uniform motion is constant.
| Table of Content |
Key Terms: Distance, Time, Motion, Speed, Uniform Motion, X-Axis, Y-Axis, Uniform Speed, Time Interval, Velocity, Distance-Time Graph
Distance-Time Graph
[Click Here for Sample Questions]
A Distance-Time graph can be defined as:
| “A graph that represents how far an object has travelled in a given time period.” |
- ‘Distance’ is the total length that is travelled by an object.
- ‘Time’ can be defined by the minutes, hours, or seconds needed to cover this distance by the object.
Distance-Time Graph
When these units of Distance and Time are placed on the X and Y axes of a graph to define the Distance covered and the time used by the object to do so, it is called a Distance-Time graph.
- On the X-axis, the time is plotted.
- On the Y-axis, the distance is plotted.
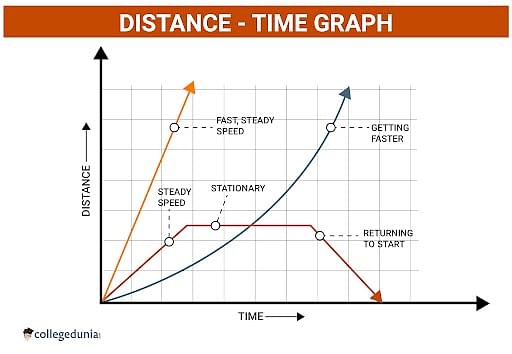
Note: The Curved lines on a distance-time graph denote that the speed is changing.
Example of Distance-Time Graph
[Click Here for Sample Questions]
To Distance-Time graph example can be shown via uniform motion.
- Suppose a driver drives at a constant speed shown by the speedometer.
- The driver measures the time taken by the bus for each kilometre. The driver finds out that the bus travels 1 kilometre for every 2 minutes.
- Thus, he creates a graph to represent the same. By this table, the speed he found is: ½ × 60 = 30 km/hr.
- The graph has been found to be in a straight line, while the motion of the bus is uniform.
- As per the graph, the speed of the bus at any instant time can be determined.

Data Table of Distance-Time Graph
The initial and final position of the car is:
= \(Speed = \frac{(Final Position-Initial position)}{Time}\)
The slope of the line can also be determined by a rectangle drawn anywhere near the straight line, helping to find the speed of the bus. In case an object is not moving, the distance-time graph can be found in a horizontal line, showing that the object is at rest.
Thus,

Distance-Time Graph
Conclusion of Distance-Time GraphSome conclusions can be derived from the above-stated points about the Distance-Time graph. These are:
|
Read Also:
Plotting Distance-Time Graph
[Click Here for Sample Questions]
In a Distance-Time graph, the values of distance and time are plotted on the Y-axis and X-axis respectively.
Note: Curved lines on a Distance-Time graph represent a change in the speed of the object, while a straight line indicates constant speed throughout the distance covered by the object.

- The Distance-Time graph is a linear graph where a line graph is plotted to denote the distance versus time values of an object on the graph.
- To do this, we have to first take a graph sheet and draw two perpendicular lines, naming them the X-axis horizontally and the Y-axis vertically.
- The X-axis shall indicate the distance travelled by the object and the Y-axis indicates the time required to cover this distance.
- Distance-Time graph for uniform motion is a straight line.
Read More: Average Acceleration Formula
Distance-Time Graph Formula
[Click Here for Sample Questions]
The values of a Distance-Time graph can be easily calculated from the slope or gradient on the linear graph. The gradient of the line drawn on a distance-time graph is equal to a moving object’s speed.
The gradient is directly proportional to the speed of the object, that is, the greater the gradient or steeper the line, the faster is the speed of the moving object. Thus, the formula of Distance-Time Graph is:
| \(Speed = \frac{Change\ in\ the\ Distance}{Change\ in\ Time}\) |
Importance of Distance-Time Graph
[Click Here for Sample Questions]
There are a number of applications of Distance-Time graphs. Some include:
- They provide great observation to study the motion of an object and determine the change in the position of an entity.
- The incline on this graph denotes the speed of the object.
- If an object’s distance and time of motion are recorded and plotted on a rectangular graph, a distance-time graph shall be constructed that corresponds to the motion of the body.
Distance vs. Time Definition
In the distance-time graph study, the three important components noted were:
- Time
- Speed
- Distance
The vertical Y-axis of the plotted graphical representation can be denoted as the vertical time axis. The horizontal X-axis can be defined as the horizontal distance axis. After the axes are determined, the values can easily be plotted on the graph.
Read More: Path Length
Things to Remember
- A Distance-Time graph is a graph that represents how far an object has travelled in a given time.
- In a Distance-Time graph, the values of distance and time are plotted on the Y-axis and X-axis respectively.
- The values of speed of an object can be easily calculated from the slope or gradient of a Distance-Time graph.
- These graphs provide great observation to study the motion of an object and determine the change in the position of an entity.
- If the line on a Distance-Time graph is uniform, then the speed of the object is constant.
Also Read:
Important Notes PDF on Motion
Notes on the chapter motion are given below:






Important Notes on Motion
Sample Questions
Ques. How can the total distance be calculated from a Distance-Time graph? (1 mark)
Ans. Apart from the Distance and Time values of a moving object, a Distance-Time graph also indicates the total distance covered by the object. This can be calculated by studying the x-axis of the graph.
Ques. What is a Distance Time Graph? (1 mark)
Ans. A distance-time graph can be expressed as a type of graph that represents how far an object has travelled in a given time period
Ques. What is a limitation of a Distance-Time graph? (1 mark)

Ans. Distance-Time graphs cannot show negative time slopes. It is impossible to move back in time and hence negative time slopes on Distance-Time graphs indicate wrong calculations or observations.
Ques. What do we derive about the speed of the moving object from the following Distance-Time graph? (1 mark)
Ans. The given distance-time graph indicates that the velocity of the object is constantly accelerating and the speed is constantly getting faster. This can be understood by studying the given slope of the graph.
Ques. How can Distance-Time graphs be plotted? (1 mark)
Ans. Distance-Time graphs are linear graphs. They can be plotted simply by drawing two perpendicular lines, with the horizontal line being the Time and the vertical line being the Distance covered by the object.
Ques. List two importance of Distance-Time graphs? (2 marks)
Ans. The two importances of Distance-Time graphs are:
- It helps to give a great observation to study the motion of an object. Thus, it aids to determine the change in the position of an entity.
- The incline on this graph helps to represent the speed of the object.
Ques. How can we differentiate between a distance-time Graph and a Speed-Time graph? (2 marks)
Ans. A Distance-Time Graph and a Speed-Time Graph can be easily differentiated by looking at the values on the two Axes.
- Time is placed on the horizontal axis, while Speed and Distance values are placed on the vertical axis.
- The former indicates the total distance traveled by a body, while the latter indicates its acceleration.
Ques. Amaira walked from her home to a bookshop to buy some stationery items. She then decided to go to the supermarket to buy groceries before returning home. The distance-time graph for her journey is as shown below:

Calculate the:
(a) Speed of Amaira when it is given that she reaches the bookstore in 20 minutes
(b) Her speed when she walked back from the supermarket to her home
(c) Her average speed for the whole journey (3 marks)
Ans. As per the question:
- s = distance travelled/time taken = 100/20
= 5 m/min
- Speed = 150/20
= 7.5 m/min
- Avg Speed = Total distance/Total time
= (100+50+150)/80
= 300/80
= 3.75 m/min
Ques. What are the types of Distance-Time graph? (3 marks)
Ans. Due to distance and time graphs, an object can represent how far it has travelled. Three basic types of graph include:
- Bar graphs
- Pie charts
- Line graphs
Ques. Rama went for a drive in his car. The distance-time graph shows her full journey. Thus, determine the total distance traveled during her journey, along with her average speed between 4:30 and 5:30. (5 marks)

Ans. Rama traveled 30 km away from her home. After stopping for a while, she again drove 20 km. And, she then stopped again shortly, travelling 50 km back home after starting the journey back.
Thus, the total distance travelled is = 30 km + 20 km + 50 km = 100km.
As per the axis shown in the image, the two big squares total 30 minutes.
This means that one big square is 15 minutes. Which is to say, from 4:30 to 4:45, Rama is at rest.
Speed between 4:30 and 4:45 = 0/0.25 = 0 km/h.
In order to calculate the average speed of Rama between 4:30 and 5:30, the slope of the graph between 4:45 and 5:00 needs to be. This specific period lasted for 15 minutes, thus equal to 0.25 hours. It can be expressed as the “change in x”.
During this period, she increased her distance from her home from 30 km up to 50 km.
Thus, she traveled 20 km in total – which can also be termed as the “change in y”.
Thus, we get, slope = 20/0.25 = 80 km/h.
Therefore, the average speed = (0 + 80)/2 = 40 km/h
Check-Out:



Comments