Collegedunia Team Content Curator
Content Curator
Derivation of the equation of motion is the mathematical method through which the three equations of motion are derived. Algebraic, Graphic, and Calculus methods are used to calculate various parameters such as time, velocity, acceleration, or distance in a given problem of motion related to daily life. Of these parameters, u, v, a, and s are vector quantities. Vectors going in one direction are positive and vectors in the opposite direction are negative. Equations of motion apply to uniformly accelerated motion. Moving objects have momentum, and forces cause variations in them. The total momentum in an explosion or collision is conserved and stays the same.
Read More: Potential Energy
| Table of Content |
Key Terms: Equations of Motion, Equations of Motion Derivation, Moment Inertia, Motion, Distance, Acceleration, Velocity, Time
Equations of Motion
[Click Here for Sample Questions]
There are three equations of motions in physics used to calculate various parameters such as time, acceleration, Velocity and Distance. These equations are as follows.
- First Equation of Motion: v = u + at
- Second Equation of Motion: s = ut + ½ at2
- Third Equation of Motion: v2 = u2 + 2as
Where
- v is final Velocity
- u is initial velocity
- t is the time taken
- a is acceleration
- s is the distance travelled

Equations of Motion
Methods to Derive Equations of Motion
[Click Here for Previous Year Questions]
There are three methods used to derive the equations of motion, these methods are as follows:
- Derivation using Algebraic Method
- Derivation using Graphical Method
- Derivation using Calculus Method
Motion in a Straight Line Video Explanation
Also Read:
Derivation of First Equation of Motion
[Click Here for Sample Questions]
Let’s imagine a moving body, travelling with uniform acceleration in a straight line. So, let the acceleration be a, initial velocity be u, the time period be t, distance travelled be s and final velocity be v.
Algebraic Method
The acceleration of a body is said to be the rate of change of velocity.
So, acceleration is represented mathematically as: a = (v-u)/t
Here v is the final velocity and u is the initial velocity.
By Rearranging the equation, we get the first equation of motion as: v = u + at
Graphical Method
In the below graph,
- The velocity changes in time t from A to B at a uniform rate.
- BC is the v and OC is t.
- A perpendicular is drawn from B to OE, A parallel line is drawn from A to D and A perpendicular is drawn from B to OC.

Derivation of First Equation of Motion
So, we know from the graph that
BC = BD + DC
Hence, v = BD + DC
and v = BD + OA (since DC = OA)
Therefore, v = BD + u (since OA = u) (Equation 1)
Now,
a = slope of line AB
a = BD/AD
Since AD = AC = t,
BD = at (Equation 2)
Equation 1 + equation 2, we get: v = u + at
Read More: Angular Momentum
Calculus Method
Since acceleration is the rate of change of velocity,
a=dv/dt
Rearranging the above equation, we get
adt=dv
Integrating both sides, we get
∫t0 adt = ∫vudv
at = v−u
Rearranging, we get v=u+at
Read More: Equations of Motion
Derivation of Second Equation of Motion
[Click Here for Previous Year Questions]
The second equation of motion can be derived via the following methods:
Algebraic Method
The rate of change of displacement is known as velocity.
Velocity = Displacement/Time
Displacement = Velocity×Time
Use average velocity in the place of velocity, if the velocity is not constant.:
Displacement={(Initial Velocity + Final Velocity)/2} × Time
s={(u+v)/2} × t
s=[{u+ (u + at)}/2] × t
s=[{2u + at/2}]×t
s=({2u/2} + {at/2})×t
s=(u + ½ at)×t
On further simplification, the equation becomes s=ut+½ at2
Read More: Application and Uses of Convex Mirror, Examples
Graphical Method
From the graph above,
Distance travelled (s) = Area of figure OABC = Area of rectangle OADC + Area of triangle ABD
s=(½ AB×BD)+(OA×OC)

Derivation of Second Equation of Motion
Since BD = EA,
s=(½ AB×EA) + (u × t)
As EA = at,
s=½ × at × t+ ut
So, the equation becomes s= ut+ ½ at2
Calculus Method
The rate of change of displacement is known as velocity.
Mathematically, this is:
v=ds/dt
ds=vdt
ds=(u + at) dt
ds=(u + at) dt = (udt + atdt)
On further simplification, the equation becomes:
∫0sds=∫0tudt+∫0tatdt
s = ut + ½ at2
Derivation of Third Equation of Motion
[Click Here for Sample Questions]
The third equation of motion can be derived by:
Algebraic Method
Displacement is an object’s rate of change of position. Mathematically, this is:
Displacement=(Initial Velocity+Final Velocity/2) × t
s=(u+v/2) × t
From the first equation of motion, we know that
v= u + at
t = (v−u)/a
s=(v+u/2) (v−u/a)
s=(v2−u2/2a)
2as=v2−u2
That results in v2 = u2 + 2as
Read More: Types of Motors and its Application
Graphical Method
s is the total distance travelled given by the Area of trapezium OABC.
S = Height × ½ (Sum of Parallel Sides)
S=(OA+CB)×OC
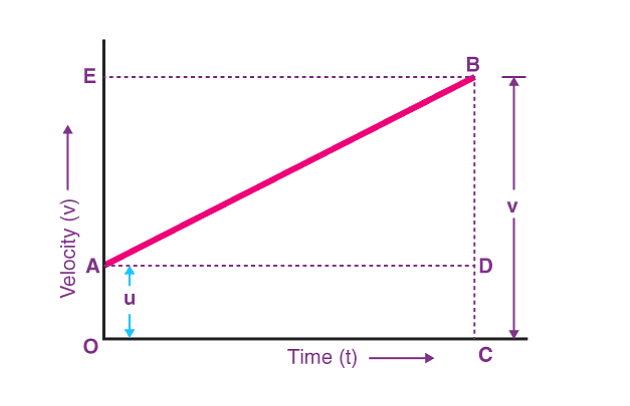
Derivation of Third Equation of Motion
Here, CB = v, OA = u and OC = t,
so,
s= ½ (u+v) × t
t = (v – u)/ a
s= ½ ((u+v) × (v-u))/a
s= ½ (v+u) × (v-u)/a
s = (v2-u2)/2a
Third equation of motion is: v2 = u2 + 2as
Read More: Unit of Frequency
Calculus Method
The rate of change of velocity is Acceleration:
a= dv/dt (1)
The rate of change of displacement is velocity.
v= ds/dt (2)
Cross multiplying (1) and (2), we get
ads/dt=vdv/dt
∫0sads=∫uvvds
as = (v2−u2)/2
This results in v2 = u2 + 2as
Read More: Capacitor Types
Things to Remember
- Derivation of the equation of motion is the mathematical method through which the three equations of motion are derived using different methods, these equations are used to calculate various parameters such as time, velocity, acceleration or distance in a given problem of motion related to daily life.
- When you know the derivation of a given equation, you tend to understand the basic concept behind that equation, and that in turn helps to solve problems in a better way.
- let the acceleration be a, initial velocity be u, the time period be t, distance traveled be s and final velocity be v.
- There are three methods used to derive the equations of motion, these methods are as follows: Derivation using Algebraic Method, Derivation using Graphical Method, Derivation using Calculus Method.
Read More:
Previous Year Questions
- A charged particle enters a uniform magnetic field with a certain speed at… [JKCET 2006]
- A person walked up a stalled escalator in 90s… [NEET 2006]
- An automobile in travelling at 50 km/h, can be stopped at a distance of… [KEAM 2003]
- An object is thrown vertically upward with a speed of… [TS EAMCET 2017]
- An automobile travelling at 50 km/h, can be stopped at a distance of… [JCECE 2005]
- A body of mass 2kg has an initial velocity of… [BHU UET]
- A body dropped from a height h with initial velocity zero… [NEET 1996]
- A ball is dropped from a high rise platform at… [NEET 2010]
- A ball is thrown vertically downward with a velocity of 20m/s from the… [NEET 2020]
- A ball is thrown vertically upward. It has a speed of… [NEET 2005]
Sample Questions
Ques: What are the three equations of motion? (3 marks)
Ans: The three equations of motion are as follows:
- v = u+at
- s = ut+ (½ ) at2
- v2 = u2+2as
Ques: In what three ways can an equation be derived? (3 marks)
Ans: There are three ways through which an equation can be derived, these are:
- By Calculus Method
- By Algebraic Method
- By Graphical Method
Ques: What is the derivation of a motion? (2 marks)
Ans: Derivation of the equation of motion is the mathematical method through which the three equations of motion are derived using different methods.
Ques: Why is a derivation of an equation necessary to understand? (2 marks)
Ans: When you know the derivation of a given equation, you tend to understand the basic concept behind that equation, and that in turn helps to solve problems in a better way.
Ques: What parameters are found out by using the equations of motion? (2 marks)
Ans: The equations of motion are used to calculate various parameters such as time, velocity, acceleration or distance in a given problem of motion related to daily life.
Read more: Electrical Resistance
Ques: What to do when the acceleration in a given situation is not constant? (2 marks)
Ans: When deriving an equation and the acceleration given is not constant, one can use average acceleration in its place.
Ques: Use the calculus method to derive the first equation of motion. (3 marks)
Ans: Since acceleration is the rate of change of velocity, it can be mathematically written as:
a=dv/dt
Rearranging the above equation, we get
adt=dv
Integrating both sides, we get
∫t0adt=∫vudv
at=v−u
Rearranging, we get v=u+at
Ques: Derive the third equation of motion using the calculus method. (3 marks)
Ans: We know that acceleration is the rate of change of velocity and can be represented as:
a= dv/dt (1)
We also know that velocity is the rate of change of displacement and can be represented as:
v= ds/dt (2)
Cross multiplying (1) and (2), we get
ads/dt=vdv/dt
∫0sads=∫uvvds
as = (v2−u2)/2
v2 = u2 + 2as
Read More: Rolling Friction
Ques: Derive the second equation of motion using the calculus method. (3 marks)
Ans: Velocity is the rate of change of displacement.
Mathematically, this is:
v=ds/dt
ds=vdt
ds=(u + at) dt
ds=(u + at) dt = (udt + atdt)
On further simplification, the equation becomes:
∫0sds=∫0tudt+∫0tatdt
s = ut + ½ at2
Read Also:







Comments