Bihar Board Class 12 Mathematics Question Paper PDF with Solutions is available for download. The Bihar School Examination Board (BSEB) conducted the Class 12 examination for a total duration of 3 hours 15 minutes, and the Bihar Board Class 12 Maths question paper was of a total of 100 marks.
Bihar Board Class 12 Mathematics 2025 Question Paper with Solutions Set A
| Bihar Board Class 12 Mathematics 2025 Question Paper with Answer Key Set A | Download PDF | Check Solutions |

\(\frac{d}{dx} (\sec^2 x - \tan^2 x) = \)
\(\frac{d}{dx} [e ^ 2 + 2ex] =\)
\(\frac{d}{dx} \left[ \lim_{x \to a} \frac{x^n + a^n}{x + a} \right] =\)
\(\frac{d}{dx} (\sin^{-1}(2x)) =\)
\(\frac{d}{dx} \left[ \frac{(x + 2)(x^2 - 2x + 4)}{x^3 + 8} \right] =\)
View Solution
We will apply the quotient rule here, where: \[ \frac{d}{dx} \left[ \frac{u(x)}{v(x)} \right] = \frac{v(x) u'(x) - u(x) v'(x)}{[v(x)]^2} \]
Here, \( u(x) = (x + 2)(x^2 - 2x + 4) \) and \( v(x) = x^3 + 8 \).
Step 1: Find the derivatives of \( u(x) \) and \( v(x) \).
- \( u'(x) = (x^2 - 2x + 4) + (x + 2)(2x - 2) \).
- \( v'(x) = 3x^2 \).
Step 2: Apply the quotient rule.
The derivative is: \[ \frac{(x^3 + 8) \cdot \left[ (x^2 - 2x + 4) + (2x - 2) \right] - \left[ (x + 2)(x^2 - 2x + 4) \right] \cdot 3x^2}{(x^3 + 8)^2}. \]
Step 3: Conclusion.
Simplifying gives us the correct result \( \frac{(x^2 - 2x + 4) + (2x - 2)}{3x^2} \).
\[ \boxed{\frac{(x^2 - 2x + 4) + (2x - 2)}{3x^2}} \] Quick Tip: When applying the quotient rule, first differentiate the numerator and denominator separately and then substitute them into the formula.
\(\frac{d}{dx} \left[ 2\sqrt{x} \right] =\)
\(\frac{d}{dx} \left[ (1 - \cos 2x) + 2 \cos^2 x \right] =\)
\(\frac{d}{dx} \left[ \log(x^2) + \log(a^2) \right] =\)
\(\frac{d}{dx} \left[ 2 \tan^{-1}(x) \right] =\)
\(\frac{d}{dx} \left[ e^{x^2} \right] =\)
\(\int \frac{dx}{x^2 + 4}\)
\(\int \frac{\cos 2x}{\cos x + \sin x} \, dx \)
\(\frac{d}{dx} \left[ \cos(\pi x + \sin \pi x) \right]\)
\(\int \tan(\tan^{-1}(x)) \, dx \)
\(\int \frac{1}{e^{-x}} \, dx \)
\(\int \log(x^2) \, dx \)
\(\int \left( \sin 3x + 4 \sin^3 x \right) \, dx \)
\(\int_{-1}^1 \sin^7 x \cos^{13} x \, dx \)
\(\int_0^1 \frac{4 \tan^{-1}(x)}{1 + x^2} \, dx \)
\(\int_0^1 3x^2 \, dx \)
View Solution
The integral is straightforward: \[ \int_0^1 3x^2 \, dx = \left[ x^3 \right]_0^1 = 1^3 - 0^3 = 1. \]
Step 2: Conclusion.
Thus, the value of the integral is \( 1 \).
\[ \boxed{1} \] Quick Tip: For basic polynomial integrals, use the power rule: \( \int x^n \, dx = \frac{x^{n+1}}{n+1} \).
\(\int_0^a x \cdot \frac{1}{2\sqrt{a^2 - x^2}} \, dx \)
View Solution
This is a standard integral involving a square root. Use the substitution: \[ x = a \sin \theta \quad so that \quad dx = a \cos \theta \, d\theta. \]
The integral becomes: \[ \int_0^{\frac{\pi}{2}} a^2 \sin \theta \cdot \frac{1}{2 \cos \theta} \, a \cos \theta \, d\theta = \frac{a^2}{2} \int_0^{\frac{\pi}{2}} d\theta = \frac{a^2}{2} \cdot \frac{\pi}{2}. \]
Step 2: Conclusion.
Thus, the value of the integral is \( \frac{a^2}{2} \).
\[ \boxed{\frac{a^2}{2}} \] Quick Tip: For integrals of the form \( \frac{x}{\sqrt{a^2 - x^2}} \), use the substitution \( x = a \sin \theta \) to simplify the square root.
\(\int_0^a \frac{1}{\sqrt{x}} \, dx \)
\(\int_0^{\frac{\pi}{2}} \frac{\sqrt{\cos x}}{\sqrt{\sin x} + \sqrt{\cos x}} \, dx \)
View Solution
This integral requires simplifying the trigonometric expressions and using symmetry. A substitution or recognizing symmetry in the integrand can show that the integral evaluates to \( \frac{\pi}{2} \).
Step 2: Conclusion.
Thus, the value of the integral is \( \frac{\pi}{2} \).
\[ \boxed{\frac{\pi}{2}} \] Quick Tip: For integrals involving trigonometric expressions like \( \sqrt{\cos x} \) and \( \sqrt{\sin x} \), look for substitutions or symmetry to simplify the problem.
\(\int_0^{\frac{\pi}{2}} \log(\tan x) \, dx \)
\(\int_0^1 e^x \, dx \)
View Solution
This is a basic exponential integral. Using the formula for the integral of \( e^x \): \[ \int e^x \, dx = e^x + C. \]
Evaluating from 0 to 1: \[ \int_0^1 e^x \, dx = e^1 - e^0 = e - 1. \]
Step 2: Conclusion.
Thus, the value of the integral is \( e - 1 \).
\[ \boxed{e - 1} \] Quick Tip: For basic exponential integrals, remember the integral \( \int e^x \, dx = e^x + C \), and apply the limits accordingly.
\(\int_0^{\frac{\pi}{2}} \sin x \cos x \, dx \)
\(\int_0^1 (x + 2x + 3x^2 + 4x^3) \, dx \)
\(\int_{-1}^1 \sin x \cos^3 x \, dx \)
100 \(\int_0^1 x^{99} \, dx \) =
2 \(\int_1^9 \frac{dx}{\sqrt{x}} \)
\(\int \frac{1}{x \log(x)} \, dx\)
\(\int \frac{x - 3}{x^2 - 9} \, dx\)
If \( n(A) = 4 \) and \( n(B) = 2 \), then \( n(A \times B) = \)
If operation 'o' is defined as \( (a \, o \, b) = a^3 + b^3 \), then \( 4\ o \, (1 \, o \, 2) = \)
\( f : A \to B \) will be an onto function if
If \( f : \mathbb{R} \to \mathbb{R} \) such that \( f(x) = 3x - 4 \), then which of the following is \( f^{-1}(x) \)?
If operation 'o' is defined as \( (a \, o \, b) = a^2 + b^2 - ab \), then \( (1 \, o \, 2) \, o \, 3 \) =
Let \( A = \{1, 2, 3, ..., n\} \). How many bijective functions \( f : A \to A \) can be defined?
\( \tan\left(\frac{1}{2} \left( \tan^{-1}(x) + \tan^{-1}\left(\frac{1}{x}\right) \right) \right) = \)
\( \cos^{-1}(x) + \sec^{-1}\left(\frac{1}{x}\right) =\)
View Solution
Using the identity \( \sec^{-1}(y) = \cos^{-1}\left(\frac{1}{y}\right) \), we can simplify the expression as: \[ \cos^{-1}(x) + \sec^{-1}\left(\frac{1}{x}\right) = \cos^{-1}(x) + \cos^{-1}(x) = \frac{\pi}{2}. \]
Step 2: Conclusion.
Thus, the value of the expression is \( \frac{\pi}{2} \).
\[ \boxed{\frac{\pi}{2}} \] Quick Tip: When dealing with inverse trigonometric functions, use known identities and relationships between the functions to simplify the expression.
Find \( \cot^{-1} \left( \tan\left( \frac{\pi}{7} \right) \right) \)
Find \( \cos^{-1} \left( \cos \left( \frac{8\pi}{5} \right) \right) \)
Find \( \tan^{-1} \left( -\sqrt{3} \right) \)
Find \( \tan^{-1}(\sqrt{3}) - \cot^{-1}(-\sqrt{3}) \)
Find \( \sin\left( \sin^{-1}\left(\frac{2\pi}{3}\right) \right) + \tan^{-1}\left(\tan\left(\frac{3\pi}{4}\right)\right) \)
Find \( \tan^{-1}\left(\frac{1}{2}\right) + \tan^{-1}\left(\frac{1}{3}\right) \)
If \( \sin\left(\sin^{-1}\frac{1}{5} + \cos^{-1}(x)\right) = 1 \), \implies \( x = \)
Find the determinant of the matrix 
Find the determinant of the matrix 
If  = 0, \implies \( x \).
= 0, \implies \( x \).
View Solution
The determinant of a 2x2 matrix  is: \[ det(A) = ad - bc. \]
is: \[ det(A) = ad - bc. \]
For the matrix \( A = \) , we have: \[ det(A) = x \times 4 - 15 \times 4 = 4x - 60. \]
, we have: \[ det(A) = x \times 4 - 15 \times 4 = 4x - 60. \]
We are given that \( det(A) = 0 \), so: \[ 4x - 60 = 0 \quad \Rightarrow \quad 4x = 60 \quad \Rightarrow \quad x = 15. \]
Step 2: Conclusion.
Thus, \( x = 15 \).
\[ \boxed{15} \] Quick Tip: For a 2x2 matrix, if the determinant is zero, the rows or columns are linearly dependent.
Find 
Find 
Given \( A = \begin{bmatrix} 1 & 2 & 3 \end{bmatrix} \), find \( A' \) (the transpose of \( A \))
Find \( \frac{d}{dx} \left( \log(5x) \right) \)
If  , then \( A^{100} \) is
, then \( A^{100} \) is
Find 
Find the product of 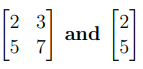

Find 
Find \( 4 \times \begin{bmatrix} 2 & -2 \end{bmatrix} \)
Find the cofactor matrix of 
Find \( \frac{d}{dx} \left( \log(x^9) \right) \)
If the direction ratios of two parallel lines are \( \frac{x - 19}{13} = \frac{y - 17}{11} = \frac{z - 15}{9} \), then the direction ratios are
Through which of the following points does the line \( \frac{x - 11}{12} = \frac{y - 12}{13} = \frac{z - 13}{14} \) pass?
If the direction ratios of two parallel lines are \( 2, 7, 9 \), then the value of \( x \) is
If the direction ratios of two parallel lines are \( a, b, c \) and \( x, y, z \), then \( az = \)
If the direction ratios of two mutually perpendicular lines are \( 5, 2, 4 \) and \( 4, 8, x \), then the value of \( x \) is
Find the equation of a plane parallel to the plane \( 9x - 8y + 7z = 10 \)
Find \( |\vec{i} - \vec{j} - 3\vec{k}| \)
Find \( (4\vec{i} + 3\vec{j})^2 \)
Find \( (7\vec{i} - 8\vec{j} + 9\vec{k}) \cdot (\vec{i} - \vec{j} + \vec{k}) \)
Find \( \vec{i} \cdot \vec{i} + \vec{i} \cdot \vec{j} + \vec{j} \cdot \vec{j} + \vec{j} \cdot \vec{k} + \vec{k} \cdot \vec{k} \)
Find \( (11\vec{i} + \vec{j} + \vec{k}) \cdot (\vec{i} + \vec{j} + 11\vec{k}) \)
Find \( (\vec{k} \times \vec{j}) \cdot \vec{i} \)
Find \( (\vec{i} - 2\vec{j} + 5\vec{k}) \cdot (-2\vec{i} + 4\vec{j} + 2\vec{k}) \)
Find \( \vec{i} \cdot \vec{j} + (\vec{i} \times \vec{i}) \)
Which of the following is an objective function?
The maximum value of \( z = 2x + y \) subject to the constraints \( x + y \leq 35 \), \( x \geq 0 \), and \( y \geq 0 \) is
The maximum value of \( z = 3x - y \) subject to constraints \[ x + y \leq 8, \quad x \geq 0, \quad y \geq 0 \]
The chance of getting a doublet in a throw of 2 dice is
The addition theorem of probability is
If odds in favour of event \( E \) are \( a : b \), then \( P(E) = \)
The multiplication theorem of probability is
Find \( \frac{d}{dx} \left( e^{3 - 2x} \right) \)
Find \( \int 2^{x + 1} \, dx \)
View Solution
We use the formula for the integral of an exponential function: \[ \int a^x \, dx = \frac{a^x}{\log a} + C. \]
Here, \( a = 2 \) and the exponent is \( x+1 \). Therefore: \[ \int 2^{x + 1} \, dx = \frac{2^{x + 1}}{\log 2} + k. \]
Thus, the correct answer is: \[ \boxed{\frac{2^{x + 1}}{\log 2} + k}. \] Quick Tip: For integrals of exponential functions with base \( a \), remember to divide by \( \log a \).
Find \( \int \frac{(\sqrt{x} + 1)^2}{x \sqrt{x} + 2x + \sqrt{x}} \, dx \)
Find \( \int_{-1}^1 \sin^{13} x \cdot \cos^{12} x \, dx \)
Find \( \int_0^2 e^x \, dx \)
Evaluate \( \int_\alpha^\beta \phi(x) \, dx + \int_\beta^\alpha \phi(x) \, dx \)
Find 
\[ \frac{d}{dx} \lim_{n \to 1} \frac{x^n - 1}{n+1} \]
Find \( \frac{d}{dx} \{ \log_3(x) \cdot \log_x(3) \} \)
Find \( \frac{d}{dx} \log(x^{100}) \)
Find \( \frac{d}{dx} \sin^{-1}(2x \sqrt{1 - x^2}) \)
Evaluate \( \int e^{2 \log(x)} \, dx \)
View Solution
Using the property of logarithms, we have \( e^{2 \log(x)} = x^2 \). Therefore, the integral becomes: \[ \int e^{2 \log(x)} \, dx = \int x^2 \, dx = \frac{x^3}{3} + k. \]
Thus, the correct answer is: \[ \boxed{\frac{x^3}{3} + k}. \] Quick Tip: Use logarithmic identities to simplify the integrand before integrating.
Find 
View Solution
The derivative of each element of the matrix is:

So, the correct answer is:  Quick Tip: When differentiating a matrix, differentiate each entry individually.
Quick Tip: When differentiating a matrix, differentiate each entry individually.
Evaluate \( \int x^m \cdot x^n \, dx \)
Evaluate \( \int e^3 \cdot e^x \, dx \)
View Solution
Since \( e^3 \) is a constant, we can factor it out of the integral: \[ \int e^3 \cdot e^x \, dx = e^3 \int e^x \, dx = e^3 e^x + k. \]
Thus, the correct answer is: \[ \boxed{e^{x+3} + k}. \] Quick Tip: When integrating exponential functions, use the fact that \( \int e^x \, dx = e^x + C \).

















Comments