Namrata Das Exams Prep Master
Exams Prep Master
Friction is an external force that opposes the relative motion between two contact surfaces. When one object is in motion compared to another, it is in relative motion. Friction acts on the surface of contact of both bodies. There are four prominent types of friction including static, sliding, rolling, and fluid. Here we will discuss sliding friction, its formula, examples along with a few important questions.
| Table of Content |
Key Terms: Friction, Force, Static Friction, Rolling Friction, Sliding Friction, Fluid Friction
What is Sliding Friction?
[Click Here for Sample Questions]
Sliding friction can be understood as the resistance created by any two objects while sliding over each other. Since it can also be defined as the force required to keep one object sliding over another, it is also known as kinetic friction. It acts in the direction opposite to the direction of application of force and resists the real relative sliding motion between the two contact surfaces. For example, consider there is a table that you wish to move. A weak force will not set the table into motion. As you increase the force applied, the table begins moving. The resistance created will be equal to the force applied but will operate in the opposite direction.

Sliding friction is dependent on the material of the object as well as the weight of the object. The shape of the objects is usually arbitrary, and friction operates independently of the shape. The weight produces a force acting normal to the surface, and the sliding friction is directly proportional to it. Sliding friction produces thermal energy, and this is dependent on the material of the objects. Sometimes, the sliding can even cause a fire, like when you light a matchstick. In most materials, sliding friction is lesser than static friction, which is the force that keeps an object at rest. In metals with static and small surfaces where molecular attraction takes over, the static force may be lesser.
Read More:
| Centripetal and Centrifugal Force | Derivation of Centripetal Acceleration | Coefficient of Static Friction |
| Aristotle Fallacy | Static Friction | Impending Motion |
Sliding Friction Formula
[Click Here for Sample Questions]
The formula for sliding friction is FS = μSFn
Where,
FS is the force of sliding friction.
μS is the coefficient of sliding friction.
Fn is the normal force.
This motion can also be interpreted by Newton’s Second Law. When the force applied or the external force is greater than the kinetic force, acceleration is experienced. When the external force is lesser than the kinetic force, the object slows down. When the two forces are equal, the object is at a constant velocity.
When an object is placed on an incline, the presence of the slope prevents gravity from pulling the object straight down, so it moves along the surface of the incline. To find the coefficient of kinetic friction on an inclined plane, it is important to understand that when the sliding force is parallel to the plane, it is equal to the force acting perpendicular to the plane. This occurs when the object is moving at a constant velocity. Then, the force perpendicular between the surfaces is reduced, according to the angle of the incline. The formula to calculate the force of sliding fraction then becomes FS = μSFsCosθ, to include the angle of the plane.

Here, we can see that the normal force is not directly opposite to the force of gravity, but perpendicular to the surface of the object. The force of gravity is then resolved into two components, one acting parallel to the surface and one acting perpendicular to the inclined surface.
The friction force that acts is generally almost independent of velocity, which results from rapid processes that occur at the sliding interface, involving local slip velocities that are not related to the macroscopic drive velocity. This does not hold true if the object is so slow that there is no thermal activation or if the object moves so fast that there is high frictional heating.

The frictional force of rolling friction, which occurs during rotational motion, is much lesser than kinetic friction. Sliding friction also produces more heat and sound. One example of this is applying the breaks on a motor vehicle.
Factors Affecting Sliding Friction
[Click Here for Sample Questions]
The amount of sliding friction created is expressed as a coefficient represented by μS. It is a ratio of two forces and hence has no dimensions. This coefficient is the result of several factors that affect kinetic friction:
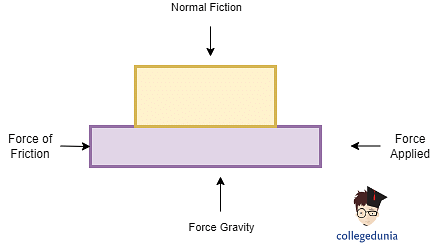
- The normal force acting upon the sliding bodies.
- The surface deformation of the objects.
- The roughness or smoothness of the sliding object.
- The roughness or smoothness of the sliding object’s surface.
- The original speed of either object.
- The shape and size of the object.
- The amount of pressure acting on either object.
Examples of Sliding Friction
[Click Here for Sample Questions]
Some of the examples of sliding friction are:
- The use of the brake of the bikes retards the wheels by creating sliding.
- Friction between bike rims and brake pads.
- Sliding of furniture/block across the floor.
- Two cards sliding against each other.
- A Speedy car.
- While sliding down through a slide in a park.
- Rubbing both hands together to create heat.
- A coaster sliding against a table.
- A washing machine pushed across the floor.
- The frame and the edge of the door sliding against one another.
- A block is being slid across the floor.
Recommended video:
Things to Remember
- When a moving body is sliding over a surface, the force acting on it is sliding friction.
- As it can also be defined as the force required to keep one object sliding over another, it is also known as kinetic friction.
- The formula for sliding friction is FS = μSFn
- This motion can also be interpreted by Newton’s Second Law.
- The frictional force of rolling friction, which occurs during rotational motion, is much lesser than kinetic friction.
- Sliding friction also produces more heat and sound.
- Friction between bike rims and brake pads, sliding of furniture/block across the floor are examples of friction.
Read More:
Sample Questions
Ques: Define coefficient of kinetic friction. (1 mark)
Ans: The kinetic friction coefficient μk is the ratio of the friction force to the normal force experienced by a body moving on a dry, non-smooth surface.
Ques: What is the measure of sliding friction? (1 mark)
Ans: The force that is required to keep the object moving at the same speed is a measure of sliding friction.
Ques: Define sliding friction. (2 marks)
Ans: Sliding friction can be understood as the resistance created by any two objects while sliding over each other. Since it can also be defined as the force required to keep one object sliding over another, it is also known as kinetic friction. It acts in the direction opposite to the direction of application of force and resists the real relative sliding motion between the two contact surfaces. For example, Rubbing both hands together to create heat.
Ques: How is sliding friction different from static friction or rolling friction? (3 marks)
Ans: Rolling friction is a type of static friction as it functions when a body is in contact with some surface and it is rotating. Whereas, sliding friction comes into play when one body slides over another body and it falls under the category of kinetic friction as the body is in motion. This is the reason why sliding friction is also known as kinetic friction.
Ques: How does sliding friction help you ride a bike? (2 marks)
Ans: Sliding friction helps us riding the bike as there is sliding friction between the brake pads and bike rims each time we use our bike’s brakes. This friction slows the rolling wheels so you can stop.
Ques: Why is it easier to move the box that is already in motion than to get it started?
or
The sliding friction is slightly smaller than the static friction. Explain. (2 marks)
Ans: When the box starts sliding or moving, the contact points on its surface do not get enough time to lock into the contact points on the floor. Therefore, the sliding friction is slightly smaller than the static friction. This is the reason why it is easier to move the box which is already in motion than to get it started.
Ques: What are the factors affecting kinetic friction? (3 marks)
Ans: The factors affecting the kinetic friction are as follows:
- The normal force acting upon the sliding bodies.
- The surface deformation of the objects.
- The roughness or smoothness of the sliding object.
- The roughness or smoothness of the sliding object’s surface.
- The original speed of either object.
Ques: What is important to notice when calculating the kinetic friction on an incline? (4 marks)
Ans: When an object is placed on an incline, the presence of the slope prevents gravity from pulling the object straight down, so it moves along the surface of the incline. To find the coefficient of kinetic friction on an inclined plane, it is important to understand that when the sliding force is parallel to the plane, it is equal to the force acting perpendicular to the plane. This occurs when the object is moving at a constant velocity. Then, the force perpendicular between the surfaces is reduced, according to the angle of the incline.
Ques: What are the examples of sliding friction? (4 marks)
Ans: Some of the examples of sliding friction are:
- The use of the brake of the bikes retards the wheels by creating sliding.
- Friction between bike rims and brake pads.
- Sliding of furniture/block across the floor.
- Two cards sliding against each other.
- A Speedy car.
- While sliding down through a slide in a park.
- Rubbing both hands together to create heat.
- A coaster sliding against a table.
Ques: Derive an expression for the acceleration of a body sliding down an inclined plane. (5 marks)
Ans:
Consider a plane is inclined to the horizontal at an angle ?. Let the body placed on the inclined plane slide down with an acceleration a, then
The reaction R = mg cos θ ------Eqn (1)
Net force on the body down the inclined plane = f = mg sin θ – F
f = ma = mg sin θ – μR as μ = F / R ---- Eqn (2)
Now substitute for R, from equation (1)
ma = mg sin θ – μ mg cos θ = mg (sin θ - μ cos θ )
a = mg (sin θ - μ cos θ)
The acceleration of the body down a rough inclined plane is always less than the acceleration due to gravity g. that is a < g
Thus, the minimum force required to push the body down the inclined plane is f (down) = mg (sin ? + μ cos ? )
The minimum force required to push the body down the inclined plane is
f (up) = mg( μ cosθ - sinθ)
For Latest Updates on Upcoming Board Exams, Click Here: https://t.me/class_10_12_board_updates
Check-Out:







Comments