Collegedunia Team Content Curator
Content Curator
Newton's laws of motion are three fundamental classical mechanics laws that define the relationship between an object's motion and the forces acting on it.
- Newton’s laws of motion express the relation established between the forces acting on a body and its motion.
- It quantifies the concept of inertia.
- Inertia is the tendency of a body wherein a body in motion continues to remain in motion, with uniform velocity and a body at rest continues to remain at rest unless it is acted upon by a force.
- ‘Force’ is a push or pull on an object as a result of the object’s interaction with another object.
- It is a vector quantity.
- An object experiences an equal and opposing force when it interacts with another object.
- When an object is in equilibrium i.e. it is not moving with a change in speed, the net force acting on it is ‘balanced’.
- When an object is not in equilibrium i.e. it is moving with a change in speed, the net force on it is ‘unbalanced’.
Key Terms: Newton’s law, Newton's second law, Newton's third law, Inertia, Laws of Motion, Force, Acceleration, Motion, Laws of inertia, Balanced forces, Unbalanced force
Newton’s Laws of Motion
[Click Here for Previous Year Questions]
Newton’s laws of motion help in determining the relations between the forces acting on a body and the motion of the body.
- A body in motion remains in motion or a body remains at rest unless the force is acted upon.
- The Force equals mass times acceleration .i.e F = m*a.
- To move a basketball that is at rest, someone must bounce it.
- Some external energy provides force to move a body from rest.
- Similarly, even to stop a motion, a force is required.
- As per Newton’s laws of motion, every action has an equal and opposite reaction.

Newton’s Three Laws of Motion
Determine the net force needed to offer an automobile mass of 1600 kg with an acceleration of 4.5 m/s2.We can determine the equation of force using the given formula: F = ma Now, upon replacing the values in the equation, we can get: F = 100kg \(\times\) 4.5m/s2 = 7200 N |
Laws of Motion Video Lecture
Also Read:
Newton’s First Law of Motion
[Click Here for Sample Questions]
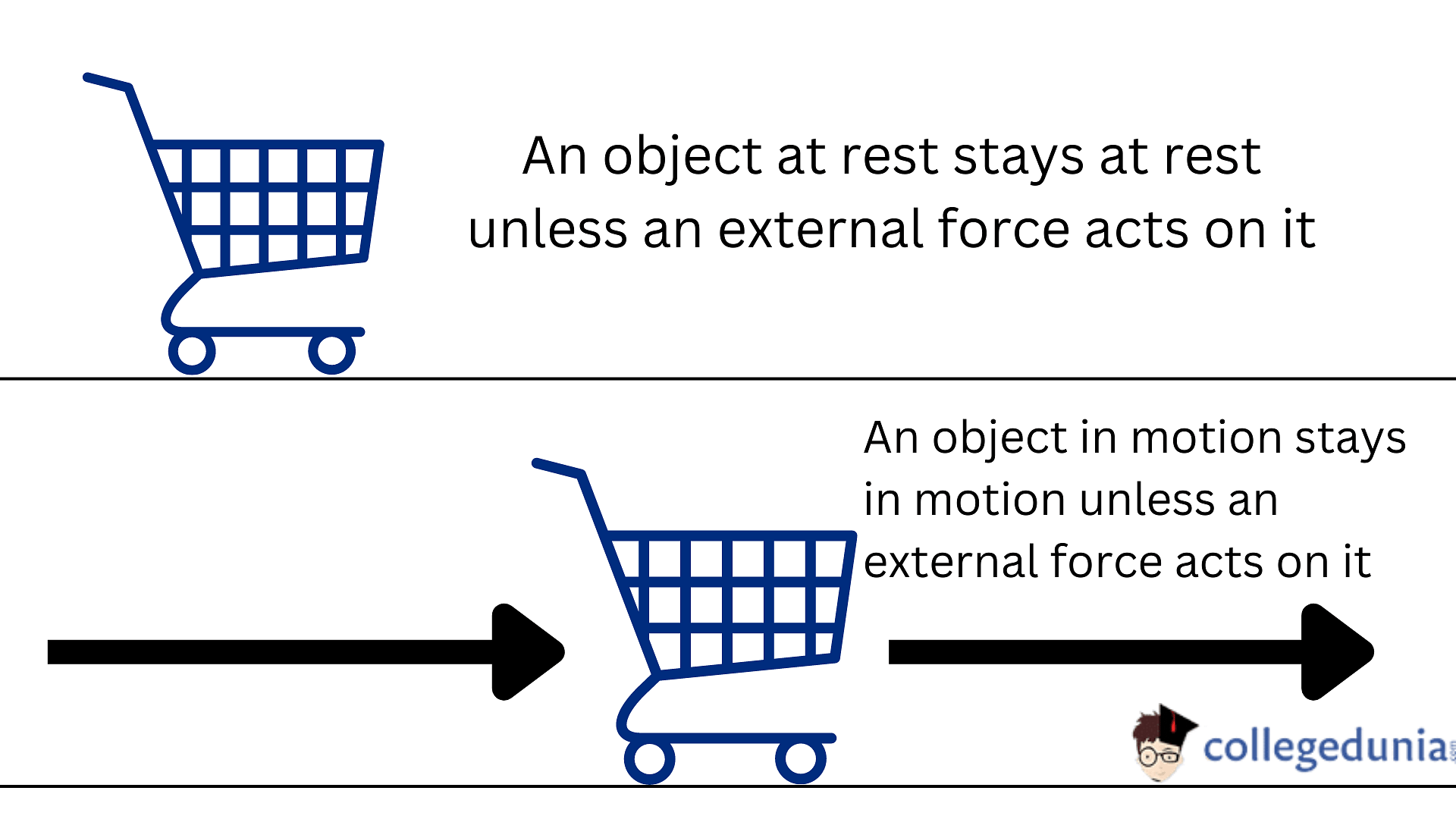
Newton’s first law of motion implies that if the net external force on a body is zero, then its acceleration is zero. An object at rest remains at rest if there is no net external force on the object.
Newton’s 1st law states that a body in uniform motion or at rest will continue to be in uniform motion or at rest until and unless a net external force acts on it.
- The first law of motion describes Inertia, which is a body's resistance to change in motion.
- If no force is applied then the object maintains a constant velocity.
- For example, a spaceship out in space, which is far from all other objects and with all its rockets turned off there is no net external force acting on it making the acceleration zero. If it is in motion, it must continue to move with a uniform velocity.
- The first law of Newton’s laws of motion is also called the law of inertia.
Examples of First Law of Motion
|
Newton’s First Law Example
Newton's Second Law of Motion
[Click Here for Previous Year Questions]
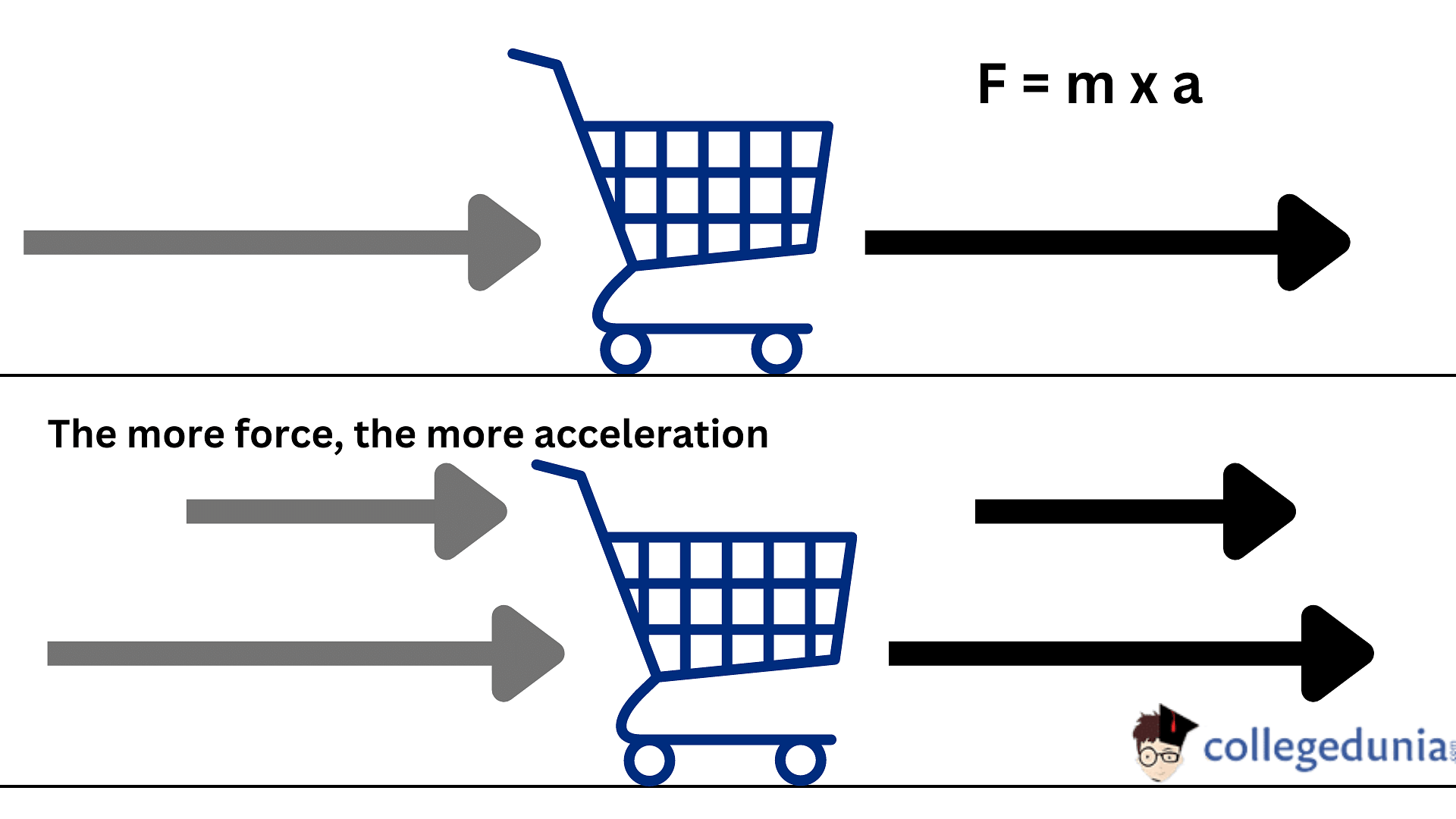
Newton’s 2nd law of motion states that the acceleration of an object produced by a net force is directly proportional to the magnitude of the force, in the same direction, and inversely proportional to the mass of the object.
- Newton's second law of motion implies that the rate of change of an object’s momentum is equal to the force acting upon it.
- The applied force is equal to the object's mass times its acceleration.
- Newton’s second law of motion states that a massive body when acted upon by an external force experiences a force equal to the product of its mass and acceleration.
- Newton’s second law describes precisely how much an object will accelerate for a given net force.
Equations for Newton’s second law of motion are:
F = Δp/Δt
F = m x a
F ∝ (mv – mu)/t
F ∝ m(v – u)/t
F ∝ ma
F = k ma
In the equation, k is the constant of proportionality and is equal to 1 when the values are taken in the SI unit. Hence, the final expression will be,
| F = ma |
In Newton’s laws of motion –
The second law of motion tells us that an external force accelerates an object. The acceleration is inversely proportional to its mass, so it’s harder to accelerate a heavier object than a lighter one.
Examples of Newton’s Second Law
|
Newton’s Laws of Motion – Second Law
Newton’s Third Law of Motion
[Click Here for Sample Questions]
Newton’s Third Law of Motion states that every action has an equal and opposite reaction.
- The third law of Newton states that when one object exerts a force on a second object, then the second object exerts an equal and opposite force on the first object.
- The third law of Newton’s laws of motion implies the conservation of momentum.
- For example – a cart resting.
- The cart applies a downward force that is equivalent to its weight on the ground.
- According to Newton’s third law of motion, the cart also applies an equal and opposite force to the cart.
- This force occurs as the cart slightly deforms the ground; as a result, the ground pushes back on the cart like a coiled spring.
Examples of Newton's Third law of Motion
|

Applications of Laws of Motion
[Click Here for Previous Year Questions]
Newton’s Laws of Motion have the following applications –
Newton’s First Law of Motion
A car traveling on a highway at a fixed speed maintains uniform motion.
- When a force from outside is applied to the car such as a sudden change in direction, the car responds to it on its own, while the passengers or objects in the car are responding to inertia, through which their motion will still be in a straight line.
- As the direction has changed, this causes the passengers or the objects to be thrown off. This is explained by the first law of motion.
Newton’s Second Law of Motion
The application of the second law of Newton’s laws of motion determines the amount of force needed to make an object stop or move. For example, stopping a moving cart or pushing a cart.
Newton’s Third Law of Motion
The application of the third law of motion can be seen by taking a glass resting on a table. Even though the glass is at rest it exerts a force on the table and the table, in return, is exerting an equal and opposite force which ensures the glass stays at rest.
Also Check:
| Concept Related Topics | ||
|---|---|---|
| Rolling Friction | Motion | Specific Gravity |
| Pseudo Force | Static Friction | Aristotle Fallacy |
Things To Remember
- Force equals mass time acceleration.i.e F= ma.
- Newton’s laws of motion are three laws of classical mechanics that describe the relationship between the motion of an object and the force acting on it.
- The first law of motion describes Inertia, which is a body's resistance to change in motion.
- If no force is applied then the object maintains a constant velocity.
- The second law of motion tells us that an external force accelerates an object.
- The third law of Newton states that when one object exerts a force on a second object, then the second object exerts an equal and opposite force on the first object.
Previous Year Questions
- What is the change in the magnetic field of a charged particle which enters a uniform magnetic field? [JKCET 2006]
- Identify the correct scenario for three objects thrown in the air. [JKCET 2007]
- An example of an inertial frame observer is? [JKCET 2009]
- Calculate the time needed by the body to cover ¼ th of the distance from a state of rest. [JIPMER 1999]
- Calculate the reading of the spring balance when a mass of 5kg is suspended on an inclined plane. [BITSAT 2006]
- Calculate the impulse experienced by the body which hits a rigid wall. [BITSAT 2018]
- What is the apparent weight of the man moving up the elevator? [DUET 2003]
- What is the work done by the inextensible spring? [BITSAT 2013]
- How much time would the man take to move up the elevator? [NEET 2006]
- During a journey from earth to moon and back … [AMUEEE 1999]
- In the arrangement shown in the figure … [JEE Advanced 1982]
- Block A of mass m and block B of mass 2 m …
- If the unit of force and length be each increased …
- The apparent weight of a person inside a lift …
- Two masses of 10 kg and 20 kg respectively … [BHU UET 2011]
Sample Questions
Ques. Find out how much net force will be needed to accelerate a 2500 kg truck at 5.50 m/s2. (3 marks)
Ans. Here we have,
Acceleration (a) = 5.50 m/s2
Mass of the Truck (m)= 2500 kg
Hence,
Force = mass × acceleration
F = 2500 × 5.5
F = 13750 N
Net force will be needed to accelerate a 2500 kg truck at 5.50 m/s2 is 13750 N.
Ques. A person drives a cart, Cart 1, to the right while pushing another cart, Cart 2, that has a massive refrigerator on it. The total mass of Cart 2, cart plus fridge, is three times the total mass of Cart 1, cart plus person. If the person is driving with enough force that the two carts accelerate to the right, what can be said for sure about the magnitudes of the forces on the carts? (2 marks)

(a) The force on cart 2 exerted by Cart 1 is larger in magnitude than the force on cart 1 exerted by cart 2.
(b) The force on Cart 2 exerted by Cart 1 is equal to the magnitude of the force on Cart 1 exerted by cart 2.
Ans. b) The force on Cart 2 exerted by Cart 1 is equal to the magnitude of the force on Cart 1 exerted by cart 2.
Explanation- Whether there is acceleration or whether the mass of one object is larger than the other object it doesn’t matter. Force reaction pairs are equal in magnitude.
Ques. What will happen If a net force of 6 N is applied on 0.5 kg-material, Calculate the acceleration of the material. (2 marks)
Ans. b Here we have Force (F) = 6 N
Mass (m) = 0.5 kg
acceleration (a) = ?
Force = mass × acceleration
F = m × a
a = \(\frac{F}{m}\)
a = \(\frac{6}{0.5}\)
a = 12 m/s2
The acceleration of the material is 12 m/s2
Ques. What will happen when a net force of 70 N is constantly applied to a 1.4 kg body at rest? What time will it take to attain the velocity of 150 m/s? (3 marks)
Ans. Here we have
Force (F) = 70 N
Mass of the body (m) = 1.4 kg
Initial velocity = 0 m/s (as body is at rest)
Final velocity = 150 m/s
We have to find t = ?
First, find the acceleration through Newton’s laws of motion –
Force = mass × acceleration
F = m × a
a = \(\frac{F}{m}\)
a = \(\frac{70}{1.4}\)
a = 50 m/s2
Now use this equation of motion
v = u + at
150 = 0 + (50 × t)
150 = 50 × t
t = \(\frac{150}{50}\)
t = 3 sec
Ques. When a train engine of mass 2500 kg is moving with some velocity. If the engine after applying brakes is brought to rest after application of brakes engine goes about 40m when the average resistance being offered to it is 5000 N. Calculate the velocity of the Train engine. (3 marks)
Ans. Here we have
Mass of the Train (m) = 2500 kg
Force (F) = – 5000 N (as negative stopping force is applied)
Distance (s) = 40 m
Final velocity (v) = 0 m/s
We have to find Initial velocity u = ?
Applying Newton’s laws of motion –
Force = mass × acceleration
First, find the acceleration
F = m × a
a = \(\frac{F}{m}\)
a = \(\frac{– 5000}{2500}\)
a = – 2 m/s2
Now we will use this equation of motion
v2 = v2 + 2as
0 = u2 + {2 × ( – 2) × 40}
u = 160 m/s
The initial velocity of the Train engine was 160 m/s
Ques. If a racing car driver on a race track in order to overtake accelerates his racing car first at the rate of 8 m/s2 and then at the rate of 16 m/s2. Find the ratio of the forces exerted by the engine for the acceleration change. (3 marks)
Ans. Here we have
a1 = 8 m/s2
a2 = 16 m/s2
We have to find the ratio of \(\frac{f_1}{f_2}\)
\(\frac{f_1}{F_2}\) = \(\frac{ma_1}{ma_2}\)
The mass of the racing car will be the same in both cases
\(\frac{F_1}{F_2}\) = \(\frac{a_1}{a_2}\) = \(\frac{8}{16}\) = \(\frac{1}{2}\)
\(\frac{f_1}{f_2}\) = 1:2
Ques. If a body of mass 10 kg is moving with a constant velocity of 4 m/s on frictionless ground. What will be the force required to keep the body moving with the same velocity? (2 marks)
Ans. Here we have
Mass (m) = 10 kg
acceleration (a) = 0
We have to find F = ?
By Newton’s laws of motion –
Force = mass × acceleration
F = 10 × 0
F = 0
Ques. When a bullet of mass of 20 gm is shot from a gun that has an initial velocity of 40 m/s the mass of the gun is 5 kg. What is the initial recoil velocity of the gun? (2 marks)
Ans. Here we have
mass of bullet (m1) = 20 gm or 0.02 kg
mass of the gun (m2) = 5 kg
Initial velocity = 40 m/s
By the law of conservation of momentum,
0 = 0.02 × 40 + 5 × v
5 × v = -0.8
v = -0.16 m/s
Ques. if a baseball ball is applying force on a ball of 1000N and the ball moves away. If the ball is applying the same force on the bat why doesn't the bat move away? (5 marks)
Ans. There are two factors to consider.
First, the masses are different. The mass of a baseball is .145kg, while a bat has a mass of about 1.0 kg. So, from F = ma, this tells us that a = F/m, and so the acceleration of the ball will be about 7 times the acceleration of the bat. We know that the average acceleration is given by a = Δv/Δt, which tells us that Δv = a * Δt. Thus, since the Δt is the same for both, and the acceleration of the ball is 7 times bigger, the Δv of the ball will be 7 times bigger.
The Second factor is that the bat is already moving at a fairly high speed, and so its momentum is much greater than the momentum of the ball, at least in the frame of reference of the spectators. Thus, the bat is only slowed down, while the ball is turned completely around. Here is an example:
mass of bat = 1kg
mass of ball = (1/7)kg
initial velocity of bat = +35 m/s
initial velocity of ball = -35 m/s
final velocity of bat = +20 m/s
final velocity of ball = +70 m/s
You can see that the Δv for the bat = 20 - 35 = -15m/s, while Δv for the ball = 70 - -35 = +105m/s, which is 7 times as big as the Δv for the bat.
If you were to watch the collision from a car moving at v = +35m/s, you would see the bat initially at rest and finally moving at -15 m/s, so you would see it "moving away" from the collision.
One final factor is that the player keeps pushing on the bat during the hit, so although the ball pushes on the bat equal and opposite to the bat pushing on the ball, there is an additional force on the bat that tends to counteract the ball pushing on the bat.
Ques. Which of the 3 Newton’s laws of motion best explains how a magician can pull a tablecloth from underneath dishes? (2 marks)
Ans. Newton’s first law of motion can explain how a magician pulls a tablecloth underneath the dishes. A negligible horizontal force is applied during the process. As per Newton’s first law of motion, the dishes and glasses remain in their state of motion (rest); as a result, they remain undisturbed. The table cloth in the trick is made so slippery that it doesn’t apply any frictional force on glasses and dishes.
Do Check Out:






Comments