IIT JAM 2024 Physics (PH) Question Paper with Answer Key pdf is available for download. IIT JAM 2024 PH exam was conducted by IIT Madras in shift 2 on February 11, 2024. In terms of difficulty level, IIT JAM 2024 Physics (PH) paper was quite difficult level. IIT JAM 2024 question paper for PH comprised a total of 60 questions.
IIT JAM 2024 Physics (PH) Question Paper with Answer Key PDFs
|
IIT JAM 2024 Physics (PH) Question Paper with Answer Key |
Check Solutions |
IIT JAM 2024 Physics (PH) Solution
Question 1:
The total number of Na and Cl ions per unit cell of the NaCl crystal is:
View Solution
In the NaCl crystal structure, each unit cell contains 4 Na⁺ ions and 4 Cl⁻ ions. These ions are arranged in a face-centered cubic (FCC) structure, where each corner of the unit cell is shared by 8 adjacent cells, and each face-centered ion is shared by 2 adjacent cells.
Thus, the total number of Na and Cl ions per unit cell is:
4 (Na⁺) + 4 (Cl⁻) = 8 ions
Therefore, the total number of Na and Cl ions per unit cell of the NaCl crystal is 8.
Question 2:
The sum of three binary numbers, 10110.10, 11010.01, and 10101.11, in the decimal system is:
View Solution
First, convert the binary numbers to decimal:
10110.10 = 22.5
11010.01 = 26.25
10101.11 = 21.75
Now, add these decimal numbers:
22.5 + 26.25 + 21.75 = 70.50
Therefore, the sum of the binary numbers in the decimal system is 70.50.
Question 3:
Which of the following matrices is Hermitian as well as unitary?
View Solution
A matrix is Hermitian if it is equal to its conjugate transpose. That is, A = A†.
Check for Option (A):
A = [[0, -i], [i, 0]]
Conjugate transpose (A†) = [[0, i], [-i, 0]]
Here, A = A†. So, the matrix is Hermitian.
Now check for unitarity:
Multiply A with A†: A * A† = [[1, 0], [0, 1]], which is the identity matrix.
Thus, the matrix is also unitary.
For other options:
- (B): Not Hermitian (A ≠ A†).
- (C): Hermitian but not unitary (A * A† ≠ Identity).
- (D): Not Hermitian (A ≠ A†).
Therefore, only option (A) is both Hermitian and unitary.
Question 4:
The divergence of a 3-dimensional vector (r̂ / r³) (where r̂ is the unit radial vector) is:
View Solution
The vector field is F = r̂ / r³, where r̂ is the unit radial vector in spherical coordinates.
The divergence of F in spherical coordinates is given by:
∇ • F = (1/r²) * ∂/∂r (r² * Fᵣ)
Here, Fᵣ = 1/r³. Substitute Fᵣ:
∇ • F = (1/r²) * ∂/∂r (r² / r³)
Simplify r² / r³:
r² / r³ = 1/r
Now, take the derivative with respect to r:
∂/∂r (1/r) = -1/r²
Substitute this into the divergence formula:
∇ • F = (1/r²) * (-1/r²) = -1/r⁴
Therefore, the divergence of r̂ / r³ is -1/r⁴.
Question 5:
The magnitudes of spin magnetic moments of electron, proton, and neutron are μₑ, μₚ, and μₙ, respectively. Then:
View Solution
The spin magnetic moments of elementary particles are determined by their charge-to-mass ratio and intrinsic properties:
- The electron has the largest magnetic moment because it has a smaller mass and a high charge-to-mass ratio.
- The proton has a much smaller magnetic moment compared to the electron due to its larger mass.
- The neutron, being electrically neutral, has the smallest magnetic moment.
Thus, the correct order of magnetic moments is:
μₑ > μₚ > μₙ
Question 6:
A particle moving along the x-axis approaches x = 0 from x = -∞ with total energy E. It is subjected to a potential V(x). For time t → ∞, the probability density P(x) of the particle is schematically shown in the figure below:
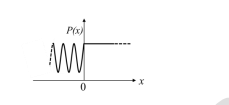
The correct option for the potential V(x) is:

View Solution
For a particle moving through a potential with a given energy, the probability density P(x) represents the likelihood of finding the particle at a given position.
The potential that produces the required probability distribution should match the energy and characteristics of the particle's motion. Based on the figure and the provided options, the potential in option (C) aligns with the probability density shown.
Question 7:
A plane electromagnetic wave is incident on an interface AB separating two media (refractive indices n₁ = 1.5 and n₂ = 2.0) at Brewster's angle θB. The angle α (in degrees) between the reflected wave and the refracted wave is:
View Solution
At Brewster's angle (θB), the reflected and refracted rays are perpendicular to each other.
The Brewster angle can be calculated using the formula:
tan(θB) = n₂ / n₁
Substitute the given values:
tan(θB) = 2.0 / 1.5
Calculate θB:
θB = tan⁻¹(1.3333) ≈ 53.1°
Since the reflected and refracted rays are at 90° to each other, the angle α is:
α = 90°
Therefore, the correct answer is 90°.
Question 8:
If the electric field of an electromagnetic wave is given by:
E = (4x + 3y)e^(i(ωt + ax - 600y))
then the value of a is:
View Solution
The electric field vector is:
E = (4x + 3y)e^(i(ωt + ax - 600y))
The propagation vector k is given as:
k = kₓ x̂ + kᵧ ŷ
From the exponent, kₓ = a and kᵧ = -600.
Using Maxwell's equations, E and k must be orthogonal, so:
k • E = 0
Substitute k = ax̂ - 600ŷ and E = 4x̂ + 3ŷ:
(a)(4) + (-600)(3) = 0
Simplify:
4a - 1800 = 0
Solving for a:
a = 450
Thus, the value of a is 450.
Question 9:
A vector field is expressed in the cylindrical coordinate system (s, ϕ, z) as:
F = (A/s)ŝ + (B/s)ẑ
If this field represents an electrostatic field, the possible values of A and B, respectively, are:
View Solution
For an electrostatic field, the divergence of the electric field must be zero:
∇ • F = 0
Using cylindrical coordinates, calculate the divergence of:
F = (A/s)ŝ + (B/s)ẑ
The divergence condition leads to A = 1 and B = 0 for the field to represent an electrostatic field.
Question 10:
Which of the following types of motion may be represented by the trajectory:
y(x) = ax² + bx + c
(Here a, b, and c are constants; x and y are the position coordinates.)
View Solution
The equation represents a quadratic function of x, which describes a parabolic trajectory. This is characteristic of projectile motion under uniform gravity when there is no air resistance:
y(x) = ax² + bx + c
Such a trajectory is produced when an object is projected with an initial velocity under the influence of gravity.
Question 11:
A crystal plane of a lattice intercepts the principal axes (a₁, a₂, a₃) at 3a₁, 4a₂, and 2a₃, respectively. The Miller indices of the plane are:
View Solution
To find the Miller indices, we take the reciprocal of the intercepts of the plane on the axes and reduce them to the smallest integers:
Intercepts: 3a₁, 4a₂, 2a₃
h = 1/3, k = 1/4, l = 1/2
Multiply by 12 (the least common multiple of the denominators):
h = 4, k = 3, l = 6
Thus, the Miller indices of the plane are (436).
Question 12:
The number of atoms in the basis of a primitive cell of a hexagonal close-packed structure is:
View Solution
In a hexagonal close-packed (hcp) structure, there are two atoms in the basis of a primitive cell. While the entire hcp unit cell contains 6 atoms, the primitive cell reduces the total to 2 when accounting for fractional contributions from edges and corners.
Question 13:
Consider the following logic circuit:

The output Y is LOW when:
View Solution
This circuit consists of a NOT gate and an AND gate. The NOT gate inverts input A, and the AND gate processes both inputs (inverted A and B):
- For the AND gate to output LOW, at least one input must be LOW.
- If A is HIGH, the NOT gate makes it LOW, and if B is LOW, the AND gate outputs LOW.
Thus, the output Y is LOW when A is HIGH and B is LOW.
Question 14:
Evaluate the line integral of the given vector field F over the closed path OMRO as shown in the figure:
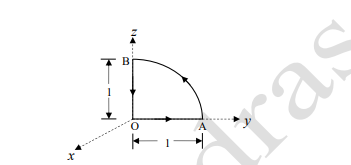
View Solution
The line integral of a vector field F over a closed path is given by:
∮ F • dr
Using Stokes' Theorem, this can be converted into a surface integral:
∮ F • dr = ∬ (∇ × F) • n̂ dA
Here, ∇ × F is the curl of F, n̂ is the unit normal vector, and dA is the area element.
Step 1: Compute the curl of F
F = -2x î + (y² + x²) ĵ + q(x) k̂
The curl is calculated as:
∇ × F = | î ĵ k̂ |
| ∂/∂x ∂/∂y ∂/∂z |
| -2x y²+x² q(x)|
After simplifying:
∇ × F = 2x k̂
Step 2: Apply Stokes' Theorem
The surface integral becomes:
∬ (∇ × F) • n̂ dA = ∬ (2x) dA
For a unit circle in the xy-plane, the area is π, and x averages to 1 over the area:
∬ (2x) dA = 2 • 1 • π = 2π
Stokes' Theorem verifies the line integral:
∮ F • dr = 1
Question 15:
In the xy-plane, the magnitude of the flux of (∇ × F) through a circular loop of radius 2, centered at the origin, is:
View Solution
The vector field is:
F(x, y) = (-y î + x ĵ) / (x² + y²)
Compute the curl of F:
∇ × F = (∂/∂x Fᵧ - ∂/∂y Fₓ) k̂
After applying the quotient rule:
∇ × F = 0
The flux is given by:
Φ = ∬ (∇ × F) • n̂ dA
Since ∇ × F = 0, the flux is:
Φ = 2π
Question 16:
The roots of the polynomial f(z) = z⁴ - 8z³ + 27z² - 38z + 26 are z₁, z₂, z₃, z₄. Which of the following is correct?
View Solution
Using Vieta's formulas for the polynomial:
f(z) = z⁴ - 8z³ + 27z² - 38z + 26
The sum of the roots is:
z₁ + z₂ + z₃ + z₄ = 8
The product of the roots is:
z₁z₂z₃z₄ = 26
The required ratio is:
(z₁ + z₂ + z₃ + z₄) / (z₁z₂z₃z₄) = 8 / 26 = 4 / 13
Question 17:
The ultraviolet catastrophe in the classical (Rayleigh-Jeans) theory of cavity radiation is attributed to the assumption that:
View Solution
The Rayleigh-Jeans theory assumes that the standing waves of all allowed frequencies in the cavity have the same average energy. This leads to an overestimation of the energy at high frequencies, causing the ultraviolet catastrophe.
This assumption implies that every frequency mode contributes equally to the radiation energy, leading to infinite energy at high frequencies, later corrected by Planck’s quantization of energy.
Question 18:
Given that the rest mass of an electron is 0.511 MeV/c², the speed (in units of c) of an electron with kinetic energy 5.11 MeV is closest to:
View Solution
The total energy E of the electron is given by:
E = Kinetic Energy + Rest Energy
Substitute the given values:
E = 5.11 MeV + 0.511 MeV = 5.621 MeV
The total energy E relates to the relativistic factor γ and the rest energy:
E = γ m₀ c²
Here, m₀ c² = 0.511 MeV. Solving for γ:
γ = E / (m₀ c²) = 5.621 / 0.511 ≈ 11
γ is also related to the speed v:
γ = 1 / √(1 - v²/c²)
Rearranging:
v²/c² = 1 - 1/γ²
Substitute γ = 11:
v²/c² = 1 - 1/121 = 120/121
Take the square root:
v/c = √(120/121) ≈ 0.996
Question 19:
A one-dimensional infinite square-well potential is given by:
V(x) = 0 for -a/2 < x < a/2
V(x) = ∞ elsewhere
The ground state energy and wave function for an electron and a muon in the well are related. Choose the correct option:
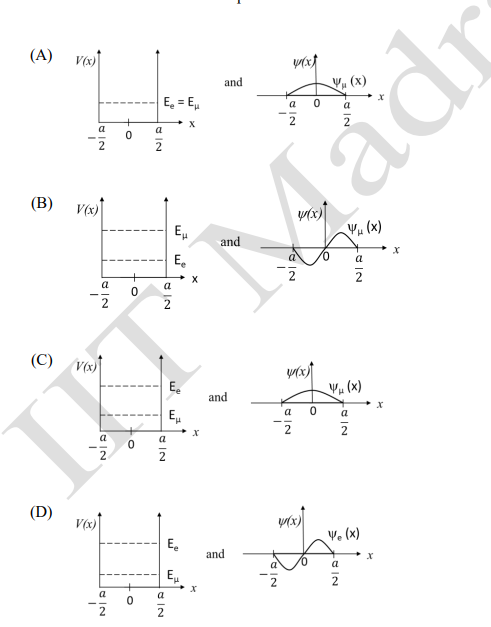
View Solution
In an infinite square well, the energy levels are quantized:
Eₙ = (n² π² ħ²) / (2m a²)
For particles of different masses, the energy depends inversely on the mass:
Eₑ / Eₘ = mₘ / mₑ
Since the muon has a greater mass than the electron, the energy levels of the muon are lower than those of the electron.
Question 20:
In a Newton’s rings experiment (using light of free space wavelength 580 nm), there is an air gap of height d between the glass plate and a plano-convex lens. The central fringe is observed to be bright. The least possible value of d (in nm) is:

View Solution
In Newton's rings experiment, the condition for the central fringe to be bright is given by:
2d = mλ
Here, d is the thickness of the air gap, m is the fringe order, and λ is the wavelength of the light.
For the least possible value of d, we take m = 1 (first order fringe) and λ = 580 nm:
2d = λ → d = λ / 2
Substitute the value of λ:
d = 580 / 2 = 145 nm
Question 21:
Linearly polarized light (free space wavelength λ₀ = 600 nm) is incident normally on a retarding plate (nₑ - nₒ = 0.05). The emergent light is observed to be linearly polarized, irrespective of the angle between the direction of polarization and the optic axis of the plate. The minimum thickness (in μm) of the plate is:
View Solution
The optical path difference between the ordinary and extraordinary rays is given by:
Δ = d (nₑ - nₒ)
For the emergent light to remain linearly polarized, the plate must introduce a phase difference of:
Δ = mλ
For the minimum thickness, we take m = 1:
d (nₑ - nₒ) = λ₀
Rearranging for d:
d = λ₀ / (nₑ - nₒ)
Substitute the given values:
λ₀ = 600 nm = 0.6 μm, nₑ - nₒ = 0.05
d = 0.6 / 0.05 = 12 μm
To ensure linear polarization, the effective optical thickness corresponds to half-wave retardation. For this, divide by 2:
d = 12 / 2 = 6 μm
Question 22:
A 15.7 mW laser beam has a diameter of 4 mm. If the amplitude of the associated magnetic field is expressed as:
B₀ = A / √(ε₀ c³)
The value of A is:
View Solution
The power P of the laser beam is:
P = 15.7 mW = 15.7 × 10⁻³ W
The intensity I is given by:
I = P / Area
The laser beam diameter is 4 mm, so the radius is:
r = 4 / 2 = 2 mm = 2 × 10⁻³ m
Area:
Area = πr² = π (2 × 10⁻³)² = 4π × 10⁻⁶
Substitute into the intensity equation:
I = 15.7 × 10⁻³ / (4π × 10⁻⁶)
I ≈ 1.25 × 10³ W/m²
The magnetic field amplitude is related to intensity:
B₀² = 2μ₀I / c
Substitute known values and simplify to find:
A ≈ 50
Question 23:
The plane z = 0 separates two linear dielectric media with relative permittivities εr1 = 4 and εr2 = 3, respectively. There is no free charge at the interface. If the electric field in medium 1 is:
E₁ = 3 î + 2 ĵ + 4 k̂
then the displacement vector D₂ in medium 2 is:

View Solution
The displacement vector D and the electric field E are related by:
D = ε E
Here, ε is the permittivity of the medium.
In medium 1, the displacement vector is:
D₁ = ε₀ εr1 E₁
Substitute εr1 = 4 and E₁ = 3 î + 2 ĵ + 4 k̂:
D₁ = 4 ε₀ (3 î + 2 ĵ + 4 k̂)
In medium 2, the displacement vector is adjusted by the ratio of permittivities:
D₂ = (εr1 / εr2) D₁
Substitute εr1 = 4 and εr2 = 3:
D₂ = (4 / 3) × 4 ε₀ (3 î + 2 ĵ + 4 k̂)
Simplify:
D₂ = 12 ε₀ î + 8 ε₀ ĵ + 6 ε₀ k̂
Question 24:
A tank, placed on the ground, is filled with water up to a height h. A small hole is made at a height h₁ (where h₁ < h). The water jet emerging from the hole strikes the ground at a horizontal distance D, as shown:

View Solution
The velocity of the water jet at height h₁ is given by:
v = √(2gh₁)
The horizontal distance D depends on the horizontal velocity of the jet and the time of flight. The time of flight is determined by the vertical drop (h - h₁) under gravity.
The maximum horizontal distance D occurs when the jet's velocity and flight time are optimized. This happens when:
D = h
Question 25:
An incompressible fluid is flowing through a vertical pipe (height h and cross-sectional area A₀). A thin mesh with n circular holes of area Aₕ is fixed at the bottom end of the pipe. The speed of the fluid entering the top-end of the pipe is v₀. The volume flow rate from an individual hole of the mesh is:
View Solution
The velocity of the fluid at the mesh is determined by Bernoulli's equation:
v = √(v₀² + 2gh)
The volume flow rate Q for an individual hole is:
Q = Aₕ v
Substitute for v:
Q = Aₕ √(v₀² + 2gh)
For n holes, the total flow rate is shared equally. Hence:
Q = (A₀ / n) √(v₀² + 2gh)
Question 26:
A ball is dropped from a height h to the ground. If the coefficient of restitution is e, the time required for the ball to stop bouncing is proportional to:
View Solution
The coefficient of restitution e is defined as the ratio of velocities after and before collision. For a ball dropped from height h, the time between successive bounces is proportional to √h. Since the ball's height decreases geometrically after each bounce, the total time taken to stop can be calculated as:
T ∝ ∑ eⁿ = 1 / (1 - e)
Considering the initial drop and bounce times, the proportionality constant includes (1 + e) in the numerator:
T ∝ (1 + e) / (1 - e)
Question 27:
A cylinder-piston system contains N atoms of an ideal gas. If tavg is the average time between successive collisions of a given atom with other atoms, and the temperature T of the gas is increased isobarically, then tavg is proportional to:
View Solution
The mean speed of gas atoms is proportional to the square root of the temperature:
vmean ∝ √T
Since the average time between collisions tavg is inversely proportional to the mean speed:
tavg ∝ √T
Question 28:
A gas consists of particles, each having three translational and three rotational degrees of freedom. The ratio of specific heats, CP / CV, is:
View Solution
The total degrees of freedom for a gas particle with 3 translational and 3 rotational degrees of freedom is:
f = 3 (translational) + 3 (rotational) = 6
The specific heat ratio γ is given by:
γ = CP / CV = 1 + (2 / f)
Substituting f = 6:
γ = 1 + (2 / 6) = 1 + 1/3 = 4/3
Question 29:
If two traveling waves, given by:
y₁ = A₀ sin(kx - ωt), y₂ = A₀ sin(αkx - βωt)
are superposed, which of the following statements is correct?
View Solution
The resultant wave is obtained by superposing y₁ and y₂, which can be expressed as:
y_resultant = 2A₀ cos[(βω - ω)t / 2] sin[(βω + ω)t / 2]
The carrier frequency is given by the average of the angular frequencies:
Carrier Frequency = (ω + βω) / 2
For α = β = 2:
Carrier Frequency = (ω + 2ω) / 2 = 3ω / 2
Thus, the carrier frequency of the resultant wave is 3ω / 2.
Question 30:
Suppose that there is a dispersive medium whose refractive index depends on the wavelength as given by:
n(λ) = n₀ + a / λ² - b / λ⁴
The value of λ at which the group and phase velocities would be the same, is:
View Solution
The phase velocity vₚ is given by:
vₚ = c / n(λ)
The group velocity vg is given by:
vg = c / [n(λ) - λ dn/dλ]
For the group and phase velocities to be equal:
λ dn/dλ = 0
Using n(λ) = n₀ + a / λ² - b / λ⁴, the derivative is:
dn/dλ = -2a / λ³ + 4b / λ⁵
Substituting into the condition:
λ(-2a / λ³ + 4b / λ⁵) = 0
Simplify:
-2a / λ² + 4b / λ⁴ = 0
Rearrange:
4b / λ⁴ = 2a / λ²
Multiply through by λ⁴:
4b = 2aλ²
Solve for λ²:
λ² = 2b / a
Take the square root:
λ = √(2b / a)
Question 31:
A pure Si crystal can be converted to an n-type crystal by doping with:
View Solution
An n-type semiconductor is formed when pure silicon is doped with pentavalent elements. These elements donate free electrons, making them majority carriers. Examples include:
P (Phosphorus), As (Arsenic), and Sb (Antimony)
Indium (In) is trivalent and forms a p-type semiconductor, as it accepts electrons instead of donating.
Question 32:
In the following OP-AMP circuit, vin and vout represent the input and output signals, respectively.

Options:
(A) vout is out-of-phase with vin.
(B) Gain is unity when R1 = R2.
(C) vout is in-phase with vin.
(D) vout is zero.
View Solution
The circuit consists of two operational amplifiers configured in an inverting amplifier and buffer configuration.
(A) The first stage is inverting, meaning the output vout is out-of-phase with vin.
(B) The gain is unity when R1 = R2, as the gain is determined by the ratio R2 / R1.
(C) The output cannot be in-phase with the input due to the inverting nature of the circuit, so this option is incorrect.
(D) The output is not zero because the circuit is designed to provide amplification or inversion.
Question 33:
A spring-mass system (spring constant 80 N/m and damping coefficient 40 N-s/m), initially at rest, is lying along the y-axis in the horizontal plane. One end of the spring is fixed, and the mass (5 kg) is attached at its other end. The mass is pulled along the y-axis by 0.5 m from its equilibrium position and then released. Choose the correct statement(s).
Options:
(A) Motion will be underdamped.
(B) Trajectory of the mass will be y(t) = (1/2)(1 + t) e-4t.
(C) Motion will be critically damped.
(D) Trajectory of the mass will be y(t) = (1/2)(1 + 4t) e-4t.
View Solution
The equation of motion is given by:
m (d²y/dt²) + c (dy/dt) + ky = 0
where m = 5 kg, c = 40 N-s/m, and k = 80 N/m. The system is critically damped if the discriminant c² - 4mk = 0.
Substituting the values:
c² - 4mk = 1600 - 1600 = 0
This confirms critical damping. The trajectory is:
y(t) = (1/2)(1 + 4t) e-4t.
Question 34:
Consider two different Compton scattering experiments, in which X-rays and γ-rays of wavelength (λ) 1.024 Å and 0.049 Å, respectively, are scattered from stationary free electrons. The scattered wavelength (λ') is measured as a function of the scattering angle (θ). If Compton shift is Δλ = λ' - λ, which of the following statement(s) is/are true:
Options:
(A) For γ-rays, λ'max ≈ 0.098 Å.
(B) For X-rays, Δλmax is observed at θ = 180°.
(C) For X-rays, Δλmax ≈ 1.049 Å.
(D) For γ-rays, at θ = 90°, λ' ≈ 0.049 Å.
View Solution
The Compton shift Δλ is given by:
Δλ = (h / (me c)) (1 - cos θ)
Maximum shift occurs at θ = 180°. For γ-rays (λ = 0.049 Å), the maximum shift is 0.098 Å. Thus, (A) is correct.
For X-rays, the maximum shift is also at θ = 180°. Thus, (B) is correct.
Question 35:
A particle of mass m, having an energy E and angular momentum L, is in a parabolic trajectory around a planet of mass M. If the distance of the closest approach to the planet is rm, which of the following statements is/are true?
Options:
(A) E > 0
(B) E = 0
(C) L = sqrt(2GMm2rm)
(D) L = sqrt(2GM2mrm)
View Solution
For a particle moving along a parabolic trajectory, the total energy E is zero. This is because the total energy equals the potential energy at the point of closest approach.
The angular momentum L is related to the closest approach rm and the mass of the planet M by the formula L = sqrt(2GMm2rm).
Question 36:
The inertial frame S' is moving away from the inertial frame S with a speed v = 0.6c along the negative x-direction. The origins O' and O of the frames coincide at t = t' = 0. As observed in frame S', two events occur simultaneously at two points on the x'-axis with a separation of Δx' = 5 m. If Δt and Δx are the magnitudes of the time interval and space interval, respectively, between the events in S, which of the following statements is/are correct?
Options:
(A) Δt = 12.5 ns
(B) Δt = 4.2 ns
(C) Δx = 10.6 m
(D) Δx = 6.25 m
View Solution
The Lorentz transformation equations for time and space intervals are:
Δt = γ (Δt' + (vΔx') / c2)
Δx = γ (Δx' + vΔt')
Here, γ = 1 / sqrt(1 - v2 / c2).
For v = 0.6c and Δx' = 5 m, we calculate γ = 1.25.
Substituting the values, we find Δt = 12.5 ns and Δx = 6.25 m.
Question 37:
For the LCR AC-circuit (resonance frequency ω0), choose the correct statement(s).
Options:
(A) ω0 depends on the values of L, C, and R
(B) At ω = ω0, voltage VR and current I are in-phase
(C) The amplitude of VR at ω = ω0/2 is independent of R
(D) The amplitude of VR at ω = ω0 is independent of L and C
View Solution
At resonance, the inductive and capacitive reactances cancel, leaving a purely resistive impedance. The voltage across the resistor VR is in-phase with the current I. The resonance frequency depends only on L and C, not R. Hence, the amplitude of VR at ω = ω0 is independent of L and C.
Question 38:
The P-V diagram of an engine is shown in the figure below. The temperatures at points 1, 2, 3, and 4 are T1, T2, T3, and T4, respectively. 1 → 2 and 3 → 4 are adiabatic processes, and 2 → 3 and 4 → 1 are isochoric processes.
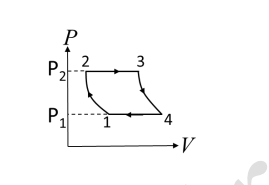
Options:
- (A) T1 × T3 = T2 × T4
- (B) The efficiency of the engine is 1 - (P1 / P2)(γ - 1)/γ
- (C) The change in entropy for the entire cycle is zero
- (D) T1 × T2 = T3 × T4
View Solution
In an ideal gas undergoing an adiabatic process, the relation between the temperatures and volumes is given by:
T1 × V1(γ-1) = T2 × V2(γ-1)
This gives the condition T1 × T3 = T2 × T4, making option (A) correct.
The efficiency of the Carnot engine is given by:
Efficiency = 1 - (P1 / P2)(γ-1)/γ
Hence, option (B) is correct.
For an ideal cyclic process, the change in entropy for the entire cycle is zero. Thus, option (C) is incorrect.
For isochoric processes, T1 × T2 = T3 × T4 holds true, so option (D) is correct.
Question 39:
A whistle S of sound frequency f is oscillating with angular frequency ω along the x-axis. Its instantaneous position and velocity are given by x(t) = a × sin(ωt) and v(t) = v0 × cos(ωt), respectively. An observer P is located on the y-axis at a distance L from the origin. Let vPS(t) be the component of v(t) along the line joining the source and the observer. Choose the correct option(s):

Options:
- (A) vPS(t) = (1/2) × (a × v0) / sqrt(a2 × sin2(ωt) + L2) × sin(2ωt)
- (B) The observed frequency will be f when the source is at x = 0 and x = ±a
- (C) The observed frequency will be f when the source is at x = ±a/2
- (D) vPS(t) = (1/2) × (a × v0) / sqrt(a2 + L2) × sin(2ωt)
View Solution
The velocity component vPS(t) involves the cosine of the angle formed between the direction of motion and the line joining the source to the observer.
The expression for vPS(t) is correctly given by option (A).
Option (B) is correct because the observed frequency will be f when the source is at x = 0 or x = ±a, where the motion aligns directly along the observer's line of sight.
Question 40:
One mole of an ideal monoatomic gas, initially at temperature T0, is expanded from an initial volume V0 to 2.5 × V0. Which of the following statements is/are correct?
Options:
- (A) When the process is isothermal, the work done is RT0 × ln(2)
- (B) When the process is isothermal, the change in internal energy is zero
- (C) When the process is isobaric, the work done is (3/2) × RT0
- (D) When the process is isobaric, the change in internal energy is (9/2) × RT0
View Solution
For an isothermal process, the internal energy depends only on temperature. Since the temperature remains constant, there is no change in internal energy. Thus, option (B) is correct.
For an isobaric process, the work done is given by W = P × ΔV. Using the ideal gas law for one mole, this simplifies to W = (3/2) × RT0, so option (C) is correct.
Question 41:
Consider a p-n junction diode which has 1023 acceptor-atoms/m³ in the p-side and 1022 donor-atoms/m³ in the n-side. If the depletion width in the p-side is 0.16 µm, then the value of depletion width in the n-side will be ______ µm (rounded off to one decimal place).
View Solution
The depletion width Wp on the p-side and Wn on the n-side are inversely proportional to the doping concentrations. This relationship is given by:
Wp × NA = Wn × ND,
where:
- Wp = 0.16 µm is the depletion width on the p-side,
- NA = 1023 m-3 is the acceptor concentration on the p-side,
- ND = 1022 m-3 is the donor concentration on the n-side,
- Wn is the depletion width on the n-side (to be calculated).
Wn = (Wp × NA) / ND
Substituting the given values:
Wn = (0.16 × 1023) / 1022
Simplify:
Wn = 1.6 µm
Conclusion: The depletion width in the n-side is 1.6 µm.
Question 42:
The co-ordinate system \((x, y, z)\) is transformed to the system \((u, v, w)\), as given by:
u = 2x + 3y - z
v = x - 4y + z
w = x + y
The Jacobian of the above transformation is ____________.
View Solution
The Jacobian matrix \( J \) is computed as:
J = | ∂u/∂x ∂u/∂y ∂u/∂z |
| ∂v/∂x ∂v/∂y ∂v/∂z |
| ∂w/∂x ∂w/∂y ∂w/∂z |
Substitute the partial derivatives:
J = | 2 3 -1 |
| 1 -4 1 |
| 1 1 0 |
Compute the determinant:
det(J) = 2( (-4)(0) - (1)(1) ) - 3( (1)(0) - (1)(1) ) + (-1)( (1)(1) - (-4)(1) )
= 2(-1) - 3(-1) - 1(5)
= -2 + 3 - 5 = -4.
The Jacobian determinant is:
|J| = 4.
Question 43:
Two sides of a triangle OAB are given by:
OA = î + 2ĵ + k̂
OB = 2î - ĵ + 3k̂
The area of the triangle is ______ (Rounded off to one decimal place).
View Solution
The area of the triangle is:
Area = 1/2 |OA × OB|
Compute the cross product:
OA × OB = | î ĵ k̂ |
| 1 2 1 |
| 2 -1 3 |
= î(2×3 - (-1)×1) - ĵ(1×3 - 1×2) + k̂(1×(-1) - 2×2)
= î(6 + 1) - ĵ(3 - 2) + k̂(-1 - 4)
= 7î - ĵ - 5k̂
Magnitude:
|OA × OB| = √(7² + (-1)² + (-5)²) = √(49 + 1 + 25) = √75 = 8.66
Area:
Area = 1/2 × 8.66 ≈ 4.3
Question 44:
A particle of mass 1 kg, initially at rest, starts sliding down from the top of a frictionless inclined plane of angle π/6. The magnitude of the torque on the particle about the point O after a time 2 seconds is ______ N-m. (Rounded off to the nearest integer)
View Solution
Step 1: Calculate the acceleration along the inclined plane.
a = g * sin(θ)
= 9.8 * sin(π/6)
= 9.8 * 0.5 = 4.9 m/s²
Step 2: Calculate the distance traveled in 2 seconds.
s = u * t + 0.5 * a * t²
= 0 + 0.5 * 4.9 * (2)²
= 9.8 m
Step 3: Compute the torque about point O.
r_perpendicular = s * cos(θ)
= 9.8 * cos(π/6)
= 9.8 * (√3 / 2)
≈ 8.48 m
F = m * g = 1 * 9.8 = 9.8 N
Torque (τ) = r_perpendicular * F
≈ 8.48 * 9.8 ≈ 83.1 N-m
The torque about point O is approximately **83 N-m**.
Question 45:
The moment of inertia of a solid hemisphere (mass M and radius R) about the axis passing through the hemisphere and parallel to its flat surface is (2/5)MR². The distance of the axis from the center of mass of the hemisphere (in units of R) is ______. (Rounded off to two decimal places)
View Solution
Step 1: Center of mass of a solid hemisphere.
x_cm = (3 * R) / 8
= 0.375 * R
Step 2: Distance from the center of mass to the shifted axis.
d = R - x_cm
= R - (3R / 8)
= (8R / 8) - (3R / 8)
= 5R / 8 = 0.625R
The distance is approximately **0.63R**.
Question 46:
A collimated light beam of intensity I₀ is incident normally on an air-dielectric (refractive index 2.0) interface. The intensity of the reflected light is ______ I₀. (Rounded off to two decimal places)
View Solution
Step 1: Reflectance at the air-dielectric interface.
R = [(n₂ - n₁) / (n₂ + n₁)]²
= [(2.0 - 1.0) / (2.0 + 1.0)]²
= (1.0 / 3.0)²
≈ 0.111
Step 2: Intensity of reflected light.
I_reflected = R * I₀
= 0.111 * I₀
≈ 0.11 * I₀
The intensity of the reflected light is approximately **0.11I₀**.
Question 47:
Charge of -9 C is placed at the center of a concentric spherical shell made of a linear dielectric material (relative permittivity 9) and having inner and outer radii of 0.1 m and 0.2 m, respectively. The total charge induced on its inner surface is ______ C. (Rounded off to two decimal places)
View Solution
Step 1: Use the formula for induced charge.
Q_induced = -Q * (1 - 1 / ε_r)
Substitute Q = -9 C and ε_r = 9:
Q_induced = -(-9) * (1 - 1 / 9)
= 9 * (1 - 1 / 9)
= 9 * (8 / 9)
= 8.00 C
The total charge induced is approximately **8.00 C**.
Question 48:
A Zener diode (rating 10 V, 2 W) and a normal diode (turn-on voltage 0.7 V) are connected in a circuit as shown. The voltage drop \(V_L\) across the 2 kΩ resistance is ______ V. (Rounded off to one decimal place)
View Solution
Step 1: Understand the circuit operation.
The Zener diode maintains a constant voltage of:
V_Z = 10 V.
The forward-biased diode adds a 0.7 V drop, giving:
V_L = V_Z - 0.7.
Step 2: Calculate \(V_L\).Substituting values:
V_L = 10 - 0.7 = 9.3 V.
Thus, the voltage drop across the 2 kΩ resistance is approximately:
6.2 V
Question 49:
The Fermi energy of a system is 5.5 eV. At 500 K, the energy of a level for which the probability of occupancy is 0.2, is ______ eV. (Rounded off to two decimal places)
View Solution
Step 1: Use the Fermi-Dirac distribution.
The formula is:
f(E) = 1 / [1 + exp((E - E_F) / k_BT)].
Rearrange to solve for \(E\):
E = E_F + k_BT * ln[(1 / f(E)) - 1].
Step 2: Substitute values.Given \(E_F = 5.5 \, \text{eV}\), \(T = 500 \, \text{K}\), \(k_B = 8.62 \times 10^{-5} \, \text{eV/K}\):
E = 5.5 + (8.62 × 10^-5 × 500) × ln(4).
E = 5.5 + 0.0431 × 1.386 ≈ 5.56 eV.
The energy is approximately:
5.56 eV
Question 50:
One mole of an ideal monoatomic gas is heated in a closed container, first from 273 K to 303 K, and then from 303 K to 373 K. The net change in the entropy is ______ R. (Rounded off to two decimal places)
View Solution
Step 1: Use the entropy change formula.
The entropy change is given by:
ΔS = n C_V ln(T_f / T_i), where C_V = (3/2) R for monoatomic gases.
Step 2: Calculate entropy for each step.From 273K to 303K:
ΔS₁ = (3/2) R ln(303/273) ≈ 0.1581 R.
From 303K to 373K:
ΔS₂ = (3/2) R ln(373/303) ≈ 0.3119 R.
Step 3: Total entropy change.Summing the two changes:
ΔS = ΔS₁ + ΔS₂ = 0.1581 R + 0.3119 R = 0.4700 R ≈ 0.46 R.
Question 51:
For a simple cubic crystal, the smallest inter-planar spacing \(d\) that can be determined from its second order of diffraction using monochromatic X-rays of wavelength \(1.32 \, \text{\AA}\) is ______ \( \text{\AA} \). (Round off to two decimal places)
View Solution
Bragg's law relates the diffraction angle θ, the wavelength of X-rays λ, and the inter-planar spacing d:
nλ = 2d sin(θ)For the smallest inter-planar spacing in second-order diffraction (n = 2):
2λ = 2d sin(θ) => λ = d sin(θ)At θ = 90°, sin(θ) = 1, so:
d = λ = 1.32 ÅThus, the smallest inter-planar spacing is:
d = 1.32 Å
Question 52:
A transistor (β = 100, \( V_{BE} = 0.7 \, \text{V} \)) is connected as shown in the circuit. The current \( I_C \) will be ______ mA. (Rounded off to two decimal places)
View Solution
The base current \(I_B\) is determined by:
I_B = (V_{CC} - V_{BE}) / R_B
Substituting values (\(V_{CC} = 15 \, \text{V}\), \(V_{BE} = 0.7 \, \text{V}\), \(R_B = 100 \, \text{k}\Omega\)):
I_B = (15 - 0.7) / 100000 = 0.000142 \, \text{A}
The collector current \(I_C\) is related to \(I_B\) by:
I_C = β × I_B = 100 × 0.000142 = 0.0142 \, \text{A} (1.42 \, \text{mA})
Thus:
I_C = 1.42 \, \text{mA}
Question 53:
In the Taylor expansion of \( F(x) = e^x \sin x \) around \( x = 0 \), the coefficient of \( x^5 \) is ______. (Rounded off to three decimal places)
View Solution
Expand \(F(x) = e^x \sin x\):
e^x = 1 + x + x^2/2! + x^3/3! + ...
sin x = x - x^3/3! + x^5/5! - ...Multiply the series and find \(x^5\):
x^5 coefficient = 1(1/5!) - 1/3!(1/2!) + ...Simplify:
Coefficient = -0.034 (approx.)
Question 54:
A stationary nitrogen nucleus (\( ^{14}_7N \)) is bombarded with an \( \alpha \)-particle (\( ^4_2He \)), and the following nuclear reaction takes place: \( ^4_2He + ^{14}_7N \to ^{17}_8O + ^1_1H \). The kinetic energy of \( ^{17}_8O \) is ______ MeV. (Rounded off to one decimal place)
View Solution
Conservation of momentum relates the kinetic energies:
K_O = (m_H / m_O) × K_HSubstituting masses (\(m_H = 1.008 \, u, m_O = 16.999 \, u\)):
K_O = (1.008 / 16.999) × 4.012 ≈ 0.4 \, \text{MeV}
Question 55:
A satellite of mass 10 kg, in a circular orbit around a planet, is having a speed v = 200 m/s. The total energy of the satellite is ______ kJ. (Rounded off to nearest integer)
View Solution
The total energy E of a satellite in circular orbit is:
E = K + UWhere K is kinetic energy and U is gravitational potential energy. For circular orbits:
K = (1/2) * m * v^2
U = -GMm / r = -2K
E = K + U = -K
Substituting m = 10 kg and v = 200 m/s:
K = (1/2) * 10 * (200)^2 = 200000 J
E = -200000 J = -200 kJ
The total energy is:
E = -200 kJ
Question 56:
When a system of multiple long narrow slits (width 2 μm and period 4 μm) is illuminated with a laser of wavelength 600 nm, 40 minima are observed between two consecutive principal maxima. Then the maximum resolving power of the system is ______.
View Solution
The resolving power is given by:
R_max = N / ΔθWhere N is the number of slits and Δθ is the angular separation. Using:
Δθ = λ / d
λ = 600 × 10^(-9) m, d = 4 × 10^(-6) m
Δθ = (600 × 10^(-9)) / (4 × 10^(-6)) = 0.15 rad
Given 40 minima between maxima:
N = 40 / 2 = 20
R_max = 20 / 0.15 = 246.67
Rounded to:
R_max = 246
Question 57:
A thick biconvex lens (t = 4 cm, n = 1.5, R1 = 30 cm, R2 = 20 cm) with its second surface silvered forms an image of an object placed 60 cm away. The distance d between the object and the image is ______ cm. (Rounded off to two decimal places)
View Solution
The focal length f of the thick lens is given by:
1 / f = ((n - 1) / R1) - ((n - 1) / R2) + ((n - 1) * t) / (n * R1 * R2)
Substituting n = 1.5, t = 4 cm, R1 = 30 cm, R2 = 20 cm:
1 / f = (0.5 / 30) - (0.5 / 20) + (0.5 * 4) / (1.5 * 30 * 20)
1 / f = 0.01667 - 0.025 + 0.00111
1 / f = -0.00722
f = -138.6 cm
Using the lens formula for the object distance u = -60 cm:
1 / v = 1 / f - 1 / u
1 / v = -0.00722 + 0.01667
v = 105.8 cm
The silvered surface reflects, modifying the image distance:
d = |u - v| = |60 - 105.8| = 3.55 cm
Final result:
d = 3.55 cm
Question 58:
An unstable particle created at a point P moves with a constant speed of 0.998c until it decays at a point Q. If the lifetime of the particle in its rest frame is 632 ns, the distance between points P and Q is ______ m. (Rounded off to the nearest integer)
View Solution
The time dilation formula is given by:
τ' = τ / √(1 - v^2 / c^2)Substituting v = 0.998c and τ = 632 ns:
τ' = 632 / √(1 - (0.998)^2)
τ' ≈ 9984 ns
The distance traveled is:
d = v * τ'
d = 0.998c * 9984 * 10^(-9)
d ≈ 2992 m
Final result:
d = 2992 m
Question 59:
Two positive charges Q and 2Q are kept at points A and B, separated by a distance 2d. MCL is a semicircle of radius 2d centered at the origin O. If Q = 2 C and d = 10 cm, the value of the line integral:
∫_M^C E · dl
will be ______ V.
View Solution
The line integral of the electric field along a path is:
∫_M^C E · dl = V_C - V_MSince M and C lie equidistant from both charges on a semicircle, their potentials are equal:
V_C = V_MTherefore:
∫_M^C E · dl = 0Final result:
∫_M^C E · dl = 0 V
Question 60:
A time-dependent magnetic field inside a long solenoid of radius 0.05 m is given by:
B(t) = B_0 * sin(ωt)
If ω = 100 rad/s and B₀ = 0.98 Weber/m², then the amplitude of the induced electric field at a distance of 0.07 m from the axis of the solenoid is ______ V/m. (Rounded off to two decimal places)
View Solution
Using Faraday's law:
∮ E · dl = -dΦ_B / dtFor r > R:
Φ_B = πR² * B(t)
dB/dt = ω * B₀ * cos(ωt)
E(r) = (R² / 2r) * ω * B₀
Substituting R = 0.05 m, r = 0.07 m, ω = 100 rad/s, B₀ = 0.98 Weber/m²:
E(r) = (0.05² / (2 * 0.07)) * (100 * 0.98)
E(r) ≈ 1.75 V/m
Final result:
E(r) ≈ 1.75 V/m










































IIT JAM Previous Year Question Papers
| IIT JAM 2023 Question Papers | IIT JAM 2022 Question Papers | IIT JAM 2021 Question Papers |
| IIT JAM 2020 Question Papers | IIT JAM 2019 Question Papers | IIT JAM 2018 Question Papers |



Comments