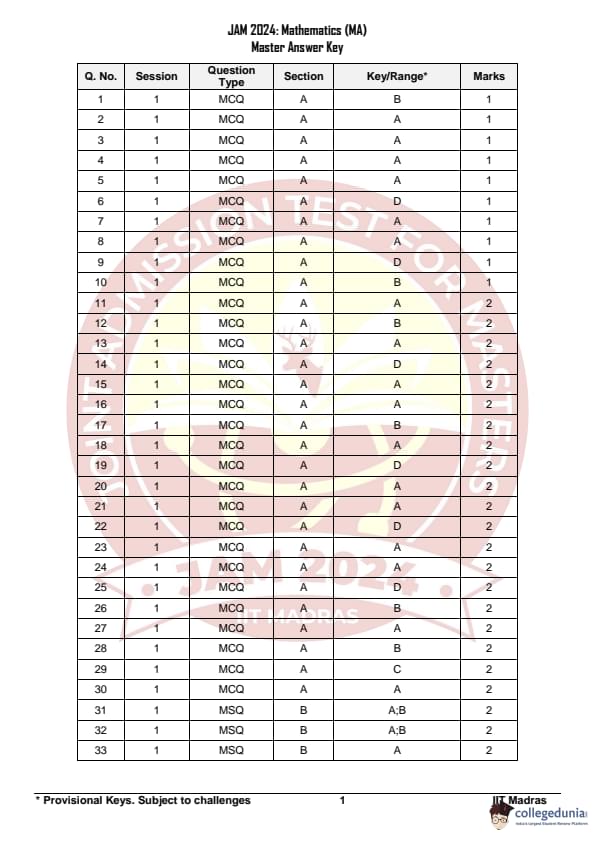
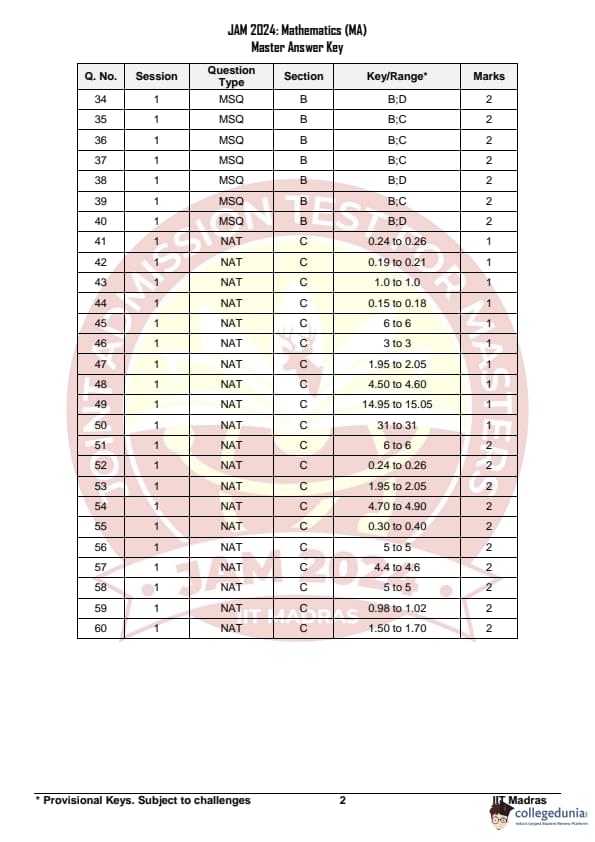
IIT JAM 2024 Mathematics (MA) Question Paper with Answer Key pdf is available for download. IIT JAM 2024 MA exam was conducted by IIT Madras in shift 1 on February 11, 2024. In terms of difficulty level, IIT JAM 2024 Mathematics (MA) paper was of difficult level. The paper comprised 60 questions.
IIT JAM 2024 Mathematics (MA) Question Paper with Answer Key PDFs
| IIT JAM 2024 Mathematics Question Paper PDF | Check Solutions |
IIT JAM Mathematics (MA) Solution
Question 1:
Let y_c : R → (0, ∞) be the solution of the Bernoulli’s equation
dy/dx - y + y^3 = 0, y(0) = c > 0.
Then, for every c > 0, which one of the following is true?
(A) lim(x → ∞) y_c(x) = 0
(B) lim(x → ∞) y_c(x) = 1
(C) lim(x → ∞) y_c(x) = e
(D) lim(x → ∞) y_c(x) does not exist
Question 2:
For a twice continuously differentiable function g: R → R, define
u_g(x, y) = 1/y ∫(-y to y) g(x + t) dt for (x, y) ∈ R², y > 0.
Which one of the following holds for all such g?
(A) d²u_g/dx² = 2/y du_g/dy + d²u_g/dy²
(B) d²u_g/dx² = 1/y du_g/dy + d²u_g/dy²
(C) d²u_g/dx² = 2/y du_g/dy - d²u_g/dy²
(D) d²u_g/dx² = 1/y du_g/dy - d²u_g/dy²
Question 3:
Let y(x) be the solution of the differential equation
dy/dx = 1 + y sec(x) for x in (-π/2, π/2),
that satisfies y(0) = 0. Then, the value of y(π/6) equals:
(A) √3 log(3/2)
(B) (√3/2) log(3/2)
(C) (√3/2) log 3
(D) √3 log 3
Question 4:
Let F be the family of curves given by
x² + 2hxy + y² = 1, -1 < h < 1.
Then, the differential equation for the family of orthogonal trajectories to F is:
(A) (x² y - y³ + y) dy/dx - (xy² - x³ + x) = 0
(B) (x² y - y³ + y) dy/dx + (xy² - x³ + x) = 0
(C) (x² y + y³ + y) dy/dx - (xy² + x³ + x) = 0
(D) (x² y + y³ + y) dy/dx + (xy² + x³ + x) = 0
Question 5:
Let G be a group of order 39 such that it has exactly one subgroup of order 3 and exactly one subgroup of order 13. Then, which one of the following statements is TRUE?
(A) G is necessarily cyclic
(B) G is abelian but need not be cyclic
(C) G need not be abelian
(D) G has 13 elements of order 13
Question 6:
For a positive integer n, let U(n) = { r in Z_n : gcd(r, n) = 1 } be the group under multiplication modulo n. Then, which one of the following statements is TRUE?
(A) U(5) is isomorphic to U(8)
(B) U(10) is isomorphic to U(12)
(C) U(8) is isomorphic to U(10)
(D) U(8) is isomorphic to U(12)
Question 7:
Which one of the following is TRUE for the symmetric group S₁₃?
(A) S₁₃ has an element of order 42
(B) S₁₃ has no element of order 35
(C) S₁₃ has an element of order 27
(D) S₁₃ has no element of order 60
Question 8:
Let G be a finite group containing a non-identity element which is conjugate to its inverse. Then, which one of the following is TRUE?
(A) The order of G is necessarily even
(B) The order of G is not necessarily even
(C) G is necessarily cyclic
(D) G is necessarily abelian but need not be cyclic
Question 9:
Consider the following statements.
P: If a system of linear equations Ax = b has a unique solution, where A is an m × n matrix and b is an m × 1 matrix, then m = n.
Q: For a subspace W of a nonzero vector space V, whenever u ∈ V \ W and v ∈ V \ W, then u + v ∈ V \ W.
Which one of the following holds?
(A) Both P and Q are true
(B) P is true but Q is false
(C) P is false but Q is true
(D) Both P and Q are false
Question 10:
Let g: R → R be a continuous function. Which one of the following is the solution of the differential equation
d²y/dx² + y = g(x) for x in R,
satisfying the conditions y(0) = 0, y'(0) = 1?
(A) y(x) = sin(x) - ∫(0 to x) sin(x - t) g(t) dt
(B) y(x) = sin(x) + ∫(0 to x) sin(x - t) g(t) dt
(C) y(x) = sin(x) + ∫(0 to x) cos(x - t) g(t) dt
(D) y(x) = sin(x) + ∫(0 to x) cos(x - t) g(t) dt
Question 11:
Which one of the following groups has elements of order 1, 2, 3, 4, 5 but does not have an element of order greater than or equal to 6?
(A) The alternating group A₆
(B) The alternating group A₅
(C) S₆
(D) S₅
Question 12:
Consider the group G = { A in M₂(R) : AAᵀ = I₂ } with respect to matrix multiplication. Let
Z(G) = { A in G : AB = BA, for all B in G }.
Then, the cardinality of Z(G) is:
(A) 1
(B) 2
(C) 4
(D) Infinite
Question 13:
Let V be a nonzero subspace of the complex vector space M₇(C) such that every nonzero matrix in V is invertible. Then, the dimension of V over C is:
(A) 1
(B) 2
(C) 7
(D) 49
Question 15:
Let:
a = [ 1/√3, -1/√2, 1/√6, 0 ]ᵀ.
Consider the following two statements:
P: The matrix I₄ - aaᵀ is invertible.
Q: The matrix I₄ - 2aaᵀ is invertible.
Which one of the following holds?
(A) P is false but Q is true.
(B) P is true but Q is false.
(C) Both P and Q are true.
(D) Both P and Q are false.
Question 16:
Let A be a 6 × 5 matrix with entries in ℝ, and B be a 5 × 4 matrix with entries in ℝ. Consider the following two statements:
P: For all such nonzero matrices A and B, there is a nonzero matrix Z such that AZB is the 6 × 4 zero matrix.
Q: For all such nonzero matrices A and B, there is a nonzero matrix Y such that BYA is the 5 × 5 zero matrix.
Which one of the following holds?
(A) Both P and Q are true.
(B) P is true but Q is false.
(C) P is false but Q is true.
(D) Both P and Q are false.
Question 17:
Let P₁₁(x) be the real vector space of polynomials, in the variable x with real coefficients and having degree at most 11, together with the zero polynomial. Let
E = {s₀(x), s₁(x), ..., s₁₁(x)}, F = {r₀(x), r₁(x), ..., r₁₁(x)}
be subsets of P₁₁(x) having 12 elements each and satisfying
s₀(3) = s₁(3) = ... = s₁₁(3) = 0, r₀(4) = r₁(4) = ... = r₁₁(4) = 1.
Then, which one of the following is TRUE?
(A) Any such E is not necessarily linearly dependent and any such F is not necessarily linearly dependent.
(B) Any such E is necessarily linearly dependent but any such F is not necessarily linearly dependent.
(C) Any such E is not necessarily linearly dependent but any such F is necessarily linearly dependent.
(D) Any such E is necessarily linearly dependent and any such F is necessarily linearly dependent.
Question 18:
For the differential equation
y(8x - 9y)dx + 2x(x - 3y)dy = 0,
which one of the following statements is TRUE?
(A) The differential equation is not exact and has x² as an integrating factor.
(B) The differential equation is exact and homogeneous.
(C) The differential equation is not exact and does not have x² as an integrating factor.
(D) The differential equation is not homogeneous and has x² as an integrating factor.
Question 19:
For x in R, let |x| denote the greatest integer less than or equal to x. For x, y in R, define
min(x, y) = {x if x ≤ y, y otherwise.}
Let f : [-2π, 2π] → R be defined by
f(x) = sin(min{x, x - |x|}) for x in [-2π, 2π].
Consider the set S = { x in [-2π, 2π] : f is discontinuous at x }. Which one of the following statements is TRUE?
(A) S has 13 elements
(B) S has 7 elements
(C) S is an infinite set
(D) S has 6 elements
Question 20:
Define the sequences {aₙ}ₙ₌₃∞ and {bₙ}ₙ₌₃∞ as
aₙ = (log n + log log n) log n and bₙ = n^(1 + 1/log n).
Which one of the following is TRUE?
(A) ∑(n=3 to ∞) 1/aₙ is convergent but ∑(n=3 to ∞) 1/bₙ is divergent.
(B) ∑(n=3 to ∞) 1/aₙ is divergent but ∑(n=3 to ∞) 1/bₙ is convergent.
(C) Both ∑(n=3 to ∞) 1/aₙ and ∑(n=3 to ∞) 1/bₙ are divergent.
(D) Both ∑(n=3 to ∞) 1/aₙ and ∑(n=3 to ∞) 1/bₙ are convergent.
Question 21:
For p, q, r in R, r ≠ 0 and n in N, let
aₙ = pⁿ nᵖ (n/(n+2))ⁿ² and bₙ = (nⁿ/n!) rⁿ (sqrt((n+2)/n))
Which one of the following statements is TRUE?
(A) If 1 < p < e² and q > 1, then Σ(1/aₙ) is convergent.
(B) If e² < p < e⁴ and q > 1, then Σ(1/aₙ) is convergent.
(C) If 1 < r < e, then Σ(1/bₙ) is convergent.
(D) If 1/e < r < 1, then Σ(1/bₙ) is convergent.
Question 22:
Let P₇(x) be the real vector space of polynomials, in the variable x with real coefficients and having degree at most 7, together with the zero polynomial. Let T: P₇(x) → P₇(x) be the linear transformation defined by
T(f(x)) = f(x) + df(x)/dx.
Then, which one of the following is TRUE?
(A) T is not a surjective linear transformation.
(B) There exists k in N such that Tᵏ is the zero linear transformation.
(C) 1 and 2 are the eigenvalues of T.
(D) There exists r in N such that (T - I)ᵣ is the zero linear transformation, where I is the identity map on P₇(x).
Question 23:
For α in R, let yₐ(x) be the solution of the differential equation
dy/dx + 2y = 1/(1 + x²) for x in R
satisfying y(0) = α. Then, which one of the following is TRUE?
(A) lim(x → ∞) yₐ(x) = 0 for every α in R
(B) lim(x → ∞) yₐ(x) = 1 for every α in R
(C) There exists an α in R such that lim(x → ∞) yₐ(x) exists but its value is different from 0 and 1.
(D) There is an α in R for which lim(x → ∞) yₐ(x) does not exist.
Question 24:
Consider the following two statements.
P: There exist functions f: R → R, g: R → R such that f is continuous at x = 1 and g is discontinuous at x = 1 but g ∘ f is continuous at x = 1.
Q: There exist functions f: R → R, g: R → R such that both f and g are discontinuous at x = 1 but g ∘ f is continuous at x = 1.
Which one of the following holds?
(A) Both P and Q are true.
(B) Both P and Q are false.
(C) P is true but Q is false.
(D) P is false but Q is true.
Question 25:
Let f: R → R be defined by
f(x) = ((x² + 1)²) / (x⁴ + x² + 1) for x ∈ R.
Then, which one of the following is TRUE?
(A) f has exactly two points of local maxima and exactly three points of local minima.
(B) f has exactly three points of local maxima and exactly two points of local minima.
(C) f has exactly one point of local maximum and exactly two points of local minima.
(D) f has exactly two points of local maxima and exactly one point of local minimum.
Question 26:
Let f: R → R be a solution of the differential equation
f''(x) - 2f'(x) + f(x) = 2e^x for x ∈ R.
Consider the following statements.
P: If f(x) > 0 for all x ∈ R, then f'(x) > 0 for all x ∈ R.
Q: If f'(x) > 0 for all x ∈ R, then f(x) > 0 for all x ∈ R.
Which one of the following holds?
(A) P is true but Q is false.
(B) P is false but Q is true.
(C) Both P and Q are true.
(D) Both P and Q are false.
Question 27:
For a > b > 0, consider
D = {(x, y, z) ∈ R³ : x² + y² + z² ≤ a² and x² + y² ≥ b²}.
Then, the surface area of the boundary of the solid D is
(A) 4π(a + b)√(a² - b²)
(B) 4π(a² - b)√(a² - b²)
(C) 4π(a - b)√(a² - b²)
(D) 4π(a² + b)√(a² - b²)
Question 28:
For n ≥ 3, let a regular n-sided polygon P_n be circumscribed by a circle of radius R_n and let r_n be the radius of the circle inscribed in P_n. Then
lim (n → ∞) (R_n / r_n)^(n²)
equals
(A) e^(π²)
(B) e^(π²/2)
(C) e^(π²/3)
(D) e^(2π²)
Question 29:
Let L1 denote the line y = 3x + 2 and L2 denote the line y = 4x + 3. Suppose that f: R → R is a four times continuously differentiable function such that the line L1 intersects the curve y = f(x) at exactly three distinct points and the line L2 intersects the curve y = f(x) at exactly four distinct points. Then, which one of the following is TRUE?
(A) df/dx does not attain the value 3 on R
(B) d²f/dx² vanishes at most once on R
(C) d³f/dx³ vanishes at least once on R
(D) df/dx does not attain the value 7/2 on R
Question 30:
Define the function f: R² → R by:
f(x, y) = 12xy * exp(-(2x + 3y - 2)).
If (a, b) is the point of local maximum of f, then f(a, b) equals:
(A) 2
(B) 6
(C) 12
(D) 0
Question 31:
Let {aₙ} (n = 1 to ∞) be a sequence of real numbers. Then, which of the following statements is/are always TRUE?
(A) If ∑aₙ (n = 1 to ∞) converges absolutely, then ∑aₙ² (n = 1 to ∞) converges absolutely.
(B) If ∑aₙ (n = 1 to ∞) converges absolutely, then ∑aₙ³ (n = 1 to ∞) converges absolutely.
(C) If ∑aₙ (n = 1 to ∞) converges, then ∑aₙ² (n = 1 to ∞) converges.
(D) If ∑aₙ (n = 1 to ∞) converges, then ∑aₙ³ (n = 1 to ∞) converges.
Question 32:
Which of the following statements is/are TRUE?
(A) ∑ n log(1 + 1/n³) is convergent
(B) ∑ (1 - cos(1/n)) log n is convergent
(C) ∑ n² log(1 + 1/n³) is convergent
(D) ∑ (1 - cos(1/√n)) log n is convergent
Question 33:
Which of the following statements is/are TRUE?
(A) The additive group of real numbers is isomorphic to the multiplicative group of positive real numbers
(B) The multiplicative group of nonzero real numbers is isomorphic to the multiplicative group of nonzero complex numbers
(C) The additive group of real numbers is isomorphic to the multiplicative group of nonzero complex numbers
(D) The additive group of real numbers is isomorphic to the additive group of rational numbers
Question 34:
Let f : (1, ∞) → (0, ∞) be a continuous function such that for every n ∈ N, f(n) is the smallest prime factor of n. Then, which of the following options is/are CORRECT?
(A) lim (x → ∞) f(x) exists
(B) lim (x → ∞) f(x) does not exist
(C) The set of solutions to the equation f(x) = 2024 is finite
(D) The set of solutions to the equation f(x) = 2024 is infinite
Question 35:
Let S = { (x, y) ∈ ℝ² : x > 0, y > 0 }, and let f : S → ℝ be given by
f(x, y) = 2x² + 3y² - log(x) - (1/6) log(y)
Then, which of the following statements is/are TRUE?
(A) There is a unique point in S at which f(x, y) attains a local maximum.
(B) There is a unique point in S at which f(x, y) attains a local minimum.
(C) For each point (x₀, y₀) ∈ S, the set { (x, y) ∈ S : f(x, y) = f(x₀, y₀) } is bounded.
(D) For each point (x₀, y₀) ∈ S, the set { (x, y) ∈ S : f(x, y) = f(x₀, y₀) } is unbounded.
Question 36:
The center Z(G) of a group G is defined as
Z(G) = { x ∈ G : xg = gx for all g ∈ G }.
Let |G| denote the order of G. Then, which of the following statements is/are TRUE for any group G?
(A) If G is non-abelian and Z(G) contains more than one element, then the center of the quotient group G/Z(G) contains only one element.
(B) If |G| ≥ 2, then there exists a non-trivial homomorphism from ℤ to G.
(C) If |G| ≥ 2 and G is non-abelian, then there exists a non-identity isomorphism from G to itself.
(D) If |G| = p³, where p is a prime number, then G is necessarily abelian.
Question 37:
For a matrix M, let Rowspace(M) denote the linear span of the rows of M and Colspace(M) denote the linear span of the columns of M. Which of the following hold(s) for all A, B, C ∈ M₁₀(ℝ) satisfying A = BC?
(A) Rowspace(A) ⊆ Rowspace(B)
(B) Rowspace(A) ⊆ Rowspace(C)
(C) Colspace(A) ⊆ Colspace(B)
(D) Colspace(A) ⊆ Colspace(C)
Question 38:
Define f : ℝ → ℝ and g : ℝ → ℝ as follows:
f(x) = Σm=0∞ (-1)m x2m / (22m (m!)2), g(x) = (x / 2) Σm=0∞ (-1)m x2m / (222m (m+1)! m!)
Let x₁, x₂, x₃, x₄ ∈ ℝ be such that 0 < x₁ < x₂, 0 < x₃ < x₄,
f(x₁) = f(x₂) = 0, f(x) ≠ 0 when x₁ < x < x₂,
g(x₃) = g(x₄) = 0, g(x) ≠ 0 when x₃ < x < x₄.
Then, which of the following statements is/are TRUE?
(A) The function f does not vanish anywhere in the interval (x₃, x₄)
(B) The function f vanishes exactly once in the interval (x₃, x₄)
(C) The function g does not vanish anywhere in the interval (x₁, x₂)
(D) The function g vanishes exactly once in the interval (x₁, x₂)
Question 39:
For 0 < α < 4, define the sequence {xₙ} of real numbers as follows:
x₁ = α and xₙ₊₁ + 2 = -xₙ(xₙ - 4) for n ∈ ℕ.
Which of the following is/are TRUE?
(A) {xₙ} converges for at least three distinct values of α ∈ (0,1)
(B) {xₙ} converges for at least three distinct values of α ∈ (1,2)
(C) {xₙ} converges for at least three distinct values of α ∈ (2,3)
(D) {xₙ} converges for at least three distinct values of α ∈ (3,4)
Question 40:
Consider G = {m + n√2 : m,n ∈ ℤ} as a subgroup of the additive group ℝ. Which of the following statements is/are TRUE?
(A) G is a cyclic subgroup of ℝ under addition
(B) G ∩ I is non-empty for every non-empty open interval I ⊆ ℝ
(C) G is a closed subset of ℝ
(D) G is isomorphic to the group ℤ × ℤ, where the group operation in ℤ × ℤ is defined by (m₁, n₁) + (m₂, n₂) = (m₁ + m₂, n₁ + n₂)
Question 41:
The area of the region
R = {(x, y) ∈ ℝ² : 0 ≤ x ≤ 1, 0 ≤ y ≤ 1 and 1/4 ≤ xy ≤ 1/2}
is _____ (rounded off to two decimal places).
Question 42:
Let y: ℝ → ℝ be the solution to the differential equation
d²y/dx² + 2 dy/dx + 5y = 1
satisfying y(0) = 0 and y'(0) = 1. Then, lim(x→∞) y(x) equals _____ (rounded off to two decimal places).
Question 43:
For α > 0, let yα(x) be the solution to the differential equation
2 d²y/dx² - dy/dx - y = 0
satisfying the conditions y(0) = 1, y'(0) = α. Then, the smallest value of α for which yα(x) has no critical points in ℝ equals _____ (rounded off to the nearest integer).
Question 44:
Consider the 4 × 4 matrix
If aᵢ,ⱼ denotes the (i, j)-th entry of M⁻¹, then a₄₁ equals _____ (rounded off to two decimal places).
Question 45:
Let P₁₂(x) be the real vector space of polynomials in the variable x with real coefficients and having degree at most 12, together with the zero polynomial. Define
V = { f ∈ P₁₂(x) : f(-x) = f(x) for all x ∈ ℝ and f(2024) = 0 }
Then, the dimension of V is _____.
Question 46:
Let
S = { f : ℝ → ℝ : f is a polynomial and f(f(x)) = f(x)¹⁰²⁴ for x ∈ ℝ }
Then, the number of elements in S is _____.
Question 46:
Let
S = { f : ℝ → ℝ : f is a polynomial and f(f(x)) = f(x)¹⁰²⁴ for x ∈ ℝ }
Then, the number of elements in S is _____.
Question 47:
Let a₁ = 1, b₁ = 2, and c₁ = 3. Consider the convergent sequences
{aₙ}ₙ₌₁ᶠ∞, {bₙ}ₙ₌₁ᶠ∞, {cₙ}ₙ₌₁ᶠ∞
defined as follows:
aₙ₊₁ = (aₙ + bₙ) / 2, bₙ₊₁ = (bₙ + cₙ) / 2, cₙ₊₁ = (cₙ + aₙ) / 2 for n ≥ 1.
Then,
Σ (bₙ cₙ (aₙ₊₁ - aₙ)) + Σ (bₙ₊₁ cₙ₊₁ - bₙ cₙ) aₙ₊₁
equals _____ (rounded off to two decimal places).
Question 48:
Let
S = {(x, y, z) ∈ ℝ³ : x² + y² + z² = 4, (x - 1)² + y² ≤ 1, z ≥ 0}.
Then, the surface area of S equals _____ (rounded off to two decimal places).
Question 49:
Let P7(x) be the real vector space of polynomials in x with degree at most 7, together with the zero polynomial. For r = 1, 2, ..., 7, define
s_r(x) = x(x - 1) ... (x - (r - 1)) and s_0(x) = 1.
Consider the fact that B = {s0(x), s1(x), ..., s7(x)} is a basis of P7(x). If
x⁵ = Σ α₅ₖ sₖ(x),
where α₅ₖ ∈ ℝ, then α₅₂ equals _____ (rounded off to two decimal places).
Question 50:
Let
M =
[ 0 0 0 0 -1 ]
[ 2 0 0 0 -4 ]
[ 0 2 0 0 0 ]
[ 0 0 2 0 3 ]
[ 0 0 0 2 2 ]
If p(x) is the characteristic polynomial of M, then p(2) - 1 equals _____.
Question 51:
For α ∈ (-2π, 0), consider the differential equation
x² d²y/dx² + αx dy/dx + y = 0 for x > 0.
Let D be the set of all α ∈ (-2π, 0) for which all corresponding real solutions to the above differential equation approach zero as x → 0+. Then, the number of elements in D ∩ ℤ equals _____.
Question 52:
The value of
lim(t -> ∞) (log(t² + 1/t²))⁻¹ ∫₁^(πt) (sin²(5x)/x) dx
equals _____ (rounded off to two decimal places).
Question 53:
Let T be the planar region enclosed by the square with vertices at the points
(0,1), (1,0), (0,-1), and (-1,0).
Then, the value of
∬_T (cos(π(x - y)) - cos(π(x + y)))² dx dy
equals _____ (rounded off to two decimal places).
Question 54:
Let
S = {(x, y, z) ∈ ℝ³ : x² + y² + z² < 1}.
Then, the value of
(1/π) ∭_S ((x - 2y + z)² + (2x - y - z)² + (x - y + 2z)²) dx dy dz
equals _____ (rounded off to two decimal places).
Question 55:
For n ∈ ℕ, if
aₙ = 1/(n³ + 1) + 2²/(n³ + 2) + ... + n²/(n³ + n),
then the sequence {aₙ}_{n=1}^{∞} converges to _____ (rounded off to two decimal places).
Question 56:
Consider the function f: ℝ → ℝ given by
f(x) = x³ - 4x² + 4x - 6.
For c ∈ ℝ, let
S(c) = { x ∈ ℝ : f(x) = c }
and |S(c)| denote the number of elements in S(c). Then, the value of
|S(-7)| + |S(-5)| + |S(3)|
equals _____ (rounded off to two decimal places).
Question 57:
Let c > 0 be such that
∫₀ᶜ e^(s²) ds = 3.
Then, the value of
∫₀ᶜ ( ∫ₓᶜ e^(x² + y²) dy ) dx
equals _____ (rounded off to one decimal place).
Question 58:
For k ∈ ℕ, let 0 = t₀ < t₁ < ... < tₖ < tₖ₊₁ = 1. A function f: [0,1] → ℝ is said to be piecewise linear with nodes t₁, ..., tₖ, if for each j = 1, 2, ..., k+1, there exist aₗ, bₗ ∈ ℝ such that
f(t) = aₗ + bₗ t for t_{ℓ-1} < t < tₗ.
Let V be the real vector space of all real-valued continuous piecewise linear functions on [0,1] with nodes 1/4, 1/2, 3/4. Then, the dimension of V equals _____.
Question 59:
For n ∈ ℕ, let
aₙ = 1/n^(n-1) Σₖ₌₀ⁿ k!n! / (n-k)! (k+1)
and β = lim(n → ∞) aₙ. Then, the value of log(β) equals _____ (rounded off to two decimal places).
Question 60:
Define the function f : (-1,1) → (-π/2, π/2) by
f(x) = sin⁻¹ x.
Let a₆ denote the coefficient of x⁶ in the Taylor series of (f(x))² about x = 0. Then, the value of 9a₆ equals _____ (rounded off to two decimal places).











































IIT JAM Previous Year Question Papers
| IIT JAM 2023 Question Papers | IIT JAM 2022 Question Papers | IIT JAM 2021 Question Papers |
| IIT JAM 2020 Question Papers | IIT JAM 2019 Question Papers | IIT JAM 2018 Question Papers |





Comments