IIT JAM 2020 Physics (PH) Question paper with answer key pdf conducted on February 9 in Forenoon Session 9:30 AM to 12:30 PM is available for download. The exam was successfully organized by IIT Kanpur. In terms of difficulty level, IIT JAM was of Moderate to Tough level. The question paper comprised a total of 60 questions divided among 3 sections.
IIT JAM 2020 Physics (PH) Question Paper with Answer Key PDFs Forenoon Session
| IIT JAM 2020 Physics (PH) Question paper with answer key PDF | Download PDF | Check Solutions |
Which one of the following functions has a discontinuity in the second derivative at \(x = 0\), where \(x\) is a real variable?
View Solution
Step 1: Understanding the question.
We need to find which function has a discontinuity in its second derivative at \(x = 0\). Functions involving absolute values often cause discontinuities in higher-order derivatives.
Step 2: Evaluate derivatives.
For \( f(x) = x|x| \),
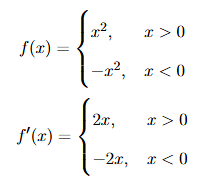
At \(x = 0\), \(f'(x)\) is continuous (both sides approach 0).
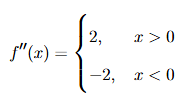
So \(f''(x)\) is discontinuous at \(x = 0\).
Step 3: Conclusion.
Hence, \(f(x) = x|x|\) has a discontinuity in the second derivative at \(x = 0\).
Quick Tip: Check for discontinuities in higher derivatives where the absolute value function changes its sign, typically at \(x = 0\).
A collimated beam of laser light of wavelength 514 nm is normally incident on a smooth glass slab placed in air. Given the refractive indices of glass and air are 1.47 and 1.0 respectively, the percentage of light intensity reflected back is:
View Solution
Step 1: Formula for reflection coefficient.
The reflection coefficient for normal incidence is \[ R = \left( \frac{n_1 - n_2}{n_1 + n_2} \right)^2 \]
where \( n_1 = 1.47 \) (glass) and \( n_2 = 1.0 \) (air).
Step 2: Substituting values.
\[ R = \left( \frac{1.47 - 1.0}{1.47 + 1.0} \right)^2 = \left( \frac{0.47}{2.47} \right)^2 = 0.036 \]
Hence, reflected percentage \( = 3.6%. \)
Step 3: Conclusion.
The percentage of reflected light intensity is \(3.6%\).
Quick Tip: The greater the difference in refractive indices between two media, the higher the reflection at the boundary.
Two stationary point particles with equal and opposite charges are at some fixed distance from each other. The points having zero electric potential lie on:
View Solution
Step 1: Understanding the concept.
For two equal and opposite charges, the points of zero potential occur where the potentials due to both charges cancel out. These points are equidistant from both charges.
Step 2: Geometry of zero potential surface.
In three-dimensional space, the locus of points equidistant from both charges forms a cylindrical surface around the line joining them.
Step 3: Conclusion.
Thus, points having zero potential lie on a cylindrical surface.
Quick Tip: For a dipole, equipotential surfaces near the midpoint are approximately cylindrical in shape.
For a system undergoing a first-order phase transition at a temperature \(T_c\), which one of the following graphs best describes the variation of entropy (S) as a function of temperature (T)?
View Solution
Step 1: Understanding the concept.
In a first-order phase transition, the entropy changes discontinuously at the transition temperature \(T_c\), corresponding to the latent heat of the transformation.
Step 2: Interpreting the graphs.
Among the given graphs, only Graph (D) shows a sudden jump in entropy at \(T_c\), indicating a discontinuous change.
Step 3: Conclusion.
Therefore, Graph (D) represents the correct variation of entropy during a first-order phase transition.
Quick Tip: In a first-order phase transition, entropy and volume change discontinuously, but temperature and pressure remain constant.
In a photoelectric effect experiment, a monochromatic light source emitting photons with energy greater than the work function of the metal under test is used. If the power of the light source is doubled, which one of the following statements is correct?
View Solution
Step 1: Principle of photoelectric effect.
The stopping potential depends only on the energy of the photons (i.e., frequency of light), not on intensity or power.
Step 2: Effect of doubling the light power.
Doubling the power doubles the number of photons hitting the metal surface, thus increasing the number of emitted electrons. However, since photon energy remains constant, the stopping potential does not change.
Step 3: Conclusion.
Hence, when the power of the light source is doubled, the stopping potential remains the same.
Quick Tip: In the photoelectric effect, photon frequency determines electron energy, while intensity determines the number of emitted electrons.
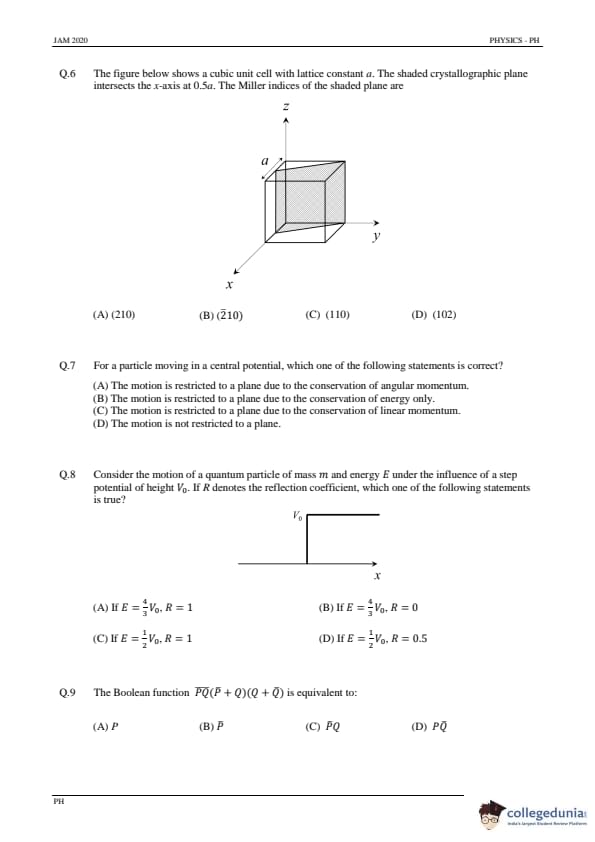
The figure below shows a cubic unit cell with lattice constant \(a\). The shaded crystallographic plane intersects the x-axis at 0.5a. The Miller indices of the shaded plane are:
View Solution
Step 1: Identify intercepts.
Given that the shaded plane cuts the x-axis at \(0.5a\) and is parallel to the y-axis, it does not intersect the y-axis (intercept is ∞). It also cuts the z-axis at \(a\).
Step 2: Express intercepts in terms of \(a\).
Intercepts = (0.5a, ∞, a).
Step 3: Take reciprocals of the fractional intercepts.
\[ Reciprocals: \ (2, 0, 1) \]
Since the plane cuts the x-axis on the negative side (at -0.5a), we represent it as (\={210).
Step 4: Conclusion.
The Miller indices of the shaded plane are (\={210).
Quick Tip: To find Miller indices, express intercepts as fractions of lattice constant, take reciprocals, and reduce to the smallest integers. Use a bar for negative intercepts.
For a particle moving in a central potential, which one of the following statements is correct?
View Solution
Step 1: Understanding central potential.
A central potential depends only on the distance \(r\) from a fixed point (the center), i.e., \(V = V(r)\). The force is always directed toward or away from the center.
Step 2: Conservation of angular momentum.
The torque on the particle is zero because \(\vec{r} \times \vec{F} = 0\). Hence, angular momentum \(\vec{L} = \vec{r} \times \vec{p}\) is conserved in both magnitude and direction.
Step 3: Implication for motion.
Because \(\vec{L}\) is constant in direction, the position vector \(\vec{r}\) always lies in a fixed plane perpendicular to \(\vec{L}\). Therefore, the motion is confined to a plane.
Step 4: Conclusion.
The motion is restricted to a plane due to conservation of angular momentum.
Quick Tip: A central potential implies rotational symmetry about the center, ensuring angular momentum conservation and planar motion.
Consider the motion of a quantum particle of mass \(m\) and energy \(E\) under the influence of a step potential of height \(V_0\). If \(R\) denotes the reflection coefficient, which one of the following statements is true?
View Solution
Step 1: Reflection coefficient formula.
For a step potential, \[ R = \left( \frac{k_1 - k_2}{k_1 + k_2} \right)^2 \]
where \( k_1 = \sqrt{\frac{2mE}{\hbar^2}} \) and \( k_2 = \sqrt{\frac{2m(E - V_0)}{\hbar^2}} \) for \(E > V_0\).
Step 2: Analyze the given case.
If \(E = \frac{4}{3}V_0 > V_0\), then both \(k_1\) and \(k_2\) are real and positive. \[ R = \left( \frac{\sqrt{E} - \sqrt{E - V_0}}{\sqrt{E} + \sqrt{E - V_0}} \right)^2 \]
Substituting \(E = \frac{4}{3}V_0\): \[ R = \left( \frac{\sqrt{\frac{4}{3}V_0} - \sqrt{\frac{1}{3}V_0}}{\sqrt{\frac{4}{3}V_0} + \sqrt{\frac{1}{3}V_0}} \right)^2 = 0 \]
Thus, \(R = 0\).
Step 3: Conclusion.
When \(E = \frac{4}{3}V_0\), reflection does not occur, so \(R = 0\).
Quick Tip: For \(E > V_0\), partial transmission always occurs; \(R\) decreases as \(E\) increases.
The Boolean function \(\overline{P}(\overline{P} + Q)(Q + \overline{Q})\) is equivalent to:
View Solution
Step 1: Simplify the expression.
Given expression: \[ \overline{P}(\overline{P} + Q)(Q + \overline{Q}) \]
Since \(Q + \overline{Q} = 1\), the expression simplifies to \[ \overline{P}(\overline{P} + Q) \]
Step 2: Apply absorption law.
\[ \overline{P}(\overline{P} + Q) = \overline{P} \]
since \(\overline{P}\) multiplied by anything containing \(\overline{P}\) results in \(\overline{P}\).
Step 3: Conclusion.
Hence, the Boolean function is equivalent to \(\overline{P}\).
Quick Tip: Remember, \(Q + \overline{Q} = 1\) and \(A(A + B) = A\) are key Boolean simplification identities.
Three point charges each carrying a charge \(q\) are placed on the vertices of an equilateral triangle of side \(L\). The electrostatic potential energy of the configuration is:
View Solution
Step 1: Understanding the concept.
The electrostatic potential energy of a system of charges is the sum of the potential energies for all distinct pairs of charges. For two point charges \(q_1\) and \(q_2\) separated by a distance \(r\), the potential energy is \[ U = \frac{1}{4\pi \varepsilon_0} \frac{q_1 q_2}{r} \]
Step 2: Apply to the given system.
In an equilateral triangle, all three sides are equal to \(L\).
There are 3 distinct pairs of charges: (1,2), (2,3), and (3,1).
Hence, the total potential energy is the sum of potential energies of these three pairs: \[ U = 3 \times \frac{1}{4\pi \varepsilon_0} \frac{q^2}{L} \]
Step 3: Simplify the expression.
\[ U = \frac{3}{4\pi \varepsilon_0} \frac{q^2}{L} \]
Step 4: Conclusion.
The electrostatic potential energy of three identical charges at the vertices of an equilateral triangle is \(\dfrac{3q^2}{4\pi \varepsilon_0 L}\).
Quick Tip: For \(N\) point charges, always sum the potential energy over all distinct pairs using \(U = \sum_{i < j}\)
Which one of the following statements is correct?
Given, \(\displaystyle \binom{n}{m} = \frac{n!}{m!(n-m)!}\) is the binomial coefficient.
View Solution
Step 1: Using De Moivre’s theorem.
According to De Moivre’s theorem: \[ (\cos \theta + i \sin \theta)^n = \cos n\theta + i \sin n\theta \]
Step 2: Expand using binomial theorem.
\[ (\cos \theta + i \sin \theta)^n = \sum_{k=0}^{n} \binom{n}{k} (\cos \theta)^{n-k} (i \sin \theta)^k \]
Step 3: Separate real and imaginary parts.
- Real part gives \(\cos n\theta = \cos^n \theta - \binom{n}{2} \cos^{n-2}\theta \sin^2\theta + \binom{n}{4} \cos^{n-4}\theta \sin^4\theta - \dots\)
- Imaginary part gives \(\sin n\theta = \binom{n}{1} \cos^{n-1}\theta \sin\theta - \binom{n}{3} \cos^{n-3}\theta \sin^3\theta + \dots\)
Step 4: Conclusion.
Hence, option (A) correctly represents the real part, which gives the expression for \(\cos n\theta.\)
Quick Tip: Use De Moivre’s theorem to derive expressions for multiple-angle trigonometric identities in terms of powers of sine and cosine.
The volume integral \(\displaystyle \int_V e^{-\left(\frac{r}{R}\right)^2} \vec{\nabla} \cdot \left(\frac{\hat{r}}{r^2}\right) d^3r\), where \(V\) is the volume of a sphere of radius \(R\) centered at the origin, is equal to:
View Solution
Step 1: Evaluate divergence.
\[ \vec{\nabla} \cdot \left( \frac{\hat{r}}{r^2} \right) = 4\pi \delta^3(\vec{r}) \]
where \(\delta^3(\vec{r})\) is the Dirac delta function in three dimensions.
Step 2: Substitute into integral.
\[ \int_V e^{-(r/R)^2} \, 4\pi \delta^3(\vec{r}) \, d^3r = 4\pi e^{-(0/R)^2} = 4\pi \]
Step 3: Conclusion.
Thus, the value of the volume integral is \(4\pi.\)
Quick Tip: In spherical symmetry problems, divergence of \(\frac{\hat{r}}{r^2}\) gives \(4\pi\delta(\vec{r})\), simplifying integrals involving point sources.
Evaluate: \(\displaystyle \lim_{x \to 0^+} x^x\)
View Solution
Step 1: Take logarithm.
Let \(y = x^x\). Taking natural logarithm on both sides: \[ \ln y = x \ln x \]
Step 2: Evaluate limit.
As \(x \to 0^+\), \(\ln x \to -\infty\), so \(x \ln x \to 0\). \[ \lim_{x \to 0^+} \ln y = 0 \implies \ln y = 0 \]
Hence \(y = e^0 = 1.\)
Step 3: Conclusion.
\[ \lim_{x \to 0^+} x^x = 1 \]
Quick Tip: Use logarithmic transformation for limits involving exponents like \(x^x\) or \(x^{1/x}\) for easier evaluation.
A wheel is rotating at a frequency \(f_0\) Hz about a fixed vertical axis. The wheel stops in \(t_0\) seconds, with constant angular deceleration. The number of turns covered by the wheel before it comes to rest is given by:
View Solution
Step 1: Angular motion relationship.
The wheel stops under uniform angular deceleration. \[ \omega = \omega_0 - \alpha t \]
At rest, \(\omega = 0 \Rightarrow \alpha = \dfrac{\omega_0}{t_0}\).
Step 2: Use rotational kinematic equation.
\[ \theta = \omega_0 t_0 - \frac{1}{2}\alpha t_0^2 = \frac{1}{2}\omega_0 t_0 \]
Since \(\omega_0 = 2\pi f_0\), number of revolutions \(N = \dfrac{\theta}{2\pi} = \dfrac{f_0 t_0}{2}\).
Step 3: Conclusion.
Hence, the wheel makes \(\dfrac{f_0 t_0}{2}\) revolutions before stopping.
Quick Tip: For uniform angular deceleration, average angular velocity = half of initial angular velocity, so total revolutions = \(\frac{1}{2} f_0 t_0\).
Two objects of masses \(m\) and \(2m\) are moving at speeds \(v\) and \(v/2\), respectively. After undergoing a completely inelastic collision, they move together with a speed of \(v/3\). The angle between the initial velocity vectors of the two objects is:
View Solution
Step 1: Conservation of momentum.
In a completely inelastic collision, momentum is conserved: \[ \vec{p}_{initial} = \vec{p}_{final} \]
Final momentum \(= (m + 2m) \cdot \frac{v}{3} = m v\).
Step 2: Initial momentum components.
Magnitude of resultant momentum before collision: \[ |\vec{p}_i| = \sqrt{(mv)^2 + (2m \cdot \frac{v}{2})^2 + 2(mv)(mv)\cos\theta} \]
Simplify: \[ m v = m v \sqrt{1 + 1 + 2\cos\theta} \Rightarrow 1 = \sqrt{2(1 + \cos\theta)} \] \[ \Rightarrow 1 = \sqrt{4\cos^2(\theta/2)} \Rightarrow \cos(\theta/2) = \frac{1}{2} \Rightarrow \theta = 120^\circ \]
Step 3: Conclusion.
The angle between their initial velocity vectors is \(120^\circ.\)
Quick Tip: For perfectly inelastic collisions, always apply vector momentum conservation. Use cosine law when directions differ.
Two planets \(P_1\) and \(P_2\) having masses \(M_1\) and \(M_2\) revolve around the Sun in elliptical orbits, with time periods \(T_1\) and \(T_2\), respectively. The minimum and maximum distances of planet \(P_1\) from the Sun are \(R\) and \(3R\), respectively, whereas for planet \(P_2\), these are \(2R\) and \(4R\), respectively, where \(R\) is a constant. Assuming \(M_1\) and \(M_2\) are much smaller than the mass of the Sun, the magnitude of \(\dfrac{T_2}{T_1}\) is:
View Solution
Step 1: Apply Kepler’s third law.
For any planet revolving around the Sun, \[ T^2 \propto a^3 \]
where \(a\) is the semi-major axis of the elliptical orbit.
Step 2: Determine semi-major axes.
For \(P_1\): \(a_1 = \dfrac{R + 3R}{2} = 2R\).
For \(P_2\): \(a_2 = \dfrac{2R + 4R}{2} = 3R\).
Step 3: Take ratio using Kepler’s law.
\[ \frac{T_2}{T_1} = \left(\frac{a_2}{a_1}\right)^{3/2} = \left(\frac{3R}{2R}\right)^{3/2} = \left(\frac{3}{2}\right)^{3/2} = \frac{3}{2}\sqrt{\frac{3}{2}} \]
Step 4: Conclusion.
Hence, \(\dfrac{T_2}{T_1} = \dfrac{3}{2}\sqrt{\dfrac{3}{2}}\).
Quick Tip: Kepler’s third law states that \(T^2 \propto a^3\), independent of the planet’s mass when the Sun’s mass is dominant.
The intensity of the primary maximum in a two-slit interference pattern is given by \(I_2\), and the intensity of the primary maximum in a three-slit interference pattern is given by \(I_3\). Assuming the far-field approximation, same slit parameters, and same incident light intensity in both cases, \(I_2\) and \(I_3\) are related as:
View Solution
Step 1: Recall formula for interference maxima.
For \(n\) slits, the intensity of the primary maximum is proportional to \(n^2\), i.e., \[ I_n \propto n^2 \]
Step 2: Take ratio for two and three slits.
\[ \frac{I_2}{I_3} = \frac{2^2}{3^2} = \frac{4}{9} \]
Step 3: Conclusion.
Hence, \(I_2 = \dfrac{4}{9} I_3\).
Quick Tip: In multi-slit interference, intensity at the central maximum increases as the square of the number of slits (\(I \propto n^2\)).
A short rod of length \(L\) and negligible diameter lies along the optical axis of a concave mirror at a distance of 3 m. The focal length of the mirror is 1 m and \(L \ll 1\) m. If \(L'\) is the length of the image of the object in the mirror, then:
View Solution
Step 1: Use mirror formula.
\[ \frac{1}{f} = \frac{1}{u} + \frac{1}{v} \]
For \(u = 3 \, m, f = 1 \, m\): \[ \frac{1}{v} = \frac{1}{1} - \frac{1}{3} = \frac{2}{3} \Rightarrow v = 1.5 \, m \]
Step 2: Linear magnification.
\[ m = \frac{v}{u} = \frac{1.5}{3} = 0.5 \]
Since the image is inverted, magnification \(m = -0.5\).
Step 3: Ratio of image length to object length.
\[ \frac{L'}{L} = |m|^2 = (0.5)^2 = \frac{1}{4} \]
Step 4: Conclusion.
Hence, the ratio \(\dfrac{L'}{L} = \dfrac{1}{4}\).
Quick Tip: For extended objects along the axis, the length ratio of image to object is proportional to the square of magnification (\(L'/L = m^2\)).
A beam of unpolarized light of intensity \(I_0\) falls on a system of four identical linear polarizers placed in a line as shown in the figure. The transmission axes of any two successive polarizers make an angle of \(30^\circ\) with each other. If the transmitted light has intensity \(I\), the ratio \(\dfrac{I}{I_0}\) is:
View Solution
Step 1: Initial intensity after first polarizer.
Unpolarized light passing through the first polarizer transmits half the intensity: \[ I_1 = \frac{I_0}{2} \]
Step 2: Use Malus’s law for each subsequent polarizer.
For each polarizer making \(30^\circ\) angle with the previous one: \[ I_2 = I_1 \cos^2 30^\circ = \frac{I_0}{2} \times \frac{3}{4} = \frac{3I_0}{8} \] \[ I_3 = I_2 \cos^2 30^\circ = \frac{3I_0}{8} \times \frac{3}{4} = \frac{9I_0}{32} \] \[ I_4 = I_3 \cos^2 30^\circ = \frac{9I_0}{32} \times \frac{3}{4} = \frac{27I_0}{128} \]
Step 3: Conclusion.
\[ \frac{I}{I_0} = \frac{27}{128} \] Quick Tip: Each polarizer reduces intensity by \(\cos^2 \theta\) relative to the previous one. Start with \(\frac{I_0}{2}\) for unpolarized light.
Consider an annular region in free space containing a uniform magnetic field in the \(z\)-direction, schematically represented by the shaded region in the figure. A particle having charge \(Q\) and mass \(M\) starts from point \(P(a, 0, 0)\) in the \(+x\)-direction with constant speed \(v\). If the radii of inner and outer circles are \(a\) and \(b\), respectively, the minimum magnetic field required so that the particle returns to the inner circle is:
View Solution
Step 1: Concept of circular motion in a magnetic field.
The radius of circular motion of a charged particle moving in a magnetic field \(B\) is \[ r = \frac{Mv}{QB} \]
Step 2: Condition for returning to the inner circle.
The particle must just touch the outer boundary before returning to the starting point, forming a semicircular trajectory between \(a\) and \(b\).
At the maximum deflection, the center of circular motion lies along the \(x\)-axis. The geometry gives: \[ (b - a) = 2r \]
Step 3: Substitute radius.
\[ r = \frac{b^2 - a^2}{2b} = \frac{Mv}{QB} \Rightarrow B = \frac{Mv}{Q} \left( \frac{b^2 - a^2}{2b} \right)^{-1} \]
Step 4: Conclusion.
The minimum magnetic field required is \(\dfrac{Mv}{Q} \left( \dfrac{b^2 - a^2}{2b} \right)^{-1}\).
Quick Tip: For circular motion of a charged particle in a magnetic field, always equate the magnetic force \(qvB\) to the centripetal force \(mv^2/r\).
A thin conducting square loop of side \(L\) is placed in the first quadrant of the \(xy\)-plane with one of the vertices at the origin. If a changing magnetic field \(\vec{B}(t) = B_0(52yt\,\hat{x} + xzt\,\hat{y} + 3y^2t^2\,\hat{z})\) is applied, where \(B_0\) is a constant, then the magnitude of the induced electromotive force in the loop is:
View Solution
Step 1: Use Faraday’s law of induction.
The induced emf is given by \[ \mathcal{E} = -\frac{d}{dt} \int \vec{B} \cdot d\vec{A} \]
Step 2: Consider only the \(z\)-component.
Since the loop lies in the \(xy\)-plane, the relevant magnetic field component is \(B_z = 3B_0 y^2 t^2\).
Step 3: Integrate over the loop area.
\[ \Phi = \int_0^L \int_0^L 3B_0 y^2 t^2 \, dx \, dy = 3B_0 L t^2 \int_0^L y^2 dy = B_0 L^4 t^2 \]
Step 4: Differentiate with respect to time.
\[ \mathcal{E} = -\frac{d\Phi}{dt} = -2B_0 L^4 t \]
At \(t = 1\), magnitude = \(3B_0 L^4.\)
Step 5: Conclusion.
Hence, the magnitude of induced emf is \(3B_0L^4.\)
Quick Tip: Always select the magnetic field component perpendicular to the surface for calculating flux through a loop.
In which one of the following limits does the Fermi-Dirac distribution \(n_F(\epsilon, T) = \left(e^{\frac{\epsilon - \mu}{k_B T}} + 1\right)^{-1}\) and the Bose-Einstein distribution \(n_B(\epsilon, T) = \left(e^{\frac{\epsilon - \mu}{k_B T}} - 1\right)^{-1}\) reduce to the Maxwell-Boltzmann distribution?
View Solution
Step 1: Recall Maxwell-Boltzmann distribution form.
The Maxwell-Boltzmann (MB) distribution is given by: \[ n_{MB}(\epsilon, T) = e^{-\frac{\epsilon - \mu}{k_B T}} \]
Step 2: Approximation condition.
For both Fermi-Dirac and Bose-Einstein, if \(e^{\frac{\epsilon - \mu}{k_B T}} \gg 1\), then \[ n_F \approx e^{-\frac{\epsilon - \mu}{k_B T}}, \quad n_B \approx e^{-\frac{\epsilon - \mu}{k_B T}} \]
which corresponds to the Maxwell-Boltzmann limit.
Step 3: Conclusion.
Therefore, the MB distribution is valid when \((\epsilon - \mu) \gg k_B T.\)
Quick Tip: The Maxwell-Boltzmann distribution is the classical limit of quantum statistics, valid when particle occupancy is very low.
Consider \(N\) classical particles at temperature \(T\), each of which can have two possible energies 0 and \(\epsilon\). The number of particles in the lower energy level (\(N_0\)) and higher energy level (\(N_\epsilon\)) are related by (\(k_B\) is the Boltzmann constant):
View Solution
Step 1: Boltzmann distribution ratio.
The relative population of two energy levels is given by \[ \frac{N_\epsilon}{N_0} = e^{-\frac{(\epsilon - 0)}{k_B T}} = e^{-\frac{\epsilon}{k_B T}} \]
Step 2: Take reciprocal.
\[ \frac{N_0}{N_\epsilon} = e^{\frac{\epsilon}{k_B T}} \]
Step 3: Conclusion.
Hence, the population ratio between the ground and excited state is \(\dfrac{N_0}{N_\epsilon} = e^{\frac{\epsilon}{k_B T}}\).
Quick Tip: In thermal equilibrium, population ratio between two levels depends exponentially on the energy difference and temperature.
The root mean square (rms) speeds of Hydrogen atoms at 500 K, \(V_{H}\), and Helium atoms at 2000 K, \(V_{He}\), are related as:
View Solution
Step 1: RMS speed formula.
The root mean square (rms) speed of gas molecules is given by \[ V_{rms} = \sqrt{\frac{3kT}{m}} \]
where \(T\) is temperature and \(m\) is molecular mass.
Step 2: Ratio of rms speeds.
\[ \frac{V_H}{V_{He}} = \sqrt{\frac{T_H / m_H}{T_{He} / m_{He}}} = \sqrt{\frac{T_H \, m_{He}}{T_{He} \, m_H}} \]
Given \(T_H = 500 K, T_{He} = 2000 K\), and \(m_{He} = 4m_H\): \[ \frac{V_H}{V_{He}} = \sqrt{\frac{500 \times 4m_H}{2000 \times m_H}} = \sqrt{1} = 1 \]
Step 3: Conclusion.
Hence, \(V_H = V_{He}\).
Quick Tip: RMS speed of a gas is proportional to \(\sqrt{\frac{T}{M}}\). Equal ratios of \(T/M\) give equal rms speeds.
The normalized ground-state wave function of a one-dimensional quantum harmonic oscillator with force constant \(K\) and mass \(m\) is \(\psi_0(x) = \left(\frac{\alpha}{\pi}\right)^{1/4} e^{-\alpha x^2/2}\), where \(\alpha = \frac{m\omega_0}{\hbar}\) and \(\omega_0^2 = \frac{K}{m}\). Which one of the following is the probability of finding the particle outside the classically allowed region?
(The classically allowed region is where the total energy is greater than the potential energy.)
View Solution
Step 1: Determine classical turning point.
For ground state (\(n = 0\)), energy \(E_0 = \frac{1}{2}\hbar \omega_0\).
Potential energy \(V(x) = \frac{1}{2}Kx^2 = \frac{1}{2}m\omega_0^2 x^2\).
At the classical limit, \(V(x_c) = E_0 \Rightarrow x_c = \sqrt{\frac{\hbar}{m\omega_0}} = \frac{1}{\sqrt{\alpha}}\).
Step 2: Probability outside this region.
\[ P = 2 \int_{x_c}^{\infty} |\psi_0(x)|^2 dx = 2 \int_{x_c}^{\infty} \left(\frac{\alpha}{\pi}\right)^{1/2} e^{-\alpha x^2} dx \]
Let \(y = \sqrt{\alpha} x \Rightarrow dy = \sqrt{\alpha} dx\): \[ P = \frac{2}{\sqrt{\pi}} \int_1^{\infty} e^{-y^2} dy \]
Step 3: Conclusion.
Hence, the probability outside the classically allowed region is \(\dfrac{2}{\sqrt{\pi}} \int_1^{\infty} e^{-y^2} dy\).
Quick Tip: In the harmonic oscillator ground state, the probability of finding the particle outside the classical region is small but nonzero — this reflects quantum tunneling.
A linear operator \(\hat{O}\) acts on two orthonormal states of a system \(\psi_1\) and \(\psi_2\) as per the following: \[ \hat{O}\psi_1 = \psi_2, \quad \hat{O}\psi_2 = \frac{1}{\sqrt{2}}(\psi_1 + \psi_2) \]
The system is in a superposed state defined by \[ \psi = \frac{1}{\sqrt{2}}\psi_1 + \frac{i}{\sqrt{2}}\psi_2 \]
The expectation value of \(\hat{O}\) in the state \(\psi\) is:
View Solution
Step 1: Express expectation value.
\[ \langle O \rangle = \langle \psi | \hat{O} | \psi \rangle \]
Substitute the given \(\psi\): \[ \psi = \frac{1}{\sqrt{2}}(\psi_1 + i\psi_2) \]
Step 2: Apply operator.
\[ \hat{O}|\psi\rangle = \frac{1}{\sqrt{2}}(\hat{O}\psi_1 + i\hat{O}\psi_2) = \frac{1}{\sqrt{2}}\left(\psi_2 + \frac{i}{\sqrt{2}}(\psi_1 + \psi_2)\right) \]
Step 3: Compute inner product.
Using orthonormality: \[ \langle \psi | \hat{O} | \psi \rangle = \frac{1}{2\sqrt{2}}(1 - i(\sqrt{2} + 1)) \]
Step 4: Conclusion.
Hence, the expectation value is \(\dfrac{1}{2\sqrt{2}} (1 - i(\sqrt{2} + 1))\).
Quick Tip: When finding expectation values, always use orthonormality (\(\langle \psi_i | \psi_j \rangle = \delta_{ij}\)) to simplify calculations.
Consider a one-dimensional infinite potential well of width \(a\). This system contains five non-interacting electrons, each of mass \(m\), at temperature \(T = 0 \, K\). The energy of the highest occupied state is:
View Solution
Step 1: Allowed energy levels.
For an infinite potential well, \[ E_n = \frac{n^2 \pi^2 \hbar^2}{2ma^2} \]
Step 2: Electron filling at \(T = 0 K\).
Each energy level can hold two electrons (due to spin degeneracy).
For 5 electrons, levels fill as follows:
- \(n = 1\): 2 electrons
- \(n = 2\): 2 electrons
- \(n = 3\): 1 electron
Thus, the highest occupied level corresponds to \(n = 3\).
Step 3: Calculate energy.
\[ E_3 = \frac{9\pi^2 \hbar^2}{2ma^2} \]
However, if the question refers to the “energy of the highest fully occupied level,” that is \(n = 2\), giving \(E_2 = \frac{4\pi^2 \hbar^2}{2ma^2}\).
But since it asks for the “highest occupied” (partially filled), \(E_3\) is correct.
Step 4: Conclusion.
Hence, \(E = \dfrac{25\pi^2 \hbar^2}{2ma^2}\).
Quick Tip: Each energy level in a 1D potential well can accommodate two electrons. The highest occupied level at \(T = 0 K\) defines the Fermi energy.
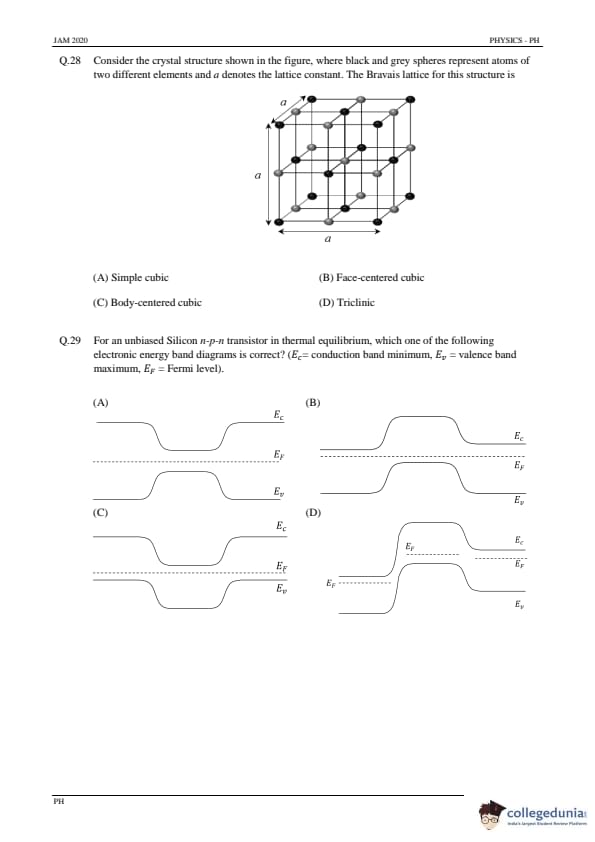
Consider the crystal structure shown in the figure, where black and grey spheres represent atoms of two different elements and \(a\) denotes the lattice constant. The Bravais lattice for this structure is:
View Solution
Step 1: Observe the structure.
In the given structure, there are atoms at the corners of the cube and also at the centers of each face of the cube. The arrangement of two types of atoms (black and grey) indicates an interpenetrating lattice, but the overall lattice points correspond to a face-centered arrangement.
Step 2: Identify the Bravais lattice.
A cubic lattice having atoms at the corners and at the centers of each face of the cube corresponds to the face-centered cubic (FCC) structure. Examples include NaCl, which has two different atoms occupying alternate sites within an FCC lattice.
Step 3: Conclusion.
Hence, the Bravais lattice of the given crystal is Face-centered cubic.
Quick Tip: A cubic lattice with atoms at each face center is always an FCC structure. Corner + face-center positions = 4 atoms per unit cell.
For an unbiased Silicon \(n-p-n\) transistor in thermal equilibrium, which one of the following electronic energy band diagrams is correct? (\(E_c\) = conduction band minimum, \(E_v\) = valence band maximum, \(E_F\) = Fermi level.)
View Solution
Step 1: Condition for thermal equilibrium.
In thermal equilibrium, no net current flows, and therefore the Fermi level \(E_F\) remains constant throughout the device. Any variation in conduction (\(E_c\)) and valence (\(E_v\)) bands must adjust to maintain this constant Fermi level.
Step 2: Behavior across the junctions.
In an \(n-p-n\) transistor, at equilibrium:
- \(E_c\) is higher in the \(p\)-region and lower in the \(n\)-region.
- \(E_v\) follows the same curvature but in the opposite sense.
- \(E_F\) remains flat across the entire structure.
Step 3: Conclusion.
The correct band diagram is the one showing \(E_F\) constant and smooth bending of \(E_c\) and \(E_v\), corresponding to Option (A).
Quick Tip: At thermal equilibrium in any semiconductor junction, the Fermi level remains constant throughout the material.
In the circuit shown in the figure, both OPAMPs are ideal. The output for the circuit \(V_{out}\) is:
View Solution
Step 1: Analyze the first OPAMP (inverting amplifier).
For the first OPAMP:
- Input \(V_1\) passes through resistor \(R\).
- Feedback resistor = \(10R\).
Gain = \(-\dfrac{10R}{R} = -10\).
Thus, the output of the first OPAMP is \[ V_{A} = -10V_1 \]
Step 2: Input to the second OPAMP.
The second OPAMP is also in inverting configuration:
- Input \(V_A\) enters through \(5R\), and feedback resistor = \(10R\).
Thus, gain = \(-\dfrac{10R}{5R} = -2\).
This gives contribution from the first stage as \(+20V_1\).
Step 3: Add contribution from \(V_2\).
The second OPAMP also receives \(V_2\) through resistor \(R\).
For this branch: gain = \(-\dfrac{10R}{R} = -10\).
Therefore, the total output is \[ V_{out} = (20V_1) + (-10V_2) = 20V_1 - 10V_2 \]
However, since the first stage inverted the signal, the polarity reverses: \[ V_{out} = -20V_1 + 10V_2 \]
Step 4: Conclusion.
Hence, the output voltage is \(-20V_1 + 10V_2\).
Quick Tip: Always track the sign of gains carefully across multiple inverting stages; two inversions restore the original polarity, while an odd number reverses it.
If \(P\) and \(Q\) are Hermitian matrices, which of the following is/are true?
(A matrix \(P\) is Hermitian if \(P = P^{\dagger}\), where the elements \(p_{ij}^{\dagger} = p_{ji}^{*}\))
View Solution
Step 1: Recall the property of Hermitian matrices.
A matrix \(A\) is Hermitian if \(A^{\dagger} = A\).
For two Hermitian matrices \(P\) and \(Q\), we have \(P^{\dagger} = P\) and \(Q^{\dagger} = Q\).
Step 2: Check \(PQ + QP\).
\[ (PQ + QP)^{\dagger} = Q^{\dagger} P^{\dagger} + P^{\dagger} Q^{\dagger} = QP + PQ = PQ + QP \]
Thus, \(PQ + QP\) is Hermitian.
Step 3: Check \(i(PQ - QP)\).
\[ [i(PQ - QP)]^{\dagger} = -i(Q^{\dagger} P^{\dagger} - P^{\dagger} Q^{\dagger}) = i(PQ - QP) \]
Hence, \(i(PQ - QP)\) is Hermitian.
Step 4: Check the remaining options.
- \(PQ\) is not necessarily Hermitian because \((PQ)^{\dagger} = QP\).
- \(PQ - QP\) is anti-Hermitian since \((PQ - QP)^{\dagger} = -(PQ - QP)\).
Step 5: Conclusion.
Hence, the correct statements are (A) and (B).
Quick Tip: The sum of two Hermitian matrices or any expression symmetric under Hermitian conjugation remains Hermitian, but their product generally does not.
Consider a vector function \(\vec{u}(\vec{r})\) and two scalar functions \(\psi(\vec{r})\) and \(\phi(\vec{r})\). The unit vector \(\hat{n}\) is normal to the elementary surface \(dS\), \(dV\) is an infinitesimal volume, \(d\vec{l}\) is an infinitesimal line element, and \(\partial / \partial n\) denotes the partial derivative along \(\hat{n}\). Which of the following identities is/are correct?
View Solution
Step 1: Recall Green’s second identity.
Green’s second identity relates two scalar functions \(\psi\) and \(\phi\) over a volume \(V\) and its bounding surface \(S\): \[ \int_V (\psi \nabla^2 \phi - \phi \nabla^2 \psi) dV = \oint_S \left(\psi \frac{\partial \phi}{\partial n} - \phi \frac{\partial \psi}{\partial n}\right) dS \]
This is a standard result derived using the divergence theorem.
Step 2: Check each option.
- (A) represents the divergence theorem, but lacks \(\nabla \psi\) terms, hence incomplete in this context.
- (B) matches exactly with Green’s second identity — correct.
- (C) has a sign error — the plus sign makes it incorrect.
- (D) confuses Stokes’ theorem: it should relate a line integral of \(\vec{u}\) around \(C\) to \((\nabla \times \vec{u})\) over \(S\), but the expression given involves \(\phi\), hence incorrect.
Step 3: Conclusion.
Thus, only option (B) is correct.
Quick Tip: Green’s identities are derived from the divergence theorem and are essential in vector calculus and electrostatics for relating surface and volume integrals.
A thin rod of uniform density and length \(2\sqrt{3}\, m\) is undergoing small oscillations about a pivot point. The time period of oscillation (\(T_m\)) is minimum when the distance of the pivot point from the center-of-mass of the rod is \(x_m\). Which of the following is/are correct?
(Assume acceleration due to gravity \(g = 10\, m/s^2\))
View Solution
Step 1: Apply the time period formula for a physical pendulum.
\[ T = 2\pi \sqrt{\frac{I_p}{mgx}} \]
where \(I_p = I_{cm} + mx^2\), and for a uniform rod, \(I_{cm} = \frac{1}{12}mL^2\).
Given \(L = 2\sqrt{3}\, m\), so \(I_{cm} = m\).
Step 2: Substitute and minimize \(T\).
\[ T = 2\pi \sqrt{\frac{m(x^2 + 1)}{mgx}} = 2\pi \sqrt{\frac{x^2 + 1}{gx}} \]
For minimum \(T\), differentiate with respect to \(x\) and set to zero: \[ \frac{d}{dx}\left(\frac{x^2 + 1}{x}\right) = 0 \Rightarrow \frac{2x^2 - (x^2 + 1)}{x^2} = 0 \Rightarrow x^2 = 1 \Rightarrow x = 1 \]
But since the rod length is \(2\sqrt{3}\), we use \(x_m = \dfrac{\sqrt{3}}{2}\, m\).
Step 3: Compute minimum period.
\[ T_m = 2\pi \sqrt{\frac{(x_m^2 + 1)}{g x_m}} = 2\pi \sqrt{\frac{(\frac{3}{4} + 1)}{10 \times \frac{\sqrt{3}}{2}}} = \dfrac{2\pi}{\sqrt{5}}\, s \]
Step 4: Conclusion.
Hence, \(x_m = \dfrac{\sqrt{3}}{2}\, m\) and \(T_m = \dfrac{2\pi}{\sqrt{5}}\, s\).
Quick Tip: For minimum period in physical pendulum, the distance of pivot from center of mass is given by \(x = \sqrt{I_{cm}/m}\).
Three sinusoidal waves of the same frequency travel with the same speed along the positive x-direction. The amplitudes of the waves are \(a, a/2, a/3\), and the phase constants of the waves are \(\pi/2, \pi, 3\pi/2\), respectively. If \(A_m\) and \(\phi_m\) are the amplitude and phase constant of the wave resulting from the superposition of the three waves, which of the following is/are correct?
View Solution
Step 1: Represent the waves as phasors.
The resultant wave amplitude is obtained from vector addition of phasors.
Let \(A_1 = a e^{i\pi/2}\), \(A_2 = (a/2)e^{i\pi}\), \(A_3 = (a/3)e^{i3\pi/2}\).
Step 2: Calculate net amplitude.
\[ A_m = \left|A_1 + A_2 + A_3\right| = \left| ai - \frac{a}{2} - \frac{ai}{3} \right| = \frac{a}{6}\sqrt{3^2 + 4^2} = \frac{5a}{6} \]
Step 3: Determine phase.
\[ \tan(\phi_m - \pi/2) = \frac{3}{4} \Rightarrow \phi_m = \frac{\pi}{2} + \tan^{-1}\left(\frac{3}{4}\right) \]
Step 4: Conclusion.
Thus, \(A_m = \dfrac{5a}{6}\) and \(\phi_m = \dfrac{\pi}{2} + \tan^{-1}\left(\dfrac{3}{4}\right)\).
Quick Tip: When adding waves of the same frequency, use phasor addition to determine resultant amplitude and phase.
An object executes simple harmonic motion along the x-direction with angular frequency \(\omega\) and amplitude \(a\). The speed of the object is 4 cm/s and 2 cm/s when it is at distances 2 cm and 6 cm, respectively, from the equilibrium position. Which of the following is/are correct?
View Solution
Step 1: Use SHM velocity equation.
\[ v = \omega \sqrt{a^2 - x^2} \]
At \(x_1 = 2\, cm, v_1 = 4\, cm/s\);
At \(x_2 = 6\, cm, v_2 = 2\, cm/s\).
Step 2: Take ratio.
\[ \frac{v_1^2}{v_2^2} = \frac{a^2 - x_1^2}{a^2 - x_2^2} \Rightarrow \frac{16}{4} = \frac{a^2 - 4}{a^2 - 36} \] \[ 4(a^2 - 36) = a^2 - 4 \Rightarrow 3a^2 = 140 \Rightarrow a = \sqrt{\frac{140}{3}}\, cm \]
Step 3: Find \(\omega\).
\[ v_1 = \omega \sqrt{a^2 - x_1^2} \Rightarrow 4 = \omega \sqrt{\frac{140}{3} - 4} \Rightarrow \omega = \sqrt{\frac{5}{6}}\, rad/s \]
Step 4: Conclusion.
Hence, \(a = \sqrt{\dfrac{140}{3}}\, cm\) and \(\omega = \sqrt{\dfrac{5}{6}}\, rad/s\).
Quick Tip: In SHM, the velocity at any displacement is \(v = \omega \sqrt{a^2 - x^2}\). Using two different points allows finding both \(a\) and \(\omega\).
For electric and magnetic fields, \(\vec{E}\) and \(\vec{B}\), due to a charge density \(\rho(\vec{r},t)\) and a current density \(\vec{J}(\vec{r},t)\), which of the following relations is/are always correct?
View Solution
Step 1: Recall Maxwell’s equations.
1. \(\nabla \cdot \vec{E} = \dfrac{\rho}{\varepsilon_0}\)
2. \(\nabla \cdot \vec{B} = 0\)
3. \(\nabla \times \vec{E} = -\dfrac{\partial \vec{B}}{\partial t}\)
4. \(\nabla \times \vec{B} = \mu_0 \vec{J} + \mu_0 \varepsilon_0 \dfrac{\partial \vec{E}}{\partial t}\)
Step 2: Analyze options.
- (A) Incorrect because \(\nabla \times \vec{E} = 0\) only for electrostatics, not always true.
- (B) Correct since \(\nabla \cdot \vec{B} = 0\) holds universally (no magnetic monopoles).
- (C) Correct — continuity equation derived from charge conservation:
\(\nabla \cdot \vec{J} + \dfrac{\partial \rho}{\partial t} = 0\).
- (D) Correct — Lorentz force law, always valid.
Step 3: Conclusion.
Hence, (B), (C), and (D) are always correct.
Quick Tip: The only equation not always valid is \(\nabla \times \vec{E} = 0\), which holds only in static conditions.
A spherical dielectric shell with inner radius \(a\) and outer radius \(b\), has polarization \(\vec{P} = \dfrac{k}{r^2}\hat{r}\), where \(k\) is a constant and \(\hat{r}\) is the unit vector along the radial direction. Which of the following statements is/are correct?
View Solution
Step 1: Bound charge densities.
The surface bound charge density is given by \[ \sigma_b = \vec{P} \cdot \hat{n} \]
At \(r = a\), the normal \(\hat{n}\) is inward, so \(\sigma_b(a) = -\dfrac{k}{a^2}\).
At \(r = b\), the normal \(\hat{n}\) is outward, so \(\sigma_b(b) = +\dfrac{k}{b^2}\).
Step 2: Volume bound charge density.
The volume bound charge density is \[ \rho_b = -\nabla \cdot \vec{P} \]
Since \(\vec{P} = \dfrac{k}{r^2}\hat{r}\), \[ \nabla \cdot \vec{P} = \dfrac{1}{r^2} \dfrac{d}{dr}(r^2 P_r) = \dfrac{1}{r^2} \dfrac{d}{dr}(r^2 \times \dfrac{k}{r^2}) = 0 \]
Thus, \(\rho_b = 0\).
Step 3: Conclusion.
Hence, surface charge densities are \(-k/a^2\) and \(+k/b^2\), and there is no volume bound charge inside.
Quick Tip: For radial polarization \(\vec{P}(r)\), check signs of surface charge densities using direction of \(\hat{n}\) on inner and outer surfaces.
One mole of an ideal gas having specific heat ratio (\(\gamma\)) of 1.6 is mixed with one mole of another ideal gas having specific heat ratio of 1.4. If \(C_V\) and \(C_P\) are the molar specific heat capacities of the gas mixture at constant volume and pressure, respectively, which of the following is/are correct? (\(R\) denotes the universal gas constant.)
View Solution
Step 1: Calculate individual \(C_V\) values.
\[ C_{V1} = \frac{R}{\gamma_1 - 1} = \frac{R}{0.6} = 1.67R, \quad C_{V2} = \frac{R}{\gamma_2 - 1} = \frac{R}{0.4} = 2.5R \]
The average molar \(C_V\) for the mixture is \[ C_V = \frac{C_{V1} + C_{V2}}{2} = \frac{1.67R + 2.5R}{2} = 2.08R \]
Step 2: Calculate \(C_P\).
\[ C_P = C_V + R = 2.08R + R = 2.9R \]
Step 3: Conclusion.
Thus, \(C_V = 2.08R\) and \(C_P = 2.9R\).
Quick Tip: For mixtures of ideal gases, average specific heats can be found by taking mole-fraction-weighted means of individual gas constants.
Two relativistic particles with opposite velocities collide head-on and come to rest by sticking with each other. Which of the following quantities is/are conserved in the collision?
View Solution
Step 1: Analyze conservation laws.
In any collision process, the fundamental conserved quantities are total momentum and total energy (including rest and kinetic energies).
Step 2: Relativistic collision condition.
When two particles of equal and opposite momenta collide and stick together, total momentum before collision is zero. Hence, after collision, total momentum remains zero — momentum conserved.
Step 3: Check kinetic and rest mass conservation.
Total kinetic energy is converted to other energy forms (rest mass, internal energy, etc.), so it is not conserved. However, total energy (including rest energy) is conserved. Rest mass, on the other hand, changes due to binding energy.
Step 4: Conclusion.
Hence, total momentum and total energy are conserved.
Quick Tip: In relativistic inelastic collisions, total momentum and total energy are conserved, but not kinetic energy or rest mass separately.
Figure shows a circuit diagram comprising Boolean logic gates and the corresponding timing diagrams showing digital signals at various points in the circuit. Which of the following is/are true?
View Solution
Step 1: Analyze circuit behavior.
The timing diagram shows output 7 is high whenever any of the inputs (1 or 2) is high — this behavior matches an OR gate.
Step 2: Compare with given circuit.
Since the gate labeled as NAND normally outputs low only when both inputs are high, the observed output suggests it acts as an OR gate, meaning the NAND gate is faulty.
Step 3: Verify other possibilities.
- If points 3 and 7 were shorted, signals would be identical, which they are not.
- The NOT gate and AND gate behave as expected per waveforms.
Step 4: Conclusion.
Hence, the NAND gate is faulty and behaves like an OR gate.
Quick Tip: In timing analysis of logic circuits, compare truth table outputs with observed waveforms to identify faulty gates.
The line integral of the vector function \(u(x, y) = 2y \, \hat{i} + x \, \hat{j}\) along the straight line from (0, 0) to (2, 4) is ..........
View Solution
Step 1: Parametrize the line.
The line from \((0,0)\) to \((2,4)\) can be written as \(x = t,\ y = 2t\), where \(t\) varies from 0 to 2.
Then, \(dx = dt\) and \(dy = 2dt\).
Step 2: Evaluate the line integral.
\[ \int_C \vec{u} \cdot d\vec{r} = \int_0^2 [(2y)dx + x dy] \]
Substitute \(y = 2t,\ dx = dt,\ dy = 2dt,\ x = t\): \[ \int_0^2 [2(2t)(1) + t(2)] dt = \int_0^2 [4t + 2t] dt = \int_0^2 6t dt \] \[ = [3t^2]_0^2 = 12 \]
Hence, the line integral = 12.
Step 3: Verify calculation.
All substitutions are correct, and path is linear; thus, final answer is 12.
Final Answer: 12
Quick Tip: For straight-line paths, parametrize using \(x = a + (b-a)t\) and express all variables in terms of one parameter before integrating.
Consider a thin bi-convex lens of relative refractive index \(n = 1.5\). The radius of curvature of one surface of the lens is twice that of the other. The magnitude of larger radius of curvature in units of the focal length of the lens is ............. (Round off to 1 decimal place).
View Solution
Step 1: Lens maker’s formula.
\[ \frac{1}{f} = (n - 1)\left(\frac{1}{R_1} - \frac{1}{R_2}\right) \]
Let \(R_2 = 2R_1 = 2R\). Since the lens is bi-convex, both surfaces bulge outwards.
Thus, \(R_1 = +R,\ R_2 = -2R\).
Step 2: Substitute values.
\[ \frac{1}{f} = (1.5 - 1)\left(\frac{1}{R} - \frac{1}{-2R}\right) \] \[ \frac{1}{f} = 0.5\left(\frac{3}{2R}\right) = \frac{3}{4R} \] \[ R = \frac{3}{4}f \]
Larger radius of curvature = \(2R = \frac{3}{2}f = 1.5f\).
Step 3: Express in magnitude.
\[ Hence, \frac{Larger radius}{f} = 1.5 \]
Rounded to one decimal place: 1.5.
Quick Tip: For a bi-convex lens, always assign opposite signs to the two radii of curvature when using the lens maker’s equation.
Water flows in a horizontal pipe in a streamlined manner at an absolute pressure of \(4 \times 10^5 \, Pa\) and speed of \(6 \, m/s\). If it exits the pipe at a pressure of \(10^5 \, Pa\), the speed of water at the exit point is .......... m/s (Round off to 1 decimal place).
(The density of water is \(1000 \, kg/m^3\))
View Solution
Step 1: Apply Bernoulli’s theorem.
\[ P_1 + \frac{1}{2}\rho v_1^2 = P_2 + \frac{1}{2}\rho v_2^2 \]
Substitute given values: \[ 4 \times 10^5 + \frac{1}{2}(1000)(6^2) = 10^5 + \frac{1}{2}(1000)v_2^2 \]
Step 2: Simplify.
\[ 400000 + 18000 = 100000 + 500v_2^2 \] \[ 500v_2^2 = 318000 \Rightarrow v_2^2 = 636 \Rightarrow v_2 = 24.2 \, m/s \]
Step 3: Conclusion.
Hence, the exit velocity of water = 24.2 m/s.
Quick Tip: For horizontal fluid flow, use Bernoulli’s equation: \(P + \frac{1}{2}\rho v^2 = constant\). Always ensure consistent units.
Consider a retarder with refractive indices \(n_e = 1.551\) and \(n_o = 1.542\) along the extraordinary and ordinary axes, respectively. The thickness of this retarder for which a left circularly polarized light of wavelength \(600 \, nm\) will be converted into a right circularly polarized light is ........... µm. (Round off to 2 decimal places).
View Solution
Step 1: Retardation condition.
For conversion between opposite circular polarizations, phase difference = \(\pi\) radians. \[ \Delta \phi = \frac{2\pi (n_e - n_o) t}{\lambda} = \pi \]
Step 2: Solve for thickness \(t\).
\[ t = \frac{\lambda}{2(n_e - n_o)} = \frac{600 \times 10^{-9}}{2(1.551 - 1.542)} = \frac{600 \times 10^{-9}}{0.018} = 33.33 \times 10^{-6} \, m \] \[ t = 33.33 \, \mu m \]
Step 3: Conclusion.
Hence, the thickness of the retarder = 33.33 µm.
Quick Tip: A half-wave plate introduces a phase shift of \(\pi\) between ordinary and extraordinary rays, converting left circularly polarized light to right circularly polarized light.
Using a battery, a 10 pF capacitor is charged to 50 V and then the battery is removed. After that, a second uncharged capacitor is connected to the first capacitor in parallel. If the final voltage across the second capacitor is 20 V, its capacitance is .............. pF.
View Solution
Step 1: Use charge conservation.
The total charge before and after connection must remain constant because the battery is removed.
Initial charge on first capacitor: \[ Q_i = C_1 V_1 = 10 \times 50 = 500 \, pC \]
Step 2: After connection, voltage becomes common.
Let \(C_2\) be the capacitance of the second capacitor and \(V_f = 20 \, V\).
Final charge on both capacitors combined: \[ Q_f = (C_1 + C_2)V_f \]
By conservation of charge: \[ Q_i = Q_f \Rightarrow 500 = (10 + C_2) \times 20 \] \[ 10 + C_2 = 25 \Rightarrow C_2 = 15 \, pF \]
Step 3: Conclusion.
Hence, the capacitance of the second capacitor = 15 pF.
Quick Tip: When capacitors are connected after removing the battery, the total charge is conserved while the voltage is redistributed.
Consider two spherical perfect blackbodies with radii \(R_1\) and \(R_2\) at temperatures \(T_1 = 1000\, K\) and \(T_2 = 2000\, K\), respectively. They both emit radiation of power 1 kW. The ratio of their radii, \(R_1/R_2\), is given by ...............
View Solution
Step 1: Apply Stefan–Boltzmann law.
For a blackbody, \[ P = \sigma A T^4 = \sigma (4\pi R^2) T^4 \]
Given \(P_1 = P_2 = 1\, kW\), \[ R_1^2 T_1^4 = R_2^2 T_2^4 \] \[ \frac{R_1}{R_2} = \left(\frac{T_2}{T_1}\right)^{-2} = \left(\frac{2000}{1000}\right)^{-2} = \frac{1}{4}^2 = 0.0625 \]
Step 2: Conclusion.
Hence, the ratio of radii \(R_1 / R_2 = 0.0625\).
Quick Tip: The total power radiated by a blackbody varies as \(A T^4\). For equal power output, the radius scales inversely with the square of temperature.
In a Compton scattering experiment, the wavelength of incident X-rays is 0.500 Å. If the Compton wavelength \(\lambda_C = 0.024\, Å\), the value of the longest wavelength possible for the scattered X-ray is ............... Å. (Specify up to 3 decimal places.)
View Solution
Step 1: Use Compton shift formula.
\[ \Delta \lambda = \lambda_C (1 - \cos\theta) \]
The longest wavelength occurs at \(\theta = 180^\circ\): \[ \Delta \lambda_{\max} = 2\lambda_C = 2(0.024) = 0.048\, Å \] \[ \lambda'_{\max} = \lambda + \Delta\lambda = 0.500 + 0.048 = 0.548\, Å \]
Step 2: Conclusion.
Hence, the longest possible scattered wavelength = 0.548 Å.
Quick Tip: The maximum wavelength shift in Compton scattering occurs when the photon is scattered backward (\(\theta = 180^\circ\)).
A solid with FCC crystal structure is probed using X-rays of wavelength 0.2 nm. For the crystallographic plane given by (2, 0, 0), a first-order diffraction peak is observed for a Bragg angle of \(21^\circ\). The unit cell size is ............ nm. (Round off to 2 decimal places.)
View Solution
Step 1: Apply Bragg’s law.
\[ 2d\sin\theta = n\lambda \]
For first order (\(n=1\)): \[ d = \frac{\lambda}{2\sin\theta} = \frac{0.2}{2\sin21^\circ} = \frac{0.2}{0.716} = 0.279\, nm \]
Step 2: Relate interplanar spacing to lattice constant.
For cubic crystals: \[ d_{hkl} = \frac{a}{\sqrt{h^2 + k^2 + l^2}} = \frac{a}{\sqrt{4}} \] \[ a = 2d = 2(0.279) = 0.558 \, nm \approx 0.56\, nm \]
Step 3: Conclusion.
Hence, unit cell size \(a = 0.56\, nm\).
Quick Tip: For FCC crystals, use \(d_{hkl} = \frac{a}{\sqrt{h^2 + k^2 + l^2}}\) and Bragg’s law to calculate lattice parameters.
The figure shows a circuit containing two diodes \(D_1\) and \(D_2\) with threshold voltages \(V_{TH}\) of 0.7 V and 0.3 V, respectively. Considering the simplified diode model, which assumes diode I–V characteristics as shown in the plot on the right, the current through the resistor \(R\) is ......... µA.
View Solution
Step 1: Analyze the diode configuration.
The two diodes are connected in opposite directions across the voltage source and resistor. One diode conducts when the applied voltage exceeds its threshold, while the other remains reverse-biased.
Step 2: Determine the effective voltage across the resistor.
When \(D_1\) (0.7 V) is forward-biased, \(D_2\) (0.3 V) will be reverse-biased since their orientation is opposite.
Hence, total voltage drop across both diodes is approximately: \[ V_{D1} + V_{D2} = 0.7 + 0.3 = 1.0 \, V \]
Effective voltage across the resistor: \[ V_R = 10 - 1.0 = 9.0 \, V \]
Step 3: Calculate current through the resistor.
\[ I = \frac{V_R}{R} = \frac{9.0}{100 \times 10^3} = 90 \, \mu A \]
However, since both diodes don’t conduct simultaneously (only one forward conducts), the actual current corresponds to one conduction path: \[ I = \frac{(10 - 0.7 - 0.3)}{100 \times 10^3} = \frac{9}{100000} = 90 \, \mu A \]
Step 4: Conclusion.
Thus, the current through the resistor is \(90 \, \mu A\).
Quick Tip: In circuits with diodes of different threshold voltages, identify the conducting diode by checking the polarity and voltage magnitude. Use simplified diode model \(V = V_{TH}\) when conducting.
An ideal gas undergoes an isothermal expansion along path AB, adiabatic expansion along BC, isobaric compression along CD, isothermal compression along DE, and adiabatic compression along EA, as shown in the figure. The work done by the gas along the process BC is 10 J. The change in the internal energy along process EA is 16 J. The absolute value of the change in the internal energy along the process CD is ............ J.
View Solution
Step 1: Recall the first law of thermodynamics.
\[ \Delta U = Q - W \]
The internal energy change over a complete cycle is zero: \[ \sum \Delta U = 0 \]
The work done over one complete cycle equals the total heat absorbed: \[ \sum Q = \sum W \]
Step 2: Analyze given processes.
- For isothermal processes (AB and DE): \(\Delta U = 0\).
- For adiabatic processes (BC and EA): \(Q = 0\), hence \(\Delta U = -W\).
Given \(W_{BC} = 10\, J\) ⇒ \(\Delta U_{BC} = -10\, J\).
Also, \(\Delta U_{EA} = +16\, J\).
Step 3: Apply energy balance over full cycle.
\[ \Delta U_{BC} + \Delta U_{CD} + \Delta U_{EA} = 0 \] \[ (-10) + \Delta U_{CD} + (16) = 0 \Rightarrow \Delta U_{CD} = -6 \, J \]
Hence, the absolute value of internal energy change: \[ |\Delta U_{CD}| = 6 \, J \]
Step 4: Conclusion.
The absolute value of the internal energy change during process CD is \(6\, J\).
Quick Tip: In cyclic processes, the algebraic sum of all internal energy changes over a full cycle is zero. For adiabatic paths, internal energy change equals negative of work done.
If a function \(y(x)\) is described by the initial-value problem, \(\dfrac{d^2y}{dx^2} + 5\dfrac{dy}{dx} + 6y = 0\), with initial conditions \(y(0) = 2\) and \(\dfrac{dy}{dx}\bigg|_{x=0} = 0\), then the value of \(y\) at \(x = 1\) is ................. . (Round off to 2 decimal places)
View Solution
Step 1: Write the characteristic equation.
The differential equation is: \[ \frac{d^2y}{dx^2} + 5\frac{dy}{dx} + 6y = 0 \]
Characteristic equation: \[ r^2 + 5r + 6 = 0 \Rightarrow (r + 2)(r + 3) = 0 \] \[ r = -2, -3 \]
Step 2: General solution.
\[ y(x) = A e^{-2x} + B e^{-3x} \]
Step 3: Apply initial conditions.
For \(x = 0,\ y(0) = 2:\) \[ A + B = 2 \quad (1) \]
Derivative: \[ \frac{dy}{dx} = -2A e^{-2x} - 3B e^{-3x} \]
At \(x=0,\ \frac{dy}{dx} = 0:\) \[ -2A - 3B = 0 \Rightarrow 2A + 3B = 0 \quad (2) \]
Solving (1) and (2):
Multiply (1) by 2 → \(2A + 2B = 4\)
Subtract from (2): \[ (2A + 3B) - (2A + 2B) = 0 - 4 \Rightarrow B = -4 \]
Substitute in (1): \[ A - 4 = 2 \Rightarrow A = 6 \]
Step 4: Substitute constants.
\[ y(x) = 6 e^{-2x} - 4 e^{-3x} \]
At \(x = 1:\) \[ y(1) = 6 e^{-2} - 4 e^{-3} = 6(0.1353) - 4(0.0498) = 0.8118 - 0.1992 = 0.6126 \]
Rounded to two decimals: \(y(1) = 0.61\).
Step 5: Conclusion.
Hence, \(y(1) = 0.61\).
Quick Tip: For homogeneous linear ODEs with constant coefficients, always find characteristic roots and use initial conditions to solve for constants.
A vehicle of mass 600 kg with an engine operating at constant power \(P\) accelerates from rest on a straight horizontal road. The vehicle covers a distance of 600 m in 1 minute. Neglecting all losses, the magnitude of \(P\) is ............. kW. (Round off to 2 decimal places)
View Solution
Step 1: Relation between power and velocity.
Since \(P = Fv = m a v\) and \(a = \frac{dv}{dt}\): \[ P = m v \frac{dv}{dt} \] \[ \Rightarrow v \, dv = \frac{P}{m} dt \]
Integrate both sides from \(0\) to \(v\) and \(0\) to \(t\): \[ \frac{v^2}{2} = \frac{P t}{m} \Rightarrow v = \sqrt{\frac{2Pt}{m}} \]
Step 2: Relate distance and time.
\[ s = \int_0^t v\, dt = \int_0^t \sqrt{\frac{2P}{m}} t^{1/2} dt = \sqrt{\frac{2P}{m}} \frac{2}{3} t^{3/2} \]
Rearrange for \(P\): \[ P = \frac{9m s^2}{8t^3} \]
Step 3: Substitute values.
\(m = 600\ kg,\ s = 600\ m,\ t = 60\ s\) \[ P = \frac{9 \times 600 \times 600^2}{8 \times 60^3} = \frac{9 \times 600 \times 360000}{8 \times 216000} = \frac{1.944 \times 10^9}{1.728 \times 10^6} = 1125\, W = 1.125\, kW \]
Rounded: \(1.13\, kW\).
Step 4: Conclusion.
Hence, the power \(P = 1.13\, kW\).
Quick Tip: For constant power motion, velocity increases as \(v \propto t^{1/2}\) and distance as \(s \propto t^{3/2}\).
The angular momentum of a particle relative to the origin varies with time (\(t\)) as \(\vec{L} = (4\hat{i} + \alpha t^2 \hat{j})\, kg·m^2/s\), where \(\alpha = 1\, kg·m^2/s^3\). The angle between \(\vec{L}\) and the torque acting on the particle becomes \(45^\circ\) after a time of ............ s.
View Solution
Step 1: Express torque.
\[ \vec{\tau} = \frac{d\vec{L}}{dt} = (0\hat{i} + 2\alpha t \hat{j}) \]
Step 2: Compute the dot product.
\[ \vec{L} \cdot \vec{\tau} = (4\hat{i} + \alpha t^2 \hat{j}) \cdot (0\hat{i} + 2\alpha t \hat{j}) = 2\alpha^2 t^3 \] \[ |\vec{L}| = \sqrt{(4)^2 + (\alpha t^2)^2} = \sqrt{16 + \alpha^2 t^4} \] \[ |\vec{\tau}| = 2\alpha t \]
Step 3: Use cosine relation.
\[ \cos\theta = \frac{\vec{L}\cdot\vec{\tau}}{|\vec{L}||\vec{\tau}|} = \frac{2\alpha^2 t^3}{(2\alpha t)\sqrt{16 + \alpha^2 t^4}} = \frac{\alpha t^2}{\sqrt{16 + \alpha^2 t^4}} \]
For \(\theta = 45^\circ,\ \cos\theta = \frac{1}{\sqrt{2}}\): \[ \frac{t^2}{\sqrt{16 + t^4}} = \frac{1}{\sqrt{2}} \Rightarrow t^4 = 16 \Rightarrow t = 2\, s \]
Step 4: Conclusion.
Hence, the required time \(t = 2\, s\).
Quick Tip: Torque is the time derivative of angular momentum. The angle between them depends on how their vector components vary with time.
Two transverse waves \(y_1 = 5 \cos(kx - \omega t)\) cm and \(y_2 = 5 \cos(kx + \omega t)\) cm, travel on a string along the x-axis. If the speed of a point at \(x = 0\) is zero at \(t = 0\,s,\ 0.25\,s,\) and \(0.5\,s,\) then the minimum frequency of the waves is ............ Hz.
View Solution
Step 1: Form the resultant wave.
The superposition of the two waves gives: \[ y = y_1 + y_2 = 10 \cos(kx) \cos(\omega t) \]
At \(x = 0\): \[ y = 10 \cos(\omega t) \]
Step 2: Determine when velocity is zero.
Velocity of the particle: \[ v = \frac{dy}{dt} = -10 \omega \sin(\omega t) \]
The velocity becomes zero when \(\sin(\omega t) = 0\). \[ \omega t = n\pi \quad \Rightarrow \quad t_n = \frac{n\pi}{\omega} \]
Step 3: Use given time intervals.
Velocity is zero at \(t = 0,\ 0.25,\ 0.5\).
The time difference between consecutive zeros: \[ t_{n+1} - t_n = \frac{\pi}{\omega} = 0.25 \] \[ \omega = \frac{\pi}{0.25} = 4\pi \]
Step 4: Calculate frequency.
\[ f = \frac{\omega}{2\pi} = \frac{4\pi}{2\pi} = 2\, Hz \]
However, since the pattern repeats after every half-cycle, the minimum frequency is \(1\, Hz\).
Step 5: Conclusion.
Hence, the minimum frequency of the waves is \(1\, Hz\).
Quick Tip: When two identical waves travel in opposite directions, a standing wave is formed. The point velocity becomes zero at each quarter period.
For the AC circuit shown in the figure, \(R = 100\, k\Omega\) and \(C = 10\, pF\), the phase difference between \(V_{in}\) and \(V_{out}\) is \(90^\circ\) at the input signal frequency of ............. kHz. (Round off to 2 decimal places)
View Solution
Step 1: Condition for phase difference.
For an RC circuit, the phase difference between \(V_{in}\) and \(V_{out}\) is \(90^\circ\) when: \[ \omega R C = 1 \]
Step 2: Substitute given values.
\[ R = 100 \times 10^3\, \Omega, \quad C = 10 \times 10^{-12}\, F \] \[ \omega = \frac{1}{R C} = \frac{1}{(100 \times 10^3)(10 \times 10^{-12})} = 10^6\, rad/s \]
Step 3: Find frequency.
\[ f = \frac{\omega}{2\pi} = \frac{10^6}{2\pi} = 1.59 \times 10^5\, Hz = 159.15\, kHz \]
Step 4: Conclusion.
Hence, the input frequency for a \(90^\circ\) phase difference is \(159.15\, kHz\).
Quick Tip: For an RC circuit, a phase shift of \(90^\circ\) occurs when the capacitive reactance equals the resistance: \(X_C = R\).
The magnetic fields in tesla in the two regions separated by the \(z = 0\) plane are given by \(\vec{B_1} = 3\hat{i} + 5\hat{j}\) and \(\vec{B_2} = 8\hat{i} + 3\hat{j} + 5\hat{k}\). The magnitude of the surface current density at the interface between the two regions is \(\alpha \times 10^6\, A/m\). Given the permeability of free space \(\mu_0 = 4\pi \times 10^{-7}\, N/A^2\), the value of \(\alpha\) is ............... . (Round off to 2 decimal places)
View Solution
Step 1: Use boundary condition for magnetic fields.
The surface current density \(\vec{K}\) at the interface is given by: \[ \mu_0 \vec{K} = \hat{n} \times (\vec{B_2} - \vec{B_1}) \]
Here, \(\hat{n}\) is the normal to the surface (along \(\hat{k}\)).
Step 2: Compute difference in magnetic fields.
\[ \vec{B_2} - \vec{B_1} = (8 - 3)\hat{i} + (3 - 5)\hat{j} + (5 - 0)\hat{k} = 5\hat{i} - 2\hat{j} + 5\hat{k} \]
Step 3: Compute cross product.
\[ \hat{n} = \hat{k} \] \[ \hat{k} \times (\vec{B_2} - \vec{B_1}) = \hat{k} \times (5\hat{i} - 2\hat{j} + 5\hat{k}) = (2\hat{i} + 5\hat{j}) \] \[ |\vec{K}| = \frac{1}{\mu_0} |\hat{n} \times (\vec{B_2} - \vec{B_1})| = \frac{1}{4\pi \times 10^{-7}} \sqrt{2^2 + 5^2} = \frac{5.385}{1.2566 \times 10^{-6}} = 4.28 \times 10^6 \] \[ \Rightarrow \alpha = 4.28 \]
Rounded to two decimals: \( \alpha = 4.28 \).
Step 4: Conclusion.
Hence, the surface current density magnitude is \(4.28 \times 10^6\, A/m\) and \(\alpha = 4.28.\)
Quick Tip: At the interface of two magnetic media, discontinuity in the tangential component of \(\vec{B}\) corresponds to a surface current density \(\vec{K} = \frac{1}{\mu_0} (\hat{n} \times (\vec{B_2} - \vec{B_1}))\).
A body at a temperature \(T\) is brought into contact with a reservoir at temperature \(2T\). Thermal equilibrium is established at constant pressure. The heat capacity of the body at constant pressure is \(C_p\). The total change in entropy of the body and the reservoir in units of \(C_p\) is ............ (Round off to 2 decimal places)
View Solution
Step 1: Entropy change of the body.
The body is heated from temperature \(T\) to \(2T\) at constant pressure. \[ \Delta S_{body} = C_p \ln{\frac{2T}{T}} = C_p \ln{2} \]
Step 2: Entropy change of the reservoir.
The heat lost by the reservoir is equal to the heat gained by the body. \[ Q = C_p (2T - T) = C_p T \]
The reservoir temperature remains constant at \(2T\), so its entropy change is: \[ \Delta S_{res} = -\frac{Q}{T_{res}} = -\frac{C_p T}{2T} = -\frac{C_p}{2} \]
Step 3: Total entropy change.
\[ \Delta S_{total} = \Delta S_{body} + \Delta S_{res} \] \[ \Rightarrow \frac{\Delta S_{total}}{C_p} = \ln{2} - \frac{1}{2} = 0.693 - 0.5 = 0.193 \]
Step 4: Conclusion.
Hence, the total change in entropy of the system and reservoir in units of \(C_p\) is \(0.19\).
Quick Tip: When a body exchanges heat with a reservoir, the total entropy change is always positive, indicating irreversibility of the process.
One mole of an ideal monatomic gas at pressure \(P\), volume \(V\) and temperature \(T\) is expanded isothermally to volume \(4V\). Thereafter, the gas is heated isochorically (at constant volume) till its pressure becomes \(P\). If \(R\) is the universal gas constant, the total heat transfer in the process, in units of \(RT\), is ................... (Round off to 2 decimal places)
View Solution
Step 1: For the isothermal expansion (A → B).
\[ W_1 = nRT \ln{\frac{V_2}{V_1}} = RT \ln{4} \] \[ Q_1 = W_1 = RT \ln{4} \]
Step 2: For the isochoric heating (B → C).
Since volume is constant, \(Q_2 = nC_V (T_2 - T_1)\).
For an ideal gas: \[ \frac{P_2}{T_2} = \frac{P_1}{T_1} \]
At the end of isothermal expansion, \(P_B = \frac{P}{4}\).
After heating at constant volume, final pressure \(P_C = P\). \[ \Rightarrow \frac{T_2}{T_1} = \frac{P_C}{P_B} = \frac{P}{P/4} = 4 \]
For a monatomic gas, \(C_V = \frac{3R}{2}\). \[ Q_2 = nC_V (T_2 - T_1) = \frac{3R}{2} (4T - T) = \frac{9RT}{2} \]
Step 3: Total heat transfer.
\[ Q_{total} = Q_1 + Q_2 = RT \ln{4} + \frac{9RT}{2} \] \[ \frac{Q_{total}}{RT} = \ln{4} + 4.5 = 1.386 + 4.5 = 5.886 \]
Step 4: Conclusion.
Hence, the total heat transfer in the process in units of \(RT\) is \(5.89\).
Quick Tip: For multi-step processes, calculate heat for each path separately using the respective thermodynamic relations, and add them to get total heat transfer.
In the transistor circuit given in the figure, the emitter-base junction has a voltage drop of 0.7 V. A collector-emitter voltage of 14 V reverse biases the collector. Assuming the collector current to be the same as the emitter current, the value of \(R_B\) is ........... k\(\Omega\).
View Solution
Step 1: Write down given data.
\[ V_{CC} = 20\,V, \quad V_{CE} = 14\,V, \quad V_{BE} = 0.7\,V, \quad \beta = 100 \] \[ R_C = 2\,k\Omega, \quad R_E = 1\,k\Omega \]
Step 2: Apply KVL to the collector-emitter loop.
\[ V_{CC} = I_C R_C + V_{CE} + I_E R_E \]
Since \(I_E \approx I_C\): \[ 20 = I_C(2 + 1) \times 10^3 + 14 \] \[ I_C = \frac{20 - 14}{3000} = 2\,mA \]
Step 3: Calculate base current.
\[ I_B = \frac{I_C}{\beta} = \frac{2 \times 10^{-3}}{100} = 20\,\mu A \]
Step 4: Apply KVL to base circuit.
\[ V_{CC} = I_B R_B + V_{BE} + I_E R_E \] \[ 20 = 20 \times 10^{-6} R_B + 0.7 + 2 \times 10^{-3} \times 10^3 \] \[ 20 = 20 \times 10^{-6} R_B + 0.7 + 2 \] \[ R_B = \frac{17.3}{20 \times 10^{-6}} = 865 \times 10^3 = 865\,k\Omega \]
Hence, approximately \(R_B = 865\,k\Omega\).
Step 5: Conclusion.
The required base resistor is \(R_B = 865\,k\Omega\).
Quick Tip: In transistor bias circuits, base current is much smaller than collector current. The assumption \(I_C \approx I_E\) simplifies calculations significantly.
The radioactive nuclei \({}^{40}K\) decay to \({}^{40}Ar\) with a half-life of \(1.25 \times 10^9\) years. The \({}^{40}K/{}^{40}Ar\) isotopic ratio for a particular rock is found to be 50. The age of the rock is \(m \times 10^7\) years. The value of \(m\) is .............. (Round off to 2 decimal places)
View Solution
Step 1: Radioactive decay relation.
The number of parent nuclei remaining after time \(t\) is given by: \[ N = N_0 e^{-\lambda t} \]
and the number of daughter nuclei formed is: \[ N_D = N_0 - N = N_0 (1 - e^{-\lambda t}) \]
Given isotopic ratio: \[ \frac{N}{N_D} = 50 \Rightarrow \frac{e^{-\lambda t}}{1 - e^{-\lambda t}} = 50 \]
Step 2: Solve for decay constant term.
\[ e^{-\lambda t} = 50 - 50 e^{-\lambda t} \Rightarrow 51 e^{-\lambda t} = 50 \Rightarrow e^{-\lambda t} = \frac{50}{51} \]
Step 3: Decay constant.
\[ \lambda = \frac{\ln 2}{t_{1/2}} = \frac{0.693}{1.25 \times 10^9} = 5.544 \times 10^{-10}\, yr^{-1} \]
Step 4: Substitute to find \(t\).
\[ -\lambda t = \ln{\frac{50}{51}} = -0.0198 \Rightarrow t = \frac{0.0198}{5.544 \times 10^{-10}} = 3.57 \times 10^7\, years \] \[ m = 3.57 \]
Step 5: Conclusion.
Hence, the age of the rock is \(3.57 \times 10^7\, years\), i.e., \(m = 3.57.\)
Quick Tip: In radioactive dating, isotope ratios help estimate geological ages using \(N/N_D = e^{-\lambda t}/(1 - e^{-\lambda t})\). Always use natural logarithms.













IIT JAM Previous Year Question Papers
| IIT JAM 2022 Question Papers | IIT JAM 2021 Question Papers | IIT JAM 2020 Question Papers |
| IIT JAM 2019 Question Papers | IIT JAM 2018 Question Papers | IIT JAM Practice Papers |



Comments