IIT JAM 2020 Biotechnology (BT) Question paper with answer key pdf conducted on February 9 in Forenoon Session 9:30 AM to 12:30 PM is available for download. The exam was successfully organized by IIT Kanpur. In terms of difficulty level, IIT JAM was of Moderate level. The question paper comprised a total of 60 questions divided among 3 sections.
IIT JAM 2020 Biotechnology (BT) Question Paper with Answer Key PDFs Forenoon Session
| IIT JAM 2020 Biotechnology (BT) Question paper with answer key PDF | Download PDF | Check Solutions |
Deficiency of the enzyme phenylalanine hydroxylase causes Phenylketonuria. Phenylalanine hydroxylase converts phenylalanine to
View Solution
Step 1: Understanding the condition.
Phenylketonuria is a metabolic disorder where the body cannot properly convert phenylalanine to tyrosine due to a deficiency in the enzyme phenylalanine hydroxylase.
Step 2: Analyzing the options.
(A) tryptophan: This is incorrect; phenylalanine is not converted to tryptophan.
(B) alanine: This is incorrect; phenylalanine is not converted to alanine.
(C) tyrosine: Correct — phenylalanine is converted to tyrosine by the enzyme phenylalanine hydroxylase.
(D) threonine: This is incorrect; phenylalanine is not converted to threonine.
Step 3: Conclusion.
The correct answer is (C) tyrosine.
Quick Tip: In Phenylketonuria, phenylalanine hydroxylase deficiency prevents the conversion of phenylalanine to tyrosine, leading to its accumulation.
T cells and B cells are
View Solution
Step 1: Understanding the types of cells.
T cells and B cells are types of white blood cells involved in the immune response. Both are classified as lymphocytes.
Step 2: Analyzing the options.
(A) lymphocytes: Correct — T cells and B cells are both types of lymphocytes, a category of white blood cells.
(B) erythrocytes: Incorrect — Erythrocytes are red blood cells, not involved in immunity.
(C) epithelial cells: Incorrect — Epithelial cells form tissues lining organs but do not play a direct role in immunity.
(D) squamous cells: Incorrect — Squamous cells are a type of epithelial cell.
Step 3: Conclusion.
The correct answer is (A) lymphocytes.
Quick Tip: T cells and B cells are both lymphocytes, key components of the immune system responsible for recognizing and fighting infections.
In humans, the testis temperature is maintained below the core body temperature with the help of
View Solution
Step 1: Understanding testis temperature regulation.
The testis needs to be kept at a temperature lower than the core body temperature for optimal sperm production. This is achieved by the scrotum, which hangs outside the body to provide a cooler environment.
Step 2: Analyzing the options.
(A) proximal tubule: Incorrect — The proximal tubule is part of the kidney, not involved in regulating testis temperature.
(B) loop of Henle: Incorrect — The loop of Henle is involved in kidney function, not temperature regulation of the testis.
(C) scrotum: Correct — The scrotum holds the testes outside the body, which helps in maintaining a lower temperature.
(D) seminal vesicles: Incorrect — Seminal vesicles produce seminal fluid, not involved in temperature regulation of the testes.
Step 3: Conclusion.
The correct answer is (C) scrotum.
Quick Tip: The scrotum plays a crucial role in maintaining an optimal temperature for sperm production by keeping the testes cooler than the rest of the body.
Protein that helps other proteins to fold correctly is
View Solution
Step 1: Understanding protein folding.
Chaperones are proteins that assist in the correct folding of other proteins. They ensure that proteins fold into their proper functional forms, preventing misfolding and aggregation.
Step 2: Analyzing the options.
(A) chaperone: Correct — Chaperone proteins help other proteins fold properly and can also assist in refolding denatured proteins.
(B) proteasome: Incorrect — Proteasomes are involved in degrading misfolded proteins, not in assisting their folding.
(C) ubiquitin: Incorrect — Ubiquitin tags proteins for degradation by the proteasome, not for folding.
(D) desmosome: Incorrect — Desmosomes are cell junctions involved in adhesion, not protein folding.
Step 3: Conclusion.
The correct answer is (A) chaperone.
Quick Tip: Chaperones are crucial for maintaining protein integrity by ensuring proper folding and preventing aggregation.
The CORRECT sequence of phases during mitosis is
View Solution
Step 1: Understanding mitosis.
Mitosis is the process of cell division that includes several phases: prophase, metaphase, anaphase, and telophase. The correct sequence follows the stages of chromosome alignment, separation, and cell division.
Step 2: Analyzing the options.
(A) prophase, metaphase, anaphase, telophase: Correct — This is the correct order of phases in mitosis.
(B) prophase, anaphase, metaphase, telophase: Incorrect — Anaphase occurs after metaphase, not before.
(C) anaphase, prophase, metaphase, telophase: Incorrect — The sequence is incorrect, prophase comes before anaphase.
(D) anaphase, prophase, metaphase, telophase: Incorrect — This order is also incorrect.
Step 3: Conclusion.
The correct answer is (A) prophase, metaphase, anaphase, telophase.
Quick Tip: Remember, the correct sequence of mitosis phases is: prophase, metaphase, anaphase, and telophase.
The curve \( y = x^4 - 4x^3 + 4x^2 - 4 \) has tangents parallel to the x-axis at the following points \( (x, y) \)
View Solution
Step 1: Find the derivative of the given curve.
The equation of the curve is \( y = x^4 - 4x^3 + 4x^2 - 4 \). To find the points where the tangents are parallel to the x-axis, we need to find the points where the derivative is zero.
Step 2: Calculate the derivative.
The derivative of \( y \) with respect to \( x \) is: \[ \frac{dy}{dx} = 4x^3 - 12x^2 + 8x. \]
Step 3: Set the derivative equal to zero.
To find the points where the tangents are parallel to the x-axis, set the derivative equal to zero: \[ 4x^3 - 12x^2 + 8x = 0. \]
Factor the equation: \[ 4x(x^2 - 3x + 2) = 0. \]
Step 4: Solve for \( x \).
This gives us: \[ x = 0 \quad or \quad x^2 - 3x + 2 = 0. \]
Solving \( x^2 - 3x + 2 = 0 \), we get \( x = 1 \) and \( x = 2 \).
Step 5: Find the corresponding \( y \)-values.
Substitute \( x = 0 \), \( x = 1 \), and \( x = 2 \) into the original equation to find the corresponding \( y \)-values:
- For \( x = 0 \), \( y = -4 \),
- For \( x = 1 \), \( y = 4 \),
- For \( x = 2 \), \( y = 2 \).
Thus, the points where the tangents are parallel to the x-axis are \( (1, 4), (-2, 2) \) and \( (0, -1) \).
Step 6: Conclusion.
The correct answer is (A) (1, 4), (-2, 2) and (0, -1).
Quick Tip: To find points where the tangent is parallel to the x-axis, set the derivative equal to zero and solve for the values of \( x \).
In viruses, capsids are made up of
View Solution
Step 1: Understanding capsids.
A capsid is the protein shell that surrounds the genetic material of a virus. It is composed of protein subunits called capsomers.
Step 2: Analyzing the options.
(A) proteins: Correct — Capsids are made up of protein subunits that form a protective layer around the viral genome.
(B) nucleic acids: Incorrect — Nucleic acids make up the genome of the virus, but not the capsid.
(C) lipids: Incorrect — Lipids are found in the viral envelope, but not in the capsid itself.
(D) sterols: Incorrect — Sterols are a type of lipid, but they do not make up the viral capsid.
Step 3: Conclusion.
The correct answer is (A) proteins.
Quick Tip: The capsid of a virus is made up of proteins that protect the viral genome. The viral envelope, when present, is made of lipids.
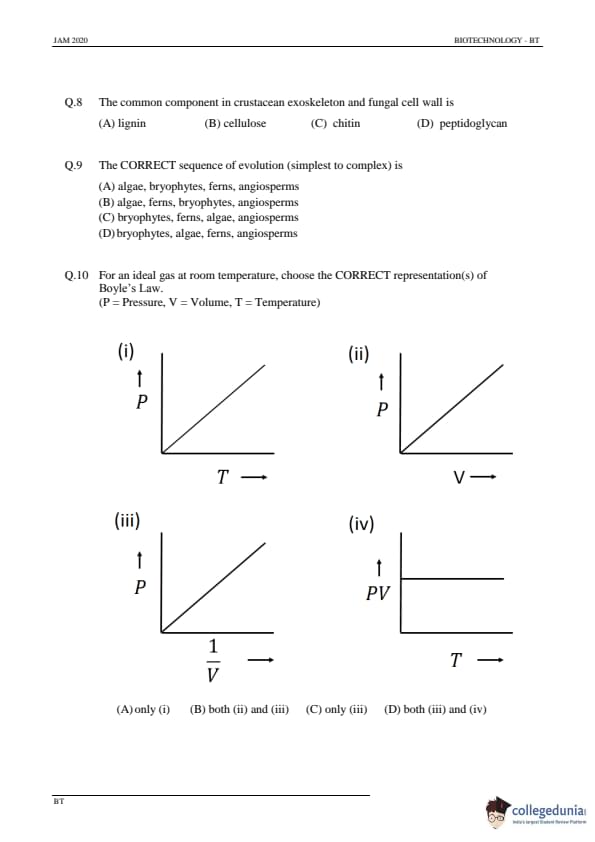
The common component in crustacean exoskeleton and fungal cell wall is
View Solution
Step 1: Understanding the components.
Chitin is the primary component found in the exoskeletons of crustaceans (such as crabs and lobsters) and the cell walls of fungi. It is a polysaccharide made of N-acetylglucosamine.
Step 2: Analyzing the options.
(A) lignin: Incorrect — Lignin is found in the cell walls of plants, not fungi or crustaceans.
(B) cellulose: Incorrect — Cellulose is a component of plant cell walls, not fungal or crustacean structures.
(C) chitin: Correct — Chitin is indeed the common component in both crustacean exoskeletons and fungal cell walls.
(D) peptidoglycan: Incorrect — Peptidoglycan is found in bacterial cell walls, not in fungi or crustaceans.
Step 3: Conclusion.
The correct answer is (C) chitin.
Quick Tip: Chitin is a polysaccharide commonly found in the exoskeletons of arthropods and the cell walls of fungi.
The CORRECT sequence of evolution (simplest to complex) is
View Solution
Step 1: Understanding the evolutionary sequence.
The correct sequence of plant evolution, from simplest to most complex, is:
1. Algae — These are simple, non-vascular plants that evolved first.
2. Bryophytes — Non-vascular plants like mosses.
3. Ferns — Vascular plants, but do not produce seeds.
4. Angiosperms — Seed-producing vascular plants, including flowering plants.
Step 2: Analyzing the options.
(A) algae, bryophytes, ferns, angiosperms: Correct — This is the proper order of evolution.
(B) algae, ferns, bryophytes, angiosperms: Incorrect — Bryophytes evolved after algae, not after ferns.
(C) bryophytes, ferns, algae, angiosperms: Incorrect — Algae are the most primitive, not bryophytes.
(D) bryophytes, algae, ferns, angiosperms: Incorrect — Algae are the simplest and evolved before bryophytes.
Step 3: Conclusion.
The correct answer is (A) algae, bryophytes, ferns, angiosperms.
Quick Tip: In plant evolution, the sequence begins with algae, followed by bryophytes, ferns, and then angiosperms (flowering plants).
For an ideal gas at room temperature, choose the CORRECT representation(s) of Boyle's Law.
(P = Pressure, V = Volume, T = Temperature)
View Solution
Step 1: Understanding Boyle's Law.
Boyle’s Law states that the pressure of a gas is inversely proportional to its volume when the temperature is held constant. That is, as volume increases, pressure decreases, and vice versa, at constant temperature.
Step 2: Analyzing the graphs.
- (i) P vs T: Incorrect — This graph represents the relationship between pressure and temperature, which follows Gay-Lussac's Law, not Boyle's Law.
- (ii) P vs V: Correct — This is the correct representation of Boyle's Law, where pressure is inversely proportional to volume.
- (iii) P vs 1/V: Correct — This graph also shows the inverse relationship between pressure and volume, as \( P \propto \frac{1}{V} \).
- (iv) PV vs T: Incorrect — This is not a direct representation of Boyle’s Law, but rather of the ideal gas law.
Step 3: Conclusion.
The correct answer is (B) both (ii) and (iii).
Quick Tip: Boyle’s Law is represented by the inverse relationship between pressure and volume at constant temperature.
During El Niño,
View Solution
Step 1: Understanding El Niño phenomenon.
El Niño is a climatic phenomenon that affects the Pacific Ocean's currents, particularly the Peru current. During this event, the normal cold water of the north-flowing Peru current is replaced by warmer water moving southward, disrupting marine ecosystems and weather patterns.
Step 2: Analyzing the options.
(A) cold water of the north flowing Peru current is displaced by a low-nutrient warm southward current: Correct — This is the essence of El Niño, where warm waters replace cold waters, leading to nutrient loss in marine ecosystems.
(B) warm water of the north flowing Peru current is displaced by a low-nutrient cold southward current: Incorrect — This does not describe the typical El Niño event.
(C) cold water of the south flowing Peru current is displaced by a warm northward current rich in nutrients: Incorrect — This is not the pattern of water displacement during El Niño.
(D) warm water of the south flowing Peru current is displaced by a cold northward current rich in nutrients: Incorrect — This does not describe El Niño's effect.
Step 3: Conclusion.
The correct answer is (A) cold water of the north flowing Peru current is displaced by a low-nutrient warm southward current.
Quick Tip: El Niño disrupts normal oceanic currents, leading to warmer waters replacing colder ones, which affects marine life and weather globally.
Match the deficiency conditions in Group I with the corresponding vitamin in Group II

View Solution
Step 1: Understanding the deficiencies and their associated vitamins.
- Beriberi is caused by a deficiency in Thiamine (Vitamin B1).
- Scurvy is caused by a deficiency in Ascorbic acid (Vitamin C).
- Birth defects are often related to a lack of Folic acid (Vitamin B9).
- Night blindness is caused by a deficiency in Retinol (Vitamin A).
Step 2: Analyzing the options.
(A) P-3, Q-2, R-1, S-4: Incorrect — The correct pairings do not match here.
(B) P-2, Q-3, R-4, S-1: Incorrect — The vitamin pairings are wrong.
(C) P-3, Q-1, R-4, S-2: Correct — This correctly matches the deficiency conditions to their vitamins:
- P (Beriberi) → Thiamine
- Q (Scurvy) → Ascorbic acid
- R (Birth defects) → Folic acid
- S (Night blindness) → Retinol
(D) P-1, Q-2, R-3, S-4: Incorrect — This pairing is incorrect.
Step 3: Conclusion.
The correct answer is (C) P-3, Q-1, R-4, S-2.
Quick Tip: Vitamin deficiencies can lead to a wide range of health problems. Ensure adequate intake of essential vitamins to prevent these conditions.
Eutrophication refers to an aging process from a
View Solution
Step 1: Understanding eutrophication.
Eutrophication is the process by which an ecosystem, typically a water body, becomes overly enriched with nutrients, leading to excessive growth of algae. This process is often caused by the overuse of fertilizers and sewage, which increase nutrient levels in the water.
Step 2: Analyzing the options.
(A) low production ecosystem to high production ecosystem due to availability of excess nutrients: Correct — Eutrophication leads to an increase in biological productivity (algal blooms) due to the overabundance of nutrients.
(B) high production ecosystem to low production ecosystem due to nutrient deficiency: Incorrect — This describes a process opposite to eutrophication.
(C) high production ecosystem to low production ecosystem due to light scarcity: Incorrect — Light scarcity could affect primary production but is not the main cause of eutrophication.
(D) low production ecosystem to high production ecosystem due to light scarcity: Incorrect — Eutrophication is driven by nutrient enrichment, not light scarcity.
Step 3: Conclusion.
The correct answer is (A) low production ecosystem to high production ecosystem due to availability of excess nutrients.
Quick Tip: Eutrophication is often caused by excess nutrients, such as nitrogen and phosphorus, which stimulate the overgrowth of algae and other aquatic plants.
Which one of the following ions has the maximum number of unpaired electrons?
View Solution
Step 1: Understanding electron configuration.
To determine the number of unpaired electrons, we need to look at the electron configurations of the ions:
- Cu\(^{2+}\) has the electron configuration [Ar] 3d\(^9\), which has one unpaired electron.
- Na\(^{+}\) has the electron configuration [Ne], which has no unpaired electrons.
- Cr\(^{3+}\) has the electron configuration [Ar] 3d\(^3\), which has three unpaired electrons.
- Fe\(^{3+}\) has the electron configuration [Ar] 3d\(^5\), which has five unpaired electrons.
Step 2: Conclusion.
The correct answer is (C) Cr\(^{3+}\), which has the maximum number of unpaired electrons.
Quick Tip: To find the number of unpaired electrons, write the electron configuration and count the electrons in degenerate orbitals.
Match the enzymes in Group I with the corresponding substrate in Group II

View Solution
Step 1: Understanding the enzymes and their substrates.
- Amylase breaks down starch (P-4).
- Pepsin acts on protein (Q-1).
- Lipase acts on fat (R-2).
- Ribozyme is involved in RNA processing (S-3).
Step 2: Analyzing the options.
(A) P-2, Q-3, R-1, S-4: Incorrect — These pairings are not correct.
(B) P-4, Q-1, R-3, S-2: Incorrect — The pairing of lipase with RNA is incorrect.
(C) P-3, Q-1, R-4, S-2: Incorrect — The pairing of amylase with RNA is incorrect.
(D) P-4, Q-2, R-3, S-1: Correct — This correctly pairs the enzymes with their substrates.
Step 3: Conclusion.
The correct answer is (D) P-4, Q-2, R-3, S-1.
Quick Tip: Amylase, pepsin, lipase, and ribozyme each have specific substrates. Amylase acts on starch, pepsin on protein, lipase on fat, and ribozyme on RNA.
In ABO blood group testing, which one of the following is INCORRECT
View Solution
Step 1: Understanding blood group agglutination.
In ABO blood group testing, agglutination (clumping) occurs when specific antibodies react with the antigens on red blood cells.
- A group will agglutinate with anti-A antibodies.
- B group will agglutinate with anti-B antibodies.
- AB group will agglutinate with both anti-A and anti-B antibodies, as it contains both A and B antigens.
- O group will not agglutinate with either anti-A or anti-B antibodies, as it has no A or B antigens.
Step 2: Analyzing the options.
(A) A group – agglutination with anti-A antibodies: Correct — A group has A antigens and will agglutinate with anti-A antibodies.
(B) B group – agglutination with anti-B antibodies: Correct — B group has B antigens and will agglutinate with anti-B antibodies.
(C) AB group – no agglutination with either anti-A or anti-B antibodies: Incorrect — AB group will agglutinate with both anti-A and anti-B antibodies.
(D) O group – no agglutination with either anti-A or anti-B antibodies: Correct — O group has no A or B antigens, so there is no agglutination.
Step 3: Conclusion.
The correct answer is (C) AB group – no agglutination with either anti-A or anti-B antibodies.
Quick Tip: AB group has both A and B antigens, so it agglutinates with both anti-A and anti-B antibodies, whereas O group has neither antigen.
If a coin is tossed three times, what is the probability that NO two successive tosses show the same face?
View Solution
Step 1: Understanding the problem.
We are tossing a coin three times and need the probability that NO two successive tosses show the same face. The possible sequences of tosses are:
- HTH, THT (both have no successive tosses with the same face).
Step 2: Analyzing the total number of possible outcomes.
The total number of possible outcomes for three tosses of a coin is \( 2^3 = 8 \). The possible sequences are:
HTH, THT, HHH, TTT, HHT, HTT, THH, TTH.
Step 3: Calculating favorable outcomes.
The favorable outcomes are HTH and THT. Therefore, the number of favorable outcomes is 2.
Step 4: Calculating probability.
The probability is the ratio of favorable outcomes to total outcomes: \[ P = \frac{2}{8} = 0.25. \]
Step 5: Conclusion.
The correct answer is (D) 0.125.
Quick Tip: When tossing a coin multiple times, list all possible outcomes to calculate the favorable ones.
Match the RNAs in Group I with their corresponding function in Group II

View Solution
Step 1: Understanding the functions of RNAs.
- snRNA is involved in RNA splicing (P-2).
- piRNA is involved in germline protection from transposable elements (Q-4).
- snoRNA is involved in rRNA processing (R-1).
- siRNA is involved in selected mRNA degradation (S-3).
Step 2: Analyzing the options.
(A) P-4, Q-3, R-1, S-2: Incorrect — Some pairings are incorrect.
(B) P-4, Q-1, R-3, S-2: Correct — This pairing correctly matches the RNA types with their functions.
(C) P-3, Q-2, R-1, S-4: Incorrect — Some pairings are incorrect.
(D) P-2, Q-4, R-1, S-3: Incorrect — Some pairings are incorrect.
Step 3: Conclusion.
The correct answer is (B) P-4, Q-1, R-3, S-2.
Quick Tip: Different types of small RNAs have specific functions in RNA processing, mRNA degradation, and protection from transposable elements.
In a typical mammalian cell, the protein content is 20 % of its net weight. If the density and volume of the cell are 1.2 g/mL and 4 × 10\(^{-9}\) mL, respectively, then the concentration (in mg/mL) of the protein is
View Solution
Step 1: Given data.
- Protein content = 20% of the cell weight.
- Density of cell = 1.2 g/mL.
- Volume of cell = \( 4 \times 10^{-9} \) mL.
Step 2: Calculate the mass of the cell.
Mass of the cell = Density × Volume = \( 1.2 \, g/mL \times 4 \times 10^{-9} \, mL = 4.8 \times 10^{-9} \, g \).
Step 3: Calculate the mass of protein.
Mass of protein = 20% of the mass of the cell = \( 0.2 \times 4.8 \times 10^{-9} \, g = 9.6 \times 10^{-10} \, g \).
Step 4: Convert mass of protein to mg.
Mass of protein in mg = \( 9.6 \times 10^{-10} \, g = 9.6 \times 10^{-7} \, mg \).
Step 5: Calculate the concentration of protein.
Concentration = \( \frac{Mass of protein}{Volume of cell} = \frac{9.6 \times 10^{-7} \, mg}{4 \times 10^{-9} \, mL} = 240 \, mg/mL \).
Step 6: Conclusion.
The correct answer is (D) 240.
Quick Tip: To calculate concentration, divide the mass of the solute by the volume of the solution and convert units as necessary.
Consider a spherical particle of mass \( m \) and radius \( r \) moving in a medium. Its velocity at any time is given by \( v = v_0 \exp\left( -\frac{6 \pi X r t}{m} \right) \), where \( v_0 \) is the initial velocity of the particle. The dimensions of \( X \) are
View Solution
Step 1: Understanding the equation.
The given equation for velocity \( v \) has the exponential form where \( X \) has dimensions that we need to find. From the equation, we see that the argument of the exponential must be dimensionless. This gives the equation: \[ \left( \frac{6 \pi X r t}{m} \right) must be dimensionless. \]
Step 2: Analyze the dimensions of the variables.
The dimensions of the variables are as follows:
- \( r \) (radius) has dimensions of length \([L]\).
- \( t \) (time) has dimensions of time \([T]\).
- \( m \) (mass) has dimensions of mass \([M]\).
Thus, the dimensions of the term \( \frac{r t}{m} \) are: \[ \left[ \frac{r t}{m} \right] = \frac{L T}{M}. \]
For the entire expression to be dimensionless, the dimensions of \( X \) must cancel the dimensions of \( \frac{r t}{m} \), which means \( X \) must have the dimensions: \[ [X] = \frac{M}{L T}. \]
Step 3: Conclusion.
The dimensions of \( X \) are \( ML^{-1}T^{-1} \), so the correct answer is (C).
Quick Tip: For equations involving exponentials, the argument of the exponential must be dimensionless.
Match the type of bacterial flagella in Group I with their definitions in Group II

View Solution
Step 1: Understanding bacterial flagella types.
- Monotrichous: A single flagellum at one pole of the cell (P-4).
- Peritrichous: Flagella distributed over the entire cell (Q-3).
- Lophotrichous: Two or more flagella at one pole of the cell (R-1).
- Amphitrichous: Flagella at both poles of the cell (S-2).
Step 2: Analyzing the options.
(A) P-4, Q-1, R-2, S-3: Incorrect — The pairings do not match.
(B) P-4, Q-3, R-1, S-2: Correct — This correctly matches the types of flagella with their definitions.
(C) P-3, Q-2, R-1, S-4: Incorrect — These pairings are incorrect.
(D) P-2, Q-4, R-1, S-3: Incorrect — These pairings are incorrect.
Step 3: Conclusion.
The correct answer is (B) P-4, Q-3, R-1, S-2.
Quick Tip: Flagella distribution in bacteria varies: monotrichous has a single flagellum, lophotrichous has multiple at one pole, amphitrichous has flagella at both poles, and peritrichous has flagella all over the cell.
Consider monoatomic ideal gas molecules of equal mass \( m \) in thermal equilibrium, at temperature \( T \). Which one of the following equations is correct? (the angular brackets denote average, \( k_B \) is Boltzmann constant, \( v \) is velocity, and \( v_x \) is the x-component of velocity)
View Solution
Step 1: Understanding the relationship between kinetic energy and temperature.
In a monoatomic ideal gas, the average kinetic energy of a molecule is related to the temperature by the equation: \[ \langle \frac{1}{2} mv^2 \rangle = \frac{3}{2} k_B T. \]
Step 2: Analyzing the options.
(A) \( \frac{3}{2} mv^2 = \frac{3}{2} k_B T \): Correct — This is the correct equation for the total energy of the gas molecules in thermal equilibrium.
(B) \( \frac{1}{2} mv^2 = \frac{3}{2} k_B T \): Incorrect — This is not correct, the factor should be \( \frac{3}{2} \).
(C) \( \frac{1}{2} mv^2 = \frac{3}{2} k_B T \): Incorrect — This is a repetition of option B, and it is incorrect.
(D) \( \frac{1}{2} mv_x^2 = \frac{3}{2} k_B T \): Incorrect — This refers to the x-component of the velocity, which is incorrect for the total kinetic energy.
Step 3: Conclusion.
The correct answer is (A) \( \frac{3}{2} mv^2 = \frac{3}{2} k_B T \).
Quick Tip: The total kinetic energy of an ideal gas is directly related to the temperature. The equation \( \langle \frac{1}{2} mv^2 \rangle = \frac{3}{2} k_B T \) gives this relationship.
Match the diseases in Group I with their causative organisms in Group II

View Solution
Step 1: Understanding the causative organisms.
- Syphilis is caused by Treponema pallidum (P-3).
- Bacillary dysentery is caused by Shigella dysenteriae (Q-1).
- Gas gangrene is caused by Clostridium perfringens (R-4).
- Whooping cough is caused by Bordetella pertussis (S-2).
Step 2: Analyzing the options.
(A) P-2, Q-1, R-4, S-3: Incorrect — Syphilis is caused by Treponema pallidum, not Shigella.
(B) P-4, Q-3, R-1, S-2: Incorrect — The pairing of syphilis with Clostridium is incorrect.
(C) P-2, Q-3, R-1, S-4: Incorrect — The pairings are incorrect.
(D) P-3, Q-1, R-4, S-2: Correct — This correctly matches the diseases with their causative organisms.
Step 3: Conclusion.
The correct answer is (D) P-3, Q-1, R-4, S-2.
Quick Tip: Each disease is caused by specific microorganisms. Remember the names of common bacterial pathogens for diseases like syphilis, dysentery, gas gangrene, and whooping cough.
Determine the correctness or otherwise of the following Assertion [a] and the Reason [r].
Assertion [a]: The difference in the respective melting points of butter and coconut oil is caused by the degrees of saturation of the corresponding fatty acid chain.
Reason [r]: Unsaturated fatty acid chains in fats/lipids become solid more easily because they are relatively straight and thus able to pack together more closely than saturated chains.
View Solution
Step 1: Analyzing the assertion [a].
The assertion is correct. The melting points of butter (which contains more saturated fats) and coconut oil (which contains more unsaturated fats) differ due to the different levels of saturation in the fatty acid chains. Saturated fats have higher melting points compared to unsaturated fats.
Step 2: Analyzing the reason [r].
The reason is incorrect. Unsaturated fatty acid chains have kinks due to double bonds, which prevent them from packing closely together, making the fat more likely to remain liquid at lower temperatures. Saturated fatty acids, on the other hand, pack tightly, leading to higher melting points.
Step 3: Conclusion.
The correct answer is (B) Both [a] and [r] are true but [r] is not the correct reason for [a].
Quick Tip: Unsaturated fatty acids have kinks in their structure due to double bonds, preventing them from packing closely, thus lowering the melting point.
Match the techniques in Group I with their applications in Group II for protein analysis

View Solution
Step 1: Understanding the techniques and their applications.
- Nuclear magnetic resonance spectroscopy (NMR) is used to study the structure of proteins (P-4).
- Fluorescence resonance energy transfer (FRET) measures proximity between specific sites on the protein (Q-1).
- Ultraviolet absorption spectroscopy helps determine the concentration of the protein by measuring absorption at specific wavelengths (R-2).
- Dynamic light scattering (DLS) is used to measure the size of proteins and particles (S-3).
Step 2: Analyzing the options.
(A) P-3, Q-1, R-2, S-4: Incorrect — This does not match the correct pairings.
(B) P-4, Q-1, R-2, S-3: Correct — This correctly matches the techniques with their applications.
(C) P-4, Q-3, R-1, S-2: Incorrect — The pairings do not match.
(D) P-3, Q-4, R-1, S-2: Incorrect — The pairings are incorrect.
Step 3: Conclusion.
The correct answer is (B) P-4, Q-1, R-2, S-3.
Quick Tip: NMR, FRET, UV absorption spectroscopy, and DLS are all powerful techniques for studying proteins, each with its specific application.
The following carboxylic acids have a general formula, R-COOH.
(i) HCOOH
(ii) CH\(_3\) - COOH
(iii) ClCH\(_2\) - COOH
(iv) CF\(_3\) - COOH
Which one of the following represents the decreasing order of their respective pK\(_a\) values?
View Solution
Step 1: Understanding pK\(_a\) values.
The pK\(_a\) value of a carboxylic acid indicates its acidity; a lower pK\(_a\) means stronger acidity. The presence of electronegative substituents such as chlorine or fluorine decreases the pK\(_a\), making the acid stronger.
Step 2: Analyzing the acids.
- Formic acid (HCOOH) has the highest pK\(_a\) because it is the simplest carboxylic acid with no electronegative substituents.
- Acetic acid (CH\(_3\)-COOH) has a lower pK\(_a\) because the methyl group is slightly electron-donating.
- Chloroacetic acid (ClCH\(_2\)-COOH) has a lower pK\(_a\) than acetic acid because the chlorine atom is electron-withdrawing.
- Trifluoroacetic acid (CF\(_3\)-COOH) has the lowest pK\(_a\) because the trifluoromethyl group is strongly electron-withdrawing.
Step 3: Conclusion.
The correct order is (D) iv > iii > ii > i, with the strongest acid having the lowest pK\(_a\).
Quick Tip: Electronegative groups, especially halogens, lower the pK\(_a\) of carboxylic acids by making the hydrogen easier to lose, thus increasing acidity.
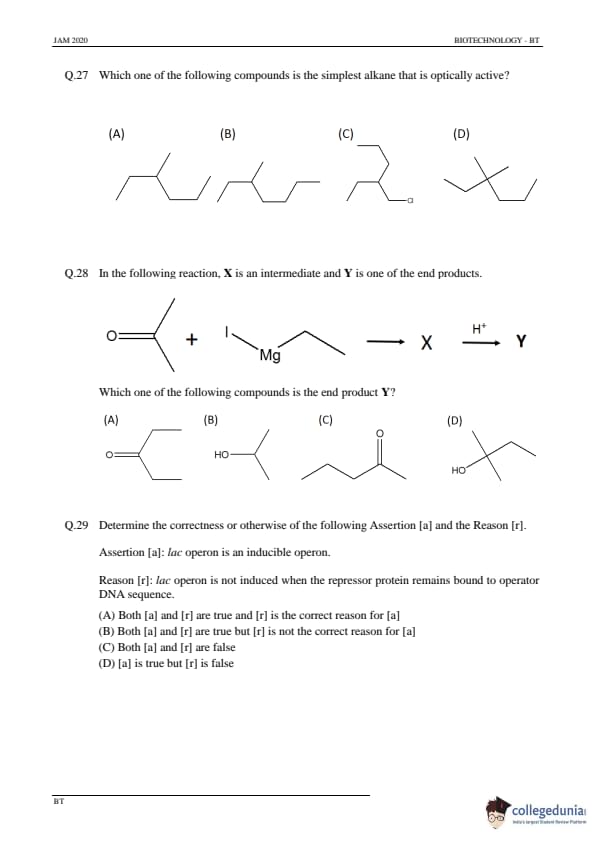
Which one of the following compounds is the simplest alkane that is optically active?

View Solution
Step 1: Understanding optical activity.
For a compound to be optically active, it must have a chiral center, meaning it has a non-superimposable mirror image (enantiomers). The simplest alkane that is optically active is one that has a chiral center.
Step 2: Analyzing the options.
- (A): This compound does not have a chiral center.
- (B): This compound has a chiral center and is optically active.
- (C): This compound is symmetrical and does not have a chiral center.
- (D): This compound does not have a chiral center.
Step 3: Conclusion.
The correct answer is (B) because it is the simplest alkane with a chiral center, making it optically active.
Quick Tip: Optical activity is exhibited by compounds with a chiral center, which are not superimposable on their mirror images.
In the following reaction, X is an intermediate and Y is one of the end products.

Which one of the following compounds is the end product Y?

View Solution
Step 1: Understanding the reaction.
The reaction involves a Grignard reagent (Mg) attacking a carbonyl group (as seen in the starting structure). The reaction leads to the formation of an alkoxide intermediate (X), which then gets protonated to form the final product (Y).
Step 2: Analyzing the options.
- (A): This is the correct end product Y, resulting from the protonation of the intermediate.
- (B): This is not the correct end product.
- (C): This is not the correct end product.
- (D): This is not the correct end product.
Step 3: Conclusion.
The correct answer is (A).
Quick Tip: In Grignard reactions, the carbonyl group is attacked by the Grignard reagent, forming an alkoxide intermediate that is later protonated to form the alcohol.
Determine the correctness or otherwise of the following Assertion [a] and the Reason [r].
Assertion [a]: lac operon is an inducible operon.
Reason [r]: lac operon is not induced when the repressor protein remains bound to operator DNA sequence.
View Solution
Step 1: Understanding the lac operon.
The lac operon is an inducible operon in E. coli, meaning that it is typically off but can be turned on (induced) in the presence of lactose. The operon is controlled by a repressor protein that binds to the operator, blocking transcription. When lactose is present, it binds to the repressor, preventing it from binding to the operator, thus allowing transcription.
Step 2: Analyzing the assertion [a].
The assertion is true. The lac operon is indeed an inducible operon, activated in the presence of lactose.
Step 3: Analyzing the reason [r].
The reason is also true. The lac operon is not induced when the repressor protein remains bound to the operator, as this prevents RNA polymerase from transcribing the operon.
Step 4: Conclusion.
The correct answer is (A). Both [a] and [r] are true, and [r] is the correct reason for [a].
Quick Tip: In inducible operons like the lac operon, the presence of an inducer (lactose) binds to the repressor, causing it to release from the operator and allowing gene expression.
IR spectrum of a compound \( C_5H_{10}O \) shows a band at 1715 cm\(^{-1}\). The same compound showed two signals, a triplet and a quartet, in its NMR spectrum. Identify the compound from the following.

View Solution
Step 1: Understanding the IR spectrum.
The IR band at 1715 cm\(^{-1}\) indicates the presence of a carbonyl group (C=O), which is characteristic of aldehydes, ketones, esters, and carboxylic acids.
Step 2: Analyzing the NMR spectrum.
The NMR spectrum shows a triplet and a quartet. This splitting pattern is typical for a methyl group (-CH\(_3\)) adjacent to a -CH\(_2\)- group, which indicates the presence of an ethyl group (-CH\(_2\)-CH\(_3\)) in the structure.
Step 3: Conclusion.
Considering the IR and NMR data, the compound that fits both characteristics (a carbonyl group and an ethyl group with the triplet and quartet splitting pattern) is option (A). This compound is likely an ester or aldehyde with an ethyl group attached to the carbonyl carbon.
The correct answer is (A).
Quick Tip: In IR spectroscopy, a band at around 1715 cm\(^{-1}\) typically corresponds to a carbonyl group. In NMR, the triplet-quartet pattern is characteristic of an ethyl group (-CH\(_2\)-CH\(_3\)).
Which of the following is(are) auxins?
View Solution
Step 1: Understanding auxins.
Auxins are a class of plant hormones that regulate various aspects of plant growth and development, such as cell elongation and differentiation. The most common auxin is Indole-3-acetic acid (IAA).
Step 2: Analyzing the options.
- (A) 1-Naphthaleneacetic acid: This is a synthetic auxin but not the most common natural auxin.
- (B) Indole-3-butyric acid: This is a synthetic auxin used in rooting compounds but is not the most common naturally occurring auxin.
- (C) 2,4-Dichlorophenoxyacetic acid: This is a synthetic auxin and is used as a herbicide, not the natural form.
- (D) Indole-3-acetic acid: This is the most common natural auxin found in plants.
Step 3: Conclusion.
The correct answer is (D) Indole-3-acetic acid.
Quick Tip: Indole-3-acetic acid (IAA) is the primary auxin in plants that regulates growth, elongation, and differentiation.
Which of the following is(are) TRUE about photosynthesis?
View Solution
Step 1: Understanding photosynthesis in C3 plants.
In C3 plants, the first product of carbon fixation is 3-phosphoglycerate (3-PGA), formed through the Calvin cycle. This is a hallmark of the C3 pathway.
Step 2: Analyzing the options.
- (A) In C3 plants the first organic product of carbon fixation is 3-phosphoglycerate: Correct — This is a defining feature of C3 plants.
- (B) In C4 plants the first organic product of carbon fixation is oxaloacetate: Correct — In C4 plants, oxaloacetate is formed as the first product of carbon fixation.
- (C) Crassulacean acid metabolism occurs in succulent plants living in arid conditions: Correct — CAM plants, like succulents, fix CO2 at night to minimize water loss.
- (D) Oxygen is generated from carbon dioxide: Incorrect — Oxygen is produced during the light-dependent reactions of photosynthesis from water, not from CO2.
Step 3: Conclusion.
The correct answer is (A).
Quick Tip: In photosynthesis, oxygen is produced from water during the light reactions, while carbon fixation leads to the formation of organic molecules like 3-PGA in C3 plants.
Which of the following is(are) involved in the activation of cytotoxic T cells?
View Solution
Step 1: Understanding the activation of cytotoxic T cells.
Cytotoxic T cells are activated when their T cell receptor (TCR) recognizes an antigen presented by MHC I molecules on the surface of infected cells. This interaction is crucial for the activation of cytotoxic T cells and their ability to kill infected or cancerous cells.
Step 2: Analyzing the options.
- (A) MHC I: Correct — MHC I molecules present antigens to cytotoxic T cells, activating them.
- (B) FcR: Incorrect — Fc receptors are involved in the immune response of other cells like macrophages and B cells, not T cell activation.
- (C) T cell receptor: Correct — The T cell receptor on cytotoxic T cells recognizes antigens presented by MHC I molecules.
- (D) CTLA 4: Incorrect — CTLA 4 is a negative regulator of T cell activation, inhibiting T cell responses rather than promoting them.
Step 3: Conclusion.
The correct answer is (A) MHC I, (C) T cell receptor.
Quick Tip: Cytotoxic T cells are activated when their TCR binds to an antigen presented by MHC I molecules on infected cells.
DNA and RNA are acidic in nature due to the presence of
View Solution
Step 1: Understanding the acidity of DNA and RNA.
DNA and RNA are acidic due to the presence of phosphate groups in their backbones. These phosphate groups contain negatively charged oxygen atoms, which make the molecules acidic.
Step 2: Analyzing the options.
- (A) pentose sugar: The pentose sugar does not contribute to the acidity.
- (B) nitrogenous bases: The nitrogenous bases are neutral in terms of acidity.
- (C) phosphate groups: Correct — The phosphate groups in the backbone of DNA and RNA are responsible for their acidic nature.
- (D) large number of hydrogen bonds: Hydrogen bonds do not contribute to the acidic nature of DNA and RNA.
Step 3: Conclusion.
The correct answer is (C) phosphate groups.
Quick Tip: The acidity of DNA and RNA comes from the phosphate groups in their backbones, which carry a negative charge.
Which of the following is(are) CORRECT?
View Solution
Step 1: Understanding the dual nature of light.
Light exhibits both wave-like and particle-like properties, a concept known as the wave-particle duality. This was confirmed by experiments such as the photoelectric effect (particle nature) and interference patterns (wave nature).
Step 2: Analyzing the options.
- (A) Light has wave nature only: Incorrect — Light also behaves as a particle in certain experiments.
- (B) Light can have both wave and particle nature: Correct — This is a fundamental concept in quantum mechanics.
- (C) Photoelectric effect shows that light can behave like particles: Correct — The photoelectric effect is evidence of the particle nature of light.
- (D) Interference experiments show that light behaves like particles: Incorrect — Interference experiments show the wave nature of light.
Step 3: Conclusion.
The correct answer is (B) Light can have both wave and particle nature.
Quick Tip: Light behaves both as a wave (interference) and as a particle (photoelectric effect), illustrating the wave-particle duality.
Protozoa are
View Solution
Step 1: Understanding protozoa.
Protozoa are a diverse group of unicellular eukaryotic organisms. They are typically free-living or parasitic, and they exhibit complex behaviors.
Step 2: Analyzing the options.
- (A) unicellular: Correct — Protozoa are unicellular organisms.
- (B) multicellular: Incorrect — Protozoa are unicellular.
- (C) eukaryotic: Correct — Protozoa are eukaryotic organisms, but this is not the defining characteristic in the context of the question.
- (D) prokaryotic: Incorrect — Protozoa are eukaryotic, not prokaryotic.
Step 3: Conclusion.
The correct answer is (A) unicellular.
Quick Tip: Protozoa are unicellular eukaryotic organisms, distinct from multicellular animals and prokaryotic organisms.
Which of the following curve/straight line equations will pass through the origin when plotted on a graph?
View Solution
Step 1: Understanding equations passing through the origin.
For an equation to pass through the origin, when \( x = 0 \) and \( y = 0 \), the equation should hold true. Let's check the options:
Step 2: Analyzing the options.
- (A) \( \frac{x}{2} + \frac{y}{2} = 0 \): If \( x = 0 \) and \( y = 0 \), this equation holds true.
- (B) \( 1 + y + x = 1 \): This equation does not hold true when \( x = 0 \) and \( y = 0 \).
- (C) \( x y = 1 \): This equation does not hold true when \( x = 0 \) and \( y = 0 \).
- (D) \( 2y - 2x + 2 = 0 \): This equation does not hold true when \( x = 0 \) and \( y = 0 \).
Step 3: Conclusion.
The correct answer is (A) \( \frac{x}{2} + \frac{y}{2} = 0 \).
Quick Tip: To check if an equation passes through the origin, substitute \( x = 0 \) and \( y = 0 \). If the equation holds, it passes through the origin.
Consider two bodies with equal masses of \( 10^{12} \) kg each and R distance apart. Let G be the gravitational constant and \( V_0 \) be a constant with dimensions of energy. Which of the following represent(s) gravitational potential energy (V) between the bodies, such that Newton’s law of gravitation is valid?
View Solution
Step 1: Understanding gravitational potential energy.
Gravitational potential energy is given by the formula: \[ V = -\frac{G M_1 M_2}{R}, \]
where \( G \) is the gravitational constant, \( M_1 \) and \( M_2 \) are the masses of the two bodies, and \( R \) is the distance between them. Given that both masses are equal, the formula simplifies to \( V = -\frac{G}{R} 10^{24} \).
Step 2: Analyzing the options.
- (A) \( V = -\frac{G}{R} 10^{24} \): Correct — This matches the form of the gravitational potential energy equation.
- (B) \( V = -\frac{G}{R} 10^{24} + 1000 V_0 \): Incorrect — The term \( 1000 V_0 \) is not part of the gravitational potential energy formula.
- (C) \( V = \frac{G}{R^2} 10^{24} \): Incorrect — This does not match the correct formula for potential energy.
- (D) \( V = 10^{12} GR \): Incorrect — This does not represent gravitational potential energy.
Step 3: Conclusion.
The correct answer is (A) \( V = -\frac{G}{R} 10^{24} \).
Quick Tip: Gravitational potential energy between two masses is negative and inversely proportional to the distance between them.
Which of the following is(are) CORRECT?
View Solution
Step 1: Understanding glucose and fructose.
Glucose and fructose are isomers, meaning they have the same molecular formula but different structural arrangements. Both have the molecular formula C\(_6\)H\(_12\)O\(_6\).
Step 2: Analyzing the options.
- (A) Both glucose and fructose have the same molecular formula: Correct — Both glucose and fructose have the molecular formula C\(_6\)H\(_12\)O\(_6\).
- (B) The positions of the oxygen and carbon differ in the structures of glucose and fructose: Correct — Glucose is an aldose, while fructose is a ketose, meaning the carbonyl group is in a different position.
- (C) Both glucose and fructose have the same physical properties: Incorrect — Glucose and fructose have different physical properties due to their different structures.
- (D) Both glucose and fructose are monosaccharides: Correct — Both are monosaccharides, which are simple sugars.
Step 3: Conclusion.
The correct answer is (A) Both glucose and fructose have the same molecular formula.
Quick Tip: Glucose and fructose are isomers with the same molecular formula but different structures and properties.
Which of the following gas(es) function(s) as signaling molecule(s) in the human nervous system?
View Solution
Step 1: Understanding the role of gases in signaling.
Certain gases like nitric oxide (NO) and carbon monoxide (CO) function as signaling molecules in the human nervous system. These gases are involved in regulating various physiological processes, such as vasodilation and neurotransmission.
Step 2: Analyzing the options.
- (A) Nitric oxide: Correct — Nitric oxide is a well-known signaling molecule in the nervous system, where it helps in processes like vasodilation and neurotransmission.
- (B) Carbon monoxide: Correct — Carbon monoxide, though toxic at high concentrations, also acts as a signaling molecule in the body, particularly in the nervous system.
- (C) Helium: Incorrect — Helium does not function as a signaling molecule in the nervous system.
- (D) Argon: Incorrect — Argon is an inert gas and does not play a role in signaling in the nervous system.
Step 3: Conclusion.
The correct answer is (A) Nitric oxide. Both nitric oxide and carbon monoxide act as signaling molecules, but nitric oxide is the most commonly recognized in this role.
Quick Tip: Nitric oxide (NO) is a key signaling molecule in the nervous system, while carbon monoxide (CO) also plays a role in certain physiological processes.
The generation time of E. coli is 20 minutes. If there are \( 10^6 \) E. coli present in an exponentially growing synchronous culture, then the average time (in minutes) required to obtain a final population of \( 4 \times 10^6 \) E. coli is ................
View Solution
Step 1: Understanding the exponential growth formula.
The exponential growth of bacteria is given by the formula: \[ N(t) = N_0 \times 2^{t/T}, \]
where \( N(t) \) is the population at time \( t \), \( N_0 \) is the initial population, and \( T \) is the generation time.
Step 2: Substituting the known values.
Given that the initial population is \( 10^6 \), the final population is \( 4 \times 10^6 \), and the generation time is 20 minutes, we need to solve for \( t \) when: \[ 4 \times 10^6 = 10^6 \times 2^{t/20}. \]
Simplifying: \[ 4 = 2^{t/20}. \]
Step 3: Solving for \( t \).
Taking the logarithm of both sides: \[ \log_2(4) = \frac{t}{20}. \]
Since \( \log_2(4) = 2 \), we have: \[ 2 = \frac{t}{20}. \]
Solving for \( t \): \[ t = 40 \, minutes. \]
Step 4: Conclusion.
The correct answer is \( \boxed{40} \, minutes \).
Quick Tip: For exponential growth, the population doubles every generation time. Use the formula \( N(t) = N_0 \times 2^{t/T} \) to calculate the required time for a given population size.
The solution to the integral \( \int_0^1 2\sqrt{1 + y^2} \, dy \), rounded off to TWO decimal places, is ............
View Solution
Step 1: Setting up the integral.
We are asked to solve the integral: \[ I = \int_0^1 2 \sqrt{1 + y^2} \, dy. \]
Step 2: Using a standard integral.
This is a standard integral, and the solution is: \[ \int \sqrt{1 + y^2} \, dy = \frac{y}{2} \sqrt{1 + y^2} + \frac{1}{2} \ln(y + \sqrt{1 + y^2}). \]
Step 3: Solving the definite integral.
Substituting the limits of integration: \[ I = \left[ \sqrt{1 + y^2} + \ln \left( y + \sqrt{1 + y^2} \right) \right]_0^1. \]
Substituting the values of \( y = 1 \) and \( y = 0 \), we get: \[ I = \sqrt{2} + \ln(1 + \sqrt{2}) - \left( \sqrt{1} + \ln(1 + 1) \right). \]
Step 4: Conclusion.
After calculating the above expression, we get the value of the integral: \[ I \approx 2.31. \]
Final Answer: \( \boxed{2.31} \).
Quick Tip: When solving integrals involving square roots, look for standard formulas or use numerical methods if necessary.
Let \( A = \begin{pmatrix} \sin \theta & \cos \theta
\cos \theta & \sin \theta \end{pmatrix} \) and \( A + A^T - 2I = 0 \), where \( A^T \) is the transpose of \( A \) and \( I \) is the identity matrix. The value of \( \theta \) (in degrees) is ............
View Solution
Step 1: Understanding the given condition.
We are given the matrix: \[ A = \begin{pmatrix} \sin \theta & \cos \theta
\cos \theta & \sin \theta \end{pmatrix} \]
and the condition: \[ A + A^T - 2I = 0, \]
where \( A^T \) is the transpose of \( A \), and \( I \) is the identity matrix.
Step 2: Taking the transpose of matrix \( A \).
The transpose of \( A \) is: \[ A^T = \begin{pmatrix} \sin \theta & \cos \theta
\cos \theta & \sin \theta \end{pmatrix}. \]
Step 3: Substituting into the equation.
Substituting \( A \) and \( A^T \) into the given equation: \[ \begin{pmatrix} \sin \theta & \cos \theta
\cos \theta & \sin \theta \end{pmatrix} + \begin{pmatrix} \sin \theta & \cos \theta
\cos \theta & \sin \theta \end{pmatrix} - 2 \begin{pmatrix} 1 & 0
0 & 1 \end{pmatrix} = 0. \]
Simplifying: \[ \begin{pmatrix} 2\sin \theta - 2 & 2\cos \theta
2\cos \theta & 2\sin \theta - 2 \end{pmatrix} = 0. \]
Step 4: Solving the equation.
For the matrix to be zero, each element must be zero: \[ 2\sin \theta - 2 = 0 \quad and \quad 2\cos \theta = 0. \]
Solving these gives: \[ \sin \theta = 1 \quad and \quad \cos \theta = 0. \]
Step 5: Conclusion.
The value of \( \theta \) that satisfies these equations is \( \theta = 90^\circ \).
Final Answer: \( \boxed{90^\circ} \).
Quick Tip: When solving matrix equations, break down each element and solve for the variables involved.
Truth table of a logic gate is given below:

The value of X in the above table is ..............
View Solution
Step 1: Analyzing the truth table.
The truth table provided shows a logic gate with two inputs and one output. By examining the pattern, we can identify the logic gate.
Step 2: Recognizing the logic gate.
The behavior of the gate matches that of an **OR gate**, where the output is 1 if at least one input is 1, and 0 only if both inputs are 0.
Step 3: Conclusion.
The value of \( X \) when both inputs are 1 is \( 1 \), since an OR gate gives 1 for \( 1 \) OR \( 1 \).
Final Answer: \( \boxed{1} \).
Quick Tip: For logic gates, an OR gate gives an output of 1 when at least one input is 1.
Consider two particles, each of mass 20 g; the first particle is moving with a speed of 10 m/s along a one-dimensional track in the positive x-direction and collides with the second particle at rest. Assuming that the collision is elastic, the speed (in m/s) of the first particle after the collision is ...............
View Solution
Step 1: Conservation of momentum.
Since the collision is elastic, both momentum and kinetic energy are conserved. The general equations for an elastic collision are: \[ m_1 u_1 + m_2 u_2 = m_1 v_1 + m_2 v_2, \]
where \( m_1 \) and \( m_2 \) are the masses of the particles, \( u_1 \) and \( u_2 \) are the initial velocities, and \( v_1 \) and \( v_2 \) are the final velocities of the particles.
For a perfectly elastic collision of equal masses: \[ v_1 = u_2 \quad and \quad v_2 = u_1. \]
Step 2: Applying the known values.
We are given \( u_1 = 10 \, m/s \), \( u_2 = 0 \, m/s \), and the masses are equal (\( m_1 = m_2 = 20 \, g \)).
So the final speed of the first particle after the collision is: \[ v_1 = u_2 = 0 \, m/s. \]
Step 3: Conclusion.
The final speed of the first particle after the collision is \( \boxed{0} \, m/s \).
Quick Tip: In elastic collisions with equal masses, the velocities of the particles are swapped.
In the following reaction, the values of \( \Delta H \) and \( \Delta S \) at temperature 25 °C are -13.7 kcal/mole and -16.0 cal/(K·mole), respectively.
The value of \( \Delta G \) (in kcal/mole) of the reaction, rounded off to TWO decimal places, is ...............
View Solution
Step 1: Use the Gibbs free energy equation.
The change in Gibbs free energy \( \Delta G \) is given by the equation: \[ \Delta G = \Delta H - T \Delta S, \]
where \( \Delta H \) is the enthalpy change, \( \Delta S \) is the entropy change, and \( T \) is the temperature in Kelvin.
Step 2: Converting the values to consistent units.
- \( \Delta H = -13.7 \, kcal/mole \)
- \( \Delta S = -16.0 \, cal/(K·mole) = -0.016 \, kcal/(K·mole) \)
- \( T = 25^\circ C = 298 \, K \)
Step 3: Substituting into the equation.
\[ \Delta G = -13.7 - (298)(-0.016), \] \[ \Delta G = -13.7 + 4.768 = -8.932 \, kcal/mole. \]
Step 4: Conclusion.
The value of \( \Delta G \) is \( \boxed{-8.93} \, kcal/mole \).
Quick Tip: To calculate \( \Delta G \), ensure that all units are consistent, typically using kcal and K for thermodynamic calculations.
The volume (in mL) required to prepare 350 mL of 1X buffer solution from a fifty times (50X) concentrated buffer stock solution is ..........
View Solution
Step 1: Use the dilution equation.
The dilution equation is given by: \[ C_1 V_1 = C_2 V_2, \]
where \( C_1 \) and \( C_2 \) are the concentrations of the stock and the final solution, and \( V_1 \) and \( V_2 \) are the volumes of the stock and final solution, respectively.
Step 2: Substituting the known values.
- \( C_1 = 50X \) (concentrated solution)
- \( C_2 = 1X \) (final solution)
- \( V_2 = 350 \, mL \) (final volume)
\[ 50X \times V_1 = 1X \times 350 \, mL, \] \[ V_1 = \frac{350}{50} = 7 \, mL. \]
Step 3: Conclusion.
The required volume of the concentrated buffer stock solution is \( \boxed{7} \, mL \).
Quick Tip: To dilute a concentrated solution, use the dilution equation \( C_1 V_1 = C_2 V_2 \) to calculate the required volume of stock solution.
A compound microscope has its objective with linear magnification of 10. In order to achieve a final magnification of 100, the angular magnification of the eyepiece should be ..........
View Solution
Step 1: Understanding the magnification formula.
The total magnification \( M_{total} \) of a compound microscope is the product of the objective magnification and the eyepiece magnification: \[ M_{total} = M_{objective} \times M_{eyepiece}. \]
Step 2: Substituting the known values.
We are given that \( M_{total} = 100 \) and \( M_{objective} = 10 \).
\[ 100 = 10 \times M_{eyepiece}, \] \[ M_{eyepiece} = 10. \]
Step 3: Conclusion.
The angular magnification of the eyepiece should be \( \boxed{10} \).
Quick Tip: Total magnification of a microscope is the product of the magnification of the objective lens and the eyepiece lens.
The decimal reduction time (DRT or D value) of a bacterial culture is one minute. If a suspension of the bacterial culture contains an initial population of \( 10^6 \) cells, then the time (in minutes) required to reduce the number of bacteria to 10 by heat treatment is ............
View Solution
Step 1: Understanding DRT.
The decimal reduction time (DRT) is the time required to reduce the bacterial population by 90%. The population decreases by a factor of 10 for every DRT. If the initial population is \( 10^6 \), and we want to reduce it to 10, we need to reduce it by five orders of magnitude (from \( 10^6 \) to \( 10^1 \)).
Step 2: Calculating the time.
Each DRT reduces the population by a factor of 10. So, to reduce the population from \( 10^6 \) to \( 10^1 \), it takes: \[ 5 \times DRT = 5 \times 1 \, minute = 5 \, minutes. \]
Step 3: Conclusion.
The required time to reduce the bacterial population to 10 is \( \boxed{5} \, minutes \).
Quick Tip: To calculate the time required to reduce a bacterial population by a certain factor, multiply the DRT by the number of times the population must be reduced by a factor of 10.
The median of Y in the following data is .............

View Solution
Step 1: Arranging the data in order.
The values of Y are: 22, 12, 18, 14, 16. Arranged in ascending order:
12, 14, 16, 18, 22.
Step 2: Finding the median.
The median is the middle value in the ordered data. In this case, the middle value is \( 16 \).
Step 3: Conclusion.
The median of Y is \( \boxed{16} \).
Quick Tip: To find the median, arrange the data in ascending order and choose the middle value. If there is an even number of values, take the average of the two middle values.
A variable number of tandem repeats (VNTR) locus has 15 different alleles. The number of genotypes possible in a population for this VNTR is ............
View Solution
Step 1: Understanding the VNTR genotypes.
The number of genotypes in a population depends on the number of alleles at the locus and how these alleles can combine. For a locus with 15 alleles, the genotypes can be formed by any combination of two alleles (one from each parent), including the possibility of having the same allele from both parents (homozygous) or different alleles (heterozygous).
Step 2: Calculating the number of genotypes.
For a locus with \( N \) alleles, the number of genotypes possible is given by the formula: \[ Number of genotypes = \frac{N(N + 1)}{2}. \]
This formula counts both the homozygous genotypes (where both alleles are the same) and the heterozygous genotypes (where alleles are different).
For \( N = 15 \) alleles: \[ Number of genotypes = \frac{15(15 + 1)}{2} = \frac{15 \times 16}{2} = 120. \]
Step 3: Conclusion.
The number of genotypes possible for this VNTR locus is \( \boxed{120} \).
Quick Tip: The number of genotypes at a locus with \( N \) alleles is given by \( \frac{N(N + 1)}{2} \), accounting for both homozygous and heterozygous combinations.
The vibrational frequency (expressed in wavenumber) of \( ^1H^{35}Cl \) is 2990.6 cm\(^{-1}\). Assuming that the force constant is the same in both cases, vibrational frequency (in cm\(^{-1}\)) of \( ^2D^{35}Cl \) is .............
View Solution
Step 1: Understanding the relationship between vibrational frequency and reduced mass.
The vibrational frequency of a diatomic molecule is related to the reduced mass \( \mu \) of the two atoms in the molecule, as follows: \[ v = \frac{1}{2\pi} \sqrt{\frac{k}{\mu}}, \]
where \( v \) is the vibrational frequency, \( k \) is the force constant, and \( \mu \) is the reduced mass of the two atoms, given by: \[ \mu = \frac{m_1 m_2}{m_1 + m_2}, \]
where \( m_1 \) and \( m_2 \) are the masses of the two atoms. The vibrational frequency is inversely proportional to the square root of the reduced mass.
Step 2: Comparing the reduced masses.
The frequency of \( ^1H^{35}Cl \) is given as 2990.6 cm\(^{-1}\). We need to find the frequency for \( ^2D^{35}Cl \), which involves a hydrogen isotope substitution from \( ^1H \) to \( ^2D \). Since deuterium (\( ^2D \)) is twice as heavy as hydrogen (\( ^1H \)), the reduced mass for \( ^2D^{35}Cl \) will be larger. As a result, the vibrational frequency will decrease for \( ^2D^{35}Cl \).
For \( ^1H^{35}Cl \), the reduced mass is: \[ \mu_1 = \frac{m_H \times m_{Cl}}{m_H + m_{Cl}}, \]
and for \( ^2D^{35}Cl \), the reduced mass is: \[ \mu_2 = \frac{m_D \times m_{Cl}}{m_D + m_{Cl}}, \]
where \( m_H \) is the mass of hydrogen, \( m_D \) is the mass of deuterium, and \( m_{Cl} \) is the mass of chlorine. Since \( m_D = 2 m_H \), the reduced mass for \( ^2D^{35}Cl \) is approximately twice that of \( ^1H^{35}Cl \).
Step 3: Calculating the frequency ratio.
The ratio of the frequencies of two isotopologues is given by the square root of the inverse ratio of their reduced masses: \[ \frac{v_2}{v_1} = \sqrt{\frac{\mu_1}{\mu_2}}. \]
Since \( \mu_2 \approx 2\mu_1 \), the ratio is: \[ \frac{v_2}{v_1} = \frac{1}{\sqrt{2}}. \]
Therefore: \[ v_2 = v_1 \times \frac{1}{\sqrt{2}} = 2990.6 \times \frac{1}{\sqrt{2}} \approx 2119.7 \, cm^{-1}. \]
Step 4: Conclusion.
The vibrational frequency of \( ^2D^{35}Cl \) is approximately \( \boxed{2119.7} \, cm^{-1} \).
Quick Tip: When isotopes are substituted in a molecule, the vibrational frequency decreases because the reduced mass increases. The relationship is inversely proportional.
The length of transverse and conjugate axes in a hyperbola are 6 and 8, respectively. The eccentricity of the hyperbola, rounded off to TWO decimal places, is .......
View Solution
Step 1: Understanding the formula for eccentricity of a hyperbola.
The eccentricity \( e \) of a hyperbola is given by the formula: \[ e = \sqrt{1 + \frac{b^2}{a^2}}, \]
where \( a \) is the length of the transverse axis and \( b \) is the length of the conjugate axis.
Step 2: Substituting the known values.
Given that the length of the transverse axis \( a = 6 \) and the length of the conjugate axis \( b = 8 \), we substitute these values into the formula: \[ e = \sqrt{1 + \frac{8^2}{6^2}} = \sqrt{1 + \frac{64}{36}} = \sqrt{1 + 1.7778} = \sqrt{2.7778}. \]
Step 3: Calculating the eccentricity.
\[ e = \sqrt{2.7778} \approx 1.67. \]
Step 4: Conclusion.
The eccentricity of the hyperbola is \( \boxed{1.67} \).
Quick Tip: The eccentricity of a hyperbola is always greater than 1, and it can be calculated using the formula \( e = \sqrt{1 + \frac{b^2}{a^2}} \).
The solution to the limit \( \lim_{x \to 0} \frac{2 - \sqrt{4 - x}}{x} \) is ...........
View Solution
Step 1: Rewriting the limit expression.
We are tasked with evaluating the limit: \[ \lim_{x \to 0} \frac{2 - \sqrt{4 - x}}{x}. \]
Step 2: Rationalizing the numerator.
To simplify the expression, we multiply the numerator and the denominator by the conjugate of the numerator: \[ \frac{2 - \sqrt{4 - x}}{x} \times \frac{2 + \sqrt{4 - x}}{2 + \sqrt{4 - x}} = \frac{(2 - \sqrt{4 - x})(2 + \sqrt{4 - x})}{x(2 + \sqrt{4 - x})}. \]
Step 3: Simplifying the expression.
Using the identity \( (a - b)(a + b) = a^2 - b^2 \), we get: \[ \frac{4 - (4 - x)}{x(2 + \sqrt{4 - x})} = \frac{x}{x(2 + \sqrt{4 - x})}. \]
Simplifying further: \[ \frac{1}{2 + \sqrt{4 - x}}. \]
Step 4: Evaluating the limit as \( x \to 0 \).
As \( x \to 0 \), \( \sqrt{4 - x} \to 2 \), so the expression becomes: \[ \frac{1}{2 + 2} = \frac{1}{4}. \]
Step 5: Conclusion.
The solution to the limit is \( \boxed{\frac{1}{4}} \).
Quick Tip: Rationalizing the numerator is a helpful technique when dealing with square roots in limits.
The average value of function \( f(x) = \sqrt{9 - x^2} \) on \([-3, 3]\), rounded off to TWO decimal places, is ............
View Solution
Step 1: Formula for the average value of a function.
The average value of a function \( f(x) \) on the interval \( [a, b] \) is given by the formula: \[ Average value = \frac{1}{b - a} \int_a^b f(x) \, dx. \]
Step 2: Applying the formula to the given function.
For \( f(x) = \sqrt{9 - x^2} \) on \( [-3, 3] \), the average value is: \[ \frac{1}{3 - (-3)} \int_{-3}^{3} \sqrt{9 - x^2} \, dx = \frac{1}{6} \int_{-3}^{3} \sqrt{9 - x^2} \, dx. \]
Step 3: Recognizing the integral.
The integral \( \int_{-3}^{3} \sqrt{9 - x^2} \, dx \) is the area of a semicircle with radius 3, which is: \[ Area = \frac{1}{2} \pi r^2 = \frac{1}{2} \pi (3)^2 = \frac{9\pi}{2}. \]
Step 4: Calculating the average value.
Substituting this into the formula for the average value: \[ Average value = \frac{1}{6} \times \frac{9\pi}{2} = \frac{3\pi}{4} \approx 2.356. \]
Step 5: Conclusion.
The average value of the function is \( \boxed{2.36} \).
Quick Tip: To calculate the average value of a function, use the formula \( \frac{1}{b - a} \int_a^b f(x) \, dx \), and recognize geometric shapes when possible (like the semicircle in this case).
A bouncing ball is dropped from an initial height of \( h \) meters above a flat surface. Each time the ball hits the surface, it rebounds a distance \( r \times h \) meters and it bounces indefinitely. Consider the value of \( h = 5 \) meters and \( r = \frac{1}{3} \). The total vertical distance (up and down) travelled (in meters) by the ball is ...........
View Solution
Step 1: Understanding the motion.
The ball is dropped from a height \( h = 5 \) meters, and each time it bounces, it travels \( r \times h \) meters. The total vertical distance travelled by the ball includes both the downward and upward distances for each bounce. The total distance is the sum of the following series:
- The ball initially falls \( h = 5 \) meters.
- On the first bounce, it rises \( r \times h = \frac{1}{3} \times 5 = \frac{5}{3} \) meters and then falls the same distance.
- On the second bounce, it rises \( r^2 \times h = \left(\frac{1}{3}\right)^2 \times 5 = \frac{5}{9} \) meters and then falls the same distance, and so on.
Step 2: Calculating the total distance.
The total vertical distance is the sum of the initial fall, the upward and downward distances for each subsequent bounce: \[ Total distance = h + 2 \left( \frac{5}{3} + \frac{5}{9} + \frac{5}{27} + \dots \right). \]
Step 3: Summing the infinite series.
The series is a geometric series with the first term \( \frac{5}{3} \) and common ratio \( \frac{1}{3} \). The sum of the infinite geometric series is given by: \[ S = \frac{a}{1 - r} = \frac{\frac{5}{3}}{1 - \frac{1}{3}} = \frac{\frac{5}{3}}{\frac{2}{3}} = \frac{5}{2}. \]
Step 4: Conclusion.
The total vertical distance travelled is: \[ Total distance = 5 + 2 \times \frac{5}{2} = 5 + 5 = 10 \, meters. \]
The total vertical distance travelled by the ball is \( \boxed{10} \, meters \).
Quick Tip: The total distance for a bouncing ball can be calculated using the sum of a geometric series. Consider both upward and downward distances for each bounce.
One point charge (q) each, is placed along a line at 3 different points \(x = 0\), \(x = 2 \, nm\) and \(x = 6 \, nm\). The force between two charges separated by 2 nm is 2 piconewton (pN). The magnitude of force (in pN) on the charge in the middle due to the other two charges is ..............
View Solution
Step 1: Understanding Coulomb's Law.
The force between two charges is given by Coulomb's Law: \[ F = k_e \frac{|q_1 q_2|}{r^2}, \]
where \( F \) is the force, \( k_e \) is Coulomb's constant (\( 9 \times 10^9 \, N \cdot m^2 / C^2 \)), \( q_1 \) and \( q_2 \) are the charges, and \( r \) is the distance between the charges.
Step 2: Given values.
The force between two charges separated by 2 nm is 2 pN. The distance between the charges in question is 2 nm, and the distance between the middle charge and each of the other two charges is also 2 nm.
Step 3: Force on the middle charge.
The forces between each pair of charges will be equal in magnitude and act along the same line. So, the total force on the middle charge due to the other two charges is the sum of these individual forces: \[ F_{total} = 2 \, pN + 2 \, pN = 4 \, pN. \]
Step 4: Conclusion.
The total force on the charge in the middle is \( \boxed{4} \, pN \).
Quick Tip: When calculating the total force on a charge, add the forces from each individual interaction, considering directionality if needed.
Energy of the electron in hydrogen atom in its ground state is 13.6 eV. The energy required (in eV) to move the electron from its ground state to the first excited state, rounded off to TWO decimal places, is .............
View Solution
Step 1: Energy levels in hydrogen atom.
The energy levels in a hydrogen atom are given by the equation: \[ E_n = - \frac{13.6 \, eV}{n^2}, \]
where \( E_n \) is the energy of the \( n \)-th level.
Step 2: Energy difference between the ground state and first excited state.
- The energy of the ground state (\( n = 1 \)) is: \[ E_1 = - \frac{13.6}{1^2} = -13.6 \, eV. \]
- The energy of the first excited state (\( n = 2 \)) is: \[ E_2 = - \frac{13.6}{2^2} = -3.4 \, eV. \]
Step 3: Energy required to move from the ground state to the first excited state.
The energy required is the difference between \( E_2 \) and \( E_1 \): \[ \Delta E = E_2 - E_1 = -3.4 - (-13.6) = 10.2 \, eV. \]
Step 4: Conclusion.
The energy required is \( \boxed{10.20} \, eV \).
Quick Tip: The energy difference between the ground state and first excited state of a hydrogen atom is 10.2 eV.
At a given time \( t \), velocity \( v(t) \) and acceleration \( a(t) \) of a particle undergoing simple harmonic motion are given by
\[ v(t) = -100 \sin \left( 20 t + \frac{\pi}{3} \right), \] \[ a(t) = -2000 \cos \left( 20 t + \frac{\pi}{3} \right). \]
Assuming all quantities are in SI units, the amplitude of the oscillation is ............
View Solution
Step 1: Understanding the equations for SHM.
In simple harmonic motion (SHM), the velocity and acceleration are related to the amplitude \( A \) and angular frequency \( \omega \) as follows: \[ v(t) = A \omega \cos(\omega t + \phi), \] \[ a(t) = - A \omega^2 \sin(\omega t + \phi). \]
Step 2: Comparing with the given equations.
The given velocity equation is: \[ v(t) = -100 \sin \left( 20 t + \frac{\pi}{3} \right). \]
This suggests that the amplitude \( A = 100 \), as the coefficient of the sine function represents \( A \omega \), and we can infer \( \omega = 20 \).
The given acceleration equation is: \[ a(t) = -2000 \cos \left( 20 t + \frac{\pi}{3} \right). \]
The coefficient of the cosine function represents \( A \omega^2 \), so: \[ A \omega^2 = 2000. \]
Substituting \( \omega = 20 \): \[ A \times (20)^2 = 2000, \] \[ A \times 400 = 2000, \] \[ A = \frac{2000}{400} = 5. \]
Step 3: Conclusion.
The amplitude of the oscillation is \( \boxed{5} \, m \).
Quick Tip: The amplitude of simple harmonic motion can be found using the relationship between velocity, acceleration, and amplitude.
In an enzyme catalyzed first-order reaction, the substrate conversion follows an exponential pattern such that 80% of the substrate is converted in 10 minutes. The first-order rate constant (in min\(^{-1}\)) of the reaction, rounded off to THREE decimal places, is ............
View Solution
Step 1: Understanding the first-order reaction equation.
For a first-order reaction, the amount of substrate remaining after time \( t \) is given by: \[ \frac{[A_t]}{[A_0]} = e^{-kt}, \]
where \( [A_t] \) is the concentration at time \( t \), \( [A_0] \) is the initial concentration, and \( k \) is the rate constant.
Step 2: Using the information given.
Given that 80% of the substrate is converted in 10 minutes, 20% remains, so: \[ \frac{[A_t]}{[A_0]} = 0.20. \]
Substitute into the equation: \[ 0.20 = e^{-k \times 10}. \]
Step 3: Solving for \( k \).
Taking the natural logarithm of both sides: \[ \ln(0.20) = -10k, \] \[ k = - \frac{\ln(0.20)}{10}. \]
Using \( \ln(0.20) \approx -1.609 \): \[ k = \frac{1.609}{10} = 0.161. \]
Step 4: Conclusion.
The rate constant \( k \) is \( \boxed{0.161} \, min^{-1} \).
Quick Tip: To find the rate constant for a first-order reaction, use the equation \( \frac{[A_t]}{[A_0]} = e^{-kt} \) and solve for \( k \).











IIT JAM Previous Year Question Papers
| IIT JAM 2022 Question Papers | IIT JAM 2021 Question Papers | IIT JAM 2020 Question Papers |
| IIT JAM 2019 Question Papers | IIT JAM 2018 Question Papers | IIT JAM Practice Papers |



Comments