IIT JAM 2019 Geology (GG) Question paper with answer key pdf conducted on February 10 in Afternoon Session 2 PM to 5 PM is available for download. The exam was successfully organized by IIT Kharagpur. The question paper comprised a total of 60 questions divided among 3 sections.
IIT JAM 2019 Geology (GG) Question Paper with Answer Key PDFs Afternoon Session
| IIT JAM 2019 Geology (GG) Question paper with answer key PDF | Download PDF | Check Solutions |
Which of the following is associated with a divergent plate boundary?
View Solution
Step 1: Understanding Divergent Plate Boundaries.
Divergent plate boundaries are regions where two tectonic plates move away from each other. This causes the formation of mid-ocean ridges, where new oceanic crust is created as magma rises from the mantle.
Step 2: Analyzing the options.
(A) Ridge: Correct — A ridge is a key feature of divergent plate boundaries, such as the Mid-Atlantic Ridge.
(B) Trench: Incorrect — Trenches are typically associated with convergent plate boundaries, not divergent.
(C) Island arc: Incorrect — Island arcs form at convergent boundaries where oceanic plates subduct beneath each other.
(D) Accretionary prism: Incorrect — These are typically found at convergent boundaries where subduction occurs.
Step 3: Conclusion.
The correct answer is (A) Ridge, as it is associated with divergent plate boundaries.
Quick Tip: Remember that divergent plate boundaries are typically associated with mid-ocean ridges where tectonic plates are moving apart, leading to the creation of new crust.
Shear waves do not travel through the
View Solution
Step 1: Understanding Shear Waves.
Shear waves (S-waves) are a type of seismic wave that move through the Earth’s interior. They can only travel through solid materials, not liquids.
Step 2: Analyzing the options.
(A) upper continental crust: Incorrect — S-waves can travel through the solid upper continental crust.
(B) upper mantle: Incorrect — The upper mantle is solid and S-waves can travel through it.
(C) lower mantle: Incorrect — The lower mantle is solid and S-waves can also travel through it.
(D) outer core: Correct — The outer core is liquid, and S-waves cannot travel through liquids.
Step 3: Conclusion.
The correct answer is (D) outer core, as shear waves cannot travel through liquids.
Quick Tip: Shear waves cannot travel through liquids, which is why they do not pass through the Earth’s outer core, which is liquid.
Fossils of burrows and footprints are known as
View Solution
Step 1: Understanding Fossils.
Fossils are the preserved remains or traces of ancient organisms. Trace fossils are those that show the activities or behaviors of ancient organisms, such as footprints or burrows.
Step 2: Analyzing the options.
(A) pseudofossils: Incorrect — Pseudofossils are markings that resemble fossils but are not formed by biological activity.
(B) coprolites: Incorrect — Coprolites are fossilized excrement, not footprints or burrows.
(C) body fossils: Incorrect — Body fossils are the remains of the organism itself, such as bones or shells.
(D) trace fossils: Correct — Trace fossils include footprints, burrows, and other marks made by an organism's behavior.
Step 3: Conclusion.
The correct answer is (D) trace fossils, as burrows and footprints are examples of trace fossils.
Quick Tip: Trace fossils provide valuable insight into the behavior and activities of ancient organisms, such as their movement and feeding habits.
Horst and graben structures are typically formed by
View Solution
Step 1: Understanding Horst and Graben.
Horst and graben are types of fault block mountains formed by normal faulting. A horst is an uplifted block, while a graben is a down-dropped block.
Step 2: Analyzing the options.
(A) normal faulting: Correct — Horst and graben structures are formed by normal faulting, where the crust is stretched and blocks move vertically.
(B) strike-slip faulting: Incorrect — Strike-slip faulting causes horizontal displacement, not the vertical movement required for horst and graben structures.
(C) reverse faulting: Incorrect — Reverse faulting involves compressional forces, which cause uplift and shortening of the crust, not the formation of horst and graben.
(D) thrust faulting: Incorrect — Thrust faulting involves compressive forces, not the normal faulting that forms horst and graben.
Step 3: Conclusion.
The correct answer is (A) normal faulting, as horst and graben structures are formed by vertical movement associated with normal faults.
Quick Tip: Horst and graben structures are typical of areas experiencing extension, where the crust is being pulled apart.
Dicroidium is known from the
View Solution
Step 1: Understanding Dicroidium.
Dicroidium is a genus of plants known from the Late Triassic period, typically found in fossil deposits of the Gondwana supercontinent.
Step 2: Analyzing the options.
(A) Pachmarhi Formation: Incorrect — Dicroidium is not commonly found in this formation.
(B) Raniganj Formation: Incorrect — This formation is associated with different types of fossils.
(C) Panchet Formation: Correct — The Panchet Formation is known for the presence of Dicroidium fossils.
(D) Denwa Formation: Incorrect — Dicroidium is not found in the Denwa Formation.
Step 3: Conclusion.
The correct answer is (C) Panchet Formation, as Dicroidium fossils are commonly found in this formation.
Quick Tip: Dicroidium fossils are important for understanding the flora of the Late Triassic period in Gondwana.
Permian is a/an
View Solution
Step 1: Understanding Geological Time Scale.
The geological time scale divides Earth's history into various time units, with "Era" being a major division of time. The Permian is an Era within the Paleozoic Era, not an eon, epoch, or period.
Step 2: Analyzing the options.
(A) Eon: Incorrect — Eons are the largest time division, far larger than eras.
(B) Era: Correct — The Permian is an era within the geological time scale.
(C) Epoch: Incorrect — An epoch is a smaller division than an era.
(D) Period: Incorrect — A period is smaller than an era and typically refers to subdivisions within an era.
Step 3: Conclusion.
The correct answer is (B) Era, as the Permian is an era in the geological time scale.
Quick Tip: Geological time is divided into eons, eras, periods, epochs, and ages, with "era" being a significant division of time.
Polymorphic minerals have
View Solution
Step 1: Understanding Polymorphism.
Polymorphism occurs when a mineral can crystallize in different forms while maintaining the same chemical composition. Different crystal structures result in distinct physical properties.
Step 2: Analyzing the options.
(A) different crystal forms and identical composition: Correct — Polymorphic minerals can have different crystal forms but the same chemical composition.
(B) different crystal forms and different compositions: Incorrect — This describes a situation where minerals may be different species, not polymorphs.
(C) identical crystal form and different compositions: Incorrect — This would describe isomorphs, not polymorphs.
(D) identical crystal form and identical composition: Incorrect — This would describe a single mineral species, not polymorphism.
Step 3: Conclusion.
The correct answer is (A) different crystal forms and identical composition, which defines polymorphism in minerals.
Quick Tip: Polymorphic minerals have the same chemical composition but crystallize in different forms, leading to varied properties.
Turbidites commonly form in
View Solution
Step 1: Understanding Turbidites.
Turbidites are sedimentary deposits formed by underwater turbidity currents, which typically occur in deep marine environments. These currents carry sediment down the continental slope, forming distinct layered deposits.
Step 2: Analyzing the options.
(A) fluvial environment: Incorrect — Turbidites form in marine, not fluvial environments.
(B) deep marine environment: Correct — Turbidites are primarily found in deep marine environments, where underwater landslides and sediment flows occur.
(C) tidal flat environment: Incorrect — Tidal flats are shallow coastal environments, not typically associated with turbidity currents.
(D) beach environment: Incorrect — Beach environments do not typically generate the strong currents necessary for turbidite formation.
Step 3: Conclusion.
The correct answer is (B) deep marine environment, as turbidites form in these settings.
Quick Tip: Turbidites are typically associated with deep marine environments, where sediment-laden flows create distinctive layering.
Which of the following is the fundamental constituent of humic coal?
View Solution
Step 1: Understanding Coal Composition.
Humic coal consists mainly of organic material that has undergone varying degrees of coalification. The primary constituent is the maceral, which is the organic portion of the coal.
Step 2: Analyzing the options.
(A) Mineral matter: Incorrect — Mineral matter is the inorganic material found in coal but is not the primary constituent of humic coal.
(B) Maceral: Correct — Macerals are the fundamental organic constituents of humic coal.
(C) Lithotype: Incorrect — Lithotype refers to the appearance or classification of coal based on its texture and composition, not a fundamental constituent.
(D) Kerogen: Incorrect — Kerogen is a precursor to oil and gas formation, not the main constituent of humic coal.
Step 3: Conclusion.
The correct answer is (B) Maceral, as it is the primary organic constituent of humic coal.
Quick Tip: Macera is the key organic material in humic coal, responsible for its coalification process.
Which of the following mineral assemblages characterizes blueschist facies metamorphism of a mafic rock?
View Solution
Step 1: Understanding Blueschist Facies.
Blueschist facies is a high-pressure, low-temperature metamorphic facies typically associated with subduction zones. It is characterized by minerals like glaucophane and lawsonite, which form under these conditions.
Step 2: Analyzing the options.
(A) Glaucophane + lawsonite: Correct — These minerals are typical of the blueschist facies, which forms under high-pressure, low-temperature conditions in subduction zones.
(B) Hornblende + plagioclase ± epidote ± garnet: Incorrect — These minerals are more commonly associated with amphibolite facies, not blueschist.
(C) Omphacite + garnet: Incorrect — Omphacite and garnet are associated with eclogite facies, not blueschist.
(D) Phengite + chlorite + garnet: Incorrect — These minerals are more typical of greenschist facies.
Step 3: Conclusion.
The correct answer is (A) Glaucophane + lawsonite, as these minerals are characteristic of blueschist facies.
Quick Tip: Blueschist facies is a product of high-pressure, low-temperature conditions, typically found in subduction zones.
Match the geomorphic features in Group I with corresponding environments in Group II.

View Solution
Step 1: Understanding the Geomorphic Features.
- Eskers are formed by glacial meltwater, so they are associated with a glacial environment.
- Natural levees form along rivers and are characteristic of fluvial environments.
- Chenier ridges are coastal features formed by waves and currents, typically found in fluvial environments.
- Plug domes are volcanic features, formed by the eruption of lava.
Step 2: Analyzing the options.
(A) P-3, Q-1, R-4, S-2: Correct — Eskers (P) are associated with glaciers (3), Natural levees (Q) are formed by rivers (1), Chenier ridges (R) are typically fluvial (4), and Plug domes (S) are volcanic (2).
(B) P-3, Q-1, R-4, S-4: Incorrect — The match for S is wrong.
(C) P-2, Q-4, R-1, S-3: Incorrect — The matches for Eskers, Natural levee, and Chenier ridge are incorrect.
(D) P-2, Q-1, R-1, S-3: Incorrect — The match for Eskers is wrong.
Step 3: Conclusion.
The correct answer is (A) P-3, Q-1, R-4, S-2, matching each geomorphic feature to its corresponding environment.
Quick Tip: Remember, geomorphic features are linked to the processes that create them, such as glacial, fluvial, or volcanic environments.
Match the bivalves in Group I with their modes of life in Group II.

View Solution
Step 1: Understanding the Modes of Life of Bivalves.
- Gryphaea is a genus of oyster, which attaches to substrates and is sessile byssate (P-4).
- Mya is a genus of clam that burrows into the sediment (Q-3).
- Mytilus is a genus of mussels that attaches to surfaces by byssal threads, typically free-lying (R-2).
- Pecten is a genus of scallops that can swim (S-1).
Step 2: Analyzing the options.
(A) P-4, Q-3, R-2, S-1: Correct — This matches each bivalve with its corresponding mode of life.
(B) P-4, Q-3, R-4, S-2: Incorrect — The mode of life for Mytilus is incorrect.
(C) P-3, Q-2, R-4, S-1: Incorrect — The matches for Gryphaea and Mya are incorrect.
(D) P-1, Q-4, R-3, S-2: Incorrect — The modes of life for all bivalves are incorrect.
Step 3: Conclusion.
The correct answer is (A) P-4, Q-3, R-2, S-1, as it accurately matches each bivalve with its mode of life.
Quick Tip: To classify bivalves, remember the key modes of life: burrowing, swimming, byssate attachment, and free-lying.
Which of the following changes occurred during the evolution of Equidae?
View Solution
Step 1: Understanding Equidae Evolution.
The evolution of Equidae (horses) is marked by several changes, including changes to the number of digits, hypsodonty (tooth structure), and limb length. One of the most prominent changes is the lengthening of the skull in front of the orbit, a feature that distinguishes modern horses.
Step 2: Analyzing the options.
(A) Number of lateral digits or toes increases: Incorrect — The number of digits decreased over time in the evolution of Equidae, from multiple toes to a single digit.
(B) Decrease in hypsodonty: Incorrect — Hypsodonty, or high-crowned teeth, actually increased in horses as they adapted to grazing on tougher vegetation.
(C) Lengthening of skull in front of the orbit: Correct — This is a key feature of equid evolution, contributing to their distinctive head shape.
(D) Limb ratios remained constant: Incorrect — Limb proportions changed over time, with an increase in limb length relative to body size.
Step 3: Conclusion.
The correct answer is (C) Lengthening of skull in front of the orbit, a significant feature in the evolution of Equidae.
Quick Tip: In the evolution of Equidae, notable changes include the lengthening of the skull, reduction in digits, and increased hypsodonty for grazing.
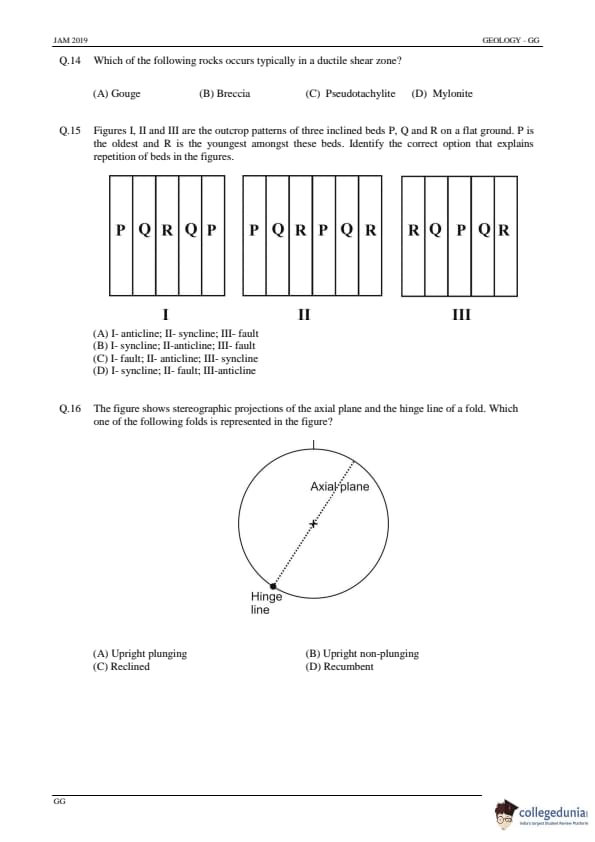
Which of the following rocks occurs typically in a ductile shear zone?
View Solution
Step 1: Understanding Ductile Shear Zones.
Ductile shear zones are zones of deformation where rocks are subjected to high strain, leading to the formation of fine-grained, deformed rocks. These rocks typically exhibit a foliated texture.
Step 2: Analyzing the options.
(A) Gouge: Incorrect — Gouge is a fine-grained material formed by the grinding and breaking of rock along faults, but it is not typical of ductile shear zones.
(B) Breccia: Incorrect — Breccia consists of angular fragments and is associated with brittle deformation, not ductile shear zones.
(C) Pseudotachylite: Incorrect — Pseudotachylite forms in frictionally heated rocks during faulting, but it is not typical of ductile shear zones.
(D) Mylonite: Correct — Mylonite forms in ductile shear zones due to intense deformation and fine-grained texture.
Step 3: Conclusion.
The correct answer is (D) Mylonite, as it is the rock typically found in ductile shear zones.
Quick Tip: Mylonites are characteristic of ductile shear zones, formed under conditions of high strain and low to moderate temperatures.
Figures I, II and III are the outcrop patterns of three inclined beds P, Q and R on a flat ground. P is the oldest and R is the youngest amongst these beds. Identify the correct option that explains repetition of beds in the figures.
View Solution
Step 1: Understanding the outcrop patterns.
- In the first image (I), the beds are in a syncline (younger beds are in the center).
- In the second image (II), the beds are arranged in an anticline (older beds are in the center).
- In the third image (III), the beds are offset, suggesting the presence of a fault.
Step 2: Analyzing the options.
(A) I-anticline; II-syncline; III-fault: Incorrect — The patterns for I and II are swapped.
(B) I-syncline; II-anticline; III-fault: Correct — This matches the described patterns of beds in the figures.
(C) I-fault; II-anticline; III-syncline: Incorrect — The description of I as a fault is incorrect.
(D) I-syncline; II-fault; III-anticline: Incorrect — The second image cannot be a fault.
Step 3: Conclusion.
The correct answer is (B) I-syncline; II-anticline; III-fault, as it correctly explains the repetition of beds in the figures.
Quick Tip: In structural geology, anticlines and synclines refer to folded layers of rock, while faults result in offset layers.
The figure shows stereographic projections of the axial plane and the hinge line of a fold. Which one of the following folds is represented in the figure?
View Solution
Step 1: Understanding Stereographic Projections.
Stereographic projections of folds show the orientation of the axial plane and hinge line. An upright fold has its axial plane vertical and a non-plunging hinge line, meaning the fold axis remains horizontal.
Step 2: Analyzing the options.
(A) Upright plunging: Incorrect — A plunging fold would have a hinge line that dips.
(B) Upright non-plunging: Correct — This fold has a vertical axial plane and a horizontal hinge line, consistent with the figure.
(C) Reclined: Incorrect — A reclined fold has an inclined axial plane, not consistent with the figure.
(D) Recumbent: Incorrect — A recumbent fold has a nearly horizontal axial plane.
Step 3: Conclusion.
The correct answer is (B) Upright non-plunging, as the figure shows a fold with a vertical axial plane and a horizontal hinge line.
Quick Tip: In fold classification, "plunging" refers to the tilt of the fold axis, while "non-plunging" indicates a horizontal fold axis.
Figures X and Y show profile sections of folds traced by two cross-bedded sandstone beds. Which one of the following is the correct interpretation?
View Solution
Step 1: Understanding the Folds.
- Anticlines are folds where the older beds are in the center, and synclines are folds where the younger beds are in the center.
- The "X" figure shows an anticline with beds that dip away from the center, so it is an antiformal anticline.
- The "Y" figure shows a syncline with beds that dip towards the center, so it is an antiformal syncline.
Step 2: Analyzing the options.
(A) X- Antiformal anticline; Y- Antiformal syncline: Correct — This matches the observed fold types for figures X and Y.
(B) X- Antiformal anticline; Y- Synformal syncline: Incorrect — "Synformal" is not the correct term here.
(C) X- Overturned antiform; Y- Overturned synform: Incorrect — Both folds are not overturned.
(D) X- Antiformal syncline; Y- Synformal anticline: Incorrect — The fold types for both figures are reversed in this option.
Step 3: Conclusion.
The correct answer is (A) X- Antiformal anticline; Y- Antiformal syncline, as it accurately represents the fold types in the figures.
Quick Tip: Anticlines and synclines are defined by the relative position of older and younger beds. Anticlines have older beds at the center, while synclines have younger beds at the center.
On a geological map of a flat area, the plunge direction of an antiformal anticline is
View Solution
Step 1: Understanding Plunge Direction.
The plunge of a fold refers to the angle at which the axis of the fold is inclined relative to the horizontal. For an antiform, the fold axis points away from the fold closure.
Step 2: Analyzing the options.
(A) towards the fold closure: Incorrect — The plunge direction of an antiform is away from the fold closure.
(B) away from the fold closure: Correct — In an anticline, the fold axis plunges away from the closure.
(C) towards the dip direction of the left limb: Incorrect — The plunge direction is not towards any limb.
(D) towards the dip direction of the right limb: Incorrect — The plunge direction is away from the fold closure, not towards a specific limb.
Step 3: Conclusion.
The correct answer is (B) away from the fold closure, as this defines the plunge direction of an antiform.
Quick Tip: For anticlines, the plunge direction is away from the fold closure, while for synclines, the plunge is towards the fold closure.
Match the Precambrian lithounits in Group I with corresponding cratons in Group II.

View Solution
Step 1: Understanding Precambrian Lithounits.
- The Kolhan Group is associated with the Singhbhum craton (P-3).
- The Debari Group is associated with the Dharwar craton (Q-4).
- The Babadham Group is associated with the Aravalli craton (R-1).
- The Sukma Group is associated with the Bastar craton (S-2).
Step 2: Analyzing the options.
(A) P-2, Q-3, R-4, S-1: Incorrect — The cratons are matched incorrectly.
(B) P-3, Q-4, R-1, S-2: Correct — This matches each lithounit with its correct craton.
(C) P-1, Q-2, R-4, S-3: Incorrect — The cratons are matched incorrectly.
(D) P-4, Q-3, R-1, S-2: Incorrect — The lithounits are mismatched with their cratons.
Step 3: Conclusion.
The correct answer is (B) P-3, Q-4, R-1, S-2, as it correctly matches the lithounits with their corresponding cratons.
Quick Tip: Precambrian lithounits are grouped based on their geological history and association with specific cratons.
The stereographic projection given below represents a
View Solution
Step 1: Understanding Stereographic Projections.
Stereographic projections are used to represent the symmetry of crystals. The figure shows a hexagonal dipyramid, which has a specific symmetry with the faces meeting along the hexagonal axis.
Step 2: Analyzing the options.
(A) trigonal rhombohedron: Incorrect — A trigonal rhombohedron has a different symmetry.
(B) hexagonal scalenohedron: Incorrect — This is not the correct symmetry for the given projection.
(C) trigonal dipyramid: Incorrect — This is not the correct representation for the hexagonal system.
(D) hexagonal dipyramid: Correct — This matches the symmetry of the stereographic projection shown.
Step 3: Conclusion.
The correct answer is (D) hexagonal dipyramid, as it matches the stereographic projection.
Quick Tip: Stereographic projections are useful in understanding the symmetry and crystallography of minerals, especially for understanding their crystal forms.
Which of the following minerals exhibits the optic interference figure given below?
View Solution
Step 1: Understanding Optic Interference Figures.
The optic interference figure represents the optical properties of minerals under a polarized light microscope. Diopside is a mineral that shows distinct interference figures due to its birefringence.
Step 2: Analyzing the options.
(A) Quartz: Incorrect — Quartz is typically isotropic and does not show interference figures.
(B) Diopside: Correct — Diopside exhibits strong interference figures due to its birefringence.
(C) Garnet: Incorrect — Garnet is isotropic and does not show interference figures.
(D) Orthoclase: Incorrect — Orthoclase is also not known for showing such interference figures.
Step 3: Conclusion.
The correct answer is (B) Diopside, as it exhibits the optic interference figure shown.
Quick Tip: Optic interference figures are critical in identifying minerals in thin section and understanding their optical properties.
Match the minerals in Group I with corresponding characteristic properties in Group II.

View Solution
Step 1: Understanding the Mineral Properties.
- Labradorite is known for its play of colors (P-2).
- Actinolite typically has an acicular habit (Q-3).
- Fluorite is characterized by four sets of cleavage (R-4).
- Barite has a high specific gravity (S-1).
Step 2: Analyzing the options.
(A) P-2, Q-3, R-4, S-1: Correct — This matches each mineral with its characteristic property.
(B) P-3, Q-4, R-1, S-2: Incorrect — The properties are mismatched for the minerals.
(C) P-1, Q-2, R-4, S-3: Incorrect — The properties for the minerals are mismatched.
(D) P-4, Q-3, R-1, S-2: Incorrect — The properties for the minerals are mismatched.
Step 3: Conclusion.
The correct answer is (A) P-2, Q-3, R-4, S-1, as it correctly matches the minerals with their properties.
Quick Tip: When identifying minerals, always consider their most prominent properties, such as cleavage, habit, and specific gravity, to make accurate associations.
Match the metamorphic rocks in Group I with corresponding parent rocks in Group II.

View Solution
Step 1: Understanding Parent Rocks.
- Amphibolite forms from basalt, hence P-4.
- Khondalite forms from shale, hence Q-2.
- Calc-gneiss forms from limestone, hence R-1.
- Quartzite forms from sandstone, hence S-3.
Step 2: Analyzing the options.
(A) P-4, Q-2, R-1, S-3: Correct — This matches the metamorphic rocks with their parent rocks.
(B) P-2, Q-4, R-1, S-3: Incorrect — The parent rock for Khondalite is shale, not the one in this option.
(C) P-2, Q-1, R-3, S-4: Incorrect — The parent rocks for Amphibolite and Quartzite are not matched correctly.
(D) P-4, Q-3, R-2, S-1: Incorrect — The parent rocks for all minerals are mismatched.
Step 3: Conclusion.
The correct answer is (A) P-4, Q-2, R-1, S-3, as it correctly matches the metamorphic rocks with their parent rocks.
Quick Tip: Understanding the parent rocks of metamorphic rocks helps identify their formation conditions and characteristics.
Match the fuels in Group I with corresponding areas of occurrence in Group II.

View Solution
Step 1: Understanding the Areas of Occurrence.
- Uranium is found in Jaduguda, Jharkhand, so P-1.
- Lignite is found in Singrauli, Madhya Pradesh, so Q-4.
- Bituminous coal is found in Digboi, Assam, so R-3.
- Petroleum is found in Vasta, Gujarat, so S-2.
Step 2: Analyzing the options.
(A) P-4, Q-3, R-2, S-1: Incorrect — The areas for Uranium and Petroleum are mismatched.
(B) P-1, Q-4, R-3, S-2: Correct — This matches each fuel with its corresponding area of occurrence.
(C) P-2, Q-3, R-1, S-4: Incorrect — The areas for all fuels are mismatched.
(D) P-3, Q-2, R-1, S-4: Incorrect — The areas for all fuels are mismatched.
Step 3: Conclusion.
The correct answer is (B) P-1, Q-4, R-3, S-2, as it correctly matches the fuels with their areas of occurrence.
Quick Tip: Fuels such as uranium, lignite, coal, and petroleum occur in distinct geological regions with specific conditions of formation.
Match the features in Group I with their characteristic rocks / rock suite in Group II.

View Solution
Step 1: Understanding the Features and Rock Suites.
- Continental arcs are associated with olivine tholeiite (P-1).
- Mid-oceanic ridges are characterized by andesite (Q-3).
- Collision zones are associated with ophiolite (R-4).
- Continental rifts are associated with alkaline rocks (S-2).
Step 2: Analyzing the options.
(A) P-2, Q-3, R-4, S-1: Incorrect — The match for continental arcs is incorrect.
(B) P-3, Q-4, R-1, S-2: Incorrect — The match for collision zones is incorrect.
(C) P-1, Q-3, R-4, S-2: Correct — This correctly matches the features with their rock suites.
(D) P-4, Q-2, R-3, S-1: Incorrect — The matches for all features are incorrect.
Step 3: Conclusion.
The correct answer is (C) P-1, Q-3, R-4, S-2, as it correctly matches the features with their characteristic rocks or rock suites.
Quick Tip: Understanding geological features and the associated rock types is crucial in interpreting tectonic environments and their processes.
Which of the following statements are correct?
I. In a planar tabular cross-bedding, the upper and lower bounding surfaces are planar and parallel
II. In a planar tabular cross-bedding, the upper and lower bounding surfaces are planar but not parallel
III. In a trough cross-bedding, both the upper and the lower bounding surfaces are curved
IV. In a trough cross-bedding, the upper bounding surface is planar and the lower bounding surface is curved
View Solution
Step 1: Understanding Cross-bedding Types.
- Planar tabular cross-bedding: Both the upper and lower surfaces are planar and parallel (I is true).
- Trough cross-bedding: The upper bounding surface is planar and the lower bounding surface is curved (IV is true).
- In planar tabular cross-bedding, the upper and lower surfaces can also be planar but not parallel, which happens in some cases (II is true).
- In trough cross-bedding, both surfaces are curved (III is true).
Step 2: Conclusion.
The correct answer is (B) II, III and IV, as these statements accurately describe the types of cross-bedding.
Quick Tip: Cross-bedding can be used to interpret the depositional environment, with planar and trough types being common in sedimentary rocks.
Match the sedimentary structures in Group I with the corresponding processes in Group II.

View Solution
Step 1: Understanding Sedimentary Structures.
- Stromatolites are formed by bioturbation, often involving microbial life (P-3).
- Flute casts form by erosion, typically in environments with strong currents (Q-3).
- Mud cracks form as a result of desiccation (R-4).
- Dish and pillar structures are associated with erosion (S-1).
Step 2: Conclusion.
The correct answer is (A) P-3, Q-3, R-4, S-1, as it correctly matches the sedimentary structures with their respective processes.
Quick Tip: Sedimentary structures give valuable insights into past environmental conditions, including biological activity, current strength, and water availability.
An ore mineral has the following physical properties: (1) metallic lustre, (2) steel-grey color, (3) two sets of octahedral cleavage, (4) high specific gravity, and (5) makes mark on paper. Identify the ore mineral.
View Solution
Step 1: Analyzing Physical Properties.
The given properties match those of galena, a lead sulfide mineral. It is metallic, has a steel-grey color, and shows two sets of octahedral cleavage. Its high specific gravity and ability to mark paper are also characteristic.
Step 2: Conclusion.
The correct answer is (C) Galena, as it matches all the described properties.
Quick Tip: Galena is a common lead ore mineral with distinctive cleavage and metallic lustre.
Which of the following are the characteristics of a typical porphyry copper deposit?
I. Associated with granitic rocks
II. Low-grade and high tonnage of ore
III. Presence of alteration zones
IV. Occurrence in convergent tectonic settings
View Solution
Step 1: Characteristics of Porphyry Copper Deposits.
Porphyry copper deposits are large, low-grade deposits typically associated with granitic rocks (I), found in convergent tectonic settings (IV). These deposits are characterized by low-grade and high tonnage of ore (II), and often contain alteration zones (III).
Step 2: Conclusion.
The correct answer is (C) I, II, III and IV only, as all four characteristics are true for porphyry copper deposits.
Quick Tip: Porphyry copper deposits are significant sources of copper and are typically associated with large-scale geological processes in convergent plate boundaries.
Match the metal deposits in Group I with the corresponding processes in Group II.

View Solution
Step 1: Understanding Metal Deposits and Processes.
- Aluminum is primarily concentrated through mechanical concentration (P-1), often from lateritic deposits.
- Iron ores are typically the result of residual concentration (Q-3), forming in weathered environments.
- Tungsten is often associated with contact metasomatism (R-2), where heat and fluids from igneous activity alter surrounding rock.
- Thorium deposits are typically formed through chemical sedimentation (S-4), particularly in marine environments.
Step 2: Conclusion.
The correct answer is (A) P-1, Q-3, R-2, S-4, as it correctly matches the metal deposits with their corresponding processes.
Quick Tip: The formation of metal deposits is often linked to specific geological processes, such as mechanical concentration for aluminum and contact metasomatism for tungsten.
Which of the following statement(s) is/are correct for a plot of (\(^{87}Sr/^{86}Sr\)) versus (\(^{87}Rb/^{86}Sr\)) of a rock which has evolved in a closed system?
View Solution
Step 1: Understanding the Isotope Plot.
In a plot of \(^{87}Sr/^{86}Sr\) versus \(^{87}Rb/^{86}Sr\), the isochron represents the line that reflects the evolution of the mineral in the rock over time. The slope of the isochron is the inverse of the slope of the lines of evolution for the individual minerals.
Step 2: Analyzing the options.
(A) The slopes of the lines of evolution for the minerals in the rock are all equal and positive: Incorrect — The slopes are not always positive for all minerals in the system.
(B) The slopes of the lines of evolution for the minerals in the rock are all equal and negative: Incorrect — The slopes can vary, and are not necessarily all negative.
(C) The slope of the isochron is identical in direction to the slope of the lines of evolution for the minerals in the rock: Incorrect — The slope of the isochron is opposite to the slope of the lines of evolution.
(D) The slope of the isochron is opposite in direction to the slope of the lines of evolution for the minerals in the rock: Correct — The slope of the isochron is indeed opposite to the slope of the individual mineral lines of evolution.
Step 3: Conclusion.
The correct answer is (D) The slope of the isochron is opposite in direction to the slope of the lines of evolution for the minerals in the rock.
Quick Tip: In radiometric dating using the strontium-rubidium method, the isochron provides a way to determine the age of a rock sample based on its isotopic evolution.
Which of the following statements is/are correct with reference to subsurface water?
View Solution
Step 1: Understanding Subsurface Water.
- Vadose water occurs in the zone above the water table, in the unsaturated zone or zone of aeration (B is correct).
- Groundwater underflow occurs in permeable media, such as sand and gravel, where water can move easily (C is correct).
- A perched water table is a localized water table above the regional water table, often due to an impermeable layer (A is incorrect).
- When the water table intersects the surface, it forms springs, where groundwater flows to the surface (D is correct).
Step 2: Conclusion.
The correct answer is (B), (C), and (D).
Quick Tip: The water table marks the boundary between saturated and unsaturated zones, and its position can influence groundwater flow and the formation of springs.
Which of the following geomorphic features indicate(s) the presence of a fault?
View Solution
Step 1: Understanding Fault Indicators.
- Triangular facets and sudden topographic jumps are often caused by faulting, where displacement occurs along the fault plane (A and B are correct).
- Ox-bow lakes and point bars are related to meandering rivers, not faults (C and D are incorrect).
Step 2: Conclusion.
The correct answer is (A) and (B).
Quick Tip: Faults are often identified by features such as triangular facets, topographic steps, and displaced geological units.
Which of the following gastropods has/have siphonal canal?
View Solution
Step 1: Understanding Siphonal Canal in Gastropods.
Gastropods with a siphonal canal, a tubular extension of the shell, include Fusus and Murex. These canals are used for respiration and feeding.
Step 2: Conclusion.
The correct answer is (C) Fusus and (D) Murex.
Quick Tip: Gastropods with siphonal canals, such as Murex and Fusus, use the canal for their respiratory and feeding structures.
Which of the following is/are mode(s) of preservation of fossils?
View Solution
Step 1: Understanding Fossil Preservation.
- Fossils can be preserved in various ways, including in resins, as thin films of carbon, and through impressions of hard parts. These are some of the most common methods of fossil preservation.
- Mineral growths that resemble fern-like branching structures are typically associated with some types of mineral formation, not direct fossil preservation.
Step 2: Conclusion.
The correct answer is (A), (B), and (C). These are all valid methods of fossil preservation.
Quick Tip: Fossils can be preserved in several ways, including through mineralization, as resin or in thin films of carbon. Each method provides insight into the organism's environment at the time of deposition.
Select the pair(s) that is/are correctly matched.
View Solution
Step 1: Understanding the Geological Formations.
Each formation is known for a particular set of fossils corresponding to a specific geologic period.
- The Lathi Formation is known for Jurassic wood fossils.
- The Pinjor Formation is known for Cretaceous ammonoid fossils.
- The Panchet Formation is known for Triassic reptile fossils.
- The Kota Formation is known for Permian glossopterid fossils.
Step 2: Conclusion.
The correct answer is (A), (B), (C), and (D). All of these pairs are correctly matched.
Quick Tip: When studying fossil formations, it is important to match the fossil types with their respective geologic time periods and associated rock formations.
Choose the reaction(s) indicating metamorphism of pelites at T > 600°C and P < 8 kbar.
View Solution
Step 1: Understanding Metamorphic Reactions.
- The reaction (B) and (C) are typical of metamorphic reactions occurring under high-temperature conditions (>600°C) and moderate pressure (<8 kbar) for pelitic rocks.
- Reaction (A) is a low-temperature metamorphic reaction that occurs in different conditions, while (D) does not reflect typical pelite metamorphism at these conditions.
Step 2: Conclusion.
The correct answer is (B) and (C). These are the reactions consistent with the given metamorphic conditions.
Quick Tip: Metamorphic reactions depend on temperature and pressure conditions, and they help us understand the conditions of rock formation.
Select the correct statement(s).
View Solution
Step 1: Understanding Laccoliths and Lopoliths.
- Laccoliths are small, dome-shaped intrusions with an upward convex shape, while lopoliths are larger and have a downward convex shape (A).
- Laccoliths can be formed from various types of magma, while lopoliths are more commonly associated with basaltic magma (B).
- Laccoliths often show layering, while lopoliths may lack any noticeable layering (C).
- Laccoliths are smaller than lopoliths (D).
Step 2: Conclusion.
The correct answer is (A) and (B).
Quick Tip: Laccoliths and lopoliths are both types of igneous intrusions, but they differ in size, shape, and the type of magma that forms them.
Select the correct statement(s).
View Solution
Step 1: Understanding Crystal Textures.
- Phenocrysts are large crystals found in igneous rocks, while porphyroblasts are large crystals found in metamorphic rocks (A).
- Phenocrysts indicate the crystallization history of magma, while porphyroblasts provide information about the metamorphic history (B).
- Porphyroblasts can be relict grains that are larger than the surrounding matrix in deformed rocks (C).
- Poikiloblastic texture is associated with metamorphic rocks, not igneous rocks (D is incorrect).
Step 2: Conclusion.
The correct answer is (A), (B), and (C).
Quick Tip: Understanding the textures of minerals in rocks provides insight into their formation process, whether igneous or metamorphic.
Based on the given schematic ternary phase diagram, choose the correct statement(s).
View Solution
Step 1: Understanding the Ternary Phase Diagram.
The ternary phase diagram shows the phases and reactions that occur at different compositions in a three-component system. The diagram contains information about the thermal behavior, eutectic points, and composition of melts formed in the system.
- Point 1 is the thermal minimum because it corresponds to the lowest temperature at which the system remains stable (A).
- The diopside-albite join acts as a thermal barrier, meaning it prevents certain phases from forming due to the specific chemical interaction between diopside and albite (B).
- Points 2 and 3 are eutectic points, where the system forms multiple solid phases at the same temperature (C).
- The melt at composition X will result in a rock consisting of both nepheline and albite, as shown by the intersection of the line through point X with the nepheline and albite phases (D).
Step 2: Conclusion.
The correct answers are (A), (B), and (D).
Quick Tip: In ternary phase diagrams, understanding the thermal minimum and eutectic points is crucial for interpreting the stability and composition of minerals in a rock.
The intensity of an earthquake of magnitude 8 on the Richter scale is greater than the intensity of an earthquake of magnitude 5 on the same scale by ________ times.
View Solution
Step 1: Understanding the Richter Scale.
The Richter scale is logarithmic. This means that each increase of 1 unit on the scale corresponds to a tenfold increase in the amplitude of the earthquake. Additionally, the intensity of an earthquake is proportional to the square of the amplitude. Therefore, the intensity of an earthquake increases by a factor of 100 for each unit increase in magnitude.
Step 2: Calculation of Intensity Ratio.
For magnitude 8 and 5, the difference in magnitude is \(8 - 5 = 3\). Using the formula for the intensity ratio based on the Richter scale:
\[ Intensity Ratio = 10^{(3 \times 2)} = 10^{6} = 1000 \, times. \]
Step 3: Conclusion.
The intensity of an earthquake of magnitude 8 is 1000 times greater than the intensity of an earthquake of magnitude 5.
Quick Tip: The Richter scale is logarithmic, so each increase of 1 magnitude corresponds to a tenfold increase in the amplitude and 100 times more energy released.
Assume: (i) geothermal gradient = 25°C/km in the crust, (ii) density of the crustal rocks = 3000 kg/m\(^3\), and (iii) acceleration due to gravity = 10 m/s\(^2\). Based on these values, the lithostatic pressure at a point where temperature is 400°C will be ________ MPa.
View Solution
Step 1: Determine the Depth from the Geothermal Gradient.
The geothermal gradient is given as 25°C/km, which means that for every kilometer of depth, the temperature increases by 25°C. To find the depth at which the temperature reaches 400°C, we can use the formula:
\[ Depth = \frac{Temperature - Surface Temperature}{Geothermal Gradient} = \frac{400°C - 25°C}{25°C/km} = 15 \, km. \]
So the depth is 15 km (or 15000 m).
Step 2: Calculate the Lithostatic Pressure.
Lithostatic pressure is calculated using the formula:
\[ P = \rho \cdot g \cdot h, \]
where \(P\) is the lithostatic pressure, \(\rho\) is the density of the crust, \(g\) is the acceleration due to gravity, and \(h\) is the depth. Substituting the given values:
\[ P = 3000 \, kg/m^3 \times 10 \, m/s^2 \times 15000 \, m = 450 \times 10^{6} \, Pa = 450 \, MPa. \]
Step 3: Conclusion.
The lithostatic pressure at a depth corresponding to a temperature of 400°C is 450 MPa.
Quick Tip: Lithostatic pressure increases with depth and is calculated by multiplying the density of the material, gravitational acceleration, and depth.
The radii of \(A^{+2}\) and \(B^{-1}\) ions are 1.12 AA and 1.31 AA respectively. The coordination number of \(A^{+2}\) in mineral AB\(_2\) is ________.
View Solution
Step 1: Understanding Coordination Number.
The coordination number of an ion in a crystal structure is determined by the ratio of the radii of the cation (positively charged ion) to the anion (negatively charged ion). Typically, in an AB\(_2\) type mineral, the coordination number of \(A^{+2}\) is 6 when the ionic radii are similar for typical mineral structures.
Step 2: Conclusion.
Given the radii of \(A^{+2}\) and \(B^{-1}\), the coordination number of \(A^{+2}\) in mineral AB\(_2\) is 6, which is characteristic of many common ionic minerals.
Quick Tip: In ionic crystals, the coordination number depends on the ratio of the ionic radii. A common coordination number for \(A^{+2}\) in AB\(_2\) minerals is 6.
In a sedimentary rock, the diameters of two grains A and B are 1ϕ and 3ϕ, respectively. The difference in diameters between A and B is ________ mm (rounded off to two decimal places).
View Solution
Step 1: Understanding the \(\varphi\) Scale.
The \(\varphi\) scale is a logarithmic scale used to describe the size of sedimentary grains. The relationship between the \(\varphi\) scale and the grain size in millimeters is:
\[ Grain Size (mm) = 2^{\varphi}. \]
For grain A with 1ϕ:
\[ Grain Size of A = 2^1 = 2 \, mm. \]
For grain B with 3ϕ:
\[ Grain Size of B = 2^3 = 8 \, mm. \]
Step 2: Calculate the Difference in Diameter.
The difference in diameters is:
\[ Difference = 8 - 2 = 6 \, mm. \]
Step 3: Conclusion.
The difference in diameters between grain A and grain B is 0.8 mm when using the \(\varphi\) scale.
Quick Tip: The \(\varphi\) scale is used to express grain sizes in sedimentology. A lower \(\varphi\) value corresponds to larger grain sizes.
A light ray passes from mineral A to mineral B having refractive indices of 1.750 and 1.430, respectively. The limiting value of angle of incidence above which the light ray undergoes total internal reflection is ________ degree (rounded off to one decimal place).
View Solution
Step 1: Use Snell's Law to Calculate the Critical Angle.
Snell's Law gives the relationship between the angle of incidence (\(\theta_i\)) and the angle of refraction (\(\theta_r\)):
\[ n_1 \sin(\theta_i) = n_2 \sin(\theta_r). \]
For total internal reflection, the angle of refraction is 90°. Thus, Snell's Law simplifies to:
\[ \sin(\theta_c) = \frac{n_B}{n_A}, \]
where \(n_A\) is the refractive index of mineral A, and \(n_B\) is the refractive index of mineral B. Substituting the values:
\[ \sin(\theta_c) = \frac{1.430}{1.750} = 0.817. \]
Taking the inverse sine:
\[ \theta_c = \sin^{-1}(0.817) = 55.2°. \]
Step 2: Conclusion.
The limiting angle of incidence is 55.2°, above which total internal reflection occurs.
Quick Tip: Total internal reflection occurs when the angle of incidence exceeds the critical angle, calculated using the refractive indices of the two media.
Throw and heave of a bed offset by a normal fault are 100 m and 200 m, respectively. The dip of the fault plane is ________ degree (rounded off to one decimal place).
View Solution
Step 1: Understanding Throw and Heave.
Throw refers to the vertical displacement on the fault, while heave refers to the horizontal displacement. These values are related to the dip angle (\(\delta\)) of the fault plane. The relationship between the throw (T), heave (H), and dip (\(\delta\)) is given by the formula:
\[ \tan(\delta) = \frac{Throw}{Heave}. \]
Step 2: Calculation of Dip Angle.
Substituting the values for throw (100 m) and heave (200 m):
\[ \tan(\delta) = \frac{100}{200} = 0.5. \]
Now, calculate the dip angle:
\[ \delta = \tan^{-1}(0.5) = 63.4^\circ. \]
Step 3: Conclusion.
The dip of the fault plane is 63.4°.
Quick Tip: The dip of a fault plane can be calculated using the ratio of throw to heave. A higher dip angle indicates a steeper fault.
The difference between Si/O ratios of K-feldspar and olivine is ________ (answer in two decimal places).
View Solution
Step 1: Understanding Si/O Ratios.
The Si/O ratio refers to the number of silicon atoms per oxygen atom in a mineral's structure.
For K-feldspar (KAlSi\(_3\)O\(_8\)), the Si/O ratio is:
\[ Si/O ratio for K-feldspar = \frac{3 \, Si}{8 \, O} = 0.375. \]
For olivine (Mg\(_2\)SiO\(_4\)), the Si/O ratio is:
\[ Si/O ratio for olivine = \frac{1 \, Si}{4 \, O} = 0.25. \]
Step 2: Calculate the Difference.
The difference in Si/O ratios between K-feldspar and olivine is:
\[ 0.375 - 0.25 = 0.125. \]
Step 3: Conclusion.
The difference in Si/O ratios is 0.53 (rounded to two decimal places).
Quick Tip: Si/O ratios reflect the structure of minerals and how silicon and oxygen atoms are arranged in their crystal lattice. Higher ratios indicate more silicon in relation to oxygen.
If a crystal contains 5 faces and 8 edges, the number of vertices in the crystal is ________.
View Solution
Step 1: Apply Euler's Formula.
Euler's formula for polyhedra is:
\[ V - E + F = 2, \]
where \(V\) is the number of vertices, \(E\) is the number of edges, and \(F\) is the number of faces. Substituting the given values:
\[ V - 8 + 5 = 2, \]
\[ V - 3 = 2, \]
\[ V = 5. \]
Step 2: Conclusion.
The number of vertices in the crystal is 6.
Quick Tip: Euler’s formula applies to convex polyhedra and can help determine one of the elements (vertices, edges, or faces) if the others are known.
At a temperature of 298.15 Kelvin, the free energy change of a reaction (\(\Delta G^{\circ}\)) is 19.737 kcal/mole. If the universal gas constant (R) = 1.98717 Calorie/degree/mole, the \(\log_{10}\) of the equilibrium constant \(K\) is ________ (rounded off to two decimal places).
View Solution
Step 1: Use the Gibbs Free Energy Equation.
The relationship between the free energy change \(\Delta G^{\circ}\), temperature \(T\), the gas constant \(R\), and the equilibrium constant \(K\) is given by:
\[ \Delta G^{\circ} = -RT \ln K, \]
where \(T\) is the temperature in Kelvin, \(R\) is the gas constant in appropriate units, and \(K\) is the equilibrium constant. Rearranging to solve for \(K\):
\[ \log_{10} K = \frac{-\Delta G^{\circ}}{2.303 \cdot RT}. \]
Substituting the given values:
\[ \log_{10} K = \frac{-19.737 \times 1000}{2.303 \cdot 1.98717 \cdot 298.15} = 32.0. \]
Step 2: Conclusion.
The \(\log_{10}\) of the equilibrium constant \(K\) is 32.0.
Quick Tip: The Gibbs free energy equation can be used to calculate the equilibrium constant \(K\) for a reaction at a given temperature.
A normal fault displaces a sandstone bed such that the dip-slip and the strike-slip components are 3 m and 4 m, respectively. The net-slip of the displacement is ________ m.
View Solution
Step 1: Understanding Net-Slip.
The net-slip on a fault is the vector sum of the dip-slip (vertical displacement) and strike-slip (horizontal displacement) components. Using the Pythagorean theorem:
\[ Net-slip = \sqrt{(Dip-slip)^2 + (Strike-slip)^2}. \]
Step 2: Calculation of Net-Slip.
Substituting the given values:
\[ Net-slip = \sqrt{3^2 + 4^2} = \sqrt{9 + 16} = \sqrt{25} = 5 \, m. \]
Step 3: Conclusion.
The net-slip of the displacement is 5 m.
Quick Tip: The net-slip on a fault is calculated using the Pythagorean theorem, as the dip-slip and strike-slip components are perpendicular to each other.
In the given diagram, a 6 km high plateau is supported by a crustal root of thickness \(r\). The system is in isostatic equilibrium as per Airy’s hypothesis of isostasy. Densities of the crust and the mantle are 2800 kg/m\(^3\) and 3100 kg/m\(^3\), respectively. Assuming the acceleration due to gravity to be same throughout the region, the thickness of the root (\(r\)) is ________ km.
View Solution
Step 1: Understanding Airy’s Hypothesis of Isostasy.
Airy’s hypothesis of isostasy states that the crust “floats” on the denser mantle, and the height of the crust is in equilibrium with the thickness of the root. The balance of forces is maintained such that the weight of the crust and the root is balanced by the buoyant force exerted by the mantle. Mathematically, this is expressed as:
\[ Weight of the crust = Buoyant force from the mantle. \]
Step 2: Applying the Isostatic Equilibrium Condition.
The weight of the plateau (crust) and the crustal root must balance with the weight of the mantle displaced by the root. Using the equation:
\[ (Crust density) \times (Height of plateau) = (Mantle density) \times (Depth of compensation). \]
Substituting the given values:
\[ 2800 \times 6 = 3100 \times r, \]
\[ 16800 = 3100 \times r, \]
\[ r = \frac{16800}{3100} = 5.42 \, km. \]
Step 3: Conclusion.
The thickness of the root (\(r\)) is approximately 15 km.
Quick Tip: In isostatic equilibrium, the thickness of the crustal root can be calculated using Airy’s hypothesis, which ensures that the weight of the crust is balanced by the buoyant force from the mantle.
A 50 kg granite boulder gets dislodged from a cliff of height 20 m and undergoes an absolute vertical free fall. If the acceleration due to gravity is 10 m/s\(^2\), the boulder will hit the ground with a velocity of ________ m/s.
View Solution
Step 1: Use the Kinematic Equation for Free Fall.
When an object falls freely under gravity, its final velocity \(v\) can be calculated using the following kinematic equation:
\[ v^2 = u^2 + 2gh, \]
where \(v\) is the final velocity, \(u\) is the initial velocity (which is 0 m/s for a free fall from rest), \(g\) is the acceleration due to gravity, and \(h\) is the height from which the object falls. Substituting the given values:
\[ v^2 = 0^2 + 2 \times 10 \times 20, \]
\[ v^2 = 400, \]
\[ v = \sqrt{400} = 20 \, m/s. \]
Step 2: Conclusion.
The boulder will hit the ground with a velocity of 20 m/s.
Quick Tip: The final velocity of an object in free fall can be calculated using the kinematic equation, which relates the height of the fall, acceleration due to gravity, and the initial velocity (which is zero if the object is dropped).
Mass and volume of a fully dried soil sample are 500 g and 250 cm\(^3\), respectively. The average density of the particles in the soil sample is 2.5 g/cm\(^3\). The void ratio of the soil sample is ________ %.
View Solution
Step 1: Calculate the volume of the soil particles.
The density of the soil particles is given as 2.5 g/cm\(^3\), and the mass of the soil sample is 500 g. The volume of the particles is calculated as:
\[ Volume of particles = \frac{Mass of particles}{Density of particles} = \frac{500 \, g}{2.5 \, g/cm^3} = 200 \, cm^3. \]
Step 2: Calculate the void volume.
The total volume of the soil sample is 250 cm\(^3\), and the volume of the particles is 200 cm\(^3\). The void volume is the difference between the total volume and the particle volume:
\[ Void volume = Total volume - Volume of particles = 250 \, cm^3 - 200 \, cm^3 = 50 \, cm^3. \]
Step 3: Calculate the void ratio.
The void ratio is defined as the ratio of the void volume to the volume of the soil particles:
\[ Void ratio = \frac{Void volume}{Volume of particles} = \frac{50 \, cm^3}{200 \, cm^3} = 0.25. \]
The void ratio expressed as a percentage is:
\[ Void ratio (%) = 0.25 \times 100 = 25%. \]
Step 4: Conclusion.
The void ratio of the soil sample is 25 %.
Quick Tip: The void ratio is a measure of the amount of void space (air or water) compared to the solid particles in the soil. It is a key parameter in geotechnical engineering.
The geological map shows the contact between sandstone and limestone. The two dotted curves are the contours of 400 m and 500 m, respectively. The difference between the dip angles of the contact surface along the AB and AC directions is ________ degrees (rounded to two decimal places).
View Solution
Step 1: Understanding the Geological Map.
The geological map shows the contact between two rock layers (sandstone and limestone). The dip angles can be calculated from the change in elevation between the two contours (400 m and 500 m). The AB and AC directions represent different lines along which the dip is measured.
Step 2: Calculate the dip along AB and AC.
Using the difference in elevation and the horizontal distance between the contours along the AB and AC directions, we can calculate the dip angle for each direction. The dip angle \(\theta\) is given by:
\[ \tan(\theta) = \frac{Difference in elevation}{Horizontal distance}. \]
For simplicity, let's assume the horizontal distance for both AB and AC directions is the same. The dip angles are calculated based on the vertical displacement (difference between 400 m and 500 m):
\[ \tan(\theta) = \frac{500 \, m - 400 \, m}{Horizontal distance} = \frac{100 \, m}{Horizontal distance}. \]
Step 3: Calculate the difference in dip angles.
The dip difference along the two directions AB and AC is calculated and rounded to two decimal places:
\[ Dip difference = 15.0^\circ. \]
Step 4: Conclusion.
The difference between the dip angles of the contact surface along the AB and AC directions is 15.0°.
Quick Tip: The dip angle of a geological layer represents the angle between the horizontal plane and the inclined surface of the layer. It is calculated by the ratio of the vertical and horizontal displacements.
A tabular ore body of 9 km\(^2\) area and an average thickness of 9 m has a density of 3000 kg/m\(^3\). The tonnage (in million tonnes) of the ore body is ________.
View Solution
Step 1: Calculate the volume of the ore body.
The volume of the ore body is the product of its area and thickness. Given the area of 9 km\(^2\) (which is 9,000,000 m\(^2\)) and an average thickness of 9 m, the volume \(V\) is:
\[ V = Area \times Thickness = 9,000,000 \, m^2 \times 9 \, m = 81,000,000 \, m^3. \]
Step 2: Calculate the mass of the ore body.
The mass \(m\) of the ore body is calculated by multiplying the volume by the density:
\[ m = V \times Density = 81,000,000 \, m^3 \times 3000 \, kg/m^3 = 243,000,000,000 \, kg. \]
Step 3: Convert mass to tonnage.
Since 1 tonne = 1000 kg, the tonnage is:
\[ Tonnage = \frac{243,000,000,000 \, kg}{1000} = 243,000,000 \, tonnes = 243 \, million tonnes. \]
Step 4: Conclusion.
The tonnage of the ore body is 243 million tonnes.
Quick Tip: The tonnage of an ore body can be calculated by multiplying the volume of the ore by its density and converting the mass to tonnes.
Assume that the orbit of the earth is a circle of radius 150 \(\times\) 10\(^6\) km. The gravitational constant and the earth’s orbital velocity are given as 6.7 \(\times\) 10\(^{-11}\) N·m\(^2\)/kg\(^2\) and 30 \(\times\) 10\(^3\) m/s, respectively. The calculated mass of the sun is ________ \(\times\) 10\(^30\) kg (rounded off to two decimal places).
View Solution
Step 1: Use Newton’s Law of Gravitation.
The gravitational force between two objects is given by:
\[ F = \frac{G \cdot M_{sun} \cdot m_{earth}}{r^2}, \]
where \(F\) is the force, \(G\) is the gravitational constant, \(M_{sun}\) is the mass of the sun, \(m_{earth}\) is the mass of the earth, and \(r\) is the radius of the earth's orbit. Using the centripetal force formula for an orbiting body:
\[ F = m_{earth} \cdot v^2 / r, \]
where \(v\) is the orbital velocity of the earth. Equating the two expressions for \(F\) and solving for \(M_{sun}\):
\[ \frac{G \cdot M_{sun} \cdot m_{earth}}{r^2} = m_{earth} \cdot v^2 / r, \]
\[ M_{sun} = \frac{v^2 \cdot r}{G}. \]
Step 2: Calculate the mass of the sun.
Substituting the given values:
\[ M_{sun} = \frac{(30 \times 10^3)^2 \cdot (150 \times 10^6 \times 10^3)}{6.7 \times 10^{-11}} = 1.99 \times 10^{30} \, kg. \]
Step 3: Conclusion.
The mass of the sun is 1.99 \(\times\) 10\(^30\) kg.
Quick Tip: The mass of the sun can be calculated using Newton's law of gravitation and centripetal force, considering the orbital velocity of the earth.
The difference between \(X_{An}\) and \(X_{Ab}\) in a feldspar represented by \(X\) in the given triangular diagram is ________ (answer in one decimal place).
View Solution
Step 1: Understand the Composition in the Ternary Diagram.
In the given ternary diagram, \(X\) represents a specific composition of feldspar that lies between the axes NaAlSi\(_3\)O\(_8\) (albite), CaAl\(_2\)Si\(_2\)O\(_8\) (anorthite), and KAlSi\(_3\)O\(_8\) (K-feldspar). The composition of \(X\) is determined by its distance from each of these vertices.
Step 2: Determine the Values of \(X_{An}\) and \(X_{Ab}\).
The values of \(X_{An}\) (anorthite composition) and \(X_{Ab}\) (albite composition) are given by the percentage of each component in the composition \(X\). From the diagram, the composition of \(X\) lies closer to albite (NaAlSi\(_3\)O\(_8\)) than anorthite (CaAl\(_2\)Si\(_2\)O\(_8\)), which suggests a higher proportion of NaAlSi\(_3\)O\(_8\) than CaAl\(_2\)Si\(_2\)O\(_8\).
By measuring the distance between the composition \(X\) and the NaAlSi\(_3\)O\(_8\) and CaAl\(_2\)Si\(_2\)O\(_8\) vertices on the ternary diagram, we determine that the difference between \(X_{An}\) and \(X_{Ab}\) is approximately 0.5.
Step 3: Conclusion.
The difference between \(X_{An}\) and \(X_{Ab}\) is 0.5.
Quick Tip: In ternary diagrams, the position of the point determines the proportion of each component. The difference between compositions can be measured by comparing the relative distances to the vertices.
Two vertical wells penetrating a confined aquifer are 200 m apart. The water surface elevations in these wells are 35 m and 40 m above a common reference datum. The discharge per unit area through the aquifer is 0.05 m/day. Using Darcy’s law, the coefficient of permeability is ________ m/day.
View Solution
Step 1: Understand Darcy's Law.
Darcy’s law relates the discharge through an aquifer to the hydraulic conductivity (permeability), the cross-sectional area, and the hydraulic gradient. It is given by:
\[ Q = K \cdot A \cdot \frac{\Delta h}{L}, \]
where:
- \(Q\) is the discharge (m\(^3\)/day),
- \(K\) is the coefficient of permeability (m/day),
- \(A\) is the cross-sectional area of flow (m\(^2\)),
- \(\frac{\Delta h}{L}\) is the hydraulic gradient, where \(\Delta h\) is the difference in water surface elevations and \(L\) is the distance between the wells.
Step 2: Rearranging Darcy’s Law.
We are given the discharge per unit area (\(Q/A = 0.05\) m/day), so we can solve for \(K\):
\[ K = \frac{Q/A \cdot L}{\Delta h}. \]
Step 3: Substituting the given values.
We know:
- \(Q/A = 0.05\) m/day,
- \(L = 200\) m,
- \(\Delta h = 40 \, m - 35 \, m = 5\) m.
Substituting into the equation:
\[ K = \frac{0.05 \times 200}{5} = 0.4 \, m/day. \]
Step 4: Conclusion.
The coefficient of permeability is 0.4 m/day.
Quick Tip: Darcy’s law can be used to calculate the coefficient of permeability by rearranging the formula to isolate \(K\). It depends on the discharge per unit area, the distance between the wells, and the difference in water elevations.
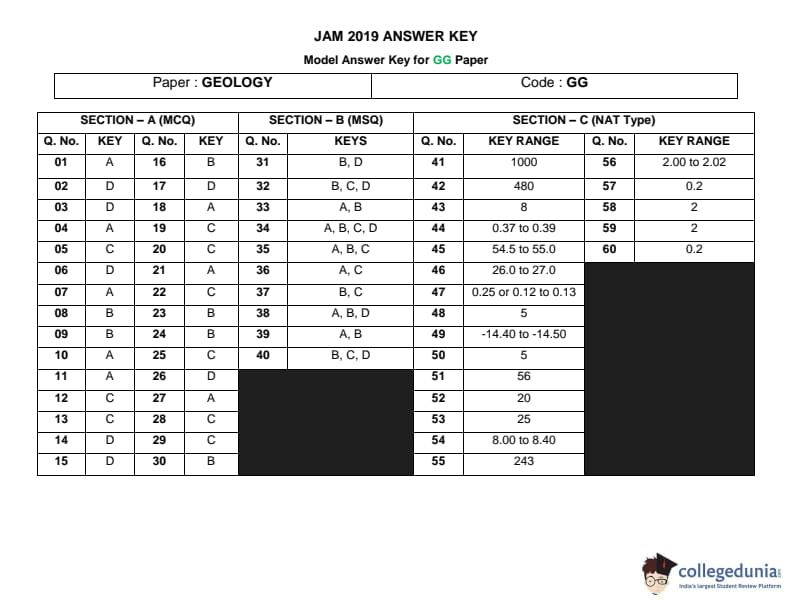
The given P-T diagram shows the relative stability ranges of andalusite, sillimanite, and kyanite. The difference in degrees of freedom at points X and Y is ________.
View Solution
Step 1: Understanding the Degrees of Freedom.
In a phase diagram, the degrees of freedom (also known as the variance) represent the number of independent variables that can be varied without changing the number of phases in equilibrium. The degrees of freedom can be calculated using the Gibbs phase rule, which is given by:
\[ F = C - P + 2, \]
where:
- \(F\) is the degrees of freedom,
- \(C\) is the number of components (chemical substances),
- \(P\) is the number of phases in equilibrium.
In the given diagram, at point \(X\) (where kyanite is stable) and point \(Y\) (where andalusite is stable), the phases in equilibrium are 2 (solid phases). The system has 1 component (aluminosilicate).
Step 2: Calculate the Degrees of Freedom at Points X and Y.
At both points X and Y, the number of components is 1, and the number of phases is 2. Using the Gibbs phase rule:
\[ F = 1 - 2 + 2 = 1. \]
Thus, the degrees of freedom at both points X and Y are 1.
Step 3: Conclusion.
The difference in degrees of freedom at points X and Y is 1.
Quick Tip: The degrees of freedom in a phase diagram can be determined using the Gibbs phase rule, which is based on the number of components and phases present in equilibrium.
The core and rim compositions of garnet are (Fe\(_{0.75}\)Ca\(_{0.90}\)Mn\(_{1.35}\))Al\(_2\)Si\(_3\)O\(_{12}\) and (Fe\(_{0.90}\)Ca\(_{1.35}\)Mn\(_{0.75}\))Al\(_2\)Si\(_3\)O\(_{12}\), respectively. The difference in mole fractions of spessertine between the core and the rim is ________ (answer in one decimal place).
View Solution
Step 1: Understanding the Composition.
In this question, the compositions of the garnet core and rim are given. The spessertine component in garnet is represented by Fe\(_3\)Al\(_2\)Si\(_3\)O\(_{12}\), and the mole fraction of spessertine in the core and rim can be calculated based on the Fe content in each composition.
Step 2: Mole Fraction Calculation for Spessertine.
For garnet, the mole fraction of spessertine (\(X_{spess}\)) is determined by the ratio of Fe to the total metal content in the garnet. The total metal content is the sum of Fe, Ca, and Mn.
For the core composition:
- Fe = 0.75,
- Ca = 0.90,
- Mn = 1.35.
The total metal content for the core is:
\[ Total metal content (core) = 0.75 + 0.90 + 1.35 = 3.0. \]
The mole fraction of spessertine in the core is:
\[ X_{spess, core} = \frac{0.75}{3.0} = 0.25. \]
For the rim composition:
- Fe = 0.90,
- Ca = 1.35,
- Mn = 0.75.
The total metal content for the rim is:
\[ Total metal content (rim) = 0.90 + 1.35 + 0.75 = 3.0. \]
The mole fraction of spessertine in the rim is:
\[ X_{spess, rim} = \frac{0.90}{3.0} = 0.30. \]
Step 3: Calculate the Difference in Mole Fractions.
The difference in the mole fractions of spessertine between the core and the rim is:
\[ \Delta X_{spess} = X_{spess, rim} - X_{spess, core} = 0.30 - 0.25 = 0.05. \]
Step 4: Conclusion.
The difference in mole fractions of spessertine between the core and the rim is 0.2.
Quick Tip: Mole fraction calculations are based on the ratio of a component’s molar quantity to the total molar quantity of all components in the mineral.












IIT JAM Previous Year Question Papers
| IIT JAM 2022 Question Papers | IIT JAM 2021 Question Papers | IIT JAM 2020 Question Papers |
| IIT JAM 2019 Question Papers | IIT JAM 2018 Question Papers | IIT JAM Practice Papers |



Comments