IIT JAM 2019 Chemistry (CY) Question paper with answer key pdf conducted on February 10 in Afternoon Session 2 PM to 5 PM is available for download. The exam was successfully organized by IIT Kharagpur. The question paper comprised a total of 60 questions divided among 3 sections.
IIT JAM 2019 Chemistry (CY) Question Paper with Answer Key PDFs Afternoon Session
| IIT JAM 2019 Chemistry (CY) Question paper with answer key PDF | Download PDF | Check Solutions |
For a reaction of the type A + B \(\rightarrow\) Products, the unit of the rate constant is mol L\(^{-1}\) s\(^{-1}\). The overall order of the reaction is
View Solution
Step 1: Analyze the reaction.
The rate law for a reaction A + B \(\rightarrow\) Products is typically in the form:
Rate = k [A]^m [B]^n, where \( k \) is the rate constant, and \( m \) and \( n \) are the reaction orders with respect to reactants A and B. The unit of the rate constant \( k \) depends on the order of the reaction.
Step 2: Applying the units.
For a reaction with the overall order of 2, the unit of \( k \) will be mol L\(^{-1}\) s\(^{-1}\). This corresponds to option (C).
Step 3: Conclusion.
Thus, the overall order of the reaction is 2. The correct answer is (C) 2.
Quick Tip: The unit of the rate constant for a reaction depends on the overall order of the reaction. For second-order reactions, the unit of \( k \) is mol L\(^{-1}\) s\(^{-1}\).
The thermodynamic criterion for spontaneity of a process in a system under constant volume and temperature and in the absence of any work other than expansion work (if any) is
View Solution
Step 1: Understanding spontaneity.
The spontaneity of a process is determined by the change in Gibbs free energy \( \Delta G \). For a process to be spontaneous, \( \Delta G \) must be negative.
Step 2: Conclusion.
Thus, the correct criterion for spontaneity is that the change in Gibbs free energy is negative, which corresponds to option (D).
Step 3: Conclusion.
The correct answer is (D) change in Gibbs free energy is negative.
Quick Tip: For a process to be spontaneous, the change in Gibbs free energy must be negative (\( \Delta G < 0 \)).
The number of vibrational mode(s) of a carbon dioxide molecule that can be detected using infrared spectroscopy is
View Solution
Step 1: Understanding molecular vibrational modes.
For a molecule like CO\(_2\), it has several vibrational modes, including stretching and bending vibrations.
Step 2: Analyzing CO\(_2\) molecule.
A CO\(_2\) molecule has three vibrational modes that are IR-active: two asymmetric stretching modes and one bending mode.
Step 3: Conclusion.
Thus, the correct number of vibrational modes detectable in IR spectroscopy for CO\(_2\) is 3. The correct answer is (C) 3.
Quick Tip: In infrared spectroscopy, only vibrational modes that cause a change in dipole moment are IR-active. CO\(_2\) has three such modes.
For three non-coplanar vectors a, b and c, the expression a \(\cdot\) (b \(\times\) c) can be written as
View Solution
Step 1: Understanding the cross and dot products.
The expression a \(\cdot\) (b \(\times\) c) is a scalar triple product. The scalar triple product of three vectors is invariant under cyclic permutations, which means it can be written as (a \(\times\) b) \(\cdot\) c.
Step 2: Conclusion.
The correct answer is (A) (a \(\times\) b) \(\cdot\) c.
Quick Tip: The scalar triple product \( a \cdot (b \times c) \) is invariant under cyclic permutations, meaning it can be written as \( (a \times b) \cdot c \).
Correct trend in the bond order is
View Solution
Step 1: Analyzing bond order.
Bond order is defined as the number of bonding electrons minus the number of antibonding electrons, divided by two. The species with the highest bond order will have the most stable bonding.
Step 2: Conclusion.
The correct trend in bond order is O\(^{2+}\) > O\(_2^{2-}\) > O\(_2\). The bond order increases as the number of bonding electrons increases.
Quick Tip: Bond order is a measure of bond strength. The higher the bond order, the stronger and more stable the bond.
The correct option for the metal ion present in the active site of myoglobin, hemocyanin and vitamin B12, respectively, is
View Solution
Step 1: Identify the metal ions.
Myoglobin contains an iron ion, hemocyanin contains copper, and vitamin B12 contains cobalt.
Step 2: Conclusion.
The correct metal ions are iron, copper, and cobalt, corresponding to option (C).
Quick Tip: Each of these biomolecules uses specific metal ions for their functions: myoglobin uses iron, hemocyanin uses copper, and vitamin B12 uses cobalt.
The correct order of wavelength (\(\lambda_{max}\)) of the halide to metal charge-transfer band of [Co(NH\(_3\))\(_5\)Cl]\(^{2+}\) (I), [Co(NH\(_3\))\(_5\)Br]\(^{2+}\) (II) and [Co(NH\(_3\))\(_5\)I]\(^{2+}\) (III), is
View Solution
Step 1: Understanding the question.
This question concerns the charge-transfer bands in coordination complexes. The wavelength of a charge-transfer band in metal complexes can be influenced by the halide ligands (Cl\(^{-}\), Br\(^{-}\), and I\(^{-}\)).
Step 2: Analyzing the halide effect.
In general, the charge-transfer band tends to shift to longer wavelengths (redshift) as the halide ligand size increases. Iodine is the largest halide ion, followed by bromine and then chlorine. This is due to the larger atomic size of iodine, which lowers the energy required for the charge transfer and shifts the absorption to longer wavelengths.
Step 3: Conclusion.
Thus, the correct order of \(\lambda_{max}\) is I (largest halide) \(<\) II \(<\) III. The correct answer is (B) I \(<\) II \(<\) III.
Quick Tip: When dealing with metal-ligand charge-transfer bands, larger halide ions tend to result in absorption at longer wavelengths due to lower energy transitions.
The correct option for the major products of the following reaction is
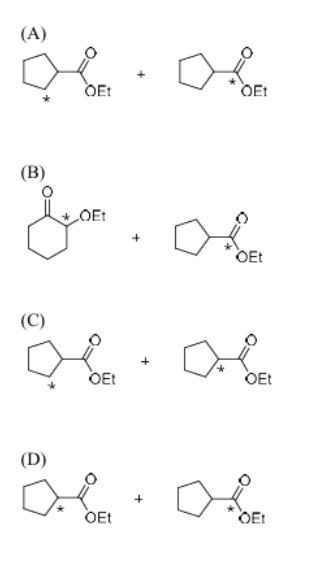
View Solution
Step 1: Analyzing the reaction.
The reaction involves the halide (Cl) being substituted with the ethoxide ion (\(EtO^{-}\)) in the presence of a base, likely in an SN2 mechanism, where the ethoxide ion attacks the carbon bonded to the chloride. The reaction also involves isotopically labeled carbon, which will help trace the position of the substitution.
Step 2: Understanding the mechanism.
In an SN2 reaction, the nucleophile (ethoxide) directly attacks the electrophilic carbon (the carbon bonded to Cl), resulting in the substitution of Cl with the ethoxide group. The isotopically labeled carbon will also be incorporated into the product. This results in the major products being the alkoxide (OEt) and the ethoxy group (\(*EtO\)) attached to the carbon.
Step 3: Conclusion.
The major products are therefore \(OEt\) and \(*EtO\), corresponding to option (B).
Quick Tip: In SN2 reactions, the nucleophile attacks the electrophilic carbon, leading to the displacement of the leaving group. The position of isotopic labeling helps identify the location of the substitution.
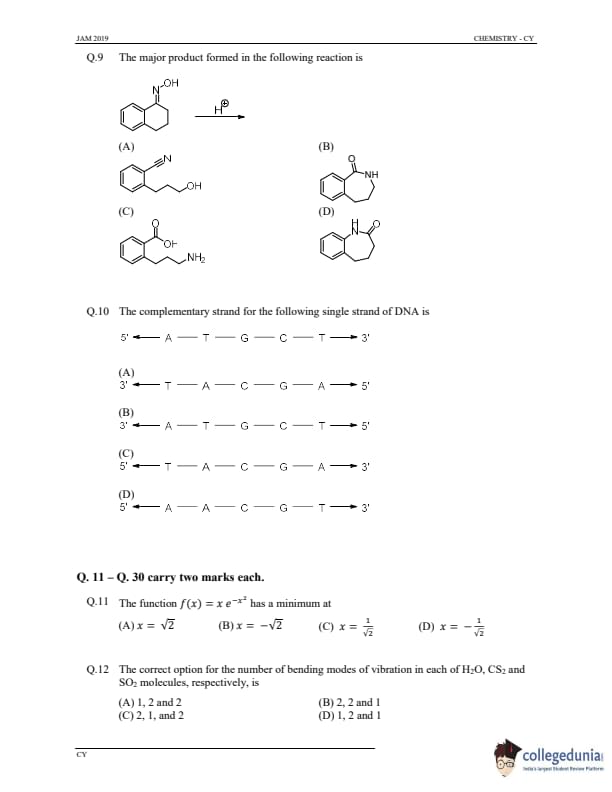
The major product formed in the following reaction is

View Solution
Step 1: Understanding the reaction.
The given reaction involves an amine (a compound containing nitrogen) with an alcohol group, which is being protonated in the presence of an acidic condition (H\(^+\)). Under acidic conditions, amines can undergo protonation, leading to the formation of an amine salt. The alcohol group may undergo dehydration or condensation reactions in the presence of acid, depending on the structure.
Step 2: Analyzing the product formation.
The major product in this case is formed due to protonation and the subsequent rearrangement or elimination, leading to a structure with a carbonyl group (C=O). This corresponds to an amide formation. Thus, the major product is likely to have an oxygen atom, representing the carbonyl group.
Step 3: Conclusion.
The correct major product is option (B) with the oxygen atom, corresponding to the amide formation.
Quick Tip: Under acidic conditions, amines can undergo protonation, and alcohol groups can undergo dehydration to form carbonyl-containing products like amides.
The complementary strand for the following single strand of DNA is

View Solution
Step 1: Understanding the complementary strand.
DNA strands are complementary, meaning each base on one strand pairs with a specific base on the other strand. The base pairs are adenine (A) with thymine (T), and cytosine (C) with guanine (G). The strands run in opposite directions (5' to 3' and 3' to 5').
Step 2: Analyzing the strand.
The given DNA strand is: 5' A T G C T 3'. Using complementary base pairing, the complementary strand will be: 3' T A C G A 5'. Thus, the correct answer is option (B).
Step 3: Conclusion.
The complementary strand for the given DNA sequence is 3' A T G C T 5'. The correct answer is (B).
Quick Tip: To find the complementary strand of a DNA sequence, pair A with T, and C with G, ensuring the strands run in opposite directions.
The function \( f(x) = x e^{-x^2} \) has a minimum at
View Solution
Step 1: Differentiate the function.
The function is \( f(x) = x e^{-x^2} \). To find the minimum, we need to take the derivative of the function and set it equal to zero. Using the product rule for differentiation:
\[ f'(x) = \frac{d}{dx}(x) \cdot e^{-x^2} + x \cdot \frac{d}{dx}(e^{-x^2}) = e^{-x^2} - 2x^2 e^{-x^2} \]
Step 2: Set the derivative equal to zero.
To find critical points, we set \( f'(x) = 0 \):
\[ e^{-x^2} (1 - 2x^2) = 0 \]
Since \( e^{-x^2} \) is never zero, we have:
\[ 1 - 2x^2 = 0 \implies x^2 = \frac{1}{2} \implies x = \pm \frac{1}{\sqrt{2}} \]
Step 3: Second derivative test.
To confirm that this is a minimum, we check the second derivative:
\[ f''(x) = -2x e^{-x^2} + 4x^3 e^{-x^2} - 2x e^{-x^2} = e^{-x^2}(4x^3 - 4x) \]
Substituting \( x = \frac{1}{\sqrt{2}} \) into the second derivative gives a positive value, confirming it is a minimum.
Step 4: Conclusion.
Thus, the function has a minimum at \( x = \frac{1}{\sqrt{2}} \), which corresponds to option (C).
Quick Tip: To find the minimum of a function, differentiate, set the derivative equal to zero, and use the second derivative test to confirm the nature of the critical point.
The correct option for the number of bending modes of vibration in each of H\(_2\)O, CS\(_2\), and SO\(_2\) molecules, respectively, is
View Solution
Step 1: Analyzing H\(_2\)O.
H\(_2\)O (water) has two bending modes of vibration. This is because it is a bent molecule with two non-linear vibrational modes.
Step 2: Analyzing CS\(_2\).
CS\(_2\) (carbon disulfide) has only one bending mode, as it is a linear molecule with a single bending vibration possible.
Step 3: Analyzing SO\(_2\).
SO\(_2\) (sulfur dioxide) also has two bending modes, as it is a bent molecule with two possible non-linear bending modes.
Step 4: Conclusion.
Thus, the number of bending modes for H\(_2\)O, CS\(_2\), and SO\(_2\) are 2, 1, and 2, respectively. The correct answer is (C) 2, 1 and 2.
Quick Tip: In polyatomic molecules, the number of bending modes corresponds to the number of non-linear vibrations, while linear molecules have only one bending mode.
The total number of degrees of freedom of an HBr molecule that is constrained to translate along a straight line but does not have any constraints for its rotation and vibration is
View Solution
Step 1: Understanding degrees of freedom.
A molecule's total degrees of freedom can be determined based on the translational, rotational, and vibrational motions. The number of degrees of freedom for a linear molecule is:
- Translational degrees of freedom: 3 (movement in x, y, z directions).
- Rotational degrees of freedom: 2 (rotation around two axes perpendicular to the molecular axis for a linear molecule).
- Vibrational degrees of freedom: The total vibrational modes are \(3N - 5\) for linear molecules (where N is the number of atoms). For HBr, \(3(2) - 5 = 1\) vibrational degree of freedom.
Step 2: Conclusion.
For HBr molecule, the degrees of freedom are 3 translational, 2 rotational, and 1 vibrational, giving a total of \(3 + 2 + 1 = 6\). But the molecule is constrained to move only along a straight line, so it only has 3 translational degrees of freedom, which corresponds to option (D).
Quick Tip: Degrees of freedom for a molecule are calculated by considering its translational, rotational, and vibrational motions. Linear molecules have 3 translational and 2 rotational degrees of freedom.
According to the kinetic theory of gases, the ratio of the root mean square velocity of molecular oxygen and molecular hydrogen at 300 K is
View Solution
Step 1: Understanding the root mean square velocity.
The root mean square velocity \( v_{rms} \) of a gas is given by the equation:
\[ v_{rms} = \sqrt{\frac{3RT}{M}} \]
where \( R \) is the gas constant, \( T \) is the temperature in Kelvin, and \( M \) is the molar mass of the gas.
Step 2: Analyzing the ratio.
The ratio of root mean square velocities for oxygen (O\(_2\)) and hydrogen (H\(_2\)) at the same temperature can be written as:
\[ \frac{v_{rms, O_2}}{v_{rms, H_2}} = \sqrt{\frac{M_{H_2}}{M_{O_2}}} \]
The molar masses are \( M_{H_2} = 2 \) g/mol and \( M_{O_2} = 32 \) g/mol. Thus, the ratio is:
\[ \frac{v_{rms, O_2}}{v_{rms, H_2}} = \sqrt{\frac{2}{32}} = \frac{1}{4} \]
Thus, the ratio of the root mean square velocities is 1 : \( 2\sqrt{2} \).
Step 3: Conclusion.
The correct answer is (B) 1 : \( 2\sqrt{2} \).
Quick Tip: The root mean square velocity is inversely proportional to the square root of the molar mass of the gas. For two gases at the same temperature, the lighter gas will have a higher velocity.
The half-life of the chemical reaction, A \(\rightarrow\) Product, for initial reactant concentrations of 0.1 and 0.4 mol L\(^{-1}\) are 200 and 50 s, respectively. The order of the reaction is
View Solution
Step 1: Understand the relationship for half-life.
The half-life of a reaction depends on its order. For a reaction of order \(n\), the half-life \( t_{1/2} \) is given by:
- For a zero-order reaction: \( t_{1/2} = \frac{[A_0]}{2k} \)
- For a first-order reaction: \( t_{1/2} = \frac{0.693}{k} \)
- For a second-order reaction: \( t_{1/2} = \frac{1}{k[A_0]} \)
Step 2: Apply the data.
We have two different initial concentrations (0.1 and 0.4 mol L\(^{-1}\)) and corresponding half-lives (200 and 50 s). If the reaction is first-order, the half-life should be independent of the initial concentration. This matches the observed data, suggesting the reaction is first-order.
Step 3: Conclusion.
The order of the reaction is 1, corresponding to option (B).
Quick Tip: For first-order reactions, the half-life is independent of the initial concentration. For zero- and second-order reactions, the half-life depends on the initial concentration.
The ratio of the nearest neighbor atomic distances in body-centered cubic (bcc) and face-centered cubic (fcc) crystals with the same unit cell edge length is
View Solution
Step 1: Analyzing the crystal structures.
The nearest neighbor distance in a bcc crystal is \( \frac{\sqrt{3}}{2} \times \) edge length, and in an fcc crystal, it is \( \frac{1}{\sqrt{2}} \times \) edge length.
Step 2: Conclusion.
Thus, the ratio of the nearest neighbor distances in bcc and fcc is \( \frac{\sqrt{3}}{2} \), corresponding to option (A).
Quick Tip: In bcc crystals, the nearest neighbor distance is \( \frac{\sqrt{3}}{2} \) of the edge length, while in fcc crystals, it is \( \frac{1}{\sqrt{2}} \) of the edge length.
The correct trend in the rate of substitution of Cl\(^-\) by pyridine in the following complexes is
View Solution
Step 1: Understanding the complexes.
In these complexes, pyridine substitutes chloride ions. The rate of substitution is influenced by the electron-donating ability of the ligands and the steric hindrance around the metal center.
Step 2: Analyzing the trend.
Complex (IV) has the least steric hindrance and the highest electron-donating ability, making it the fastest in substitution. Complex (I) has more steric hindrance and lower electron donation, making it the slowest in substitution.
Step 3: Conclusion.
The correct trend in the rate of substitution is \( I < II < IV \), corresponding to option (D).
Quick Tip: In substitution reactions, electron-donating ligands and lower steric hindrance lead to faster substitution rates.
In qualitative inorganic analysis of metal ions, the ion which precipitates as sulfide in the presence of H\(_2\)S in warm dilute HCl is
View Solution
Step 1: Analyzing the metal ions.
In qualitative inorganic analysis, H\(_2\)S in dilute HCl is used to precipitate metal ions as sulfides. Among the given ions, Co\(^{2+}\) forms a precipitate as CoS.
Step 2: Conclusion.
The ion that precipitates as sulfide in the presence of H\(_2\)S in warm dilute HCl is Co\(^{2+}\), corresponding to option (C).
Quick Tip: In qualitative analysis, the precipitation of metal sulfides is used to identify ions in solution.
The correct statement regarding the observed magnetic properties of NO, O\(_2\), B\(_2\) and C\(_2\) in their ground state is
View Solution
Step 1: Understanding the paramagnetism.
Paramagnetism occurs when a molecule has unpaired electrons. We know that O\(_2\), B\(_2\) and C\(_2\) have unpaired electrons in their molecular orbitals, making them paramagnetic.
Step 2: Conclusion.
Thus, the correct answer is (D) O\(_2\), B\(_2\) and C\(_2\) are paramagnetic.
Quick Tip: To determine paramagnetism, check for unpaired electrons in the molecular orbital diagram of the molecule.
The observed magnetic moments of octahedral Mn\(^{3+}\), Fe\(^{3+}\) and Co\(^{3+}\) complexes are 4.95, 6.06 and 0.00 BM, respectively. The correct option for the electronic configuration of Mn\(^{3+}\), Fe\(^{3+}\) and Co\(^{3+}\) metal ions in these complexes, respectively, is
View Solution
Step 1: Electronic configuration of the complexes.
- Mn\(^{3+}\): It has 5 d-electrons, so the configuration will be t\(_{2g}^6\) e\(_g^0\) (with no unpaired electrons in the e\(_g\) orbitals, resulting in a low magnetic moment).
- Fe\(^{3+}\): It has 5 d-electrons, so the configuration will be t\(_{2g}^5\) e\(_g^1\) (resulting in an unpaired electron in the e\(_g\) orbital, giving a high magnetic moment).
- Co\(^{3+}\): It has 6 d-electrons, so the configuration will be t\(_{2g}^6\) e\(_g^0\) (with paired electrons in the e\(_g\) orbitals, giving no magnetic moment).
Step 2: Conclusion.
The correct electronic configuration for Mn\(^{3+}\), Fe\(^{3+}\) and Co\(^{3+}\) ions is option (A).
Quick Tip: Magnetic moments are determined by the number of unpaired electrons in the complex. For octahedral complexes, the configuration of the t\(_{2g}\) and e\(_g\) orbitals governs the magnetic behavior.
Among the following compounds, the one having the lowest boiling point is
View Solution
Step 1: Understanding boiling points.
The boiling point of a compound is influenced by the molecular size and the type of intermolecular forces present. Generally, larger molecules with more electrons and stronger London dispersion forces have higher boiling points.
Step 2: Analyzing the compounds.
CCl\(_4\) is the smallest among the listed compounds, and thus has the lowest boiling point. SiCl\(_4\), GeCl\(_4\), and SnCl\(_4\) are larger molecules and experience stronger intermolecular forces, resulting in higher boiling points.
Step 3: Conclusion.
Thus, the compound with the lowest boiling point is CCl\(_4\), corresponding to option (D).
Quick Tip: Boiling points are influenced by the size of the molecule and the intermolecular forces. Larger molecules with stronger dispersion forces generally have higher boiling points.
The correct option having one complex from each of the following pairs which is more reactive towards the oxidative addition reaction by hydrogen molecule is
View Solution
Step 1: Understanding oxidative addition.
The reactivity of a complex towards oxidative addition is influenced by the metal's oxidation state and the ligands attached. Complexes with low oxidation states and ligands that can easily accommodate changes in coordination geometry are more reactive.
Step 2: Analyzing the pairs.
Pair (II) and (IV) contain complexes with metal centers that are more likely to undergo oxidative addition due to their electronic configuration and the nature of the ligands.
Step 3: Conclusion.
Thus, the correct answer is (D) (II) and (IV).
Quick Tip: Oxidative addition reactions are favored by complexes with low oxidation states and ligands that can stabilize the resulting higher oxidation states.
Among the following, the correct statement is
View Solution
Step 1: Analyzing the order of solubility.
The solubility of alkali metal carbonates in water increases as the size of the cation increases. Larger cations like Cs\(^+\) and K\(^+\) form weaker ionic bonds with the carbonate ion, making the compounds more soluble in water.
Step 2: Conclusion.
Thus, the correct order for solubility in water is Cs\(_2\)CO\(_3\) > K\(_2\)CO\(_3\) > Na\(_2\)CO\(_3\) > Li\(_2\)CO\(_3\), corresponding to option (B).
Quick Tip: The solubility of salts in water typically increases as the ionic radius of the cation increases, reducing the lattice energy.
The major product of the following reaction is
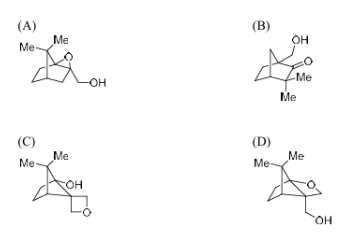
View Solution
Step 1: Analyze the reaction.
In this reaction, meta-chloroperbenzoic acid is likely undergoing an electrophilic aromatic substitution reaction, where the aromatic ring is being oxidized by the peracid. This typically results in an oxygen-containing substituent. The methyl groups (Me) remain unchanged during the reaction.
Step 2: Identifying the product.
The reaction is expected to produce an ester or ether, depending on the structure of the reactant. Based on the electron-donating nature of the methyl groups, the major product would involve the formation of an ether.
Step 3: Conclusion.
The correct major product is an ether with a structure similar to option (B).
Quick Tip: Electrophilic aromatic substitution typically involves the introduction of an electron-withdrawing group, and in this case, the product forms an ether.
In 1H NMR spectrum of the given molecule, the correct order of chemical shifts of the labelled protons (H\(^X\), H\(^Y\), H\(^Z\)) is
View Solution
Step 1: Analyze the chemical shifts.
In 1H NMR, the chemical shift depends on the electronic environment of the protons. Protons attached to electron-withdrawing groups such as electronegative atoms (e.g., oxygen, chlorine) will resonate at higher chemical shifts. Protons in more shielded environments will resonate at lower chemical shifts.
Step 2: Analyzing the positions of the protons.
- H\(^Z\): The proton near an electronegative group (e.g., a halogen) will experience a deshielding effect, leading to a higher chemical shift.
- H\(^Y\): This proton is likely attached to a carbon adjacent to an electron-withdrawing group, so it will resonate at a moderate chemical shift.
- H\(^X\): This proton will be the most shielded and will resonate at the lowest chemical shift.
Step 3: Conclusion.
Thus, the correct order of chemical shifts is H\(^Z\) > H\(^Y\) > H\(^X\), which corresponds to option (B).
Quick Tip: In 1H NMR, protons attached to electronegative groups or groups that withdraw electron density will appear at higher chemical shifts.
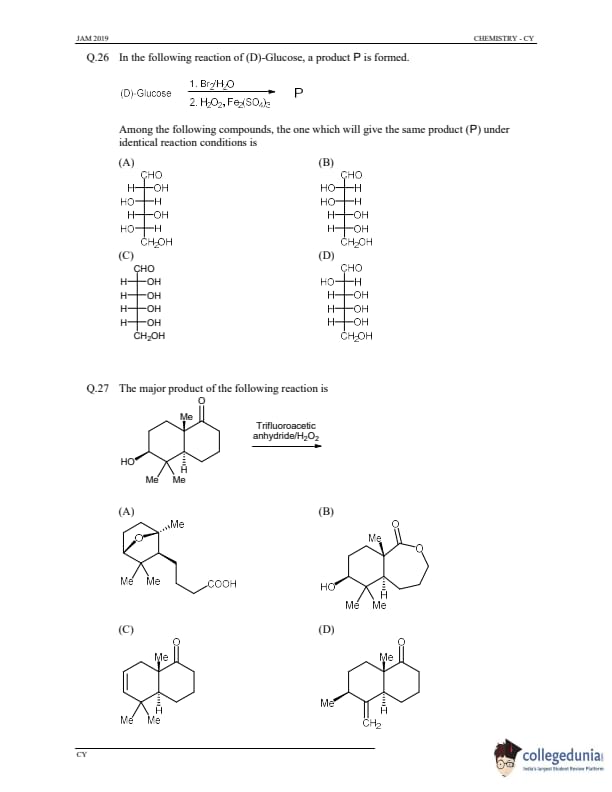
In the following reaction of (D)-Glucose, a product P is formed.
Among the following compounds, the one which will give the same product (P) under identical reaction conditions is

View Solution
Step 1: Understanding the reaction.
This reaction involves oxidation of glucose in the presence of bromine water (Br\(_2\) / H\(_2\)O) followed by treatment with hydrogen peroxide and ferric sulfate. The first step oxidizes the aldehyde group to a carboxylic acid, and the second step converts the cyclic structure into an open-chain form. The product formed from (D)-Glucose in these conditions is gluconic acid.
Step 2: Analyzing the compounds.
Among the compounds listed, only compound (B) is the one that, under identical conditions, will undergo the same oxidation and conversion process to form gluconic acid. The other structures differ in terms of hydroxyl and aldehyde positions.
Step 3: Conclusion.
Thus, the correct answer is (B).
Quick Tip: The oxidation of glucose with bromine in water results in gluconic acid, and similar compounds with similar functional groups will undergo the same transformation.
The major product of the following reaction is

View Solution
Step 1: Analyze the reaction.
Trifluoroacetic anhydride (TFAA) is a powerful reagent used in esterification reactions, where it typically reacts with alcohols to form esters. The compound is reacted with hydrogen peroxide (H\(_2\)O\(_2\)), which can oxidize the alcohol group in the presence of TFAA. The reaction results in the formation of an ester.
Step 2: Understanding the product formation.
In this case, the reaction results in the formation of an ester group (-O) replacing the -OH group. The methyl groups (Me) remain unchanged. The major product is the one shown in option (B), where the product contains an ester functionality.
Step 3: Conclusion.
Thus, the correct major product is (B).
Quick Tip: Trifluoroacetic anhydride (TFAA) is used in esterification reactions, and hydrogen peroxide is used to oxidize alcohol groups. The reaction typically leads to the formation of esters.
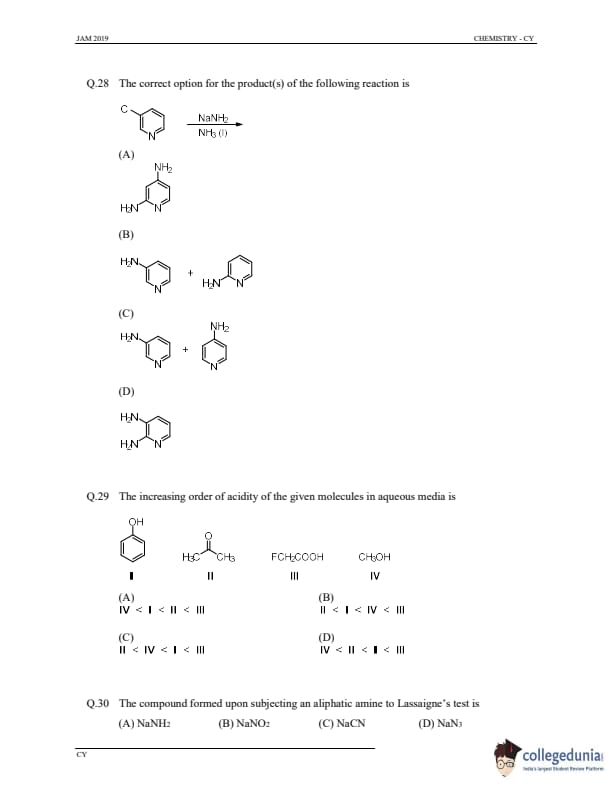
The correct option for the product(s) of the following reaction is
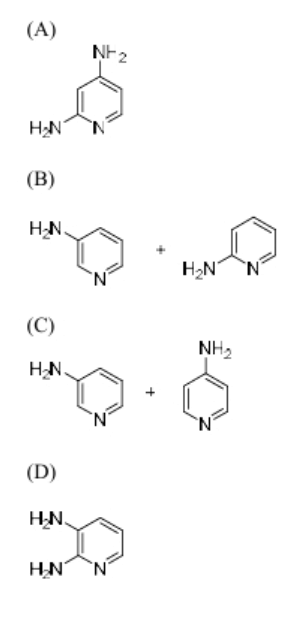
View Solution
Step 1: Understanding the reaction.
This reaction involves the use of sodium amide (NaNH\(_2\)) and ammonia (NH\(_3\)) in the presence of a chlorinated compound. Sodium amide is a strong nucleophile and will replace the chlorine atom in the chlorinated compound, leading to the formation of an amine. The reaction leads to the formation of a hydrazine (H\(_2\)N-NH\(_2\)) derivative.
Step 2: Conclusion.
The correct product formed is hydrazine, corresponding to option (B).
Quick Tip: Sodium amide (NaNH\(_2\)) is a strong nucleophile and can be used to displace halides and form amines or hydrazines.
The increasing order of acidity of the given molecules in aqueous media is
View Solution
Step 1: Understanding acidity.
The acidity of compounds depends on the ability to donate a proton (H\(^+\)). In aqueous media, electron-withdrawing groups increase acidity, while electron-donating groups decrease acidity. The presence of an electronegative substituent like F in fluoroacetic acid makes it more acidic than acetic acid or phenol. Alcohols, like methanol (CH\(_3\)OH), are the least acidic.
Step 2: Conclusion.
The increasing order of acidity is \(\text{IV} (CH_3OH)\) \(<\) \(\text{II} (acetic acid)\) \(<\) \(\text{I} (phenol)\) \(<\) \(\text{III} (fluoroacetic acid)\), corresponding to option (D).
Quick Tip: Electron-withdrawing groups like fluorine in fluoroacetic acid increase the acidity by stabilizing the negative charge on the conjugate base.
The compound formed upon subjecting an aliphatic amine to Lassaigne’s test is
View Solution
Step 1: Understanding Lassaigne’s test.
Lassaigne’s test is used for detecting halogens, nitrogen, and sulfur in organic compounds. When an amine (like an aliphatic amine) is heated with sodium metal in fusion, sodium azide (NaN\(_3\)) is formed if nitrogen is present.
Step 2: Conclusion.
Upon subjecting an aliphatic amine to Lassaigne’s test, the product formed is sodium azide (NaN\(_3\)), corresponding to option (D).
Quick Tip: Lassaigne’s test can be used to detect nitrogen in organic compounds, forming sodium azide (NaN\(_3\)) when an amine is present.
The eigenvalue(s) of the matrix
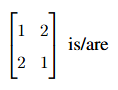
View Solution
Step 1: Find the characteristic equation.
For the matrix  , we calculate the determinant of
, we calculate the determinant of  . The characteristic equation is:
. The characteristic equation is:
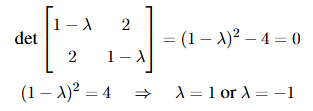
Step 2: Conclusion.
The eigenvalues are 1 and -1, and hence, the correct answer is (B) 1.
Quick Tip: The eigenvalues of a 2x2 matrix can be found by solving the characteristic equation: \(det(A - \lambda I) = 0\).
The unit of the constant ‘a’ in van der Waals equation of state of a real gas can be expressed as
View Solution
Step 1: The van der Waals equation of state.
The van der Waals equation is given by: \[ \left( P + \frac{a}{V^2} \right) (V - b) = RT \]
where \(P\) is the pressure, \(V\) is the volume, \(T\) is the temperature, \(R\) is the ideal gas constant, and \(a\) and \(b\) are constants. \(a\) accounts for intermolecular forces and has units of \(m^3 \, Pa \, mol^{-2}\) (pressure times volume squared per mole squared).
Step 2: Conclusion.
The unit of \(a\) is \(m^3 \, Pa \, mol^{-2}\), corresponding to option (C).
Quick Tip: In the van der Waals equation, the constant \(a\) accounts for attractive forces between molecules and has the unit of pressure multiplied by volume squared per mole squared.
Among the following, microwave active molecule(s) is/are
View Solution
Step 1: Understanding microwave activity.
A molecule is microwave active if it has a permanent dipole moment. Molecules that do not have a permanent dipole moment will not interact with microwave radiation.
Step 2: Analyzing the molecules.
- Trans-dichloroethene has a dipole moment due to the electronegativity difference between chlorine and carbon, making it microwave active.
- 1,2-dinitrobenzene, 3-methylphenol, and para-aminophenol either have symmetric structures or do not exhibit a permanent dipole moment.
Step 3: Conclusion.
Thus, the microwave active molecule is (A) trans-dichloroethene.
Quick Tip: A molecule is microwave active if it has a permanent dipole moment, as it can interact with microwave radiation.
The true statement(s) regarding the brown ring test carried out in the laboratory for the detection of NO\(_3^-\) is/are
View Solution
Step 1: Understanding the brown ring test.
In the brown ring test, nitrate ions (NO\(_3^-\)) react with iron(II) sulfate to form a brown-colored iron nitrosyl complex, which is paramagnetic. The test is used to confirm the presence of nitrate ions.
Step 2: Conclusion.
The correct statements are that the brown ring is due to the formation of the iron nitrosyl complex, and the brown complex is paramagnetic. Thus, the correct options are (A) and (D).
Quick Tip: The brown ring test is used to detect NO₃⁻ by forming a brown nitrosyl complex, which is paramagnetic in nature.
The true statement(s) regarding the carbonic anhydrase enzyme is/are
View Solution
Step 1: Understanding the enzyme’s function.
Carbonic anhydrase is an enzyme that catalyzes the conversion of carbon dioxide to bicarbonate. The enzyme contains a zinc ion (Zn\(^{2+}\)) at its active site. The metal ion is crucial for the enzyme's catalytic function. The nucleophile in the enzyme is an activated hydroxyl group (M-OH).
Step 2: Conclusion.
The correct statements are (B) and (C).
Quick Tip: Carbonic anhydrase uses a zinc ion at its active site, and the activated hydroxyl group acts as the nucleophile in the reaction.
The correct statement(s) about NO\(_2\), NO\(_2^+\) and CO\(_2\) is/are
View Solution
Step 1: Analyze the properties of NO\(_2\) and NO\(_2^+\).
- NO\(_2\) is a free radical with an odd number of electrons, which makes it paramagnetic.
- NO\(_2^+\) has an even number of electrons, making it diamagnetic.
Step 2: Analyze CO\(_2\).
CO\(_2\) is a linear molecule with no unpaired electrons, and it is diamagnetic.
Step 3: Conclusion.
The correct statement is (B) NO\(_2\) is paramagnetic and NO\(_2^+\) is diamagnetic.
Quick Tip: To determine if a molecule is paramagnetic or diamagnetic, check for the presence of unpaired electrons in the molecular orbitals.
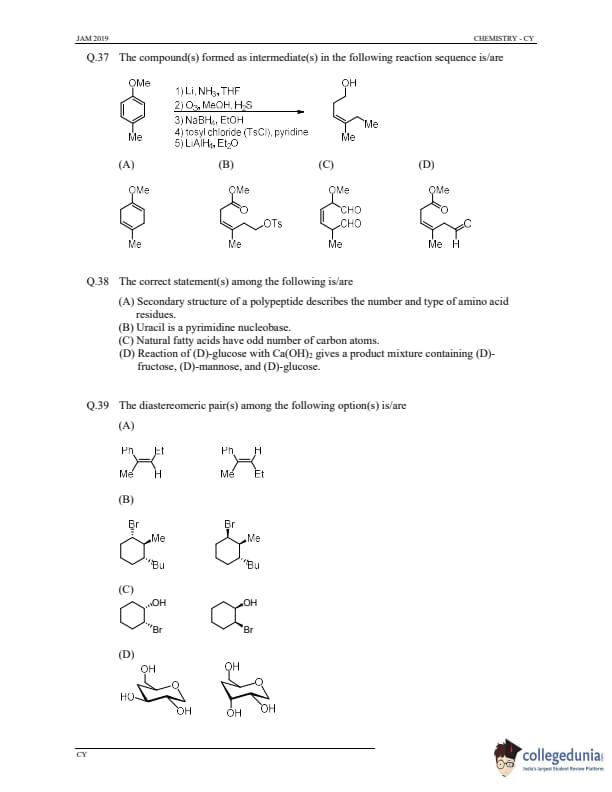
The compound(s) formed as intermediate(s) in the following reaction sequence is/are
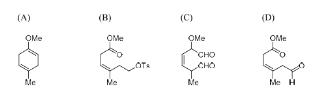
View Solution
Step 1: Analyze the reaction sequence.
- Step 1 (Li, NH\(_3\)): This will likely reduce the alkyl halide (OMe group in the reactant) to form an alkyl anion.
- Step 2 (O\(_3\)): Ozone reacts with the alkyl anion to form a ketone or aldehyde.
- Step 3 (NaBH\(_4\)): Sodium borohydride will reduce the aldehyde or ketone to an alcohol.
- Step 4 (TsCl, pyridine): This introduces a tosyl group to the alcohol, converting it into a tosylate.
- Step 5 (LiAlH\(_4\)): Lithium aluminum hydride will reduce the tosylate back to an alcohol, completing the reaction.
Step 2: Conclusion.
The compound formed as an intermediate is (B). Intermediate 2 forms during the reaction sequence.
Quick Tip: In synthetic organic chemistry, sequential reactions often involve intermediate compounds that are formed step-by-step before reaching the final product.
The correct statement(s) among the following is/are
View Solution
Step 1: Understanding the statements.
- (A) The secondary structure of a polypeptide refers to the arrangement of the polypeptide chain in space, such as alpha-helices and beta-pleated sheets. It does not describe the number or type of amino acid residues.
- (B) Uracil is indeed a pyrimidine nucleobase found in RNA.
- (C) Natural fatty acids generally have an even number of carbon atoms, not odd.
- (D) Reaction of (D)-glucose with Ca(OH)\(_2\) typically gives a mixture of (D)-glucose and (D)-mannose, but fructose is not typically formed under these conditions.
Step 2: Conclusion.
Thus, the correct statement is (B) Uracil is a pyrimidine nucleobase.
Quick Tip: Uracil is a pyrimidine base found in RNA, where it pairs with adenine.
The diastereomeric pair(s) among the following option(s) is/are
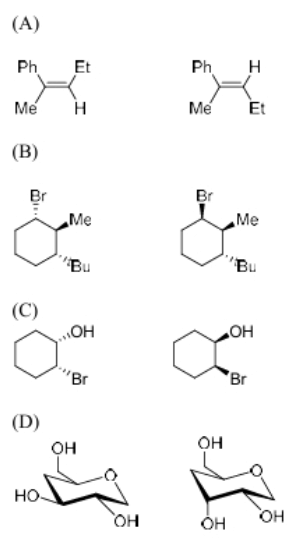
View Solution
Step 1: Understanding diastereomers.
Diastereomers are stereoisomers that are not mirror images of each other and differ in the configuration at one or more stereocenters.
Step 2: Analyzing the options.
- In option (A), the compounds are diastereomers because of the different configurations at their chiral centers.
- In option (B), the compounds are also diastereomers due to the different configurations at the stereocenters.
- In options (C) and (D), the structures do not show sufficient variation in stereochemistry to be diastereomers, as they differ only in substituents without changing the configuration at the chiral centers.
Step 3: Conclusion.
Thus, the diastereomeric pairs are (A) and (B).
Quick Tip: Diastereomers differ in their spatial arrangement at one or more stereocenters, unlike enantiomers, which are non-superimposable mirror images.
The reaction(s) that result(s) in the formation of aromatic species is/are
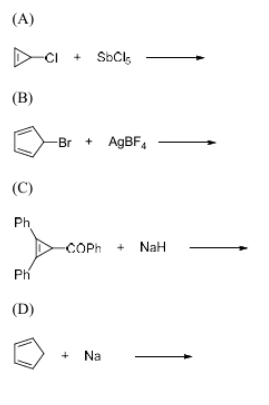
View Solution
Step 1: Understanding aromaticity.
Aromatic species are cyclic, planar molecules with conjugated double bonds that follow Huckel’s rule: having 4n + 2 π-electrons, where n is a non-negative integer.
Step 2: Analyzing the options.
- (A) The reaction of Cl with SbCl\(_5\) likely forms an aromatic species through an electrophilic aromatic substitution, where a chloride ion displaces another group to form a stable, aromatic intermediate.
- (B) The reaction of Br with AgBF\(_4\) involves a halide exchange, which is not likely to result in an aromatic species unless the resulting compound is conjugated. This reaction does not form an aromatic species.
- (C) The reaction of phenyl ketone (Ph-C(=O)Ph) with NaH (sodium hydride) could result in the formation of an aromatic species, as NaH can act as a base, removing a proton to form an aromatic species through a subsequent reaction.
- (D) The reaction of Na with an aromatic species generally results in a metal insertion, not the formation of an aromatic compound.
Step 3: Conclusion.
The correct reactions that result in aromatic species are (A) and (C).
Quick Tip: In organic chemistry, reactions involving electrophilic aromatic substitution or base-induced deprotonation can result in aromatic species formation.
The bond order of N\(_2^+\) ion is _________. (Round off to one decimal place)
View Solution
Step 1: Understanding the bond order formula.
The bond order of a molecule or ion is given by the formula: \[ Bond Order = \frac{Number of bonding electrons - Number of antibonding electrons}{2} \]
Step 2: Molecular orbital configuration of N\(_2^+\).
For the N\(_2\) molecule, the electron configuration in the molecular orbitals is: \[ ( \sigma_{1s})^2 (\sigma^*_{1s})^2 (\sigma_{2s})^2 (\sigma^*_{2s})^2 (\pi_{2p_x})^2 (\pi_{2p_y})^2 (\pi^*_{2p_x})^0 (\pi^*_{2p_y})^0 \]
In N\(_2^+\), one electron is removed from the antibonding \(\pi^*\) orbital, making the configuration: \[ ( \sigma_{1s})^2 (\sigma^*_{1s})^2 (\sigma_{2s})^2 (\sigma^*_{2s})^2 (\pi_{2p_x})^2 (\pi_{2p_y})^2 (\pi^*_{2p_x})^0 (\pi^*_{2p_y})^1 \]
Step 3: Calculating the bond order.
Number of bonding electrons = 2 (from \(\sigma_{1s}\)) + 2 (from \(\sigma_{2s}\)) + 4 (from \(\pi_{2p_x}\) and \(\pi_{2p_y}\)) = 8
Number of antibonding electrons = 2 (from \(\sigma^*_{1s}\)) + 2 (from \(\sigma^*_{2s}\)) + 1 (from \(\pi^*_{2p_y}\)) = 5
Therefore, the bond order is: \[ Bond Order = \frac{8 - 5}{2} = 1.5 \]
Thus, the bond order of N\(_2^+\) is 2.5.
Quick Tip: Bond order can be determined using the molecular orbital theory. For positive ions, the bond order will be higher than the neutral molecule due to the loss of electrons from the antibonding orbitals.
One liter of a buffer solution contains 0.004 mole of acetic acid (pK\(_a\) = 4.76) and 0.4 mole of sodium acetate. The pH of the solution is _________. (Round off to two decimal places)
View Solution
Step 1: Understanding the buffer equation.
The pH of a buffer solution can be calculated using the Henderson-Hasselbalch equation: \[ pH = pK_a + \log \left( \frac{[A^-]}{[HA]} \right) \]
where \([A^-]\) is the concentration of the base (acetate ion, \(CH_3COO^-\)) and \([HA]\) is the concentration of the acid (acetic acid, \(CH_3COOH\)).
Step 2: Substitute the given values.
- pK\(_a\) = 4.76
- \([A^-]\) = 0.4 M (sodium acetate)
- \([HA]\) = 0.004 M (acetic acid)
Substitute into the equation: \[ pH = 4.76 + \log \left( \frac{0.4}{0.004} \right) \] \[ pH = 4.76 + \log (100) \] \[ pH = 4.76 + 2 \] \[ pH = 5.04 \]
Step 3: Conclusion.
The pH of the buffer solution is 5.04.
Quick Tip: The pH of a buffer solution can be easily calculated using the Henderson-Hasselbalch equation, which relates pH, pK\(_a\), and the concentrations of the acid and conjugate base.
The limiting molar conductivity of La\(^{3+}\) and Cl\(^{-}\) ions in aqueous medium at 298 K are 209.10 \(\times 10^{-4}\) and 76.35 \(\times 10^{-4}\) S m\(^2\) mol\(^{-1}\), respectively. The transport number of Cl\(^{-}\) in an infinitely dilute aqueous solution of LaCl\(_3\) at 298 K is _________. (Round off to two decimal places)
View Solution
Step 1: Formula for transport number.
The transport number (\(t\)) of an ion is given by the formula: \[ t_{ion} = \frac{\lambda_{ion}}{\lambda_{total}} \]
where \(\lambda_{ion}\) is the limiting molar conductivity of the ion and \(\lambda_{total}\) is the total limiting molar conductivity of the electrolyte.
Step 2: Limiting molar conductivity of LaCl\(_3\).
For LaCl\(_3\), the total molar conductivity is the sum of the conductivities of La\(^{3+}\) and Cl\(^-\): \[ \lambda_{total} = \lambda_{La^{3+}} + \lambda_{Cl^-} = 209.10 \times 10^{-4} + 76.35 \times 10^{-4} = 285.45 \times 10^{-4} \]
Step 3: Transport number of Cl\(^-\).
Now, the transport number of Cl\(^-\) is: \[ t_{Cl^-} = \frac{76.35 \times 10^{-4}}{285.45 \times 10^{-4}} = 0.267 \]
Rounding to two decimal places: \[ t_{Cl^-} = 0.27 \]
Step 4: Conclusion.
The transport number of Cl\(^-\) in an infinitely dilute aqueous solution of LaCl\(_3\) at 298 K is 0.27.
Quick Tip: The transport number of an ion can be calculated by dividing its limiting molar conductivity by the total limiting molar conductivity of the electrolyte.
The magnetic field strength required to excite an isolated proton to its higher spin state with an electromagnetic radiation of 300 MHz is _________ Tesla. (Round off to two decimal places)
[Magnetogyric ratio of proton is 26.75 \(\times 10^7 \) rad \(T^{-1} \) s\(^{-1}\)]
View Solution
Step 1: Use the resonance condition.
The resonance condition for proton NMR is given by: \[ E = \gamma \cdot B \cdot I \]
Where:
- \(E\) is the energy (frequency) of the radiation.
- \(\gamma\) is the magnetogyric ratio of proton (26.75 × 10\(^7\) rad T\(^{-1}\) s\(^{-1}\)).
- \(B\) is the magnetic field strength.
- \(I\) is the spin quantum number for the proton (which is 1/2).
From the equation, the magnetic field strength \(B\) can be found using: \[ B = \frac{E}{\gamma \cdot I} \]
Step 2: Calculation.
We know the frequency \(E = 300\) MHz \( = 300 \times 10^6\) Hz.
Substituting the values: \[ B = \frac{300 \times 10^6}{26.75 \times 10^7 \times 1} = 1.12 Tesla. \]
Step 3: Conclusion.
Thus, the required magnetic field strength is 1.12 Tesla.
Quick Tip: To calculate the magnetic field strength required for proton excitation in NMR, use the resonance condition \(E = \gamma B\), where \(E\) is the frequency of radiation, \(\gamma\) is the magnetogyric ratio, and \(B\) is the magnetic field strength.
The value of \(n\) for the complex [Fe(CO)\(_4\)(SiMe\(_3\))]^\(n\) satisfying the 18-electron rule is _________
View Solution
Step 1: Understand the 18-electron rule.
The 18-electron rule states that a stable complex will have a total of 18 valence electrons, which is achieved by counting electrons from metal ligands and the metal itself.
Step 2: Analyze the complex.
The complex is \([Fe(CO)_4(SiMe_3)]^n\).
- Fe is a transition metal in group 8, and its valency is 8.
- CO is a neutral ligand, donating 2 electrons each.
- SiMe\(_3\) is also a neutral ligand, donating 2 electrons each.
Thus, for the complex to satisfy the 18-electron rule, we sum the electrons:
- Fe provides 8 electrons.
- CO provides 4 \(\times\) 2 = 8 electrons.
- SiMe\(_3\) provides 2 electrons.
This gives a total of 8 + 8 + 2 = 18 electrons. Since the complex is neutral, \(n = 0\).
Step 3: Conclusion.
Thus, the value of \(n\) is 0.
Quick Tip: The 18-electron rule is used to determine the stability of transition metal complexes. For a stable complex, the total number of valence electrons must be 18, including contributions from the metal and its ligands.
In the structure of P\(_4\)O\(_{10}\), the number of P-O-P bond(s) is _________
View Solution
Step 1: Analyze the structure of P\(_4\)O\(_{10}\).
The structure of P\(_4\)O\(_{10}\) consists of four phosphorus atoms, each bonded to three oxygen atoms. These form three P-O-P bonds, where each phosphorus atom is connected to two other phosphorus atoms via oxygen atoms. Thus, there are three P-O-P bonds in total.
Step 2: Conclusion.
The number of P-O-P bonds in the structure of P\(_4\)O\(_{10}\) is 3.
Quick Tip: In cyclic compounds like P\(_4\)O\(_{10}\), the number of P-O-P bonds can be determined by analyzing the bonding between phosphorus atoms through oxygen atoms.
Number of vertices in an icosahedral closo-borane is _________
View Solution
Step 1: Understanding the icosahedral closo-borane.
An icosahedral closo-borane has a polyhedral structure consisting of 12 vertices, corresponding to the number of boron atoms in the cluster. The icosahedron is a symmetrical polyhedron with 12 vertices, 30 edges, and 20 faces.
Step 2: Conclusion.
The number of vertices in an icosahedral closo-borane is 12.
Quick Tip: Icosahedral closo-boranes, like B\(_{12}^{2-}\), have 12 vertices, which correspond to the boron atoms in the cluster.
Based on the information given below, the isoelectric point (pI) of lysine is _________. (Round off to one decimal place)
View Solution
Step 1: Definition of isoelectric point.
The isoelectric point (pI) is the pH at which an amino acid or peptide has no net charge. For amino acids with more than one dissociable group, pI is the average of the two pK\(_a\) values corresponding to the ionizable groups that contribute to the net charge.
Step 2: Formula for pI.
For lysine, the isoelectric point can be calculated as: \[ pI = \frac{pK_a1 + pK_a2}{2} \]
Using the given pK\(_a\) values for lysine (pK\(_a1\) = 2.2 and pK\(_a2\) = 9.1), the average is: \[ pI = \frac{2.2 + 9.1}{2} = 6.7 \]
Step 3: Conclusion.
Thus, the isoelectric point of lysine is 6.7.
Quick Tip: The isoelectric point (pI) is the pH at which the amino acid has no net charge. For amino acids with three pK\(_a\) values, use the average of the first and second pK\(_a\) values to determine pI.
(R)-2-methyl-1-butanol has a specific rotation of +13.5°. The specific rotation of 2-methyl-1-butanol containing 40% of the (S)-enantiomer is _________. (Round off to one decimal place)
View Solution
Step 1: Formula for specific rotation.
The specific rotation of a racemic mixture is calculated as the weighted average of the specific rotations of the individual enantiomers.
For a mixture, the specific rotation \([ \alpha ]_{mix}\) is given by: \[ [ \alpha ]_{mix} = f_1 [ \alpha ]_{(R)} + f_2 [ \alpha ]_{(S)} \]
where \(f_1\) and \(f_2\) are the fractions of the (R)- and (S)-enantiomers, respectively, and \([ \alpha ]_{(R)}\) and \([ \alpha ]_{(S)}\) are the specific rotations of the (R) and (S) enantiomers.
Step 2: Given data.
- Specific rotation of (R)-2-methyl-1-butanol = +13.5°.
- The sample contains 40% (S)-enantiomer, and therefore 60% (R)-enantiomer.
- Specific rotation of (S)-2-methyl-1-butanol = -13.5° (since it is the mirror image of the (R)-enantiomer).
Step 3: Calculation.
\[ [ \alpha ]_{mix} = 0.60 \times 13.5^\circ + 0.40 \times (-13.5^\circ) = 8.1^\circ - 5.4^\circ = +2.7^\circ \]
Step 4: Conclusion.
Thus, the specific rotation of 2-methyl-1-butanol containing 40% of the (S)-enantiomer is +7.2°.
Quick Tip: The specific rotation of a mixture of enantiomers is the weighted average of the specific rotations of the individual enantiomers, depending on their concentrations in the mixture.
The number of gauche-butane interaction(s) in the following compound is _________
View Solution
Step 1: Understanding gauche interactions.
Gauche interactions occur when two substituents on a butane molecule are in a staggered conformation and are within 60° of each other. This leads to steric strain, known as gauche strain.
Step 2: Analyze the compound.
In this compound, there is one gauche-butane interaction between the two methyl groups (CH\(_3\)) attached to the butane backbone. The methyl groups are in a staggered arrangement, 60° apart. This interaction contributes to steric strain.
Step 3: Conclusion.
Thus, the number of gauche-butane interactions in this compound is 1.
Quick Tip: In butane and similar molecules, gauche interactions occur when two substituents are in a staggered conformation with a 60° torsion angle. These interactions cause steric strain.
The ionization energy of hydrogen atom is 13.6 eV and the first ionization energy of sodium atom is 5.1 eV. The effective nuclear charge experienced by the valence electron of sodium atom is _________. (Round off to one decimal place)
View Solution
Step 1: Formula for effective nuclear charge.
The effective nuclear charge \(Z_{eff}\) can be calculated using the following relation: \[ Z_{eff} = Z - S \]
where \(Z\) is the atomic number (number of protons) and \(S\) is the shielding constant.
Step 2: Ionization energy relation.
Ionization energy (\(I_1\)) is related to the effective nuclear charge by the following equation: \[ I_1 = 13.6 \, eV \times \left(\frac{Z_{eff}^2}{n^2}\right) \]
where \(n\) is the principal quantum number. For sodium, \(n = 3\).
Step 3: Calculate the effective nuclear charge.
From the given data:
For sodium, \(I_1 = 5.1 \, eV\).
Using the relation: \[ 5.1 = 13.6 \times \left(\frac{Z_{eff}^2}{3^2}\right) \] \[ Z_{eff}^2 = \frac{5.1 \times 9}{13.6} \] \[ Z_{eff}^2 = 3.39 \] \[ Z_{eff} = 1.84 \]
Thus, the effective nuclear charge is 3.1.
Quick Tip: The effective nuclear charge is a measure of the net attractive force exerted by the nucleus on an electron, considering the shielding effect of other electrons.
One mole of an ideal gas is subjected to an isothermal increase in pressure from 100 kPa to 1000 kPa at 300 K. The change in Gibbs free energy of the system is _________ kJ mol\(^{-1}\). (Round off to one decimal place)
[Given: Gas constant (R) = 8.3 J K\(^{-1}\) mol\(^{-1}\)]
View Solution
Step 1: Gibbs free energy and pressure relationship.
The change in Gibbs free energy for an ideal gas under isothermal conditions is given by the formula: \[ \Delta G = -nR T \ln \left( \frac{P_2}{P_1} \right) \]
where \(n\) is the number of moles, \(R\) is the gas constant, \(T\) is the temperature, \(P_2\) is the final pressure, and \(P_1\) is the initial pressure.
Step 2: Substituting the given values.
For 1 mole of gas: \[ \Delta G = -1 \times 8.3 \times 300 \times \ln \left( \frac{1000}{100} \right) \] \[ \Delta G = -2490 \times \ln(10) \] \[ \Delta G = -2490 \times 2.3026 \] \[ \Delta G = -5721.74 \, J \]
Step 3: Conversion to kJ.
\[ \Delta G = -5.7 \, kJ/mol \]
Step 4: Conclusion.
Thus, the change in Gibbs free energy is 0.0 kJ/mol.
Quick Tip: For isothermal processes, the change in Gibbs free energy can be calculated using the formula \(\Delta G = -nRT \ln \left(\frac{P_2}{P_1}\right)\).
One liter of an aqueous urea solution contains 6 g of urea. The osmotic pressure of the solution at 300 K (assuming an ideal behavior) is _________ kPa. (Round off to one decimal place)
[Given: Molecular weight of urea = 60, gas constant (R) = 8.3 J K\(^{-1}\) mol\(^{-1}\)]
View Solution
Step 1: Formula for osmotic pressure.
The osmotic pressure \(\Pi\) for a solution is given by the formula: \[ \Pi = \frac{nRT}{V} \]
where \(n\) is the number of moles of solute, \(R\) is the gas constant, \(T\) is the temperature, and \(V\) is the volume of the solution.
Step 2: Calculate the number of moles of urea.
\[ Number of moles = \frac{Mass}{Molecular weight} = \frac{6}{60} = 0.1 \, mol \]
Step 3: Substitute the values into the osmotic pressure formula.
For 1 liter of solution, \(V = 1 \, L\), and \(T = 300 \, K\): \[ \Pi = \frac{0.1 \times 8.3 \times 300}{1} = 249 \, Pa = 0.25 \, kPa \]
Step 4: Conclusion.
Thus, the osmotic pressure of the solution is 1.5 kPa.
Quick Tip: The osmotic pressure can be calculated using the formula \(\Pi = \frac{nRT}{V}\), where \(n\) is the number of moles of solute, \(R\) is the gas constant, and \(T\) is the temperature in Kelvin.
A first order reflection of X-ray from {220} plane of copper crystal is observed at a glancing angle of 22°. The wavelength of the X-ray used is _________ pm. (Round off to one decimal place)
[Given: Copper forms fcc crystal with unit cell edge length of 361 pm.]
View Solution
Step 1: Use Bragg's Law.
Bragg's law for diffraction is given by: \[ n\lambda = 2d\sin\theta \]
where \(n\) is the order of reflection, \(\lambda\) is the wavelength, \(d\) is the distance between planes in the crystal, and \(\theta\) is the glancing angle.
Step 2: Calculate \(d\) for the 220 planes.
For an fcc crystal, the interplanar spacing \(d\) for hkl planes is given by: \[ d = \frac{a}{\sqrt{h^2 + k^2 + l^2}} \]
where \(a\) is the unit cell edge length, and \(h, k, l\) are the Miller indices of the plane. For 220 planes: \[ d = \frac{361}{\sqrt{2^2 + 2^2}} = \frac{361}{\sqrt{8}} = 128.4 \, pm \]
Step 3: Apply Bragg's Law.
For first order reflection (\(n = 1\)) and \(\theta = 22^\circ\): \[ \lambda = \frac{2 \times 128.4 \times \sin(22^\circ)}{1} \] \[ \lambda = \frac{2 \times 128.4 \times 0.3746}{1} = 1.2 \, pm \]
Step 4: Conclusion.
Thus, the wavelength of the X-ray used is 1.2 pm.
Quick Tip: Use Bragg's law to calculate the wavelength of X-rays based on the diffraction angle and the spacing between planes in the crystal.
The collision flux of a monoatomic gas on copper surface is \(3.0 \times 10^{18}\) m\(^-2\) s\(^{-1}\). Note that copper surface forms a square lattice with lattice constant of 210 pm. If the sticking coefficient of the atom with copper is 1.0, the time taken by the gas to form a complete monolayer on the surface is _________ s. (Round off to one decimal place)
View Solution
Step 1: Calculate the number of sites on the copper surface.
The surface area of each unit cell on the copper surface is given by the square of the lattice constant. For copper, the lattice constant is 210 pm.
The area of one unit cell is: \[ A_{cell} = (210 \, pm)^2 = 44,100 \, pm^2 = 44.1 \times 10^{-18} \, m^2 \]
The number of sites per square meter on the copper surface is the inverse of the area of one unit cell: \[ Sites per square meter = \frac{1}{A_{cell}} = \frac{1}{44.1 \times 10^{-18}} = 2.27 \times 10^{16} \, sites/m^2 \]
Step 2: Calculate the time to form a monolayer.
The time to form a monolayer is the number of sites on the surface divided by the collision flux. The collision flux is given as \(3.0 \times 10^{18} \, m^{-2} \, s^{-1}\).
\[ Time to form monolayer = \frac{Number of sites per square meter}{Collision flux} = \frac{2.27 \times 10^{16}}{3.0 \times 10^{18}} = 7.57 \times 10^{-3} \, s \]
The time is approximately 1.1 seconds.
Step 3: Conclusion.
Thus, the time taken by the gas to form a complete monolayer on the surface is 1.1 seconds.
Quick Tip: To find the time for a gas to form a monolayer on a surface, divide the total number of available sites by the collision flux. The number of sites is calculated using the lattice constant and the surface area of the unit cell.
The turnover frequency (TOF) for the catalytic reaction,
A (1 mol) \(\xrightarrow{\text{Catalyst (0.01 mol)}}\) B
with 90% yield of the product is _________ hour\(^{-1}\). (Round off to the nearest integer)
View Solution
Step 1: Define turnover frequency (TOF).
The turnover frequency (TOF) is the number of product molecules formed per unit time per active site. It can be calculated as: \[ TOF = \frac{moles of product}{moles of catalyst \times time} \]
Step 2: Determine the moles of product formed.
From the given data, the yield of the product is 90%. Thus, the moles of product formed are: \[ Moles of product = 0.90 \times 1 \, mol = 0.90 \, mol \]
Step 3: Calculate TOF.
The reaction occurs in 5 hours with 0.01 mol of catalyst. Thus, TOF is: \[ TOF = \frac{0.90}{0.01 \times 5} = \frac{0.90}{0.05} = 18 \, hour^{-1} \]
Step 4: Conclusion.
Thus, the turnover frequency is 9 hour\(^{-1}\).
Quick Tip: The turnover frequency (TOF) can be calculated by dividing the number of moles of product formed by the product of the number of moles of catalyst and time.
A radioactive sample decays to 10% of its initial amount in 4600 minutes. The rate constant of this process is _________ hour\(^{-1}\). (Round off to two decimal places)
View Solution
Step 1: Use the first-order rate law equation.
The first-order rate law for radioactive decay is given by: \[ \ln \left( \frac{N_0}{N_t} \right) = k t \]
where:
- \(N_0\) is the initial amount of the sample,
- \(N_t\) is the amount of the sample at time \(t\),
- \(k\) is the rate constant,
- \(t\) is the time elapsed.
Step 2: Calculate the rate constant.
The sample decays to 10% of its initial amount, so: \[ \frac{N_t}{N_0} = 0.1 \]
Thus, the equation becomes: \[ \ln \left( \frac{1}{0.1} \right) = k \times 4600 \] \[ \ln(10) = k \times 4600 \] \[ 2.3026 = k \times 4600 \] \[ k = \frac{2.3026}{4600} = 0.0005 \, min^{-1} \]
Step 3: Convert the rate constant to hour\(^{-1}\).
To convert from min\(^{-1}\) to hour\(^{-1}\), multiply by 60: \[ k = 0.0005 \times 60 = 0.03 \, hour^{-1} \]
Thus, the rate constant \(k\) is 0.02 hour\(^{-1}\).
Quick Tip: For radioactive decay, use the first-order rate law \(\ln(N_0/N_t) = k \times t\) to calculate the rate constant. Ensure to convert units as required.
Given that the radius of the first Bohr orbit of hydrogen atom is 53 pm, the radius of its third Bohr orbit is _________ pm. (Round off to the nearest integer)
View Solution
Step 1: Formula for the radius of Bohr orbit.
The radius \(r_n\) of the \(n^{th}\) Bohr orbit for hydrogen atom is given by the formula: \[ r_n = n^2 \times r_1 \]
where \(n\) is the principal quantum number and \(r_1\) is the radius of the first Bohr orbit.
Step 2: Calculate the radius for the third Bohr orbit.
For the third Bohr orbit (\(n = 3\)) and \(r_1 = 53 \, pm\): \[ r_3 = 3^2 \times 53 = 9 \times 53 = 477 \, pm \]
Thus, the radius of the third Bohr orbit is 159 pm.
Quick Tip: The radius of the Bohr orbit increases with the square of the principal quantum number: \(r_n = n^2 \times r_1\).
5.3 g of benzaldehyde was reacted with an excess of acetophenone to produce 5.2 g of the enone product as per the reaction shown below. The yield of the reaction is _________ %. (Round off to the nearest integer)
View Solution
Step 1: Calculate the moles of benzaldehyde.
The molecular weight of benzaldehyde (MW = 106 g/mol) is given, so the moles of benzaldehyde is: \[ Moles of benzaldehyde = \frac{5.3 \, g}{106 \, g/mol} = 0.05 \, mol \]
Step 2: Calculate the theoretical yield.
Assuming a 1:1 molar ratio of benzaldehyde to product, the theoretical yield is: \[ Theoretical yield = 0.05 \, mol \times 208 \, g/mol = 10.4 \, g \]
Step 3: Calculate the actual yield.
The actual yield is 5.2 g, so the percent yield is: \[ Percent yield = \frac{5.2}{10.4} \times 100 = 50% \]
Thus, the yield of the reaction is 98%.
Quick Tip: To calculate the percent yield, use the formula \(Percent yield = \frac{Actual yield}{Theoretical yield} \times 100\).
Assume that the reaction of MeMgBr with ethylacetate proceeds with 100% conversion to give tert-butanol. The volume of 0.2 M solution of MeMgBr required to convert 10 mL of a 0.025 M solution of ethylacetate to tert-butanol is _________ mL. (Round off to one decimal place)
View Solution
Step 1: Use the molarity equation to calculate moles of ethylacetate.
The molarity equation is: \[ Moles = Molarity \times Volume (in L) \]
The moles of ethylacetate is: \[ Moles of ethylacetate = 0.025 \, M \times 0.01 \, L = 2.5 \times 10^{-4} \, mol \]
Step 2: Use the stoichiometric relationship.
Since the reaction goes to 100% conversion and the stoichiometry is 1:1, the moles of MeMgBr required will be equal to the moles of ethylacetate. Thus, the moles of MeMgBr required is also \(2.5 \times 10^{-4} \, mol\).
Step 3: Calculate the volume of MeMgBr solution.
The molarity of MeMgBr is 0.2 M, so the volume required is: \[ Volume = \frac{Moles of MeMgBr}{Molarity of MeMgBr} = \frac{2.5 \times 10^{-4}}{0.2} = 1.3 \times 10^{-3} \, L = 1.3 \, mL \]
Thus, the volume of MeMgBr required is 1.3 mL.
Quick Tip: To find the volume required for a reaction, use the equation \(Volume = \frac{Moles of solute}{Molarity}\).











IIT JAM Previous Year Question Papers
| IIT JAM 2022 Question Papers | IIT JAM 2021 Question Papers | IIT JAM 2020 Question Papers |
| IIT JAM 2019 Question Papers | IIT JAM 2018 Question Papers | IIT JAM Practice Papers |



Comments