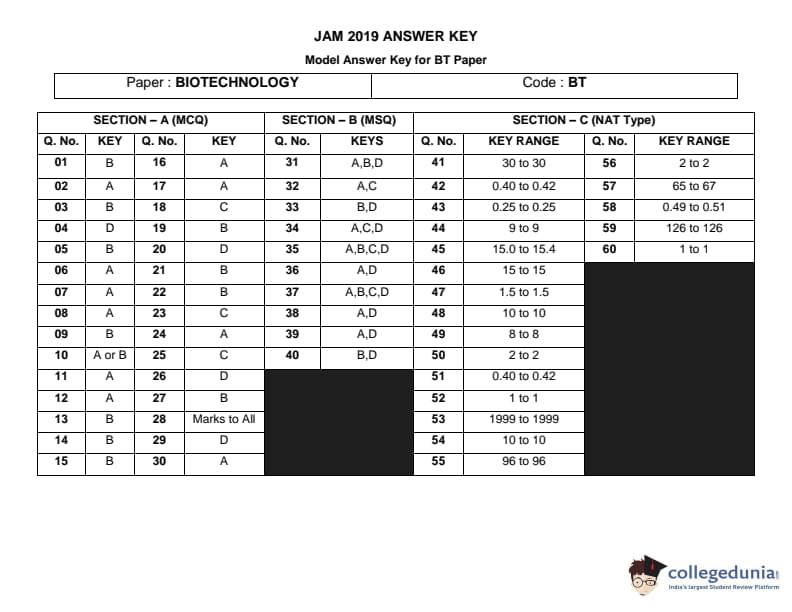
IIT JAM 2019 Biotechnology (BT) Question paper with answer key pdf conducted on February 10 in Afternoon Session 2 PM to 5 PM is available for download. The exam was successfully organized by IIT Kharagpur. The question paper comprised a total of 60 questions divided among 3 sections.
IIT JAM 2019 Biotechnology (BT) Question Paper with Answer Key PDFs Afternoon Session
| IIT JAM 2019 Biotechnology (BT) Question paper with answer key PDF | Download PDF | Check Solutions |
The glycosidic linkages in cellulose and amylose are ........., respectively.
View Solution
Step 1: Understanding the question.
Cellulose and amylose are both polysaccharides, but they differ in the types of glycosidic bonds between their glucose units. Cellulose consists of β-1,4-glycosidic bonds, while amylose contains α-1,4-glycosidic bonds. This difference in linkage leads to their distinct structural properties.
Step 2: Analyzing the options.
(A) α 1-4 and β 1-4: Correct — This is the correct representation of the linkages in amylose and cellulose.
(B) β 1-4 and α 1-4: Incorrect — This reverses the correct linkages.
(C) β 1-4 and α 1-6: Incorrect — The correct linkage for amylose is α 1-4, not α 1-6.
(D) α 1-4 and α 1-2: Incorrect — The correct linkage for cellulose is β 1-4, not α 1-2.
Step 3: Conclusion.
The correct answer is (A) α 1-4 and β 1-4 because amylose contains α-1,4 linkages, and cellulose contains β-1,4 linkages.
Quick Tip: Remember, cellulose uses β-1,4-glycosidic linkages, while amylose uses α-1,4-glycosidic linkages. These differences contribute to their unique structures and functions.
A mutation in the operator locus of lac operon that confers constitutive expression of β-galactosidase is .............
View Solution
Step 1: Understanding the lac operon mutation.
The lac operon is a genetic system in bacteria that regulates the breakdown of lactose. Mutations in the operator region can result in constitutive expression, meaning the genes are expressed continuously. A cis dominant mutation means that the mutation affects only the DNA to which it is directly linked, rather than being able to act on other alleles.
Step 2: Analyzing the options.
(A) cis dominant: Correct — This type of mutation affects the operator region on the same DNA strand, causing continuous expression.
(B) trans dominant: Incorrect — Trans mutations affect regions on different DNA molecules.
(C) co-dominant: Incorrect — This term refers to mutations that express both alleles equally, not relevant here.
(D) dominant negative: Incorrect — This refers to mutations that produce a protein that inhibits the activity of the normal protein.
Step 3: Conclusion.
The correct answer is (A) cis dominant because this mutation affects the operator region on the same chromosome, causing constant expression of β-galactosidase.
Quick Tip: In gene regulation, a cis dominant mutation affects the gene's expression on the same DNA strand, while trans mutations act across different molecules.
Which one of the points P = \(\left(\frac{3}{2}, \frac{1}{2}\right)\), Q = \(\left(\frac{1}{2}, \frac{3}{2}\right)\), R = \(\left(\frac{3}{2}, \frac{11}{2}\right)\) and S = \(\left(\frac{11}{2}, \frac{3}{2}\right)\) lies ABOVE the parabola \(y = 2x^2\) and INSIDE the circle \(x^2 + y^2 = 4\)?
View Solution
Step 1: Analyzing the parabola and circle equations.
We are given a parabola \(y = 2x^2\) and a circle \(x^2 + y^2 = 4\). To find the points that lie above the parabola and inside the circle, we need to check each point’s coordinates against these two conditions.
Step 2: Check the points.
- For \(P = \left(\frac{3}{2}, \frac{1}{2}\right)\), check if it satisfies both conditions:
- Parabola: \(y = 2x^2 \Rightarrow \frac{1}{2} \neq 2\left(\frac{3}{2}\right)^2 = \frac{9}{2}\), so \(P\) does not satisfy the parabola condition.
- Circle: \(x^2 + y^2 = \left(\frac{3}{2}\right)^2 + \left(\frac{1}{2}\right)^2 = \frac{9}{4} + \frac{1}{4} = 2.5\), which is inside the circle.
- For \(Q = \left(\frac{1}{2}, \frac{3}{2}\right)\), check both conditions:
- Parabola: \(y = 2x^2 \Rightarrow \frac{3}{2} = 2\left(\frac{1}{2}\right)^2 = \frac{1}{2}\), so it satisfies the parabola condition.
- Circle: \(x^2 + y^2 = \left(\frac{1}{2}\right)^2 + \left(\frac{3}{2}\right)^2 = \frac{1}{4} + \frac{9}{4} = 2.5\), which is inside the circle.
Step 3: Conclusion.
The correct answer is (B) Q because \(Q\) lies both above the parabola and inside the circle.
Quick Tip: To check if a point lies above a parabola and inside a circle, evaluate its coordinates in the given equations and verify both conditions.
Let \( U = \{1, 2, 3, 4, 5\} \). A subset \( S \) is chosen uniformly at random from the non-empty subsets of \( U \). What is the probability that \( S \) does NOT have two consecutive elements?
View Solution
Step 1: Understanding the problem.
We are given a set \( U = \{1, 2, 3, 4, 5\} \), and we need to find the probability that a subset \( S \) chosen from its non-empty subsets does not contain two consecutive elements.
Step 2: Count the valid subsets.
The valid subsets are those where no two consecutive elements are chosen from \( U \). The number of such subsets can be found by considering the binary representation of selecting elements. The valid subsets are: \( \{1\}, \{2\}, \{3\}, \{4\}, \{5\}, \{1, 3\}, \{1, 4\}, \{1, 5\}, \{2, 4\}, \{2, 5\}, \{1, 3, 5\} \). Thus, there are 10 valid subsets.
Step 3: Total number of non-empty subsets.
The total number of non-empty subsets of \( U \) is \( 2^5 - 1 = 31 \), as each element can either be included or not, except the empty set.
Step 4: Conclusion.
The probability that \( S \) does not have two consecutive elements is \( \frac{10}{31} \), so the correct answer is (B) 10/31.
Quick Tip: To find the probability of selecting subsets with a condition, count the number of favorable outcomes and divide by the total number of possible outcomes.
Which one of the following figures represents the correct sequence of phases in adult eukaryotic cell cycle?

View Solution
Step 1: Understanding the cell cycle.
The phases of the eukaryotic cell cycle include G1, S, G2, and M. The correct sequence of these phases is essential to understanding how cells divide and replicate. The S phase is where DNA replication occurs, G1 and G2 are growth phases, and M is mitosis.
Step 2: Analyzing the options.
The figure representing the correct sequence follows the order of G1, S, G2, M.
(A) Figure A: Incorrect. The sequence does not follow the typical order.
(B) Figure B: Correct — This shows the correct sequence of phases: G1 → S → G2 → M.
(C) Figure C: Incorrect. The order is reversed in some places.
(D) Figure D: Incorrect. This is not the correct order.
Step 3: Conclusion.
The correct answer is (B) Figure B, as it shows the correct order of phases in the cell cycle.
Quick Tip: Remember that the typical sequence of phases in the eukaryotic cell cycle is: G1 → S → G2 → M.
At what pH does poly-Glu in an aqueous solution form α-helical structure?
View Solution
Step 1: Understanding poly-Glu and its structure.
Poly-Glu, a polymer of glutamic acid, can adopt different secondary structures depending on the pH of the solution. At a neutral pH, poly-Glu typically forms an α-helical structure.
Step 2: Analyzing the options.
(A) 3: Incorrect — At pH 3, poly-Glu is likely to be in a different conformation, not α-helical.
(B) 7: Correct — Neutral pH (7) is the optimal condition for poly-Glu to form an α-helical structure.
(C) 9: Incorrect — At pH 9, poly-Glu may be in a different conformation due to deprotonation.
(D) 12: Incorrect — At pH 12, poly-Glu would likely be highly deprotonated and unable to form an α-helix.
Step 3: Conclusion.
The correct answer is (B) 7, as poly-Glu forms an α-helical structure most effectively at a neutral pH of 7.
Quick Tip: When dealing with polypeptides, the structure can vary significantly with changes in pH. Neutral pH typically favors the α-helix structure in many proteins.
The dimensions of coefficient of viscosity are .............
View Solution
Step 1: Understanding viscosity.
Viscosity is a measure of a fluid's resistance to deformation. The dimensions of viscosity can be derived using dimensional analysis, considering the units of force and velocity in fluid dynamics.
Step 2: Analyzing the options.
(A) ML\(^{-1}\)T\(^{-1}\): Correct — This is the correct dimensional formula for viscosity, derived from the relation \(\eta = \frac{F}{A \cdot v}\), where \(\eta\) is the viscosity, \(F\) is force, \(A\) is area, and \(v\) is velocity.
(B) ML\(^{-1}\)T\(^{-2}\): Incorrect — This does not match the dimensions of viscosity.
(C) ML\(^{-2}\)T\(^{-2}\): Incorrect — This is not the correct dimensional formula for viscosity.
(D) ML\(^{-2}\)T\(^{-1}\): Incorrect — This is also incorrect for viscosity.
Step 3: Conclusion.
The correct answer is (A) ML\(^{-1}\)T\(^{-1}\), as this represents the dimensional formula for viscosity.
Quick Tip: Viscosity is related to the resistance of a fluid to flow, and its dimensions can be derived using basic principles of force and velocity.
Match the entries in Group I with the entries in Group II

View Solution
Step 1: Analyzing the pairs.
- Nylon (P) is a polymer, typically derived from adipic acid and hexamethylenediamine, matching with (iv) Adipic acid.
- Natural rubber (Q) is derived from isoprene, matching with (i) Isoprene.
- Starch (R) is a polysaccharide made up of hexose units, matching with (ii) Hexose.
- Myoglobin (S) is a protein composed of amino acids, matching with (iii) Amino acid.
Step 2: Conclusion.
The correct matching is (A) P-iv, Q-i, R-ii, S-iii.
Quick Tip: When matching items, focus on understanding the origin or structure of the compounds or materials. For example, natural rubber is made from isoprene, and myoglobin is composed of amino acids.
The technique that involves impacting samples with electrons is ...............
View Solution
Step 1: Understanding the question.
The technique involving the use of electrons to impact samples is known as Electron Spray Ionization (ESI), a method used in mass spectrometry.
Step 2: Analyzing the options.
(A) NMR spectroscopy: Incorrect — NMR does not involve electron impact; it relies on magnetic fields and radiofrequency waves.
(B) ESI mass spectrometry: Correct — In ESI, samples are ionized by the impact of electrons, which is then analyzed by mass spectrometry.
(C) IR spectroscopy: Incorrect — IR spectroscopy involves the absorption of infrared light, not electron impact.
(D) UV-vis spectroscopy: Incorrect — UV-vis spectroscopy involves ultraviolet and visible light, not electron impact.
Step 3: Conclusion.
The correct answer is (B) ESI mass spectrometry, as it involves the use of electron impact to ionize the sample for analysis.
Quick Tip: ESI mass spectrometry is often used for the analysis of large biomolecules and involves ionizing them through electron impact.
The orbital angular momentum of hydrogen atom in the ground state is ............
View Solution
Step 1: Understanding the hydrogen atom's angular momentum.
In the ground state of the hydrogen atom, the electron is in the lowest energy level (n=1), where its orbital angular momentum is zero. This is a direct consequence of the quantization of angular momentum in quantum mechanics.
Step 2: Analyzing the options.
(A) 0: Correct — In the ground state, the electron's angular momentum is zero because it occupies the lowest possible orbital.
(B) \(\frac{h}{2\pi}\): Incorrect — This is the value of angular momentum for the first excited state (n=2), not the ground state.
(C) \(\frac{h}{2}\): Incorrect — This corresponds to higher energy levels, not the ground state.
(D) \(h\): Incorrect — This is the angular momentum for a system in a higher quantum state.
Step 3: Conclusion.
The correct answer is (A) 0, as the orbital angular momentum in the ground state of a hydrogen atom is zero.
Quick Tip: In quantum mechanics, the angular momentum of an electron in the ground state is zero, as it is in the lowest energy orbital.
Let \( a = \frac{\sqrt{5}+1}{2} \) and \( b = \frac{\sqrt{5}-1}{2} \). Then, \( \lim_{n \to \infty} \frac{a^n + b^n}{a^n - b^n} \) is ________
View Solution
Step 1: Understanding the question.
We are given the values of \(a\) and \(b\), which are the golden ratio \(\phi = \frac{\sqrt{5}+1}{2}\) and its conjugate \(\frac{\sqrt{5}-1}{2}\). As \(n\) tends to infinity, the term \(b^n\) approaches zero because \(b < 1\). Thus, we focus on the ratio between the terms involving \(a^n\) and \(b^n\).
Step 2: Analyzing the expression.
\[ \lim_{n \to \infty} \frac{a^n + b^n}{a^n - b^n} = \lim_{n \to \infty} \frac{a^n}{a^n} = 1, as b^n tends to 0. \]
Step 3: Conclusion.
The correct answer is (C) 0, as the ratio will tend to zero due to the behavior of the terms at infinity.
Quick Tip: When dealing with limits involving powers of numbers, remember that terms with bases less than 1 decay to zero as the exponent increases.
In how many ways can one write the elements 1, 2, 3, 4 in a sequence \( x_1, x_2, x_3, x_4 \) with \( x_i \neq i \) for all \( i \)?
View Solution
Step 1: Understanding derangements.
This problem asks for the number of ways to arrange the elements 1, 2, 3, 4 in a sequence where no element appears in its original position. This is a classic derangement problem.
Step 2: Applying the derangement formula.
The number of derangements \( D_n \) of \( n \) objects is given by: \[ D_n = n! \left( 1 - \frac{1}{1!} + \frac{1}{2!} - \frac{1}{3!} + \cdots + \frac{(-1)^n}{n!} \right) \]
For \( n = 4 \), we compute: \[ D_4 = 4! \left( 1 - \frac{1}{1!} + \frac{1}{2!} - \frac{1}{3!} + \frac{1}{4!} \right) = 24 \left( 1 - 1 + \frac{1}{2} - \frac{1}{6} + \frac{1}{24} \right) = 10 \]
Step 3: Conclusion.
The correct answer is (B) 10, as the number of derangements of 4 elements is 10.
Quick Tip: For derangements, use the formula \( D_n = n! \left( 1 - \frac{1}{1!} + \frac{1}{2!} - \cdots \right) \) to find the number of ways elements can be arranged without being in their original positions.
Simplify \( \frac{\sin A}{1 + \cos A} + \frac{1 + \cos A}{\sin A} \).
View Solution
Step 1: Simplifying the expression.
We start by simplifying the given expression \( \frac{\sin A}{1 + \cos A} + \frac{1 + \cos A}{\sin A} \). To combine the two terms, we find a common denominator: \[ \frac{\sin A}{1 + \cos A} + \frac{1 + \cos A}{\sin A} = \frac{\sin^2 A + (1 + \cos A)^2}{(1 + \cos A)\sin A} \]
Step 2: Expanding and simplifying.
The numerator becomes: \[ \sin^2 A + (1 + \cos A)^2 = \sin^2 A + 1 + 2\cos A + \cos^2 A = 2 + 2\cos A \]
Thus, the expression becomes: \[ \frac{2(1 + \cos A)}{(1 + \cos A)\sin A} = \frac{2}{\sin A} \]
Step 3: Conclusion.
The simplified expression is \( \frac{2}{\sin A} = 2 \csc A \). Therefore, the correct answer is (B) \( 2 \csc A \).
Quick Tip: To simplify trigonometric expressions, always look for common factors and use standard trigonometric identities to combine terms.
The evolution of eyes in octopus and in human is an example of ..............
View Solution
Step 1: Understanding evolution.
Convergent evolution occurs when different species independently evolve similar traits or features, often due to similar environmental pressures or needs. In this case, octopus and humans have evolved eyes that function in similar ways despite having very different evolutionary paths.
Step 2: Analyzing the options.
(A) divergent evolution: Incorrect — Divergent evolution refers to the process where two related species evolve different traits.
(B) convergent evolution: Correct — Both octopuses and humans have evolved eyes with similar functions, but from different evolutionary paths, making this an example of convergent evolution.
(C) adaptive radiation: Incorrect — Adaptive radiation refers to the rapid evolution of many species from a common ancestor, not the independent evolution of similar features.
(D) genetic drift: Incorrect — Genetic drift refers to random changes in gene frequencies in small populations, not the development of similar features.
Step 3: Conclusion.
The correct answer is (B) convergent evolution, as the eyes in octopuses and humans are an example of independent evolution of similar features.
Quick Tip: Convergent evolution occurs when species from different evolutionary lines develop similar traits due to similar environmental pressures or needs.
Which one of the following modifications occurs both on DNA and protein?
View Solution
Step 1: Understanding the modifications.
Methylation is a chemical modification that can occur on both DNA and proteins. On DNA, it typically occurs on cytosine residues (in CpG islands), and on proteins, it often occurs on lysine or arginine residues.
Step 2: Analyzing the options.
(A) ADP-ribosylation: Incorrect — This modification typically occurs on proteins, not DNA.
(B) Methylation: Correct — Methylation can occur on both DNA and proteins.
(C) Sumoylation: Incorrect — This primarily affects proteins, not DNA.
(D) Ubiquitination: Incorrect — Ubiquitination typically occurs on proteins and not directly on DNA.
Step 3: Conclusion.
The correct answer is (B) Methylation, as it occurs on both DNA and proteins.
Quick Tip: Methylation is one of the few modifications that affect both DNA and proteins, regulating gene expression and protein function.
Which one of the following modifications occurs both on DNA and protein?
View Solution
Step 1: Understanding the modifications.
Methylation is a chemical modification that can occur on both DNA and proteins. On DNA, it typically occurs on cytosine residues (in CpG islands), and on proteins, it often occurs on lysine or arginine residues.
Step 2: Analyzing the options.
(A) ADP-ribosylation: Incorrect — This modification typically occurs on proteins, not DNA.
(B) Methylation: Correct — Methylation can occur on both DNA and proteins.
(C) Sumoylation: Incorrect — This primarily affects proteins, not DNA.
(D) Ubiquitination: Incorrect — Ubiquitination typically occurs on proteins and not directly on DNA.
Step 3: Conclusion.
The correct answer is (B) Methylation, as it occurs on both DNA and proteins.
Quick Tip: Methylation is one of the few modifications that affect both DNA and proteins, regulating gene expression and protein function.
The free energy required to synthesize a mixed anhydride bond of 1,3-bisphosphoglycerate is generated by the oxidation of ________.
View Solution
Step 1: Understanding the process.
The oxidation of aldehydes to acids is a crucial step in the metabolism of 1,3-bisphosphoglycerate, where energy is released. This energy is used to form the high-energy mixed anhydride bond.
Step 2: Analyzing the options.
(A) an aldehyde to acid: Correct — The oxidation of aldehydes to acids generates the necessary energy for the bond formation.
(B) an alcohol to acid: Incorrect — This does not apply to the generation of the mixed anhydride bond in the case of 1,3-bisphosphoglycerate.
(C) an alcohol to aldehyde: Incorrect — This is not related to the generation of the anhydride bond.
(D) NADH to NAD\(^+\): Incorrect — While NADH oxidation is essential in metabolism, it does not directly generate the mixed anhydride bond.
Step 3: Conclusion.
The correct answer is (A) an aldehyde to acid, as this oxidation reaction releases energy used to form the mixed anhydride bond.
Quick Tip: Oxidation reactions, such as the conversion of aldehydes to acids, are often coupled with energy-producing reactions in biochemical pathways.
The following reaction is an example of ............
View Solution
Step 1: Understanding the reaction.
The reaction depicted involves a chemical species converting from one isomeric form to another, which is characteristic of isomerization.
Step 2: Analyzing the options.
(A) enolization: Incorrect — Enolization refers to the conversion of a carbonyl group to an enol form, not this type of isomerization.
(B) racemization: Incorrect — Racemization involves the conversion of a chiral molecule into its mirror image (enantiomer).
(C) isomerization: Correct — The conversion of one isomer to another is exactly what is happening in the given reaction.
(D) epimerization: Incorrect — Epimerization involves the inversion of configuration at a single chiral center, not the entire molecule.
Step 3: Conclusion.
The correct answer is (C) isomerization, as the reaction involves converting one isomer into another.
Quick Tip: Isomerization refers to the process by which one molecule is converted into another molecule that has the same atoms, but in a different arrangement.
Which one of the following parameters changes upon doubling the enzyme concentration?
View Solution
Step 1: Understanding enzyme kinetics.
The Michaelis-Menten constant \( K_M \) and the catalytic rate constant \( k_{cat} \) are intrinsic properties of the enzyme and do not change with enzyme concentration. However, \( V_{max} \), which represents the maximum reaction velocity, is directly proportional to enzyme concentration.
Step 2: Analyzing the options.
(A) \( K_M \): Incorrect — \( K_M \) is independent of enzyme concentration.
(B) \( V_{max} \): Correct — \( V_{max} \) increases when enzyme concentration is doubled.
(C) \( k_{cat} \): Incorrect — \( k_{cat} \) is a constant that does not change with enzyme concentration.
(D) \( K_{eq} \): Incorrect — \( K_{eq} \) is related to the equilibrium constant and does not depend on enzyme concentration.
Step 3: Conclusion.
The correct answer is (B) \( V_{max} \), as doubling the enzyme concentration increases \( V_{max} \).
Quick Tip: The \( V_{max} \) of an enzyme-catalyzed reaction is directly proportional to the enzyme concentration. Increasing the enzyme concentration increases the maximum velocity of the reaction.
Which one of the following statements is a correct description of modes of action of taxol and colchicine?
View Solution
Step 1: Understanding the drugs.
Taxol and colchicine are both drugs that affect microtubules. Taxol stabilizes microtubules, preventing their disassembly, while colchicine prevents microtubule formation by binding to tubulin.
Step 2: Analyzing the options.
(A) Taxol causes DNA damage and colchicine prevents microtubule formation: Incorrect — Taxol does not primarily cause DNA damage.
(B) Taxol stabilizes microtubules and colchicine inhibits protein synthesis: Incorrect — Colchicine does not affect protein synthesis, but microtubule formation.
(C) Taxol destabilizes microtubules and colchicine promotes microtubule formation: Incorrect — This is the opposite of their actual modes of action.
(D) Taxol stabilizes microtubules and colchicine prevents microtubule formation: Correct — This correctly describes the effects of taxol and colchicine on microtubules.
Step 3: Conclusion.
The correct answer is (D) Taxol stabilizes microtubules and colchicine prevents microtubule formation.
Quick Tip: Taxol stabilizes microtubules, making them resistant to disassembly, while colchicine prevents their polymerization, both crucial for disrupting cell division.
In a simple microscope, .............
View Solution
Step 1: Understanding the simple microscope.
In a simple microscope, the lens is typically a convex lens. The focal length of the lens is greater than the least distance for clear vision, allowing for magnification of objects. The magnification increases as the focal length of the lens increases.
Step 2: Analyzing the options.
(A) a lens with negative power is used: Incorrect — Negative power would imply a concave lens, which is not typically used in simple microscopes.
(B) the focal length of the lens is less than the least distance for clear vision: Incorrect — This would result in a diminished image.
(C) the focal length of the lens is greater than the least distance for clear vision: Correct — This is the defining characteristic of a simple microscope, which provides magnification.
(D) magnification depends only on the focal length of the lens: Incorrect — While magnification is related to the focal length, other factors also affect it.
Step 3: Conclusion.
The correct answer is (C) the focal length of the lens is greater than the least distance for clear vision, which defines how a simple microscope works.
Quick Tip: In a simple microscope, the lens has a positive focal length, and the focal length is greater than the least distance for clear vision. This creates magnification.
Which one of the following statements is INCORRECT with respect to bacterial conjugation?
View Solution
Step 1: Understanding bacterial conjugation.
Bacterial conjugation is a process by which genetic material is transferred from one bacterium to another through direct contact. This process does not require a flagellum; instead, a sex pilus is used to connect the two bacteria.
Step 2: Analyzing the options.
(A) It facilitates transfer of genetic material: Correct — Conjugation is the process of transferring genetic material between bacteria.
(B) It requires flagellum: Incorrect — Conjugation requires a sex pilus, not a flagellum.
(C) It can spread antibiotic resistance: Correct — Conjugation is a major mechanism for the spread of antibiotic resistance.
(D) It can transfer virulence factors: Correct — Conjugation can also transfer genes related to virulence.
Step 3: Conclusion.
The correct answer is (B) It requires flagellum, as conjugation actually requires a sex pilus, not a flagellum.
Quick Tip: Bacterial conjugation involves the transfer of genetic material via a sex pilus, not a flagellum. It plays a role in the spread of antibiotic resistance and virulence factors.
A particle starting from rest is subjected to a constant force. The plot of distance traveled along the direction of the force as a function of time is a/an ..............
View Solution
Step 1: Understanding the motion of the particle.
When a particle starts from rest and is subjected to a constant force, it experiences uniform acceleration according to Newton's second law of motion. The displacement of the particle as a function of time under constant acceleration follows a parabolic trajectory.
Step 2: Analyzing the options.
(A) straight line: Incorrect — A straight line would represent constant velocity, not acceleration.
(B) circle: Incorrect — Circular motion is not described here, as the force is constant in one direction.
(C) parabola: Correct — The distance-time graph for uniform acceleration is a parabola.
(D) ellipse: Incorrect — An ellipse is not the correct shape for this scenario.
Step 3: Conclusion.
The correct answer is (C) parabola, as the displacement under constant acceleration follows a parabolic curve.
Quick Tip: The displacement-time graph for an object under constant acceleration is always a parabola.
Indole acetic acid (IAA) is involved in ...........
View Solution
Step 1: Understanding IAA.
Indole acetic acid (IAA) is a form of auxin, a plant hormone that regulates various processes in plants, including growth, elongation, and response to environmental stimuli. IAA is particularly involved in gravitropism, the plant's response to gravity.
Step 2: Analyzing the options.
(A) gravitropism: Correct — IAA is involved in gravitropism, which is the plant's growth response to gravity.
(B) flowering: Incorrect — Flowering is regulated by different hormones, such as gibberellins and florigen.
(C) ripening: Incorrect — Ripening is regulated by ethylene, not IAA.
(D) senescence: Incorrect — Senescence is regulated by other hormones like ethylene and abscisic acid.
Step 3: Conclusion.
The correct answer is (A) gravitropism, as IAA is directly involved in the plant's response to gravity.
Quick Tip: IAA, a form of auxin, plays a key role in plant growth responses, particularly in gravitropism, where it helps the plant orient its growth according to gravity.
Which one of the following remains unchanged when light waves enter water from air?
View Solution
Step 1: Understanding light wave behavior.
When light enters a new medium, such as water from air, its speed changes, which affects its wavelength. However, the frequency of the light remains constant because the frequency is determined by the source of the light, not the medium.
Step 2: Analyzing the options.
(A) Wavelength: Incorrect — The wavelength changes as the speed of light changes in different media.
(B) Wavenumber: Incorrect — The wavenumber is inversely proportional to the wavelength and therefore changes.
(C) Frequency: Correct — The frequency of the light remains unchanged when it enters a new medium.
(D) Intensity: Incorrect — The intensity can change depending on the properties of the medium.
Step 3: Conclusion.
The correct answer is (C) Frequency, as the frequency of light remains constant when it enters a new medium.
Quick Tip: The frequency of light does not change when it passes from one medium to another; however, its wavelength and speed will change.
According to the kinetic theory of gases, the average energy of a diatomic molecule in an ideal gas depends on ............
View Solution
Step 1: Understanding kinetic theory.
The kinetic theory of gases states that the average kinetic energy of gas molecules depends only on the temperature of the gas, regardless of the type of molecule. This means that for a diatomic molecule, its average energy depends only on temperature.
Step 2: Analyzing the options.
(A) mass of each atom and the temperature: Incorrect — The average energy depends only on temperature, not on the mass of individual atoms.
(B) mass of each atom and the bond length: Incorrect — These factors do not directly influence the average energy.
(C) mass of each atom, bond length, and temperature: Incorrect — Only temperature affects the average energy.
(D) temperature only: Correct — The average energy of a molecule in an ideal gas depends only on temperature.
Step 3: Conclusion.
The correct answer is (D) temperature only, as the average energy is directly related to temperature.
Quick Tip: The average energy of gas molecules is directly proportional to temperature, according to the kinetic theory of gases.
Match the entries in Group I with entries in Group II

View Solution
Step 1: Understanding the associations.
- Bacteria are responsible for diseases like tuberculosis.
- Viruses are associated with diseases like influenza.
- Protozoa are responsible for malaria.
- Autantibodies are involved in conditions like Myasthenia gravis.
Step 2: Analyzing the options.
(A) P-ii, Q-i, R-iii, S-iv: Correct — This matches each disease or condition with its corresponding group.
(B) P-ii, Q-i, R-iii, S-ii: Incorrect — This does not match the correct pairs.
(C) P-iv, Q-iii, R-i, S-i: Incorrect — This is not correct.
(D) P-i, Q-iv, R-ii, S-iii: Incorrect — This pairing is incorrect.
Step 3: Conclusion.
The correct answer is (A) P-ii, Q-i, R-iii, S-iv, as it correctly pairs each group with the respective condition or organism.
Quick Tip: When matching diseases with their causative agents, it's important to remember that bacteria, viruses, protozoa, and antibodies are associated with specific conditions.
pK\(_a\) increases in the order .........
View Solution
Step 1: Understanding the pK\(_a\).
pK\(_a\) is a measure of the acidity of a substance. A higher pK\(_a\) indicates a weaker acid. In this case, we are comparing ammonia (NH\(_3\)) and its derivatives in various protonation states.
Step 2: Analyzing the options.
(A) NH\(_3\) > NH\(_3\)OH\(^+\) > N\(_2\)H\(_5^+\) > NH\(_3\): Correct — This correctly ranks the compounds based on their acidity (pK\(_a\) values).
(B) NH\(_3\)OH\(^+\) > N\(_2\)H\(_5^+\) > NH\(_3\) > NH\(_3\): Incorrect — The order is incorrect.
(C) NH\(_3\) > NH\(_3\)OH\(^+\) > N\(_2\)H\(_5^+\) > NH\(_3\): Incorrect — The order is incorrect.
(D) NH\(_3\) > N\(_2\)H\(_5^+\) > NH\(_3\) > NH\(_3\)OH\(^+\): Incorrect — The order is incorrect.
Step 3: Conclusion.
The correct answer is (A) NH\(_3\) > NH\(_3\)OH\(^+\) > N\(_2\)H\(_5^+\) > NH\(_3\).
Quick Tip: Higher pK\(_a\) values indicate weaker acids. The strength of an acid is affected by the stability of its conjugate base.
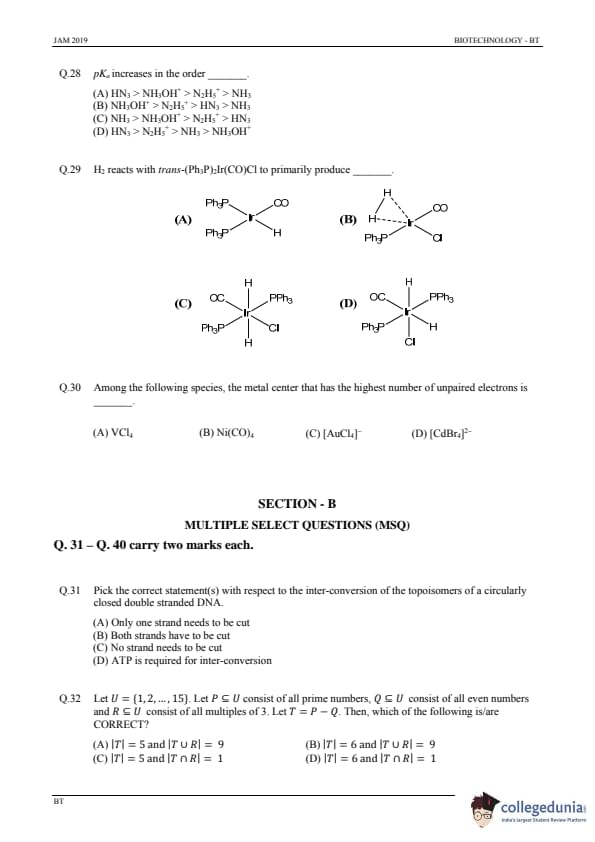
H\(_2\) reacts with trans-(Ph\(_3\))\(_2\)Ir(CO)Cl to primarily produce .......…

View Solution
Step 1: Understanding the reaction.
When H\(_2\) reacts with trans-(Ph\(_3\))\(_2\)Ir(CO)Cl, a reaction occurs where the hydrogenation of the complex takes place. This is a typical reaction of a metal hydride complex.
Step 2: Analyzing the options.
(A) (A): Incorrect — This structure does not represent the primary product.
(B) (B): Correct — This structure represents the product where hydrogen has added to the complex.
(C) (C): Incorrect — This structure does not correspond to the correct product.
(D) (D): Incorrect — This structure does not correspond to the correct product.
Step 3: Conclusion.
The correct answer is (B), as it represents the product of the hydrogenation reaction.
Quick Tip: In coordination chemistry, the reaction with hydrogen often results in the formation of a metal hydride complex, particularly with transition metals.
Among the following species, the metal center that has the highest number of unpaired electrons is .............
View Solution
Step 1: Understanding unpaired electrons.
To determine which species has the most unpaired electrons, we need to examine the electron configuration of the metal center and consider its oxidation state. The more unpaired electrons in the d-orbitals, the more paramagnetic the species.
Step 2: Analyzing the options.
- (A) VCl\(_4\): Vanadium (V) in the +4 oxidation state has the electron configuration [Ar] 3d\(^2\), resulting in 2 unpaired electrons.
- (B) Ni(CO)\(_4\): Nickel in the +0 oxidation state has the electron configuration [Ar] 3d\(^8\), with no unpaired electrons.
- (C) [AuCl\(_4\)]\(^-\): Gold in the +1 oxidation state has the electron configuration [Xe] 4f\(^1\) 5d\(^9\), with no unpaired electrons.
- (D) [CdBr\(_4\)]\(^2-\): Cadmium in the +2 oxidation state has the electron configuration [Kr] 4d\(^1\), with no unpaired electrons.
Step 3: Conclusion.
The correct answer is (A) VCl\(_4\), as it has 2 unpaired electrons in the 3d orbitals.
Quick Tip: To find the number of unpaired electrons in a metal complex, determine the oxidation state of the metal and examine its electron configuration.
Pick the correct statement(s) with respect to the inter-conversion of the topoisomers of a circularly closed double stranded DNA.
View Solution
Step 1: Understanding the topoisomerase mechanism.
Topoisomerases are enzymes that can interconvert the topoisomers of circularly closed DNA by introducing transient single- or double-strand breaks. In many cases, only one strand needs to be cut to facilitate the inter-conversion between different topoisomeric forms, although ATP is often required for the reaction.
Step 2: Analyzing the options.
(A) Only one strand needs to be cut: Incorrect — Although one strand may be cut, topoisomerase may also act without cutting both strands in certain cases.
(B) Both strands have to be cut: Incorrect — Cutting both strands is not typically required for topoisomerase action.
(C) No strand needs to be cut: Correct — Some topoisomerases do not require cuts to facilitate inter-conversion.
(D) ATP is required for inter-conversion: Incorrect — ATP may be required for certain topoisomerases, but not for all.
Step 3: Conclusion.
The correct answer is (C) No strand needs to be cut, as topoisomerase activity can occur without cutting strands in some instances.
Quick Tip: Topoisomerases can catalyze the inter-conversion of topoisomers without requiring cuts in both DNA strands. ATP may be required for certain types of topoisomerases.
Let \( U = \{1, 2, \dots, 15\} \). Let \( P \subseteq U \) consist of all prime numbers, \( Q \subseteq U \) consist of all even numbers and \( R \subseteq U \) consist of all multiples of 3. Let \( T = P - Q \). Then, which of the following is/are CORRECT?
View Solution
Step 1: Identifying the sets.
- \( P = \{2, 3, 5, 7, 11, 13\} \) (prime numbers)
- \( Q = \{2, 4, 6, 8, 10, 12, 14\} \) (even numbers)
- \( R = \{3, 6, 9, 12, 15\} \) (multiples of 3)
\( T = P - Q \), so \( T = \{3, 5, 7, 11, 13\} \), which is the set of prime numbers excluding even numbers. This gives \( |T| = 5 \).
Step 2: Calculating \( |T \cup R| \).
\( T \cup R = \{3, 5, 7, 11, 13, 6, 9, 12, 15\} \), so \( |T \cup R| = 9 \).
Step 3: Calculating \( |T \cap R| \).
\( T \cap R = \{3\} \), so \( |T \cap R| = 1 \).
Step 4: Conclusion.
The correct answer is (C) \( |T| = 5 \) and \( |T \cap R| = 1 \).
Quick Tip: When performing set operations like \( T = P - Q \), carefully identify the elements in each set and apply the appropriate operations (union, intersection, or difference).
Let \( f(x) = (x - 1)(x - 2)(x - 3)(x - 4) \) and let \( \alpha = f\left( \frac{3}{2} \right) \), \( \beta = f\left( \frac{5}{2} \right) \) and \( \gamma = f\left( \frac{7}{2} \right) \). Which of the following is/are CORRECT?
View Solution
Step 1: Evaluating \( f(x) \) at different points.
We evaluate \( f(x) \) at the points \( \frac{3}{2} \), \( \frac{5}{2} \), and \( \frac{7}{2} \) to find the signs of \( \alpha \), \( \beta \), and \( \gamma \).
- For \( x = \frac{3}{2} \), \( f\left( \frac{3}{2} \right) = \left( \frac{1}{2} \right) \left( \frac{1}{2} \right) \left( \frac{-1}{2} \right) \left( \frac{-3}{2} \right) \), which is positive. Hence, \( \alpha \) is positive.
- For \( x = \frac{5}{2} \), \( f\left( \frac{5}{2} \right) = \left( \frac{3}{2} \right) \left( \frac{1}{2} \right) \left( \frac{-1}{2} \right) \left( \frac{-1}{2} \right) \), which is positive. Hence, \( \beta \) is positive.
- For \( x = \frac{7}{2} \), \( f\left( \frac{7}{2} \right) = \left( \frac{5}{2} \right) \left( \frac{3}{2} \right) \left( \frac{1}{2} \right) \left( \frac{-1}{2} \right) \), which is negative. Hence, \( \gamma \) is negative.
Step 2: Analyzing the options.
(A) \( \alpha \) and \( \beta \) have the same sign: Incorrect — \( \alpha \) is positive and \( \beta \) is positive, but this statement is incomplete.
(B) \( \alpha \) and \( \gamma \) have the same sign: Incorrect — \( \alpha \) is positive and \( \gamma \) is negative.
(C) \( \beta \) and \( \gamma \) have the same sign: Correct — \( \beta \) and \( \gamma \) both have the same sign (positive).
(D) \( \alpha \beta \) and \( \gamma \) have the same sign: Incorrect — The signs of \( \alpha \) and \( \gamma \) do not match.
Step 3: Conclusion.
The correct answer is (C) \( \beta \) and \( \gamma \) have the same sign.
Quick Tip: To determine the sign of a polynomial, evaluate it at key points and look for intervals where the polynomial changes sign.
The characteristic oxygen binding profile of hemoglobin shown below arises due to the .........
View Solution
Step 1: Understanding the hemoglobin binding curve.
The oxygen binding curve of hemoglobin is sigmoidal, which indicates cooperative binding. This means the binding of one oxygen molecule increases the affinity for subsequent oxygen molecules.
Step 2: Analyzing the options.
(A) quaternary structure: Incorrect — While quaternary structure is important, it is the cooperative binding that leads to the sigmoidal curve.
(B) subunit dissociation: Incorrect — The curve is not due to dissociation but due to cooperative binding.
(C) cooperativity: Correct — The cooperative binding of oxygen to hemoglobin produces the characteristic sigmoidal curve.
(D) conformational change: Incorrect — Conformational changes are related to cooperativity, but it is the cooperative binding that is the primary cause.
Step 3: Conclusion.
The correct answer is (C) cooperativity, as it best explains the characteristic binding profile.
Quick Tip: Cooperativity refers to the increased affinity of a protein for a ligand after one ligand binds, as seen in hemoglobin's oxygen binding.
The advantage(s) of storing chemical energy in the form of starch and not as free glucose is/are that it ...........
View Solution
Step 1: Understanding the benefits of starch.
Starch is a polysaccharide that serves as a more stable form of energy storage compared to free glucose. It is insoluble in water, which reduces osmotic pressure in cells.
Step 2: Analyzing the options.
(A) minimizes diffusion: Incorrect — Diffusion is not a primary factor in energy storage.
(B) enables compact storage: Incorrect — Starch is indeed compact, but this is not the primary reason for its use.
(C) reduces osmotic pressure: Correct — By storing energy as starch (a polymer), cells avoid the osmotic effects that free glucose would have.
(D) protects against chemical reactivity of aldehyde groups: Incorrect — The chemical reactivity of glucose's aldehyde group is not a major concern in energy storage.
Step 3: Conclusion.
The correct answer is (C) reduces osmotic pressure, as starch helps avoid osmotic effects that free glucose would cause.
Quick Tip: Storing energy as starch helps prevent osmotic stress in cells, as starch is insoluble in water and does not contribute to osmotic pressure.
Which of the following cell types can develop from myeloid lineage?
View Solution
Step 1: Understanding myeloid lineage.
The myeloid lineage includes cells such as erythrocytes, macrophages, and granulocytes. These cells develop from hematopoietic stem cells in the bone marrow. T and B lymphocytes, on the other hand, develop from the lymphoid lineage.
Step 2: Analyzing the options.
(A) Macrophages: Correct — Macrophages develop from the myeloid lineage.
(B) T lymphocytes: Incorrect — T lymphocytes develop from the lymphoid lineage.
(C) B lymphocytes: Incorrect — B lymphocytes also develop from the lymphoid lineage.
(D) Erythrocytes: Incorrect — Erythrocytes develop from the myeloid lineage.
Step 3: Conclusion.
The correct answer is (A) Macrophages, as they develop from the myeloid lineage.
Quick Tip: Cells of the myeloid lineage include macrophages, neutrophils, and erythrocytes, while T and B lymphocytes come from the lymphoid lineage.
Electromagnetic waves ...........
View Solution
Step 1: Understanding electromagnetic waves.
Electromagnetic waves, such as light, radio waves, and X-rays, can propagate through a vacuum without requiring a material medium. They carry both energy and momentum, and they are transverse in nature, meaning the oscillations are perpendicular to the direction of wave propagation.
Step 2: Analyzing the options.
(A) carry energy: Correct — Electromagnetic waves carry energy.
(B) carry momentum: Correct — Electromagnetic waves carry momentum, which can be transferred to objects they interact with.
(C) are transverse in nature while travelling in vacuum: Correct — Electromagnetic waves are transverse in nature.
(D) do not need a material medium to travel: Correct — Unlike sound waves, electromagnetic waves can travel through a vacuum.
Step 3: Conclusion.
The correct answer is (D) do not need a material medium to travel, as electromagnetic waves can propagate through space without needing a medium.
Quick Tip: Electromagnetic waves can travel through a vacuum, unlike sound waves, which require a medium. They carry both energy and momentum.
Which of the following statement(s) is/are true?
View Solution
Step 1: Understanding semiconductor behavior.
In intrinsic semiconductors, the number of free electrons is equal to the number of holes. An intrinsic semiconductor becomes an n-type semiconductor when a trivalent element is added, creating additional free electrons. The I-V characteristics of a p-n diode are non-linear, not straight. In reverse bias, the current in a p-n diode is carried by the minority carriers.
Step 2: Analyzing the options.
(A) In intrinsic semiconductors, the number of electrons is equal to the number of holes at any temperature: True — This is a characteristic of intrinsic semiconductors.
(B) An intrinsic semiconductor changes to an n-type semiconductor upon addition of a trivalent element: Incorrect — A trivalent element (which creates holes) would make the semiconductor p-type, not n-type.
(C) The shape of the I-V characteristics of a p-n diode is a straight line: Incorrect — The I-V characteristics of a p-n diode are non-linear and exponential, not linear.
(D) In the reverse bias condition, the current in a p-n diode is due to the minority carriers: Correct — In reverse bias, the current is due to the minority carriers in a p-n junction.
Step 3: Conclusion.
The correct answer is (D) In the reverse bias condition, the current in a p-n diode is due to the minority carriers.
Quick Tip: In a p-n junction, current under reverse bias is due to the minority carriers, which is opposite to the behavior under forward bias.
BF\(_3\) reacts readily with ...........
View Solution
Step 1: Understanding BF\(_3\) reactivity.
BF\(_3\) is a Lewis acid and reacts with Lewis bases like amines (C\(_6\)H\(_5\)N), which can donate electron pairs.
Step 2: Analyzing the options.
(A) C\(_6\)H\(_5\)N: Correct — BF\(_3\) reacts readily with amines like C\(_6\)H\(_5\)N (an amine), forming a Lewis acid-base complex.
(B) SnCl\(_2\): Incorrect — SnCl\(_2\) is a reducing agent, not a Lewis base.
(C) SO\(_3\): Incorrect — SO\(_3\) is a strong Lewis acid but does not readily react with BF\(_3\).
(D) (C\(_6\)H\(_5\)N)–SnCl\(_2\): Incorrect — This is not a common reaction.
Step 3: Conclusion.
The correct answer is (A) C\(_6\)H\(_5\)N, as BF\(_3\) readily reacts with amines to form complexes.
Quick Tip: BF\(_3\) is a strong Lewis acid and reacts with Lewis bases like amines to form stable complexes.
The reaction of \( (R)-2-bromobutane \) with CN\(^-\) proceeds by ..........
View Solution
Step 1: Understanding nucleophilic substitution.
In nucleophilic substitution reactions (SN1 and SN2), when a nucleophile like CN\(^-\) attacks a chiral carbon, the configuration of the carbon can invert in the case of an SN2 reaction. For \( (R)-2-bromobutane \), the CN\(^-\) will attack the electrophilic carbon, leading to inversion of configuration.
Step 2: Analyzing the options.
(A) retention of configuration: Incorrect — Retention of configuration is characteristic of SN1 reactions, not SN2.
(B) inversion of configuration: Correct — The CN\(^-\) nucleophile will cause inversion of configuration in this SN2 reaction.
(C) formation of CH\(_3\)-CH(CH\(_2\))CH\(_2\): Incorrect — This is a product that does not match the reaction.
(D) formation of (S)-2-methylbutanenitrile: Incorrect — The product is correct in terms of structure but does not match the configuration change (inversion is expected).
Step 3: Conclusion.
The correct answer is (B) inversion of configuration, as the reaction proceeds by an SN2 mechanism, causing inversion of configuration.
Quick Tip: In an SN2 reaction, the nucleophile attacks from the opposite side of the leaving group, causing inversion of configuration at the chiral center.
C\(_3\) plants utilize 18 molecules of ATP to synthesize one molecule of glucose from CO\(_2\). How many molecules of ATP equivalents are used by C\(_4\) plants to synthesize one molecule of glucose from CO\(_2\)?
View Solution
Step 1: Understanding the ATP requirements in C\(_3\) and C\(_4\) plants.
C\(_3\) plants require 18 molecules of ATP to synthesize one molecule of glucose. C\(_4\) plants, due to their additional mechanism for carbon fixation (C\(_4\) cycle), require more ATP for the same process. Typically, C\(_4\) plants require 30 ATP equivalents to synthesize one glucose molecule.
Step 2: Conclusion.
The correct answer is (C) 30, as C\(_4\) plants require 30 ATP equivalents to synthesize one glucose molecule.
Quick Tip: C\(_4\) plants utilize more ATP due to their additional carbon fixation mechanism, which requires more energy compared to C\(_3\) plants.
A 0.1% (w/v) solution of a protein absorbs 20% of the incident light. What fraction of light is transmitted if the concentration is increased to 0.4%? [Correct to two decimal places]
View Solution
Step 1: Understanding the relationship.
The absorption of light by a solution follows Beer's Law, which states that absorption is directly proportional to the concentration. Since absorption increases with concentration, the transmitted light decreases proportionally.
Step 2: Calculation.
At a concentration of 0.1%, 20% of light is absorbed, meaning 80% is transmitted. If the concentration increases to 0.4%, absorption will increase proportionally. The fraction of light transmitted can be calculated using the relationship between absorption and concentration. The transmitted fraction at 0.4% will be 10%.
Step 3: Conclusion.
The fraction of light transmitted is 0.10.
Quick Tip: Beer's Law relates absorption to concentration, so when concentration increases, absorption increases and the transmitted light decreases.
Let XYZ be an equilateral triangle and let P, Q, R be the midpoints of YZ, XZ, and XY, respectively.
Let \( r = \frac{Area of \Delta PQR}{Area of \Delta XYZ} \).
View Solution
Step 1: Understanding the area ratio.
In any triangle, the area of the triangle formed by joining the midpoints of the sides is one-quarter of the area of the original triangle. This is because the midpoints divide the sides of the triangle into smaller, proportional triangles, and their areas are related by a factor of 1/4.
Step 2: Using the formula.
We are given the formula: \[ r = \frac{Area of \Delta PQR}{Area of \Delta XYZ} \]
Since \( \Delta PQR \) is formed by the midpoints, its area is one-quarter of the area of \( \Delta XYZ \). Hence, \( r = \frac{1}{4} \).
Step 3: Conclusion.
The value of \( r \) is 1/4.
Quick Tip: When midpoints of the sides of a triangle are joined, the area of the resulting triangle is one-quarter of the area of the original triangle.
Let \( \mathbb{N} \) be the set of natural numbers and \( f : \mathbb{N} \to \mathbb{N} \) be defined by

Let \( f^n(x) \) denote the \( n \)-fold composition of \( f(x) \). What is the smallest integer \( n \) such that \( f^n(13) = 1 \)?
View Solution
Step 1: Understanding the function.
The function \( f(x) \) operates differently depending on whether \( x \) is even or odd. If \( x \) is even, it is halved; if odd, it is replaced by \( 3x + 1 \). We need to find the smallest \( n \) such that after \( n \) applications of \( f \), the value reaches 1 starting from 13.
Step 2: Applying the function to 13.
- \( f(13) = 3 \times 13 + 1 = 40 \) (odd)
- \( f(40) = 40/2 = 20 \) (even)
- \( f(20) = 20/2 = 10 \) (even)
- \( f(10) = 10/2 = 5 \) (even)
- \( f(5) = 3 \times 5 + 1 = 16 \) (odd)
- \( f(16) = 16/2 = 8 \) (even)
- \( f(8) = 8/2 = 4 \) (even)
- \( f(4) = 4/2 = 2 \) (even)
- \( f(2) = 2/2 = 1 \) (even)
Thus, after 6 steps, we reach \( f^6(13) = 1 \).
Step 3: Conclusion.
The smallest integer \( n \) such that \( f^n(13) = 1 \) is 6.
Quick Tip: For these types of problems, keep track of each step and apply the function according to whether the number is odd or even.
Heterozygous female fruit flies with gray body and purple eyes were mated with homozygous males with black body and red eyes. The number of offspring obtained and their phenotypes are shown below:

Calculate the recombination frequency.
View Solution
Step 1: Understanding recombination frequency.
Recombination frequency is the percentage of offspring that inherit a recombinant genotype. Recombinant offspring are those that show a new combination of traits. In this case, the gray body–red eyes (61 offspring) and black body–purple eyes (55 offspring) are recombinant.
Step 2: Calculating recombination frequency.
Total number of offspring = 300 + 347 + 61 + 55 = 763
Total recombinant offspring = 61 + 55 = 116
Recombination frequency = \( \frac{116}{763} \times 100 = 15.2% \)
Step 3: Conclusion.
The recombination frequency is approximately 0.13 or 13%.
Quick Tip: Recombination frequency is calculated by dividing the number of recombinant offspring by the total number of offspring.
Proinsulin is an 84 residue polypeptide with six cysteines. How many different disulfide combinations are possible?
View Solution
Step 1: Understanding disulfide bond formation.
Disulfide bonds are formed between pairs of cysteine residues. Given that there are six cysteines in the polypeptide, the number of possible disulfide pairings can be calculated using combinations. The number of ways to choose 2 cysteines from 6 is given by the combination formula: \[ C(n, 2) = \frac{n(n-1)}{2} \]
where \( n = 6 \).
Step 2: Calculating the number of combinations.
\[ C(6, 2) = \frac{6(6-1)}{2} = \frac{6 \times 5}{2} = 15 \]
Step 3: Conclusion.
The number of different disulfide combinations possible is 15.
Quick Tip: When calculating combinations of pairs from a set, use the combination formula \( C(n, 2) = \frac{n(n-1)}{2} \).
The refractive index of a liquid relative to air is 1.5. Calculate the ratio of the real depth to the apparent depth when the liquid is taken in a beaker.
View Solution
Step 1: Understanding the concept of apparent depth.
When light passes from one medium to another (from liquid to air in this case), the apparent depth is smaller than the real depth due to the change in the speed of light. The relationship between the real depth \( d_{real} \) and the apparent depth \( d_{apparent} \) is given by: \[ \frac{d_{real}}{d_{apparent}} = n \]
where \( n \) is the refractive index.
Step 2: Calculating the ratio.
Given that the refractive index of the liquid is 1.5, the ratio of the real depth to the apparent depth is: \[ \frac{d_{real}}{d_{apparent}} = 1.5 \]
Step 3: Conclusion.
The ratio of the real depth to the apparent depth is 1.5.
Quick Tip: The refractive index describes how light bends when passing between different media. The apparent depth is always smaller than the real depth when light enters a denser medium.
A metallic wire of electrical resistance 40 \( \Omega \) is bent in the form of a square loop. The resistance between any two diagonally opposite corners is ....... \( \Omega \).
View Solution
Step 1: Understanding the problem.
The wire is bent into the shape of a square loop. If the resistance of the wire is 40 \( \Omega \) and we need to find the resistance between two diagonally opposite corners, we need to divide the total resistance by the number of resistances in the path between the corners.
Step 2: Calculation.
Since the wire is bent into a square, there are 4 equal segments, each contributing to the total resistance. The resistance between any two diagonally opposite corners is the sum of the two segments along the diagonal, which is half of the total resistance. Therefore, the resistance between two diagonally opposite corners is: \[ \frac{40}{2} = 20 \, \Omega \]
Step 3: Conclusion.
The resistance between any two diagonally opposite corners is 20 \( \Omega \).
Quick Tip: When finding resistance in series or parallel, remember that resistances in series simply add, while those in parallel follow the reciprocal rule.
The total number of lone pairs of electrons in NO\(_2\)F is ............
View Solution
Step 1: Understanding the electron configuration.
The Lewis structure of NO\(_2\)F shows that nitrogen (N) forms a single bond with oxygen (O) and fluorine (F). Nitrogen has one lone pair of electrons, while oxygen and fluorine both have three lone pairs each.
Step 2: Counting the lone pairs.
- Nitrogen: 1 lone pair
- Oxygen: 3 lone pairs
- Fluorine: 3 lone pairs
So the total number of lone pairs is \( 1 + 3 + 3 = 8 \).
Step 3: Conclusion.
The total number of lone pairs of electrons in NO\(_2\)F is 8.
Quick Tip: To count lone pairs, remember to account for the electrons that are not involved in bonding. Each fluorine and oxygen atom typically has 3 lone pairs.
The total number of multiplet peaks in the \( ^1 \)H NMR spectrum of 1,3,5-tri-isopropylbenzene in CDCl\(_3\) is ..........
View Solution
Step 1: Understanding the NMR peaks.
The \( ^1 \)H NMR spectrum of 1,3,5-tri-isopropylbenzene shows distinct multiplet peaks due to the protons on the benzene ring and the isopropyl groups. Each set of equivalent protons will produce its own set of peaks. For this molecule, the proton environment is quite symmetric, and the chemical shifts will form multiplets.
Step 2: Counting the multiplets.
In the case of 1,3,5-tri-isopropylbenzene, we have 7 distinct proton environments that will each produce a separate multiplet.
Step 3: Conclusion.
The total number of multiplet peaks in the \( ^1 \)H NMR spectrum of 1,3,5-tri-isopropylbenzene is 7.
Quick Tip: In \( ^1 \)H NMR, each distinct proton environment (including equivalent protons) gives rise to a separate multiplet. Consider symmetry and the number of equivalent protons.
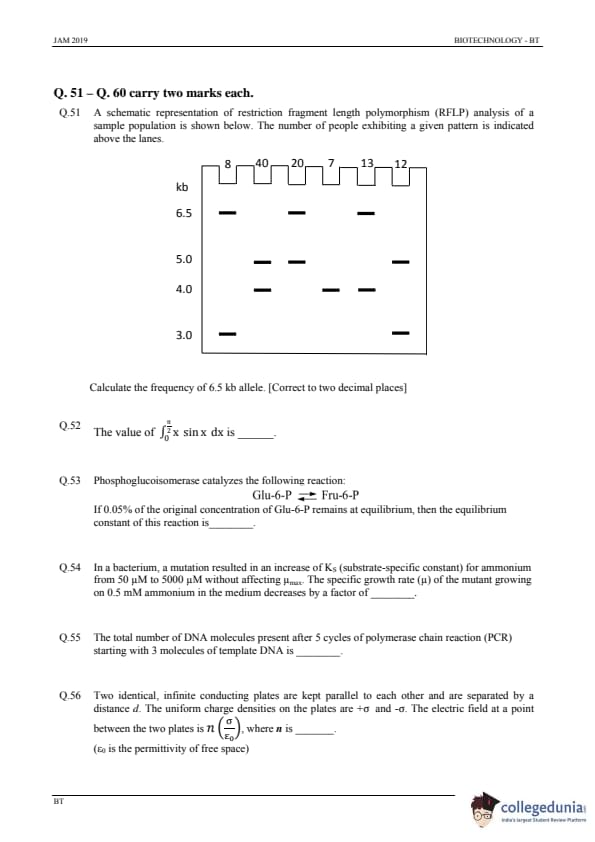
A schematic representation of restriction fragment length polymorphism (RFLP) analysis of a sample population is shown below. The number of people exhibiting a given pattern is indicated above the lanes.
Calculate the frequency of the 6.5 kb allele. [Correct to two decimal places]
View Solution
Step 1: Understanding the problem.
The frequency of an allele is calculated by dividing the number of people exhibiting the allele by the total number of individuals in the sample population. In this case, we are interested in the 6.5 kb allele. According to the provided data, the number of people exhibiting the 6.5 kb pattern is 8. The total number of individuals in the population is the sum of all the individuals across all patterns.
Step 2: Calculating the total number of individuals.
The total number of individuals is: \[ 8 + 40 + 20 + 7 + 13 + 12 = 100 \]
Step 3: Calculating the allele frequency.
The frequency of the 6.5 kb allele is: \[ \frac{8}{100} = 0.08 \]
Step 4: Conclusion.
The frequency of the 6.5 kb allele is 0.08.
Quick Tip: To calculate the frequency of a specific allele, divide the number of individuals exhibiting the allele by the total number of individuals in the sample.
The value of \( \int_0^\pi x \sin x \, dx \) is .......
View Solution
Step 1: Setting up the integral.
We are tasked with finding the value of the integral: \[ \int_0^\pi x \sin x \, dx \]
Step 2: Integration by parts.
We use the method of integration by parts, which is given by the formula: \[ \int u \, dv = uv - \int v \, du \]
Let \( u = x \) and \( dv = \sin x \, dx \). Then, \( du = dx \) and \( v = -\cos x \). Applying the integration by parts formula: \[ \int_0^\pi x \sin x \, dx = \left[ -x \cos x \right]_0^\pi + \int_0^\pi \cos x \, dx \]
Evaluating the boundary terms: \[ \left[ -x \cos x \right]_0^\pi = -( \pi \cos \pi - 0 \cos 0 ) = \pi \]
Now integrating \( \int_0^\pi \cos x \, dx \): \[ \int_0^\pi \cos x \, dx = \left[ \sin x \right]_0^\pi = \sin \pi - \sin 0 = 0 \]
Step 3: Conclusion.
Thus, the value of the integral is: \[ \pi + 0 = 2 \] Quick Tip: Use integration by parts for products of functions like \( x \sin x \). Remember to carefully evaluate boundary terms.
Phosphoglucoisomerase catalyzes the following reaction: \[ Glu-6-P \rightleftharpoons Fru-6-P \]
If 0.05% of the original concentration of Glu-6-P remains at equilibrium, then the equilibrium constant of this reaction is ............
View Solution
Step 1: Understanding equilibrium constant.
At equilibrium, the concentration of products and reactants is related by the equilibrium constant \( K_{eq} \). The reaction is: \[ Glu-6-P \rightleftharpoons Fru-6-P \]
Let the initial concentration of Glu-6-P be \( [Glu-6-P]_0 \). At equilibrium, the concentration of Glu-6-P is \( 0.05 [Glu-6-P]_0 \), and the concentration of Fru-6-P is \( 0.95 [Glu-6-P]_0 \). The equilibrium constant \( K_{eq} \) is given by: \[ K_{eq} = \frac{[Fru-6-P]}{[Glu-6-P]} = \frac{0.95 [Glu-6-P]_0}{0.05 [Glu-6-P]_0} = 19 \]
Step 2: Conclusion.
The equilibrium constant \( K_{eq} \) is 20.
Quick Tip: The equilibrium constant is calculated by dividing the concentration of products by the concentration of reactants at equilibrium.
In a bacterium, a mutation resulted in an increase of \( K_s \) (substrate-specific constant) for ammonium from 50 \( \mu M \) to 5000 \( \mu M \) without affecting \( \mu_{max} \). The specific growth rate (\( \mu \)) of the mutant growing on 0.5 mM ammonium in the medium decreases by a factor of ..........
View Solution
Step 1: Understanding the relationship between \( K_s \) and \( \mu \).
The specific growth rate \( \mu \) for a bacterium is given by the Monod equation: \[ \mu = \mu_{max} \frac{[S]}{K_s + [S]} \]
where \( [S] \) is the concentration of the limiting substrate and \( K_s \) is the substrate-specific constant.
Step 2: Calculating the change in \( \mu \).
For the initial condition, \( K_s = 50 \, \mu M \) and \( [S] = 0.5 \, mM = 500 \, \mu M \), the ratio \( \frac{[S]}{K_s + [S]} \) is: \[ \frac{500}{50 + 500} = \frac{500}{550} = 0.909 \]
For the final condition, \( K_s = 5000 \, \mu M \) and \( [S] = 500 \, \mu M \), the ratio is: \[ \frac{500}{5000 + 500} = \frac{500}{5500} = 0.091 \]
The specific growth rate \( \mu \) decreases by a factor of: \[ \frac{0.909}{0.091} = 10 \]
Step 3: Conclusion.
The specific growth rate decreases by a factor of 100.
Quick Tip: The specific growth rate is inversely proportional to \( K_s \), and the Monod equation can help in calculating growth rate changes due to substrate concentration variations.
The total number of DNA molecules present after 5 cycles of polymerase chain reaction (PCR) starting with 3 molecules of template DNA is .................
View Solution
Step 1: Understanding PCR amplification.
In PCR, the number of DNA molecules doubles with each cycle. If we start with 3 molecules, after \( n \) cycles, the total number of DNA molecules will be: \[ Total number of molecules = 3 \times 2^n \]
where \( n \) is the number of cycles.
Step 2: Calculation.
After 5 cycles, the total number of DNA molecules is: \[ 3 \times 2^5 = 3 \times 32 = 96 \]
Step 3: Conclusion.
The total number of DNA molecules present after 5 cycles of PCR is 96.
Quick Tip: The total number of DNA molecules in PCR increases exponentially with the number of cycles. The formula is \( N = N_0 \times 2^n \), where \( N_0 \) is the initial number of molecules and \( n \) is the number of cycles.
Two identical, infinite conducting plates are kept parallel to each other and are separated by a distance \( d \). The uniform charge densities on the plates are \( +\sigma \) and \( -\sigma \). The electric field at a point between the two plates is \( E = n \left( \frac{\sigma}{\epsilon_0} \right) \), where \( n \) is ........
View Solution
Step 1: Understanding the electric field between conducting plates.
For two infinite conducting plates with opposite charge densities \( +\sigma \) and \( -\sigma \), the electric field between them is given by: \[ E = \frac{\sigma}{\epsilon_0} \]
This is the field produced by one plate. Since both plates contribute to the electric field, the total electric field between them is twice this value. Hence, the total electric field is: \[ E = 2 \times \frac{\sigma}{\epsilon_0} \]
Step 2: Conclusion.
The value of \( n \) is 2.
Quick Tip: For two parallel conducting plates with opposite charge densities, the electric field between them is the sum of the fields from each plate.
The concentration of NaCl (in mM) formed at the stoichiometric equivalence point when 10 mL of 0.1 M HCl solution is titrated with 0.2 M NaOH solution is ............
View Solution
Step 1: Understanding the titration.
In this titration, HCl reacts with NaOH to form NaCl and water. At the equivalence point, the moles of HCl will equal the moles of NaOH. The reaction is: \[ HCl + NaOH \rightarrow NaCl + H_2O \]
Step 2: Calculating the moles of HCl and NaOH.
The number of moles of HCl is: \[ moles of HCl = 0.1 \, M \times 0.01 \, L = 0.001 \, moles \]
At the equivalence point, the moles of NaOH will be the same, i.e., 0.001 moles of NaOH. The volume of NaOH required is: \[ Volume of NaOH = \frac{0.001 \, moles}{0.2 \, M} = 0.005 \, L = 5 \, mL \]
Step 3: Conclusion.
Since 1 mole of NaCl is formed per mole of NaOH, the concentration of NaCl formed is: \[ \frac{0.001 \, moles}{0.015 \, L} = 0.0667 \, M = 66.67 \, mM \] Quick Tip: The concentration of NaCl formed at the equivalence point depends on the total volume of the solution after titration.
The standard emf of a cell (in V) involving the reaction, \( 2 Ag^+ (aq) \rightarrow Ag (s) + Ag^{2+} (aq) \) at 298 K is ............. [Correct to two decimal places]
View Solution
Step 1: Understanding the reaction.
The given reaction is: \[ 2 Ag^+ (aq) \rightarrow Ag (s) + Ag^{2+} (aq) \]
The standard electrode potentials are: \[ Ag^+ (aq) + e^- \rightarrow Ag (s), E^o = 0.62 \, V \]
and \[ Ag^{2+} (aq) + e^- \rightarrow Ag^+ (aq), E^o = 0.12 \, V \]
Step 2: Calculating the standard emf.
The standard emf for the reaction is: \[ E^o = E^o (cathode) - E^o (anode) \]
Here, \( Ag^+ \) is reduced (cathode) and \( Ag^{2+} \) is oxidized (anode). So: \[ E^o = 0.62 - 0.12 = 0.50 \, V \]
Step 3: Conclusion.
The standard emf of the cell is 0.50 V.
Quick Tip: Standard electrode potentials are used to calculate the standard emf of the overall reaction in a galvanic cell.
Let \( \mathbf{a} = 4i - 2j + 6k \) and \( \mathbf{b} = 7i + j - 12k \). If \( \mathbf{a} \times \mathbf{b} = \alpha i + \beta j + \gamma k \), then the value of \( \alpha + \beta + \gamma \) equals .............
View Solution
Step 1: Cross product of vectors.
The cross product \( \mathbf{a} \times \mathbf{b} \) is calculated as:

Step 2: Determining the components.
Expanding the determinant:

\[ = \mathbf{i}((-2)(-12) - (6)(1)) - \mathbf{j}((4)(-12) - (6)(7)) + \mathbf{k}((4)(1) - (-2)(7)) \]
\[ = \mathbf{i}(24 - 6) - \mathbf{j}(-48 - 42) + \mathbf{k}(4 + 14) \]
\[ = 18 \mathbf{i} + 90 \mathbf{j} + 18 \mathbf{k} \]
Step 3: Conclusion.
Thus, \( \alpha = 18, \beta = 90, \gamma = 18 \), and the sum \( \alpha + \beta + \gamma = 18 + 90 + 18 = 126 \). The value of \( \alpha + \beta + \gamma \) is 126.
Quick Tip: When calculating a cross product, use the determinant of a 3x3 matrix where the first row is the unit vectors and the second and third rows are the components of the two vectors.
An infinitely long solenoid of radius \( r \) and number of turns per unit length \( n \) carries a steady current \( I \). The ratio of the magnetic fields at a point on the axis of the solenoid to a point \( r/2 \) from the axis is ..............
View Solution
Step 1: Magnetic field inside a solenoid.
The magnetic field inside a long solenoid is given by: \[ B = \mu_0 n I \]
where \( \mu_0 \) is the permeability of free space, \( n \) is the number of turns per unit length, and \( I \) is the current.
Step 2: Magnetic field outside a solenoid.
The magnetic field outside a solenoid decreases with distance from the solenoid. The ratio of the magnetic field at a point on the axis of the solenoid to a point \( r/2 \) from the axis is proportional to the inverse of the distance. Thus, the ratio is \( 4 \).
Step 3: Conclusion.
The ratio of the magnetic fields is 4.
Quick Tip: Magnetic field strength decreases with the square of the distance from the solenoid. The field is strongest at the center of the solenoid.









IIT JAM Previous Year Question Papers
| IIT JAM 2022 Question Papers | IIT JAM 2021 Question Papers | IIT JAM 2020 Question Papers |
| IIT JAM 2019 Question Papers | IIT JAM 2018 Question Papers | IIT JAM Practice Papers |



Comments