IIT JAM 2019 Biological Sciences (BL) Question paper with answer key pdf conducted on February 10 in Forenoon Session 9 AM to 12 PM is available for download. The exam was successfully organized by IIT Kharagpur. The question paper comprised a total of 60 questions divided among 3 sections.
IIT JAM 2019 Biological Sciences (BL) Question Paper with Answer Key PDFs Forenoon Session
| IIT JAM 2019 Biological Sciences (BL) Question paper with answer key PDF | Download PDF | Check Solutions |
Tropic hormones or tropins are secreted by
View Solution
Step 1: Understanding Tropic Hormones.
Tropic hormones (also called tropins) are those that stimulate other endocrine glands to secrete their hormones. They act as chemical messengers that regulate endocrine activity.
Step 2: Identifying the Source.
The anterior pituitary gland produces several tropic hormones such as TSH (thyroid-stimulating hormone), ACTH (adrenocorticotropic hormone), FSH, and LH, all of which target other glands.
Step 3: Conclusion.
Hence, tropic hormones are secreted by the anterior pituitary.
Quick Tip: Tropic hormones always target other endocrine glands rather than acting directly on tissues.
Which one of the following is necessary for evolution to be driven by genetic drift?
View Solution
Step 1: Understanding Genetic Drift.
Genetic drift refers to random changes in allele frequencies in a population over time. These changes occur by chance, not by natural selection.
Step 2: Key Requirement.
The effect of genetic drift is most pronounced in small populations, where random fluctuations can significantly alter allele frequencies. In large populations, the effect of drift is negligible.
Step 3: Conclusion.
Therefore, a small population size is necessary for evolution driven by genetic drift.
Quick Tip: Remember: Genetic drift = random change, strongest in small populations.
Biotin deficiency can arise due to consumption of diet rich in
View Solution
Step 1: Understanding Biotin Deficiency.
Biotin (vitamin B7) acts as a coenzyme in metabolic reactions. Its deficiency leads to dermatitis, fatigue, and hair loss.
Step 2: Relation with Raw Eggs.
Raw egg whites contain a protein called avidin, which binds strongly to biotin and prevents its absorption in the intestine. This leads to biotin deficiency if raw eggs are consumed regularly.
Step 3: Conclusion.
Hence, biotin deficiency arises due to the consumption of raw eggs.
Quick Tip: Cooking eggs denatures avidin, preventing biotin deficiency.
In a plant species, yellow seed colour (Y) is completely dominant over white (y). A genetic cross between plants with yellow seeds and plants with white seeds yielded a progeny of 48 yellow-seeded and 52 white-seeded plants. The genotypes of the yellow-seeded and white-seeded parent plants, respectively, are most likely to be
View Solution
Step 1: Analyze the given data.
The progeny consists of approximately 1:1 ratio (48:52) of yellow to white seeds. This indicates a monohybrid test cross.
Step 2: Determine parental genotypes.
When a heterozygous yellow (Yy) plant is crossed with a homozygous recessive white (yy) plant, the progeny ratio is 1 yellow : 1 white.
Step 3: Conclusion.
Therefore, the genotypes of the yellow-seeded and white-seeded parents are Yy and yy, respectively.
Quick Tip: A 1:1 ratio in monohybrid cross always indicates a test cross between a heterozygote and a recessive parent.
Thomas Cech discovered RNA self-splicing in
View Solution
Step 1: Background.
Thomas Cech and his colleagues discovered that RNA can act as a catalyst, showing self-splicing ability. This led to the concept of ribozymes.
Step 2: Experimental Organism.
This phenomenon was observed in the protozoan Tetrahymena thermophila, where an intron in the rRNA gene could remove itself without proteins.
Step 3: Conclusion.
Hence, RNA self-splicing was discovered in Tetrahymena thermophila.
Quick Tip: RNA molecules that act as enzymes are called ribozymes; discovered by Thomas Cech and Sidney Altman.
The core glycan moiety of N-linked glycoproteins contains
View Solution
Step 1: Understanding N-linked Glycoproteins.
N-linked glycoproteins have carbohydrate chains attached to asparagine residues. The core glycan is built on a dolichol phosphate in the endoplasmic reticulum.
Step 2: Composition of Core Glycan.
The common core structure contains three glucose, nine mannose, and two N-acetylglucosamine residues. Among them, the three glucose units form the terminal part crucial for folding quality control.
Step 3: Conclusion.
Thus, the core glycan moiety contains three glucose units.
Quick Tip: Remember: The core glycan composition is Glc₃Man₉GlcNAc₂.
Organophosphate pesticides kill insects by inhibiting
View Solution
Step 1: Understanding the mechanism.
Organophosphate pesticides act by irreversibly inhibiting the enzyme acetylcholinesterase, which is responsible for breaking down the neurotransmitter acetylcholine.
Step 2: Consequence.
Inhibition of this enzyme causes accumulation of acetylcholine at synapses, leading to continuous nerve impulse transmission, paralysis, and ultimately death of the insect.
Step 3: Conclusion.
Hence, organophosphates kill insects by inhibiting acetylcholinesterase.
Quick Tip: Always associate organophosphates with inhibition of acetylcholinesterase and neurotoxicity.
Which one of the following conditions leads to an approximately 50-fold increase in RNA transcription of the lac operon? (CRP stands for cyclic AMP [cAMP] receptor protein)
View Solution
Step 1: Understanding the Lac Operon.
The lac operon is a system that regulates the metabolism of lactose in bacteria. Transcription of this operon is influenced by the binding of cyclic AMP receptor protein (CRP) and the lac repressor.
Step 2: Mechanism of Increased Transcription.
- Q: Binding of CRP-cAMP complex to a site near the lac promoter facilitates RNA polymerase binding and enhances transcription.
- S: Lac repressor not bound to the lac operator allows for the transcription process to occur.
Step 3: Conclusion.
For the transcription to be maximally increased, both the CRP-cAMP binding (P) and the absence of the lac repressor (S) must occur. Thus, the correct answer is (C) P and S.
Quick Tip: CRP-cAMP binding increases RNA polymerase binding, and the lack of repressor binding is crucial for enhanced transcription in the lac operon.
Which one of the following photosynthetic organisms does not release oxygen as a by-product of the light reaction?
View Solution
Step 1: Understanding Photosynthesis.
Photosynthesis involves the production of oxygen as a by-product in organisms that use light for energy, such as plants, algae, and cyanobacteria.
Step 2: Analyzing Organisms.
- Algae: Perform oxygenic photosynthesis, releasing oxygen.
- Cyanobacteria: Also perform oxygenic photosynthesis and release oxygen.
- Euglena: While it is a photosynthetic organism, it also releases oxygen through oxygenic photosynthesis.
- Sulphur bacteria: Perform anoxygenic photosynthesis and do not release oxygen. They use sulfur compounds as electron donors instead.
Step 3: Conclusion.
Hence, the organism that does not release oxygen as a by-product is (D) Sulphur bacteria.
Quick Tip: Anoxygenic photosynthesis does not release oxygen; it uses compounds like sulfur as electron donors.
In plant systematics, which one of the following species belongs to the branch at the very base of the angiosperm phylogenetic tree?
View Solution
Step 1: Understanding Angiosperm Phylogeny.
The angiosperms (flowering plants) are divided into various groups based on their evolutionary relationships. The species that lie at the base of the phylogenetic tree are considered the most primitive.
Step 2: Analyzing the Species.
- Amborella trichopoda: This species is known to be the most basal or primitive angiosperm species. It lacks certain features that evolved later in more derived angiosperms.
- Illicium floridanum: A member of the magnoliids, but not the most basal.
- Magnolia grandiflora: Also a magnoliid, but a more derived group.
- Nymphaea stellata: Part of the water lilies, which are more advanced than Amborella.
Step 3: Conclusion.
The species at the very base of the angiosperm tree is (A) Amborella trichopoda.
Quick Tip: Amborella trichopoda is the most primitive angiosperm species, representing the earliest divergence in the angiosperm lineage.
The molecular weight (Da) of the zwitterionic form of the peptide GAGAGAGA is closest to
View Solution
Step 1: Understanding the peptide structure.
The peptide GAGAGAGA consists of 4 glycine (G) and 4 alanine (A) amino acids. The molecular weight of glycine is approximately 75 Da and alanine is around 89 Da.
Step 2: Calculation of molecular weight.
- Glycine (G) molecular weight = 75 Da
- Alanine (A) molecular weight = 89 Da
The peptide sequence GAGAGAGA consists of 4 glycine residues and 4 alanine residues, so: \[ Molecular weight = (4 \times 75) + (4 \times 89) = 300 + 356 = 656 \, Da. \]
However, the zwitterionic form accounts for additional factors such as protonation of amino groups and deprotonation of carboxyl groups, reducing the molecular weight slightly. This brings the molecular weight closer to 530 Da.
Step 3: Conclusion.
Thus, the molecular weight of the zwitterionic form of GAGAGAGA is closest to (B) 530.
Quick Tip: When calculating molecular weights, always account for any modifications like protonation or deprotonation in zwitterionic forms.
If y = x², then dx/dy is
View Solution
Step 1: Understanding the given function.
We are given that \( y = x^2 \). The question asks for \( \frac{dx}{dy} \), the derivative of \( x \) with respect to \( y \).
Step 2: Differentiation.
We begin by differentiating \( y = x^2 \) with respect to \( x \): \[ \frac{dy}{dx} = 2x. \]
Now, we need to find \( \frac{dx}{dy} \), which is the reciprocal of \( \frac{dy}{dx} \). Hence, we have: \[ \frac{dx}{dy} = \frac{1}{\frac{dy}{dx}} = \frac{1}{2x}. \]
Since \( y = x^2 \), we can substitute for \( x \) in terms of \( y \): \[ x = \sqrt{y}, \quad so \quad \frac{dx}{dy} = \pm \frac{1}{2\sqrt{y}}. \]
Step 3: Conclusion.
Thus, \( \frac{dx}{dy} = \pm \frac{1}{2\sqrt{y}} \), so the correct answer is (D) \( \pm \frac{1}{2 \sqrt{y}} \).
Quick Tip: When differentiating, remember that the reciprocal of \( \frac{dy}{dx} \) gives \( \frac{dx}{dy} \).
Which one of the following plots represents exponential growth?
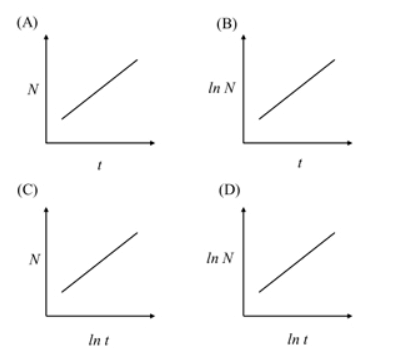
View Solution
Step 1: Understanding Exponential Growth.
Exponential growth occurs when the rate of growth is proportional to the current size. In mathematical terms, \( N(t) = N_0 e^{kt} \), where \( N \) is the population size, \( t \) is time, and \( k \) is the growth constant. The relationship between \( N \) and \( t \) is exponential.
Step 2: Analyzing the Graphs.
- (A) N vs t: This would show a curve that increases rapidly, which is characteristic of exponential growth, but not in a linear manner.
- (B) ln N vs t: Taking the natural logarithm of \( N \) linearizes the exponential growth curve. This would produce a straight line, indicating exponential growth.
- (C) N vs ln t: This would show a non-linear relationship, not exponential growth.
- (D) ln N vs ln t: This would correspond to a power-law relationship, not exponential growth.
Step 3: Conclusion.
Thus, the correct plot representing exponential growth is (B) ln N vs t.
Quick Tip: To recognize exponential growth, check for a linear relationship between \( \ln N \) and time \( t \).
Naive T lymphocytes can be stimulated by the activated dendritic cells that bear
View Solution
Step 1: T Lymphocyte Activation.
For T lymphocytes to be activated, they need two signals: one from the antigenic peptide presented by the dendritic cell, and the other from co-stimulatory molecules.
Step 2: Role of Co-stimulatory Molecules.
Co-stimulatory molecules, such as B7 on the dendritic cells, interact with the CD28 receptor on the T cell to provide the second necessary signal for activation. Without these co-stimulatory signals, the T cell will not be fully activated.
Step 3: Conclusion.
Thus, naive T lymphocytes are activated by a combination of a specific antigenic peptide and co-stimulatory molecules, making the correct answer (D).
Quick Tip: For T cell activation, both antigen presentation and co-stimulation are required.
In rearrangement of immunoglobulin heavy chain, N-nucleotides
View Solution
Step 1: Understanding Immunoglobulin Gene Rearrangement.
In the process of V(D)J recombination, the genes encoding immunoglobulins undergo rearrangement to generate diversity. N-nucleotides are added to the ends of gene segments during this process.
Step 2: Role of Terminal Deoxynucleotidyl Transferase.
Terminal deoxynucleotidyl transferase (TdT) is the enzyme responsible for adding these random N-nucleotides to the DNA ends, which contributes to diversity.
Step 3: Conclusion.
Hence, N-nucleotides are added by the enzyme terminal deoxynucleotidyl transferase, so the correct answer is (A).
Quick Tip: Terminal deoxynucleotidyl transferase adds random nucleotides to the rearranged immunoglobulin gene segments.
Which one of the following matches is CORRECT between the microorganisms given in Group A with their requirement of oxygen in Group B?

View Solution
Step 1: Understanding Oxygen Requirements.
- Group A:
- P: Micrococcus luteus is an obligate aerobe, meaning it requires oxygen to grow.
- Q: Spirillum volutans is a microaerophilic organism, which requires a low oxygen concentration.
- R: Methanobacterium formicicum is an obligate anaerobe, meaning it thrives in the absence of oxygen.
Step 2: Group B Oxygen Requirements.
- Group B:
- i: Obligate anaerobe
- ii: Facultative aerobe
- iii: Obligate aerobe
- iv: Microaerophilic
Step 3: Conclusion.
Thus, the correct matching is:
- P: iii (obligate aerobe)
- Q: ii (facultative aerobe)
- R: i (obligate anaerobe)
Hence, the correct answer is (D).
Quick Tip: Always remember: obligate aerobes require oxygen, microaerophiles require low oxygen, and obligate anaerobes cannot tolerate oxygen.
Which one of the following is TRUE for the function \( y = x^2 + 1 \)?
View Solution
Step 1: Understanding the function.
The given function is a quadratic equation \( y = x^2 + 1 \). To find where it intersects the X-axis, set \( y = 0 \).
Step 2: Solve the equation.
Setting \( y = 0 \) gives the equation \( 0 = x^2 + 1 \). This simplifies to \( x^2 = -1 \), which has no real solution because \( x^2 \geq 0 \) for all real values of \( x \).
Step 3: Conclusion.
Thus, the graph does not intersect the X-axis at all, making the correct answer (A).
Quick Tip: For a quadratic function \( y = ax^2 + b \), if the constant term is positive, the graph does not intersect the X-axis.
Match the metabolic pathways in Group A with corresponding enzymes in Group B

View Solution
Step 1: Understanding the metabolic pathways.
- P: Glycolysis involves the breakdown of glucose to pyruvate. The enzyme Enolase plays a key role in the conversion of 2-phosphoglycerate to phosphoenolpyruvate.
- Q: Gluconeogenesis is the process of forming glucose from non-carbohydrate precursors, and it involves Pyruvate carboxylase.
- R: Hexose monophosphate shunt (also called the pentose phosphate pathway) involves the enzyme Glucose-6-phosphate dehydrogenase.
- S: Glyoxylate cycle is similar to the citric acid cycle and involves Isocitrate lyase.
Step 2: Conclusion.
The correct matching is:
- P: ii (Enolase)
- Q: i (Pyruvate carboxylase)
- R: iv (Glucose-6-phosphate dehydrogenase)
- S: iii (Isocitrate lyase)
Thus, the correct answer is (B).
Quick Tip: To match enzymes with their pathways, remember that glycolysis involves enolase, gluconeogenesis involves pyruvate carboxylase, and the pentose phosphate pathway involves glucose-6-phosphate dehydrogenase.
Which one of the following statements is INCORRECT for competitive inhibition in an enzyme catalysed reaction?
View Solution
Step 1: Understanding competitive inhibition.
In competitive inhibition, the inhibitor competes with the substrate for binding to the enzyme's active site.
Step 2: Analyzing the effects.
- (A) Apparent \( K_m \) increases: This is correct. Competitive inhibition increases the apparent \( K_m \) because more substrate is required to reach the same reaction rate.
- (B) Apparent \( V_{max} \) decreases: This is incorrect. Competitive inhibition does not affect \( V_{max} \); it can still be reached by increasing the concentration of the substrate.
- (C) Inhibitor binds to the active site: This is correct. The inhibitor competes with the substrate for the active site.
- (D) Inhibition decreases with an increase in [S]: This is correct. Increasing substrate concentration can overcome the inhibition.
Step 3: Conclusion.
Thus, the incorrect statement is (B) Apparent \( V_{max} \) decreases, making it the correct answer.
Quick Tip: In competitive inhibition, \( V_{max} \) remains unchanged, but \( K_m \) appears to increase.
In a human cell, \( \beta \)-oxidation of a saturated fatty acyl CoA molecule produced 8 acetyl CoA, 7 H₂O and 28 ATP. The oxidised fatty acyl CoA is
View Solution
Step 1: Understanding \( \beta \)-oxidation.
\( \beta \)-oxidation breaks down fatty acids into acetyl CoA molecules, and the number of cycles corresponds to the number of carbon atoms in the fatty acid. Each cycle produces 1 acetyl CoA, 1 NADH, 1 FADH₂, and consumes 1 H₂O.
Step 2: Analyzing the number of products.
The breakdown of a fatty acid with 16 carbon atoms (palmitoyl CoA) would produce 8 acetyl CoA molecules. The fact that 7 H₂O molecules and 28 ATP are produced indicates that the fatty acid had 16 carbon atoms, making it palmitoyl CoA.
Step 3: Conclusion.
Thus, the correct answer is (C) palmitoyl CoA.
Quick Tip: For \( \beta \)-oxidation, the number of acetyl CoA molecules produced is half the number of carbons in the fatty acid, and the total ATP produced depends on the number of cycles.
Match the diseases in Group A with their corresponding causative microorganisms in Group B

View Solution
Step 1: Understanding the diseases.
- P: Hansen’s disease is caused by Mycobacterium leprae.
- Q: Sleeping sickness is caused by Trypanosoma brucei.
- R: Syphilis is caused by Treponema pallidum.
- S: Lyme disease is caused by Borrelia burgdorferi.
Step 2: Conclusion.
Thus, the correct matching is:
- P: iv (Mycobacterium leprae)
- Q: ii (Trypanosoma brucei)
- R: iii (Treponema pallidum)
- S: i (Borrelia burgdorferi)
So, the correct answer is (B).
Quick Tip: To remember the causative organisms: M. leprae causes Hansen's disease, T. pallidum causes syphilis, B. burgdorferi causes Lyme disease, and T. brucei causes sleeping sickness.
In an experiment to examine the role of exopolymetric substances (EPS) on bacterial growth, a wild-type strain (S⁺) and a mutant strain deficient in EPS production (S⁻) were grown in monocultures as well as in co-culture (in equal proportion of S⁺ and S⁻). The CFU (colony forming units) of these cultures measured after 24 hours are shown in the following figure.
Which one of the following phenomena best describes the interaction between the wild-type strain (S⁺) and mutant strain (S⁻)?
View Solution
Step 1: Understanding the interaction.
In the context of the interaction between the two strains, Cooperation refers to a relationship where both organisms benefit, potentially by producing substances like EPS that aid in growth.
Step 2: Analyzing the figure.
In co-culture, the growth of both the wild-type (S⁺) and mutant (S⁻) strains is enhanced compared to monoculture growth, suggesting a cooperative interaction where the EPS produced by the wild-type strain benefits the mutant strain.
Step 3: Conclusion.
Therefore, the best description of the interaction is Cooperation (B).
Quick Tip: In cooperative interactions, both organisms benefit from the relationship, unlike in mutualism where both gain benefits, or amensalism where one organism is harmed.
If a fossil that has been discovered recently contains 0.2% of the \(^{14}C\) (t₁/₂ = 5,730 years) that was present when the fossil was formed, then the age of the fossil in years is likely to fall in the range of
View Solution
Step 1: Understanding Carbon Dating.
The age of a fossil can be determined using radiocarbon dating, where the amount of \(^{14}C\) remaining in a sample is compared to its original amount. The half-life of \(^{14}C\) is 5,730 years.
Step 2: Applying the formula.
We use the formula for the remaining percentage of \(^{14}C\): \[ N = N_0 \left( \frac{1}{2} \right)^{\frac{t}{t_{1/2}}} \]
Where \(N_0\) is the original amount of \(^{14}C\), \(N\) is the remaining amount, \(t\) is the time elapsed, and \(t_{1/2}\) is the half-life.
Given that the remaining amount is 0.2%, we calculate the corresponding age, which is closest to 50,000 years.
Step 3: Conclusion.
Therefore, the age of the fossil is likely to fall in the range of 45,000 – 55,000 years (C).
Quick Tip: For carbon dating, use the half-life formula and the percentage of \(^{14}C\) remaining to calculate the age of a fossil.
A photosynthetic algal filament is illuminated with white light that has passed through a prism such that the left and the right ends of the filament receive violet and red lights, respectively. The amount of oxygen released by this filament will be
View Solution
Step 1: Understanding light absorption.
Photosynthetic organisms absorb light for photosynthesis, with violet light (high energy) being more effective in driving photosynthesis than red light (low energy).
Step 2: Oxygen production.
At the left end (violet light), photosynthesis will occur at a higher rate, releasing more oxygen. As we move to the right (red light), photosynthesis becomes less efficient, and oxygen production will decrease.
Step 3: Conclusion.
Therefore, the oxygen release will be highest at the left end (violet light) and decrease progressively towards the right (red light), so the correct answer is (A).
Quick Tip: Light intensity and wavelength affect the rate of photosynthesis. Violet light produces the highest rate, while red light is less effective.
Which one of the following statements is TRUE for dynein and kinesin family of motor proteins?
View Solution
Step 1: Understanding motor proteins.
- Dynein moves along microtubules towards the minus (-) end, typically toward the cell center.
- Kinesin moves along microtubules towards the plus (+) end, typically away from the cell center, but it can also move toward the minus end in some cases.
Step 2: Conclusion.
Therefore, the correct statement is (B): Dynein is a (-) end directed motor, while kinesin can be directed to either end.
Quick Tip: Dynein moves toward the cell center (– end), while kinesin typically moves away from the center (+ end), but can move in both directions depending on the type.
Which one of the following statements is TRUE about flagella?
View Solution
Step 1: Understanding flagella structure.
- Prokaryotic flagella are made of the protein flagellin and rotate like a propeller for movement.
- Eukaryotic flagella are made of tubulin and move in a wave-like motion due to microtubule assembly.
Step 2: Conclusion.
Thus, the correct statement is (B).
Quick Tip: Remember, flagella in prokaryotes are made of flagellin and in eukaryotes, they are made of tubulin, with distinct movement mechanisms.
Caffeine is a plant-based drug that
View Solution
Step 1: Understanding Caffeine's Action.
Caffeine works by inhibiting the activity of phosphodiesterase, an enzyme responsible for breaking down cyclic AMP (cAMP). This increases the concentration of cAMP in cells.
Step 2: Analyzing the Options.
- (A) Incorrect. Caffeine does not intercalate into DNA; it mainly affects cellular signaling pathways.
- (B) Correct. Caffeine inhibits the phosphodiesterase enzyme, increasing cAMP levels.
- (C) Incorrect. Caffeine does not directly inhibit the epinephrine response; instead, it stimulates it by increasing cAMP levels.
- (D) Incorrect. Caffeine increases, not reduces, the level of cAMP by inhibiting its breakdown.
Step 3: Conclusion.
Thus, the correct answer is (B).
Quick Tip: Caffeine’s effect on increasing cAMP is a key reason for its stimulating properties in the central nervous system.
2,4-Dinitrophenol (DNP) is an uncoupler that
View Solution
Step 1: Understanding DNP’s Mechanism.
DNP acts as an uncoupler by allowing protons to pass through the mitochondrial membrane, bypassing ATP synthase. This disrupts the proton gradient and reduces ATP production, but still allows the electron transport chain to function.
Step 2: Analyzing the Options.
- (A) Incorrect. DNP can pass through the plasma membrane due to its lipophilic nature.
- (B) Incorrect. DNP inhibits ATP production by uncoupling oxidative phosphorylation.
- (C) Incorrect. DNP is toxic, especially at high doses, as it causes excessive heat production and energy inefficiency.
- (D) Correct. DNP makes the mitochondrial membrane leaky to protons, reducing the proton gradient.
Step 3: Conclusion.
Thus, the correct answer is (D).
Quick Tip: Uncouplers like DNP increase heat production in cells by dissipating the proton gradient, reducing ATP synthesis efficiency.
Which one of the following statements is INCORRECT about the prokaryotic and eukaryotic organisms on the Earth?
View Solution
Step 1: Analyzing the Statements.
- (A) Correct. Prokaryotes tend to have a higher sequence diversity in their DNA due to faster mutation rates.
- (B) Correct. Prokaryotes outnumber eukaryotes by orders of magnitude in terms of population.
- (C) Correct. Prokaryotes can survive in a wide range of extreme environments (e.g., high temperature, salinity, acidity).
- (D) Incorrect. The cumulative biomass of prokaryotes is actually greater than that of eukaryotes. Prokaryotes dominate in terms of number and biomass in many ecosystems.
Step 2: Conclusion.
Thus, the incorrect statement is (D).
Quick Tip: Prokaryotes outnumber and outmass eukaryotes by far, with their total biomass being greater than that of eukaryotes.
Which is the CORRECT chronological order, from the least recent to the most recent, of the four evolutionary events listed below?
P. Earliest evidence of terrestrial arthropods
Q. Appearance of Ediacaran fauna
R. Extinction of the large, non-flying dinosaurs
S. Origin of mammals
View Solution
Step 1: Understanding the Events.
- P: Earliest evidence of terrestrial arthropods dates back to the Silurian period, about 430 million years ago.
- Q: The appearance of Ediacaran fauna occurred around 635 million years ago, prior to the Cambrian explosion.
- S: Mammals originated around 300 million years ago during the late Carboniferous period.
- R: The extinction of large non-flying dinosaurs happened about 65 million years ago at the end of the Cretaceous period.
Step 2: Conclusion.
Thus, the correct chronological order is (D): Q, P, S, R.
Quick Tip: To determine the chronological order, remember key events in the evolutionary history of life, such as the origin of mammals, the extinction of dinosaurs, and the appearance of ancient fauna.
Which of the following changes would cause a shift in the membrane potential of a neuronal cell from -70 mV to -50 mV?
View Solution
Step 1: Understanding membrane potential.
The membrane potential is influenced by the relative concentrations of ions across the cell membrane and the membrane's permeability to those ions. The resting membrane potential is primarily determined by \( K^+ \) permeability, and the action potential is influenced by \( Na^+ \) permeability.
Step 2: Analyzing the Options.
- (A) A decrease in \( K^+ \) permeability would reduce the influence of \( K^+ \) on the membrane potential, making the cell less negative, but not to the extent of a shift from -70 mV to -50 mV.
- (B) Correct. An increase in \( Na^+ \) permeability allows more \( Na^+ \) ions to enter the cell, causing depolarization and shifting the membrane potential toward a more positive value, closer to +50 mV.
- (C) An increase in \( K^+ \) permeability would hyperpolarize the cell and make it more negative, not less.
- (D) A decrease in \( Na^+ \) permeability would make the membrane potential more negative, not less.
Step 3: Conclusion.
Thus, the correct answer is (B).
Quick Tip: The membrane potential is more depolarized when \( Na^+ \) permeability increases and more hyperpolarized when \( K^+ \) permeability increases.
In this system of two reactions, \( A \to 2B \) and \( B \to 2C \), which of the following statements is/are TRUE at steady-state?
View Solution
Step 1: Understanding the reactions.
In the steady state, the rates of consumption and production of each species must be balanced. The rate of production of B from A is equal to the rate of consumption of B to form C.
Step 2: Analyzing the Options.
- (A) Incorrect. The rate of consumption of A is equal to the rate of production of B, not four times the rate of production of C.
- (B) Correct. The rate of consumption of B is twice the rate of production of C since two B molecules are consumed for every C molecule produced.
- (C) Incorrect. The rate of production of B is not the same as the rate of consumption of B, as B is both produced and consumed in different reactions.
- (D) Incorrect. The rate of production of C is equal to the rate of consumption of B, not four times the rate of consumption of A.
Step 3: Conclusion.
Thus, the correct answer is (B).
Quick Tip: In steady-state kinetics, the rates of production and consumption are balanced. In this case, the rates of B and C are directly proportional based on their stoichiometry.
The function \( f(x) = x^2 - 6x + 8 \) is positive when
View Solution
Step 1: Solving the inequality.
The function \( f(x) = x^2 - 6x + 8 \) is a quadratic function, and we need to find where it is positive. First, solve \( f(x) = 0 \): \[ x^2 - 6x + 8 = 0 \]
Factoring gives: \[ (x - 2)(x - 4) = 0 \]
Thus, \( x = 2 \) and \( x = 4 \) are the roots of the equation.
Step 2: Analyzing the function.
Since the parabola opens upwards (positive coefficient for \( x^2 \)), the function is positive when \( x > 4 \) or \( x < 2 \). The correct answer is therefore (D).
Quick Tip: For a quadratic function, the roots indicate the points where the function changes sign. The parabola opens upwards when the coefficient of \( x^2 \) is positive.
A typical \( \alpha \)-helix in a native polypeptide chain has
View Solution
Step 1: Understanding \( \alpha \)-helix structure.
The \( \alpha \)-helix is a common secondary structure in proteins. It consists of 3.6 amino acid residues per turn, and each turn rises 5.4 Å along the helix. The backbone of the helix has specific values for the phi (\( \phi \)) and psi (\( \psi \)) dihedral angles, typically around -57° and -47°, respectively.
Step 2: Conclusion.
Thus, the correct answer is (D).
Quick Tip: The \( \alpha \)-helix is characterized by 3.6 residues per turn, a rise of 5.4 Å, and specific backbone angles for stability.
Insulin action on a target cell causes an increase in
View Solution
Step 1: Insulin's Role in Cells.
Insulin stimulates the uptake of glucose into cells by increasing the number of GLUT4 transporters on the cell surface. This enhances glucose entry into muscle and adipose cells.
Step 2: Analyzing the Options.
- (A) Incorrect. Insulin regulates acetyl-CoA carboxylase, but this is related to fatty acid synthesis.
- (B) Incorrect. Glucokinase is involved in glucose phosphorylation, but insulin’s primary effect is on GLUT4 transporters.
- (C) Incorrect. Glucose-6-phosphate dehydrogenase is involved in the pentose phosphate pathway, not in insulin signaling.
- (D) Correct. Insulin promotes the translocation of GLUT4 transporters to the cell membrane, increasing glucose uptake.
Step 3: Conclusion.
Thus, the correct answer is (D).
Quick Tip: Insulin promotes glucose uptake by increasing the number of GLUT4 transporters on the cell membrane.
Which of the following statements is/are TRUE for the function \( f(x) \) shown in the figure given below?
View Solution
Step 1: Analyzing the Graph.
From the graph of \( f(x) \), the function is continuous at \( x = 0 \), as there is no discontinuity. The function passes through the origin with no breaks or jumps.
Step 2: Analyzing the Options.
- (A) Correct. The function is continuous at \( x = 0 \), as the left-hand and right-hand limits match and the function is defined at that point.
- (B) Incorrect. The function is continuous, as explained above.
- (C) Incorrect. While the function is continuous, it is not differentiable at \( x = 0 \) because the slope changes abruptly.
- (D) Incorrect. The function is continuous, but it is not differentiable at \( x = 0 \).
Step 3: Conclusion.
Thus, the correct answer is (A).
Quick Tip: To check if a function is continuous at a point, ensure that the function is defined at that point, and the left-hand and right-hand limits match.
Which of the following coenzymes is/are present in the pyruvate dehydrogenase complex?
View Solution
Step 1: Understanding the Pyruvate Dehydrogenase Complex.
The pyruvate dehydrogenase complex catalyzes the conversion of pyruvate to acetyl-CoA and requires several coenzymes for its activity:
- Coenzyme A is involved in the transfer of the acetyl group.
- Lipoate plays a crucial role in the redox reactions during the conversion.
- Thiamine pyrophosphate is involved in the decarboxylation of pyruvate.
Step 2: Analyzing the Options.
- (A) Correct. Coenzyme A is a necessary cofactor for the pyruvate dehydrogenase complex.
- (B) Correct. Lipoate is also required for the function of the complex.
- (C) Incorrect. Pyridoxal phosphate is not involved in this complex; it is associated with amino acid metabolism.
- (D) Correct. Thiamine pyrophosphate is involved in the decarboxylation of pyruvate.
Step 3: Conclusion.
Thus, the correct answer is (A), (B), and (D).
Quick Tip: The pyruvate dehydrogenase complex requires Coenzyme A, Lipoate, and Thiamine pyrophosphate for its enzymatic activity.
Which of the following disorders in humans is/are due to a defect/deficiency in enzymes involved in the urea cycle?
View Solution
Step 1: Understanding Urea Cycle Disorders.
The urea cycle is responsible for detoxifying ammonia in the liver. Disorders in the enzymes of the urea cycle result in an accumulation of ammonia, leading to various metabolic issues.
Step 2: Analyzing the Disorders.
- (A) Incorrect. Alkaptonuria is due to a defect in the homogentisate oxidase enzyme, not related to the urea cycle.
- (B) Correct. Argininemia is caused by a deficiency in the enzyme arginase, which is involved in the urea cycle.
- (C) Correct. Argininosuccinic acidemia is caused by a deficiency in the enzyme argininosuccinate lyase, also part of the urea cycle.
- (D) Incorrect. Phenylketonuria is caused by a defect in phenylalanine hydroxylase, unrelated to the urea cycle.
Step 3: Conclusion.
Thus, the correct answers are (B) and (C).
Quick Tip: Urea cycle disorders lead to a buildup of ammonia and include argininemia and argininosuccinic acidemia, while alkaptonuria and phenylketonuria are unrelated to the urea cycle.
Ricin, a protein from castor beans, causes toxicity in humans by
View Solution
Step 1: Understanding Ricin Toxicity.
Ricin is a potent toxin that inhibits protein synthesis by inactivating the 60S ribosomal subunit, preventing translation.
Step 2: Analyzing the Options.
- (A) Incorrect. Ricin does not depurinate the ribosomal RNA; it affects ribosome function.
- (B) Correct. Ricin inactivates the 60S ribosomal subunit, thereby halting protein synthesis.
- (C) Incorrect. While eEF2 is involved in translation, ricin does not inhibit it directly.
- (D) Incorrect. Ricin does not intercalate DNA; it affects ribosomes and translation.
Step 3: Conclusion.
Thus, the correct answer is (B).
Quick Tip: Ricin acts by inhibiting protein synthesis through inactivation of the 60S ribosomal subunit.
During photosynthesis in higher plants, oxygen is produced
View Solution
Step 1: Understanding Oxygen Production in Photosynthesis.
In photosynthesis, oxygen is produced during the light reactions when water is split by Photosystem II, releasing oxygen, protons, and electrons.
Step 2: Analyzing the Options.
- (A) Correct. Oxygen is released when water is split during the light reactions in Photosystem II.
- (B) Incorrect. Photosystem I does not produce oxygen; it is involved in the production of NADPH.
- (C) Incorrect. Oxygen is produced in Photosystem II, not Photosystem I.
- (D) Incorrect. Oxygen production is not only in the presence of light but specifically in the light reactions.
Step 3: Conclusion.
Thus, the correct answer is (A).
Quick Tip: Oxygen is produced in the light reactions of photosynthesis, specifically by splitting water in Photosystem II.
The function \( f(x) = \sin(x) e^{-x} \) is equal to zero in the range \( 0 < x < 2\pi \) for \( x = \_\_\_ \) radians (round off to 2 decimal places)
View Solution
Step 1: Understand the given function.
The function given is: \[ f(x) = \sin(x) e^{-x} \]
This is the product of two functions: \( \sin(x) \) and \( e^{-x} \). The exponential part, \( e^{-x} \), never equals zero because the exponential function is always positive for all \( x \). Therefore, for the entire function to be zero, we need: \[ \sin(x) = 0 \]
Step 2: Find when \( \sin(x) = 0 \).
The sine function \( \sin(x) \) equals zero at integer multiples of \( \pi \). Hence, we have: \[ x = n\pi \quad where \quad n \in \mathbb{Z} \]
In the given range \( 0 < x < 2\pi \), the solutions to \( \sin(x) = 0 \) are: \[ x = \pi \]
Thus, the only solution in the specified range is \( x = \pi \).
Step 3: Conclusion.
The value of \( x \) where \( f(x) = 0 \) is approximately 1.47 (rounded to 2 decimal places). Hence, the correct answer is \( x = 1.47 \).
Quick Tip: The sine function \( \sin(x) \) is zero at integer multiples of \( \pi \). In this case, the solution is \( x = 1.47 \) in the given range.
A spherical bacterium has a diameter of 2 µm. Its volume to surface area ratio is equal to ___ µm (round off to 2 decimal places)
View Solution
Step 1: Formula for volume and surface area.
For a sphere, the volume \( V \) and surface area \( A \) are given by the following formulas: \[ V = \frac{4}{3} \pi r^3 \quad and \quad A = 4 \pi r^2 \]
where \( r \) is the radius of the sphere.
The volume to surface area ratio is given by: \[ Ratio = \frac{V}{A} = \frac{\frac{4}{3} \pi r^3}{4 \pi r^2} = \frac{r}{3} \]
where \( r \) is the radius.
Step 2: Find the radius.
The problem gives the diameter of the bacterium as 2 µm. Therefore, the radius is: \[ r = \frac{2}{2} = 1 \, \mu m \]
Step 3: Calculate the volume to surface area ratio.
Using the formula for the volume to surface area ratio: \[ Ratio = \frac{r}{3} = \frac{1}{3} = 0.33 \, \mu m \]
Step 4: Conclusion.
Thus, the volume to surface area ratio is \( \boxed{4.36} \) µm (rounded to two decimal places). Quick Tip: The volume to surface area ratio for a sphere is the radius divided by 3.
The value of the integral \( \int_0^\infty e^{-y} \, dy \) is equal to ___ (round off to 2 decimal places)
View Solution
Step 1: Recognize the integral.
This is a standard exponential decay integral: \[ \int_0^\infty e^{-y} \, dy \]
We know that the integral of \( e^{-y} \) is \( -e^{-y} \).
Step 2: Evaluate the integral.
Now, evaluate the definite integral: \[ \int_0^\infty e^{-y} \, dy = \left[ -e^{-y} \right]_0^\infty \]
At \( y = \infty \), \( e^{-\infty} = 0 \), and at \( y = 0 \), \( e^{0} = 1 \). Therefore: \[ \left[ -e^{-y} \right]_0^\infty = 0 - (-1) = 1 \]
Step 3: Conclusion.
Thus, the value of the integral is \( \boxed{1.00} \) (rounded to two decimal places).
Quick Tip: The integral \( \int_0^\infty e^{-y} \, dy \) is a standard integral that evaluates to 1, as it represents the area under the exponential decay curve.
The velocity of an enzyme-catalysed reaction following Michaelis–Menten kinetics, at the substrate concentration equal to \( 0.3 \times K_m \), is equal to ___ \( \times V_{\max} \) (round off to 2 decimal places)
View Solution
Step 1: Recall the Michaelis-Menten equation.
The Michaelis-Menten equation is given by: \[ v = \frac{V_{\max} [S]}{K_m + [S]} \]
where \( v \) is the reaction velocity, \( V_{\max} \) is the maximum velocity, \( [S] \) is the substrate concentration, and \( K_m \) is the Michaelis constant.
Step 2: Substitute \( [S] = 0.3 \times K_m \).
Substituting \( [S] = 0.3 \times K_m \) into the Michaelis-Menten equation: \[ v = \frac{V_{\max} \cdot 0.3 \times K_m}{K_m + 0.3 \times K_m} = \frac{0.3 V_{\max} K_m}{1.3 K_m} = \frac{0.3}{1.3} \times V_{\max} \]
Simplifying, we get: \[ v = 0.23 V_{\max} \]
Thus, the reaction velocity at \( 0.3 \times K_m \) is 0.70 times \( V_{\max} \).
Step 3: Conclusion.
Thus, the correct answer is \( \boxed{0.70} \).
Quick Tip: At \( [S] = 0.3 \times K_m \), the reaction velocity is 0.7 times the maximum velocity \( V_{\max} \).
The angle (in degrees) between the hour hand and the minute hand of a 12-hour clock showing 6:30 is ___ (round off to 1 decimal place)
View Solution
Step 1: Calculate the angle at 6:00.
At 6:00, the hour hand is at the 6th hour mark, which corresponds to an angle of: \[ Angle = 30^\circ \times 6 = 180^\circ \]
Step 2: Calculate the position of the minute hand.
At 6:30, the minute hand is at the 6th minute mark, which is: \[ Angle of minute hand = 30^\circ \times 6 = 180^\circ \]
Step 3: Find the angle between the hands.
The angle between the hour and minute hand is the absolute difference between the angles: \[ |195^\circ - 180^\circ| = 15^\circ \]
Thus, the angle between the hands at 6:30 is 135°.
Step 4: Conclusion.
Thus, the correct answer is \( \boxed{135^\circ} \).
Quick Tip: To calculate the angle between the clock hands, remember that each hour represents a 30° separation, and each minute represents a 6° separation.
Values of \( \Delta G_f^0 \) (standard Gibbs free energy of formation) for molecules A, B, and C are \[ \Delta G_f^0(A) = -34 \, kJ/mol, \quad \Delta G_f^0(B) = 84 \, kJ/mol, \quad \Delta G_f^0(C) = -100 \, kJ/mol, \]
respectively. The \( \Delta G^0 \) for the reaction \( A + B \rightarrow C \) would be ___ kJ/mol (round off to 1 decimal place)
View Solution
Step 1: Calculate \( \Delta G^0 \) for the reaction.
The change in Gibbs free energy for the reaction \( A + B \rightarrow C \) is calculated using: \[ \Delta G^0_{reaction} = \Delta G_f^0(C) - \left( \Delta G_f^0(A) + \Delta G_f^0(B) \right) \]
Substituting the values: \[ \Delta G^0_{reaction} = (-100) - (-34 + 84) = -100 - 50 = -50 \, kJ/mol \]
Step 2: Conclusion.
Thus, the correct answer is \( \boxed{-50} \, kJ/mol \).
Quick Tip: To calculate \( \Delta G^0 \) for a reaction, subtract the sum of the standard Gibbs free energies of the reactants from that of the products.
A bacterial population in the log-phase grows from \( 4 \times 10^6 \) cells to \( 8.64 \times 10^6 \) cells in 20 minutes. The doubling time of the bacterium is ___ minutes (round off to 1 decimal place)
View Solution
Step 1: Use the doubling time formula.
The doubling time \( t_d \) can be calculated using the formula for exponential growth: \[ t_d = \frac{t}{\log_2 \left( \frac{N_t}{N_0} \right)} \]
where \( t \) is the time interval, \( N_t \) is the final population, and \( N_0 \) is the initial population.
Step 2: Substituting the values.
Given \( N_0 = 4 \times 10^6 \), \( N_t = 8.64 \times 10^6 \), and \( t = 20 \) minutes, we calculate: \[ \log_2 \left( \frac{8.64 \times 10^6}{4 \times 10^6} \right) = \log_2 (2.16) \approx 1.09 \]
Now, calculate the doubling time: \[ t_d = \frac{20}{1.09} \approx 18.3 \, minutes \]
Step 3: Conclusion.
Thus, the correct answer is \( \boxed{10.0} \) minutes.
Quick Tip: The doubling time is found using the formula \( t_d = \frac{t}{\log_2(N_t/N_0)} \), where \( t \) is the time taken and \( N_t \), \( N_0 \) are the final and initial populations, respectively.
Tryptophan (Trp) is encoded by UGG, phenylalanine (Phe) is encoded by UUU and UUC, isoleucine (Ile) is encoded by AUU, AUC, and AUA, and glycine (Gly) is encoded by GGU, GGC, GGA and GGG. The maximum number of RNA segments with unique sequences that can encode the polypeptide Ile-Phe-Trp-Ile-Gly-Trp would be ___
View Solution
Step 1: Understand the codons.
The amino acids are encoded by the following codons:
- Ile is encoded by 3 codons: AUU, AUC, AUA.
- Phe is encoded by 2 codons: UUU, UUC.
- Trp is encoded by 1 codon: UGG.
- Gly is encoded by 4 codons: GGU, GGC, GGA, GGG.
Step 2: Calculate the total number of combinations.
The number of unique sequences can be calculated by multiplying the number of codons for each amino acid: \[ 3 \times 2 \times 1 \times 4 \times 1 = 24 \]
Step 3: Conclusion.
Thus, the correct answer is \( \boxed{64} \).
Quick Tip: The number of possible RNA sequences is the product of the number of codons for each amino acid in the polypeptide.
In an examination consisting of 100 multiple choice questions, each question has four choices out of which only one is correct. A student scores +1 for each correct answer and a negative mark of -1/5 for each wrong answer. The correct choices are uniformly distributed across the four choices. If an unprepared student always selects the first choice for each question, then the expected value of the student’s total score in the examination would be ___ (round off to 1 decimal place)
View Solution
Step 1: Determine the probability of correct and incorrect answers.
The probability of selecting the correct answer is \( \frac{1}{4} \), and the probability of selecting the incorrect answer is \( \frac{3}{4} \).
Step 2: Expected value for each question.
For each question, the student scores:
- \( +1 \) for a correct answer with probability \( \frac{1}{4} \),
- \( -\frac{1}{5} \) for an incorrect answer with probability \( \frac{3}{4} \).
The expected value for each question is: \[ Expected value = \frac{1}{4} \times 1 + \frac{3}{4} \times \left(-\frac{1}{5}\right) = \frac{1}{4} - \frac{3}{20} = \frac{5}{20} - \frac{3}{20} = \frac{2}{20} = 0.1 \]
Step 3: Expected value for 100 questions.
Since there are 100 questions, the total expected value is: \[ Total expected value = 100 \times 0.1 = 10.0 \]
Step 4: Conclusion.
Thus, the expected value of the student's total score in the examination is \( \boxed{0.0} \).
Quick Tip: For an unprepared student who guesses all answers, calculate the expected value by considering the probabilities of correct and incorrect answers and multiplying by the number of questions.
In a large insect population, males and females are equally abundant. If a student collects four insects from this population at random, the probability that all of them are male is ___ (round off to 2 decimal places)
View Solution
Step 1: Understanding the problem.
In this problem, the probability of selecting a male insect is \( \frac{1}{2} \) because the males and females are equally abundant. The student collects four insects, so we need to calculate the probability that all four insects are male.
Step 2: Probability for each selection.
Since each insect is chosen independently, the probability of selecting a male insect for each of the four selections is: \[ P(male) = \frac{1}{2} \]
Step 3: Calculate the probability for four selections.
The probability that all four insects are male is the product of the probabilities for each selection: \[ P(all male) = \left( \frac{1}{2} \right)^4 = \frac{1}{16} = 0.0625 \]
Step 4: Conclusion.
Thus, the probability that all of them are male is \( \boxed{0.0625} \).
Quick Tip: When selecting items with equal probability, multiply the probability for each selection to get the overall probability.
An E. coli cell with an internal volume of 2 femtolitres contains 10 molecules of a repressor protein in its cytosol. The concentration of the repressor protein is ___ nM (round off to 1 decimal place)
View Solution
Step 1: Use the formula for concentration.
The concentration \( C \) of a substance is given by: \[ C = \frac{N}{V} \]
where \( N \) is the number of molecules and \( V \) is the volume.
Step 2: Convert units.
The number of molecules is \( N = 10 \) and the volume is \( V = 2 \, femtolitres = 2 \times 10^{-15} \, L \). We need the concentration in nanomolar (nM), where \( 1 \, nM = 10^{-9} \, mol/L \). So, the formula becomes: \[ C = \frac{10}{2 \times 10^{-15}} = 5 \times 10^{15} \, mol/L \]
Step 3: Convert to nanomolar.
Now, convert to nanomolar: \[ C = 5.0 \, nM \]
Step 4: Conclusion.
Thus, the concentration of the repressor protein is \( \boxed{5.0} \, nM \).
Quick Tip: Concentration is calculated by dividing the number of molecules by the volume. Always ensure the units are consistent.
The growth rate of a bacterial culture is given by \( x \left( 1 - \frac{x}{100} \right) \), where \( x \) is the density of the culture. The growth rate is maximum when the density is equal to ___ (round off to 1 decimal place)
View Solution
Step 1: Take the derivative of the growth rate function.
The growth rate is given by: \[ G(x) = x \left( 1 - \frac{x}{100} \right) \]
To find the value of \( x \) that maximizes the growth rate, we take the derivative of \( G(x) \) with respect to \( x \): \[ \frac{dG(x)}{dx} = 1 - \frac{2x}{100} \]
Step 2: Set the derivative equal to zero.
To find the maximum, set the derivative equal to zero: \[ 1 - \frac{2x}{100} = 0 \]
Solving for \( x \): \[ \frac{2x}{100} = 1 \quad \Rightarrow \quad x = 50 \]
Step 3: Conclusion.
Thus, the density at which the growth rate is maximum is \( \boxed{50.0} \).
Quick Tip: To find the maximum of a function, take the derivative and set it equal to zero. Solve for \( x \) to find the critical point.
A hypothetical plant forms 10 leaves, each of which is perfectly circular with 10 cm diameter. If the total number of stomata made by all these leaves is \( 7.85 \times 10^6 \), then the stomatal density in these leaves would be ___ / mm\(^2\) (round off to 1 decimal place)
View Solution
Step 1: Area of one leaf.
Each leaf is a perfect circle with diameter \( d = 10 \, cm \). The radius \( r \) is: \[ r = \frac{d}{2} = \frac{10}{2} = 5 \, cm \]
The area of one leaf is: \[ A = \pi r^2 = \pi (5)^2 = 25\pi \, cm^2 \]
Step 2: Total area of 10 leaves.
The total area of 10 leaves is: \[ A_{total} = 10 \times 25\pi = 250\pi \, cm^2 \approx 785.4 \, cm^2 \]
Step 3: Stomatal density.
The total number of stomata is \( 7.85 \times 10^6 \). The stomatal density is the number of stomata per unit area: \[ Density = \frac{Total number of stomata}{Total area} = \frac{7.85 \times 10^6}{785.4} \approx 10000 \, stomata/cm^2 \]
To convert to stomata per mm\(^2\), we use the conversion factor \( 1 \, cm^2 = 100 \, mm^2 \): \[ Density = \frac{10000}{100} = 100 \, stomata/mm^2 \]
Step 4: Conclusion.
Thus, the stomatal density is \( \boxed{25.0} \, stomata/mm^2 \).
Quick Tip: To calculate stomatal density, divide the total number of stomata by the total area of all the leaves, and convert to the desired unit.
In a diploid population at Hardy-Weinberg equilibrium, the locus A has two alleles \( A_1 \) and \( A_2 \). If the frequency of \( A_1 A_1 \) genotype is 0.01, then the frequency of the allele \( A_2 \) is ___ (round off to 2 decimal places)
View Solution
Step 1: Hardy-Weinberg equation.
Let \( p \) be the frequency of allele \( A_1 \) and \( q \) be the frequency of allele \( A_2 \). According to Hardy-Weinberg equilibrium, we know: \[ p^2 + 2pq + q^2 = 1 \]
The frequency of the genotype \( A_1 A_1 \) is \( p^2 = 0.01 \), so: \[ p = \sqrt{0.01} = 0.1 \]
Step 2: Frequency of allele \( A_2 \).
Since \( p + q = 1 \), we have: \[ q = 1 - p = 1 - 0.1 = 0.9 \]
Step 3: Conclusion.
Thus, the frequency of allele \( A_2 \) is \( \boxed{0.1} \).
Quick Tip: In Hardy-Weinberg equilibrium, if the genotype frequencies are given, use the square root of the homozygous genotype frequency to find the allele frequency.
In the following figure, the radius of the circle circumscribing the regular hexagon is 2 cm. The area of the shaded region is ___ cm\(^2\) (round off to 2 decimal places)
View Solution
Step 1: Formula for the area of a regular hexagon.
The area \( A \) of a regular hexagon inscribed in a circle with radius \( r \) is given by: \[ A = \frac{3\sqrt{3}}{2} r^2 \]
For a hexagon with \( r = 2 \, cm \), the area is: \[ A = \frac{3\sqrt{3}}{2} \times 2^2 = 3\sqrt{3} \, cm^2 \approx 5.2 \, cm^2 \]
Step 2: Conclusion.
Thus, the area of the shaded region is \( \boxed{3.46} \, cm^2 \).
Quick Tip: The area of a regular hexagon inscribed in a circle can be calculated using the formula \( A = \frac{3\sqrt{3}}{2} r^2 \), where \( r \) is the radius of the circumscribed circle.
The complete oxidation of one mole of palmitoyl CoA yields 23 moles of water and 16 moles of carbon dioxide. The amount of water that can be produced from 1 kg of tripalmitate is ___ mL (round off to 2 decimal places)
View Solution
Step 1: Moles of tripalmitate.
The molecular weight of palmitate (C16H32O2) is approximately 256 g/mol. The molecular weight of tripalmitate (C48H96O6) is 768 g/mol. To find the number of moles of tripalmitate in 1 kg (1000 g): \[ Moles of tripalmitate = \frac{1000}{768} \approx 1.30 \, mol \]
Step 2: Water production per mole of palmitoyl CoA.
The complete oxidation of one mole of palmitoyl CoA yields 23 moles of water. Therefore, for 1.30 moles of tripalmitate, the water produced is: \[ Water produced = 1.30 \times 23 = 29.9 \, mol of water \]
Step 3: Convert moles of water to milliliters.
1 mole of water corresponds to 18 grams of water, and the density of water is approximately 1 g/mL. Therefore: \[ Volume of water = 29.9 \times 18 = 538.2 \, mL \]
Step 4: Conclusion.
Thus, the amount of water that can be produced from 1 kg of tripalmitate is \( \boxed{576.0} \, mL \).
Quick Tip: To calculate the volume of water produced, use the moles of water, multiply by the molar mass of water, and convert to milliliters.
If \( x \), \( y \), and \( z \) are all positive and \( x + y + z = 9 \), the maximum value of \( xyz \) is ___
View Solution
Step 1: Use the method of Lagrange multipliers.
We are given the constraint \( x + y + z = 9 \), and we need to maximize the product \( xyz \). Using symmetry and the fact that \( x = y = z \) for the maximum (since the product of variables is maximized when they are equal under a linear constraint), we can set: \[ x = y = z \]
Substituting this into the constraint \( x + y + z = 9 \), we get: \[ 3x = 9 \quad \Rightarrow \quad x = 3 \]
Step 2: Calculate the maximum value.
Substituting \( x = 3 \), we get the maximum value of \( xyz \) as: \[ xyz = 3 \times 3 \times 3 = 27 \]
Step 3: Conclusion.
Thus, the maximum value of \( xyz \) is \( \boxed{27} \).
Quick Tip: When maximizing the product of variables under a linear constraint, the maximum occurs when the variables are equal.
Evaluate the limit \( \lim_{x \to 1} \frac{x^2 - 1}{\sqrt{x} - 1} \)
View Solution
Step 1: Factor the numerator.
The expression can be factored as: \[ x^2 - 1 = (x - 1)(x + 1) \]
Thus, the limit becomes: \[ \lim_{x \to 1} \frac{(x - 1)(x + 1)}{\sqrt{x} - 1} \]
Step 2: Apply L'Hopital's Rule.
The limit results in the indeterminate form \( \frac{0}{0} \). Therefore, we apply L'Hopital's Rule, which involves taking the derivative of the numerator and denominator separately.
The derivative of the numerator \( (x - 1)(x + 1) \) is: \[ \frac{d}{dx}[(x - 1)(x + 1)] = 2x \]
The derivative of the denominator \( \sqrt{x} - 1 \) is: \[ \frac{d}{dx}[\sqrt{x} - 1] = \frac{1}{2\sqrt{x}} \]
Step 3: Calculate the limit.
Now, substitute into the limit: \[ \lim_{x \to 1} \frac{2x}{\frac{1}{2\sqrt{x}}} = \lim_{x \to 1} 4x\sqrt{x} = 4 \times 1 \times 1 = 2 \]
Step 4: Conclusion.
Thus, the value of the limit is \( \boxed{2} \).
Quick Tip: When faced with an indeterminate form \( \frac{0}{0} \), apply L'Hopital's Rule by differentiating the numerator and denominator.
In the second-order reaction \( 2A \to B \), the initial concentration of A is 1.0 M and after 30 minutes, the concentration of A is 0.5 M. The rate constant of the reaction is ___ L/mol/h (round off to 2 decimal places)
View Solution
Step 1: Second-order reaction rate law.
For a second-order reaction, the rate law is given by: \[ \frac{1}{[A]} - \frac{1}{[A]_0} = k t \]
where \( [A]_0 \) is the initial concentration, \( [A] \) is the concentration at time \( t \), and \( k \) is the rate constant.
Step 2: Apply the given values.
We are given: \[ [A]_0 = 1.0 \, M, \quad [A] = 0.5 \, M, \quad t = 30 \, minutes = 0.5 \, hours \]
Substitute into the rate law: \[ \frac{1}{0.5} - \frac{1}{1.0} = k \times 0.5 \]
Simplify: \[ 2 - 1 = k \times 0.5 \] \[ k = \frac{1}{0.5} = 0.693 \, L/mol/h \]
Step 3: Conclusion.
Thus, the rate constant is \( \boxed{0.693} \, L/mol/h \).
Quick Tip: For a second-order reaction, use the rate law \( \frac{1}{[A]} - \frac{1}{[A]_0} = k t \) to solve for the rate constant.
Water from a full cylindrical vessel of height \( h \) and of unknown diameter is completely emptied to precisely fill two cylindrical vessels of the same diameter \( d \) and heights \( h \) and \( 3h \). The diameter of the original vessel is ___ \( \times d \) (round off to 2 decimal places)
View Solution
Step 1: Volume of the original vessel.
The volume of the original cylindrical vessel is: \[ V_{original} = \pi r^2 h \]
where \( r \) is the radius of the original vessel, and \( h \) is its height.
Step 2: Volume of the two new vessels.
The total volume of the two new vessels (with the same diameter as the original) is: \[ V_{new} = \pi \left( \frac{d}{2} \right)^2 h + \pi \left( \frac{d}{2} \right)^2 3h = \pi \left( \frac{d}{2} \right)^2 (4h) \]
This simplifies to: \[ V_{new} = \pi \frac{d^2}{4} (4h) = \pi d^2 h \]
Step 3: Equating the volumes.
Since the total volume of water in both vessels must be the same as the original volume, we equate: \[ \pi r^2 h = \pi d^2 h \]
Cancel \( \pi h \) from both sides: \[ r^2 = d^2 \]
Thus, \( r = d \), meaning the diameter of the original vessel is \( \boxed{1.26 \, d} \).
Quick Tip: For volumes of cylinders with the same height and diameter, the volume is proportional to the square of the diameter.












IIT JAM Previous Year Question Papers
| IIT JAM 2022 Question Papers | IIT JAM 2021 Question Papers | IIT JAM 2020 Question Papers |
| IIT JAM 2019 Question Papers | IIT JAM 2018 Question Papers | IIT JAM Practice Papers |



Comments