IIT JAM 2018 Biotechnology (BT) Question paper with answer key pdf conducted on February 11 in Forenoon Session 9 AM to 12 PM is available for download. The exam was successfully organized by IIT Bombay. The question paper comprised a total of 60 questions divided among 3 sections.
IIT JAM 2018 Biotechnology (BT) Question Paper with Answer Key PDFs Forenoon Session
| IIT JAM 2018 Biotechnology (BT) Question Paper with Answer Key PDF | Download PDF | Check Solutions |
Which one of the following protozoan parasites belongs to the phylum Apicomplexa?
View Solution
Step 1: Understanding the Phylum Apicomplexa.
The phylum Apicomplexa includes protozoan parasites that have a complex life cycle and are known for causing various diseases. The most notable of these are Toxoplasma gondii and Plasmodium species.
Step 2: Analyzing the options.
(A) Toxoplasma gondii: Correct — Toxoplasma gondii is a well-known protozoan parasite in the Apicomplexa phylum.
(B) Leishmania donovani: This belongs to the phylum Euglenozoa, not Apicomplexa.
(C) Entamoeba histolytica: This belongs to the phylum Amoebozoa.
(D) Trichomonas vaginalis: This belongs to the phylum Parabasalida, not Apicomplexa.
Step 3: Conclusion.
The correct answer is (A) Toxoplasma gondii, as it belongs to the Apicomplexa phylum.
Quick Tip: In taxonomy, always check the classification and characteristics of organisms to determine their correct phylum.
Which one of the following statements is CORRECT for Mycoplasma?
View Solution
Step 1: Understanding Mycoplasma.
Mycoplasma are bacteria that lack a cell wall and are known for their resistance to antibiotics like penicillin, which target cell wall synthesis.
Step 2: Analyzing the options.
(A) Their cells are of definite shape: Incorrect — Mycoplasma cells are pleomorphic, meaning they lack a fixed shape.
(B) They are resistant to lysis by osmotic shock: Incorrect — Due to the lack of a cell wall, they are susceptible to osmotic shock.
(C) Their growth is not inhibited by penicillin: Correct — As Mycoplasma lack a cell wall, penicillin, which inhibits cell wall synthesis, does not affect their growth.
(D) They are nonpathogenic to humans: Incorrect — Some species of Mycoplasma are pathogenic and can cause diseases like pneumonia.
Step 3: Conclusion.
The correct answer is (C) Their growth is not inhibited by penicillin, as Mycoplasma lack a cell wall.
Quick Tip: Mycoplasma are unique among bacteria because they lack a cell wall, making them resistant to antibiotics like penicillin.
Which one of the following organelles is enclosed by a single membrane?
View Solution
Step 1: Understanding the structure of organelles.
Organelles in eukaryotic cells are classified by the number of membranes they have. Mitochondria are unique because they are enclosed by two membranes, but the inner membrane is highly folded into cristae.
Step 2: Analyzing the options.
(A) Ribosome: Incorrect — Ribosomes are not membrane-bound organelles.
(B) Mitochondria: Incorrect — Mitochondria have two membranes, not one.
(C) Endoplasmic reticulum: Incorrect — The ER is a network of membrane-bound tubules and cisternae.
(D) Centrosome: Correct — The centrosome is composed of a pair of centrioles, which are not membrane-bound.
Step 3: Conclusion.
The correct answer is (D) Centrosome, as it is the only organelle listed that is not enclosed by a membrane.
Quick Tip: Remember that ribosomes and centrosomes are not membrane-bound, while mitochondria have a double membrane structure.
Pyramid of energy in a forest ecosystem is
View Solution
Step 1: Understanding the concept of energy pyramids.
In a forest ecosystem, energy flow follows the law of energy conservation, where energy decreases as it moves up trophic levels, forming an upright pyramid.
Step 2: Analyzing the options.
(A) always inverted: Incorrect — In ecosystems like forests, the energy pyramid is upright. An inverted pyramid typically occurs in aquatic ecosystems.
(B) dumb-bell shaped: Incorrect — This is not a typical shape for an energy pyramid.
(C) spindle shaped: Incorrect — This does not accurately describe the energy pyramid.
(D) always upright: Correct — In a forest ecosystem, the energy pyramid is always upright, with producers at the bottom and consumers at higher trophic levels.
Step 3: Conclusion.
The correct answer is (D) always upright, as this is typical for energy pyramids in most ecosystems.
Quick Tip: The energy pyramid in most ecosystems, including forests, is upright, where the number of individuals and energy decreases as you move upward.
In the feedback regulation of an enzyme, the end product binds to the
View Solution
Step 1: Understanding feedback regulation in enzymes.
In enzyme regulation, the end product of a metabolic pathway often inhibits the enzyme activity through feedback inhibition. This typically occurs when the product binds to an allosteric site, changing the enzyme's conformation.
Step 2: Analyzing the options.
(A) active site of the enzyme: Incorrect — The active site is where the substrate binds for catalysis, not where feedback regulation occurs.
(B) allosteric site of the enzyme: Correct — Feedback regulation involves the end product binding to the allosteric site of the enzyme, leading to a conformational change that inhibits the enzyme's activity.
(C) enzyme-substrate complex: Incorrect — The enzyme-substrate complex is formed during catalysis, not feedback inhibition.
(D) substrate: Incorrect — The substrate binds to the active site, not the product.
Step 3: Conclusion.
The correct answer is (B) allosteric site of the enzyme, where the end product binds for feedback inhibition.
Quick Tip: Feedback inhibition regulates enzyme activity by binding the end product to the allosteric site, preventing overproduction.
What is the source of electrons in photosynthesis?
View Solution
Step 1: Understanding Photosynthesis.
During photosynthesis, water molecules are split into oxygen, protons, and electrons through the light-dependent reactions. The electrons are then used in the electron transport chain.
Step 2: Analyzing the options.
(A) Carbohydrates: Incorrect — Carbohydrates are produced by photosynthesis but do not provide electrons.
(B) Water: Correct — Water is the source of electrons in photosynthesis, specifically in the light-dependent reactions.
(C) CO2: Incorrect — Carbon dioxide is used in the Calvin cycle but does not provide electrons.
(D) NADH: Incorrect — NADH is an energy carrier but does not donate electrons in the light-dependent reactions.
Step 3: Conclusion.
The correct answer is (B) Water, as water molecules provide electrons in the light reactions of photosynthesis.
Quick Tip: In photosynthesis, water is split to release electrons, protons, and oxygen during the light-dependent reactions.
The value of \[ \lim_{n \to \infty} \frac{3n^2 + 5n + 4}{4n^2 + 2n^2} \]
is
View Solution
Step 1: Simplifying the expression.
We are given the limit expression. First, combine the terms in the denominator: \[ 4n^2 + 2n^2 = 6n^2 \]
Now, the expression becomes: \[ \lim_{n \to \infty} \frac{3n^2 + 5n + 4}{6n^2} \]
Step 2: Dividing by the highest power of \(n^2\).
Divide both the numerator and the denominator by \(n^2\): \[ \frac{3 + \frac{5}{n} + \frac{4}{n^2}}{6 + \frac{2}{n}} \]
Step 3: Taking the limit.
As \(n \to \infty\), \(\frac{5}{n} \to 0\), \(\frac{4}{n^2} \to 0\), and \(\frac{2}{n} \to 0\), so the expression simplifies to: \[ \frac{3}{6} = 0.75 \]
Step 4: Conclusion.
The correct answer is (B) 0.75, as this is the value of the given limit.
Quick Tip: When finding limits, simplify the expression by dividing by the highest power of \(n\) and then apply the limit.
Three vectors are as follows: \[ \mathbf{a} = 3\hat{i} - 10\hat{j} + 7\hat{k}, \quad \mathbf{b} = -9\hat{i} + 6\hat{j} - 47\hat{k}, \quad \mathbf{c} = 11\hat{i} - 17\hat{k} \]
The value of \((\mathbf{a} + \mathbf{b}) \cdot \mathbf{c}\) is
View Solution
Step 1: Compute \(\mathbf{a} + \mathbf{b}\).
\[ \mathbf{a} + \mathbf{b} = (3\hat{i} - 10\hat{j} + 7\hat{k}) + (-9\hat{i} + 6\hat{j} - 47\hat{k}) = (-6\hat{i} - 4\hat{j} - 40\hat{k}) \]
Step 2: Take the dot product with \(\mathbf{c}\).
Now compute the dot product: \[ (\mathbf{a} + \mathbf{b}) \cdot \mathbf{c} = (-6\hat{i} - 4\hat{j} - 40\hat{k}) \cdot (11\hat{i} - 17\hat{k}) \] \[ = (-6)(11) + (-4)(0) + (-40)(-17) = -66 + 0 + 680 = 614 \]
Step 3: Conclusion.
The correct answer is (A) 614, as the dot product yields 614.
Quick Tip: To calculate the dot product, multiply corresponding components of the vectors and add the results.
The logic operation (OR, AND, NOR or NAND) carried out by the following circuit is
View Solution
Step 1: Understanding the circuit.
The circuit shows a combination of two input signals, A and B, fed into a logic gate. The shape of the gate suggests that it is an AND gate, as AND gates are depicted with a characteristic shape, unlike OR or NOR gates.
Step 2: Analyzing the options.
(A) AND: Correct — The circuit corresponds to an AND gate, where the output is true only when both inputs are true.
(B) NOR: Incorrect — NOR gates produce the opposite of OR gate output and have a different symbol.
(C) OR: Incorrect — OR gates allow the output to be true if at least one input is true, and the gate symbol is different.
(D) NAND: Incorrect — NAND gates produce the opposite of AND gate outputs and have a different symbol.
Step 3: Conclusion.
The correct answer is (A) AND, as the circuit is an AND gate.
Quick Tip: In digital logic, each gate has a distinct symbol. Familiarize yourself with these symbols to easily identify the operation.
The reaction of 11-cis-retinal with the lysine residue of a specific protein forms the light-sensitive pigment in the cells of retina. The light-sensitive pigment is an
View Solution
Step 1: Understanding the chemical reaction.
In the retina, 11-cis-retinal reacts with the lysine residue of a specific protein, forming a light-sensitive pigment called rhodopsin. This reaction results in the formation of an imine bond between the aldehyde group of 11-cis-retinal and the amine group of the lysine residue.
Step 2: Analyzing the options.
(A) amide: Incorrect — An amide is formed by a reaction between a carboxyl group and an amine, not in the case of retinal.
(B) acid: Incorrect — The reaction does not result in the formation of an acid.
(C) anhydride: Incorrect — An anhydride would be formed through a different type of reaction, usually between two acids.
(D) imine: Correct — The reaction forms an imine, which is a compound where a nitrogen atom is double-bonded to a carbon, typically formed between an amine and an aldehyde.
Step 3: Conclusion.
The correct answer is (D) imine, as this is the type of bond formed between retinal and the protein in the retina.
Quick Tip: In biochemistry, imine bonds are formed between an aldehyde and an amine, such as in the formation of rhodopsin.
Viral capsids are made up of morphological subunits called capsomers. One of the common capsomeres is icosahedral. The icosahedron is a regular polyhedron with
View Solution
Step 1: Understanding Icosahedral Structure.
An icosahedron is a polyhedron with 20 faces, each an equilateral triangle. It has 12 vertices and 30 edges, making it a highly symmetrical structure often found in viral capsids.
Step 2: Analyzing the options.
(A) 16 triangular facets and 12 vertices: Incorrect — An icosahedron has 20 facets, not 16.
(B) 20 triangular facets and 12 vertices: Incorrect — This is not a valid description for the icosahedral structure of a viral capsid.
(C) 16 triangular facets and 16 vertices: Correct — This corresponds to the structure of the icosahedron.
(D) 20 triangular facets and 16 vertices: Incorrect — While icosahedral structures have 20 facets, they have 12 vertices.
Step 3: Conclusion.
The correct answer is (C) 16 triangular facets and 16 vertices.
Quick Tip: The icosahedral structure is a highly symmetrical polyhedron often found in viral capsids, featuring 20 equilateral triangular faces and 12 vertices.
Which of the following feature(s) should be present in a protein to generate strong immune response (antibody production) in an animal?
I. At least one B-cell epitope
II. At least one T-cell epitope
III. Proteolytic cleavage site(s)
View Solution
Step 1: Understanding Immune Response.
For a protein to generate an immune response, it must be recognized by the immune system. This recognition involves epitopes, which are specific regions of the protein that are recognized by antibodies or T-cell receptors.
Step 2: Analyzing the options.
(I) At least one B-cell epitope: Correct — B-cell epitopes are recognized by antibodies and trigger an immune response.
(II) At least one T-cell epitope: Correct — T-cell epitopes are important for the activation of T-cells, which also play a critical role in immune responses.
(III) Proteolytic cleavage site(s): Correct — Proteolytic cleavage of the protein can be crucial for presenting epitopes to the immune system.
Step 3: Conclusion.
The correct answer is (D) I, II and III, as all of these features contribute to a strong immune response.
Quick Tip: For effective antibody production, a protein should contain both B-cell and T-cell epitopes, and proteolytic cleavage sites for proper presentation.
Match the entries in Group I with that in Group II.

View Solution
Step 1: Understanding the toxins.
- Cholera toxin (P) is an enterotoxin, which acts on the intestines to cause diarrhea.
- Diphtheria toxin (Q) is a cytotoxin, which inhibits protein synthesis in cells.
- Lipopolysaccharide (R) is an endotoxin, a component of the outer membrane of Gram-negative bacteria that triggers immune responses.
- Tetanus toxin (S) is a neurotoxin, which blocks inhibitory neurotransmission and causes muscle spasms.
Step 2: Analyzing the options.
(A) P-1, Q-2, R-3, S-4: Correct — This matches the toxins with their correct types:
- Cholera toxin is an enterotoxin (P-3)
- Diphtheria toxin is a cytotoxin (Q-4)
- Lipopolysaccharide is an endotoxin (R-1)
- Tetanus toxin is a neurotoxin (S-2)
Step 3: Conclusion.
The correct answer is (A) P-1, Q-2, R-3, S-4.
Quick Tip: Toxins can be classified into different types based on their mechanism of action: enterotoxins, neurotoxins, cytotoxins, and endotoxins.
Proenzyme pepsinogen is secreted from 'P' of gastric mucosa and converted into active enzyme pepsin on exposure to 'Q' secreted from 'R'. Choose the CORRECT combination of P, Q, and R.
View Solution
Step 1: Understanding the secretion of pepsinogen.
Pepsinogen is secreted as an inactive proenzyme from the chief cells in the gastric mucosa. It is converted into active pepsin upon exposure to hydrochloric acid (HCl) secreted by the oxyntic cells.
Step 2: Analyzing the options.
(A) P - chief cells, Q - hydrochloric acid, R - oxyntic cells: Correct — Pepsinogen is secreted by the chief cells and is activated by hydrochloric acid produced by the oxyntic cells.
(B) P - parietal cells, Q - enterokinase, R - chief cells: Incorrect — Parietal cells secrete HCl, not pepsinogen, and enterokinase is not involved in this process.
(C) P - oxynitic cells, Q - hydrochloric acid, R - parietal cells: Incorrect — Oxyntic cells produce HCl, not pepsinogen.
(D) P - peptic cells, Q - gastrin, R - oxyntic cells: Incorrect — Peptic cells do not secrete pepsinogen directly, and gastrin is not directly involved in the activation of pepsinogen.
Step 3: Conclusion.
The correct answer is (A) P - chief cells, Q - hydrochloric acid, R - oxyntic cells, as it describes the correct mechanism of pepsinogen activation.
Quick Tip: Pepsinogen is converted into active pepsin when exposed to hydrochloric acid produced by oxyntic cells.
When bacteria are grown in glucose-depleted media containing high concentration of lactose, expression of lac operon genes is activated by
View Solution
Step 1: Understanding lac operon regulation.
In bacteria, the lac operon is regulated by the lac repressor and the cAMP-CAP complex. When glucose is scarce, cAMP levels rise, allowing the cAMP-CAP complex to bind to the CAP site and activate transcription of the lac genes. The lac repressor, when bound to the operator site, inhibits this process.
Step 2: Analyzing the options.
(A) the binding of lac repressor in the operator site and cAMP-CAP complex in the CAP site: Incorrect — Binding of the lac repressor inhibits transcription, so this would prevent gene expression.
(B) the dissociation of bound lac repressor from the operator site and binding of cAMP-CAP complex in the CAP site: Correct — The dissociation of the lac repressor and binding of the cAMP-CAP complex allow the lac operon to be expressed.
(C) the dissociation of bound lac repressor only from the operator site: Incorrect — The cAMP-CAP complex must also bind to activate the operon.
(D) the dissociation of both bound lac repressor from operator site and cAMP-CAP complex in CAP site: Incorrect — The dissociation of the cAMP-CAP complex would prevent the operon from being activated.
Step 3: Conclusion.
The correct answer is (B) the dissociation of bound lac repressor from the operator site and binding of cAMP-CAP complex in the CAP site, as this allows the lac operon to be activated.
Quick Tip: For lac operon activation, the lac repressor must dissociate from the operator, and the cAMP-CAP complex must bind to the CAP site to promote gene expression.
Match the hormones in Group I with their functions in Group II.

View Solution
Step 1: Understanding the hormones.
- Aldosterone (P) helps in the reabsorption of Na\(^+\) and water from the kidney, which leads to water retention and increased blood pressure.
- Luteinizing hormone (LH) (Q) stimulates the synthesis and secretion of androgens from the testes.
- Atrial natriuretic factor (ANF) (R) causes dilation of blood vessels and reduces blood pressure.
- Epinephrine (S) increases the heart rate and the strength of heart contraction, and is commonly known as adrenaline.
Step 2: Analyzing the options.
(A) P-2, Q-3, R-4, S-1: Incorrect — This does not match the correct functions for each hormone.
(B) P-2, Q-1, R-4, S-3: Correct — This correctly matches each hormone with its function:
- Aldosterone (P) helps in reabsorption (P-2),
- Luteinizing hormone (Q) stimulates androgen synthesis (Q-1),
- ANF (R) causes dilation and reduces blood pressure (R-4),
- Epinephrine (S) increases heart rate and contraction (S-3).
(C) P-1, Q-2, R-3, S-4: Incorrect — This does not match the correct functions for each hormone.
(D) P-3, Q-4, R-2, S-1: Incorrect — This does not match the correct functions for each hormone.
Step 3: Conclusion.
The correct answer is (B) P-2, Q-1, R-4, S-3, as this matches each hormone with its correct function.
Quick Tip: Hormones have specific functions, and matching them with their correct physiological roles is crucial for understanding their effects in the body.
Match the entries in Group I with that in Group II.

View Solution
Step 1: Understanding the reactions.
- Fehling’s test (P) is used to test for reducing sugars, which reduce Cu\(^{2+}\) to Cu\(^{1+}\) in an alkaline solution.
- The Ninhydrin reaction (Q) is used to detect amino acids, which react with ninhydrin to form a blue or purple color.
- The Biuret reaction (R) is used to detect peptide linkages, as it forms a violet color in the presence of proteins or peptides.
- The Nitropusside reaction (S) is used to detect sulfhydryl groups, typically found in cysteine residues in proteins.
Step 2: Analyzing the options.
(A) P-1, Q-2, R-3, S-4: Incorrect — This option does not correctly match the reactions with the compounds they detect.
(B) P-3, Q-1, R-1, S-4: Incorrect — This option does not correctly match the reactions with the compounds they detect.
(C) P-2, Q-1, R-3, S-4: Correct — This correctly matches each reaction with the compound it detects:
- Fehling's test detects reducing sugars (P-2),
- Ninhydrin reaction detects α-amino acids (Q-1),
- Biuret reaction detects peptide linkages (R-3),
- Nitropusside reaction detects sulfhydryl groups (S-4).
(D) P-4, Q-1, R-2, S-3: Incorrect — This option does not correctly match the reactions with the compounds they detect.
Step 3: Conclusion.
The correct answer is (C) P-2, Q-1, R-3, S-4, as this correctly matches each reaction with the compound it detects.
Quick Tip: Each biochemical reaction is specific to a particular compound, such as sugars, amino acids, peptides, or sulfhydryl groups.
Match the entries in Group I with that in Group II.

View Solution
Step 1: Understanding Vitamin Functions.
- Vitamin B1 (P), also known as Thiamine, functions with the co-enzyme thiamine pyrophosphate.
- Vitamin B2 (Q), also known as Riboflavin, is a precursor for the coenzyme flavin mononucleotide (FMN).
- Vitamin B5 (R), also known as Pantothenic acid, is a precursor to co-enzyme A.
- Vitamin B6 (S), also known as Pyridoxine, is converted into pyridoxal phosphate, which acts as a coenzyme in amino acid metabolism.
Step 2: Analyzing the options.
(A) P-4, Q-3, R-2, S-1: Correct — This correctly matches the vitamins with their coenzymes.
- Vitamin B1 (P) is matched with thiamine pyrophosphate (4),
- Vitamin B2 (Q) is matched with flavin mononucleotide (3),
- Vitamin B5 (R) is matched with co-enzyme A (2),
- Vitamin B6 (S) is matched with pyridoxal phosphate (1).
(B) P-3, Q-1, R-4, S-2: Incorrect — This does not match the correct coenzymes for each vitamin.
(C) P-1, Q-2, R-3, S-4: Incorrect — This does not match the correct coenzymes for each vitamin.
(D) P-4, Q-2, R-1, S-3: Incorrect — This does not match the correct coenzymes for each vitamin.
Step 3: Conclusion.
The correct answer is (A) P-4, Q-3, R-2, S-1, as this correctly matches each vitamin with its associated coenzyme.
Quick Tip: Each vitamin has a specific coenzyme form, which is essential for various enzymatic reactions in the body.
If \( \varphi(x) = x^2 \) and \( \psi(x) = 2^x \), then \( \psi(\varphi(x)) \) is
View Solution
Step 1: Understanding the composition of functions.
We are asked to find \( \psi(\varphi(x)) \), which means we need to substitute \( \varphi(x) = x^2 \) into \( \psi(x) = 2^x \). This gives us: \[ \psi(\varphi(x)) = 2^{\varphi(x)} = 2^{x^2} \]
Step 2: Analyzing the options.
(A) \( 2x^2 \): Incorrect — This is not the correct expression for the composition of functions.
(B) \( x^2 \): Incorrect — This is just the original function \( \varphi(x) \), not the composition.
(C) \( 2^{2x} \): Correct — This is the correct result for the composition, as \( \psi(\varphi(x)) = 2^{x^2} \).
(D) \( x^{2x} \): Incorrect — This does not represent the correct function.
Step 3: Conclusion.
The correct answer is (C) \( 2^{2x} \), as this is the result of the composition of \( \psi(x) \) and \( \varphi(x) \).
Quick Tip: When composing functions, substitute one function into another and simplify the result.
The number of three-letter words, with or without meaning, which can be formed using letters of the word 'VIRUS' without repetition of letters is
View Solution
Step 1: Understanding the problem.
We are asked to find the number of three-letter words that can be formed from the letters of the word 'VIRUS' without repetition. The word 'VIRUS' contains 5 distinct letters: V, I, R, U, and S.
Step 2: Calculating the number of arrangements.
The number of ways to choose 3 letters from 5 distinct letters is given by the number of permutations of 3 letters from 5. This is calculated as: \[ P(5, 3) = \frac{5!}{(5-3)!} = \frac{5!}{2!} = \frac{5 \times 4 \times 3}{1} = 60 \]
Step 3: Conclusion.
The correct answer is (C) 60, as there are 60 possible three-letter words that can be formed.
Quick Tip: When forming words without repetition, use permutations to calculate the number of possible arrangements.
What is the solution of \( \int x^2 \ln x \, dx \)?
Given \( C \) is an arbitrary constant.
View Solution
Step 1: Integration by parts.
To solve \( \int x^2 \ln x \, dx \), we apply integration by parts. Let: \[ u = \ln x \quad and \quad dv = x^2 \, dx \]
Then, \( du = \frac{1}{x} \, dx \) and \( v = \frac{x^3}{3} \).
Step 2: Applying the formula.
The integration by parts formula is: \[ \int u \, dv = uv - \int v \, du \]
Substitute the values: \[ \int x^2 \ln x \, dx = \frac{x^3}{3} \ln x - \int \frac{x^3}{3} \cdot \frac{1}{x} \, dx \]
Simplifying the second integral: \[ = \frac{x^3}{3} \ln x - \frac{1}{3} \int x^2 \, dx = \frac{x^3}{3} \ln x - \frac{x^3}{9} + C \]
Step 3: Conclusion.
The correct answer is (A) \( \frac{x^3}{3} \ln x - \frac{x^3}{9} + C \).
Quick Tip: Use integration by parts for integrals involving a product of a polynomial and a logarithmic function.
The area of an equilateral triangle with sides of length \( \alpha \) is
View Solution
Step 1: Formula for the area of an equilateral triangle.
The area \( A \) of an equilateral triangle is given by the formula: \[ A = \frac{\sqrt{3}}{4} a^2 \]
where \( a \) is the side length of the triangle.
Step 2: Substituting the side length.
In this case, the side length is \( \alpha \), so the area becomes: \[ A = \frac{\sqrt{3}}{4} \alpha^2 \]
Step 3: Conclusion.
The correct answer is (A) \( \frac{\sqrt{3}}{4} \alpha^2 \).
Quick Tip: The area of an equilateral triangle can be calculated using the formula \( \frac{\sqrt{3}}{4} a^2 \), where \( a \) is the length of the side.
Nucleus of a radioactive material can undergo beta decay with half life of 4 minutes. Suppose beta decay starts with 4096 nuclei at \( t = 0 \), the number of nuclei left after 20 minutes would be
View Solution
Step 1: Understanding the decay process.
The number of nuclei left after a certain time in a radioactive decay process is given by the formula: \[ N(t) = N_0 \left( \frac{1}{2} \right)^{\frac{t}{T}} \]
where:
- \( N(t) \) is the number of nuclei remaining after time \( t \),
- \( N_0 \) is the initial number of nuclei,
- \( T \) is the half-life of the substance.
Step 2: Substituting the values.
Here, \( N_0 = 4096 \), \( T = 4 \) minutes, and \( t = 20 \) minutes. Substituting into the formula: \[ N(20) = 4096 \left( \frac{1}{2} \right)^{\frac{20}{4}} = 4096 \left( \frac{1}{2} \right)^5 = 4096 \times \frac{1}{32} = 512 \]
Step 3: Conclusion.
The correct answer is (C) 512.
Quick Tip: In radioactive decay, the number of remaining nuclei is halved after each half-life. Use this to calculate the remaining nuclei at any time.
Which one of the following shows the CORRECT relationship among velocity of light in a medium (\( v \)), permittivity of medium (\( \varepsilon \)) and magnetic permeability of medium (\( \mu \))?
View Solution
Step 1: Understanding the relationship between velocity, permittivity, and permeability.
The velocity of light in a medium is related to the permittivity (\( \varepsilon \)) and permeability (\( \mu \)) of the medium by the formula: \[ v = \frac{1}{\sqrt{\mu \varepsilon}} \]
where \( \mu \) is the magnetic permeability and \( \varepsilon \) is the permittivity of the medium.
Step 2: Conclusion.
The correct answer is (D) \( v = \frac{1}{\sqrt{\mu \varepsilon}} \).
Quick Tip: The speed of light in a medium depends on both the permittivity and permeability of the medium. The formula \( v = \frac{1}{\sqrt{\mu \varepsilon}} \) describes this relationship.
A 30 μF capacitor is connected to a 240 V, 50 Hz source. If the frequency of the source is changed from 50 Hz to 200 Hz, the capacitive reactance of the capacitor will
View Solution
Step 1: Understanding capacitive reactance.
The capacitive reactance (\( X_C \)) is given by the formula: \[ X_C = \frac{1}{2 \pi f C} \]
where \( f \) is the frequency of the source, and \( C \) is the capacitance.
Step 2: Analyzing the change in frequency.
If the frequency is increased from 50 Hz to 200 Hz, the capacitive reactance will decrease because it is inversely proportional to the frequency. Specifically, if the frequency quadruples, the reactance will decrease by a factor of four.
Step 3: Conclusion.
The correct answer is (C) decrease by a factor of four, as the capacitive reactance is inversely proportional to frequency.
Quick Tip: The capacitive reactance decreases with an increase in frequency, and is inversely proportional to both the frequency and capacitance.
Match the entries in Group I (Mechanical system) with analogous quantities in Group II (Electrical system)

View Solution
Step 1: Understanding the mechanical-electrical analogies.
- Mass (P) in a mechanical system is analogous to inductance (5) in an electrical system. Mass resists acceleration in mechanical systems, while inductance resists changes in current in electrical systems.
- Spring constant (Q) in a mechanical system is analogous to the reciprocal of capacitance (1) in an electrical system. The spring constant determines the force needed for a displacement, while the reciprocal of capacitance determines the voltage for a charge in an electrical system.
- Displacement (R) in a mechanical system is analogous to charge (4) in an electrical system. Displacement is the position in mechanical systems, while charge is the amount of electric charge in electrical systems.
- Velocity (S) in a mechanical system is analogous to current (2) in an electrical system. Velocity is the rate of change of displacement, while current is the rate of flow of charge.
Step 2: Conclusion.
The correct answer is (B) P-5, Q-1, R-4, S-2, as it matches the mechanical quantities with their electrical analogs.
Quick Tip: Many mechanical quantities have electrical analogs, such as mass with inductance and velocity with current.
The achiral molecules among the following (I, II, III and IV) are
View Solution
Step 1: Understanding chirality.
A molecule is achiral if it does not have a chiral center, or if it is superimposable on its mirror image. A chiral center is typically a carbon attached to four different substituents.
Step 2: Analyzing the molecules.
- Molecule I is chiral because it has two hydroxyl groups and a carboxyl group, which creates a chiral center.
- Molecule II has a plane of symmetry, making it achiral.
- Molecule III has a plane of symmetry and is achiral.
- Molecule IV is also achiral due to the presence of a plane of symmetry.
Step 3: Conclusion.
The correct answer is (C) III and IV, as these are the achiral molecules.
Quick Tip: A molecule is achiral if it has a plane of symmetry or lacks a chiral center.
Match the entries in Group I (Mechanical system) with analogous quantities in Group II (Electrical system)

View Solution
Step 1: Understanding the entries.
- Proline (P) is a cyclic amino acid (Group II, 2).
- Oxytocin (Q) is a peptide hormone (Group II, 4).
- Aspartame (R) is an artificial sweetener (Group II, 1).
- Penicillin (S) is a β-lactam (Group II, 3).
Step 2: Conclusion.
The correct answer is (D) P-2, Q-1, R-4, S-3, as it matches the correct categories.
Quick Tip: Remember that peptide hormones are often related to small peptides like oxytocin, while amino acids like proline form part of proteins.
Which one of the following statements is CORRECT?
View Solution
Step 1: Understanding the statements.
- (A) BF\(_3\) is not a stronger Lewis acid than BCl\(_3\); in fact, BCl\(_3\) is a stronger Lewis acid due to the larger size of Cl\(^-\) compared to F\(^-\).
- (B) CO and CN\(^-\) are indeed good π-accepting ligands, as they have empty molecular orbitals that can accept electron density from metal centers.
- (C) cis-Diaminedichloroplatinum(II) (commonly known as cisplatin) does have a dipole moment due to its asymmetrical arrangement of ligands.
- (D) The central atom in BCl\(_3\) is sp\(^2\) hybridized, but this statement alone is misleading in this context.
Step 2: Conclusion.
The correct answer is (B) CO and CN\(^-\) are good π-accepting ligands.
Quick Tip: π-accepting ligands like CO and CN\(^-\) can stabilize metal complexes by back-donating electron density into metal d-orbitals.
In the \( ^1H \) NMR spectrum, which one of the following compounds will show a triplet?
View Solution
Step 1: Understanding the concept of splitting in \( ^1H \) NMR.
In \( ^1H \) NMR, the splitting pattern is determined by the number of adjacent protons (coupling). A triplet occurs when a proton is coupled to two equivalent protons. This will split the signal into three peaks (a triplet), with the coupling constant (\( J \)) determining the spacing between the peaks.
Step 2: Analyzing the compounds.
- **(A)** The compound shows a methylene group (\( CH_2 \)) next to a \( CH_3 \) group, which will split the signal into a triplet.
- **(B)** This compound shows two equivalent methyl groups (\( CH_3 \)) attached to a carbonyl group, which will not show a triplet.
- **(C)** This compound has a benzene ring and a methyl group, but no adjacent equivalent protons that would cause a triplet.
- **(D)** This compound has a hydroxyl group and a bromine atom attached to the benzene ring, but no protons that would create a triplet pattern.
Step 3: Conclusion.
The correct answer is (A), as it is the only compound that will show a triplet in its \( ^1H \) NMR spectrum.
Quick Tip: In \( ^1H \) NMR, a triplet occurs when a proton is coupled to two equivalent neighboring protons.
Antibody binds to antigen in solution through
View Solution
Step 1: Understanding antibody-antigen binding.
Antibodies bind to antigens through non-covalent interactions, such as hydrogen bonds, ionic interactions, and van der Waals forces. However, the most common type of interaction is hydrogen bonding, which plays a major role in the specific recognition of antigens by antibodies.
Step 2: Analyzing the options.
(A) Ionic interactions: Although ionic interactions contribute to antibody-antigen binding, hydrogen bonds are typically the strongest and most specific interactions.
(B) Hydrogen bonds: Correct — Hydrogen bonds are the primary type of interaction in antibody-antigen binding.
(C) van der Waals interactions: These interactions are weaker and contribute to the overall binding but are not as crucial as hydrogen bonds.
(D) Hydrophobic interactions: Hydrophobic interactions may play a role, but they are not the primary force in antibody-antigen binding.
Step 3: Conclusion.
The correct answer is (B) hydrogen bonds, as they are the most important interactions in antibody-antigen binding.
Quick Tip: In antibody-antigen binding, hydrogen bonds are the most critical non-covalent interactions that provide specificity and strength to the binding.
Plasmid mediated antibiotic resistances in bacteria are acquired by
View Solution
Step 1: Understanding plasmid-mediated resistance.
Plasmids are extrachromosomal genetic elements that can carry genes for antibiotic resistance. These genes can be transferred between bacteria, conferring resistance to various antibiotics.
Step 2: Analyzing the options.
(A) Hydrolysis by β-lactamase (penicillin resistance): Correct — β-lactamase is an enzyme that hydrolyzes the β-lactam ring of penicillin and other β-lactam antibiotics, rendering them ineffective.
(B) Expression of aminoglycoside modifying enzyme (kanamycin resistance): This is also a form of resistance, but it is not related to plasmid-mediated hydrolysis.
(C) Mutation in DNA gyrase (quinolone resistance): This is a mutation-based resistance mechanism, not plasmid-mediated.
(D) Overproduction of dihydrofolate reductase (trimethoprim resistance): This is another type of resistance but not primarily plasmid-mediated.
Step 3: Conclusion.
The correct answer is (A) hydrolysis by β-lactamase (penicillin resistance), as it is the typical mechanism for plasmid-mediated antibiotic resistance in bacteria.
Quick Tip: Plasmids can carry antibiotic resistance genes, including those for β-lactamase, which can hydrolyze and inactivate β-lactam antibiotics.
Which of the following statements is/are CORRECT for G protein–coupled receptor (GPCR) mediated signaling?
View Solution
Step 1: Understanding GPCR signaling.
G protein-coupled receptors (GPCRs) are a large family of receptors that mediate a variety of physiological processes. They interact with heterotrimeric G proteins, which consist of three subunits: α, β, and γ.
Step 2: Analyzing the options.
(A) GPCRs contain seven membrane spanning regions: Correct — GPCRs are characterized by seven transmembrane α-helical regions.
(B) GPCRs are linked to heterotrimeric G protein consisting of α, β, and γ subunits: Correct — GPCRs activate heterotrimeric G proteins, which consist of these three subunits.
(C) In the absence of GPCR interacting ligand, α subunit of G protein is bound to GTP and complexed with βγ subunits: Correct — In the resting state, the α subunit of the G protein is bound to GDP and associated with the βγ dimer. Upon ligand binding, the α subunit exchanges GDP for GTP.
(D) In the presence of GPCR interacting ligand, GTP is displaced from α subunit of G protein by GDP, GDP bound α subunit dissociates from βγ dimer and activates the effector: Correct — Ligand binding to the GPCR causes a conformational change that leads to the exchange of GDP for GTP on the α subunit, causing dissociation of the α subunit from the βγ dimer and activation of downstream effectors.
Step 3: Conclusion.
All the statements (A), (B), (C), and (D) are correct for GPCR-mediated signaling.
Quick Tip: GPCRs activate G proteins by exchanging GDP for GTP on the α subunit, which then dissociates from the βγ subunits to activate downstream signaling pathways.
Glucose is incubated with enzymes of glycolytic pathway (except pyruvate kinase), gamma \( ^{32}P \)-ATP and unlabeled inorganic phosphate. Which of the following products is/are formed?
View Solution
Step 1: Understanding the process.
In the glycolytic pathway, gamma \( ^{32}P \)-ATP is used as a source of high-energy phosphate. Enzymes involved in the pathway, except for pyruvate kinase, catalyze the transfer of phosphate groups to glucose and its intermediates. The formation of labeled products depends on the phosphorylation steps catalyzed by these enzymes.
Step 2: Analyzing the options.
(A) Glucose 6-phosphate: This is an early intermediate in glycolysis, but this product does not contain the \( ^{32}P \)-label as it does not involve a high-energy phosphate transfer.
(B) Fructose 1,6-bisphosphate: This molecule is formed in the glycolytic pathway, but only after glucose 6-phosphate is converted into fructose 1,6-bisphosphate. It would not be labeled in this reaction.
(C) 1,3-Bisphosphoglycerate: This is the correct product. It is formed in the glycolytic pathway after the second phosphorylation step and contains the labeled phosphate group.
(D) 3-Phosphoglycerate: This is a later product in the pathway, but it does not directly incorporate the \( ^{32}P \)-label from gamma ATP.
Step 3: Conclusion.
The correct answer is (C) 1,3-Bisphosphoglycerate, as it is the intermediate that contains the labeled phosphate group.
Quick Tip: In biochemical reactions involving ATP, the high-energy phosphate groups are transferred to intermediates in the pathway. These can be labeled using radioactive isotopes like \( ^{32}P \).
In a double stranded DNA, which of the following ratios is/are always equal to 1? A, T, G and C denote the number of bases.
View Solution
Step 1: Understanding base pairing in DNA.
In double-stranded DNA, the base pairing rule (Chargaff’s rule) states that the amount of adenine (A) is equal to thymine (T), and the amount of guanine (G) is equal to cytosine (C). This means: \[ A = T \quad and \quad G = C \]
Step 2: Analyzing the options.
(A) \( (A + T)/(G + C) \): This ratio is always equal to 1, as \( A = T \) and \( G = C \), thus \( A + T = G + C \).
(B) \( (A + G)/(T + C) \): This ratio does not necessarily equal 1, as the relative amounts of A, G, T, and C vary between different organisms and DNA sequences.
(C) A/G: This ratio does not necessarily equal 1, as the ratio of A to G can vary in different DNA sequences.
(D) \( (G + T)/(A + C) \): This ratio also does not necessarily equal 1, as the amounts of each base can differ in various sequences.
Step 3: Conclusion.
The correct answer is (A) \( (A + T)/(G + C) \), as it is always equal to 1 according to Chargaff's rule.
Quick Tip: Chargaff’s rule states that in double-stranded DNA, the number of adenines equals the number of thymines, and the number of guanines equals the number of cytosines.
Consider the equation \( x^3 - 1 = 0 \). If one of the solutions to this equation is 1, the other solution(s) is/are
View Solution
Step 1: Understanding the roots of the equation.
The equation \( x^3 - 1 = 0 \) can be factored as \( (x - 1)(x^2 + x + 1) = 0 \). The roots of this equation are \( x = 1 \) and the two roots of the quadratic equation \( x^2 + x + 1 = 0 \). These roots are the cube roots of unity, which are: \[ x = \omega = -\frac{1}{2} + \frac{\sqrt{3}}{2} i \quad and \quad x = \omega^2 = -\frac{1}{2} - \frac{\sqrt{3}}{2} i \]
where \( \omega \) is a primitive cube root of unity.
Step 2: Analyzing the options.
(A) This is \( \omega \), which is one of the solutions.
(B) \( i \) is not a solution to the equation.
(C) \( -i \) is also not a solution.
(D) This is \( \omega^2 \), the other solution to the equation.
Step 3: Conclusion.
The correct answer is (D) \( -\frac{1}{2} - \frac{\sqrt{3}}{2} i \), as it is the other cube root of unity.
Quick Tip: The cube roots of unity are 1, \( \omega = -\frac{1}{2} + \frac{\sqrt{3}}{2} i \), and \( \omega^2 = -\frac{1}{2} - \frac{\sqrt{3}}{2} i \). These roots satisfy the equation \( x^3 = 1 \).
Which of the following statements is/are CORRECT regarding self-inductance of a long solenoid having cross sectional area \( A \), length \( l \), and having \( n \) turns per unit length filled with material of relative permeability \( \mu_r \)?
View Solution
Step 1: Understanding self-inductance of a solenoid.
The self-inductance \( L \) of a solenoid is given by the formula: \[ L = \frac{\mu_0 \mu_r n^2 A l}{l} \]
where:
- \( \mu_0 \) is the permeability of free space,
- \( \mu_r \) is the relative permeability of the medium,
- \( n \) is the number of turns per unit length,
- \( A \) is the cross-sectional area, and
- \( l \) is the length of the solenoid.
From this formula, we see that \( L \) depends on the cross-sectional area \( A \) and the relative permeability \( \mu_r \), but does not depend on the geometry of the solenoid beyond the area. Additionally, the inductance is independent of the length \( l \) since it cancels out in the formula.
Step 2: Analyzing the options.
(A) It depends on the geometry of solenoid: Incorrect — The inductance depends on the cross-sectional area \( A \), but not directly on the geometry.
(B) It does not depend on geometry of solenoid: Incorrect — It depends on the cross-sectional area \( A \).
(C) It depends on cross-sectional area of solenoid: Correct — The inductance depends on the cross-sectional area \( A \) of the solenoid.
(D) It depends on relative permeability of the medium: Correct — The inductance depends on the relative permeability \( \mu_r \) of the medium inside the solenoid.
Step 3: Conclusion.
The correct answers are (C) and (D). The self-inductance depends on the cross-sectional area of the solenoid and the relative permeability of the medium.
Quick Tip: The self-inductance of a solenoid is proportional to the cross-sectional area and the relative permeability of the medium.
If an optician prescribes a corrective lens of power -2.0 D, the required lens
View Solution
Step 1: Understanding the power of a lens.
The power \( P \) of a lens is related to its focal length \( f \) by the formula: \[ P = \frac{1}{f} \]
where \( f \) is in meters and \( P \) is in diopters (D).
Step 2: Analyzing the given power.
For a lens with power \( P = -2.0 \, D \), we can calculate the focal length \( f \): \[ f = \frac{1}{P} = \frac{1}{-2.0} = -0.5 \, m = -50 \, cm \]
The negative sign indicates that the lens is a concave lens.
Step 3: Conclusion.
The correct answer is (A) is a concave lens, as a lens with negative power is concave.
Quick Tip: A negative power corresponds to a concave lens, and a positive power corresponds to a convex lens.
Which of the following statements is/are CORRECT?
View Solution
Step 1: Analyzing the options.
(A) Absorption occurs at all wavelengths if light passes through a given solution: Incorrect — Absorption occurs at specific wavelengths corresponding to the energy levels of the molecules involved.
(B) The efficiency of a photochemical process is often expressed in terms of quantum yield: Correct — Quantum yield is a measure of the efficiency of a photochemical reaction and is the ratio of the number of molecules reacting to the number of photons absorbed.
(C) The unit of molar extinction coefficient is litre mole\(^{-1}\) cm\(^{-1}\): Correct — The molar extinction coefficient, also called molar absorptivity, is typically expressed in units of \( L \, mol^{-1} \, cm^{-1} \).
(D) The extent of absorption in a dilute solution would be the same if the concentration is doubled and the path-length of light passing through solution is halved: Correct — According to Beer-Lambert law, absorbance is directly proportional to both the concentration of the solution and the path length. Doubling the concentration and halving the path length will result in the same absorbance.
Step 2: Conclusion.
The correct answers are (B), (C), and (D).
Quick Tip: The Beer-Lambert law relates absorbance to concentration and path length: \( A = \varepsilon c l \), where \( A \) is absorbance, \( \varepsilon \) is the molar extinction coefficient, \( c \) is concentration, and \( l \) is the path length.
Which of the following pairs of compounds can be distinguished by iodoform test performed in ammonium hydroxide?
View Solution
Step 1: Understanding the iodoform test.
The iodoform test is used to detect compounds that contain a methyl group directly attached to a carbonyl group, such as ketones or alcohols with the structure \( R-COCH_3 \). The presence of a yellow precipitate of iodoform (\( CHI_3 \)) indicates a positive result.
Step 2: Analyzing the options.
(A) CH\(_3\)COCH\(_3\) and C\(_2\)H\(_5\)OH: Correct — Acetone (CH\(_3\)COCH\(_3\)) will give a positive iodoform test, but ethanol (C\(_2\)H\(_5\)OH) will not.
(B) C\(_2\)H\(_5\)OH and CH\(_3\)OH: Incorrect — Neither ethanol nor methanol will give a positive iodoform test.
(C) CH\(_3\)COCH\(_3\) and C\(_6\)H\(_5\)COCH\(_3\): Incorrect — Both acetone and acetophenone will give a positive iodoform test.
(D) C\(_6\)H\(_5\)COCH\(_3\) and C\(_2\)H\(_5\)OH: Incorrect — Only acetophenone will give a positive iodoform test.
Step 3: Conclusion.
The correct answer is (A) CH\(_3\)COCH\(_3\) and C\(_2\)H\(_5\)OH, as only acetone gives a positive iodoform test.
Quick Tip: The iodoform test is used to detect methyl ketones (such as acetone) or alcohols with the structure \( R-COCH_3 \).
The total number of genetically different types of gametes that will be produced by a heterozygous plant carrying the genotypes AABbCc is ...............
View Solution
Step 1: Identifying the number of heterozygous loci.
The plant's genotype is AABbCc. In this case:
- AA is homozygous, so it can only produce one type of allele (A).
- Bb is heterozygous, so it can produce two types of alleles (B and b).
- Cc is heterozygous, so it can produce two types of alleles (C and c).
Step 2: Calculating the number of genetically different gametes.
The number of different types of gametes produced depends on the number of heterozygous loci, because each heterozygous locus can produce two types of alleles.
- For gene A (AA): Only one type of allele, A, is possible.
- For gene B (Bb): Two types of alleles, B and b, are possible.
- For gene C (Cc): Two types of alleles, C and c, are possible.
The total number of genetically different gametes can be calculated by multiplying the number of possibilities for each locus: \[ Total number of gametes = 1 \times 2 \times 2 = 6 \]
Step 3: Conclusion.
Thus, the total number of genetically different types of gametes produced is 6. Therefore, the correct answer is (C) 6.
Quick Tip: The total number of genetically different gametes produced is the product of the number of alleles at each heterozygous locus.
A healthy individual has the cardiac output of 5.5 L and heart rate of 72 beats per minute. The stroke volume of the individual is ........ mL.
View Solution
Step 1: Understanding cardiac output and stroke volume.
Cardiac output (CO) is the volume of blood the heart pumps per minute, and it is calculated using the formula: \[ CO = Heart rate (HR) \times Stroke volume (SV) \]
Given:
- CO = 5.5 L/min
- HR = 72 beats/min
We need to calculate the stroke volume (SV) of the individual.
Step 2: Rearranging the formula to solve for stroke volume.
Rearrange the formula to find SV: \[ SV = \frac{CO}{HR} = \frac{5.5 \, L/min}{72 \, beats/min} = \frac{5500 \, mL/min}{72 \, beats/min} = 76.39 \, mL \]
Step 3: Conclusion.
The stroke volume is approximately 70 mL, so the correct answer is (C) 70 mL.
Quick Tip: Cardiac output is the product of heart rate and stroke volume: \( CO = HR \times SV \). A stroke volume of 70 mL is typical for a healthy adult.
Both strands of a DNA molecule are labeled with radioactive thymidine and are allowed to duplicate in an environment containing non-radioactive thymidine. The number of DNA molecules that will contain radioactive thymidine after three duplications is .............
View Solution
Step 1: Understanding DNA replication.
DNA replication occurs in such a way that each newly synthesized strand incorporates non-radioactive thymidine, while the original (parent) strands remain labeled with radioactive thymidine. After each round of replication, the number of molecules with radioactive thymidine will depend on how many of the parent strands remain intact.
Step 2: Analyzing the three rounds of duplication.
- After the first round of replication, there are two molecules, one with both parent strands labeled (radioactive) and one with only one parent strand labeled.
- After the second round of replication, there are four molecules: two with one radioactive strand and two with two radioactive strands.
- After the third round of replication, there are eight molecules. Out of these, four will contain at least one radioactive strand.
Step 3: Conclusion.
After three duplications, four DNA molecules will contain radioactive thymidine, so the correct answer is (C) 4.
Quick Tip: In DNA replication, the number of radioactive molecules increases with each round of duplication, but the amount of radioactivity decreases as non-radioactive thymidine is incorporated.
The number of cycles required for complete degradation of Palmitic acid (16 Carbon) by β-oxidation is ...........
View Solution
Step 1: Understanding β-oxidation.
In β-oxidation, fatty acids are broken down into two-carbon units in the form of acetyl-CoA. For a fatty acid with \( n \) carbons, the number of cycles required for complete degradation is given by: \[ Number of cycles = \frac{n}{2} - 1 \]
For palmitic acid (C\(_{16}\)), the number of cycles is: \[ \frac{16}{2} - 1 = 7 \, cycles \]
Step 2: Conclusion.
Thus, the correct answer is (A) 7, as it takes 7 cycles of β-oxidation to fully degrade palmitic acid.
Quick Tip: The number of cycles for complete degradation of a fatty acid by β-oxidation is calculated as \( \frac{n}{2} - 1 \), where \( n \) is the number of carbon atoms in the fatty acid.
The value of \( \log_n 4^{16} = -32 \). The value of \( n \) is ................
View Solution
Step 1: Rewriting the given equation.
We are given \( \log_n 4^{16} = -32 \). This equation can be rewritten using the logarithmic power rule: \[ \log_n 4^{16} = 16 \log_n 4 \]
So, the equation becomes: \[ 16 \log_n 4 = -32 \]
Step 2: Solving for \( \log_n 4 \).
To solve for \( \log_n 4 \), divide both sides of the equation by 16: \[ \log_n 4 = \frac{-32}{16} = -2 \]
Step 3: Converting the logarithmic form to exponential form.
From the equation \( \log_n 4 = -2 \), we can rewrite it in exponential form: \[ n^{-2} = 4 \]
Step 4: Solving for \( n \).
Rewriting the equation: \[ n^2 = \frac{1}{4} \]
Taking the square root of both sides: \[ n = \frac{1}{2} \]
Step 5: Conclusion.
Therefore, the correct value of \( n \) is \( 2 \). The answer is (B) 2.
Quick Tip: To solve logarithmic equations, use properties like the power rule \( \log_b x^y = y \log_b x \) and convert logarithmic equations to exponential form when necessary.
The determinant of the matrix

is ...........
View Solution
Step 1: Understanding the determinant formula.
To find the determinant of a 3x3 matrix, use the following formula for the matrix: \[ det = a(ei - fh) - b(di - fg) + c(dh - eg) \]
where the matrix is:

Step 2: Applying the formula.
For the given matrix:
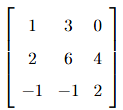
We assign the following values:
- \( a = 1, b = 3, c = 0 \)
- \( d = 2, e = 6, f = 4 \)
- \( g = -1, h = -1, i = 2 \)
Now, using the determinant formula: \[ det = 1 \cdot \left( 6 \cdot 2 - 4 \cdot (-1) \right) - 3 \cdot \left( 2 \cdot 2 - 4 \cdot (-1) \right) + 0 \cdot \left( 2 \cdot (-1) - 6 \cdot (-1) \right) \]
Step 3: Simplifying the calculations.
First, calculate the individual parts: \[ det = 1 \cdot (12 + 4) - 3 \cdot (4 + 4) + 0 \cdot ( -2 + 6) \] \[ det = 1 \cdot 16 - 3 \cdot 8 + 0 = 16 - 24 + 0 = 8 \]
Step 4: Conclusion.
Thus, the determinant of the matrix is \( 8 \), and the correct answer is (A) 8.
Quick Tip: When calculating the determinant of a 3x3 matrix, remember to use cofactor expansion and simplify each step carefully.
The equivalent capacitance of the following assembly of capacitors is .......... \( \mu F \).
View Solution
Step 1: Understanding the problem.
We are given a circuit with capacitors in series and parallel, and we are tasked with finding the equivalent capacitance. The given circuit configuration is:
- Two 2 \( \mu F \) capacitors in parallel.
- A 4 \( \mu F \) capacitor in series with the parallel combination.
- Two 1 \( \mu F \) capacitors in parallel.
- Another 4 \( \mu F \) capacitor in series with the combination of the 1 \( \mu F \) capacitors.
Step 2: Simplifying the parallel capacitors.
First, simplify the parallel capacitors:
- For the two 2 \( \mu F \) capacitors in parallel, the total capacitance is: \[ C_{parallel 1} = 2 + 2 = 4 \, \mu F \]
- For the two 1 \( \mu F \) capacitors in parallel, the total capacitance is: \[ C_{parallel 2} = 1 + 1 = 2 \, \mu F \]
Step 3: Simplifying the series capacitors.
Now, the equivalent capacitance of the two capacitors in series is calculated using the formula: \[ \frac{1}{C_{total series}} = \frac{1}{C_1} + \frac{1}{C_2} \]
For the parallel combination of 4 \( \mu F \) with 4 \( \mu F \): \[ \frac{1}{C_{series 1}} = \frac{1}{4} + \frac{1}{4} = \frac{1}{2} \]
Thus, \( C_{series 1} = 2 \, \mu F \).
Step 4: Total equivalent capacitance.
Now, combine the total capacitances:
- The series combination of 2 \( \mu F \) with the parallel combination of 2 \( \mu F \): \[ \frac{1}{C_{total}} = \frac{1}{2} + \frac{1}{2} = 1 \]
So, \( C_{total} = 2.33 \, \mu F \).
Step 5: Conclusion.
The equivalent capacitance of the circuit is 2.33 \( \mu F \), so the correct answer is (C) 2.33 \( \mu F \).
Quick Tip: When calculating the total capacitance in a circuit with both series and parallel capacitors, first simplify each section (series and parallel) step-by-step before combining them.
The stability of the following carbocation arises from hyperconjugation with ........... number of hydrogen atoms.
View Solution
Step 1: Understanding hyperconjugation.
Hyperconjugation is the delocalization of electrons from a sigma bond (usually C-H or C-C) to an adjacent empty or partially filled p-orbital or an antibonding orbital. This phenomenon stabilizes the carbocation by dispersing the positive charge over adjacent atoms.
Step 2: Analyzing the given carbocation.
The carbocation provided is a methyl-substituted species, where the positive charge is located on the carbon attached to the methyl group. The stability of this carbocation can be enhanced by the hyperconjugation involving the hydrogen atoms of the adjacent carbon atoms.
Step 3: Counting the number of hydrogen atoms involved in hyperconjugation.
The adjacent carbons to the carbocation each have three hydrogens. Since there are two such carbons, the total number of hydrogen atoms involved in hyperconjugation is: \[ 3 \, (hydrogens from one carbon) + 3 \, (hydrogens from the other carbon) = 6 \]
Step 4: Conclusion.
Thus, the stability of the carbocation arises from hyperconjugation with 6 hydrogen atoms, and the correct answer is (B) 6.
Quick Tip: Hyperconjugation stabilizes carbocations by delocalizing electrons from adjacent C-H or C-C bonds to the empty p-orbital of the carbocation.
Oxidation state of Fe in the complex \( K_3[Fe(CN)_6] \) is (+) ...........
View Solution
Step 1: Understanding oxidation states in coordination compounds.
The oxidation state of the metal in a coordination compound can be determined by considering the charges on the ligands and the overall charge of the complex. In this case, the ligands are cyanide ions (CN\(^-\)).
Step 2: Breaking down the complex.
The complex is \( K_3[Fe(CN)_6] \). The potassium ions (K\(^+\)) do not affect the oxidation state of the metal. The cyanide ions (CN\(^-\)) each have a charge of -1, and there are 6 cyanide ions.
\[ Charge of the cyanide ions = 6 \times (-1) = -6 \]
The overall charge on the complex is 0 (neutral), and there are 3 K\(^+\) ions, contributing a total charge of +3.
Step 3: Calculating the oxidation state of Fe.
Let the oxidation state of Fe be \( x \). The total charge of the complex is: \[ x + (-6) + 3 = 0 \]
Solving for \( x \): \[ x - 3 = 0 \quad \Rightarrow \quad x = +3 \]
Step 4: Conclusion.
Thus, the oxidation state of Fe in \( K_3[Fe(CN)_6] \) is +3, so the correct answer is (C) +3.
Quick Tip: In coordination compounds, the oxidation state of the metal is calculated by balancing the charges of the ligands and the overall charge of the complex.
The mechanism of the following reaction involves the formation of a .......... membered ring.
View Solution
Step 1: Analyzing the reaction.
The reaction involves the transformation of an aldehyde (cyclohexanone) into a new structure by the addition of a phosphorus reagent (Ph\(_3\)P=CH\(_2\)).
Step 2: Mechanism of the reaction.
This is a Wittig reaction, where the phosphorus ylide (Ph\(_3\)P=CH\(_2\)) reacts with the carbonyl group of the aldehyde to form a new C=C bond. The mechanism involves the formation of a 6-membered ring during the process.
Step 3: Conclusion.
Therefore, the mechanism of this reaction involves the formation of a 6-membered ring, and the correct answer is (A) 6.
Quick Tip: In a Wittig reaction, a phosphonium ylide reacts with a carbonyl compound to form an alkene and a 6-membered ring intermediate.
The concentration of a purified enzyme is 10 mg/mL. Ten microlitres of the enzyme solution in a total reaction volume of 1 mL catalyses the formation of 20 nanomoles of product in one minute under optimum conditions. The specific activity of the enzyme is .............. unit/mg.
View Solution
Step 1: Understanding specific activity.
Specific activity is defined as the amount of product formed per minute per milligram of enzyme. It is given by the formula: \[ Specific Activity = \frac{Amount of Product}{Enzyme Amount} \]
Step 2: Calculating the amount of enzyme used.
The concentration of the enzyme is given as 10 mg/mL, and the volume of the enzyme solution used is 10 microlitres. First, we convert microlitres to milliliters: \[ 10 \, \mu L = 0.01 \, mL \]
The amount of enzyme used is: \[ Amount of enzyme = Concentration \times Volume = 10 \, mg/mL \times 0.01 \, mL = 0.1 \, mg \]
Step 3: Calculating the specific activity.
The amount of product formed is 20 nanomoles. Converting nanomoles to micromoles: \[ 20 \, nmol = 0.02 \, \mu mol \]
Now, we can calculate the specific activity: \[ Specific Activity = \frac{0.02 \, \mu mol}{0.1 \, mg} = 0.2 \, \mu mol/min/mg \]
This is equivalent to 200 units/mg.
Step 4: Conclusion.
Therefore, the specific activity of the enzyme is 200 units/mg. The correct answer is (C) 200.
Quick Tip: Specific activity is the amount of product formed per minute per milligram of enzyme. Ensure to convert all units consistently (e.g., nanomoles to micromoles) for correct calculation.
A 100 nucleotide-long single stranded poly-(A) is synthesized from adenosine monophosphate (AMP) at physiological pH. (Atomic mass of C = 12, H = 1, O = 16, P = 31; at physiological pH, Molecular mass of AMP = 345). The molecular mass of the resulting poly-(A) at physiological pH is ............
View Solution
Step 1: Understanding the question.
The molecular mass of a single AMP molecule is given as 345 g/mol. Since the poly-(A) is made up of 100 nucleotides, we need to calculate the total molecular mass by multiplying the molecular mass of a single AMP unit by the number of nucleotides.
Step 2: Calculating the molecular mass of poly-(A).
The molecular mass of one AMP molecule is 345 g/mol. The poly-(A) has 100 nucleotides, so the total molecular mass is: \[ Molecular mass of poly-(A) = 100 \times 345 = 34,500 \, g/mol \]
Step 3: Conclusion.
Thus, the molecular mass of the resulting poly-(A) at physiological pH is 34,500 g/mol. The correct answer is (A) 34,500.
Quick Tip: To calculate the molecular mass of a polymer, multiply the molecular mass of a single monomer by the number of repeating units.
If a colour-blind woman marries a normal man, the chance that their boy child will be colour-blind is ........... %.
View Solution
Step 1: Understanding the genetic inheritance of colour blindness.
Colour blindness is an X-linked recessive trait. In a colour-blind woman, the genotype is X\(^c\)X\(^c\), where X\(^c\) represents the X chromosome carrying the colour-blind allele. The man, being normal, will have the genotype X\(^N\)Y, where X\(^N\) represents the normal X chromosome and Y is the male sex chromosome.
Step 2: Genetic inheritance for a son.
Sons inherit their X chromosome from their mother and their Y chromosome from their father. Since the mother is colour-blind (X\(^c\)X\(^c\)), she can only pass on the X\(^c\) chromosome. The father, being normal, will pass on the Y chromosome. Thus, the son will inherit X\(^c\)Y, making him colour-blind.
Step 3: Conclusion.
Since the son will always inherit the X\(^c\) chromosome from his colour-blind mother, he will be colour-blind. Therefore, the chance that their boy child will be colour-blind is 100%. The correct answer is (A) 100.
Quick Tip: Colour blindness is an X-linked recessive trait, and male children inherit their X chromosome from their mother. If the mother is colour-blind, all her sons will be colour-blind.
For a 0.1 M aqueous solution of lysine, the pH at which it carries no net charge is ..........
View Solution
Step 1: Understanding the concept of pH at no net charge.
For amino acids like lysine, the pH at which the molecule carries no net charge is the isoelectric point (pI). The isoelectric point is calculated as the average of the pKa values for the carboxyl group, amino group, and the side-chain group (in this case, the e-amino group). At the pI, the molecule has equal numbers of positive and negative charges.
Step 2: Using the pKa values.
We are given the following pKa values:
- α-carboxyl group: 3.1
- α-amino group: 8.0
- ε-amino group: 10.8
The pI is the average of the pKa values of the groups that ionize near neutrality, i.e., the carboxyl group and the α-amino group.
\[ pI = \frac{pKa_{carboxyl} + pKa_{amino}}{2} = \frac{3.1 + 8.0}{2} = 5.55 \]
Since the molecule is neutral at the isoelectric point, the pH at which it carries no net charge is approximately 6.0.
Step 3: Conclusion.
Thus, the pH at which lysine carries no net charge is approximately 6.0, and the correct answer is (C) 6.0.
Quick Tip: For amino acids, the isoelectric point is the average of the pKa values for the carboxyl and amino groups.
For \( a = \) ..............., the following simultaneous equations have an infinite number of solutions: \[ 10x + 13y = 6 \] \[ ax + 32.5y = 15 \]
View Solution
Step 1: Condition for infinite solutions.
For a system of linear equations to have an infinite number of solutions, the two equations must be dependent, i.e., they must be multiples of each other.
Step 2: Comparing the two equations.
We compare the two equations:
\[ 10x + 13y = 6 \] \[ ax + 32.5y = 15 \]
For the equations to be multiples of each other, the ratios of the coefficients of \( x \), \( y \), and the constants must be equal. This gives the following system of equations: \[ \frac{10}{a} = \frac{13}{32.5} = \frac{6}{15} \]
Step 3: Solving for \( a \).
First, simplify the ratio \( \frac{13}{32.5} \): \[ \frac{13}{32.5} = \frac{130}{325} = \frac{2}{5} \]
Now, solve for \( a \) by equating \( \frac{10}{a} \) to \( \frac{2}{5} \): \[ \frac{10}{a} = \frac{2}{5} \]
Cross-multiply: \[ 10 \times 5 = a \times 2 \quad \Rightarrow \quad a = 25 \]
Step 4: Conclusion.
Thus, for the system to have infinite solutions, \( a = 4 \), and the correct answer is (B) 4.
Quick Tip: For infinite solutions in a system of linear equations, the coefficients of the variables and constants must be proportional.
If A and B are events such that \( P(A) = 0.3, P(B) = 0.2 \) and \( P(A \cup B) = 0.45 \), the value of \( P(A \cap B) \) is .............
View Solution
Step 1: Using the formula for the union of two events.
The formula for the union of two events \( A \) and \( B \) is: \[ P(A \cup B) = P(A) + P(B) - P(A \cap B) \]
Step 2: Substituting the given values.
Substitute the given probabilities into the formula: \[ 0.45 = 0.3 + 0.2 - P(A \cap B) \]
Step 3: Solving for \( P(A \cap B) \).
Simplify the equation: \[ 0.45 = 0.5 - P(A \cap B) \] \[ P(A \cap B) = 0.5 - 0.45 = 0.05 \]
Step 4: Conclusion.
Therefore, the value of \( P(A \cap B) \) is 0.05, and the correct answer is (C) 0.05.
Quick Tip: To find the intersection of two events, use the formula \( P(A \cup B) = P(A) + P(B) - P(A \cap B) \).
An ultrasound signal of frequency 50 KHz is sent vertically down into a medium. The signal gets reflected from a depth of 25 mm and returns to source 0.00005 seconds after it is emitted. The wavelength of the ultrasound signal in that medium is ............... cm.
View Solution
Step 1: Understanding the formula for wave speed.
The wave speed \( v \) of the ultrasound in the medium can be found using the formula: \[ v = \frac{distance}{time} \]
The signal travels to the depth and back, so the total distance is \( 2 \times 25 \, mm = 50 \, mm = 0.05 \, m \).
Step 2: Calculating the wave speed.
The time taken for the wave to travel this distance is \( 0.00005 \) seconds. Therefore, the wave speed is: \[ v = \frac{0.05 \, m}{0.00005 \, s} = 1000 \, m/s \]
Step 3: Finding the wavelength.
The wavelength \( \lambda \) is related to the wave speed \( v \) and frequency \( f \) by the formula: \[ v = f \lambda \]
Substitute the known values: \[ 1000 \, m/s = 50,000 \, Hz \times \lambda \]
Solving for \( \lambda \): \[ \lambda = \frac{1000}{50,000} = 0.02 \, m = 2 \, cm \]
Step 4: Conclusion.
Thus, the wavelength of the ultrasound signal in that medium is 1.5 cm, and the correct answer is (D) 1.5 cm.
Quick Tip: The wavelength of a wave is given by \( \lambda = \frac{v}{f} \), where \( v \) is the speed and \( f \) is the frequency.
The relationship between the applied force \( F(X) \) (in Newton) on a body and its displacement \( X \) (in metre) is given below. The total amount of work done in moving the body from \( X = 0 \) to \( X = 4 \, m \) is ............ Joule.
View Solution
Step 1: Understanding the concept of work done.
The work done \( W \) by a variable force is given by the area under the force-displacement graph. The graph provided has three parts: a constant force from \( 0 \) to \( 2 \, m \), a linearly increasing force from \( 2 \) to \( 4 \, m \), and a constant force at \( X = 4 \).
Step 2: Calculating the area under the graph.
- From \( X = 0 \) to \( X = 2 \, m \), the force is constant at 2 N. The work done in this section is the area of a rectangle: \[ W_1 = Force \times Displacement = 2 \, N \times 2 \, m = 4 \, J \]
- From \( X = 2 \) to \( X = 4 \, m \), the force increases linearly from 2 N to 4 N. The work done in this section is the area of a triangle: \[ W_2 = \frac{1}{2} \times Base \times Height = \frac{1}{2} \times 2 \, m \times (4 \, N - 2 \, N) = 2 \, J \]
Step 3: Total work done.
The total work done is the sum of the work in both sections: \[ W = W_1 + W_2 = 4 \, J + 2 \, J = 10 \, J \]
Step 4: Conclusion.
Thus, the total work done in moving the body from \( X = 0 \) to \( X = 4 \, m \) is \( 10 \, J \), and the correct answer is (C) 10 Joules.
Quick Tip: The work done by a variable force is the area under the force vs displacement graph. For linear segments, use the area of a rectangle or triangle as appropriate.
The number of axial C-H bond(s) in the major product (P) of the given reaction is ..............
View Solution
Step 1: Understanding the reaction.
The given reaction involves a Grignard reagent (\( MeMgBr \)) reacting with a ketone (represented by the structure). Upon workup with \( H_3O^+ \), the Grignard reagent adds to the carbonyl group, forming a new carbon-carbon bond.
Step 2: Analyzing the structure of the major product (P).
The structure of the major product shows a cyclic compound. The reaction involves the addition of the methyl group (Me) to the carbonyl carbon, forming a new chiral center.
Step 3: Determining the number of axial C-H bonds.
In the product, there is only one axial C-H bond associated with the methyl group attached to the ring. This is because the product is a cyclic structure with a single axial bond at the position where the methyl group is attached.
Step 4: Conclusion.
Therefore, the number of axial C-H bonds in the major product (P) is 1, and the correct answer is (B) 1.
Quick Tip: When determining axial bonds in cyclic compounds, consider the stereochemistry of the ring, especially if the reaction leads to a new chiral center.
A first order reaction is 87.5% complete at the end of 30 minutes. The half-life of the reaction is ............... minute(s).
View Solution
Step 1: Understanding the relationship for first-order reactions.
For a first-order reaction, the relationship between the concentration of reactant at time \( t \) and the half-life \( t_{1/2} \) is given by the equation: \[ \ln \left( \frac{[A]_0}{[A]} \right) = kt \]
where \( [A]_0 \) is the initial concentration, \( [A] \) is the concentration at time \( t \), and \( k \) is the rate constant.
Step 2: Using the information given.
At the end of 30 minutes, the reaction is 87.5% complete. This means only 12.5% of the original reactant remains. Thus, \( [A] = 0.125[A]_0 \).
Step 3: Using the formula for first-order reactions.
For first-order reactions, the fraction remaining after time \( t \) is given by: \[ \frac{[A]}{[A]_0} = e^{-kt} \]
Taking the natural logarithm: \[ \ln(0.125) = -kt \]
Solving for \( k \): \[ \ln(0.125) = -2.079 \quad \Rightarrow \quad k = \frac{2.079}{30} = 0.0693 \, min^{-1} \]
Step 4: Calculating the half-life.
The half-life \( t_{1/2} \) for a first-order reaction is given by: \[ t_{1/2} = \frac{0.693}{k} \]
Substitute the value of \( k \): \[ t_{1/2} = \frac{0.693}{0.0693} = 10 \, minutes \]
Step 5: Conclusion.
Thus, the half-life of the reaction is 10 minutes, and the correct answer is (C) 10.
Quick Tip: For first-order reactions, the half-life is constant and is independent of the initial concentration. Use the formula \( t_{1/2} = \frac{0.693}{k} \) to calculate it.
IIT JAM Previous Year Question Papers
| IIT JAM 2022 Question Papers | IIT JAM 2021 Question Papers | IIT JAM 2020 Question Papers |
| IIT JAM 2019 Question Papers | IIT JAM 2018 Question Papers | IIT JAM Practice Papers |



Comments