
Content Strategy Manager
Parallel and Perpendicular Axis Theorem are related to the moment of inertia, which is a property where the body resists angular acceleration. The parallel axis theorem states that:
The moment of inertia of a body about an axis is equal to the sum of the moment of inertia of the body about the parallel axis passing through the centre and the product of the mass of the body and the square of the perpendicular distance between the two axes.
The perpendicular axis theorem states that the moment of inertia of a planar body about an axis that is perpendicular to its plane is equivalent to the moment of inertia about 2 perpendicular axes.
Read More: Rotation formula
Key Terms: Motion, Moment of Inertia, Axis of Rotation, Mass, Centre of Gravity, Plane, Rod, Centre
Parallel Axis Theorem
[Click Here for Sample Questions]
Parallel Axis Theorem states that:
| The sum of a body’s Moment of Inertia covers the axis passing through its centre and the product of the body’s mass. This is multiplied by the square of the distance between two axes that is equal to the calculated sum. |

Parallel Axis Theorem
Read Also:
Parallel Axis Theorem Formula
[Click Here for Previous Year Questions]
The formulation of the parallel axis theorem is as follows:
I = Ic + Md2
Here,
- I = Moment of inertia of the body
- Ic = Moment of inertia about the centre
- M = Mass of the body
- d2 = Square of the distance between the two axis
Parallel Axis Theorem Derivation
[Click Here for Sample Questions]
Let Ic be the moment of inertia of an axis passing through the centre of mass (AB in the diagram), and I will be the moment of inertia about the axis A'B' at d.
Consider a particle with mass m and a distance x from the body's centre of gravity.

The distance from A'B' is thus equal to x + d.
As a result, parallel axis theorem formula is as follows:
I = ∑m (x + d)2
I = ∑m (x2 + d2 + 2xd)
I = ∑mx2 + ∑md2 + ∑2xd
I = Ic + d2∑m + 2d∑mx
I = Ic + Md2 + 0
| I = Ic + Md2 |
Parallel Axis Theorem of Rod
[Click Here for Previous Year Questions]
The moment of inertia of a rod can be used to derive the parallel axis theorem. The rod's moment of inertia is calculated as follows:
I = 1/3 ML2
The distance between the rod's end and its centre is calculated as follows:
h = L/2
As a result, the rod's parallel axis theorem is:
Ic = 1/3ML2 – ML/22
Ic = 1/3ML2 – 1/4ML2
Ic = 1/12 ML2
Perpendicular Axis Theorem
[Click Here for Sample Questions]
Perpendicular Axis Theorem states that:
| The Moment of Inertia of a plain body's perpendicular axis is equal to the sum of the Moment of Inertia of any two perpendicular axes in the plane that intersect the first axis in the plane. |
This theorem can be used when the body is symmetric in shape around two of the three axes. If the Moment of Inertia around the two axes is given, then the moment of inertia around the third axis can be calculated using the formula given below.
Ia = Ib + Ic
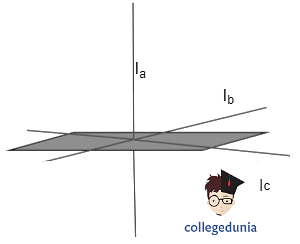
Perpendicular Axis Theorem
Solved Example on Perpendicular Axis Theorem Formula
Example: Using the perpendicular axis theorem, find the M.I. of a disc about an axis passing through its diameter.
Solution: According to perpendicular axis theorem, IZ = IX + IY
We know that IX = IY due to the geometrical symmetry of the disc, where IX and IY are M.I. of the disc about an axis passing through its diameter.
⇒ IZ = IX + IY
⇒IX = IY = IZ/2
Where, IZ = ML of the disc about Z−axis passing through its centre perpendicular to its plane =mr2/2
Thus, M.I. about diameter = IX = IY = ¼ MR2
Read Also:
If in an engineering application, the moment of inertia of a body is to be determined, but the body is irregularly shaped.
The parallel axis theorem can be used to get the moment of inertia at any point as long as the centre of gravity of the body is known.
- In space physics, the calculation of the moment of inertia of satellites and spacecraft makes it possible for us to reach outer planets and deep space.
- The theorem of the perpendicular axis helps in situations where access to one axis of a body is not provided yet it is important for us to calculate the moment of inertia of the body in that axis.
Things to Remember
- The perpendicular axis theorem only applies to flat bodies. Bodies that are flat and have little or no thickness.
- The perpendicular axis theorem allows for the computation of the moment of inertia about the third axis.
- The perpendicular axis theorem can be used to calculate the moment of inertia for three-dimensional objects.
- The moment of inertia for an object spinning along an axis that does not pass through the center of mass may be calculated using the parallel axis theorem.
- The parallel axis theorem can be used to calculate the moment of inertia or the second moment of the area of a rigid body around any axis.
Previous Year Questions
- The reduced mass of two particles having masses…
- Four small objects each of mass m are fixed at the corners of a rectangular…
- If the Earth were to suddenly contract to…
- A ball rolls without slipping. The radius of gyration of… [BHU UET 2007]
- The moment of inertia of a body about a given axis is… [BHU UET 2007]
- Four balls each of radius 10cm10cm and mass… [UPSEE 2010]
- A thin wire of mass M and length L is bent to form a circular ring… [UPSEE 2008]
- If linear density of a rod of length 3 m varies as… [BCECE 2005]
- If the moment of inertia of a disc about an axis tangential… [BCECE 2010]
- If torque is zero then… [BCECE 2004]
- A solid sphere, a hollow sphere and a disc having same mass and… [BCECE 2004]
- A pulley fixed to the ceiling carries a string with blocks of masses… [JCECE 2011]
- A solid sphere rolls down two different inclined planes of same height… [BCECE 2008]
- A ball moves one-fourth of a circle of radius… [TS EAMCET 2019]
- A rocket motor consumes 100kg100kg of fuel per second exhausting it… [TS EAMCET 2019]
- A solid sphere of mass 5kg rolls on a plane surfaces… [TS EAMCET 2019]
- A mass of 0.1 kg is hung at the 20 cm mark from a 1 m rod weighing… [COMEDK UGET 2012]
- A ring rolls down an inclined plane. The ratio of rotational kinetic energy… [COMEDK UGET 2012]
- The centre of mass of a system of two bodies of masses… [COMEDK UGET 2014]
- A person sitting firmly over a rotating stool has his arms stretched… [COMEDK UGET 2015]
Sample Questions
Ques. Calculate the moment of inertia of a 30 kgs rod with a length of 30 cm. (2 Marks)
I = (1/12) ML2
Adding the values to the formula
I = 0.225 Kg m2
Ques. What role does distance play in the parallel axis theorem? If a body's moment of inertia along a perpendicular axis going through its centre of gravity is 50 kg m2 and its mass is 30 kg, what is the moment of inertia of the identical body along an axis 50 cm distant from and parallel to the present axis? (3 Marks)
With the help of parallel axis theorem:
I=IG+Mb2
I=50+(30×0.5)2
I=57.5kg−m2
Ques. What is the moment of inertia of a propeller with six blades (considered as rods) of mass m and length L, each at 60 degrees relative to one another? (4 Marks)
The moment of inertia of a rod of length L and mass m about an axis passing through one of its ends
I = 1/3mL2
m is mass of each blade
L is the length of each blade
N is the total number of blades in the propeller = 6
θ is the angle between two blades = 60o
Ib=1/3mbL2
The moment of inertia of one blade
Ib=1/3mL2
The moment of inertia of the propeller consists of 6 blades
I=6×Ib
I=6×1/3mL2
I=2mL2
Hence, the moment of inertia of the propeller is 2mL2
Ques. What is the gyration radius? When a body rotates along an axis that passes through its centre of mass, its gyration radius is 18 cm. The perpendicular distance between two parallel axis is: If the radius of gyration of the same body is 30 cm around a parallel axis to the first axis, then: (3 Marks)
ICM = MK² where K is the body's gyration radius. 18 cm = K The moment of inertia around the axis parallel to the axis running through the centre of mass is calculated as follows:
I = ICM = Mx²
The radius of gyration for this new moment of inertia is 30 cm, and X is the perpendicular distance of the axis from the CM axis.
As a result, x = 24 cm.
Ques. Is the perpendicular axis theorem applicable to three-dimensional bodies? (2 Marks)
Ques. I is the moment of inertia of a thin uniform rod of mass M and length L passing through its centre on an axis perpendicular to the rod. The rod's moment of inertia around an axis perpendicular to the rod at its endpoint is: (2 Marks)
Iendpoint = ML²/3 = 4I
Ques. What is the Parallel Axis Outer Product? (2 Marks)
Ans. Inertia tensor is received about any set of orthogonal/perpendicular axis parallel to the reference set of axis viz: x, y, and z, coupled with the reference inertia tensor, but it is not sure if they would pass through the centre of mass by generalising the parallel axis theorem.
Ques. In terms of perpendicular axis, what is the relationship between the H – vertical axis, I – the moment of inertia, and K – radius of gyration? (2 Marks)
Ans. In terms of the perpendicular axis, the relationship between H – vertical axis, I – the moment of inertia, and K – radius of gyration is Izz = Ixx + Iyy.
Also Check:





Comments