Gravitational Force: Law of Gravitation, Derivation, Principle of Superposition

Gravitational Force is the force of attraction between all masses in the universe. For example, the attraction of the earth's mass for bodies near its surface. Newton's law of gravitation states that particles of matter in the universe attract each other with a force. This force varies directly as the product of the masses and inversely as the square of the distance between them. 

Read Also: Gravitational Potential Energy

Key Terms: Gravitation, Newton's law of gravitation, Earth gravity, Gravitation on Moon, Principle of Superposition, Vector Form

What is Gravitational Force?

[Click Here for Sample Questions]

Gravitation is a study of how two masses interact, one of which is heavier and the other lighter, and force is the force that attracts all bodies towards itself in this universe. All bodies are pulled by gravity, and it is the force that moves objects towards themselves. Gravitational force is a central force that is exerted along the line joining the q of two masses, and the direction of that force depends only on their position with respect to the source mass.

\(\overrightarrow{F} (f) = f (r) r\hat{}\)

Gravitation Detailed Video Explanation

History of Gravitational Theory

[Click Here for Previous Year Questions]

Ptolemy presented the geocentric model of the solar system. For over 1500 years, Ptolemy’s geocentric model has been relied upon for astrological and astronomical predictions. Later, it failed to explain planetary motions. This lead Nicholas Copernicus to develop the heliocentric model which states that the test mass rotates in circular orbits around the source mass. Despite accurately predicting the position and motion of the planet, the model has failed to account for many aspects such as seasons. This resulted in the formulation of a model based on Kepler’s laws of planetary motion.

Newton's Law of Gravitation

[Click Here for Sample Questions]

According to Newton’s law of gravitation, “every particle in the universe is attracted by every other particle with force, no matter how big the difference between them.”

• Force is directly proportional to the product of their masses between two particles, i.e., F ∝ M₁M₂ …….. (equation 1)
• Force is inversely proportional to the square of the distance between their centre, i.e., F ∝ 1/r² ……… (equation 2)

When we combine equation 1 and equation 2, we get

\(F=G\frac{m_1m_2}{r^2}\)

• F(r) is a variable, non-contact, and conservative force.
• The inverse square law force f(r) is also known as the gravitational constant since it varies as a square of r. The proportionality constant (G) lies in the above equation and represents gravity.
• A dimension formula for G is [M^-1L³T^-2].
• The value for gravitational constant in SI Unit is 6.67 × 10^-11 Nm² kg^-2.
• The value in CGS Unit is 6.67×10^-8 dyne cm² g^-2.

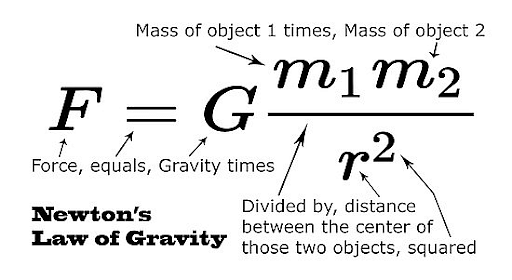
Law of Gravitation Formula

Check Also: Weightlessness

Vector Form of Newton's Law

[Click Here for Previous Year Questions]

Gravitational forces on the two particles create an action-reaction pair when they are represented by a vector form of Newton’s law of gravitation.

According to the above figure, the two particles of mass has been placed a distance apart.

\(\overrightarrow{r_{21}} = (\overrightarrow{r_2} - \overrightarrow{r_1})\)

The direction of the vector is from M₁ to M₂.

The force applied on M₂ by M₁ is as follows:

The negative sign indicates the attractive nature of the force.

The force on M₁ and M₂ is as follows:

\(\overrightarrow{F_12} = -\frac{GM_{1}M_{2}}{r^{2}_{12}}\hat{r_{12}}\)

\(\text{Since, } \hat{r_{12}} = -\hat{r_{21}}\)

\(\overrightarrow{F_{12}} = \frac{GM_{1}M_{2}}{(-r_{21})^{2}}[\hat{-r_{21}}]\)

\(\overrightarrow{F_{12}} = \frac{GM_{1}M_{2}}{(r_{21})^{2}}[\hat{r_{21}}]\)

\(- \overrightarrow{F_{21}}\)

Therefore, the applied forces are equal and opposite as per Newton's third law which also applies to gravitational forces.

Also check: Specific Gravity

Formula of Newton's Law

[Click Here for Sample Questions]

Newton’s Law of Gravitation defines what gravity is, and shows how it determines how much weight we carry and how far we jump before falling.

In accordance with Newton’s laws of gravitation, every particle in the universe attracts every other particle with a force directly proportionate to their mass products and inversely proportional to their distances.

The mathematical representation is as follows.

• F = Gravitational force between two objects (in Newton)
• G = Universal Gravitational Constant, i.e., 6.674 × 10-11 Nm²kg^-2
• M₁ = mass of one massive body (kilograms)
• M₂ = mass of another massive body (kilograms)
• R = separation between the bodies (kilometres)

Check Important Relation between G and g

Principle of Superposition of Gravitational Force

[Click Here for Previous Year Questions]

When a system consists of ‘n’ particles, Newton’s law of gravitation only applies to interactions between particles. If the system contains n(n – 1)/2 particles, there are n(n – 1)/2 interactions.

The principle of superposition states that the sum of each of these interactions if each act independently, can be expressed as the vector sum of those interactions.

F = F₁₂ + F₁₃ + F_{14 .} . . . . . + F₁n

Gravitational force F acts on a particle when the number of point masses in a system equals the vector sum of the forces exerted by the other masses on the particle.

Derivation of Newton's Law of Gravitation from Karl's Law

[Click Here for Sample Questions]

An object rotates in a nearly circular orbit of radius “r” around a source mass with a constant angular velocity.

The centripetal force is as follows.

F = mrω₂ = mr × (2π/T)²

Using Kepler’s Third Law, we get, T² ∝ r³

Substituting this value in the equation of force, we get

F = 4π²mr/Kr³

Where K = 4π²/GM

The equation of Newton’s law of gravitation is as follows.

F = GMm/r²

Read Further: Earth Satellites

Things to Remember

• Gravitational force and the law of gravitation is one of the most significant topics of the electricity chapter. Around 2-3 questions can come from this topic. The overall weightage of generators and electricity is around 10 marks. 
• Almost all things that exist in the universe attract each other. Gravitational force is the force that one object exerts on another while attracting it towards itself.
• The formula for the force of gravitation, F = G × [M₁M₂]/r²
• The value for gravitational constant in SI Unit is 6.67 × 10^-11 Nm² kg^-2.
• The value in CGS Unit is 6.67×10^-8 dyne cm² g^-2.
• The equation of Newton’s law of gravitation is F = GMm/r².

Previous Year Questions

1. The time period of a satellite of earth is 5 hours. If the separation between the… [BITSAT 2019]
2. There is a shell of mass M and density of the shell is uniform… [BITSAT 2013]
3. If the earth shrinks such that its density becomes 8 times to the present value… [AP EAPCET]
4. Four identical particles of equal masses 1kg made to move along the… [JEE Main 2021]
5. Acceleration due to gravity is g on the surface of the earth… [JKCET 2004]
6. The acceleration due to gravity at a height h above the earths surface is… [AP EAPCET]
7. A synchronous relay satellite reflects TV signals and transmits TV programmer… [BHU UET]
8. A body weighs 72 N on the surface of the earth. What is the gravitational force on… [NEET 2020]
9. The dependence of acceleration due to gravity g on the distance r from the centre… [NEET 2010]
10. The escape velocity from earth is 11.2 km/s. If a body is to be projected in… [NEET 1993]
11. The time period of a satellite of earth is 5 hours. If the separation between… [BITSAT 2019]
12. There is a shell of mass M and density of the shell is uniform… [BITSAT 2013]
13. If the earth shrinks such that its density becomes 8 times to the present value… [AP EAPCET]
14. Four identical particles of equal masses 1kg made to move along the… [JEE Main 2021]
15. Acceleration due to gravity is g on the surface of the earth. Then the value of… [JKCET 2004]