CMAT 2018 Quantitative Techniques and Data Interpretation Question paper with answer key pdf conducted on January 20 in Forenoon Session 9:30 AM to 12:30 PM is available for download. The exam was successfully organized by All India Council for Technical Education (AICTE). The question paper comprised a total of 25 questions. (PDF Source: cracku.in)
CMAT 2018 Quantitative Techniques and Data Interpretation Question Paper with Answer Key PDFs Forenoon Session
| CMAT 2018 Quantitative Techniques and Data Interpretation Question Paper with Solutions PDF | Download PDF | Check Solutions |
How many iron balls, each of radius \(1\) cm, can be made from a sphere whose radius is \(8\) cm?
View Solution
Step 1: Use the volume formula for a sphere.
The volume of a sphere of radius \(R\) is:
\[ V=\frac{4}{3}\pi R^{3} \]
Step 2: Find the volume of the big sphere.
Here, \(R=8\) cm, so:
\[ V=\frac{4}{3}\pi (8)^{3}=\frac{4}{3}\pi (512) \]
Step 3: Find the volume of one small iron ball.
Each small ball has radius \(r=1\) cm, so its volume is:
\[ v=\frac{4}{3}\pi (1)^{3}=\frac{4}{3}\pi \]
Step 4: Find the number of iron balls formed.
Let \(n\) balls be formed. Since volume is conserved:
\[ n \times v = V \]
\[ n \times \frac{4}{3}\pi = \frac{4}{3}\pi (512) \]
\[ n = 512 \]
Quick Tip: Whenever an object is melted and reshaped, total volume remains the same. Divide total volume by volume of one piece.
If \(a\) is between \(0\) and \(1\), which of the following statements is (are) true?
(i) \(a^{2}-1>0\)
(ii) \(a^{2}+1>0\)
(iii) \(a^{2}-a>0\)
View Solution
Step 1: Use the given condition.
We are given:
\[ 0 < a < 1 \]
Step 2: Check statement (i) \(a^{2}-1>0\).
Squaring \(0 < a < 1\), we get:
\[ 0 < a^{2} < 1 \]
Subtract \(1\) from all sides:
\[ -1 < a^{2}-1 < 0 \]
So \(a^{2}-1\) is negative, hence statement (i) is false.
Step 3: Check statement (ii) \(a^{2}+1>0\).
Since \(a^{2}>0\), adding \(1\) gives:
\[ a^{2}+1>0 \]
So statement (ii) is true.
Step 4: Check statement (iii) \(a^{2}-a>0\).
Factor:
\[ a^{2}-a=a(a-1) \]
Here \(a>0\) but \(a-1 < 0\), so product is negative:
\[ a(a-1) < 0 \]
Hence statement (iii) is false.
Quick Tip: If \(0 < a < 1\), then squaring makes it smaller: \(a^{2} < a\).
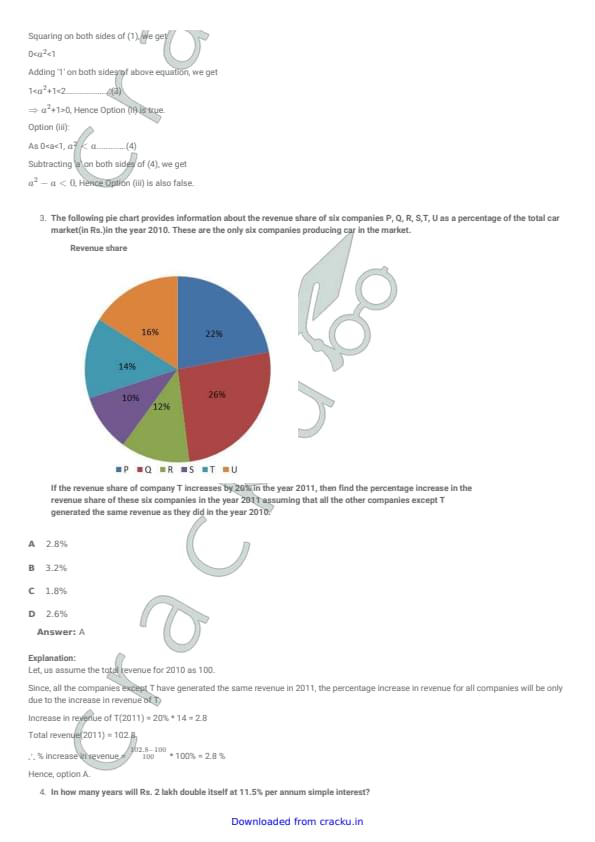
The following pie chart provides information about the revenue share of six companies \(P, Q, R, S, T, U\) as a percentage of the total car market (in Rs.) in the year 2010. These are the only six companies producing car in the market.
If the revenue share of company \(T\) increases by \(20%\) in the year 2011, then find the percentage increase in the revenue share of these six companies in the year 2011 assuming that all the other companies except \(T\) generated the same revenue as they did in the year 2010.
View Solution
Step 1: Assume total revenue in 2010 as 100.
Let total revenue in 2010 be \(100\).
Step 2: Find revenue of company \(T\) in 2010.
From pie chart, \(T=14%\).
So revenue of \(T\) in 2010 is:
\[ 14 \]
Step 3: Increase in revenue of \(T\) in 2011.
Revenue increases by \(20%\):
\[ 20% of 14 = \frac{20}{100}\times 14 = 2.8 \]
Step 4: Total revenue in 2011.
Only \(T\) increases, others remain same.
So total revenue becomes:
\[ 100 + 2.8 = 102.8 \]
Step 5: Percentage increase in total revenue.
\[ \frac{102.8-100}{100}\times 100 = 2.8% \]
Quick Tip: If only one component increases and the rest remain constant, the increase in total equals that component's increase.
In how many years will Rs. 2 lakh double itself at \(11.5%\) per annum simple interest?
View Solution
Step 1: Condition for doubling in simple interest.
If money doubles, final amount \(A=2P\).
So interest earned:
\[ I=A-P=2P-P=P \]
Step 2: Use simple interest formula.
\[ I=\frac{PTR}{100} \]
Step 3: Substitute values.
Here \(P=200000\), \(R=11.5\), \(I=P=200000\):
\[ 200000=\frac{200000 \times T \times 11.5}{100} \]
Step 4: Solve for \(T\).
Cancel \(200000\):
\[ 1=\frac{T \times 11.5}{100} \]
\[ T=\frac{100}{11.5}=8.695 \]
So time is approximately \(8.7\) years, which lies between \(8\) and \(9\).
Quick Tip: For doubling in simple interest: \(T=\frac{100}{R}\). It is independent of principal amount.
If \(AB + C = D\), find \(A\) and \(C\) given that when \(B=6\), \(D=30\) and when \(B=8\), \(D=36\).
View Solution
Step 1: Write the given relation.
\[ AB + C = D \]
Step 2: Substitute \(B=6\) and \(D=30\).
\[ 6A + C = 30 \qquad ...(1) \]
Step 3: Substitute \(B=8\) and \(D=36\).
\[ 8A + C = 36 \qquad ...(2) \]
Step 4: Subtract equation (1) from equation (2).
\[ (8A+C)-(6A+C)=36-30 \]
\[ 2A = 6 \Rightarrow A = 3 \]
Step 5: Substitute \(A=3\) in equation (1).
\[ 6(3)+C=30 \]
\[ 18+C=30 \Rightarrow C=12 \]
Quick Tip: To find unknowns quickly, form two equations and subtract them to eliminate one variable.
If \(y^{2}+3y-18 \geq 0\), which of the following is true?
View Solution
Step 1: Factorize the quadratic expression.
\[ y^{2}+3y-18 \geq 0 \]
We factorize:
\[ y^{2}+3y-18 = (y+6)(y-3) \]
Step 2: Use the sign rule for product inequality.
\[ (y+6)(y-3) \geq 0 \]
A product is non-negative when:
\[ y+6 \geq 0 and y-3 \geq 0 \quad or \quad y+6 \leq 0 and y-3 \leq 0 \]
Step 3: Solve both cases.
Case 1:
\[ y \geq -6 and y \geq 3 \Rightarrow y \geq 3 \]
Case 2:
\[ y \leq -6 and y \leq 3 \Rightarrow y \leq -6 \]
Step 4: Final solution interval.
\[ y \geq 3 \quad or \quad y \leq -6 \]
Quick Tip: For \((x-a)(x-b)\ge 0\), the solution is always \(x \le \min(a,b)\) or \(x \ge \max(a,b)\).
In how many different ways can 3 red balls, 2 blue balls and 4 yellow balls be arranged so that the balls of the same color come together?
View Solution
Step 1: Treat each color group as one unit.
Since balls of the same color must stay together, we consider:
- 3 red balls as 1 unit
- 2 blue balls as 1 unit
- 4 yellow balls as 1 unit
So, we have 3 units to arrange.
Step 2: Arrange the 3 units.
Number of ways to arrange these 3 units:
\[ 3! = 6 \]
Step 3: Arrange balls inside each unit.
Red balls can be arranged in:
\[ 3! = 6 \]
Blue balls can be arranged in:
\[ 2! = 2 \]
Yellow balls can be arranged in:
\[ 4! = 24 \]
Step 4: Multiply all arrangements.
\[ 3! \times 3! \times 2! \times 4! = 6 \times 6 \times 2 \times 24 = 1728 \]
Quick Tip: When items must stay together, treat them as a single block, then multiply by internal arrangements of each block.
The following table shows the courier charges (in Rs.) for sending 1 kg parcel from one city to another. Among the following, the charges will be the least for sending a parcel from:-
View Solution
Step 1: Read the values from the table for each given option.
We check courier charges for each route mentioned.
Step 2: Compare charges.
From the table:
- Ahmedabad to Jaipur = Rs. 10
- Mumbai to Bangalore = Rs. 25
- Jaipur to Bangalore = Rs. 10
- Kolkata to Mumbai = Rs. 7
Step 3: Select the minimum charge.
The least charge is Rs. 7 for Kolkata to Mumbai.
Quick Tip: For table-based questions, always locate exact row-column intersections carefully before comparing values.
Three numbers \(X, Y,\) and \(Z\) are in the ratio of \(12:15:25\). If the sum of twice of these numbers is \(614\), the ratio between the difference of \(Y\) and \(X\) and the difference of \(Z\) and \(Y\) is:-
View Solution
Step 1: Represent the numbers in terms of a constant.
Given ratio \(X:Y:Z = 12:15:25\).
Let:
\[ X=12k,\quad Y=15k,\quad Z=25k \]
Step 2: Find required differences.
Difference between \(Y\) and \(X\):
\[ Y-X = 15k-12k = 3k \]
Difference between \(Z\) and \(Y\):
\[ Z-Y = 25k-15k = 10k \]
Step 3: Ratio of differences.
\[ (Y-X):(Z-Y) = 3k:10k = 3:10 \]
Quick Tip: In ratio questions, you can directly compare differences using the ratio values without finding actual numbers.
Ankush and Babulal walk around a circular track. They start at 9 a.m. from the same point in the opposite directions. Ankush and Babulal walk at a speed of 3 rounds per hour and 5 rounds per hour respectively. How many times shall they cross each other until 10.30 a.m.?
View Solution
Step 1: Understand relative speed concept.
Since they move in opposite directions, relative speed is the sum of speeds.
Step 2: Calculate relative speed.
Speed of Ankush = 3 rounds/hour
Speed of Babulal = 5 rounds/hour
\[ Relative speed = 3 + 5 = 8 rounds/hour \]
Step 3: Find total time interval.
From 9:00 a.m. to 10:30 a.m. = 1.5 hours
Step 4: Find number of crossings.
They cross each other once every 1 round of relative motion.
So number of crossings:
\[ 8 \times 1.5 = 12 \]
Quick Tip: For opposite directions: \(Relative speed = v_1 + v_2\). Crossings \(=Relative speed \times Time\).
The monthly incomes of Amit and Bharat are in the ratio of \(5:4\), their monthly expenses are in the ratio of \(19:21\), and their monthly savings are in the ratio of \(37:18\). If the total annual savings of Amit and Bharat is Rs. 1,32,000, Amit's monthly income is:-
View Solution
Step 1: Use savings ratio to find monthly savings.
Savings ratio of Amit and Bharat = \(37:18\).
Let savings be \(37k\) and \(18k\).
Total monthly savings:
\[ 37k+18k = 55k \]
Step 2: Convert annual savings to monthly savings.
Total annual savings = Rs. 1,32,000
So total monthly savings:
\[ \frac{132000}{12} = 11000 \]
Step 3: Find value of \(k\).
\[ 55k = 11000 \Rightarrow k = 200 \]
Step 4: Find individual monthly savings.
Amit's saving = \(37 \times 200 = 7400\)
Bharat's saving = \(18 \times 200 = 3600\)
Step 5: Use income and expense ratios.
Income ratio = \(5:4\). Let incomes be \(5x\) and \(4x\).
Expense ratio = \(19:21\). Let expenses be \(19y\) and \(21y\).
Savings = Income - Expense
So:
\[ 5x - 19y = 7400 \qquad ...(1) \]
\[ 4x - 21y = 3600 \qquad ...(2) \]
Step 6: Solve the equations.
Multiply (1) by 4 and (2) by 5:
\[ 20x - 76y = 29600 \]
\[ 20x - 105y = 18000 \]
Subtract:
\[ 29y = 11600 \Rightarrow y = 400 \]
Substitute in (2):
\[ 4x - 21(400)=3600 \]
\[ 4x - 8400 = 3600 \Rightarrow 4x = 12000 \Rightarrow x = 3000 \]
Step 7: Find Amit's income.
Amit's income = \(5x = 5 \times 3000 = 15000\).
Quick Tip: When multiple ratios are given, convert each into equations using the relation: \(Savings = Income - Expense\).
In a circle of radius \(6\) cm, arc \(AB\) makes an angle of \(114^\circ\) with centre of the circle \(O\). What is angle \(ABO\)?
View Solution
Step 1: Use property of radii in a circle.
Since \(OA = OB\) (both are radii), triangle \(AOB\) is isosceles.
Step 2: Use angle sum property of a triangle.
Given central angle:
\[ \angle AOB = 114^\circ \]
So remaining two angles are equal:
\[ \angle ABO = \angle BAO \]
\[ \angle ABO = \frac{180^\circ - 114^\circ}{2} \]
\[ \angle ABO = \frac{66^\circ}{2} = 33^\circ \]
Quick Tip: In an isosceles triangle, angles opposite equal sides are equal. Always split the remaining angle equally.
In a survey conducted among 120 houses, it was found that 50 read Times of India, 60 read Indian Express and 48 read Hindustan Times; 20 read Times of India and Indian Express, 18 read Times of India and Hindustan Times and 24 read Indian Express and Hindustan Times. If 10 read all three, how many read only one newspaper?
View Solution
Step 1: Represent the information using a Venn diagram.
We use three sets:
- TOI = 50
- IE = 60
- HT = 48
Step 2: Fill the intersections.
Given:
\[ TOI\cap IE = 20,\quad TOI\cap HT = 18,\quad IE\cap HT = 24 \]
And:
\[ TOI\cap IE\cap HT = 10 \]
So only two-set regions become:
\[ (TOI\cap IE) only = 20-10=10 \]
\[ (TOI\cap HT) only = 18-10=8 \]
\[ (IE\cap HT) only = 24-10=14 \]
Step 3: Find only one newspaper readers.
Only TOI:
\[ 50-(10+8+10)=22 \]
Only IE:
\[ 60-(10+14+10)=26 \]
Only HT:
\[ 48-(8+14+10)=16 \]
Step 4: Total who read only one newspaper.
\[ 22+26+16 = 64 \]
Quick Tip: In 3-set Venn problems, always subtract the common 3-set value first from all pairwise intersections.
The length of the minute of a watch is 42 mm. The area swept by it in 30 minutes (in \(mm^{2}\)) by taking \(\pi\) as 3.14 is:-
View Solution
Step 1: Understand the movement of the minute hand.
In 60 minutes, minute hand completes \(360^\circ\).
So in 30 minutes, it covers:
\[ \frac{30}{60}\times 360^\circ = 180^\circ \]
Step 2: Recognize it forms a semicircle.
A \(180^\circ\) sweep forms a semicircle.
Radius \(r = 42\) mm.
Step 3: Calculate area of semicircle.
\[ A = \frac{1}{2}\pi r^{2} \]
\[ A = \frac{1}{2}\times 3.14 \times 42^{2} \]
\[ A = \frac{1}{2}\times 3.14 \times 1764 \]
\[ A = \frac{5539.0}{2} = 2769.5 \]
Quick Tip: Minute hand makes \(360^\circ\) in 60 minutes, so in \(t\) minutes it makes \(\frac{t}{60}\times 360^\circ\).
If \((x+4)\) is a factor of \(x^{3}+2x^{2}+bx+68\), what is the value of \(b\)?
View Solution
Step 1: Use factor theorem.
If \((x+4)\) is a factor of \(f(x)\), then:
\[ f(-4)=0 \]
Step 2: Form the polynomial function.
\[ f(x)=x^{3}+2x^{2}+bx+68 \]
Step 3: Substitute \(x=-4\).
\[ f(-4)=(-4)^{3}+2(-4)^{2}+b(-4)+68=0 \]
\[ -64+2(16)-4b+68=0 \]
\[ -64+32-4b+68=0 \]
\[ 36-4b=0 \Rightarrow 4b=36 \Rightarrow b=9 \]
Quick Tip: Factor theorem: If \((x-a)\) is a factor of \(f(x)\), then \(f(a)=0\).
Rakesh covers 12 km at 6 km/hr, 36 km at 9 km/hr and then 32 km at 4 km/hr. Find the approximate average speed in covering the whole distance.
View Solution
Step 1: Use the formula for average speed.
Average speed is given by:
\[ Average Speed=\frac{Total Distance}{Total Time} \]
Step 2: Find the total distance covered.
\[ 12 + 36 + 32 = 80 km \]
Step 3: Find the total time taken.
Time for 12 km at 6 km/hr:
\[ \frac{12}{6}=2 hr \]
Time for 36 km at 9 km/hr:
\[ \frac{36}{9}=4 hr \]
Time for 32 km at 4 km/hr:
\[ \frac{32}{4}=8 hr \]
Total time:
\[ 2+4+8=14 hr \]
Step 4: Calculate average speed.
\[ Average Speed=\frac{80}{14}=5.71 km/hr \]
Quick Tip: Average speed is always \(\frac{Total Distance}{Total Time}\), not the average of speeds.
Two pipes A and B can fill a cistern in 120 minutes and 150 minutes respectively. There is also an outlet C. If all the three pipes are opened together, the cistern gets filled in 100 minutes. How much time will be taken by C to empty full tank?
View Solution
Step 1: Convert filling times into rates.
Rate of pipe A:
\[ \frac{1}{120} tank/min \]
Rate of pipe B:
\[ \frac{1}{150} tank/min \]
Let rate of outlet C be \(\frac{1}{x}\) tank/min (it empties, so it will be subtracted).
Step 2: Use combined rate formula.
All three together fill the tank in 100 minutes:
\[ \frac{1}{120}+\frac{1}{150}-\frac{1}{x}=\frac{1}{100} \]
Step 3: Solve the equation.
LCM of \(120,150,100\) is \(600\).
\[ \frac{5}{600}+\frac{4}{600}-\frac{1}{x}=\frac{6}{600} \]
\[ \frac{9}{600}-\frac{1}{x}=\frac{6}{600} \]
\[ \frac{3}{600}=\frac{1}{x} \]
\[ x=200 minutes \]
Step 4: Convert minutes into hours and minutes.
\[ 200 minutes = 3 hours 20 minutes \]
Quick Tip: In pipe problems, always convert time into rate. Outlet rate is negative since it empties the tank.
Ramesh works \(A\) hours a day and rests \(B\) hours a day. This pattern continues for 1 week, with an exactly opposite pattern next week, and so on for four weeks. Every fifth week he adopts a new pattern which continues for the next four weeks. When he works longer than he rests, his wage per hour is three times that he earns per hour when he rests longer than he works. The following table shows his daily working hours for the week numbered 1 to 13. A week consists of six days and a month consists of four weeks. If Ramesh is paid Rs. 60 per working hour in the 1st week, what is his salary for the 1st month? (Assume that he is paid half his wages for his resting hours on duty)
View Solution
Step 1: Identify work and rest hours in week 1.
From the table for 1st week:
Work = 6 hours/day, Rest = 3 hours/day.
Since work \(>\) rest, wage per working hour = Rs. 60.
Rest wage is half of working wage:
\[ Rest wage per hour = \frac{60}{2}=30 \]
Step 2: Find daily earning for week 1 and week 3.
Daily earning:
\[ (60 \times 6) + (30 \times 3) = 360 + 90 = 450 \]
Each week has 6 days, so week earning:
\[ 450 \times 6 = 2700 \]
Weeks 1 and 3 have same pattern, so total for week 1 and 3:
\[ 2700 \times 2 = 5400 \]
Step 3: Identify work and rest hours in week 2 and week 4.
Opposite pattern means:
Work = 3 hours/day, Rest = 6 hours/day.
Now rest \(>\) work, so wage per working hour becomes \(\frac{60}{3}=20\).
Rest wage = half of 20 = 10.
Step 4: Find daily earning for week 2 and week 4.
Daily earning:
\[ (20 \times 3) + (10 \times 6) = 60 + 60 = 120 \]
Week earning:
\[ 120 \times 6 = 720 \]
Weeks 2 and 4 total:
\[ 720 \times 2 = 1440 \]
Step 5: Total salary for the 1st month (4 weeks).
\[ 5400 + 1440 = 6840 \]
Quick Tip: In pattern wage problems, compare work and rest hours first, then apply wage-rate conditions week-wise.
In a box, there are eight yellow and four black balls. If three balls are drawn at random, what is the probability that two are yellow and one black?
View Solution
Step 1: Find total number of ways to choose 3 balls from 12 balls.
Total balls = \(8+4=12\).
\[ Total ways=\binom{12}{3} \]
\[ \binom{12}{3}=\frac{12 \times 11 \times 10}{3 \times 2 \times 1}=220 \]
Step 2: Find favorable outcomes.
Choose 2 yellow balls out of 8:
\[ \binom{8}{2}=28 \]
Choose 1 black ball out of 4:
\[ \binom{4}{1}=4 \]
Favorable ways:
\[ 28 \times 4 = 112 \]
Step 3: Find probability.
\[ P=\frac{112}{220}=\frac{28}{55} \]
Quick Tip: In probability without replacement, use combinations: \(\frac{favorable selections}{total selections}\).
If \(\tan A + \cot A = \sqrt{5}\), what is the value of \(\tan^{3} A + \cot^{3} A\)?
View Solution
Step 1: Let \(\tan A = x\).
Then:
\[ \cot A = \frac{1}{x} \]
Given:
\[ x+\frac{1}{x}=\sqrt{5} \]
Step 2: Cube both sides.
\[ \left(x+\frac{1}{x}\right)^{3}=(\sqrt{5})^{3} \]
\[ x^{3}+\frac{1}{x^{3}}+3\left(x+\frac{1}{x}\right)=5\sqrt{5} \]
Step 3: Substitute \(x+\frac{1}{x}=\sqrt{5}\).
\[ x^{3}+\frac{1}{x^{3}}+3\sqrt{5}=5\sqrt{5} \]
\[ x^{3}+\frac{1}{x^{3}}=2\sqrt{5} \]
Step 4: Convert back to trigonometric form.
\[ \tan^{3}A+\cot^{3}A = 2\sqrt{5} \]
Quick Tip: Use \((a+b)^{3}=a^{3}+b^{3}+3ab(a+b)\). Here \(ab=\tan A \cdot \cot A = 1\).
Two balls were bought for Rs. 37.40 at a discount of \(15%\). What must be the marked price of each of the ball?
View Solution
Step 1: Let marked price of two balls be \(X\).
A discount of \(15%\) means selling price is \(85%\) of marked price.
Step 2: Form the equation.
\[ \frac{85}{100}X = 37.40 \]
Step 3: Solve for \(X\).
\[ X = \frac{37.40 \times 100}{85} = 44 \]
Step 4: Find marked price of each ball.
\[ \frac{44}{2}=22 \]
Quick Tip: After discount: \(Selling Price = \frac{100-d}{100} \times Marked Price\).
Find the value of \(a\), if: \(|2a-3| = 3a+2\).
View Solution
Step 1: Use modulus definition.
\[ |x| = \begin{cases} x, & x \ge 0
-x, & x < 0 \end{cases} \]
Here \(x=2a-3\).
Step 2: Case 1: \(2a-3 \ge 0\).
\[ 2a-3 \ge 0 \Rightarrow a \ge \frac{3}{2} \]
Then:
\[ |2a-3| = 2a-3 \]
Equation becomes:
\[ 2a-3 = 3a+2 \Rightarrow -a = 5 \Rightarrow a = -5 \]
But \(a=-5\) does not satisfy \(a \ge \frac{3}{2}\).
So this case is rejected.
Step 3: Case 2: \(2a-3 < 0\).
\[ 2a-3 < 0 \Rightarrow a < \frac{3}{2} \]
Then:
\[ |2a-3| = -(2a-3)=3-2a \]
Equation becomes:
\[ 3-2a = 3a+2 \Rightarrow 1 = 5a \Rightarrow a = \frac{1}{5} \]
This satisfies \(a < \frac{3}{2}\), so it is valid.
Quick Tip: For modulus equations, always solve in two cases and then verify if the solution satisfies the assumed condition.
From a jar of wine containing 32 litres, 4 litres is drawn out, and the jar is filled up with water. If the same proportion of wine is further drawn out two more times, what proportion of wine to water will be there in the resulting mixture?
View Solution
Step 1: Identify fraction removed each time.
Each time 4 litres is removed from 32 litres, so fraction removed is:
\[ \frac{4}{32}=\frac{1}{8} \]
So fraction of wine remaining after each operation is:
\[ 1-\frac{1}{8}=\frac{7}{8} \]
Step 2: Apply repeated replacement formula.
After 3 operations, wine left:
\[ 32 \left(\frac{7}{8}\right)^{3} \]
\[ = 32 \times \frac{343}{512} = \frac{343}{16} = 21.4375 \]
Step 3: Find water in the jar.
Total volume remains 32 litres.
\[ Water = 32 - 21.4375 = 10.5625 \]
Step 4: Find ratio wine : water.
\[ 21.4375 : 10.5625 \]
Multiply both by 16:
\[ 343 : 169 \]
Quick Tip: In repeated replacement, wine left after \(n\) operations \(= V\left(1-\frac{x}{V}\right)^n\).
The geometric mean proportion between \(30+\sqrt{200}\) and \(54-\sqrt{648}\) is:
View Solution
Step 1: Use formula for geometric mean.
Geometric mean between \(a\) and \(b\) is:
\[ \sqrt{a \times b} \]
Step 2: Simplify the two given numbers.
\[ 30+\sqrt{200}=30+10\sqrt{2}=10(3+\sqrt{2}) \]
\[ 54-\sqrt{648}=54-18\sqrt{2}=18(3-\sqrt{2}) \]
Step 3: Multiply the two expressions.
\[ a \times b = 10(3+\sqrt{2}) \times 18(3-\sqrt{2}) \]
\[ =180 \left((3+\sqrt{2})(3-\sqrt{2})\right) \]
\[ =180(3^{2}-(\sqrt{2})^{2}) =180(9-2) =180 \times 7 =1260 \]
Step 4: Take the square root.
\[ \sqrt{1260}=\sqrt{36 \times 35}=6\sqrt{35} \]
Quick Tip: Use \((a+b)(a-b)=a^{2}-b^{2}\) to simplify products involving surds.
Anil is twice as good a student as Bharat and is able to finish a work in 30 minutes less than Bharat's time. Find the time in which both of them can finish the same work together?
View Solution
Step 1: Convert efficiency relation into time relation.
Anil is twice as efficient as Bharat.
\[ Efficiency of Anil : Efficiency of Bharat = 2:1 \]
Time is inversely proportional to efficiency, so:
\[ Time of Anil : Time of Bharat = 1:2 \]
Step 2: Assume Bharat takes \(t\) minutes.
Then Anil takes \(t-30\) minutes.
So:
\[ \frac{t-30}{t} = \frac{1}{2} \]
Step 3: Solve for \(t\).
\[ 2(t-30)=t \Rightarrow 2t-60=t \Rightarrow t=60 \]
So Bharat takes 60 min and Anil takes 30 min.
Step 4: Find combined time.
Combined work rate:
\[ \frac{1}{30}+\frac{1}{60}=\frac{2+1}{60}=\frac{3}{60}=\frac{1}{20} \]
So together time:
\[ 20 minutes \]
Quick Tip: If two people take \(x\) and \(y\) time, together time \(=\frac{xy}{x+y}\).
















Comments