CMAT 2018 Quantitative Techniques and Data Interpretation Question paper with answer key pdf conducted on January 20 in Afternoon Session 2:30 PM to 5:30 PM is available for download. The exam was successfully organized by All India Council for Technical Education (AICTE). The question paper comprised a total of 25 questions. (PDF Source: cracku.in)
CMAT 2018 Quantitative Techniques and Data Interpretation Question Paper with Answer Key PDFs Afternoon Session
| CMAT 2018 Quantitative Techniques and Data Interpretation Question Paper with Solutions PDF | Download PDF | Check Solutions |
What is the probability of getting a 'nine' or 'ten' on a single throw of two dice?
View Solution
Step 1: Find the total number of outcomes.
When two dice are thrown, each die has 6 outcomes.
So total possible outcomes = \(6 \times 6 = 36\).
Step 2: Find outcomes that give sum 9.
Sum 9 occurs for the pairs:
\((3,6), (4,5), (5,4), (6,3)\)
So, number of outcomes for sum 9 = 4.
Step 3: Find outcomes that give sum 10.
Sum 10 occurs for the pairs:
\((4,6), (5,5), (6,4)\)
So, number of outcomes for sum 10 = 3.
Step 4: Compute probability.
Total favourable outcomes = \(4 + 3 = 7\).
\[ P = \frac{7}{36} \]
Quick Tip: For two dice, total possible outcomes are always \(36\). Count favourable cases and divide by \(36\).
The length of a room exceeds its breadth by 2 meters. If the length be increased by 4 meters and the breadth decreased by 2 meters, the area remains the same. Find the surface area of its walls if the height is 3 meters.
View Solution
Step 1: Assume breadth and length.
Let breadth \(= x\) meters.
Then length \(= x + 2\) meters.
Step 2: Write the original area.
\[ A = x(x+2) \]
Step 3: Apply new dimensions.
New length \(= (x+2)+4 = x+6\).
New breadth \(= x-2\).
New area:
\[ A' = (x+6)(x-2) \]
Step 4: Since area remains same, equate.
\[ x(x+2) = (x+6)(x-2) \]
\[ x^2 + 2x = x^2 + 4x - 12 \]
\[ 2x = 4x - 12 \]
\[ 2x = 12 \Rightarrow x = 6 \]
So breadth \(= 6\)m and length \(= 8\)m.
Step 5: Find surface area of walls.
Height \(h = 3\)m.
Surface area of four walls:
\[ 2h(l+b) = 2 \times 3 \times (8+6) \]
\[ = 6 \times 14 = 84m^2 \]
Quick Tip: Surface area of four walls of a room = \(2h(l+b)\).
A bus covers a distance of first 50 km in 40 minutes, next 50 km at a speed of 2 km per minute and the next 30 km at a speed of 1.0 km per minute. What is its average speed during the entire journey?
View Solution
Step 1: Total distance covered.
\[ 50 + 50 + 30 = 130 km \]
Step 2: Find time for each part.
First part: 50 km in 40 minutes.
Second part: speed = 2 km/min
\[ Time = \frac{50}{2} = 25 minutes \]
Third part: speed = 1 km/min
\[ Time = \frac{30}{1} = 30 minutes \]
Step 3: Total time.
\[ 40 + 25 + 30 = 95 minutes \]
Step 4: Convert time into hours and find average speed.
\[ 95 minutes = \frac{95}{60} hours \]
\[ Average speed = \frac{130}{95/60} = \frac{130 \times 60}{95} = 82.1 kmph \]
Quick Tip: Average speed always depends on total distance and total time, not individual speeds.
Three wheels making 60, 36 and 24 revolutions in a minute start with a certain point in their circumference onwards. Find when they will again come together in the same position.
View Solution
Step 1: Convert revolutions per minute into time per revolution.
First wheel: 60 rev/min means 1 rev/sec.
So it completes 1 revolution in 1 second.
Second wheel: 36 rev/min
\[ 36 rev in 60 sec \Rightarrow 1 rev in \frac{60}{36} = \frac{5}{3} sec \]
Third wheel: 24 rev/min
\[ 24 rev in 60 sec \Rightarrow 1 rev in \frac{60}{24} = \frac{5}{2} sec \]
Step 2: Find LCM of these time intervals.
We need the smallest time when all complete an integer number of revolutions together.
So required time = LCM of \(1, \frac{5}{3}, \frac{5}{2}\).
LCM \(= 5\) seconds.
Step 3: Conclusion.
Thus, after 5 seconds, all wheels will again be in the same starting position.
Quick Tip: In wheel/revolution problems, convert to time per revolution and take LCM.
A certain amount of money invested at 10% per annum compound interest for two years became Rs. 2000. What is the initial investment?
View Solution
Step 1: Use compound interest formula.
\[ A = P\left(1+\frac{R}{100}\right)^n \]
Given \(A = 2000\), \(R = 10\), \(n = 2\).
Step 2: Substitute values.
\[ 2000 = P\left(1+\frac{10}{100}\right)^2 \]
\[ 2000 = P(1.1)^2 = P(1.21) \]
Step 3: Solve for P.
\[ P = \frac{2000}{1.21} \approx 1653 \]
Quick Tip: For CI, principal = \(\dfrac{Amount}{(1+R/100)^n}\).
If the height of a right circular cone is increased by 200% and the radius of the base is reduced by 50%, then the volume of the cone
View Solution
Step 1: Volume of a cone.
\[ V = \frac{1}{3}\pi r^2 h \]
Step 2: Apply the changes.
Height increased by 200%:
\[ h' = h + 2h = 3h \]
Radius reduced by 50%:
\[ r' = \frac{r}{2} \]
Step 3: Compute new volume.
\[ V' = \frac{1}{3}\pi \left(\frac{r}{2}\right)^2 (3h) \]
\[ V' = \frac{1}{3}\pi \frac{r^2}{4} \cdot 3h \]
\[ V' = \frac{3}{4}\left(\frac{1}{3}\pi r^2 h\right) = \frac{3}{4}V \]
Step 4: Find percentage change.
\[ Decrease = 1 - \frac{3}{4} = \frac{1}{4} = 25% \]
Quick Tip: When radius changes, volume changes as \(r^2\), so radius has a stronger effect than height.
An electric appliance is priced at Rs. 600 initially. Because of market recession, price was successively reduced three times, each time by 10% of the price after the earlier reduction. What is the current price?
View Solution
Step 1: Initial price.
Price = 600.
Step 2: Apply successive 10% reduction 3 times.
After first reduction:
\[ 600 \times 0.9 = 540 \]
After second reduction:
\[ 540 \times 0.9 = 486 \]
After third reduction:
\[ 486 \times 0.9 = 437.4 \]
Step 3: Final price.
So the current price is Rs. 437.40.
Quick Tip: Successive reductions are multiplied: \(600 \times 0.9^3\).
Below given is the Table showing Age-wise Ownership of mobiles:
If 1 crore mobiles were sold last year, how many LG sets were sold?
View Solution
Step 1: Understand what the table represents.
The table provides age-wise distribution within each brand.
For example, for LG, 15% of LG mobiles are up to 1 year old, 45% are 1-2 years old, etc.
Step 2: Missing information.
We are given total mobiles sold last year = 1 crore.
But we are not told how many of these were LG mobiles.
Let total LG mobiles sold last year = \(A\).
Then 15% of \(A\) would represent LG mobiles up to 1 year old.
But \(A\) itself is unknown.
Step 3: Conclusion.
Since the number of LG mobiles sold last year is not provided, the exact number cannot be found.
Quick Tip: If only internal percentage distribution is given, totals cannot be calculated unless overall brand totals are provided.
\(\sqrt{188 + \sqrt{51} + \sqrt{169}}\)
View Solution
Step 1: Rewrite the expression correctly.
From the given explanation in the image:
\[ \sqrt{188 + \sqrt{51} + \sqrt{169}} \]
Step 2: Evaluate the perfect square.
\[ \sqrt{169} = 13 \]
Step 3: Simplify further (as shown in the solution).
\[ \sqrt{188 + \sqrt{51} + 13} = \sqrt{188 + \sqrt{64}} = \sqrt{188 + 8} \]
Step 4: Final evaluation.
\[ \sqrt{188 + 8} = \sqrt{196} = 14 \]
Quick Tip: Always check if the expression under root can be converted into a perfect square for quick simplification.
In what time will Rs. 6,250 amount to Rs. 6,632.55 at 4% compound interest payable half-yearly?
View Solution
Step 1: Identify rate per half-year and number of periods.
Compound interest is payable half-yearly.
So rate per half-year:
\[ \frac{4%}{2} = 2% \]
If time is \(n\) years, number of half-year periods = \(2n\).
Step 2: Apply compound interest formula.
\[ A = P\left(1+\frac{2}{100}\right)^{2n} \]
Given: \(A = 6632.55\), \(P = 6250\).
Step 3: Substitute values.
\[ 6632.55 = 6250(1.02)^{2n} \]
\[ \frac{6632.55}{6250} = (1.02)^{2n} \]
\[ 1.061 = (1.02)^{2n} \]
Step 4: Solve for \(n\).
From the given solution in the image:
\[ 1.061 = 1.02^3 \Rightarrow 2n = 3 \Rightarrow n = \frac{3}{2} \]
So time required = \(\dfrac{3}{2}\) years.
Quick Tip: For half-yearly CI:
Rate becomes \(R/2\) and time periods become \(2n\).
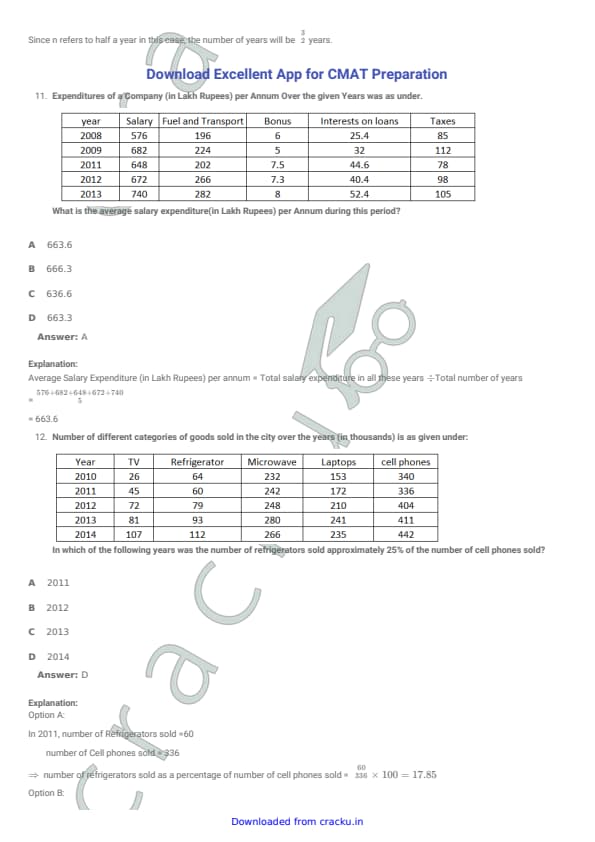
Expenditures of a Company (in Lakh Rupees) Per Annum Over the given Years was as under. What is the average salary expenditure (in Lakh Rupees) per annum during this period?
View Solution
Step 1: Understand what is asked.
We need the average salary expenditure per annum for the given years.
Step 2: Add all salary expenditures.
\[ 576 + 682 + 648 + 672 + 740 = 3318 \]
Step 3: Divide by number of years.
There are 5 years.
\[ Average = \frac{3318}{5} = 663.6 \]
Quick Tip: Average = \(\dfrac{Sum of all values}{Number of values}\).
Number of different categories of goods sold in the city over the years (in thousands) is as given under. In which of the following years was the number of refrigerators sold approximately 25% of the number of cell phones sold?
View Solution
Step 1: Condition required.
We need:
\[ \frac{Refrigerators}{Cell Phones} \times 100 \approx 25% \]
Step 2: Check each option.
For 2011:
\[ \frac{60}{336}\times 100 = 17.85% \]
For 2012:
\[ \frac{79}{404}\times 100 = 19.55% \]
For 2013:
\[ \frac{93}{411}\times 100 = 22.63% \]
For 2014:
\[ \frac{112}{442}\times 100 = 25.33% \]
Step 3: Conclusion.
2014 gives approximately 25%. Hence the correct option is 2014.
Quick Tip: To check “x is y% of z”, compute \(\dfrac{x}{z}\times 100\).
In the figure, PQ is a diameter of the circle. Angle PQS = \(35^\circ\). Find angle QRS.
View Solution
Step 1: Use property of diameter.
Since \(PQ\) is the diameter, the angle subtended by it at the circumference is \(90^\circ\).
So,
\[ \angle PRQ = 90^\circ \]
Step 2: Use angle subtended by the same chord.
Chord \(RQ\) subtends equal angles at the circumference.
So,
\[ \angle RPQ = \angle RSQ = \theta \]
Step 3: Apply angle sum property in triangle RSQ.
In triangle \(RSQ\):
\[ \angle QRS + \angle RSQ + \angle RQS = 180^\circ \]
\[ \angle QRS + \theta + 35^\circ = 180^\circ \]
Step 4: Use angle at R is 90°.
At point R:
\[ \angle PRQ = \angle QRS + \angle SRP = 90^\circ \]
So total angle used results in:
\[ \angle QRS = 180^\circ - (35^\circ + 90^\circ) = 55^\circ \]
Quick Tip: If a chord is a diameter, the angle subtended at the circumference is always \(90^\circ\).
If \(x = \sqrt[5]{5}\) and \(y = \sqrt[4]{4}\), which of the following is true?
View Solution
Step 1: Rewrite both numbers with common form.
\[ x = \sqrt[5]{5} = 5^{1/5} \]
\[ y = \sqrt[4]{4} = 4^{1/4} = (2^2)^{1/4} = 2^{1/2} \]
Step 2: Compare values.
\[ y = 2^{1/2} \approx 1.414 \]
\[ x = 5^{1/5} \approx 1.379 \]
Step 3: Conclusion.
Since \(1.414 > 1.379\), we get:
\[ y > x \]
Quick Tip: To compare surds, convert them into exponential form and approximate values if required.
If \(a\) and \(b\) are positive real numbers and \(a*b\) denotes \(\sqrt{a \times b}\), what is the value of \(8*(4*16)\)?
View Solution
Step 1: Understand the operation.
Given \(a*b = \sqrt{ab}\).
Step 2: Solve inner operation first.
\[ 4*16 = \sqrt{4 \times 16} = \sqrt{64} = 8 \]
Step 3: Now apply the operation with 8.
\[ 8*(4*16) = 8*8 = \sqrt{8 \times 8} = \sqrt{64} = 8 \]
Quick Tip: Always solve the bracket part first, then apply the operation step-by-step.
The average age of three men is 50 years and their ages are in the proportion 3:5:7. The age of the youngest man is:
View Solution
Step 1: Convert ratio into actual ages.
Let ages be \(3k\), \(5k\), and \(7k\).
Step 2: Use average condition.
\[ \frac{3k + 5k + 7k}{3} = 50 \]
\[ \frac{15k}{3} = 50 \]
\[ 5k = 50 \Rightarrow k = 10 \]
Step 3: Find youngest age.
Youngest = \(3k = 3 \times 10 = 30\) years.
Quick Tip: If ages are in ratio, write them as multiples of a constant and use the average equation.
By selling mangoes at the rate of 64 for Rs. 2000, the vendor loses 40%. How many should he sell for Rs. 1000 so as to gain 20%?
View Solution
Step 1: Find selling price per mango in first case.
64 mangoes sold for Rs. 2000.
\[ SP per mango = \frac{2000}{64} = 31.25 \]
Step 2: Use loss percentage to find cost price.
Loss = 40%, so SP = 60% of CP.
\[ 31.25 = 0.6 \times CP \Rightarrow CP = \frac{31.25}{0.6} \approx 52.08 \approx 52 \]
Step 3: Find SP per mango for 20% gain.
Gain = 20%, so SP = 120% of CP.
\[ SP = 1.2 \times 52 = 62.4 \approx 62.5 \]
Step 4: Find number of mangoes for Rs. 1000.
\[ Number = \frac{1000}{62.5} = 16 \]
Quick Tip: Loss 40% means SP = 60% of CP, and gain 20% means SP = 120% of CP.
The area of a triangle metal plate with base 88 cm and altitude 64 cm is to be reduced to one-fourth of its original area by making a hole of circular shape at the center. The radius of this hole will be:
View Solution
Step 1: Find area of triangle.
\[ A = \frac{1}{2} \times 88 \times 64 = 2816 cm^2 \]
Step 2: Area to be removed.
Final area is one-fourth, so removed area is:
\[ A - \frac{A}{4} = \frac{3A}{4} \]
\[ = \frac{3}{4} \times 2816 = 2112 cm^2 \]
Step 3: Area of removed part is circle.
\[ \pi r^2 = 2112 \]
Step 4: Solve for r.
Using \(\pi = \frac{22}{7}\):
\[ r^2 = \frac{2112 \times 7}{22} = 672 \]
\[ r = \sqrt{672} = \sqrt{16 \times 42} = 4\sqrt{42} \]
Quick Tip: If area becomes one-fourth, area removed = \(\frac{3}{4}\) of original.
Find the value of \(\sqrt{\dfrac{2+\sqrt{3}}{2-\sqrt{3}}}\) correct to three places of decimal.
View Solution
Step 1: Consider the expression.
\[ \sqrt{\frac{2+\sqrt{3}}{2-\sqrt{3}}} \]
Step 2: Rationalize the denominator inside the root.
Multiply numerator and denominator by \((2+\sqrt{3})\):
\[ \frac{2+\sqrt{3}}{2-\sqrt{3}} \times \frac{2+\sqrt{3}}{2+\sqrt{3}} = \frac{(2+\sqrt{3})^2}{4-3} \]
\[ = (2+\sqrt{3})^2 \]
Step 3: Take square root.
\[ \sqrt{(2+\sqrt{3})^2} = 2+\sqrt{3} \]
Step 4: Approximate value.
\[ 2+\sqrt{3} \approx 2+1.732 = 3.732 \]
Quick Tip: If expression becomes \(\sqrt{(a)^2}\), the answer is \(a\) (for positive values).
A mixture of petrol and kerosene weighing 5 kg contains 5% kerosene. How much more kerosene (approx.) must be added into it to make it 10%?
View Solution
Step 1: Find initial amount of kerosene.
Total mixture = 5 kg = 5000 gm.
Kerosene = 5% of 5000 gm.
\[ \frac{5}{100} \times 5000 = 250 gm \]
Step 2: Let x grams kerosene be added.
New kerosene = \(250 + x\).
New total mixture = \(5000 + x\).
Step 3: New kerosene percentage is 10%.
\[ \frac{250+x}{5000+x} = \frac{10}{100} \]
\[ 250 + x = \frac{1}{10}(5000 + x) \]
\[ 250 + x = 500 + 0.1x \]
\[ x - 0.1x = 500 - 250 \]
\[ 0.9x = 250 \Rightarrow x = \frac{250}{0.9} \approx 277.7 \]
Step 4: Approximate answer.
\[ x \approx 275 gm \]
Quick Tip: For mixture percentage problems, use equation: \(\dfrac{new part}{new total} = required fraction\).
A student who gets 20% marks fails by 20 marks, but another student who gets 36% marks gets 44 marks more than minimum passing marks. Find the maximum number of marks and percentage necessary for passing.
View Solution
Step 1: Assume maximum marks and passing marks.
Let maximum marks = \(x\).
Let minimum passing marks = \(y\).
Step 2: Form equation from first condition.
A student getting 20% fails by 20 marks.
So, his marks = \(y - 20\).
\[ \frac{20}{100}x = y - 20 \]
\[ \frac{x}{5} = y - 20 \Rightarrow x = 5y - 100 \quad ...(1) \]
Step 3: Form equation from second condition.
A student getting 36% gets 44 marks more than passing marks.
So, his marks = \(y + 44\).
\[ \frac{36}{100}x = y + 44 \]
\[ \frac{9}{25}x = y + 44 \Rightarrow 9x = 25y + 1100 \quad ...(2) \]
Step 4: Substitute (1) into (2).
From (1), \(x = 5y - 100\).
\[ 9(5y - 100) = 25y + 1100 \]
\[ 45y - 900 = 25y + 1100 \]
\[ 20y = 2000 \Rightarrow y = 100 \]
Step 5: Find maximum marks.
\[ x = 5y - 100 = 5(100) - 100 = 400 \]
Step 6: Find passing percentage.
\[ Passing percentage = \frac{y}{x}\times 100 = \frac{100}{400}\times 100 = 25% \]
Quick Tip: For such problems, assume maximum marks \(x\) and passing marks \(y\), then form equations using percentages and differences.
If 26 horses or 20 bullocks eat up the fodder in store in 170 days, in what time will 10 horses and 8 bullocks finish the same quantity of fodder?
View Solution
Step 1: Assume daily consumption of horse and bullock.
Let one horse eat \(h\) units per day.
Let one bullock eat \(b\) units per day.
Step 2: Total fodder in store.
Given, 26 horses finish in 170 days:
\[ Total fodder = 26h \times 170 \]
Also, 20 bullocks finish in 170 days:
\[ Total fodder = 20b \times 170 \]
Equating both:
\[ 26h = 20b \Rightarrow b = \frac{26}{20}h = 1.3h \]
Step 3: Daily consumption of 10 horses and 8 bullocks.
\[ 10h + 8b = 10h + 8(1.3h) = 10h + 10.4h = 20.4h \]
Step 4: Total fodder in terms of h.
\[ Total fodder = 26h \times 170 \]
Step 5: Time required.
\[ Time = \frac{26h \times 170}{20.4h} = \frac{26 \times 170}{20.4} = 216.67 days \]
Quick Tip: When two groups finish the same work in same time, equate their daily efficiencies to relate their unit rates.
A boat covers 24 km upstream and 72 km downstream in 8 hours, while it covers 48 km upstream and 108 km downstream in 14 hours. Find the speed of the boat in still water and the speed of the stream respectively.
View Solution
Step 1: Assume speed of boat and stream.
Let speed of boat in still water = \(V\) km/h.
Let speed of stream = \(v\) km/h.
Upstream speed = \(V-v\).
Downstream speed = \(V+v\).
Step 2: Form equation from first condition.
\[ \frac{24}{V-v} + \frac{72}{V+v} = 8 \quad ...(1) \]
Step 3: Form equation from second condition.
\[ \frac{48}{V-v} + \frac{108}{V+v} = 14 \quad ...(2) \]
Step 4: Simplify equations.
Multiply (1) by 3:
\[ \frac{72}{V-v} + \frac{216}{V+v} = 24 \quad ...(3) \]
Multiply (2) by 3:
\[ \frac{144}{V-v} + \frac{324}{V+v} = 42 \quad ...(4) \]
Now subtract (3) from (4):
\[ \frac{72}{V-v} + \frac{108}{V+v} = 18 \]
Step 5: Solve gives values.
From the given calculation in the image:
\[ V = 12,\quad v = 6 \]
Step 6: Conclusion.
Speed of boat in still water = 12 km/h.
Speed of stream = 6 km/h.
Quick Tip: In boat-stream problems: Upstream \(= V-v\) and Downstream \(= V+v\). Always form equations using time = distance/speed.
A shopkeeper sells rice at the cost price, but uses false weight. He gains 20% in this process. What weight does he use for one kilogram?
View Solution
Step 1: Assume cost price of 1 kg.
Let cost price of 1 kg rice = Rs. 100.
Since he sells at cost price, selling price for "1 kg" = Rs. 100.
Step 2: Understand the trick.
He charges for 1000 g but gives less weight = \(x\) g.
So he is actually selling \(x\) grams for Rs. 100.
Step 3: Cost price of x grams.
If 1000 g costs 100, then 1 g costs \(\frac{100}{1000} = 0.1\).
So cost price of \(x\) g = \(0.1x\).
Step 4: Use gain percentage.
Gain = 20%, so:
\[ SP = 1.2 \times CP \]
\[ 100 = 1.2 \times (0.1x) \]
\[ 100 = 0.12x \Rightarrow x = \frac{100}{0.12} = 833.33 \]
Step 5: Conclusion.
So he gives approximately \(833\frac{1}{3}\) g instead of 1 kg.
Quick Tip: If selling at cost price but gaining due to underweight, assume CP of 1 kg and use gain formula: \(SP = 1.2 \times CP\) to find actual weight.
Working together, Rakesh, Prakash and Ashok can finish the same job in an hour. Also, if Prakash works for an hour, and then Ashok works for four hours, the job will be completed. If Rakesh can do the job an hour quicker than Prakash, how many hours would Ashok take to complete the job alone?
View Solution
Step 1: Assume efficiencies.
Let efficiency of Rakesh = \(r\).
Let efficiency of Prakash = \(p\).
Let efficiency of Ashok = \(a\).
Step 2: Together they finish work in 1 hour.
So total work = 1 unit.
\[ (r+p+a)\times 1 = 1 \Rightarrow r+p+a = 1 \quad ...(1) \]
Step 3: Second condition.
Prakash works 1 hour and Ashok works 4 hours to complete job.
\[ p(1) + a(4) = 1 \quad ...(2) \]
Step 4: Relation between Rakesh and Prakash.
Rakesh takes 1 hour less than Prakash.
Let Prakash take \(t\) hours alone.
Then Rakesh takes \((t-1)\) hours.
So,
\[ p = \frac{1}{t}, \quad r = \frac{1}{t-1} \]
Step 5: Using given solution steps (as per image).
After simplifying and solving, it comes:
\[ a = \frac{1}{6} \]
Step 6: Time taken by Ashok alone.
\[ Time = \frac{1}{a} = \frac{1}{1/6} = 6 hours \]
Quick Tip: Convert time into efficiency: If a person takes \(t\) hours, efficiency = \(\frac{1}{t}\). Use equations based on total work = 1 unit.




















Comments