Muskan Shafi Education Content Expert
Education Content Expert
Relative Velocity is the velocity of an object with respect to another object or observer. Relative Velocity is the time rate of change of the relative position of one object with respect to another object.
- Relative Velocity gives us a measure of how fast two objects are moving with respect to each other.
- Relative Velocity helps to understand how objects move and interact with one another.
- It can be measured for many different types and cases of interactions among objects.
Relative Velocity is the vector difference between the velocities of two bodies. It is the velocity of a body with respect to another regarded as being at rest. Relative Velocity Formula is given as VAB = VA – VB. Here, VAB denotes the relative velocity of body A with respect to body B and VA and VB are the velocities of body A and body B respectively.
Read More: NCERT Solutions for Class 11 Physics Motion in a Plane
Key Terms: Relative Velocity, Speed, Velocity, Motion, Unit of Velocity, Position-Time Graph, Distance, Vector, Motion in a Straight Line
What is Relative Velocity?
[Click Here for Sample Questions]
Relative Velocity is defined as an object’s velocity with respect to another observer.
- Relative Velocity is the pace at which a body's relative location changes with regard to another object over time.
- It can be expressed as a measure of how fast two objects are moving with respect to one another.
- Relative Velocity can be calculated considering the velocity of object A with respect to object B.
- The SI unit of Relative velocity is Meter per second (m/s).
- The dimension of relative velocity is M0L1T-1.
Check More:
Relative Velocity Formula
[Click Here for Previous Years' Questions]
Consider two objects A and B which are moving relative to each other. The relative velocity will be the velocity that body A that would appear to an observer on body B and vice versa. Mathematically, the relative velocity is the vector difference between the velocities of two bodies.
Relative Velocity = Velocity of the Body A – Velocity of the Body B
The Relative Velocity Formula is
| VAB = VA – VB |
Where
- VAB: Relative Velocity of object A with respect to Object B
- VA: Velocity of Object A
- VB: Velocity of the Object B

Relative Velocity Formula
Solved ExampleExample: Hot balloon A flies to the north with a velocity of 350 m/s. Another hot balloon B flies to the south with a velocity of 500 m/s beside balloon A. Calculate:
Solution: Substitute the values in the relative velocity formula,
Here, the velocity of balloon B is taken as negative since it flies in opposite direction to balloon A.
The velocity of the balloon B is taken as positive because it flies in the same direction as balloon A |
Examples of Relative Velocity
[Click Here for Sample Questions]
Consider two objects A and B travelling evenly in one dimension, say along the x-axis, with average velocities VA and VB. If xA (0) and xB (0) are locations of objects A and B at time t = 0, then xA (t) and xB (t) at time t are given by:
- xA (t) = xA (0) + VA t …(1)
- xB (t) = xB (0) + VB t …(2)
Then, the transition from object A to object B is given by:
xBA (t) = xB (t) - xA (t) = [xB (0) - xA (0) ] + (VB - VA) t … (3)
Because the displacement from A to B varies continuously by the amount VB – VA in each unit of time, it indicates that object B has a velocity VB – VA as observed from object A.
- The relative velocity of object A in relation to object B is calculated as follows: VAB = VA - VB
- In the same way, the velocity of object B in relation to object A is given by: VBA = VB – VA
We may observe from the two statements above that:
Relative Velocity of A with Respect to B = – Relative velocity of B with Respect to A
| VAB = - VBA |
Thus, the magnitude of both relative velocities is equal to each other. Mathematically,
|VAB| = |VBA|
Read More: Motion in a Straight Line
Important Cases of Relative Velocity
[Click Here for Previous Years' Questions]
Relative Velocity is applicable in a variety of interactions. Here are a few cases related to the application of related velocity:
Case 1
“Relative Velocity for Two Objects moving in the Same Direction with Equal Velocities.”
Suppose two cars A and B are moving in the same direction with equal velocities (VA = VB). For a person who is sitting in car A, car B would appear to be at rest. Therefore the velocity of B relative to A is zero.
VBA = VB – VA = 0 (As VA = VB)
Similarly, for a person who is seated in car B and observes car A, the relative velocity of A with respect to B is also zero.
VAB = VA – VB = 0 (As VA = VB)
Thus, if Vb – Va = 0, it means the two cars are moving in the same direction and have the same distance between them always. Thus, the position-time graphs for the situation will be two parallel straight lines.

Relative Velocity in Same Direction with Equal Velocities
Read More: Motion in a Plane Important Questions
Case 2
“Relative Velocity for Two Objects starting from the Same Point and moving in the Same Direction with Unequal Velocities.”
Suppose Car A is moving with a velocity VA and Car B is moving with a greater velocity VB in the same direction. The person in car A would feel that bus B is moving away from him with velocity,
VBA = VB – VA
For a person in car B, car A appears to go back with a velocity,
VAB = VA-VB = – (VB – VA)
Therefore, the velocity of A in relation to B is the negative of the velocity of B in relation to A.
Relative Velocity in Same Direction with Unequal Velocities
Case 3
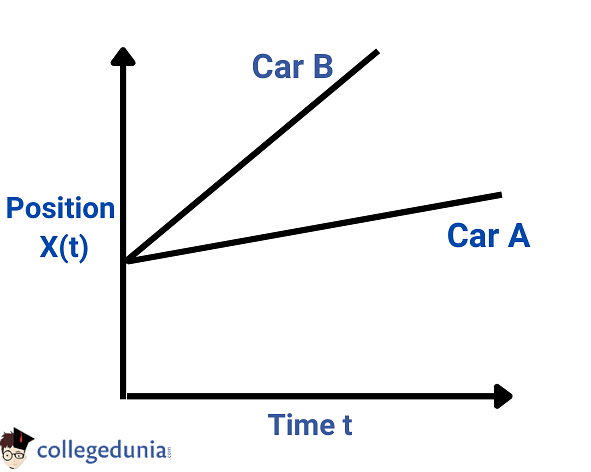
“Relative Velocity for Two Objects starting from Different Positions and moving in the Same Direction with Unequal Velocities.”
Consider that Va> Vb. If car A has higher velocity and is moving behind car B, then car A will overtake car B at some point and the position-time graphs of the two cars will intersect at a point.
Vab = Va – Vb ≠ 0
Vba = Vb - Va ≠ 0 as Va > Vb

Now consider that, Vb > Va. If car B has a higher velocity and is moving ahead, there is no chance of overtaking the other car A and hence the position-time graphs will not intersect. Thus, both the lines move far from each other as shown in the graph.
Vab = Va-Vb ≠0
Vba = Vb - Va ≠ 0 as Vb > Va

In this case, the position-time graphs are straight lines inclined to the time axis and one of them will be steeper than the other.
Case 4
“Relative Velocity for Two Objects moving in the Opposite Direction.”
Consider that both the cars are moving in opposite directions, so, the relative velocity of VBA or VAB will be
VBA = VB - (-VA) = VB + VA
Similarly,
VAB = VA - (-VB) = VA+VB
VAB = VBA = VA+VB
Thus, when two objects are moving in opposite directions, each seems to go very fast relative to the other.

Relative Velocity in Opposite Direction
Read More: Velocity Formula
Relative Velocity Problems
[Click Here for Sample Questions]
Problem 1: Car A travels at a speed of 40 m/s towards the North and Car B travels at a speed of 60 m/s towards the South. Find out the relative velocity.
Solution: It is given that,
- Velocity of Bus A= VA = 40 m/s (Towards North)
- Velocity of Bus B= VB = 60 m/s (Towards South)
Since both the buses are moving in the opposite direction, so relative velocity will be
VAB = VA – (-VB)
= 40 – (-60)
= 100 m/s
Problem 2: A bus motorcycle travelling on the highway at a velocity of 120 km/h passes a car that is travelling at a velocity of 90 km/h. What will be the relative velocity of the bus from the point of view of a passenger in the car?
Solution: Let us consider
- Velocity of Bus: VA
- Velocity of Car: VB
The velocity of the bus relative to the point of view of a passenger will be calculated as
- VAB = VA – VB
- VAB = 120 km/h – 90 km/h
- VAB = 30 km/h
Thus, the velocity of the bus from the viewpoint of the passenger of the car is 30 km/h.
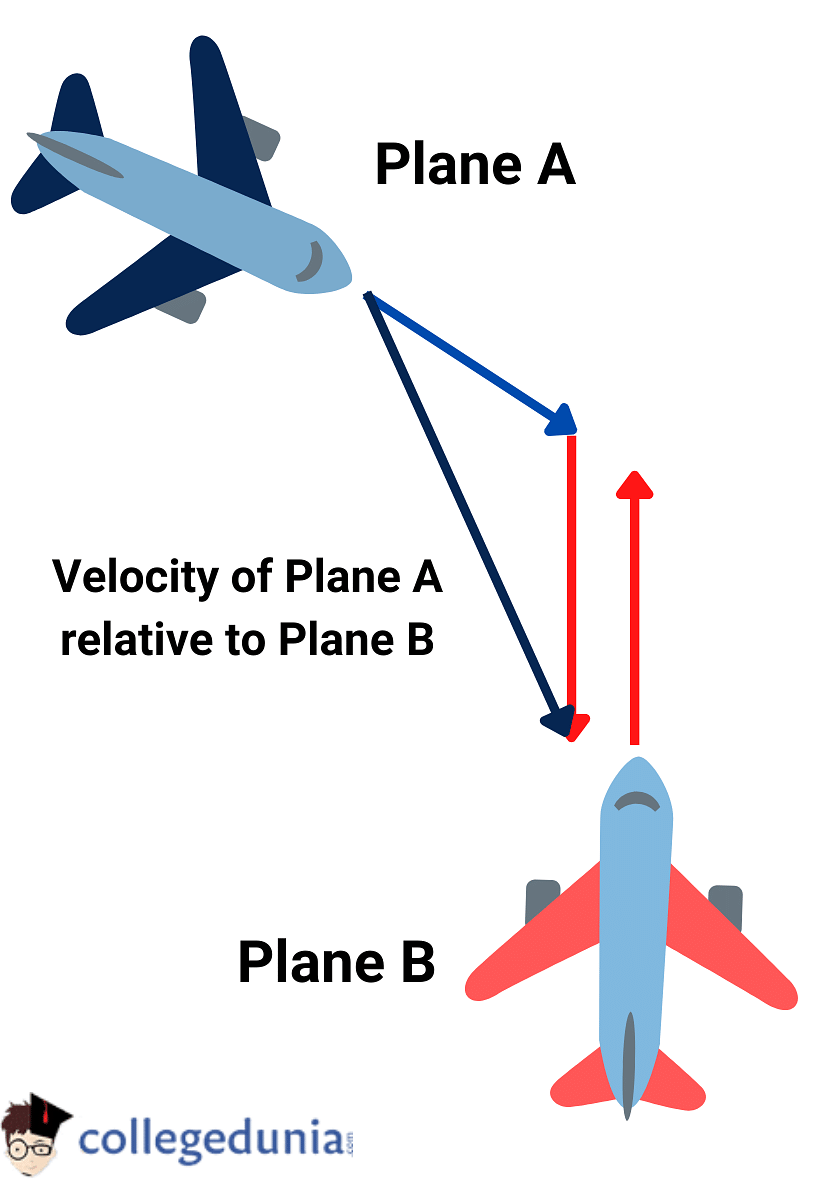
Problem 3: Aeroplane A flies with a velocity of 450 m/s to the north. Another aeroplane B travels at a velocity of 500 m/s to the south beside aeroplane A. What will be the relative velocity of aeroplane A with respect to aeroplane B?
Solution: Using the relative velocity formula, the relative velocity of aeroplane A with respect to the velocity of aeroplane B will be calculated as
VAB = VA – VB
Substituting the values in the formula,
VAB = 450 m/s – (–500 m/s) = 950 m/s
Therefore, the relative velocity of aeroplane A with respect to aeroplane B is 950 m/s.
Also Check:
Motion in a Straight Line Class 11 Handwritten Notes
[Click Here for Previous Years' Questions]
Here are the handwritten notes on Class 11 Motion in a Straight Line and other related topics:

















Things to Remember
- Relative Velocity is the velocity of an object with respect to another object.
- In mathematical terms, the relative velocity is the vector difference between the velocities of two bodies.
- Relative Velocity Formula is vAB = vA – vB, where VA and VB are the velocities of two objects.
- The unit of velocity is the ratio of the unit of distance and that of time.
- The SI unit of Relative velocity is m/s.
- The dimension of relative velocity is M0L1T-1.
Previous Year Questions
- Preeti reached the metro station and found that the escalator … [NEET 2017]
- An eagle flies at constant velocity horizontally across the sky … [UPSEE 2018]
- Consider a ship travelling due east along the equator … [TS EAMCET 2018]
- The position x of a particle with respect to time t along … [NEET 2007]
- The apparent frequency observed by a moving observer away … [KEAM]
- A child is swinging a swing. Minimum and maximum … [JCECE 2004]
- The nature of a graph drawn for a freely falling body … [TS EAMCET 2019]
- In a vertical circular motion, the ratio of the kinetic energy of a particle … [MHT CET 2016]
- Speeds of 20m/s and 15m/s relative to the ground … [BITSAT 2019]
- An object is thrown vertically upward with a speed of 30m/s … [TS EAMCET 2017]
- An automobile travelling at 50 km/h … [JCECE 2005]
- A rifle shoots a bullet with a muzzle velocity of … [JCECE 2005]
Sample Questions
Ques. What is Relative Velocity? (1 Mark)
Ans. Relative Velocity is defined as the velocity of an object in relation to another observer. Relative velocity is the time rate of change of the relative position of one object with respect to another object.
Ques. How long will a person sitting near the window of a train travelling at 36 km/h see a train passing by in the opposite direction with a speed of 18 km/h? The length of the slower-moving train is given as 90 m. (3 Marks)
Ans. It is given that,
Velocity of train = Vt = 36 Km/h = 36 × 5/18 m/s = 10 m/s
Velocity of passenger moving in opposite direction = Vp = 18 Km/h = 18 × 5/18 m/s = 5 m/s
The relative velocity of the slow-moving train with respect to the person sitting in the train is
Vtp = Vt – (-Vp) = Vt + Vp
Vtp = (10 + 5) m/s = 15 m/s
Since the person watches the full length of the other train, the time taken to watch the full train would be
Speed = Distance / Time
15 = 90/t
t = 90/15
= 6 sec
Ques. What is the formula for relative velocity? (3 Marks)
Ans. The Relative Velocity Formula is given as
VAB = VA – VB
Here
- vAB refers to the Relative Velocity of Object A with respect to Object B.
- vA refers to the Velocity of Object A.
- vB refers to the Velocity of the Object B.
Ques. What will happen if the velocities of the two objects are equal? (1 Mark)
Ans. If the velocities of two objects are equal, then the relative velocity of both objects will be zero. It implies that they will be moving at the same speed and in the same direction.
Ques. Two cars that were initially 900 m distant apart, start moving towards each other with speeds of 1 m/s and 2 m/s along a straight road. In what time will they meet each other? (3 Marks)
Ans. Let the relative velocity of two cars be VBA = VB - VA
Consider that the direction VA is moving in a positive direction.
- VA = 1 m/s
- VB = -2 m/s.
Thus, the relative velocity of the two cars will be VBA = − 2 − 1 = − 3 m / s
It means that car B is approaching car A with a speed of -3 m/s along the straight road. Similarly, car A is approaching car B with a speed of 3 m/s along the straight road. Therefore, the two cars are approaching at a speed of 3 m/s.
t = Displacement ⁄ Relative velocity
= 900/3 = 30 sec.
Ques. “Relative velocity can be negative.” True or False? (1 Mark)
Ans. True. Negative relative velocity is possible. It is possible for relative velocity to be negative since it is the difference between two velocities regardless of their magnitude.
Ques. What is the difference between velocity and relative velocity? (2 Marks)
Ans. The difference between velocity and relative velocity is that velocity is measured with respect to a reference point, which is relative to a different point. On the other hand, the relative velocity is measured in a frame where an object is either at rest or moving with respect to the absolute frame.
Ques. Give a situation in which relative velocity needs to be calculated. (3 Marks)
Ans. Consider that we are travelling on a bus. Now, think that another bus overtakes us. Here, we will not be able to feel the actual speed of the overtaking bus, as felt by a person who looks at it, standing by the side of the road. If both buses are moving at the same speed in the same direction, a person sitting in one bus observes a person in the other bus at rest, even though both people are in motion. If both buses are in the opposite direction, then the passengers would observe a greater speed, greater than their individual speed. Thus, in all such situations, the relative velocity is calculated.
Ques. What is the need of using relative velocity? (1 Mark)
Ans. The usage of relative velocity is necessary since it is required to determine whether an object is at rest or moving.
Ques. How to describe Relative Motion Velocity in a Plane? (2 Marks)
Ans. In a plane, relative motion velocity is similar to that of a straight line. The only distinction is that we examine numerous objects moving in a frame that is non-stationary with regard to another observer in the case of relative motion in a plane.
Ques. Two trains each 50 m long are traveling in opposite directions with velocity 10 m/s and 15 m/s. At what time do they cross each other? (4 marks)
Ans. Given
- The velocity of the first train, VA = 10 m/s
- The velocity of the second train, VB = 15 m/s
- The length of each train, L = 50 m
Since both the trains are moving in opposite directions of each other, therefore the relative velocity of train A with respect to train B is given by
VAB = VA - (-VB)
⇒ VAB = VA + VB
On substituting the values, we get
⇒ VAB = 10 + 15 = 25 m/s
The total distance traveled by each train while crossing each other is given by
S = Own length + Length of the oppositely moving train
⇒ S = 50 + 50 = 100 m
Now time taken by the trains to cross each other is given by
T = S/VAB
On substituting the values, we get
T = 100/25 = 4 seconds
Ques. Two cars are moving in the same direction at the same speed 30 km/hr. They are separated by a distance of 5 km, What will be the speed of a car moving in the opposite direction if it meets these two cars at an interval of 4 minutes? (4 marks)
Ans. The two cars (say A and B) are moving with the same velocity, the relative velocity of one (say B) with respect to the other A is given by
VBA = VB - VA
⇒ VBA = v - v = 0
So the relative separation between them (= 5 km) always remains the same.
Now if the velocity of the car (say C) moving in the opposite direction to A and B is VC relative to the ground then the velocity of car C relative to A and B will be
Vrel = VC - v
But as v is opposite to VC
So Vrel = VC - (-30)
⇒ Vrel = VC + 30 km/h
Therefore the time taken by it to cross cars A and B is
T = d/Vrel
⇒ 4/60 = 5/(VC + 30)
On solving, we get
Velocity of car C, VC = 45 km/h
Ques. If two bodies are moving in opposite directions with non-zero velocities, which of the following statements is true? (2 marks)
(a) Relative velocity < Absolute velocity
(b) Relative velocity <= Absolute velocity
(c) Relative velocity > Absolute velocity
(d) Relative velocity = Absolute velocity
Ans. The correct answer is c. Relative velocity > Absolute velocity
Explanation: The formula for relative velocity is given by
Vector VR = Vector VA - Vector VB
When both velocities are pointing in opposing directions, the equation becomes
VR = VA - (-VB)
As a result, the magnitudes get added, resulting in a relative velocity larger than the absolute velocity of either of the two bodies.
Ques. An observer is sitting on a car moving with some constant velocity. The observer sees things around him, in the (2 marks)
(a) An absolute frame of reference
(b) Relative frame of reference
(c) Valid frame of reference
(d) Ground frame of reference
Ans. The correct answer is b. Relative frame of reference
Explanation: The observer is not stationary with respect to the ground. The observer is at rest with respect to the moving car's frame, i.e., the relative frame of reference. The observer will see everything around him with respect to the relative frame of reference.
For Latest Updates on Upcoming Board Exams, Click Here:https://t.me/class_10_12_board_updates
Check-Out:




Comments