| Updated On - Nov 10, 2025
The IIT JAM 2025 Mathematics(MA), being conducted Today by IIT Delhi in Shift 1, from 9:30 AM to 12:30 PM is now over.
According to the initial feedback the exam was moderately difficult. All sections had questions of roughly similar difficulty and variety. Questions from MCQ were a little tough, and questions from NAT and MSQs were comparatively easier.
According to the exam pattern, students are expected to answer 60 questions in which there will be 30 MCSs,10 MSQs, and 20 NATs questions with negative markings applicable only to MCQs.
The question paper along with the answer key is now available for download.
Also Check: IIT JAM 2025 Question Paper
IIT JAM 2025 Mathematics (MA) Question Paper with Answer Key PDFs
| IIT JAM 2025 Mathematics (MA) Question Paper with Answer Key PDFs | Download PDF | Check Solutions |

The sum of the infinite series \[ \sum_{n=1}^{\infty} \frac{(-1)^{n+1} \pi^{2n+1}}{2^{2n+1} (2n)!} \]
is equal to
For which one of the following choices of \( N(x, y) \), is the equation \[ (e^x \sin y - 2y \sin x) \, dx + N(x, y) \, dy = 0 \]
an exact differential equation?
Let \( f, g : \mathbb{R} \to \mathbb{R} \) be two functions defined by

and
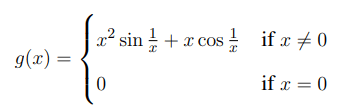
Then, which one of the following is TRUE?
Let \( f, g : \mathbb{R} \to \mathbb{R} \) be two functions defined by
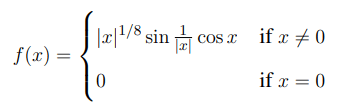
and
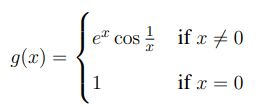
Then, which one of the following is TRUE?
Which one of the following is the general solution of the differential equation \[ \frac{d^2 y}{dx^2} - 8 \frac{dy}{dx} + 16y = 2e^{4x} ? \]
Define \( T : \mathbb{R}^3 \to \mathbb{R}^3 \) by \[ T(x, y, z) = (x + z, 2x + 3y + 5z, 2y + 2z), \quad for all (x, y, z) \in \mathbb{R}^3 \]
Then, which one of the following is TRUE?
Let
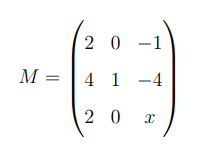
for some real number \( x \). If 0 is an eigenvalue of \( M \), then  is equal to
is equal to
Let \( T : P_2(\mathbb{R}) \to P_2(\mathbb{R}) \) be the linear transformation defined by \[ T(p(x)) = p(x + 1), \quad for all p(x) \in P_2(\mathbb{R}) \]
If \( M \) is the matrix representation of \( T \) with respect to the ordered basis \( \{1, x, x^2\} \) of \( P_2(\mathbb{R}) \), then which one of the following is TRUE?
Let \( G \) be a finite abelian group of order 10. Let \( x_0 \) be an element of order 2 in \( G \).
If \( X = \{ x \in G : x^3 = x_0 \} \), then which one of the following is TRUE?
The value of \[ \int_0^1 \left( \int_0^{\sqrt{y}} 3e^{x^3} \, dx \right) dy \]
is equal to
Let \( C \) denote the family of curves described by \( yx^2 = \lambda \), for \( \lambda \in (0, \infty) \) and lying in the first quadrant of the \( xy \)-plane. Let \( O \) denote the family of orthogonal trajectories of \( C \).
Which one of the following curves is a member of \( O \), and passes through the point \( (2, 1) \)?
Let \( \varphi : (0, \infty) \to \mathbb{R} \) be the solution of the differential equation \[ x \frac{dy}{dx} = \left( \ln y - \ln x \right) y, \]
satisfying \( \varphi(1) = e^2 \). Then, the value of \( \varphi(2) \) is equal to:
Let \( X = \{ x \in S_4 : x^3 = id \} \) and \( Y = \{ x \in S_4 : x^2 \neq id \} \).
If \( m \) and \( n \) denote the number of elements in \( X \) and \( Y \), respectively, then which one of the following is TRUE?
Let \( \varphi : \mathbb{R} \to \mathbb{R} \) be the solution of the differential equation \[ x \frac{dy}{dx} = (y - 1)(y - 3), \]
satisfying \( \varphi(0) = 2 \). Then, which one of the following is TRUE?
Let

Consider the system \( S \) of linear equations given by: \[ 6x_1 + 2x_2 - 6x_3 + 8x_4 = 8 \] \[ 5x_1 + 3x_2 - 9x_3 + 8x_4 = 16 \] \[ 3x_1 + x_2 - 2x_3 + 4x_4 = 32 \]
where \( x_1, x_2, x_3, x_4 \) are unknowns.
Then, which one of the following is TRUE?
Let

for some real number \( x \). Suppose that \( -2 \) and \( 3 \) are eigenvalues of \( M \). If  then which one of the following is TRUE?
then which one of the following is TRUE?
Let \( f(x) = 10x^2 + e^x - \sin(2x) - \cos x \), \( x \in \mathbb{R} \). The number of points at which the function \( f \) has a local minimum is:
For \( n \in \mathbb{N} \), define \( x_n \) and \( y_n \) by \[ x_n = (-1)^n \cos \frac{1}{n} \quad and \quad y_n = \sum_{k=1}^{n} \frac{1}{n + k}. \]
Then, which one of the following is TRUE?
Let \( x_1 = \frac{5}{2} \) and for \( n \in \mathbb{N} \), define \[ x_{n+1} = \frac{1}{5} \left( x_n^2 + 6 \right). \]
Then, which one of the following is TRUE?
Let \( x_1 = 2 \) and \( x_{n+1} = 2 + \frac{1}{2x_n} \) for all \( n \in \mathbb{N} \).
Then, which one of the following is TRUE?
For \( n \in \mathbb{N} \), define \( x_n \) and \( y_n \) by \[ x_n = (-1)^n \frac{3n}{n^3} \quad and \quad y_n = \left(4n^3 + (-1)^n 3n^3 \right)^{1/n}. \]
Then, which one of the following is TRUE?
Let \( M = (m_{ij}) \) be a \( 3 \times 3 \) real, invertible matrix and \( \sigma \in S_3 \) be the permutation defined by \( \sigma(1) = 2, \sigma(2) = 3 \) and \( \sigma(3) = 1 \). The matrix \( M_\sigma \) is defined by \( n_{ij} = m_{i\sigma(j)} \) for all \( i,j \in \{1, 2, 3\} \).
Then, which one of the following is TRUE?
Let \( \mathbb{R}/\mathbb{Z} \) denote the quotient group, where \( \mathbb{Z} \) is considered as a subgroup of the additive group of real numbers \( \mathbb{R} \).
Let \( m \) denote the number of injective (one-one) group homomorphisms from \( \mathbb{Z}_3 \) to \( \mathbb{R}/\mathbb{Z} \) and \( n \) denote the number of group homomorphisms from \( \mathbb{R}/\mathbb{Z} \) to \( \mathbb{Z}_3 \).
Then, which one of the following is TRUE?
Let \( f_1, f_2, f_3 \) be nonzero linear transformations from \( \mathbb{R}^4 \) to \( \mathbb{R} \) and \[ \ker(f_1) \subset \ker(f_2) \cap \ker(f_3). \]
Let \( T : \mathbb{R}^4 \to \mathbb{R}^3 \) be the linear transformation defined by \[ T(v) = (f_1(v), f_2(v), f_3(v)) \quad for all v \in \mathbb{R}^4. \]
Then, the nullity of \( T \) is equal to:
Let \( x_1 = 1 \). For \( n \in \mathbb{N} \), define \[ x_{n+1} = \left( \frac{1}{2} + \frac{\sin^2 n}{n} \right) x_n. \]
Then, which one of the following is TRUE?
Let \( x_1 > 0 \). For \( n \in \mathbb{N} \), define \[ x_{n+1} = x_n + 4. \]
If \[ \lim_{n \to \infty} \left( \frac{1}{x_1 x_2 x_3} + \frac{1}{x_2 x_3 x_4} + \cdots + \frac{1}{x_{n+1} x_{n+2} x_{n+3}} \right) = \frac{1}{24}, \]
then the value of \( x_1 \) is equal to:
Let \( f : \mathbb{R}^2 \to \mathbb{R} \) be defined by \[ f(x, y) = e^{y}(x^2 + y^2) \quad for all (x, y) \in \mathbb{R}^2. \]
Then, which one of the following is TRUE?
Let \( \Omega \) be the bounded region in \( \mathbb{R}^3 \) lying in the first octant \( (x \geq 0, y \geq 0, z \geq 0) \), and bounded by the surfaces \( z = x^2 + y^2 \), \( z = 4 \), \( x = 0 \) and \( y = 0 \).
Then, the volume of \( \Omega \) is equal to:
Let \( x_1 = 1 \). For \( n \in \mathbb{N} \), define \[ x_{n+1} = \left( \frac{1}{2} + \frac{\sin^2 n}{n} \right) x_n. \]
Then, which one of the following is TRUE?
The number of elements in the set \[ \{ x \in \mathbb{R} : 8x^2 + x^4 + x^8 = \cos x \} \]
is equal to:
Let \( f : \mathbb{R}^2 \to \mathbb{R} \) be defined by

Then, which of the following is/are TRUE?
If \( M, N, \mu, w : \mathbb{R}^2 \to \mathbb{R} \) are differentiable functions with continuous partial derivatives, satisfying \[ \mu(x, y) M(x, y) \, dx + \mu(x, y) N(x, y) \, dy = dw, \]
then which one of the following is TRUE?
Let \( \varphi : (-1, \infty) \to (0, \infty) \) be the solution of the differential equation \[ \frac{dy}{dx} = 2 y e^x = 2 e^x \sqrt{y}, \]
satisfying \( \varphi(0) = 1 \). Then, which of the following is/are TRUE?
Let \( f : \mathbb{R}^2 \to \mathbb{R} \) be defined by

Then, which of the following is/are TRUE?
Let \( u_1 = (1, 0, 0, -1) \), \( u_2 = (2, 0, 0, -1) \), \( u_3 = (0, 0, 1, -1) \), \( u_4 = (0, 0, 0, 1) \) be elements in the real vector space \( \mathbb{R}^4 \).
Then, which of the following is/are TRUE?
For \( n \in \mathbb{N} \), let \[ x_n = \sum_{k=1}^{n} \frac{k}{n^2 + k}. \]
Then, which of the following is/are TRUE?
Let \( f : \mathbb{R} \to \mathbb{R} \) be a twice differentiable function such that \[ f(0) = 0, \, f'(0) = 2, \, f(1) = -3. \]
Then, which of the following is/are TRUE?
Let \( f : \mathbb{R} \to \mathbb{R} \) be a twice differentiable function such that \[ f(0) = 4, \, f(1) = -2, \, f(2) = 8, \, f(3) = 2. \]
Then, which of the following is/are TRUE?
For \( n \in \mathbb{N} \), consider the set \( U(n) = \{ x \in \mathbb{Z}_n : \gcd(x, n) = 1 \} \) as a group under multiplication modulo \( n \).
Then, which of the following is/are TRUE?
Consider the following subspaces of the real vector space \( \mathbb{R}^3 \):

Then, which of the following is/are TRUE?
The radius of convergence of the power series \[ \sum_{n=1}^{\infty} \frac{(x + \frac{1}{4})^n}{(-2)^n n^2} \]
about \( x = -\frac{1}{4} \) is equal to ___________ (rounded off to two decimal places).
The value of \[ \lim_{n \to \infty} 8n \left( \left( e^{\frac{1}{2n}} - 1 \right) \left( \sin \frac{1}{2n} + \cos \frac{1}{2n} \right) \right) \]
is equal to ______________ (rounded off to two decimal places).
Let \( \alpha \) be the real number such that \[ \lim_{x \to 0} \frac{(1 - \cos x)(22x^2 + x - 4)}{x^3} = \alpha \ln 2. \]
Then, the value of \( \alpha \) is equal to ___________ (rounded off to two decimal places).
Let \( \varphi : \mathbb{R} \to \mathbb{R} \) be the solution of the differential equation \[ 4 \frac{d^2 y}{dx^2} + 16 \frac{dy}{dx} + 25y = 0 \]
satisfying \( \varphi(0) = 1 \) and \( \varphi'(0) = -\frac{1}{2} \).
Then, the value of \( \lim_{x \to \infty} e^{2x} \varphi(x) \) is equal to ___________ (rounded off to two decimal places).
Let \( S \) be the surface area of the portion of the plane \( z = x + y + 3 \), which lies inside the cylinder \( x^2 + y^2 = 1 \).
Then, the value of \( \left( \frac{S}{\pi} \right)^2 \) is equal to ____________ (rounded off to two decimal places).
Consider the following subspaces of \( \mathbb{R}^4 \): \[ V_1 = \left\{ (x, y, z, w) \in \mathbb{R}^4 : x + y + 2w = 0 \right\}, \quad V_2 = \left\{ (x, y, z, w) \in \mathbb{R}^4 : 2y + z + w = 0 \right\}, \quad V_3 = \left\{ (x, y, z, w) \in \mathbb{R}^4 : x + 3y + z + 3w = 0 \right\}. \]
Then, the dimension of the subspace \( V_1 \cap V_2 \cap V_3 \) is equal to ______________ (rounded off to two decimal places).
Consider the real vector space \( \mathbb{R}^3 \). Let \( T : \mathbb{R}^3 \to \mathbb{R} \) be a linear transformation such that \[ T(1, 1, 1) = 0, \quad T(1, -1, 1) = 0, \quad T(0, 0, 1) = 16. \]
Then, the value of \( T \left( \frac{1}{2}, \frac{2}{3}, \frac{3}{4} \right) \) is equal to ______________ (rounded off to two decimal places).
Let \( T \) denote the triangle in the \( xy \)-plane bounded by the \( x \)-axis and the lines \( y = x \) and \( x = 1 \). The value of the double integral (over \( T \)) \[ \iint_T (5 - y) \, dx \, dy \]
is equal to ____________ (rounded off to two decimal places).
Let \( T, S : P_4(\mathbb{R}) \to P_4(\mathbb{R}) \) be the linear transformations defined by \[ T(p(x)) = xp'(x), \quad S(p(x)) = (x + 1)p'(x) \]
for all \( p(x) \in P_4(\mathbb{R}) \).
Then, the nullity of the composition \( S \circ T \) is ______________
Let \( f : \mathbb{R}^2 \to \mathbb{R} \) be defined by
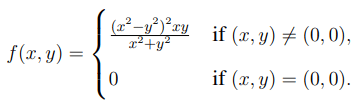
Then, the value of \( \frac{\partial f}{\partial y}(0, 0) \) and \( \frac{\partial f}{\partial x}(0, 0) \) is equal to ___________ (rounded off to two decimal places).
Let \( f : \mathbb{R} \to \mathbb{R} \) be a continuous function satisfying \[ \int_0^{\frac{\pi}{4}} \left( \sin(x) f(x) + \cos(x) \int_0^x f(t) \, dt \right) \, dx = \sqrt{2}. \]
Then, the value of \[ \int_0^{\frac{\pi}{4}} f(x) \, dx \]
is equal to ________ (rounded off to two decimal places).
Let \( \sigma \in S_4 \) be the permutation defined by \( \sigma(1) = 2 \), \( \sigma(2) = 3 \), \( \sigma(3) = 1 \), and \( \sigma(4) = 4 \).
The number of elements in the set \[ \{ \tau \in S_4 : \tau \circ \sigma^{-1} = \sigma \} \]
is equal to ___________
Let \( f(x) = 2x - \sin(x) \), for all \( x \in \mathbb{R} \). Let \( k \in \mathbb{N} \) be such that \[ \lim_{x \to 0} \left( \frac{1}{x} \sum_{i=1}^{k} i^2 f \left( \frac{x}{i} \right) \right) = 45. \]
Then, the value of \( k \) is equal to ___________
The value of the infinite series \[ \sum_{n=1}^{\infty} n \left( \frac{3}{4} \right)^{2n-1} \]
is equal to ___________ (rounded off to two decimal places).
Let \( \varphi : (0, \infty) \to \mathbb{R} \) be the solution of the differential equation \[ x^2 \frac{d^2 y}{dx^2} - x \frac{dy}{dx} + y = 6x \ln x, \]
satisfying \( \varphi(1) = -3 \) and \( \varphi(e) = 0 \).
Then, the value of \( \varphi'(1) \) is equal to ___________ (rounded off to two decimal places).
Let \( \varphi : \mathbb{R} \to \mathbb{R} \) be the solution of the differential equation \[ \frac{dy}{dx} + 2xy = 2 + 4x^2, \]
satisfying \( \varphi(0) = 0 \).
Then, the value of \( \varphi(2) \) is equal to ___________ (rounded off to two decimal places).
Let \( \Omega \) be the solid bounded by the planes \( z = 0 \), \( y = 0 \), \( x = \frac{1}{2} \), \( 2y = x \) and \( 2x + y + z = 4 \).
If \( V \) is the volume of \( \Omega \), then the value of \( 64V \) is equal to ___________ (rounded off to two decimal places).
Let the subspace \( H \) of \( P_3(\mathbb{R}) \) be defined as \[ H = \{ p(x) \in P_3(\mathbb{R}) : xp'(x) = 3p(x) \}. \]
Then, the dimension of \( H \) is equal to ___________
Let \( G \) be an abelian group of order 35. Let \( m \) denote the number of elements of order 5 in \( G \), and let \( n \) denote the number of elements of order 7 in \( G \).
Then, the value of \( m + n \) is equal to ___________
The number of surjective (onto) group homomorphisms from \( S_4 \) to \( \mathbb{Z}_6 \) is equal to ______________







.png?h=175&w=350&mode=stretch)
.jpeg?h=175&w=350&mode=stretch)
.jpeg?h=175&w=350&mode=stretch)

Comments