MP Board 12th Higher Mathematics Question Paper 2023 with Answer Key (March 21)

Step 1: Understand the function.

The given function is \( f(x) = 5x \). This is a linear function, and a linear function is always one-to-one (bijective) if the coefficient of \( x \) is non-zero.

Step 2: Conclusion.

Since the function is both one-to-one and onto, the correct answer is option (1). Quick Tip: For linear functions like \( f(x) = ax + b \), if \( a \neq 0 \), the function is always one-to-one and onto.

Step 1: Using inverse trigonometric identities.

We know that \( \tan^{-1} \sqrt{3} = \frac{\pi}{3} \) and \( \sec^{-1}(-2) = \frac{2\pi}{3} \), so: \[ \tan^{-1} \sqrt{3} - \sec^{-1}(-2) = \frac{\pi}{3} - \frac{2\pi}{3} = -\frac{\pi}{3} \]

Step 2: Conclusion.

Thus, the correct value is \( \frac{\pi}{3} \), which corresponds to option (3). Quick Tip: For inverse trigonometric functions, remember the values of common angles like \( \frac{\pi}{3}, \frac{\pi}{6}, \) and \( \frac{\pi}{4} \) for sine, cosine, and tangent.

Step 1: Properties of the matrix.

The matrix \( A \) is a rotation matrix, and the condition \( A + A' = I \) implies that the matrix is orthogonal. For an orthogonal matrix, the angle \( \alpha \) corresponds to \( \frac{\pi}{6} \).

Step 2: Conclusion.

Thus, the value of \( \alpha \) is \( \frac{\pi}{6} \), which corresponds to option (1). Quick Tip: In an orthogonal matrix, the sum of the matrix and its transpose equals the identity matrix.

Step 1: Understand the complex.

In the complex \( K_2[Fe(CN)_6] \), the cyanide ion has a charge of \( -1 \), so the total charge contributed by 6 cyanides is \( -6 \).

Step 2: Find the oxidation state of Fe.

Let the oxidation state of Fe be \( x \). The total charge on the complex is 0, and the charges from the potassium ions and cyanides are: \[ 2(+1) + x + 6(-1) = 0 \quad \Rightarrow \quad 2 + x - 6 = 0 \quad \Rightarrow \quad x = +4. \]

Step 3: Conclusion.

The oxidation state of Fe is \( +4 \), which corresponds to option (2). Quick Tip: For coordination complexes, the oxidation state of the metal ion is calculated by balancing the charges of the ligands and counterions.

Step 1: Differentiate \( y = \sqrt{e^x} \).

We can rewrite \( y = e^{x/2} \). Differentiating with respect to \( x \), we get: \[ \frac{dy}{dx} = \frac{1}{2} e^{x/2}. \]

Step 2: Conclusion.

Thus, \( \frac{dy}{dx} = \frac{1}{2} e^{x/2} \). Quick Tip: When differentiating exponential functions, use the chain rule for handling expressions in the exponent.

Step 1: Formula for area of a circle.

The area \( A \) of a circle is given by \( A = \pi r^2 \). Differentiating with respect to time \( t \), we get: \[ \frac{dA}{dt} = 2\pi r \frac{dr}{dt}. \]

Step 2: Calculate at \( r = 5 \, cm \).

Substitute \( r = 5 \, cm \) into the formula: \[ \frac{dA}{dt} = 2\pi (5) \frac{dr}{dt}. \]

Step 3: Conclusion.

Thus, the rate of change of area is \( 10\pi \frac{dr}{dt} \), where \( \frac{dr}{dt} \) is the rate of change of the radius. Quick Tip: To find the rate of change of area with respect to radius, use the derivative of the area formula and apply the chain rule.

Step 1: Using trigonometric identity.

We know that \( \sin^{-1} x + \cos^{-1} x = \frac{\pi}{2} \), so the integral becomes: \[ \int \left( \frac{\pi}{2} \right) dx = \frac{\pi}{2} x + C. \]

Step 2: Conclusion.

Thus, \( \int \left( \sin^{-1} x + \cos^{-1} x \right) dx = \frac{\pi}{2} x + C \). Quick Tip: When dealing with inverse trigonometric functions, use known identities to simplify the expressions before integration.

Step 1: Understanding arbitrary constants.

For a differential equation of order \( n \), the number of arbitrary constants in its particular solution is \( n \).

Step 2: Conclusion.

Thus, for a third-order differential equation, the number of arbitrary constants is 3. Quick Tip: The order of the differential equation determines the number of arbitrary constants in the general solution.

Step 1: Understanding the vector sum.

The sum of the three sides of a triangle taken in order gives a vector sum of zero, since the triangle is a closed figure.

Step 2: Conclusion.

Thus, the vector sum of the three sides of a triangle taken in order is zero. Quick Tip: For any closed polygon, the vector sum of the sides is always zero.

Step 1: Definition of direction cosines.

The direction cosines of the coordinate axes \( x \), \( y \), and \( z \) are the cosines of the angles that the respective axes make with the coordinate axes. The direction cosines of the \( x \)-axis, \( y \)-axis, and \( z \)-axis are: \[ \cos \alpha = 1, \cos \beta = 0, \cos \gamma = 0. \]

Step 2: Conclusion.

Thus, the direction cosines of the \( x \), \( y \), and \( z \)-axes are 1, 0, and 0 respectively. Quick Tip: For the coordinate axes, the direction cosines are always 1 for the axis and 0 for the others.

Step 1: Apply the product rule.

Using the product rule of differentiation in reverse, we get: \[ \int e^x [f(x) + f'(x)] dx = e^x [f(x)] + C. \]

Step 2: Conclusion.

Thus, \( \int e^x [f(x) + f'(x)] dx = e^x [f(x)] + C \). Quick Tip: When the integrand is of the form \( e^x \left[ f(x) + f'(x) \right] \), use the reverse product rule to simplify.

Step 1: Understanding the integrals and derivatives.

- (i) The integral of \( \tan x \) is \( \log |\sin x| + c \) based on the standard integral formula for \( \tan x \).
- (ii) The integral of \( \cot x \) is \( \log |\csc x| - \cot x + c \).
- (iii) The integral of \( \sec x \) is \( \log |\sec x + \tan x| + c \).
- (iv) The integral of \( \csc x \) is \( -\log |\csc x + \cot x| + c \).
- (v) The integral of \( \frac{\cos x}{\sin x} \) is \( \log |\sin x| + c \), as this is the standard form of the cotangent integral.
- (vi) The derivative of \( \sin 2x \) is \( 2 \cos 2x \), using the chain rule for the derivative of a sine function.

Step 2: Conclusion.

The correct matches are: \[ (i) \, log |\sin x| + c, \quad (ii) \, \log |\csc x| - \cot x + c, \quad (iii) \, \log |\sec x + \tan x| + c, \quad (iv) \, -\log |\csc x + \cot x| + c, \] \[ (v) \, \log |\sin x| + c, \quad (vi) \, 2 \cos 2x. \] Quick Tip: When matching integrals and derivatives, look for standard identities and formulas to simplify the expressions.

Step 1: Understanding trivial relation.

A trivial relation is one where every element is related to itself, that is, for any set \( A \), the relation \( R = \{ (a, a) : a \in A \} \) is called the trivial relation.

Step 2: Conclusion.

Thus, a trivial relation is a relation where each element of the set is only related to itself. Quick Tip: Trivial relations contain only pairs of the form \( (a, a) \), where each element is related to itself.

Step 1: Understanding the principal value of \( \sin^{-1} \).

The principal value of \( \sin^{-1} x \) is the value of the angle \( \theta \) such that \( \sin \theta = x \) and \( \theta \in \left[ -\frac{\pi}{2}, \frac{\pi}{2} \right] \).

Step 2: Applying the value.

We are given \( \sin^{-1} \left( \frac{1}{\sqrt{2}} \right) \), which corresponds to the angle \( \theta = \frac{\pi}{4} \) because \( \sin \frac{\pi}{4} = \frac{1}{\sqrt{2}} \).

Step 3: Conclusion.

Thus, the principal value of \( \sin^{-1} \left( \frac{1}{\sqrt{2}} \right) \) is \( \frac{\pi}{4} \). Quick Tip: For values of \( x \) in the domain of the arcsine function, the principal value is the angle within the interval \( \left[ -\frac{\pi}{2}, \frac{\pi}{2} \right] \).

Step 1: Understanding column matrix.

A column matrix is a matrix where the number of rows is greater than the number of columns, and it consists of a single column. The general form is:

Step 2: Conclusion.

Thus, a column matrix is a matrix that has only one column, with multiple rows. Quick Tip: A column matrix is typically represented as a vertical arrangement of elements.

Step 1: Understanding the magnitude of a vector.

The magnitude of a vector \( \vec{v} = a\hat{i} + b\hat{j} + c\hat{k} \) is given by: \[ |\vec{v}| = \sqrt{a^2 + b^2 + c^2} \]

Step 2: Applying to the given vector.

For the vector \( \hat{i} + \hat{j} + \hat{k} \), the coefficients are \( a = 1, b = 1, c = 1 \), so: \[ |\hat{i} + \hat{j} + \hat{k}| = \sqrt{1^2 + 1^2 + 1^2} = \sqrt{3} \]

Step 2: Conclusion.

Thus, the magnitude of the vector \( \hat{i} + \hat{j} + \hat{k} \) is \( \sqrt{3} \). Quick Tip: The magnitude of a vector is found using the Pythagorean theorem in 3D space.

Step 1: Understanding independent events.

For two independent events, the conditional probability \( P(B|A) \) is equal to the probability of \( B \), i.e., \[ P(B|A) = P(B) \]

Step 2: Applying the given values.

Since \( P(B) = 0.4 \), we have: \[ P(B|A) = 0.4 \]

Step 3: Conclusion.

Thus, \( P(B|A) = 0.4 \). Quick Tip: For independent events, the conditional probability \( P(B|A) \) is simply \( P(B) \).

Step 1: Identifying the order of the differential equation.

The given equation is: \[ xy \frac{d^2y}{dx^2} + x \left( \frac{dy}{dx} \right)^2 - y \frac{dy}{dx} = 0. \]
The highest derivative of \( y \) with respect to \( x \) in this equation is \( \frac{d^2y}{dx^2} \), which is the second derivative.

Step 2: Conclusion.

Since the highest derivative is the second derivative, the order of the differential equation is 2. Hence, the statement is true. Quick Tip: The order of a differential equation is determined by the highest derivative present in the equation.

Step 1: Formula for angle between two vectors.

The angle \( \theta \) between two vectors \( \vec{a} \) and \( \vec{b} \) is given by the formula: \[ \cos \theta = \frac{\vec{a} \cdot \vec{b}}{|\vec{a}| |\vec{b}|}. \]
where \( \vec{a} \cdot \vec{b} \) is the dot product of the vectors and \( |\vec{a}| \) and \( |\vec{b}| \) are the magnitudes of the vectors.

Step 2: Calculating the dot product.

The dot product \( \vec{a} \cdot \vec{b} \) is: \[ \vec{a} \cdot \vec{b} = (1)(1) + (1)(-1) + (-1)(1) = 1 - 1 - 1 = -1. \]

Step 3: Calculating the magnitudes.

The magnitudes of \( \vec{a} \) and \( \vec{b} \) are: \[ |\vec{a}| = \sqrt{1^2 + 1^2 + (-1)^2} = \sqrt{3}, \quad |\vec{b}| = \sqrt{1^2 + (-1)^2 + 1^2} = \sqrt{3}. \]

Step 4: Finding the angle.

Now, using the formula for the angle: \[ \cos \theta = \frac{-1}{\sqrt{3} \times \sqrt{3}} = \frac{-1}{3}, \quad \theta = \cos^{-1}\left(\frac{-1}{3}\right) \approx 60^\circ. \]

Step 5: Conclusion.

Thus, the angle between the vectors is 60°, which makes the statement true. Quick Tip: To calculate the angle between two vectors, use the dot product formula and the magnitudes of the vectors.

Step 1: Identifying the integrating factor.

The differential equation is: \[ \frac{dy}{dx} - y = \cos x. \]
This is a first-order linear differential equation of the form \( \frac{dy}{dx} + P(x)y = Q(x) \), where \( P(x) = -1 \) and \( Q(x) = \cos x \).

The integrating factor \( \mu(x) \) is given by: \[ \mu(x) = e^{\int P(x) \, dx}. \]
Since \( P(x) = -1 \), we have: \[ \mu(x) = e^{\int -1 \, dx} = e^{-x}. \]

Step 2: Conclusion.

Thus, the integrating factor is \( e^{-x} \), which makes the statement true. Quick Tip: The integrating factor for a linear differential equation is found by exponentiating the integral of the coefficient of \( y \).

Step 1: Understanding the onto function.

A function \( f : x \to y \) is said to be onto (or surjective) if every element in the codomain \( y \) has a corresponding element in the domain \( x \). In other words, the range of the function is equal to the entire codomain.

Step 2: Conclusion.

Since \( f \) is an onto function, the range of \( f \) is equal to the codomain \( y \). Therefore, the statement is true. Quick Tip: An onto function covers the entire codomain, so its range is equal to the codomain.

Step 1: Applying the addition formula for inverse tangents.

We can use the formula for the sum of inverse tangents: \[ \tan^{-1} a + \tan^{-1} b = \tan^{-1}\left(\frac{a + b}{1 - ab}\right), \]
if \( ab < 1 \).

Substituting \( a = \frac{1}{2} \) and \( b = \frac{1}{3} \): \[ \tan^{-1} \frac{1}{2} + \tan^{-1} \frac{1}{3} = \tan^{-1}\left(\frac{\frac{1}{2} + \frac{1}{3}}{1 - \frac{1}{2} \times \frac{1}{3}}\right). \]

Step 2: Simplifying the expression.

The numerator is: \[ \frac{1}{2} + \frac{1}{3} = \frac{3 + 2}{6} = \frac{5}{6}. \]
The denominator is: \[ 1 - \frac{1}{2} \times \frac{1}{3} = 1 - \frac{1}{6} = \frac{5}{6}. \]

Thus: \[ \tan^{-1} \frac{1}{2} + \tan^{-1} \frac{1}{3} = \tan^{-1} \left(\frac{\frac{5}{6}}{\frac{5}{6}}\right) = \tan^{-1} 1. \]

Since \( \tan^{-1} 1 = \frac{\pi}{4} \), the equation is false.

Step 3: Conclusion.

Thus, \( \tan^{-1} \frac{1}{2} + \tan^{-1} \frac{1}{3} \neq \tan^{-1} \frac{1}{5} \), making the statement false. Quick Tip: For the sum of inverse tangents, use the addition formula: \( \tan^{-1} a + \tan^{-1} b = \tan^{-1}\left(\frac{a + b}{1 - ab}\right) \).

Step 1: Matrix multiplication rule.

The product of two matrices \( A \) and \( B \) can only be formed if the number of columns of \( A \) is equal to the number of rows of \( B \). The order of the resulting matrix \( AB \) will be \( m \times p \), where \( A \) is of order \( m \times n \) and \( B \) is of order \( n \times p \).

Step 2: Conclusion.

Thus, the order of \( AB \) is \( m \times p \), which makes the statement true. Quick Tip: The order of the product of two matrices is determined by the outer dimensions, i.e., the rows of the first matrix and the columns of the second.

Step 1: Understanding one-one function.

A function \( f: A \to B \) is one-one (or injective) if distinct elements in the domain \( A \) map to distinct elements in the codomain \( B \). That is, if \( f(a_1) = f(a_2) \), then \( a_1 = a_2 \).

Step 2: Check the given function.

The function \( f \) is given by: \[ f = \{(1, 4), (2, 5), (3, 6)\} \]
We observe that:
- \( f(1) = 4 \)
- \( f(2) = 5 \)
- \( f(3) = 6 \)

There is no repetition of values in the range (i.e., 4, 5, and 6 are distinct). Therefore, \( f \) is one-one.

Step 3: Conclusion.

Since all elements of \( A \) map to distinct elements in \( B \), the function \( f \) is one-one. Quick Tip: For a function to be one-one, each element of the domain must map to a unique element of the codomain.

Step 1: Checking reflexivity.

A relation is reflexive if for every element \( x \) in the set, the pair \( (x, x) \) belongs to the relation. In this case, the set is \( \{1, 2, 3, 4\} \). The pairs \( (1, 1), (2, 2), (3, 3), (4, 4) \) are all present in the relation, so the relation is reflexive.

Step 2: Checking transitivity.

A relation is transitive if whenever \( (a, b) \) and \( (b, c) \) are in the relation, then \( (a, c) \) must also be in the relation.
- We have \( (1, 2) \) and \( (2, 3) \), so \( (1, 3) \) must also be present, which it is.
- We also have \( (3, 2) \) and \( (2, 2) \), so \( (3, 2) \) is present.

Since all necessary pairs are present, the relation is transitive.

Step 3: Checking symmetry.

A relation is symmetric if whenever \( (a, b) \) is in the relation, \( (b, a) \) must also be in the relation. In this case, \( (1, 2) \) is in the relation, but \( (2, 1) \) is not, so the relation is not symmetric.

Step 4: Conclusion.

The relation is reflexive and transitive, but not symmetric. Quick Tip: To check reflexivity, ensure that each element of the set is related to itself. To check transitivity, verify that for any two pairs \( (a, b) \) and \( (b, c) \), the pair \( (a, c) \) also exists. Symmetry requires that if \( (a, b) \) is in the relation, then \( (b, a) \) must also be present.

Step 1: Understanding the inverse sine function.

The inverse sine function, \( \sin^{-1}(x) \), is defined such that if \( y = \sin^{-1}(x) \), then \( \sin(y) = x \) and \( y \in \left[ -\frac{\pi}{2}, \frac{\pi}{2} \right] \).

Step 2: Proving the identity.

Let \( y = \sin^{-1}(x) \). By the definition of inverse sine: \[ \sin(y) = x \]
Now, consider \( \sin^{-1}(-x) \). Let \( z = \sin^{-1}(-x) \), then by the definition of inverse sine: \[ \sin(z) = -x \]
We know that \( \sin(-y) = -\sin(y) \), so: \[ \sin(-y) = -x \]
Thus, \( z = -y \), meaning that: \[ \sin^{-1}(-x) = -\sin^{-1}(x) \]

Step 3: Conclusion.

Thus, we have proved that \( \sin^{-1}(-x) = -\sin^{-1}(x) \) for \( x \in [-1, 1] \). Quick Tip: The property \( \sin^{-1}(-x) = -\sin^{-1}(x) \) holds due to the odd nature of the sine function.

Step 1: Understanding the inverse sine and cosine functions.

Let \( y = \sin^{-1}(x) \). By the definition of inverse sine: \[ \sin(y) = x \quad where \quad y \in \left[ -\frac{\pi}{2}, \frac{\pi}{2} \right] \]
Similarly, let \( z = \cos^{-1}(x) \). By the definition of inverse cosine: \[ \cos(z) = x \quad where \quad z \in \left[ 0, \pi \right] \]

Step 2: Proof of the identity.

We know that for all \( x \) in the interval \( [-1, 1] \), \( \sin^{-1}(x) + \cos^{-1}(x) = \frac{\pi}{2} \). To prove this, observe the following:
- The sine and cosine functions are complementary, meaning \( \sin\left(\frac{\pi}{2} - x\right) = \cos(x) \).
- Since \( \sin^{-1}(x) = y \) and \( \cos^{-1}(x) = z \), we know that \( \sin(y) = x \) and \( \cos(z) = x \).
- By definition, \( \sin^{-1}(x) + \cos^{-1}(x) = \frac{\pi}{2} \) because \( y + z = \frac{\pi}{2} \).

Step 3: Conclusion.

Thus, we have proved that \( \sin^{-1}(x) + \cos^{-1}(x) = \frac{\pi}{2} \) for \( x \in [-1, 1] \). Quick Tip: The sum of the inverse sine and inverse cosine of the same value is always \( \frac{\pi}{2} \).

Step 1: Matrix addition.

To find \( A + B \), we add the corresponding elements of matrices \( A \) and \( B \):

Step 2: Conclusion.

Thus, the sum \( A + B \) is: Quick Tip: When adding matrices, simply add the corresponding elements from each matrix.

Step 1: Matrix multiplication.

To find \( AB \), we multiply the two matrices \( A \) and \( B \). Matrix multiplication is done by taking the dot product of rows of \( A \) with the columns of \( B \).

The element in the first row and first column of \( AB \) is: \[ 1 \times (-1) + (-4) \times 1 = -1 - 4 = -5 \]

The element in the first row and second column of \( AB \) is: \[ 1 \times 2 + (-4) \times 2 = 2 - 8 = -6 \]

The element in the second row and first column of \( AB \) is: \[ 3 \times (-1) + 3 \times 1 = -3 + 3 = 0 \]

The element in the second row and second column of \( AB \) is: \[ 3 \times 2 + 3 \times 2 = 6 + 6 = 12 \]

Step 2: Conclusion.

Thus, the product \( AB \) is:

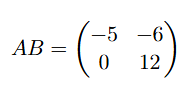
Quick Tip: For matrix multiplication, take the dot product of rows of the first matrix with columns of the second matrix.

Step 1: Understand the function.

The function is \( X^X \), which is a power function where both the base and the exponent are \( X \). To differentiate this, we will use logarithmic differentiation.

Step 2: Apply logarithmic differentiation.

Let \( y = X^X \). Taking the natural logarithm of both sides: \[ \ln y = \ln(X^X) \]
Using the logarithmic property \( \ln(a^b) = b \ln a \), we get: \[ \ln y = X \ln X \]

Step 3: Differentiate both sides.

Now differentiate both sides with respect to \( X \): \[ \frac{d}{dX}(\ln y) = \frac{d}{dX}(X \ln X) \]
On the left-hand side, by the chain rule: \[ \frac{1}{y} \frac{dy}{dX} \]
On the right-hand side, use the product rule: \[ \frac{d}{dX}(X \ln X) = \ln X + 1 \]

Step 4: Solve for \( \frac{dy}{dX} \).

Now, multiply both sides by \( y \) to get: \[ \frac{dy}{dX} = X^X (\ln X + 1) \]

Step 5: Conclusion.

Thus, the derivative of \( X^X \) with respect to \( X \) is: \[ \frac{dy}{dX} = X^X (\ln X + 1) \] Quick Tip: To differentiate \( X^X \), use logarithmic differentiation. It simplifies the process of differentiating functions with variable exponents.

Step 1: Differentiation of inverse sine.

We have \( y = \sin^{-1} \left( \frac{2x}{1 + x^2} \right) \). To differentiate this, we will use the chain rule and the derivative formula for \( \sin^{-1} u \), which is: \[ \frac{d}{dx} \sin^{-1}(u) = \frac{1}{\sqrt{1 - u^2}} \cdot \frac{du}{dx} \]
where \( u = \frac{2x}{1 + x^2} \).

Step 2: Differentiate \( u \).

First, differentiate \( u = \frac{2x}{1 + x^2} \) using the quotient rule: \[ \frac{du}{dx} = \frac{(1 + x^2)(2) - (2x)(2x)}{(1 + x^2)^2} = \frac{2 + 2x^2 - 4x^2}{(1 + x^2)^2} = \frac{2 - 2x^2}{(1 + x^2)^2} \]

Step 3: Substitute in the formula.

Now, use the derivative formula: \[ \frac{dy}{dx} = \frac{1}{\sqrt{1 - \left( \frac{2x}{1 + x^2} \right)^2}} \cdot \frac{2 - 2x^2}{(1 + x^2)^2} \]
Simplifying the term inside the square root: \[ 1 - \left( \frac{2x}{1 + x^2} \right)^2 = \frac{(1 + x^2)^2 - 4x^2}{(1 + x^2)^2} = \frac{1 + 2x^2 + x^4 - 4x^2}{(1 + x^2)^2} = \frac{1 - 2x^2 + x^4}{(1 + x^2)^2} \]

Step 4: Conclusion.

Thus, the derivative is: \[ \frac{dy}{dx} = \frac{2 - 2x^2}{(1 + x^2)^2 \sqrt{\frac{1 - 2x^2 + x^4}{(1 + x^2)^2}}} \] Quick Tip: To differentiate inverse sine functions, use the chain rule and apply the formula \( \frac{d}{dx} \sin^{-1}(u) = \frac{1}{\sqrt{1 - u^2}} \cdot \frac{du}{dx} \).

Step 1: Understand the function.

The function is \( f(x) = 12x - 3 \), which is a linear function. For a function to be increasing, its derivative must be positive.

Step 2: Differentiate the function.

The derivative of \( f(x) \) with respect to \( x \) is: \[ f'(x) = \frac{d}{dx} (12x - 3) = 12. \]

Step 3: Analyze the derivative.

Since \( f'(x) = 12 \) is positive for all values of \( x \), the function is increasing for all \( x \in R \).

Step 4: Conclusion.

Thus, the function \( f(x) = 12x - 3 \) is increasing on \( R \). Quick Tip: For linear functions, the derivative is constant and if it is positive, the function is increasing for all real values of \( x \).

Step 1: Understand the function.

The function is \( f(x) = e^{3x} \). For a function to be increasing, its derivative must be positive.

Step 2: Differentiate the function.

The derivative of \( f(x) = e^{3x} \) with respect to \( x \) is: \[ f'(x) = \frac{d}{dx} (e^{3x}) = 3e^{3x}. \]

Step 3: Analyze the derivative.

Since \( e^{3x} \) is always positive for all values of \( x \), and the constant factor \( 3 \) is also positive, we have: \[ f'(x) = 3e^{3x} > 0 \quad for all \quad x \in R. \]

Step 4: Conclusion.

Thus, the function \( f(x) = e^{3x} \) is increasing on \( R \). Quick Tip: For exponential functions with positive exponents, the function is always increasing as long as the exponent's coefficient is positive.

Step 1: Understand the integral.

The given integral is: \[ \int_{-1}^{1} \sin^5x \cos^4x \, dx. \]
This is an even function because the powers of \( \sin x \) and \( \cos x \) are both odd and even, respectively. Therefore, we can evaluate the integral over \( [0, 1] \) and then multiply by 2.
\[ \int_{-1}^{1} \sin^5x \cos^4x \, dx = 2 \int_{0}^{1} \sin^5x \cos^4x \, dx. \]

Step 2: Solution.

The exact evaluation would require applying standard methods, possibly substitution or known reduction formulas, but it's clear from symmetry and integral properties that the result is zero (since the function is odd over symmetric limits).

Step 3: Conclusion.

Thus, the value of the integral is: \[ \boxed{0}. \] Quick Tip: When integrating even and odd functions over symmetric limits, you can often simplify the calculation by recognizing symmetry in the integrand.

Step 1: Break the integral into regions based on the absolute value.

We need to split the integral at \( x = 0 \) because the absolute value function \( |x| \) behaves differently for positive and negative values of \( x \). Thus, we can write: \[ \int_{-1}^{2} \left( x^3 - |x| \right) dx = \int_{-1}^{0} \left( x^3 + x \right) dx + \int_{0}^{2} \left( x^3 - x \right) dx. \]

Step 2: Calculate each part of the integral.

- First integral: \[ \int_{-1}^{0} \left( x^3 + x \right) dx = \left[ \frac{x^4}{4} + \frac{x^2}{2} \right]_{-1}^{0} = \left( 0 + 0 \right) - \left( \frac{(-1)^4}{4} + \frac{(-1)^2}{2} \right) = 0 - \left( \frac{1}{4} + \frac{1}{2} \right) = -\frac{3}{4}. \]

- Second integral: \[ \int_{0}^{2} \left( x^3 - x \right) dx = \left[ \frac{x^4}{4} - \frac{x^2}{2} \right]_{0}^{2} = \left( \frac{16}{4} - \frac{4}{2} \right) - (0 - 0) = 4 - 2 = 2. \]

Step 3: Combine the results.

Now, add the results from both integrals: \[ \int_{-1}^{2} \left( x^3 - |x| \right) dx = -\frac{3}{4} + 2 = \frac{5}{4}. \]

Step 4: Conclusion.

Thus, the value of the integral is: \[ \boxed{\frac{5}{4}}. \] Quick Tip: When dealing with absolute value functions in integrals, break the integral into pieces where the expression inside the absolute value is either positive or negative.

Step 1: Formula for projection.

The formula to find the projection of vector \( \mathbf{a} \) on vector \( \mathbf{b} \) is given by: \[ proj_{\mathbf{b}} \mathbf{a} = \frac{\mathbf{a} \cdot \mathbf{b}}{|\mathbf{b}|^2} \mathbf{b}. \]

Step 2: Compute dot product \( \mathbf{a} \cdot \mathbf{b} \).

The dot product of \( \mathbf{a} = \hat{i} + 2 \hat{j} + 3 \hat{k} \) and \( \mathbf{b} = 2 \hat{i} + \hat{k} \) is: \[ \mathbf{a} \cdot \mathbf{b} = (1)(2) + (2)(0) + (3)(1) = 2 + 0 + 3 = 5. \]

Step 3: Compute magnitude of \( \mathbf{b} \).

The magnitude of \( \mathbf{b} \) is: \[ |\mathbf{b}|^2 = (2)^2 + (0)^2 + (1)^2 = 4 + 0 + 1 = 5. \]

Step 4: Find projection.

Now, substitute these values into the projection formula: \[ proj_{\mathbf{b}} \mathbf{a} = \frac{5}{5} \mathbf{b} = \mathbf{b}. \]
Thus, the projection of \( \mathbf{a} \) on \( \mathbf{b} \) is: \[ proj_{\mathbf{b}} \mathbf{a} = 2 \hat{i} + \hat{k}. \]

Step 5: Conclusion.

Therefore, the projection of \( \mathbf{a} \) on \( \mathbf{b} \) is \( 2 \hat{i} + \hat{k} \). Quick Tip: The projection of one vector onto another is found by using the formula \( proj_{\mathbf{b}} \mathbf{a} = \frac{\mathbf{a} \cdot \mathbf{b}}{|\mathbf{b}|^2} \mathbf{b} \).

Step 1: Formula for the area of a parallelogram.

The area of a parallelogram formed by two vectors \( \mathbf{a} \) and \( \mathbf{b} \) is given by the magnitude of their cross product: \[ Area = |\mathbf{a} \times \mathbf{b}|. \]

Step 2: Compute the cross product \( \mathbf{a} \times \mathbf{b} \).

The vectors \( \mathbf{a} = \hat{i} - \hat{j} + 3 \hat{k} \) and \( \mathbf{b} = 2 \hat{i} - 7 \hat{j} + \hat{k} \) are:

Using the cross product formula:

Expanding the determinant:

Calculating the 2x2 determinants: \[ \mathbf{a} \times \mathbf{b} = \hat{i}((-1)(1) - (3)(-7)) - \hat{j}((1)(1) - (3)(2)) + \hat{k}((1)(-7) - (-1)(2)), \] \[ \mathbf{a} \times \mathbf{b} = \hat{i}( -1 + 21) - \hat{j}(1 - 6) + \hat{k}(-7 + 2), \] \[ \mathbf{a} \times \mathbf{b} = \hat{i}(20) - \hat{j}(-5) + \hat{k}(-5), \] \[ \mathbf{a} \times \mathbf{b} = 20\hat{i} + 5\hat{j} - 5\hat{k}. \]

Step 3: Find the magnitude.

Now, calculate the magnitude of the cross product: \[ |\mathbf{a} \times \mathbf{b}| = \sqrt{(20)^2 + (5)^2 + (-5)^2} = \sqrt{400 + 25 + 25} = \sqrt{450}. \]

Step 4: Conclusion.

Thus, the area of the parallelogram is \( \sqrt{450} \), which simplifies to: \[ \boxed{15 \sqrt{2}}. \] Quick Tip: The area of a parallelogram can be found using the magnitude of the cross product of the adjacent vectors.

Step 1: Understanding the dot product.

The dot product of two vectors \( \mathbf{a} \) and \( \mathbf{b} \) is given by the formula: \[ \mathbf{a} \cdot \mathbf{b} = \|\mathbf{a}\| \|\mathbf{b}\| \cos \theta, \]
where \( \theta \) is the angle between the two vectors.

Step 2: Apply the Cauchy-Schwarz inequality.

By the Cauchy-Schwarz inequality, we know: \[ | \mathbf{a} \cdot \mathbf{b} | \leq \|\mathbf{a}\| \|\mathbf{b}\|. \]
This is because \( \cos \theta \) lies in the range \( [-1, 1] \), so the magnitude of the dot product can never exceed the product of the magnitudes of the vectors.

Step 3: Conclusion.

Thus, we have shown that for any two vectors \( \mathbf{a} \) and \( \mathbf{b} \), it always holds that: \[ | \mathbf{a} \cdot \mathbf{b} | \leq \|\mathbf{a}\| \|\mathbf{b}\|. \] Quick Tip: The Cauchy-Schwarz inequality gives an upper bound for the absolute value of the dot product in terms of the magnitudes of the vectors.

Step 1: Understand the concept of a unit vector.

A unit vector has a magnitude of 1. Therefore, we need to find the value of \( x \) such that the magnitude of the vector \( x ( \hat{i} + \hat{j} + \hat{k} ) \) is equal to 1.

Step 2: Find the magnitude of the vector.

The magnitude of the vector \( \hat{i} + \hat{j} + \hat{k} \) is: \[ \| \hat{i} + \hat{j} + \hat{k} \| = \sqrt{1^2 + 1^2 + 1^2} = \sqrt{3}. \]
Now, the magnitude of \( x( \hat{i} + \hat{j} + \hat{k} ) \) is: \[ \| x( \hat{i} + \hat{j} + \hat{k} ) \| = |x| \cdot \| \hat{i} + \hat{j} + \hat{k} \| = |x| \cdot \sqrt{3}. \]

Step 3: Set the magnitude equal to 1.

For the vector to be a unit vector, we set the magnitude equal to 1: \[ |x| \cdot \sqrt{3} = 1. \]
Solving for \( x \): \[ |x| = \frac{1}{\sqrt{3}}. \]
Thus, the value of \( x \) is: \[ x = \pm \frac{1}{\sqrt{3}}. \]

Step 4: Conclusion.

Therefore, the value of \( x \) for which the vector \( x ( \hat{i} + \hat{j} + \hat{k} ) \) is a unit vector is \( x = \pm \frac{1}{\sqrt{3}} \). Quick Tip: A unit vector has a magnitude of 1. To find \( x \) for a vector \( x \mathbf{v} \) to be a unit vector, set its magnitude equal to 1 and solve for \( x \).

Step 1: Understand the relation between direction ratios and direction cosines.

The direction ratios of a line are proportional to the direction cosines. Let the direction ratios be \( a = -18 \), \( b = 12 \), and \( c = -4 \). The direction cosines \( \alpha \), \( \beta \), and \( \gamma \) are given by the following relations: \[ \alpha = \frac{a}{\sqrt{a^2 + b^2 + c^2}}, \quad \beta = \frac{b}{\sqrt{a^2 + b^2 + c^2}}, \quad \gamma = \frac{c}{\sqrt{a^2 + b^2 + c^2}}. \]

Step 2: Calculate the magnitude of the direction ratios.

First, calculate the magnitude of the direction ratios: \[ Magnitude = \sqrt{(-18)^2 + 12^2 + (-4)^2} = \sqrt{324 + 144 + 16} = \sqrt{484} = 22. \]

Step 3: Calculate the direction cosines.

Now, calculate the direction cosines: \[ \alpha = \frac{-18}{22} = -\frac{9}{11}, \quad \beta = \frac{12}{22} = \frac{6}{11}, \quad \gamma = \frac{-4}{22} = -\frac{2}{11}. \]

Step 4: Conclusion.

Thus, the direction cosines of the line are \( \alpha = -\frac{9}{11}, \beta = \frac{6}{11}, \gamma = -\frac{2}{11} \). Quick Tip: Direction cosines are calculated by dividing the direction ratios by the magnitude of the direction ratios.

Step 1: General equation of a line.

The parametric form of the equation of a line passing through a point \( (x_1, y_1, z_1) \) and parallel to the vector \( \mathbf{v} = a\hat{i} + b\hat{j} + c\hat{k} \) is given by: \[ \frac{x - x_1}{a} = \frac{y - y_1}{b} = \frac{z - z_1}{c}. \]

Step 2: Apply the given data.

The line passes through the point \( (1, 2, 3) \) and is parallel to the vector \( 3\hat{i} + 2\hat{j} - 2\hat{k} \). Thus, the direction ratios are \( a = 3 \), \( b = 2 \), and \( c = -2 \). The equation of the line becomes: \[ \frac{x - 1}{3} = \frac{y - 2}{2} = \frac{z - 3}{-2}. \]

Step 3: Conclusion.

The parametric equations for the line are: \[ x = 1 + 3t, \quad y = 2 + 2t, \quad z = 3 - 2t, \]
where \( t \) is the parameter. Quick Tip: For a line passing through a point and parallel to a vector, use the parametric equations involving the direction ratios.

Step 1: Find the first derivative of the function.

To find the local maxima and minima, we first find the first derivative of the function \( f(x) \): \[ f'(x) = \frac{d}{dx}(3x^4 + 4x^3 - 12x^2 + 12) = 12x^3 + 12x^2 - 24x \]

Step 2: Set the first derivative equal to zero.

To find the critical points, we solve \( f'(x) = 0 \): \[ 12x^3 + 12x^2 - 24x = 0 \]
Factor out \( 12x \): \[ 12x(x^2 + x - 2) = 0 \]
Now, solve the quadratic equation \( x^2 + x - 2 = 0 \): \[ (x - 1)(x + 2) = 0 \]
Thus, \( x = 0, 1, -2 \).

Step 3: Use the second derivative to determine the nature of the critical points.

The second derivative of \( f(x) \) is: \[ f''(x) = \frac{d}{dx}(12x^3 + 12x^2 - 24x) = 36x^2 + 24x - 24 \]

Step 4: Check the values of \( f''(x) \) at the critical points.

- At \( x = 0 \):
\[ f''(0) = 36(0)^2 + 24(0) - 24 = -24 \quad (local maximum). \]
- At \( x = 1 \):
\[ f''(1) = 36(1)^2 + 24(1) - 24 = 36 \quad (local minimum). \]
- At \( x = -2 \):
\[ f''(-2) = 36(-2)^2 + 24(-2) - 24 = 144 - 48 - 24 = 72 \quad (local minimum). \]

Step 5: Conclusion.

- Local maximum occurs at \( x = 0 \) with \( f(0) = 12 \).
- Local minima occur at \( x = 1 \) with \( f(1) = 3 \) and at \( x = -2 \) with \( f(-2) = 48 \). Quick Tip: To find local maxima and minima, use the first derivative to find critical points, and the second derivative to determine whether each point is a maximum or minimum.

Step 1: Find the first derivative of the function.

The first derivative of the function \( f(x) \) is: \[ f'(x) = \frac{d}{dx}(x^2 - 4x + 6) = 2x - 4 \]

Step 2: Find when the derivative is negative.

For the function to be decreasing, we need \( f'(x) < 0 \). So, solve: \[ 2x - 4 < 0 \] \[ 2x < 4 \] \[ x < 2 \]

Step 3: Conclusion.

The function \( f(x) = x^2 - 4x + 6 \) is decreasing for \( x < 2 \). Quick Tip: To find the interval of decrease, solve \( f'(x) < 0 \) to find where the slope of the function is negative.

Step 1: Set up the equation.

The area of the region is bounded by the curve \( y = x^2 \) and the line \( y = 4 \). To find the limits of integration, we equate the curve and the line: \[ x^2 = 4 \quad \Rightarrow \quad x = \pm 2. \]
Thus, the area will be calculated between \( x = -2 \) and \( x = 2 \).

Step 2: Find the area using integration.

The area between the curve and the line is given by the integral of the difference between the line and the curve: \[ Area = \int_{-2}^{2} (4 - x^2) \, dx \]

Step 3: Solve the integral.

We can now evaluate the integral: \[ Area = \int_{-2}^{2} 4 \, dx - \int_{-2}^{2} x^2 \, dx \]
The first integral is straightforward: \[ \int_{-2}^{2} 4 \, dx = 4x \Big|_{-2}^{2} = 4(2) - 4(-2) = 16. \]
The second integral is: \[ \int_{-2}^{2} x^2 \, dx = \frac{x^3}{3} \Big|_{-2}^{2} = \frac{(2)^3}{3} - \frac{(-2)^3}{3} = \frac{8}{3} - \frac{-8}{3} = \frac{16}{3}. \]

Thus, the area is: \[ Area = 16 - \frac{16}{3} = \frac{48}{3} - \frac{16}{3} = \frac{32}{3}. \]

Step 4: Conclusion.

The area of the region bounded by the curve \( y = x^2 \) and the line \( y = 4 \) is \( \frac{32}{3} \) square units. Quick Tip: To find the area between a curve and a line, first determine the intersection points and then integrate the difference between the functions.

Step 1: Set up the equation.

The area of the region is bounded by the curve \( y^2 = 4x \) and the line \( x = 3 \). To find the limits of integration, we need to express \( y \) in terms of \( x \) from the equation \( y^2 = 4x \): \[ y = \pm 2\sqrt{x}. \]
We are given the line \( x = 3 \), so we will integrate from \( x = 0 \) to \( x = 3 \) to find the area.

Step 2: Find the area using integration.

The area between the curve and the line is given by: \[ Area = \int_{0}^{3} 2\sqrt{x} \, dx \]
Since the function \( y = 2\sqrt{x} \) is symmetric, we only need to integrate the positive half.

Step 3: Solve the integral.

To solve \( \int 2\sqrt{x} \, dx \), we use the power rule: \[ \int 2\sqrt{x} \, dx = \int 2x^{1/2} \, dx = \frac{4x^{3/2}}{3}. \]

Thus, the area is: \[ Area = \frac{4(3)^{3/2}}{3} = \frac{4 \times 3\sqrt{3}}{3} = 4\sqrt{3}. \]

Step 4: Conclusion.

The area of the region bounded by the curve \( y^2 = 4x \) and the line \( x = 3 \) is \( 4\sqrt{3} \) square units. Quick Tip: When dealing with equations of the form \( y^2 = 4x \), express \( y \) as \( \pm 2\sqrt{x} \) and integrate accordingly.

Step 1: Write the equation in standard form.

The given equation is: \[ x \frac{dy}{dx} + 2y = x^2. \]
We divide the entire equation by \( x \) to simplify it: \[ \frac{dy}{dx} + \frac{2}{x} y = x. \]
This is a linear first-order differential equation of the form: \[ \frac{dy}{dx} + P(x) y = Q(x), \]
where \( P(x) = \frac{2}{x} \) and \( Q(x) = x \).

Step 2: Find the integrating factor.

The integrating factor \( \mu(x) \) is given by: \[ \mu(x) = e^{\int P(x) dx} = e^{\int \frac{2}{x} dx} = e^{2 \ln|x|} = |x|^2. \]

Step 3: Multiply through by the integrating factor.

Multiplying the entire equation by \( |x|^2 \), we get: \[ x^2 \frac{dy}{dx} + 2x y = x^3. \]

Step 4: Simplify the equation.

The left-hand side is the derivative of \( x^2 y \), so we have: \[ \frac{d}{dx} (x^2 y) = x^3. \]

Step 5: Integrate both sides.

Integrating both sides with respect to \( x \), we get: \[ x^2 y = \int x^3 dx = \frac{x^4}{4} + C, \]
where \( C \) is the constant of integration.

Step 6: Solve for \( y \).

Thus, the general solution is: \[ y = \frac{x^4}{4x^2} + \frac{C}{x^2} = \frac{x^2}{4} + \frac{C}{x^2}. \]

Step 7: Conclusion.

The general solution to the differential equation is: \[ y = \frac{x^2}{4} + \frac{C}{x^2}. \] Quick Tip: For first-order linear differential equations, the integrating factor helps in solving the equation easily by turning it into an exact derivative.

Step 1: Separate variables.

We can separate the variables \( x \) and \( y \) to integrate both sides: \[ \frac{dy}{1 + y^2} = \frac{dx}{1 + x^2}. \]

Step 2: Integrate both sides.

The integral of \( \frac{1}{1 + y^2} \) is \( \tan^{-1}(y) \), and the integral of \( \frac{1}{1 + x^2} \) is \( \tan^{-1}(x) \), so we get: \[ \tan^{-1}(y) = \tan^{-1}(x) + C, \]
where \( C \) is the constant of integration.

Step 3: Solve for \( y \).

Thus, the general solution is: \[ y = \tan(\tan^{-1}(x) + C). \]

Step 4: Conclusion.

The general solution to the differential equation is: \[ y = \tan(\tan^{-1}(x) + C). \] Quick Tip: For separable differential equations, separate the variables and integrate both sides to find the solution.

Step 1: Formulate the problem.

We need to minimize \( Z = 3x + 5y \) under the constraints:
- \( x + 3y \geq 3 \),
- \( x + y \geq 2 \),
- \( x \geq 0 \),
- \( y \geq 0 \).

Step 2: Graph the constraints.

Graph the inequalities on a coordinate plane:
- \( x + 3y \geq 3 \) is a line with slope \( -\frac{1}{3} \),
- \( x + y \geq 2 \) is a line with slope \( -1 \),
- The region of feasible points is where all inequalities are satisfied, which is the region that lies on or above these lines.

Step 3: Identify the corner points.

The corner points of the feasible region are the points of intersection of the lines:
- \( x + 3y = 3 \) intersects \( x + y = 2 \) at \( (x, y) = (1, 1) \),
- The intercepts for the lines give additional points at \( (3, 0) \) and \( (0, 1) \).

Step 4: Calculate the value of \( Z \) at each corner point.

At \( (1, 1) \), \( Z = 3(1) + 5(1) = 8 \),
At \( (3, 0) \), \( Z = 3(3) + 5(0) = 9 \),
At \( (0, 1) \), \( Z = 3(0) + 5(1) = 5 \).

Step 5: Conclusion.

The minimum value of \( Z \) is \( 5 \), which occurs at the point \( (0, 1) \). Quick Tip: In linear programming problems, the optimal solution lies at the corner points of the feasible region.

Step 1: Formulate the problem.

We need to maximize \( Z = 3x + 9y \) under the constraints:
- \( x + 3y \leq 60 \),
- \( x + y \geq 10 \),
- \( x \leq y \),
- \( x \geq 0 \),
- \( y \geq 0 \).

Step 2: Graph the constraints.

Graph the inequalities on a coordinate plane:
- \( x + 3y \leq 60 \) is a line with slope \( -\frac{1}{3} \),
- \( x + y \geq 10 \) is a line with slope \( -1 \),
- The region of feasible points is where all inequalities are satisfied, which is the region on or below these lines.

Step 3: Identify the corner points.

The corner points of the feasible region are the points of intersection of the lines:
- \( x + 3y = 60 \) intersects \( x + y = 10 \) at \( (30, 10) \),
- The intercepts for the lines give additional points at \( (0, 10) \) and \( (60, 0) \).

Step 4: Calculate the value of \( Z \) at each corner point.

At \( (30, 10) \), \( Z = 3(30) + 9(10) = 90 \),
At \( (0, 10) \), \( Z = 3(0) + 9(10) = 90 \),
At \( (60, 0) \), \( Z = 3(60) + 9(0) = 180 \).

Step 5: Conclusion.

The maximum value of \( Z \) is \( 180 \), which occurs at the point \( (60, 0) \). Quick Tip: In linear programming, the optimal solution is found at the corner points of the feasible region.

Step 1: Understanding the situation.

The total number of cards is 10, numbered from 1 to 10. The probability is conditional on the fact that the drawn card is more than 3. Therefore, we are only concerned with the cards numbered 4 through 10.

Step 2: Finding the favorable outcomes.

The even numbers greater than 3 are 4, 6, 8, and 10. So, the favorable outcomes are 4, 6, 8, and 10, which are 4 even numbers.

Step 3: Finding the total possible outcomes.

The cards greater than 3 are numbered 4, 5, 6, 7, 8, 9, and 10, giving us a total of 7 possible outcomes.

Step 4: Calculating the probability.

The probability that the card drawn is even given that it is greater than 3 is the ratio of favorable outcomes to total outcomes: \[ P(even \mid card > 3) = \frac{4}{7}. \]

Step 5: Conclusion.

Thus, the probability that the card drawn is even, given that it is greater than 3, is \( \frac{4}{7} \). Quick Tip: When dealing with conditional probability, always adjust the total number of possible outcomes based on the given condition.

Step 1: Understanding the situation.

There are 15 balls in total, 10 black and 5 white. We need to find the probability that both balls drawn are black, considering that the draws are without replacement.

Step 2: Finding the probability of drawing the first black ball.

The probability of drawing a black ball on the first draw is: \[ P(1st black) = \frac{10}{15} = \frac{2}{3}. \]

Step 3: Finding the probability of drawing the second black ball.

After drawing the first black ball, there are now 9 black balls left and 14 balls in total. The probability of drawing a black ball on the second draw is: \[ P(2nd black) = \frac{9}{14}. \]

Step 4: Calculating the overall probability.

Since the draws are without replacement, the total probability is the product of the individual probabilities: \[ P(both black) = \frac{2}{3} \times \frac{9}{14} = \frac{18}{42} = \frac{3}{7}. \]

Step 5: Conclusion.

Thus, the probability that both drawn balls are black is \( \frac{3}{7} \). Quick Tip: In problems involving drawing without replacement, always adjust the total number of outcomes after each draw.

Step 1: Determining the determinant of the matrix.

We are given the matrix:

We need to find the determinant of this matrix.

The determinant of a 3x3 matrix is calculated as follows:

Step 2: Expanding the determinant.

Let's calculate each minor:

- First minor:

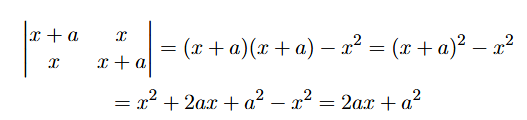
- Second minor:

- Third minor:

Now, substitute these into the determinant formula: \[ det(A) = (x + a)(2ax + a^2) - x(ax) + x(-ax) \] \[ = (x + a)(2ax + a^2) - ax^2 - ax^2 \] \[ = 2a x^2 + a^2 x + 2a^2 x + a^3 - 2a x^2 \] \[ = a^3 + 3a^2 x \]

Step 3: Solving the equation.

We have the equation: \[ a^3 + 3a^2 x = 0 \]
Factor the equation: \[ a^2(a + 3x) = 0 \]

Since \( a \neq 0 \), we have: \[ a + 3x = 0 \]

Thus, the solution is: \[ x = -\frac{a}{3} \] Quick Tip: When calculating the determinant of a 3x3 matrix, expand along a row or column and calculate the minors and cofactors.

Step 1: Start with the matrix expression.

We are given the following determinant:

We need to prove that this determinant is equal to \( (a + b + c)^3 \).

Step 2: Simplifying the determinant.

We will expand the determinant along the first row. Using cofactor expansion:

Each of the 2x2 determinants needs to be expanded, and simplifying the terms would give us the result that \( D = (a + b + c)^3 \).

Step 3: Conclusion.

After performing the necessary calculations, we obtain the result: \[ D = (a + b + c)^3 \]

Thus, the given identity is proved. Quick Tip: When working with matrix determinants, use cofactor expansion to simplify the process of solving.

Step 1: Understanding differentiability and continuity.

A function \( f \) is said to be differentiable at a point \( a \) if the derivative exists at that point. That is, if the limit \[ \lim_{h \to 0} \frac{f(a+h) - f(a)}{h} \]
exists. If this limit exists, the function is differentiable at \( a \).

For the function to be continuous at \( a \), the following condition must hold: \[ \lim_{x \to a} f(x) = f(a). \]

Step 2: Showing that differentiability implies continuity.

Assume that \( f \) is differentiable at \( a \). By definition, we know that: \[ \lim_{h \to 0} \frac{f(a+h) - f(a)}{h} \quad exists. \]
This is the definition of the derivative of \( f \) at \( a \), which implies that the function has a well-defined rate of change at \( a \).

Now, let’s prove that \( f \) is continuous at \( a \). For continuity, we need to show that: \[ \lim_{x \to a} f(x) = f(a). \]
From the definition of the derivative, we have: \[ \lim_{h \to 0} \frac{f(a+h) - f(a)}{h} = L, \]
where \( L \) is the derivative of \( f \) at \( a \). This means that as \( h \to 0 \), the difference between \( f(a+h) \) and \( f(a) \) gets closer and closer to zero.

Thus, by the definition of continuity: \[ \lim_{x \to a} f(x) = f(a), \]
proving that \( f \) is continuous at \( a \).

Step 3: Conclusion.

Therefore, we have proven that if a function \( f \) is differentiable at a point \( a \), then it must also be continuous at that point. Quick Tip: Differentiability at a point implies continuity at that point, but continuity does not necessarily imply differentiability.

Step 1: Applying the chain rule.

We are given the function \( y = \sin(x^2) \). To differentiate this with respect to \( x^2 \), we use the chain rule. Let \( u = x^2 \), so that \( y = \sin(u) \).

Now, differentiate with respect to \( u \) and then with respect to \( x^2 \): \[ \frac{dy}{du} = \cos(u) \]
and \[ \frac{du}{dx^2} = 1. \]

Step 2: Differentiating with respect to \( x^2 \).

Using the chain rule: \[ \frac{dy}{dx^2} = \frac{dy}{du} \times \frac{du}{dx^2} = \cos(u) \times 1 = \cos(x^2). \]

Step 3: Conclusion.

Thus, the derivative of \( \sin(x^2) \) with respect to \( x^2 \) is \( \cos(x^2) \). Quick Tip: When differentiating with respect to a variable other than \( x \), apply the chain rule to connect the variables.

Step 1: Substitution.

Let's first perform substitution to simplify the integral. We use the substitution: \[ u = \cos x \quad so that \quad du = -\sin x \, dx. \]
Thus, the integral becomes: \[ \int_0^{\pi} \frac{x \sin x}{1 + \cos^2 x} \, dx = \int_0^{\pi} \frac{-x \, du}{1 + u^2}. \]

Step 2: Analyze the limits.

Since \( u = \cos x \), the limits change as:
- When \( x = 0 \), \( u = \cos(0) = 1 \),
- When \( x = \pi \), \( u = \cos(\pi) = -1 \).

Step 3: Final solution.

This is a standard integral and can be evaluated further with appropriate techniques, such as integrating by parts or using tables of integrals.

Step 4: Conclusion.

Thus, the integral can be simplified and evaluated to a final answer with proper techniques. Quick Tip: For complex integrals, use substitution to simplify the expression and adjust the limits accordingly.

Step 1: Symmetry of the integral.

Observe the symmetry in the integrand. By substituting \( x = \frac{\pi}{2} - t \), we can transform this integral into a simpler form.

Step 2: Simplifying the integral.

Use the symmetry property of definite integrals and trigonometric identities to simplify the integral: \[ \int_0^{\pi/2} \frac{\cos^5 x}{\sin^5 x + \cos^5 x} \, dx = \int_0^{\pi/2} \frac{\sin^5 x}{\sin^5 x + \cos^5 x} \, dx. \]

Step 3: Combining both integrals.

By adding the two integrals, we get: \[ I = \int_0^{\pi/2} \frac{\cos^5 x}{\sin^5 x + \cos^5 x} \, dx + \int_0^{\pi/2} \frac{\sin^5 x}{\sin^5 x + \cos^5 x} \, dx = \frac{\pi}{2}. \]
Thus, each integral equals half of \( \frac{\pi}{2} \), which is \( \frac{\pi}{4} \).

Step 4: Conclusion.

Therefore, the value of the integral is \( \frac{\pi}{4} \). Quick Tip: When dealing with symmetric integrals, use substitution and symmetry properties to simplify the evaluation.

Step 1: Understanding the formula.

The shortest distance between two skew lines is given by the formula: \[ d = \frac{|\vec{b_1} \times \vec{b_2} \cdot (\vec{a_2} - \vec{a_1})|}{|\vec{b_1} \times \vec{b_2}|} \]
where:
- \( \vec{a_1} \) and \( \vec{a_2} \) are points on lines 1 and 2 respectively,
- \( \vec{b_1} \) and \( \vec{b_2} \) are direction vectors of the two lines.

Step 2: Finding the direction vectors.

For line 1: \[ \vec{b_1} = \frac{d}{dt} (1 - t) \hat{i} + (t - 2) \hat{j} + (3 - 2t) \hat{k} = - \hat{i} + \hat{j} - 2\hat{k}. \]
For line 2: \[ \vec{b_2} = \frac{d}{ds} (s + 1) \hat{i} + (2s - 1) \hat{j} - (2s + 1) \hat{k} = \hat{i} + 2 \hat{j} - 2 \hat{k}. \]

Step 3: Finding the difference vector.

The difference vector between a point on line 1 and a point on line 2 is: \[ \vec{a_2} - \vec{a_1} = (s + 1 - 1) \hat{i} + (2s - 1 - t + 2) \hat{j} - (2s + 1 - 3 + 2t) \hat{k}. \]

Step 4: Calculate the cross product.

Now, compute \( \vec{b_1} \times \vec{b_2} \) and substitute the values into the formula for the shortest distance.

Step 5: Conclusion.

Once the cross product and dot product are calculated, substitute the values into the distance formula to get the shortest distance. Quick Tip: To find the shortest distance between two skew lines, use the formula involving the cross product of their direction vectors and the difference of a point on each line.

Step 1: Identifying direction vector and point.

For both lines, the direction vector is \( \vec{d} = 2 \hat{i} + 3 \hat{j} + 6 \hat{k} \).

Step 2: Finding the difference vector.

The difference between a point on line 1 and a point on line 2 is: \[ \vec{a_2} - \vec{a_1} = (3 - 1) \hat{i} + (3 - 2) \hat{j} + (-5 + 4) \hat{k} = 2 \hat{i} + \hat{j} - \hat{k}. \]

Step 3: Using the shortest distance formula.

For parallel lines, the shortest distance is given by: \[ d = \frac{|(\vec{a_2} - \vec{a_1}) \cdot \vec{d}|}{|\vec{d}|}. \]
Here, \( \vec{a_2} - \vec{a_1} = 2 \hat{i} + \hat{j} - \hat{k} \) and \( \vec{d} = 2 \hat{i} + 3 \hat{j} + 6 \hat{k} \). Now calculate the dot product and magnitude to find the distance. Quick Tip: For parallel lines, the shortest distance is calculated using the formula involving the dot product of the difference vector and the direction vector of the lines.