TS EAMCET 2024 Question Paper May 9 Shift 2: Download MPC Question Paper with Solutions PDF

SECTION-A
(Mathematics)

Question 1:

The domain of the real valued function: \[ f(x) \;=\; \sqrt[3]{\frac{x \,-\, 2}{2x^2 \,-\, 7x \,+\,5}} \;+\; \log\bigl(x^2 \,-\, x \,-\, 2\bigr). \]

• (1) \(\displaystyle (-\infty,\,-1)\;\cup\;\Bigl(2,\,\tfrac{5}{2}\Bigr)\;\cup\;\Bigl(\tfrac{5}{2},\,\infty\Bigr)\)
• (2) \(\displaystyle \mathbb{R}\setminus\Bigl\{1,\,\tfrac{5}{2}\Bigr\}\)
• (3) \(\displaystyle (-\infty,\,-1)\;\cup\;(2,\,\infty)\)
• (4) \(\displaystyle (-1,\,2)\)

\(f\) is a real valued function satisfying the relation \(f\bigl(3x + \tfrac{1}{2x}\bigr) \;=\; 9x^2 + \tfrac{1}{4x^2}\). If \(f\bigl(x + \tfrac{1}{x}\bigr) = 1\) then \(x =\) ?

• (1) \(\pm 2\)
• (2) \(\pm 1\)
• (3) \(\pm 3\)
• (4) \(\pm 6\)

\(\frac{1}{3.6} + \frac{1}{6.9} + \frac{1}{9.12} + \dots\) up to 9 terms \(=\)

• (1) \(\tfrac{10}{99}\)
• (2) \(\tfrac{11}{108}\)
• (3) \(\tfrac{1}{10}\)
• (4) \(\tfrac{1}{90}\)

If \(\alpha,\,\beta,\,\gamma\) are the roots of the equation

then \(2\alpha + 3\beta + 4\gamma =\)?

• (1) \(6\)
• (2) \(8\)
• (3) \(-6\)
• (4) \(-8\)

If

then \[ \sum_{1\le i\le 3 \atop 1\le j\le 3} a_{ij} \;=\; ? \]

• (1) \(\tfrac{2}{3}\)
• (2) \(\tfrac{1}{3}\)
• (3) \(1\)
• (4) \(17\)

If \(AX = D\) represents the system of linear equations \[ 3x - 4y + 7z + 6=0,\quad 5x + 2y - 4z + 9=0,\quad 8x - 6y - z + 5=0, \]
then AX = D ?

• (1) \(Rank(A) = Rank([A|D])= 1\)
• (2) \(Rank(A) = Rank([A|D])= 2\)
• (3) \(Rank(A) = Rank([A|D])= 3\)
• (4) \(Rank(A) \neq Rank([A|D])\)

If \((x,y,z)=(\alpha,\beta,\gamma)\) is the unique solution of the system of simultaneous linear equations \[ \begin{cases} 3x - 4y + 2z + 7 = 0,
2x + 3y - z = 10,
x - 2y - 3z = 3, \end{cases} \]
then \(\alpha = ?\)

• (1) \(3\)
• (2) \(-3\)
• (3) \(-1\)
• (4) \(1\)

If \[ \frac{(2 - i)\,x + (1 + i)}{2 + i} \;+\; \frac{(1 - 2i)\,y + (1 - i)}{1 + 2i} \;=\; 1 - 2i, \quad then\quad 2x + 4y =\;? \]

• (1) \(5\)
• (2) \(-2\)
• (3) \(1\)
• (4) \(-1\)

If \(z = 1 - \sqrt{3}\,i\), then \(z^3 - 3z^2 + 3z = \;?\)

• (1) \(0\)
• (2) \(1 + 3\sqrt{3}\,i\)
• (3) \(1\)
• (4) \(2 + 3\sqrt{3}\,i\)

The product of all the values of \(\bigl(\sqrt{3} - i\bigr)^{\tfrac{2}{5}}\) is \;?

• (1) \(2\,(\sqrt{3} - i)\)
• (2) \(2\,(\sqrt{3} + i)\)
• (3) \(2\,(1 - \sqrt{3}\,i)\)
• (4) \(2\,(1 + \sqrt{3}\,i)\)

The number of common roots among the 12^th and 30^th roots of unity is \;?

• (1) \(12\)
• (2) \(9\)
• (3) \(8\)
• (4) \(6\)

If \(\alpha\) is a root of the equation \[ \frac{x - 1}{\sqrt{2x^2 - 5x + 2}} \;=\; \frac{41}{60}, \quad and \quad -\tfrac{1}{2} < \alpha < 0, \textbf{\;then\;} \alpha =\; ? \]

• (1) \(-\tfrac{5}{31}\)
• (2) \(-\tfrac{7}{34}\)
• (3) \(-\tfrac{9}{37}\)
• (4) \(-\tfrac{11}{41}\)

If \(4+3x-7x^2\) attains its maximum value \(M\) at \(x=\alpha\) and \(5x^2-2x+1\) attains its minimum value at \(x=\beta\), then \[ \frac{28\,(M - \alpha)}{5\,(m + \beta)} =\,? \]
\textit{(Assume \(m\) is that minimum value of \(5x^2 -2x +1\) at \(x=\beta\))

• (1) \(28\)
• (2) \(23\)
• (3) \(5\)
• (4) \(1\)

If \(\alpha,\,\beta,\,\gamma\) are the roots of the equation \[ 2x^3 \;-\; 5x^2 \;+\; 4x \;-\; 3 \;=\; 0, \]
then \[ \sum \alpha\beta(\alpha+\beta) \;=\;? \]

• (1) \(8\)
• (2) \(4\)
• (3) \(2\)
• (4) \(\tfrac{1}{2}\)

If \(\alpha,\beta,\gamma,2,\varepsilon\) are the roots of the equation \[ x^5 \;+\;4x^4 \;-\;13x^3 \;-\;52x^2 \;+\;36x \;+\;144\;=\;0, \alpha<\beta<\gamma<2<\varepsilon, \]
then \[ \alpha \;+\;2\beta \;+\;3\gamma \;+\;5\,\varepsilon =\;? \]

• (1) \(-1\)
• (2) \(25\)
• (3) \(-36\)
• (4) \(48\)

Among the 4-digit numbers that can be formed using the digits \(\{1,2,3,4,5,6\}\) without repeating any digit, the number of such numbers which are divisible by 6 is \;?

• (1) \(60\)
• (2) \(66\)
• (3) \(52\)
• (4) \(57\)

If the number of circular permutations of 9 distinct things taken 5 at a time is \(n_1\), and the number of linear permutations of 8 distinct things taken 4 at a time is \(n_2\), then what is \(\frac{n_1}{n_2}\)?

• (1) \(\frac{5}{9}\)
• (2) \(2\)
• (3) \(\tfrac{1}{2}\)
• (4) \(\frac{9}{5}\)

The number of ways in which 4 different things can be distributed to 6 persons so that no person gets all the things is \;?

• (1) \(1292\)
• (2) \(1296\)
• (3) \(1290\)
• (4) \(4090\)

If the coefficients of three consecutive terms in the expansion of \((1 + x)^{23}\) are in arithmetic progression, then those terms are \;?

• (1) \(T_{10},\,T_{11},\,T_{12}\)
• (2) \(T_{8},\,T_{9},\,T_{10}\)
• (3) \(T_{13},\,T_{14},\,T_{15}\)
• (4) \(T_{14},\,T_{15},\,T_{16}\)

The numerically greatest term in the expansion of \((3x - 16y)^{15}\) when \(x = \tfrac{2}{3}\) and \(y = \tfrac{3}{2}\) is \;?

• (1) 13^th term
• (2) 14^th term
• (3) 15^th term
• (4) 16^th term

If \[ \frac{3x^4 - 2x^2 +1}{(x-2)^4} = A + \frac{B}{x-2} + \frac{C}{(x-2)^2} + \frac{D}{(x-2)^3} + \frac{E}{(x-2)^4}, \]
then \(2A + 3B - C - D + E =\;?\)

• (1) \(0\)
• (2) \(1\)
• (3) \(-11\)
• (4) \(-39\)

The maximum value of the function \[ f(x) = 3\sin^{12}x + 4\cos^{16}x \]
is \;?

• (1) \(4\)
• (2) \(5\)
• (3) \(6\)
• (4) \(7\)

If \(A + B + C = 2S\), then \[ \sin(S - A)\,\cos(S - B)\;-\;\sin(S - C)\,\cos S \;=\;? \]

• (1) \(\cos A\,\sin B\,\sin C\)
• (2) \(\sin A\,\cos B\,\cos C\)
• (3) \(\cos A\,\sin B\)
• (4) \(\sin A\,\cos B\)

If \(\cos x + \cos y = \tfrac{2}{3}\) and \(\sin x - \sin y = \tfrac{3}{4}\), then \[ \sin(x - y) \;+\; \cos(x - y) \;=\;? \]

• (1) \(\tfrac{161}{145}\)
• (2) \(\tfrac{127}{145}\)
• (3) \(\tfrac{1}{2}\)
• (4) \(\tfrac{8}{9}\)

The solution set of the equation \(\cos^2(2x) + \sin^2(3x) = 1\) is \;?

• (1) \(\bigl\{\,x \mid x = n\pi + \tfrac{\pi}{2},\,n \in \mathbb{Z}\bigr\}\)
• (2) \(\bigl\{\,x \mid x = 2n\pi \pm \tfrac{\pi}{4},\,n \in \mathbb{Z}\bigr\}\)
• (3) \(\bigl\{\,x \mid x = \tfrac{n\pi}{5},\,n \in \mathbb{Z}\bigr\}\)
• (4) \(\bigl\{\,x \mid x = n\pi + (-1)^n \tfrac{\pi}{6},\,n\in \mathbb{Z}\bigr\}\)

If \(2\,\tan^{-1}x = 3\,\sin^{-1}x\) and \(x \neq 0\), then \(8x^2 +1 =\;?\)

• (1) \(13\)
• (2) \(5\)
• (3) \(\sqrt{7}\)
• (4) \(\sqrt{17}\)

Match the functions in List--I with their corresponding properties in List--II:

• (1) A—II,  B—III,  C—IV,  D—V 
• (2) A—V, B—I, C—II, D—III 
• (3) A—IV,  B—II, C—I,  D—V 
• (4) A—IV, B—III, C—V, D—II 

In a triangle \(ABC\), if \(\tan\tfrac{A}{2} : \tan\tfrac{B}{2} : \tan\tfrac{C}{2} = 15 : 10 : 6\), then \(\frac{a}{b - c} = \,?\)

• (1) \(\tfrac{8}{3}\)
• (2) \(\tfrac{7}{3}\)
• (3) \(5\)
• (4) \(4\)

In a triangle \(ABC\), \(\displaystyle \frac{a(rr_1+r_2r_3)}{r_1-r+r_2r_3} =\;?\)

• (1) \(\sqrt{rr_1r_2r_3}\)
• (2) \(\frac{r_1 + r_2}{r_1 + r_3}\)
• (3) \(2(R + r)\)
• (4) \(\frac{p + \frac{r}{2R}}{\dots}\) [ truncated in the image ]

If \(\vec{a},\,\vec{b},\,\vec{c}\) are non-coplanar vectors. If the three points \[ \lambda \vec{a} - 2\vec{b} + \vec{c},\quad 2 \vec{a} + \lambda\vec{b} - 2\vec{c},\quad 4\vec{a} + 7\vec{b} - 8\vec{c} \]
are collinear, then \(\lambda = \,?\)

• (1) \(-1\)
• (2) \(-2\)
• (3) \(2\)
• (4) \(1\)

If \(\mathbf{i} + \mathbf{j},\; \mathbf{j} + \mathbf{k},\; \mathbf{k} + \mathbf{i},\; \mathbf{i} - \mathbf{j},\; \mathbf{j} - \mathbf{k}\) are the position vectors of the points \(A, B, C, D, E\) respectively, then the point of intersection of the line \(AB\) and the plane passing through \(C, D, E\) is:

• (1) \(\mathbf{i} + \mathbf{j} + \mathbf{k}\)
• (2) \(\tfrac{1}{2}\,\mathbf{i} \;+\;\,\mathbf{j} \;+\;\tfrac{1}{2}\,\mathbf{k}\)
• (3) \(\tfrac{1}{2}\bigl(\mathbf{i} + \mathbf{j} + \mathbf{k}\bigr)\)
• (4) \(\tfrac{1}{2}\,\mathbf{i} \;-\;\mathbf{j} \;+\;\tfrac{1}{2}\,\mathbf{k}\)

If \(\vec{a},\vec{b}\) are two vectors such that \(\lvert \vec{a}\rvert =3,\;\lvert \vec{b}\rvert =4,\;\lvert \vec{a}+\vec{b}\rvert =\sqrt{37},\;\lvert \vec{a}-\vec{b}\rvert = k,\) and the angle between \(\vec{a}\) and \(\vec{b}\) is \(\theta,\) then \(\frac{4}{13}\,(k \sin \theta)^2 =\,?\)

• (1) \(1\)
• (2) \(2\)
• (3) \(3\)
• (4) \(4\)

\(\vec{r}\) is a vector perpendicular to the plane determined by \(\vec{r_1}=2\mathbf{i}-\mathbf{j}\) and \(\vec{r_2}=\mathbf{j}+2\mathbf{k}\). If the magnitude of the projection of \(\vec{r}\) on the vector \(2\mathbf{i}+\mathbf{j}+2\mathbf{k}\) is 1, then \(\lvert \vec{r}\rvert =\,?\)

• (1) \(\sqrt{6}\)
• (2) \(3\sqrt{6}\)
• (3) \(\frac{2\sqrt{6}}{3}\)
• (4) \(\frac{3\sqrt{6}}{2}\)

If \(\vec{b} = \mathbf{i}-\mathbf{j} +2\mathbf{k},\;\vec{c} = \mathbf{i} +2\mathbf{j} -\mathbf{k}\) are two vectors and \(\vec{a}\) is a vector such that \(\cos\angle(\vec{a},\vec{b}\times \vec{c}) = \frac{2}{\sqrt{3}}\). If \(\vec{a}\) is a unit vector, then \(\lvert \vec{a}\times(\vec{b}\times \vec{c})\rvert =\,?\)

• (1) \(3\)
• (2) \(2\)
• (3) \(1\)
• (4) \(4\)

The variance of the following continuous frequency distribution is:

• (1) \(\frac{128}{7}\)
• (2) 15
• (3) 19
• (4) \(\frac{130}{7}\)

Among the 5 married couples, if the names of 5 men are matched with the names of their wives randomly, then the probability that no man is matched with the name of his own wife is \;?

• (1) \(\tfrac{9}{20}\)
• (2) \(\tfrac{1}{5}\)
• (3) \(\tfrac{11}{30}\)
• (4) \(\tfrac{17}{60}\)

If 3 dice are thrown, the probability of getting 10 as the sum of the three numbers on the top faces is \;?

• (1) \(\tfrac{1}{9}\)
• (2) \(\tfrac{7}{72}\)
• (3) \(\tfrac{5}{36}\)
• (4) \(\tfrac{1}{8}\)

Three similar urns \(A,B,C\) contain \(2\) red and \(3\) white balls; \(3\) red and \(2\) white balls; \(1\) red and \(4\) white balls, respectively. If a ball is selected at random from one of the urns is found to be red, then the probability that it is drawn from urn \(C\) is \;?

• (1) \(\tfrac{1}{6}\)
• (2) \(\tfrac{1}{3}\)
• (3) \(\tfrac{1}{2}\)
• (4) \(\tfrac{2}{9}\)

If a random variable \(X\) has the following probability distribution, then the mean of \(X\) is:

• (1) \(\frac{26}{9}\)
• (2) \(\frac{22}{9}\)
• (3) \(\frac{24}{9}\)
• (4) \(\frac{28}{9}\)

A fair coin is tossed a fixed number of times. If the probability of getting 5 heads is equal to the probability of getting 4 heads, then the probability of getting 6 heads is:

• (1) \(\frac{7}{64}\)
• (2) \(\frac{9}{32}\)
• (3) \(\frac{21}{128}\)
• (4) \(\frac{35}{256}\)

If the ratio of the distances of a variable point \(P\) from the point \((1,1)\) and the line \(x - y + 2 = 0\) is \(1/\sqrt{2}\), then the equation of the locus of \(P\) is:

• (1) \(x^2 + 2xy + y^2 - 8x = 0\)
• (2) \(3x^2 + 2xy + 3y^2 - 12x - 4y + 4 = 0\)
• (3) \(x^2 + 2xy + y^2 - 12x + 4y + 4 = 0\)
• (4) \(x^2 + 2xy + y^2 - 8x + 8y = 0\)

If the origin is shifted to the point \(\left(\frac{3}{2}, -2\right)\) by the translation of axes, then the transformed equation of \(2x^2 + 4xy + y^2 + 2x - 2y + 1 = 0\) is:

• (1) \(4x^2 + 8xy + 2y^2 - 16 = 0\)
• (2) \(2x^2 - 4xy + y^2 = 0\)
• (3) \(4x^2 + 8xy + 2y^2 + 9 = 0\)
• (4) \(2x^2 - 4xy + y^2 + 16 = 0\)

If the line \(L = x \cos \alpha + y \sin \alpha - p = 0\) represents a line perpendicular to the line \(x + y + 1 = 0\) and \(p\) is positive, \(a\) lies in the fourth quadrant and perpendicular distance from \(\left(\sqrt{2}, \sqrt{2}\right)\) to the line \(L = 0\) is 5 units, then find \(p\):

• (1) 5
• (2) \(\frac{5}{2}\)
• (3) 10
• (4) \(\frac{15}{2}\)

If \(A(3, 2, -1)\), \(B(4, 1, 0)\), and \(C(2, 1, 4)\) are the vertices of a triangle and \((\frac{2}{3}, \frac{5}{3})\) is its orthocenter, then the third vertex of that triangle is \((m, n)\) where \(m + n =\):

• (1) \(-4\)
• (2) \(-2\)
• (3) \(5\)
• (4) \(8\)

The lengths of two equal sides of an isosceles triangle are given by \(L_1 = 2x + y - 3 = 0\) and \(L_2 = ax + by + c = 0\). If \(L_3 = x + 2y + 1 = 0\) is the third side of this triangle and \((5, 1)\) is a point on \(L_2\), then \(b^2/|ac|\) is:

• (1) \(\frac{121}{2}\)
• (2) \(\frac{49}{52}\)
• (3) \(\frac{81}{49}\)
• (4) \(\frac{25}{4}\)

The slope of one of the pair of lines \(2x^2 + hxy + 6y^2 = 0\) is three times the slope of the other line, \(h = ?\)

• (1) \(16\)
• (2) \(9\)
• (3) \(18\)
• (4) \(8\)

If \(P\left( \frac{\pi}{4} \right)\), \(Q\left( \frac{\pi}{3} \right)\) are two points on the circle \(x^2 + y^2 - 2x - 2y - 1 = 0\), then the slope of the tangent to this circle which is parallel to the chord \(PQ\) is:

• (1) \(2 + \sqrt{2} - \sqrt{3} - \sqrt{6}\)
• (2) \(2 + \sqrt{2} + \sqrt{3} + \sqrt{6}\)
• (3) \(\sqrt{2} - \sqrt{3}\)
• (4) \(2 + \sqrt{2}\)

The power of a point \( (2,0) \) with respect to a circle \( S \) is \(-4\) and the length of the tangent drawn from the point \( (1,1) \) to \( S \) is \( 2 \). If the circle \( S \) passes through the point \( (-1,-1) \), then the radius of the circle \( S \) is:

• (1) \( 2 \)
• (2) \( \sqrt{13} \)
• (3) \( 3 \)
• (4) \( \sqrt{10} \)

The pole of the line \(x - 5y - 7 = 0\) with respect to the circle \(S \equiv x^2 + y^2 - 2x - 2y + 1 = 0\) is \(P(a,b)\). If \(C\) is the centre of the circle \(S = 0\) then \(PC =\):

• (1) \( \sqrt{a + b - 1} \)
• (2) \( \sqrt{a^2 + b^2 - 1} \)
• (3) \( \sqrt{a^3 + b^3 - 1} \)
• (4) \( 3ab \)

The equation of the pair of transverse common tangents drawn to the circles \( x^2 + y^2 + 2x + 2y + 1 = 0 \) and \( x^2 + y^2 - 2x - 2y + 1 = 0 \) is:

• (1) \(x^2 - y^2 = 0\)
• (2) \(xy = 0\)
• (3) \(x^2 - y^2 + 2x + 1 = 0\)
• (4) \(x^2 - y^2 - 2y - 1 = 0\)

If a circle passing through the point \((1,1)\) cuts the circles \(x^2 + y^2 + 4x - 5 = 0\) and \(x^2 + y^2 - 4x + 3 = 0\) orthogonally, then the center of that circle is:

• (1) \(\frac{3}{4}, \frac{5}{4}\)
• (2) \(\frac{3}{2}, \frac{5}{2}\)
• (3) \(\frac{-3}{2}, \frac{5}{2}\)
• (4) \(\frac{-3}{4}, \frac{-5}{2}\)

Length of the common chord of the circles \(x^2 + y^2 - 6x + 5 = 0\) and \(x^2 + y^2 + 4y - 5 = 0\) is:

• (1) \(\sqrt{13}\)
• (2) \(\frac{12}{\sqrt{13}}\)
• (3) \(\frac{6}{\sqrt{13}}\)
• (4) \(2\sqrt{13}\)

P and Q are the extremities of a focal chord of the parabola \(y^2 = 4ax\). If \(P = (9, 9)\) and \(Q = (p, q)\), then \(p - q =\):

• (1) \(\frac{27}{16}\)
• (2) \(\frac{63}{16}\)
• (3) \(\frac{45}{16}\)
• (4) \(\frac{81}{16}\)

The number of normals that can be drawn through the point \((9,6)\) to the parabola \(y^2 = 4x\) is:

• (1) \(0\)
• (2) \(1\)
• (3) \(2\)
• (4) \(3\)

The equations of the directrices of the ellipse \(9x^2 + 4y^2 - 18x - 16y - 11 = 0\) are:

• (1) \(y = 2 \pm \frac{9}{\sqrt{5}}\)
• (2) \(x = 1 \pm \frac{6}{\sqrt{5}}\)
• (3) \(x = 2 \pm \frac{9}{\sqrt{5}}\)
• (4) \(y = 1 \pm \frac{6}{\sqrt{5}}\)

The end of a latus rectum of the ellipse \(3x^2 + 4y^2 = 12\) is lying in the third quadrant. If the normal drawn at \(L_1\) to this ellipse intersects the ellipse again at the point \(P(a,b)\), then find the value of \(a\):

• (1) \(\frac{63}{38}\)
• (2) \(\frac{11}{19}\)
• (3) \(\frac{-11}{19}\)
• (4) \(\frac{-63}{38}\)

The point \((p, q)\) is the point of intersection of a latus rectum and an asymptote of the hyperbola \(9x^2 - 16y^2 = 144\). If \(p > 0\) and \(q > 0\), then \(q = \ldots\)

• (1) \(\frac{9}{4}\)
• (2) \(\frac{7}{4}\)
• (3) \(\frac{15}{4}\)
• (4) \(\frac{13}{4}\)

A, B, C are the vertices of a triangle ABC. If the bisector of \( \angle BAC \) intersects the side BC at D\((p,q,r)\), then \( \sqrt{2p+q+r} = ? \)

• (1) \( 1 \)
• (2) \( 2 \)
• (3) \( 3 \)
• (4) \( 4 \)

If the direction ratios of two lines are \( (3,0,2) \) and \( (0,2,k) \), and \( \theta \) is the angle between them, and if \( |\cos \theta| = \frac{6}{13} \), then \( k = \)

• (1) \( \pm 2 \)
• (2) \( \pm 3 \)
• (3) \( \pm 5 \)
• (4) \( \pm 7 \)

A plane \( (\pi) \) passing through the point \( (1,2,-3) \) is perpendicular to the planes \( x + y - z + 4 = 0 \) and \( 2x - y + z + 1 = 0 \). If the equation of the plane \( (\pi) \) is \( ax + by + cz + 1 = 0 \), then \( a^2 + b^2 + c^2 \) is equal to:

• (1) \( 4 \)
• (2) \( 3 \)
• (3) \( 2 \)
• (4) \( 1 \)

Evaluate the limit: \[ \lim_{\theta \to \frac{\pi}{2}} \frac{8\tan^4\theta + 4\tan^2\theta + 5}{(3 - 2\tan\theta)^4} \]

• (1) \( -\frac{1}{2} \)
• (2) \( \frac{1}{2} \)
• (3) \( -4 \)
• (4) \( 1 \)

Define \( f: \mathbb{R} \to \mathbb{R} \) by \[ f(x) = \begin{cases} \frac{1 - \cos 4x}{x^2}, & x < 0
a, & x = 0
\frac{\sqrt{x}}{\sqrt{16 + \sqrt{x}} - 4}, & x > 0 \end{cases} \]
Find the value of \( a \) such that \( f \) is continuous at \( x = 0 \).

• (1) \( 8 \)
• (2) \( 4 \)
• (3) \( 2 \)
• (4) \( 1 \)

If \( y = \frac{\tan x \cos^{-1}x}{\sqrt{1 - x^2}} \), then the value of \( \frac{dy}{dx} \) when \( x = 0 \) is:

• (1) \( 0 \)
• (2) \( \frac{\pi}{2} \)
• (3) \( 1 \)
• (4) \( \frac{\pi}{6} \)

If \( y (\cos x)^{\sin x} = (\sin x)^{\sin x} \), then the value of \( \frac{dy}{dx} \) at \( x = \frac{\pi}{4} \) is:

• (1) \( 0 \)
• (2) \( 1 \)
• (3) \( \sqrt{2} \)
• (4) \( \frac{\sqrt{3}}{2} \)

If \( x = \cos 2t + \log (\tan t) \) and \( y = 2t + \cot 2t \), then \( \frac{dy}{dx} \) is:

• (1) \( \tan 2t \)
• (2) \( -\csc 2t \)
• (3) \( -\cot 2t \)
• (4) \( \sec 2t \)

If \( y = 44x^{45} + 45x^{44} \), then \( y'' \) is:

• (1) \( \frac{1980y}{x^2} \)
• (2) \( \frac{2020x^2}{y} \)
• (3) \( \frac{2024y}{x^2} \)
• (4) \( \frac{1990x^2}{y} \)

The approximate value of \( \sqrt[3]{730} \) obtained by the application of derivatives is:

• (1) \( 9.0041 \)
• (2) \( 9.01 \)
• (3) \( 9.006 \)
• (4) \( 9.05 \)

If \( \theta \) is the acute angle between the curves \( y^2 = x \) and \( x^2 + y^2 = 2 \), then \( \tan \theta \) is:

• (1) \( 1 \)
• (2) \( 3 \)
• (3) \( 2 \)
• (4) \( 4 \)

The vertical angle of a right circular cone is \( 60^\circ \). If water is being poured into the cone at the rate of \( \frac{1}{\sqrt{3}} \) m\(^3\)/min, then the rate (m/min) at which the radius of the water level is increasing when the height of the water level is 3m is:

• (1) \( \frac{1}{3\sqrt{3}\pi} \)
• (2) \( \frac{1}{9\sqrt{3}\pi} \)
• (3) \( \frac{1}{9\pi} \)
• (4) \( \frac{1}{3\pi} \)

A right circular cone is inscribed in a sphere of radius 3 units. If the volume of the cone is maximum, then the semi-vertical angle of the cone is:

• (1) \( \frac{\pi}{4} \)
• (2) \( \frac{\pi}{6} \)
• (3) \( \tan^{-1} (\sqrt{2}) \)
• (4) \( \tan^{-1} \left(\frac{1}{\sqrt{2}}\right) \)

If \( f(x) = kx^3 - 3x^2 - 12x + 8 \) is strictly decreasing for all \( x \in \mathbb{R} \), then:

• (1) \( k < -\frac{1}{4} \)
• (2) \( k > -\frac{1}{4} \)
• (3) \( k > \frac{1}{4} \)
• (4) \( k < \frac{1}{4} \)

Evaluate the integral: \[ \int e^{-2x} \left( \tan 2x - 2\sec^2 2x \tan 2x \right) dx. \]

• (1) \( e^{-2x} \tan 2x + c \)
• (2) \( -\frac{e^{-2x}}{2} \left[ \sec^2 2x + \tan 2x \right] + c \)
• (3) \( -\frac{e^{-2x}}{2} \left[ \tan 2x - \sec^2 2x \right] + c \)
• (4) \( -e^{-2x} \sec^2 2x + c \)

If \( \int x^3 \sin 3x \,dx = f(x) \cos 3x + g(x) \sin 3x + c \), then evaluate \( 27(f(x) + xg(x)) \):

• (1) \( 18x^3 + 4x \)
• (2) \( 8x \)
• (3) \( 4x \)
• (4) \( 18x^3 + 8x \)

Evaluate the integral: \[ \int \frac{dx}{9\cos^2 2x + 16\sin^2 2x} \]

• (1) \( \frac{1}{25} \tan^{-1} \left( \frac{3}{4} \sec^2 2x \right) + c \)
• (2) \( \frac{1}{25} \tan^{-1} \left( \frac{4}{3} \sec^2 2x \right) + c \)
• (3) \( \frac{1}{24} \tan^{-1} \left( \frac{3}{4} \tan 2x \right) + c \)
• (4) \( \frac{1}{24} \tan^{-1} \left( \frac{4}{3} \tan 2x \right) + c \)

Evaluate the integral: \[ \int \frac{2\cos 3x - 3\sin 3x}{\cos 3x + 2\sin 3x} dx. \]

• (1) \( \frac{7}{15} \log |\cos 3x + 2\sin 3x| - \frac{4}{5} x + c \)
• (2) \( -\frac{4}{5} \log |\cos 3x + 2\sin 3x| + \frac{7x}{5} + c \)
• (3) \( \frac{7}{5} \log |\cos 3x + 2\sin 3x| - \frac{4}{5} x + c \)
• (4) \( -\frac{8}{15} \log |\cos 3x + 2\sin 3x| + \frac{x}{5} + c \)

Evaluate the definite integral: \[ \int_{\frac{-\pi}{6}}^{\frac{-3\pi}{4}} \log (\sin (4x + 3)) dx. \]

• (1) \( -\frac{\pi}{2} \log 2 \)
• (2) \( -\frac{\pi}{8} \log 2 \)
• (3) \( -\frac{\pi}{14} \log 2 \)
• (4) \( -\frac{\pi}{28} \log 2 \)

Evaluate the integral: \[ \int_0^{16} \frac{\sqrt{x}}{1 + \sqrt{x}} dx. \]

• (1) \( 8 + 2\log 2 \)
• (2) \( 8 + \log 2 \)
• (3) \( 8 + 2\log 5 \)
• (4) \( 8 + \log 5 \)

Evaluate the integral: \[ \int_0^{32\pi} \sqrt{1 - \cos 4x} \, dx. \]

• (1) \( 16\sqrt{2} \)
• (2) \( 32\sqrt{2} \)
• (3) \( 128\sqrt{2} \)
• (4) \( 64\sqrt{2} \)

The general solution of the differential equation \[ (9x - 3y + 5) dy = (3x - y + 1) dx. \]

• (1) \( 4x - 3y - \log |12x - 4y + 7| = c \)
• (2) \( 4x - 12y - \log |12x - 4y + 7| = c \)
• (3) \( 4x - 12y + \log |6x - 2y + 7| = c \)
• (4) \( 4x - 6y + \log |12x - 4y + 7| = c \)

The general solution of the differential equation \[ \frac{dy}{dx} = \frac{2y^2 + 1}{2y^3 - 4xy + y}. \]

• (1) \( 4xy^2 + 2x = y^4 + y^2 + c \)
• (2) \( 2xy^2 + x = y^4 - y^2 + c \)
• (3) \( 4xy^2 - 2x = y^4 + y^2 + c \)
• (4) \( 4xy^2 + 2x = y^4 - y^2 + c \)

SECTION-B
(Physics)

Question 81:

The related effort to derive the properties of a bigger, more complex system from the properties and interactions of its constituent simpler parts is:

• (1) Unification
• (2) Reductionism
• (3) Classical approach
• (4) Quantum approach

The error in the measurement of resistance, when \( (10 \pm 0.5) \) A current passing through it produces a potential difference of \( (100 \pm 6) \) V across it, is:

• (1) \( 1% \)
• (2) \( 5.5% \)
• (3) \( 6.5% \)
• (4) \( 11% \)

A stone is thrown vertically up from the top end of a window of height 1.8 m with a velocity of 8 m/s\(^1\). The time taken by the stone to cross the window during its downward journey is:

(Acceleration due to gravity \( g = 10 \) ms\(^{-2}\))

• (1) \( 0.8 \) s
• (2) \( 1.6 \) s
• (3) \( 1.0 \) s
• (4) \( 0.2 \) s

A cannon placed on a cliff at a height of 375 m fires a cannonball with a velocity of 100 m/s\(^{-1}\) at an angle of 30° above the horizontal. The horizontal distance between the cannon and the target is:

(Acceleration due to gravity \( g = 10 \) ms\(^{-2}\))

• (1) \( 750\sqrt{3} \) m
• (2) \( 500\sqrt{3} \) m
• (3) \( 250\sqrt{3} \) m
• (4) \( 750 \) m

A 20-ton truck is traveling along a curved path of radius 240 m. If the center of gravity of the truck above the ground is 2 m and the distance between its wheels is 1.5 m, the maximum speed of the truck with which it can travel without toppling over is:

(Acceleration due to gravity \( g = 10 \) ms\(^{-2}\))

• (1) \( 43 \) ms\(^{-1}\)
• (2) \( 40 \) ms\(^{-1}\)
• (3) \( 38 \) ms\(^{-1}\)
• (4) \( 30 \) ms\(^{-1}\)

A block of mass \( m \) with an initial kinetic energy \( E \) moves up an inclined plane of inclination \( \theta \). If \( \mu \) is the coefficient of friction between the plane and the body, the work done against friction before coming to rest is:

• (1) \( \mu E \cos \theta \)
• (2) \( \frac{\mu E \cos \theta}{\sin \theta - \mu \cos \theta} \)
• (3) \( \frac{E \mu \cos \theta}{\cos \theta + \sin \theta} \)
• (4) \( \frac{\mu E \cos \theta}{\sin \theta + \mu \cos \theta} \)

A man of mass 80 kg goes to the market on a scooter of mass 100 kg with certain speed. On applying brakes, the stopping distance is \( S_1 \). The man returns home on the same scooter, with the same speed, with a 60 kg bag of rice. If \( S_2 \) is the new stopping distance when the brakes are applied with the same force, then:

• (1) \( 7S_1 = 4S_2 \)
• (2) \( 2S_1 = S_2 \)
• (3) \( 3S_1 = 4S_2 \)
• (4) \( 4S_1 = 3S_2 \)

A thin uniform wire of mass \( m \) and linear mass density \( \rho \) is bent in the form of a circular loop. The moment of inertia of the loop about its diameter is:

• (1) \( \frac{m^2}{4\pi^2 p^2} \)
• (2) \( \frac{m^3}{4p^2} \)
• (3) \( \frac{m^3}{8\pi^2 p^2} \)
• (4) \( \frac{m^3}{8p} \)

Three particles A, B, and C of masses \( m \), \( 2m \), and \( 3m \) are moving towards north, south, and east, respectively. If the velocities of the particles A, B, and C are \( 6 \) m/s, \( 12 \) m/s, and \( 8 \) m/s respectively, then the velocity of the center of mass of the system of particles is:

• (1) \( 7 \) m/s
• (2) \( 5 \) m/s
• (3) \( 26 \) m/s
• (4) \( 8 \) m/s

A particle of mass 4 mg is executing simple harmonic motion along x-axis with an angular frequency of 40 rad/s. If the potential energy of the particle is \( V(x) = a + bx^2 \), where \( V(x) \) is in joule and \( x \) is in meter, then the value of \( b \) is:

• (1) \( 800 \times 10^{-6} \) J/m\(^2\)
• (2) \( 1600 \times 10^{-6} \) J/m\(^2\)
• (3) \( 3200 \times 10^{-6} \) J/m\(^2\)
• (4) \( 6400 \times 10^{-6} \) J/m\(^2\)

The ratio of the accelerations due to gravity at heights 1280 km and 3200 km above the surface of the earth is:
(Radius of the earth = 6400 km)

• (1) \( 25:16 \)
• (2) \( 5:2 \)
• (3) \( 1:1 \)
• (4) \( 25:4 \)

If the length of a string is \(P\) when the tension in it is 6 N and its length is \(Q\) when the tension in it is 8 N, then the original length of the string is:

• (1) \( 3P + 4Q \)
• (2) \( 3P - 4Q \)
• (3) \( 4P + 3Q \)
• (4) \( 4P - 3Q \)

The excess pressure inside a soap bubble of radius 0.5 cm is balanced by the pressure due to an oil column of height 4 mm. If the density of the oil is 900 kg m\(^-3\), then the surface tension of the soap solution is:

• (1) \(9 \times 10^{-2} \, Nm^{-1}\)
• (2) \(2.25 \times 10^{-2} \, Nm^{-1}\)
• (3) \(4.5 \times 10^{-2} \, Nm^{-1}\)
• (4) \(7 \times 10^{-2} \, Nm^{-1}\)

Water flows through a horizontal pipe of variable cross-section at the rate of 12\(\pi\) litres per minute. The velocity of the water at the point where the diameter of the pipe becomes 2 cm is:

• (1) \(6 \, ms^{-1}\)
• (2) \(8 \, ms^{-1}\)
• (3) \(4 \, ms^{-1}\)
• (4) \(2 \, ms^{-1}\)

When 54 g of ice at \(-20^\circ C\) is mixed with 25 g of steam at \(100^\circ C\), then the final mixture at thermal equilibrium contains:

• (1) 20 g of water at 100°C
• (2) 100°C water and 20 g of steam
• (3) 73 g of water at 100°C and 6 g of steam at 100°C
• (4) 8 g of steam at 100°C and 12 g of water at 0°C

A solid sphere at a temperature \( T \) K is cut into two hemispheres. The ratio of energies radiated by one hemisphere to the whole sphere per second is:

• (1) \( 1:1 \)
• (2) \( 1:2 \)
• (3) \( 3:4 \)
• (4) \( 1:4 \)

If \( dQ, dU, dW \) are heat energy absorbed, change in internal energy, and external work done respectively by a diatomic gas at constant pressure, then \( dW : dU : dQ \) is:

• (1) \( 5:3:2 \)
• (2) \( 7:5:2 \)
• (3) \( 4:3:1 \)
• (4) \( 2:5:7 \)

If the temperature of a gas is increased from \( 27^\circ C \) to \( 159^\circ C \), the increase in the rms speed of the gas molecules is:

• (1) \( 142% \)
• (2) \( 71% \)
• (3) \( 80% \)
• (4) \( 20% \)

A boy standing on a platform observes the frequency of a train horn as it passes by. The change in the frequency noticed as the train approaches and recedes from him with a velocity of 108 km/h (speed of sound in air = 330 m/s) is:

• (1) \( 18.33% \)
• (2) \( 16.67% \)
• (3) \( 21.27% \)
• (4) \( 15.23% \)

If three sources of sound of frequencies \( (n-1), n, (n+1) \) are vibrated together, the number of beats produced and heard per second respectively are:

• (1) 4 and 2
• (2) 4 and 4
• (3) 2 and 2
• (4) 2 and 4

A small-angled prism is made of a material of refractive index \( \frac{3}{2} \). The ratio of the angles of minimum deviations when the prism is placed in air and in water of refractive index \( \frac{4}{3} \) is:

• (1) \( 4:1 \)
• (2) \( 3:4 \)
• (3) \( 2:3 \)
• (4) \( 1:3 \)

If you are using eyeglasses of power \( 2D \), your near point is:

• (1) \( 25 \) cm
• (2) \( 50 \) cm
• (3) \( 43 \) cm
• (4) \( 32 \) cm

A conductor carrying current is placed in a uniform magnetic field. The force experienced by the conductor is maximum when the angle between the conductor and the magnetic field is:

• (1) \( 0^\circ \)
• (2) \( 30^\circ \)
• (3) \( 45^\circ \)
• (4) \( 90^\circ \)

Two point charges of magnitudes \( -8 \mu C \) and \( +32 \mu C \) are separated by a distance of 15 cm in air. The position of the point from the \( -8 \mu C \) charge at which the resultant electric field becomes zero is:

• (1) \( 15 \) cm
• (2) \( 30 \) cm
• (3) \( 7.5 \) cm
• (4) \( 5 \) cm

If half of the space between the plates of a parallel plate capacitor is filled with a medium of dielectric constant 4, the capacitance is \( C_1 \). If one-third of the space between the plates of the capacitor is filled with the medium of dielectric constant 4, the capacitance is \( C_2 \). If in both cases, the dielectric is placed parallel to the plates of the capacitor, then \( C_1 : C_2 \) is:

• (1) \( 2:3 \)
• (2) \( 4:3 \)
• (3) \( 6:5 \)
• (4) \( 7:5 \)

The potential difference between the ends of a straight conductor of length 20 cm is 16 V. If the drift speed of the electrons is \( 2.4 \times 10^{-4} \) m/s, the electron mobility in \( m^2 V^{-1} s^{-1} \) is:

• (1) \( 3.6 \times 10^{-6} \)
• (2) \( 2.4 \times 10^{-6} \)
• (3) \( 2 \times 10^{-6} \)
• (4) \( 3 \times 10^{-6} \)

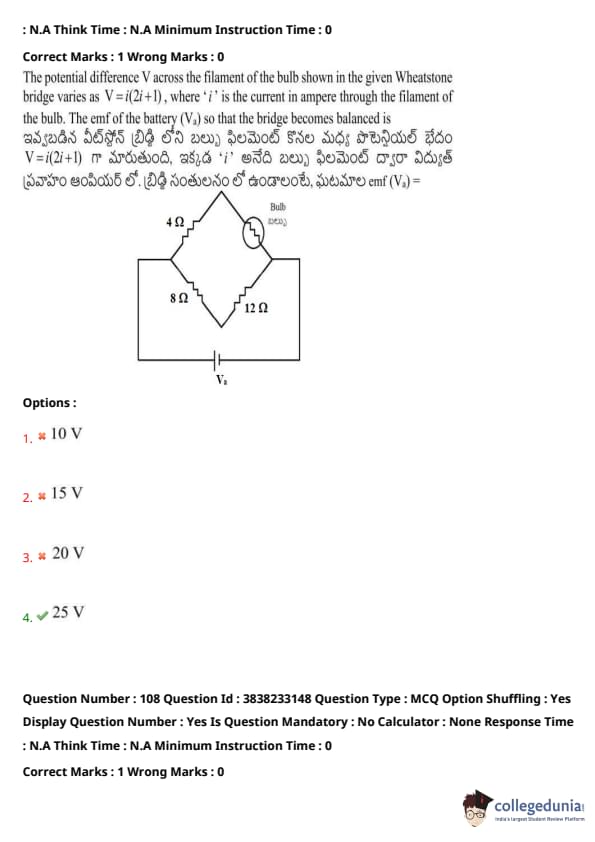
The potential difference \( V \) across the filament of the bulb shown in the given Wheatstone bridge varies as \( V = i(2i + 1) \), where \( i \) is the current in ampere through the filament of the bulb. The emf of the battery (\( V_a \)) so that the bridge becomes balanced is:

• (1) \( 10 \) V
• (2) \( 15 \) V
• (3) \( 20 \) V
• (4) \( 25 \) V

Two points A and B on the axis of a circular current loop are at distances of 4 cm and \( 3\sqrt{3} \) cm from the center of the loop. If the ratio of the induced magnetic fields at points A and B is 216:125, the radius of the loop is:

• (1) \( 3 \) cm
• (2) \( 4 \) cm
• (3) \( 5 \) cm
• (4) \( 6 \) cm

Two charged particles A and B of masses \( m \) and \( 2m \), charges \( 2q \) and \( 3q \) respectively, are moving with the same velocity into a uniform magnetic field such that both particles make the same angle \( \theta (<90^\circ) \) with the direction of the magnetic field. Then the ratio of the pitches of the helical paths of the particles A and B is:

• (1) \( 4:3 \)
• (2) \( 3:2 \)
• (3) \( 3:4 \)
• (4) \( 2:3 \)

If a bar magnet of moment \( 10^{-4} \) Am\(^2\) is kept in a uniform magnetic field of \( 12 \times 10^{-3} \) T such that it makes an angle of \( 30^\circ \) with the direction of the magnetic field, then the torque acting on the magnet is:

• (1) \( 6 \times 10^{-7} \) Nm
• (2) \( 6 \times 10^{-5} \) Nm
• (3) \( 12 \times 10^{-7} \) Nm
• (4) \( 12 \times 10^{-5} \) Nm

A train with an axle of length 1.66 m is moving towards north with a speed of 90 km/h. If the vertical component of the earth’s magnetic field is \( 0.2 \times 10^{-4} \) T, the emf induced across the ends of the axle is:

• (1) \( 16.6 \) mV
• (2) \( 1.66 \) mV
• (3) \( 0.83 \) mV
• (4) \( 8.3 \) mV

The natural frequency of an LC circuit is 120 kHz. When the capacitor in the circuit is totally filled with a dielectric material, the natural frequency of the circuit decreases by 20 kHz. The dielectric constant of the material is:

• (1) \( 3.33 \)
• (2) \( 1.44 \)
• (3) \( 2.12 \)
• (4) \( 1.91 \)

A plane electromagnetic wave of electric and magnetic fields \( E_0 \) and \( B_0 \) respectively incidents on a surface. If the total energy transferred to the surface in a time of \( t \) is \( U \), then the magnitude of the total momentum delivered to the surface for complete absorption is:

• (1) \( \frac{U E_0}{B_0} \)
• (2) \( \frac{U B_0}{E_0} \)
• (3) \( \frac{U}{E_0 B_0} \)
• (4) \( \frac{U B_0}{E_0^2} \)

If the de Broglie wavelength of a neutron at a temperature of 77°C is \( \lambda \), then the de Broglie wavelength of the neutron at a temperature of 1127°C is:

• (1) \( \frac{\lambda}{2} \)
• (2) \( \frac{\lambda}{3} \)
• (3) \( \frac{\lambda}{4} \)
• (4) \( \frac{\lambda}{9} \)

The ratio of the wavelengths of radiation emitted when an electron in the hydrogen atom jumps from the 4th orbit to the 2nd orbit and from the 3rd orbit to the 2nd orbit is:

• (1) \( 27:25 \)
• (2) \( 20:25 \)
• (3) \( 20:27 \)
• (4) \( 25:27 \)

The half-lives of two radioactive materials A and B are respectively \( T \) and \( 2T \). If the ratio of the initial masses of the materials A and B is 8:1, then the time after which the ratio of the masses of the materials A and B becomes 4:1 is:

• (1) \( 2T \)
• (2) \( T \)
• (3) \( 4T \)
• (4) \( 8T \)

The energy released by the fission of one uranium nucleus is 200 MeV. The number of fissions per second required to produce 128 W power is:

• (1) \( 6 \times 10^{12} \)
• (2) \( 8 \times 10^{12} \)
• (3) \( 2 \times 10^{12} \)
• (4) \( 4 \times 10^{12} \)

A zener diode of zener voltage 30 V is connected in a circuit as shown in the figure. The maximum current through the zener diode is:

• (1) \( 5 \) mA
• (2) \( 14 \) mA
• (3) \( 9 \) mA
• (4) \( 7 \) mA

Two logic gates are connected as shown in the figure. If the inputs are \( A = 1 \) and \( B = 0 \), then the values of \( y_1 \) and \( y_2 \) respectively are:

• (1) \( 1, 1 \)
• (2) \( 1, 0 \)
• (3) \( 0, 1 \)
• (4) \( 0, 0 \)

A message signal of peak voltage 12 V is used to amplitude modulate a carrier signal of frequency 1.2 MHz. The amplitude of the side bands is:

• (1) \( 12 \) V
• (2) \( 3 \) V
• (3) \( 6 \) V
• (4) \( 8 \) V

SECTION-C
(Chemistry)

Question 121:

The kinetic energy of electrons emitted, when radiation of frequency \( 1.0 \times 10^{15} \) Hz hits a metal, is \( 2 \times 10^{-19} \) J. What is the threshold frequency of the metal (in Hz)? (\( h = 6.6 \times 10^{-34} \) Js)

• (1) \( 3.5 \times 10^{15} \)
• (2) \( 3.3 \times 10^{14} \)
• (3) \( 6.97 \times 10^{15} \)
• (4) \( 6.97 \times 10^{14} \)

In which of the following species, the ratio of s-electrons to p-electrons is the same?

• (1) \( K^+, Cr^{3+} \)
• (2) \( Zn, Fe^{2+} \)
• (3) \( Zn, Cr^{3+} \)
• (4) \( Na^+, K^+ \)

Identify the pair of elements in which the difference in atomic radii is maximum.

• (1) \( C, N \)
• (2) \( O, F \)
• (3) \( P, S \)
• (4) \( Li, Be \)

Match the following elements with their respective blocks in the periodic table:

• (1) A - II; B - III; C - IV; D - I
• (2) A - III; B - II; C - I; D - IV
• (3) A - III; B - IV; C - II; D - I
• (4) A - II; B - I; C - IV; D - III

Identify the pair in which the difference in bond order value is maximum.

• (1) \( O_2^-, O_2^+ \)
• (2) \( O_2^{2-}, O_2^{2+} \)
• (3) \( O_2, O_2^{2+} \)
• (4) \( O_2^+, O_2^{2+} \)

The pair of molecules/ions with same geometry but central atoms in different states of hybridization is:

• (1) \( SnCl_2, H_2O \)
• (2) \( SF_4, XeF_4 \)
• (3) \( NH_4^+, CO_3^{2-} \)
• (4) \( PF_5, BrF_5 \)

If the density of a mixture of nitrogen and oxygen gases at 400 K and 1 atm pressure is 0.920 g L\(^{-1}\), what is the mole fraction of nitrogen in the mixture?

• (1) \( 0.456 \)
• (2) \( 0.554 \)
• (3) \( 0.432 \)
• (4) \( 0.568 \)

The incorrect rule regarding the determination of significant figures is:

• (1) Zeros preceding to first non-zero digit are not significant.
• (2) Zeros between two non-zero digits are not significant.
• (3) Zeros at the right end of the number are significant if they are on the right side of decimal point.
• (4) All non-zero digits are significant.

At 61 K, one mole of an ideal gas of 1.0 L volume expands isothermally and reversibly to a final volume of 10.0 L. What is the work done in the expansion?

• (1) \( -11.52 \) L atm
• (2) \( -23.04 \) L atm
• (3) \( -46.08 \) L atm
• (4) \( -5.76 \) L atm

At T(K), \( K_c \) for the dissociation of \( PCl_5 \) is \( 2 \times 10^{-2} \) mol L\(^{-1}\). The number of moles of \( PCl_5 \) that must be taken in 1.0 L flask at the same temperature to get 0.2 mol of chlorine at equilibrium is

• (1) \( 2.2 \)
• (2) \( 1.1 \)
• (3) \( 1.8 \)
• (4) \( 4.4 \)

The dihedral angles in gaseous and solid phases of H\(_2\)O\(_2\) molecule respectively are

• (1) \( 90.2^\circ, 111.5^\circ \)
• (2) \( 111.5^\circ, 90.2^\circ \)
• (3) \( 101.9^\circ, 94.8^\circ \)
• (4) \( 94.8^\circ, 101.9^\circ \)

Identify the compound which gives CO\(_2\) more readily on heating.

• (1) \( CaCO_3 \)
• (2) \( NaHCO_3 \)
• (3) \( Na_2CO_3 \)
• (4) \( Li_2CO_3 \)

The major components of cement are:

• (1) \( SiO_2, Al_2O_3 \)
• (2) \( SiO_2, Fe_2O_3 \)
• (3) \( Al_2O_3, Fe_2O_3 \)
• (4) \( SiO_2, CaO \)

Consider the following (unbalanced) reactions: \[ BF_3 + NaH \xrightarrow{450\,\mathrm{K}} X + NaF \] \[ X + H_2O \rightarrow Y + H_2 \uparrow \]
The correct statements about \(X\) and \(Y\) are:

X is an electron-deficient molecule
In X, a B--B bond is present
Y is a weak tribasic acid
Y acts as a Lewis acid

• (1) I \& IV
• (2) II \& III
• (3) II \& IV
• (4) I \& III

Which of the following does not exist?

• (1) \([ GeCl_6 ]^{2-}\)
• (2) \([ SiF_6 ]^{2-}\)
• (3) \([ SiCl_6 ]^{2-}\)
• (4) \([ Sn(OH)_6 ]^{2-}\)

Methemoglobinemia is due to:

• (1) Excess of nitrate concentration in drinking water
• (2) Excess of sulphate concentration in drinking water
• (3) Excess of fluoride concentration in drinking water
• (4) Excess of lead in drinking water

The IUPAC name of the following compound is:

• (1) 6-ethyl-2-methyldec-4-en-7-ol
• (2) 2-methyl-6-ethyldec-4-en-7-ol
• (3) 5-ethyl-9-methyldec-6-en-4-ol
• (4) 9-methyl-5-ethyldec-6-en-4-ol

The functional groups present in the product ‘X’ of the reaction given below are:

• (1)
• (2)
• (3)
• (4)

Identify the major product \((P)\) in the following reaction sequence:
\[ (CH_3)_3CBr \xrightarrow[\Delta]{Alcoholic KOH} X \xrightarrow{HBr} P \]

• (1) \((CH_3)_3CBr\)
• (2) \((CH_3)_2CHCH_2Br\)
• (3) \(CH_3 - CH - CH - CH_3\;(with Br substituent on one of the middle carbons)\)
• (4) \(CH_3 - CH = CH - CH_2Br\)

What is the percentage of carbon in the product ‘X’ formed in the following reaction?

• (1) 85.6 %
• (2) 80.6 %
• (3) 90.6 %
• (4) 70.6 %

Identify the correct statement about the crystal defects in solids:

• (1) Frenkel defect is observed when the difference between sizes of cation and anion is very small
• (2) Frenkel defect is not a dislocation effect
• (3) Schottky defects have no effect on the physical properties of solids
• (4) Trapping of electrons in lattice leads to the formation of F-centers

Dry air contains 79% \(N_2\) and 21% \(O_2\). At temperature T(K), the Henry’s law constants for \(N_2\) and \(O_2\) are \(8.57\times 10^4 \,atm\) and \(4.56\times 10^4 \,atm\), respectively. If this air is in contact with water at 1 atm, what is the ratio of the mole fractions \(\frac{X_{N_2}}{X_{O_2}}\) of \(N_2\) and \(O_2\) dissolved in water?

• (1) 4 : 1
• (2) 1 : 4
• (3) 2 : 1
• (4) 1 : 2

If the degree of dissociation of formic acid is 11.0%, what is the molar conductivity of its 0.02 M solution? \[ Given: \Lambda^\infty (\mathrm{H}^+) = 349.6 \, S cm^2 mol^{-1}, \quad \Lambda^\infty (\mathrm{HCOO}^-) = 54.6 \, S cm^2 mol^{-1}. \]

• (1) \(44.46\, S cm^2 mol^{-1}\)
• (2) \(44.46\, S cm^2 mol^{-1}\)
• (3) \(22.23\, S cm^2 mol^{-1}\)
• (4) \(22.23\, S cm^2 mol^{-1}\)

Consider the gaseous reaction: \[ A_2 + B_2 \;\longrightarrow\; 2\,AB \]
The following initial-rate data were obtained for the above reaction (rate of formation of AB):



The value of the rate constant for the above reaction is:

• (1) \(1.25\times 10^{-2}\)
• (2) \(1.25\times 10^{-3}\)
• (3) \(2.5\times 10^{-2}\)
• (4) \(2.5\times 10^{-3}\)

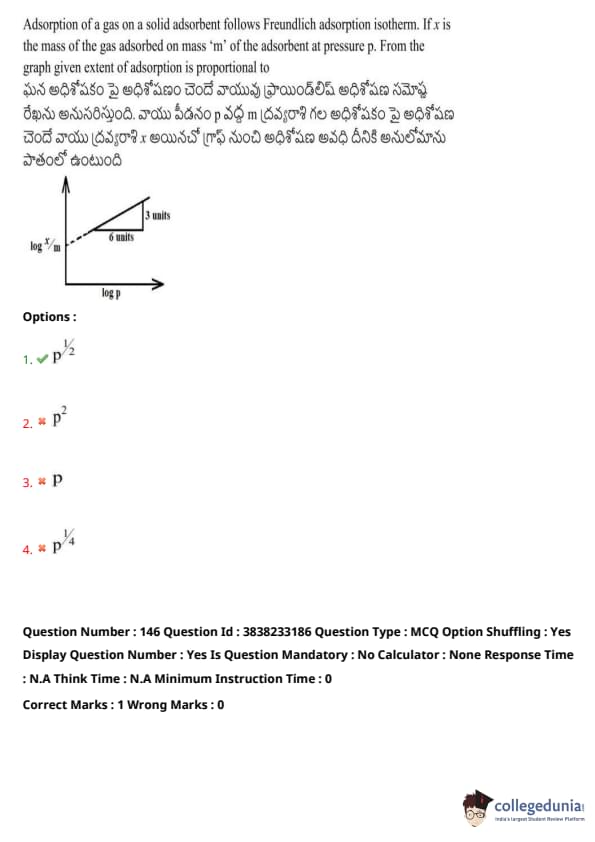
Adsorption of a gas on a solid adsorbent follows the Freundlich adsorption isotherm. If \(x\) is the mass of the gas adsorbed on mass \(m\) of the adsorbent at pressure \(p\), and from the graph of \(\log\left(\frac{x}{m}\right)\) vs. \(\log p\) we obtain a slope of \(\tfrac{1}{2}\), then the extent of adsorption is proportional to:

• (1) \(p^{\tfrac{1}{2}}\)
• (2) \(p^2\)
• (3) \(p\)
• (4) \(p^{\tfrac{1}{4}}\)

Consider the following reactions: \[ X + O_2 \;\longrightarrow\; Cu_2O + SO_2 \] \[ Cu_2O + 2\,H_2 \;\longrightarrow\; 2\,Cu + H_2O \]
If the molecule \(Y\) is formed in the first reaction, the shape of molecule \(Y\) is:

• (1) Linear
• (2) Tetrahedral
• (3) Pyramidal
• (4) Angular

In the given sequence of reactions: \[ P_4 + NaOH + H_2O \;\longrightarrow\; \dots \;\longrightarrow\; X \;+\; 2\,NaH_2PO_2 \;\longrightarrow\; \dots \]
The final product obtained with copper and \(H_2SO_4\) is:

• (1) \(Cu_3(PO_4)_2\)
• (2) \(Cu_3P_2\)
• (3) \(Cu(OH)_2\)
• (4) \(CuCO_3\)

In the contact process of manufacturing \(H_2SO_4\), the arsenic purifier used in the industrial plant contains:

• (1) \(Al_2O_3 \cdot xH_2O\)
• (2) \(Fe_2O_3 \cdot xH_2O\)
• (3) \(Cr_2O_3 \cdot xH_2O\)
• (4) \(Fe_2O_3 \cdot xH_2O\)

In the reaction: \[ Pt + 3:1 \,mixture of \,(conc. HCl + conc. HNO_3) \rightarrow [X]^{2-}, \]
What is the oxidation state of Pt in the complex ion \([X]^{2-}\)?

• (1) \(+2\)
• (2) \(+3\)
• (3) \(+4\)
• (4) \(+6\)

In which of the following, ions are correctly arranged in the increasing order of oxidizing power?

• (1) \(Cr_2O_7^{2-} < MnO_4^{-} < VO_2^{+}\)
• (2) \(VO_2^{+} < Cr_2O_7^{2-} < MnO_4^{-}\)
• (3) \(VO_2^{+} < MnO_4^{-} < Cr_2O_7^{2-}\)
• (4) \(MnO_4^{2-} < Cr_2O_7^{2-} < VO_2^{+}\)

Which of the following will have a spin-only magnetic moment of 2.86 BM?

• (1) \([CoF_6]^{3-}\)
• (2) \([Co(NH_3)_6]^{3+}\)
• (3) \([NiCl_4]^{2-}\)
• (4) \([Ni(CN)_4]^{2-}\)

The monomer which is present in both Bakelite and Melamine polymers is:

• (1) Methanal
• (2) Methanol
• (3) Phenol
• (4) Ethane-1, 2-diol

Cellulose is a polysaccharide and is made of:

• (1) \(\beta\)-\(D-glucose\) units joined through 1,4-glycosidic linkages
• (2) \(\alpha\)-\(D-glucose\) units joined through 1,4-glycosidic linkages
• (3) \(\alpha\)-\(D-glucose\) units joined through 1,6-glycosidic linkages
• (4) \(\beta\)-\(D-glucose\) units joined through 1,6-glycosidic linkages

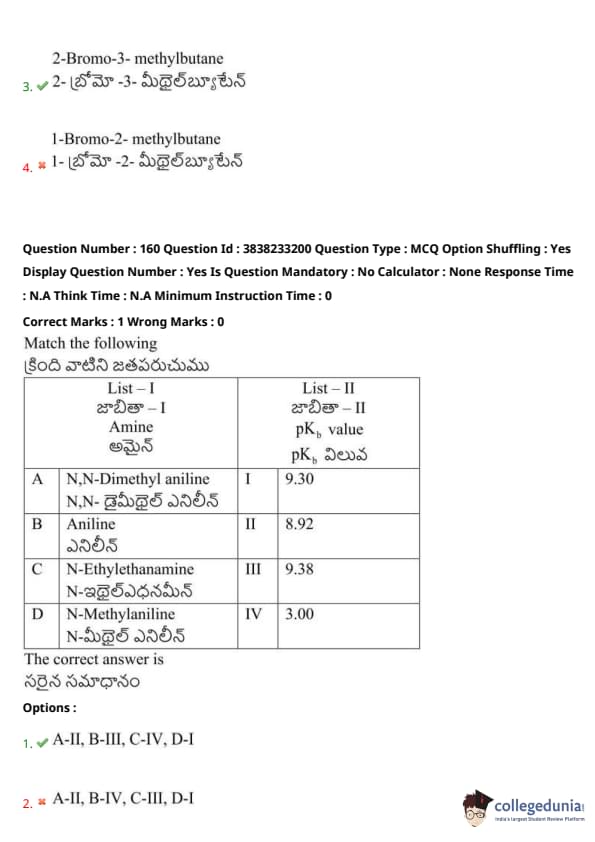
Match the following:

• (1) A-III, B-I, C-IV, D-II
• (2) A-II, B-III, C-I, D-I
• (3) A-III, B-II, C-I, D-IV
• (4) A-II, B-III, C-I, D-IV

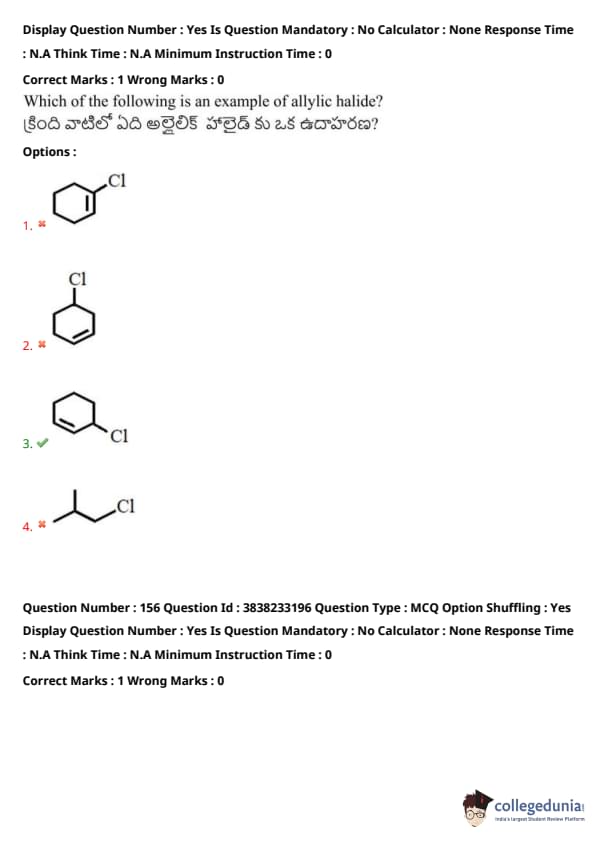
Which of the following is an example of allylic halide?

• (1)
• (2)
• (3)
• (4)

Correct Answer: (3)
View Solution

Identify the correct statements about Z:



I. \(Z\) is an aldehyde.

II. \(Z\) undergoes Cannizzaro reaction.

III. \(Z\) gives iodoform test.

IV. \(Z\) does not give test with Tollen's reagent.

• (1) I and III
• (2) II and IV
• (3) I and IV
• (4) II and III

Assertion (A): Aldehydes are more reactive than ketones towards nucleophilic addition reactions.

Reason (R): In aldehydes, the carbonyl carbon is less electrophilic compared to ketones.

• (1) (A) and (R) are correct. (R) is the correct explanation of (A)
• (2) (A) and (R) are correct, but (R) is not the correct explanation of (A)
• (3) (A) is correct but (R) is not correct
• (4) (A) is not correct but (R) is correct

Arrange the following in the correct order of their boiling points:

• (1) I \(>\) III \(>\) II \(>\) IV
• (2) II \(>\) I \(>\) III \(>\) IV
• (3) II \(>\) III \(>\) I \(>\) IV
• (4) III \(>\) II \(>\) IV \(>\) I

What is the major product Z in the given reaction sequence?

• (1) 1-Bromo-2-methylpropene
• (2) 2-Methoxy-2-methylbutane
• (3) 2-Bromo-3-methylbutane
• (4) 1-Bromo-2-methylbutane

Match the following:

• (1) A-II, B-III, C-I, D-IV
• (2) A-I, B-IV, C-III, D-II
• (3) A-III, B-II, C-I, D-IV
• (4) A-IV, B-III, C-I, D-II