TS EAMCET 2024 Question Paper May 10 Shift 2: Download MPC Question Paper with Solutions PDF

The domain of the real valued function \( f(x) = \sin^{-1} \left( \log_2 \left( \frac{x^2}{2} \right) \right) \) is

• (1) \( [-2,0) \cup (1,2] \)
• (2) \( [-2,-1] \cup [1,2] \)
• (3) \( [-1,0] \cup [1,2] \)
• (4) \( [1,\infty) \cup (-2,0) \)

The range of the real valued function \( f(x) = \log_3 (5 + 4x - x^2) \) is

• (1) \( (0,2) \)
• (2) \( [0,2] \)
• (3) \( (-\infty,2] \)
• (4) \( [-1,5] \)

If \( 3^{2n+2} - 8n - 9 \) is divisible by \( 2^p \) \(\forall n \in \mathbb{N}\), then the maximum value of \( p \) is

• (1) \( 8 \)
• (2) \( 7 \)
• (3) \( 6 \)
• (4) \( 9 \)

Let \( A = [a_{ij}] \) be a \( 3 \times 3 \) matrix with positive integers as its elements. The elements of \( A \) are such that the sum of all the elements of each row is equal to 6, and \( a_{22} = 2 \).

• (1) \( 6 \)
• (2) \( 18 \)
• (3) \( 3 \)
• (4) \( 12 \)

If \( |Adj \ A| = x \) and \( |Adj \ B| = y \), then \( \left( |Adj(AB)| \right)^{-1} \) is

• (1) \( \frac{1}{x} + \frac{1}{y} \)
• (2) \( xy \)
• (3) \( \frac{1}{xy} \)
• (4) \( x + y \)

The system of equations \[ x + 3by + bz = 0, \quad x + 2ay + az = 0, \quad x + 4cy + cz = 0 \]
has:

• (1) only zero solution for any values of \( a, b, c \).
• (2) non-zero solution for any values of \( a, b, c \).
• (3) non-zero solution whenever \( b(a+c) = 2ac \).
• (4) non-zero solution whenever \( a+c = 2b \).

Evaluate the determinant: \[ \begin{vmatrix} -\frac{bc}{a^2} & \frac{c}{a} & \frac{b}{a}
\frac{c}{b} & -\frac{ac}{b^2} & \frac{a}{b}
\frac{b}{c} & \frac{a}{c} & -\frac{ab}{c^2} \end{vmatrix}= \]

• (1) \( 0 \)
• (2) \( 4 \)
• (3) \( -1 \)
• (4) \( \frac{a^2 + b^2 + c^2}{a^2 b^2 c^2} \)

If \( z = x + iy \) satisfies the equation \[ z^2 + az + a^2 = 0, \quad a \in \mathbb{R}, \]
then:

• (1) \( |z| = |a| \)
• (2) \( |z - a| = a \)
• (3) \( z = |a| \)
• (4) \( z = a \)

If \( Z_1, Z_2, Z_3 \) are three complex numbers with unit modulus such that \[ |Z_1 - Z_2|^2 + |Z_1 - Z_3|^2 = 4 \]
then \[ Z_1 Z_2 + \overline{Z_1} Z_2 + Z_1 Z_3 + \overline{Z_1} Z_3 = \]

• (1) \( 0 \)
• (2) \( |Z_2|^2 + |Z_3|^2 \)
• (3) \( |Z_2|^2 - |Z_2 + Z_3|^2 \)
• (4) \( 1 \)

If \( \omega \) is the complex cube root of unity and \[ \left( \frac{a + b\omega + c\omega^2}{c + a\omega + b\omega^2} \right)^k + \left( \frac{a + b\omega + c\omega^2}{b + a\omega^2 + c\omega} \right)^2 = 2, \]
then \( 2k + 1 \) is always:

• (1) divisible by 2
• (2) divisible by 6
• (3) divisible by 3
• (4) divisible by 5

If \( Z_1 = \sqrt{3} + i\sqrt{3} \) and \( Z_2 = \sqrt{3} + i \), and \[ \left( \frac{Z_1}{Z_2} \right)^{50} = x + iy, \]
then the point \( (x,y) \) lies in:

• (1) first quadrant
• (2) second quadrant
• (3) third quadrant
• (4) fourth quadrant

The solution set of the inequality \[ 3^x + 3^{1-x} - 4 < 0 \]
contained in \( \mathbb{R} \) is:

• (1) \( (1,2) \)
• (2) \( (1,3) \)
• (3) \( (0,2) \)
• (4) \( (0,1) \)

The common solution set of the inequalities \[ x^2 - 4x \leq 12 \quad and \quad x^2 - 2x \geq 15 \]
taken together is:

• (1) \( (5,6) \)
• (2) \( [5,6] \)
• (3) \( [-3,5] \)
• (4) \( (-\infty,-3] \cup [5,\infty) \)

The roots of the equation \( x^3 - 3x^2 + 3x + 7 = 0 \) are \( \alpha, \beta, \gamma \) and \( w, w^2 \) are complex cube roots of unity. If the terms containing \( x^2 \) and \( x \) are missing in the transformed equation when each one of these roots is decreased by \( h \), then

• (1) \( \frac{3}{w^2} \)
• (2) \( 3w \)
• (3) \( 0 \)
• (4) \( 3w^2 \)

With respect to the roots of the equation \( 3x^3 + bx^2 + bx + 3 = 0 \), match the items of List-I with those of List-II.

The number of ways of arranging all the letters of the word "COMBINATIONS" around a circle so that no two vowels come together is

• (1) \( \frac{7!}{(2!)^4} \)
• (2) \( \frac{7!}{(2!)^3} \)
• (3) \( \frac{^8P_5 \times 6!}{(2!)^3} \)
• (4) \( \frac{7! \times ^8P_5}{(2!)^3} \)

If all the numbers which are greater than 6000 and less than 10000 are formed with the digits \( 3,5,6,7,8 \) without repetition of the digits, then the difference between the number of odd numbers and the number of even numbers among them is:

• (1) \( ^{4}P_3 \)
• (2) \( 3(^{4}P_2) \)
• (3) \( ^{5}P_3 \)
• (4) \( 2(^{4}P_3) \)

A man has 7 relatives, 4 of them are ladies and 3 gents; his wife has 7 other relatives, 3 of them are ladies and 4 gents. The number of ways they can invite them to a party of 3 ladies and 3 gents so that there are 3 of man's relatives and 3 of wife's relatives, is

• (1) \( 341 \)
• (2) \( 161 \)
• (3) \( 485 \)
• (4) \( 435 \)

If the coefficient of \( x^r \) in the expansion of \( (1 + x + x^2)^{100} \) is \( a_r \), and \( S = \sum\limits_{r=0}^{300} a_r \), then \[ \sum\limits_{r=0}^{300} r a_r = \]

• (1) \( (50) S \)
• (2) \( (25) S \)
• (3) \( (150) S \)
• (4) \( (100) S \)

Given below are two statements, one is labelled as Assertion (A) and the other one labelled as Reason (R).

Assertion (A): \[ 1 + \frac{2.1}{3.2} + \frac{2.5.1}{3.6.4} + \frac{2.5.8.1}{3.6.9.8} + \dots \infty = \sqrt{4} \]

Reason (R): \[ |x| < 1, \quad (1 - x)^{-1} = 1 + nx + \frac{n(n+1)}{1.2} x^2 + \frac{n(n+1)(n+2)}{1.2.3} x^3 + \dots \]

• (1) Both (A) and (R) are correct and (R) is the correct explanation of (A)
• (2) Both (A) and (R) are correct but (R) is NOT the correct explanation of (A)
• (3) (A) is correct but (R) is false.
• (4) (A) is false but (R) is true.

If \[ \frac{1}{x^4 + x^2 + 1} = \frac{Ax + B}{x^2 + ax + 1} + \frac{Cx + D}{x^2 - ax + 1} \]
then \( A + B - C + D = ? \)

• (1) \( a \)
• (2) \( 2a \)
• (3) \( 3a \)
• (4) \( 4a \)

If \( 0 < \theta < \frac{\pi}{4} \) and \( 8\cos\theta + 15\sin\theta = 15 \), then \( 15\cos\theta - 8\sin\theta = \)

• (1) \( 15 \)
• (2) \( 7 \)
• (3) \( 8 \)
• (4) \( 23 \)

Evaluate: \[ \sin 20^\circ (4 + \sec 20^\circ) = ? \]

• (1) \( \sqrt{3} \)
• (2) \( -\sqrt{3} \)
• (3) \( 1 \)
• (4) \( -1 \)

Suppose \( \theta_1 \) and \( \theta_2 \) are such that \( (\theta_1 - \theta_2) \) lies in the 3rd or 4th quadrant. If \[ \sin\theta_1 + \sin\theta_2 = \frac{21}{65} \quad and \quad \cos\theta_1 + \cos\theta_2 = \frac{27}{65} \]
then \[ \cos\left(\frac{\theta_1 - \theta_2}{2}\right) = \]

• (1) \( \frac{3}{\sqrt{150}} \)
• (2) \( \frac{3}{\sqrt{130}} \)
• (3) \( \frac{-3}{\sqrt{130}} \)
• (4) \( \frac{-3}{\sqrt{150}} \)

If \( A \) is the solution set of the equation \( \cos^2 x = \cos^2 \frac{\pi}{6} \) and \( B \) is the solution set of the equation \( \cos^2 x = \log_{10} P \) where \( P + \frac{16}{P} = 10 \), then \( B - A = ? \)

• (1) \( \left\{ x \in \mathbb{R} \mid x = 2n\pi + \frac{\pi}{4}, 2n\pi \pm \frac{\pi}{3}, n = 0,1,2,3, \dots \right\} \)
• (2) \( \left\{ x \in \mathbb{R} \mid x = 2n\pi + \frac{\pi}{3}, 2n\pi \pm \frac{2\pi}{3}, n = 0,1,2,3, \dots \right\} \)
• (3) \( \left\{ x \in \mathbb{R} \mid x = 2n\pi + \frac{\pi}{6}, 2n\pi \pm \frac{\pi}{12}, n = 0,1,2,3, \dots \right\} \)
• (4) \( \left\{ x \in \mathbb{R} \mid x = 2n\pi + \frac{\pi}{8}, 2n\pi \pm \frac{\pi}{16}, n = 0,1,2,3, \dots \right\} \)

The trigonometric equation \( \sin^{-1}x = 2\sin^{-1}a \) has a solution. Find the valid range for \( a \).

• (1) \(only when \frac{1}{\sqrt{2}} < a < \frac{1}{2}\)
• (2) \(for all real values of a\)
• (3) \(only when |a| \leq \frac{1}{\sqrt{2}}\)
• (4) \(only when |a| \geq \frac{1}{\sqrt{2}}\)

If \( \sinh x = \frac{12}{5} \), then \( \sinh 3x + \cosh 3x \) = ?

• (1) \( 125 \)
• (2) \( 144 \)
• (3) \( 169 \)
• (4) \( 216 \)

If \( \triangle ABC \) is an isosceles triangle with base \( BC \), then \( r_1 = ? \)

• (1) \( R^2 \cos^2 A \)
• (2) \( \frac{a^2}{2} \)
• (3) \( \frac{r}{R} \)
• (4) \( R^2 \sin^2 A \)

In \( \triangle ABC \), if \( r_1 + r_2 = 3R \), \( r_2 + r_3 = 2R \), then what type of triangle is \( \triangle ABC \)?

• (1) \( ABC is a right-angled isosceles triangle \)
• (2) \( B = \frac{\pi}{3} \)
• (3) \( A = 90^\circ, \quad a \neq b \neq c \)
• (4) \( C = 90^\circ, \quad a:b:c = 2:1:\sqrt{3} \)

Let \( \bar{n} \) be a unit vector normal to the plane \( \pi \) containing the vectors \( \bar{T} + 3\bar{k} \) and \( 2\bar{i} + \bar{j} - \bar{k} \). If this plane \( \pi \) passes through the point \( (-3,7,1) \) and \( p \) is the perpendicular distance from the origin to this plane, then \( \sqrt{p^2 + 5} \) is:

• (1) \( 59 \)
• (2) \( 8 \)
• (3) \( 64 \)
• (4) \( 51 \)

If \( \bar{a} = \bar{i} - \bar{j} + 3\bar{k} \), \( \bar{c} = -\bar{k} \) are position vectors of two points and \( \bar{b} = 2\bar{i} - \bar{j} + \lambda \bar{k} \),
\( \bar{d} = \bar{i} + \bar{j} - \bar{k} \) are two vectors, then the lines \( r = \bar{a} + t \bar{b} \), \( r = \bar{c} + s \bar{d} \) are:

• (1) skew lines when \( \lambda \neq \frac{19{3} \)}
• (2) \textbf{coplanar} \quad \forall \lambda \in \mathbb{R}
• (3) skew lines when \( \lambda \neq \frac{19{3} \)}
• (4) coplanar when \( \lambda = \frac{19{3} \)}

Let \( \bar{a}, \bar{b}, \bar{c} \) be three vectors each having \( \sqrt{2} \) magnitude such that \[ (\bar{a}, \bar{b}) = (\bar{b}, \bar{c}) = (\bar{c}, \bar{a}) = \frac{\pi}{3}. \]
If \( \bar{x} = \bar{a} \times (\bar{b} \times \bar{c}) \) and \( \bar{y} = \bar{b} \times (\bar{c} \times \bar{a}) \), then

• (1) \( |\bar{x}| = |\bar{y}| \)
• (2) \( |\bar{x}| = \sqrt{2} |\bar{y}| \)
• (3) \( |\bar{x}| = 2 |\bar{y}| \)
• (4) \( |\bar{x}| + |\bar{y}| = 2 \)

Let \( \bar{a} \) be a vector perpendicular to the plane containing non-zero vectors \( \bar{b} \) and \( \bar{c} \). If \( \bar{a}, \bar{b}, \bar{c} \) are such that \[ |\bar{a} + \bar{b} + \bar{c}| = \sqrt{|\bar{a}|^2 + |\bar{b}|^2 + |\bar{c}|^2}, \]
then \[ |(\bar{a} \times \bar{b}) \cdot (\bar{a} \times \bar{c})| = \]

• (1) \( |\bar{a}| + |\bar{b}| + |\bar{c}| \)
• (2) \( |\bar{a}| |\bar{b}| |\bar{c}| \)
• (3) \( |\bar{a}|^2 + |\bar{b}|^2 + |\bar{c}|^2 \)
• (4) \( |\bar{a}|^2 |\bar{c}|^2 \)

If \( \bar{a} = \mathbf{i} + 2\mathbf{j} + \mathbf{k} \), \( \bar{b} = 3(\mathbf{i} - \mathbf{j} + \mathbf{k}) \), and \( \bar{c} \) is a vector such that \( \bar{a} \times \bar{c} = \bar{b} \) and \( \bar{a} \cdot \bar{x} = 3 \), then \( \bar{a} \cdot (\bar{x} \times \bar{b} - \bar{c}) = \)

• (1) \( 32 \)
• (2) \( 24 \)
• (3) \( 20 \)
• (4) \( 36 \)

The variance of the first 10 natural numbers which are multiples of 3 is:

• (1) \( 53 \)
• (2) \( 73 \)
• (3) \( 52.5 \)
• (4) \( 74.25 \)

If three numbers are randomly selected from the set \( \{1,2,3,\dots,50\} \), then the probability that they are in arithmetic progression is:
 

• (1) \( \frac{3}{50} \)
• (2) \( \frac{3}{98} \)
• (3) \( \frac{3}{49} \)
• (4) \( \frac{3}{25} \)

The probability that exactly 3 heads appear in six tosses of an unbiased coin, given that the first three tosses resulted in 2 or more heads, is:

• (1) \( \frac{3}{16} \)
• (2) \( \frac{5}{16} \)
• (3) \( \frac{1}{4} \)
• (4) \( \frac{9}{16} \)

A student has to write the words ABILITY, PROBABILITY, FACILITY, MOBILITY. He wrote one word and erased all the letters in it except two consecutive letters. If ‘LI’ is left after erasing then the probability that the boy wrote the word PROBABILITY is:

• (1) \( \frac{21}{116} \)
• (2) \( \frac{72}{116} \)
• (3) \( \frac{3}{5} \)
• (4) \( \frac{4}{9} \)

Two cards are drawn at random one after the other with replacement from a pack of playing cards. If \( X \) is the random variable denoting the number of ace cards drawn, then the mean of the probability distribution of \( X \) is:

• (1) \( 2 \)
• (2) \( \frac{2}{13} \)
• (3) \( 1 \)
• (4) \( \frac{1}{13} \)

If \( X \sim B(6, p) \) is a binomial variate and \[ \frac{P(X=4)}{P(X=2)} = \frac{1}{9}, \]
then the value of \( p \) is:

• (1) \( \frac{1}{2} \)
• (2) \( \frac{1}{9} \)
• (3) \( \frac{1}{3} \)
• (4) \( \frac{1}{4} \)

If the locus of the centroid of the triangle with vertices \( A(a,0) \), \( B(\cos t, a\sin t) \) and \( C(\sin t, -b\cos t) \) (\( t \) is a parameter) is given by \[ 9x^2 + 9y^2 - 6x = 49, \]
then the area of the triangle formed by the line \[ \frac{x}{a} + \frac{y}{b} = 1 \]
with the coordinate axes is:

• (1) \( \frac{49}{2} \)
• (2) \( \frac{7}{2} \)
• (3) \( 4 \)
• (4) \( 47 \)

By shifting the origin to the point \( (h,5) \) by the translation of coordinate axes, if the equation \[ y = x^2 - 9x^2 + cx - d \]
transforms to \( Y = X^2 \), then \( \left( \frac{d - c}{h} \right) \) is:

• (1) \( 0 \)
• (2) \( 13 \)
• (3) \( 11 \)
• (4) \( 25 \)

The equation of the straight line whose slope is \( -\frac{2}{3} \) and which divides the line segment joining \( (1,2) \) and \( (-3,5) \) in the ratio 4:3 externally is:

• (1) \( 2x + 3y - 12 = 0 \)
• (2) \( 3x + 2y + 27 = 0 \)
• (3) \( 2x + 3y - 9 = 0 \)
• (4) \( 2x + 3y + 12 = 0 \)

The equations \[ 7x + y - 24 = 0 \quad and \quad x + 7y - 24 = 0 \]
represent the equal sides of an isosceles triangle. If the third side passes through \( (-1,1) \), then a possible equation for the third side is:

• (1) \( 3x - y = -4 \)
• (2) \( x + y = 0 \)
• (3) \( x - 2y = -3 \)
• (4) \( 3x + y = -2 \)

The combined equation of a possible pair of adjacent sides of a square with area 16 square units whose centre is the point of intersection of the lines \[ x + 2y - 3 = 0 \quad and \quad 2x - y - 1 = 0 \]
is:

• (1) \( (2x - y - 1 + 4\sqrt{5})(x + 2y - 3 + 4\sqrt{5}) = 0 \)
• (2) \( (2x - y - 1 - 4\sqrt{5})(x + 2y - 3 - 4\sqrt{5}) = 0 \)
• (3) \( (2x - y - 2\sqrt{5})(x + 2y + 2\sqrt{5}) = 0 \)
• (4) \( (2x - y - 1 - 2\sqrt{5})(x + 2y - 3 + 2\sqrt{5}) = 0 \)

If the line \[ 2x + by + 5 = 0 \]
forms an equilateral triangle with \[ ax^2 - 96bxy + ky^2 = 0, \]
then \( a + 3k \) is:

• (1) \( 3b \)
• (2) \( 192 \)
• (3) \( 4b^2 \)
• (4) \( 102 \)

A rhombus is inscribed in the region common to the two circles \[ x^2 + y^2 - 4x - 12 = 0 \]
and \[ x^2 + y^2 + 4x - 12 = 0. \]
If the line joining the centres of these circles and the common chord of them are the diagonals of this rhombus, then the area (in Sq. units) of the rhombus is:

• (1) \( 16\sqrt{3} \)
• (2) \( 4\sqrt{3} \)
• (3) \( 12\sqrt{3} \)
• (4) \( 8\sqrt{3} \)

If \( m \) is the slope and \( P(\beta, \beta) \) is the midpoint of a chord of contact of the circle \[ x^2 + y^2 = 125, \]
then the number of values of \( \beta \) such that \( \beta \) and \( m \) are integers is:

• (1) \( 2 \)
• (2) \( 4 \)
• (3) \( 6 \)
• (4) \( 8 \)

A rectangle is formed by the lines \[ x = 4, \quad x = -2, \quad y = 5, \quad y = -2 \]
and a circle is drawn through the vertices of this rectangle. The pole of the line \[ y + 2 = 0 \]
with respect to this circle is:

• (1) \( \left( 1, \frac{-85}{14} \right) \)
• (2) \( \left( 1, \frac{-32}{7} \right) \)
• (3) \( (-2, -2) \)
• (4) \( (1, -4) \)

The equation of a circle which passes through the points of intersection of the circles \[ 2x^2 + 2y^2 - 2x + 6y - 3 = 0, \quad x^2 + y^2 + 4x + 2y + 1 = 0 \]
and whose centre lies on the common chord of these circles is:

• (1) \( 2x^2 + 2y^2 - 3x + 4y - 2 = 0 \)
• (2) \( x^2 + y^2 + 2x + 5y - 2 = 0 \)
• (3) \( 3x^2 + 3y^2 - 2x + 4y - 3 = 0 \)
• (4) \( 4x^2 + 4y^2 + 6x + 10y - 1 = 0 \)

If the equation of the circle which cuts each of the circles \[ x^2 + y^2 = 4, \] \[ x^2 + y^2 - 6x - 8y + 10 = 0, \] \[ x^2 + y^2 + 2x - 4y - 2 = 0 \]
at the extremities of a diameter of these circles is \[ x^2 + y^2 + 2gx + 2fy + c = 0, \]
then the value of \( g + f + c \) is:

• (1) \( 9 \)
• (2) \( -9 \)
• (3) \( 12 \)
• (4) \( -12 \)

The equation of the circle passing through the origin and cutting the circles \[ x^2 + y^2 + 6x - 15 = 0 \]
and \[ x^2 + y^2 - 8y - 10 = 0 \]
orthogonally is:

• (1) \( 2x^2 + 2y^2 - 5x + 10y = 0 \)
• (2) \( 2x^2 + 2y^2 - 10x + 5y = 0 \)
• (3) \( x^2 + y^2 - 2x + 5y = 0 \)
• (4) \( x^2 + y^2 - 5x + 2y = 0 \)

The equation of a circle which passes through the points of intersection of the circles \[ 2x^2 + 2y^2 - 2x + 6y - 3 = 0, \quad x^2 + y^2 + 4x + 2y + 1 = 0 \]
and whose centre lies on the common chord of these circles is:

• (1) \( 2x^2 + 2y^2 - 3x + 4y - 2 = 0 \)
• (2) \( x^2 + y^2 + 2x + 5y - 2 = 0 \)
• (3) \( 3x^2 + 3y^2 - 2x + 4y - 3 = 0 \)
• (4) \( 4x^2 + 4y^2 + 6x + 10y - 1 = 0 \)

S = (-1,1) is the focus, \( 2x - 3y + 1 = 0 \) is the directrix corresponding to S and \( \frac{1}{2} \) is the eccentricity of an ellipse. If \( (a,b) \) is the centre of the ellipse, then \( 3a + 2b \) is:

• (1) \( \frac{30}{13} \)
• (2) \( \frac{4}{13} \)
• (3) \( -1 \)
• (4) \( 0 \)

Given the two parabolas: \[ S = y^2 - 4ax = 0, \quad S' = y^2 + ax = 0 \]
where \( P(t) \) is a point on the parabola \( S' = 0 \). If \( A \) and \( B \) are the feet of the perpendiculars from \( P \) to the coordinate axes and \( AB \) is a tangent to the parabola \( S = 0 \) at the point \( Q(t_1) \), then the value of \( t_1 \) is:

• (1) \( t \)
• (2) \( \frac{t}{4} \)
• (3) \( \frac{3t}{4} \)
• (4) \( \frac{t}{2} \)

Given that \( a \) and \( b \) are the semi-major and semi-minor axes of an ellipse whose axes are along the coordinate axes. If its latus rectum is of length 4 units and the distance between its foci is \( 4\sqrt{2} \), then the value of \( a^2 + b^2 \) is:

• (1) \( 24 \)
• (2) \( 18 \)
• (3) \( 16 \)
• (4) \( 12 \)

If the extremities of the latus recta having positive ordinate of the ellipse \[ \frac{x^2}{a^2} + \frac{y^2}{b^2} = 1 \]
(where \( a > b \)) lie on the parabola \[ x^2 + 2ay - 4 = 0, \]
then the points \( (a, b) \) lie on the curve:

• (1) \( xy = 4 \)
• (2) \( x^2 + y^2 = 4 \)
• (3) \( \frac{x^2}{4} + \frac{y^2}{4} = 1 \)
• (4) \( \frac{x^2}{4} - \frac{y^2}{4} = 1 \)

If the tangent drawn at a point \( P(t) \) on the hyperbola \[ x^2 - y^2 = c^2 \]
cuts the X-axis at \( T \) and the normal drawn at the same point \( P \) cuts the Y-axis at \( N \), then the equation of the locus of the midpoint of \( TN \) is:

• (1) \( \frac{c^2}{4x^2} - \frac{y^2}{c^2} = 1 \)
• (2) \( \frac{x^2}{4c^2} - \frac{y^2}{c^2} = 1 \)
• (3) \( \frac{x^2}{c^2} - \frac{y^2}{4c^2} = 1 \)
• (4) \( x^2 + y^2 = 4c^2 \)

If the harmonic conjugate of \( P(2,3,4) \) with respect to the line segment joining the points \[ A(3,-2,2) \quad and \quad B(6,-17,-4) \]
is \( Q(\alpha, \beta, \gamma) \), then the value of \( \alpha + \beta + \gamma \) is:

• (1) \( \frac{2}{5} \)
• (2) \( -\frac{3}{5} \)
• (3) \( \frac{7}{5} \)
• (4) \( \frac{8}{5} \)

If \( L \) is the line of intersection of two planes \[ x + 2y + 2z = 15 \quad and \quad x - y + z = 4 \]
and the direction ratios of the line \( L \) are \( (a, b, c) \), then the value of \[ \frac{a^2 + b^2 + c^2}{b^2} \]
is:

• (1) \( 14 \)
• (2) \( 10 \)
• (3) \( 22 \)
• (4) \( 26 \)

The foot of the perpendicular drawn from \( A(1,2,2) \) onto the plane \[ x + 2y + 2z - 5 = 0 \]
is \( B(a, \beta, \gamma) \). If \( \pi(x,y,z) = x + 2y + 2z + 5 = 0 \) is a plane then \(-\pi(A):\pi(B) \) is:

• (1) \( 15:32 \)
• (2) \( -7:5 \)
• (3) \( -15:47 \)
• (4) \( -27:20 \)

If \( 0 \leq x \leq \frac{\pi}{2} \), then \[ \lim\limits_{x \to a} \frac{2\cos x - 1}{2\cos x - 1} \]

Options:

• (1) does not exist at all points in \( \left[0, \frac{\pi}{2} \right] \)
• (2)
• (3) \( = -1, \) when \( a = \frac{\pi}{3} \)
• (4) \( = 1, \) when \( 0 \leq a < \frac{\pi}{3} \)

The real-valued function \[ f(x) = \frac{|x - a|}{x - a} \]
is analyzed as follows:

• (1) continuous only at \( x = a \)
• (2) discontinuous only for \( x > a \)
• (3) a constant function when \( x > a \)
• (4) strictly increasing when \( x < a \)

If \[ f(x) = 3x^{15} - 5x^{10} + 7x^5 + 50\cos(x - 1), \]
then \[ \lim_{h \to 0} \frac{f(1 - h) - f(1)}{h^2 + 3h} \]
is:

• (1) \( -25 \)
• (2) \( 25 \)
• (3) \( -10 \)
• (4) \( 10 \)

If the function \[ f(x) = \begin{cases} \frac{(e^x - 1) \sin kx}{4 \tan x}, & x \neq 0
P, & x = 0 \end{cases} \]
is differentiable at \( x = 0 \), then:

• (1) \( P = 0, f'(0) = \frac{k^2}{4} \)
• (2) \( P = 0, f'(0) = -\frac{1}{2} \)
• (3) \( P = k, f'(0) = -\frac{k^2}{4} \)
• (4) \( P = k, f'(0) = \frac{1}{4} \)

If \[ y = \log \left( x - \sqrt{x^2 - 1} \right), \]
then \[ (x^2 - 1)y'' + xy' + e^y + \sqrt{x^2 - 1} = \]
evaluates to:

• (1) \( 0 \)
• (2) \( 1 \)
• (3) \( \sqrt{x^2 - 1} \)
• (4) \( x \)

The maximum interval in which the slopes of the tangents drawn to the curve \[ y = x^4 + 5x^3 + 9x^2 + 6x + 2 \]
increase is:

• (1) \( \left[ -\frac{3}{2}, -1 \right] \)
• (2) \( \left[ 1, \frac{3}{2} \right] \)
• (3) \( R - \left[ 1, \frac{3}{2} \right] \)
• (4) \( R - \left[ -\frac{3}{2}, -1 \right] \)

If \[ A = \{ P(\alpha, \beta) \mid the tangent drawn at P to the curve y^3 - 3xy + 2 = 0 is a horizontal line \} \]
and B =  Q(a, b)  the tangent drawn at Q to the curve y^3 - 3xy + 2 = 0 is a vertical line 

then n(A) + n(B) =
 

• (1) \( 12 \)
• (2) \( 1 \)
• (3) \( 0 \)
• (4) \( 4 \)

In a \( \triangle ABC \), the sides \( b, c \) are fixed. In measuring angle \( A \), if there is an error of \( \delta A \), then the percentage error in measuring the length of the side \( a \) is:

• (1) \( \frac{2\Delta \delta A}{R \sin A} \times 100 \)
• (2) \( \frac{2 \times \Delta \delta A}{R \sin A} \times 100 \)
• (3) \( \frac{\delta A}{2R^2 \sin^2 A} \times 100 \)
• (4) \( \frac{5 \delta A}{R \sin A} \times 100 \)

Consider the curves \( y = f(x) \) and \( x = g(y) \), and let \( P(x,y) \) be a common point of these curves.

If at \( P \), on the curve \( y = f(x) \),
\[ \frac{dy}{dx} = Q(x), \]

and at the same point \( P \) on the curve \( x = g(y) \),
\[ \frac{dx}{dy} = -Q(x), \]

then:

• (1) The two curves have a common tangent.
• (2) The angle between two curves is \( 45^\circ \).
• (3) The tangent drawn at \( P \) to one curve is normal to the other curve at \( P \).
• (4) The two curves never intersect orthogonally.

If Rolle's Theorem is applicable for the function \[ f(x) = \begin{cases} x^p \log x, & x \neq 0
0, & x = 0 \end{cases} \]
on the interval \([0,1]\), then a possible value of \( p \) is:

• (1) \( -2 \)
• (2) \( -1 \)
• (3) \( 0 \)
• (4) \( 1 \)

The sum of the maximum and minimum values of the function \[ f(x) = \frac{x^2 - x + 1}{x^2 + x + 1} \]
is:

• (1) \( \frac{17}{4} \)
• (2) \( \frac{5}{2} \)
• (3) \( \frac{10}{3} \)
• (4) \( 0 \)

If \[ \int \frac{1}{x^4 + 8x^2 + 9} dx = \frac{1}{k} \left[ \frac{1}{\sqrt{14}} \tan^{-1} (f(x)) - \frac{1}{\sqrt{2}} \tan^{-1} (g(x)) \right] + c, \]
then \[ \frac{k}{\sqrt{2}} + f(\sqrt{3}) + g(1) = \]

• (1) \( 3 - 2\sqrt{2} \)
• (2) \( \sqrt{2} - 1 \)
• (3) \( \sqrt{3} + 2\sqrt{2} \)
• (4) \( \sqrt{2} + 1 \)

If \[ \int (1 + x - x^x) e^{x + x^x} dx = f(x) + c, \]
then \( f(1) - f(-1) = \)

• (1) \( \frac{e^2 - 1}{e^2} \)
• (2) \( e^2 + 1 \)
• (3) \( \frac{e + 1}{e} \)
• (4) \( \frac{e - 1}{e} \)

Evaluate the integral: \[ I = \int \frac{1}{x^m \sqrt[m]{x^m + 1}} dx. \]

• (1) \( \frac{1}{m-1} \left( \frac{\sqrt[m]{x^m + 1}}{x} \right)^m + C \)
• (2) \( \frac{-1}{m-1} \left( \frac{\sqrt[m]{x^m + 1}}{x} \right)^{m-1} + C \)
• (3) \( \frac{1}{m-1} \left( \frac{\sqrt[m]{x^m + 1}}{x} \right) + C \)
• (4) \( \frac{1}{m} \left( \frac{\sqrt[m]{x^m + 1}}{x} \right) + C \)

If \[ \int \sqrt{\csc x + 1} \, dx = k \tan^{-1} (f(x)) + c, \]
then \[ \frac{1}{k} f\left(\frac{\pi}{6}\right) = ? \]

• (1) \( \frac{1}{2} \)
• (2) \( \frac{1}{4} \)
• (3) \( \frac{1}{3} \)
• (4) \( \frac{1}{\sqrt{3}} \)

Evaluate the integral: \[ \frac{3}{25} \int_{0}^{25\pi} \sqrt{|\cos x - \cos^3 x|} \, dx. \]

• (1) \( 8 \)
• (2) \( 4 \)
• (3) \( 1 \)
• (4) \( 0 \)

If the area of the region enclosed by the curve \( ay = x^2 \) and the line \( x + y = 2a \) is \( k a^3 \), then \( k \) is:

• (1) \( \frac{2}{9} \)
• (2) \( \frac{9}{2} \)
• (3) \( \frac{3}{2} \)
• (4) \( \frac{2}{3} \)

If \( m, l, r, s, n \) are integers such that \( 9 > m > l > s > n > r > 2 \) and \[ \int_{0}^{\frac{\pi}{2}} \sin^n x \cos^r x \, dx = 4 \int_{0}^{\frac{\pi}{2}} \sin^m x \cos^r x \, dx, \] \[ \int_{0}^{\frac{\pi}{2}} \sin^l x \cos^r x \, dx = 4 \int_{0}^{\frac{\pi}{2}} \sin^s x \cos^r x \, dx, \] \[ \int_{0}^{\frac{\pi}{2}} \sin^n x \cos^r x \, dx = 0, \]
then the equation involving \( s, l, m, r \) is:

• (1) \( (s-2)(l-2) = mr \)
• (2) \( (s-2)(l+2) = rm + 5 \)
• (3) \( (s-2)(s+2) = ln - 3 \)
• (4) \( (l-2)(l+2) = ms - 5 \)

The order and degree of the differential equation \[ \frac{dy}{dx} + \left( \frac{d^2y}{dx^2} + 2 \right)^{\frac{1}{2}} + \frac{d^3y}{dx^3} + 5 = 0 \]
are respectively:

• (1) \( 2, 1 \)
• (2) \( 2, 4 \)
• (3) \( 2, 2 \)
• (4) \( 2, 3 \)

If \( y = \sin x + A \cos x \) is the general solution of \[ \frac{dy}{dx} + f(x)y = \sec x, \]
then an integrating factor of the differential equation is:

• (1) \( \sec x \)
• (2) \( \tan x \)
• (3) \( \cos x \)
• (4) \( \sin x \)

Wave picture of light has failed to explain

• (1) photoelectric effect
• (2) interference of light 
• (3) diffraction of light
• (4) polarization of light 

A capacitor of capacitance \( (4.0 \pm 0.2) \) \(\mu F\) is charged to a potential of \( (10.0 \pm 0.1) \) V. The charge on the capacitor is:

(4.0 \pm 0.2) \(\mu F\) :

• (1) \( 2.5 \ \mu C \pm 3% \)
• (2) \( 2.5 \ \mu C \pm 6% \)
• (3) \( 40 \ \mu C \pm 3% \)
• (4) \( 40 \ \mu C \pm 6% \)

A body is thrown vertically upwards with a velocity of \( 35 \ ms^{-1} \) from the ground. The ratio of the speeds of the body at times 3 s and 4 s of its motion is:
 

• (1) \( 3:4 \)
• (2) \( 1:1 \)
• (3) \( 2:1 \)
• (4) \( 3:2 \)

From a height of ‘h’ above the ground, a ball is projected up at an angle \( 30^\circ \) with the horizontal. If the ball strikes the ground with a speed of 1.25 times its initial speed of \( 40 \ ms^{-1} \), the value of ‘h’ is:

• (1) \( 75 \ m \)
• (2) \( 60 \ m \)
• (3) \( 30 \ m \)
• (4) \( 45 \ m \)

A block is kept on a rough horizontal surface. The acceleration of the block increases from \( 6 \ ms^{-2} \) to \( 11 \ ms^{-2} \) when the horizontal force acting on it increases from \( 20 \ N \) to \( 30 \ N \). The coefficient of kinetic friction between the block and the surface is:

(Acceleration due to gravitiy = 10ms-^2)

• (1) \( 0.2 \)
• (2) \( 0.3 \)
• (3) \( 0.4 \)
• (4) \( 0.5 \)

The kinetic energy of a body of mass \(4 \, kg\) moving with a velocity of \( (2\hat{i} - 4\hat{j} - \hat{k}) \, ms^{-1} \) is?

• (1) \( 84 \, J \)
• (2) \( 63 \, J \)
• (3) \( 42 \, J \)
• (4) \( 21 \, J \)

A ball P of mass \( 0.5 \) kg moving with a velocity of \( 10 \, ms^{-1} \) collides with another ball Q of mass \( 1 \) kg at rest. If the coefficient of restitution is \( 0.4 \), the ratio of the velocities of the balls P and Q after the collision is?

• (1) \( 1:7 \)
• (2) \( 2:7 \)
• (3) \( 2:5 \)
• (4) \( 5:6 \)

A circular plate of radius \( r \) is removed from a uniform circular plate P of radius \( 4r \) to form a hole. If the distance between the centre of the hole formed and the centre of the plate P is \( 2r \), then the distance of the centre of mass of the remaining portion from the centre of the plate P is?

• (1) \( \frac{r}{3} \)
• (2) \( \frac{r}{15} \)
• (3) \( \frac{2r}{15} \)
• (4) \( 2r \)

A hollow cylinder and a solid cylinder initially at rest at the top of an inclined plane are rolling down without slipping. If the time taken by the hollow cylinder to reach the bottom of the inclined plane is \( 2 \) s, the time taken by the solid cylinder to reach the bottom of the inclined plane is?

• (1) \( 2 \) s
• (2) \( 1.414 \) s
• (3) \( 1 \) s
• (4) \( 1.732 \) s

A block kept on a frictionless horizontal surface is connected to one end of a horizontal spring of constant \( 100 \, Nm^{-1} \), whose other end is fixed to a rigid vertical wall. Initially, the block is at its equilibrium position. The block is pulled to a distance of \( 8 \) cm and released. The kinetic energy of the block when it is at a distance of \( 3 \) cm from the mean position is?

• (1) \( 0.65 \, J \)
• (2) \( 0.325 \, J \)
• (3) \( 0.275 \, J \)
• (4) \( 0.5 \, J \)

The ratio of the radii of a planet and the earth is \( 1:2 \), the ratio of their mean densities is \( 4:1 \). If the acceleration due to gravity on the surface of the earth is \( 9.8 \, ms^{-2} \), then the acceleration due to gravity on the surface of the planet is?

• (1) \( 4.9 \, ms^{-2} \)
• (2) \( 8.9 \, ms^{-2} \)
• (3) \( 29.4 \, ms^{-2} \)
• (4) \( 19.6 \, ms^{-2} \)

A wire of cross-sectional area \( 10^{-6} \, m^2 \) is elongated by \( 0.1 % \) when the tension in it is \( 1000 \, N \). The Young’s modulus of the material of the wire is (Assume radius of the wire is constant)?

• (1) \( 10^{11} \, Nm^{-2} \)
• (2) \( 10^{12} \, Nm^{-2} \)
• (3) \( 10^{10} \, Nm^{-2} \)
• (4) \( 10^{9} \, Nm^{-2} \)

The work done in blowing a soap bubble of volume \( V \) is \( W \). The work done in blowing the bubble of volume \( 2V \) from the same soap solution is?

• (1) \( \frac{W}{2} \)
• (2) \( \sqrt{2} W \)
• (3) \( (2)^{\frac{1}{3}} W \)
• (4) \( (4)^{\frac{1}{3}} W \)

Three identical vessels are filled up to the same height with three different liquids A, B, and C of densities \( \rho_A \), \( \rho_B \), and \( \rho_C \) respectively. If \( \rho_A > \rho_B > \rho_C \), then the pressure at the bottom of the vessels is?

• (1) equal in all vessels
• (2) maximum in vessel containing liquid C
• (3) maximum in vessel containing liquid B
• (4) maximum in vessel containing liquid A

Steam of mass 60 g at a temperature \( 100^\circ C \) is mixed with water of mass 360 g at a temperature \( 40^\circ C \). The ratio of the masses of steam and water in equilibrium is?


\textit{(Latent heat of steam = \( 540 \) cal/g and specific heat capacity of water = \( 1 \) cal/g\(^\circ C\))

• (1) \( 1:20 \)
• (2) \( 1:10 \)
• (3) \( 1:5 \)
• (4) \( 1:3 \)

The temperature difference between the ends of two cylindrical rods A and B of the same material is \( 2:3 \). In steady state, the ratio of the rates of flow of heat through the rods A and B is \( 5:9 \). If the radii of the rods A and B are in the ratio \( 1:2 \), then the ratio of lengths of the rods A and B is?

• (1) \( 2:7 \)
• (2) \( 3:7 \)
• (3) \( 2:5 \)
• (4) \( 3:10 \)

When \( Q \) amount of heat is supplied to a monatomic gas, the work done by the gas is \( W \). When \( Q_1 \) amount of heat is supplied to a diatomic gas, the work done by the gas is \( 2W \). Then \( Q:Q_1 \) is:

• (1) \( 2:3 \)
• (2) \( 3:5 \)
• (3) \( 5:7 \)
• (4) \( 5:14 \)

The temperature at which the rms speed of oxygen molecules is 75% of the rms speed of nitrogen molecules at a temperature of \( 287^\circ C \) is:

• (1) \( 87^\circ C \)
• (2) \( 127^\circ C \)
• (3) \( 227^\circ C \)
• (4) \( 360^\circ C \)

The path difference between two particles of a sound wave is \( 50 \) cm and the phase difference between them is \( 1.8\pi \). If the speed of sound in air is \( 340 \) m/s, the frequency of the sound wave is?

• (1) \( 672 \) Hz
• (2) \( 306 \) Hz
• (3) \( 612 \) Hz
• (4) \( 340 \) Hz

A source at rest emits sound waves of frequency \( 102 \) Hz. Two observers are moving away from the source of sound in opposite directions each with a speed of \( 10% \) of the speed of sound. The ratio of the frequencies of sound heard by the observers is?

• (1) \( 9:11 \)
• (2) \( 1:1 \)
• (3) \( 7:9 \)
• (4) \( 2:3 \)

The power of a thin convex lens placed in air is \( +4D \). The refractive index of the material of the convex lens is \( \frac{3}{2} \). If this convex lens is immersed in a liquid of refractive index \( \frac{5}{3} \), then:

• (1) it behaves like a convex lens of focal length 75 cm
• (2) it behaves like a convex lens of focal length 125 cm
• (3) it behaves like a concave lens of focal length 125 cm
• (4) it behaves like a concave lens of focal length 75 cm

The refractive index of the material of a small angled prism is \( 1.6 \). If the angle of minimum deviation is \( 4.2^\circ \), the angle of the prism is?

• (1) \( 4.2^\circ \)
• (2) \( 7^\circ \)
• (3) \( 4.8^\circ \)
• (4) \( 9^\circ \)

The Brewster angle for air to glass transition of light is


\textit{(Refractive index of glass = \( 1.5 \))

• (1) \( \sin^{-1} \left(\frac{3}{2}\right) \)
• (2) \( \cos^{-1} \left(\frac{3}{2}\right) \)
• (3) \( \tan^{-1} \left(\frac{3}{2}\right) \)
• (4) \( \cos^{-1} \left(\frac{2}{3}\right) \)

A proton and an \( \alpha \) particle are both accelerated from rest in a uniform electric field. The ratio of works done by the electric field on the proton and the \( \alpha \)-particle in a given time is?

• (1) \( 1:1 \)
• (2) \( 1:2 \)
• (3) \( 1:4 \)
• (4) \( 4:1 \)

Two capacitors of capacitances \( 1\mu F \) and \( 2\mu F \) can separately withstand potentials of \( 6 \) kV and \( 4 \) kV respectively. The total potential, they together can withstand when they are connected in series is:

• (1) \( 9 \) kV
• (2) \( 3 \) kV
• (3) \( 6 \) kV
• (4) \( 2 \) kV

The resistance of a wire is \(2.5 \Omega\) at a temperature \(373 K\). If the temperature coefficient of resistance of the material of the wire is \(3.6 \times 10^{-3} K^{-1}\), its resistance at a temperature \(273 K\) is nearly:

• (1) \( 1.84 \Omega \)
• (2) \( 2.46 \Omega \)
• (3) \( 0.82 \Omega \)
• (4) \( 4.58 \Omega \)

When two identical resistors are connected in series to an ideal cell, the current through each resistor is \( 2 \) A. If the resistors are connected in parallel to the cell, the current through each resistor is?

• (1) \( 4 \) A
• (2) \( 2 \) A
• (3) \( 8 \) A
• (4) \( 1 \) A

An electron falling freely under the influence of gravity enters a uniform magnetic field directed towards south. The electron is initially deflected towards?

• (1) east
• (2) west
• (3) north
• (4) south

Two long straight parallel wires A and B separated by \( 5 \) m carry currents \( 2 \) A and \( 6 \) A respectively in the same direction. The resultant magnetic field due to the two wires at a point \( 2 \) m distance from the wire A in between the two wires is?

• (1) \( 2 \times 10^{-6} \) T
• (2) \( 2 \times 10^{-7} \) T
• (3) \( 4 \times 10^{-7} \) T
• (4) \( 4 \times 10^{-6} \) T

A short bar magnet placed in a uniform magnetic field making an angle with the field experiences a torque. If the angle made by the magnet with the field is changed from \(30^\circ\) to \(45^\circ\), the torque on the magnet?

• (1) increases by \(50%\)
• (2) decreases by \(50%\)
• (3) decreases by \(41.4%\)
• (4) increases by \(41.4%\)

The mutual inductance of two coils is \( 8 \) mH. The current in one coil changes according to the equation \( I = 12 \sin 100t \), where \( I \) is in amperes and \( t \) is time in seconds. The maximum value of emf induced in the second coil is?

• (1) \( 9.6 \) V
• (2) \( 4.8 \) V
• (3) \( 3.2 \) V
• (4) \( 12.8 \) V

An inductor of inductive reactance \( R \), a capacitor of capacitive reactance \( 2R \), and a resistor of resistance \( R \) are connected in series to an AC source. The power factor of the series LCR circuit is?

• (1) \( \frac{1}{\sqrt{2}} \)
• (2) \( \frac{1}{\sqrt{3}} \)
• (3) \( \frac{1}{4} \)
• (4) \( \frac{1}{2} \)

The efficiency of a bulb of power \( 60 \) W is \( 16% \). The peak value of the electric field produced by the electromagnetic radiation from the bulb at a distance of \( 2 \) m from the bulb is?
\[ \left(\frac{1}{4\pi \epsilon_0} = 9 \times 10^9 Nm^2C^{-2} \right) \]

• (1) \( 24 \) V/m
• (2) \( 16 \) V/m
• (3) \( 9 \) V/m
• (4) \( 12 \) V/m

The work function of a photosensitive metal surface is \( 1.1 \) eV. Two light beams of energies \( 1.5 \) eV and \( 2 \) eV incident on the metal surface. The ratio of the maximum velocities of the emitted photoelectrons is?

• (1) \( 3:4 \)
• (2) \( 1:1 \)
• (3) \( 2:3 \)
• (4) \( 4:9 \)

The ground state energy of a hydrogen atom is \( -13.6 \) eV. The potential energy of the electron in the first excited state of hydrogen is?

• (1) \( -6.8 \) eV
• (2) \( -3.4 \) eV
• (3) \( -13.6 \) eV
• (4) \( -27.2 \) eV

After the decay of a single \( \beta^- \) particle, the parent and daughter nuclei are?

• (1) isotopes
• (2) isobars
• (3) isomers
• (4) isotones

A \(_{92}^{238}U\) nucleus decays to a \(_{82}^{206}Pb\) nucleus. The number of \( \alpha \) and \( \beta^- \) particles emitted are?

• (1) \( 6 \) and \( 2 \)
• (2) \( 3 \) and \( 3 \)
• (3) \( 2 \) and \( 6 \)
• (4) \( 3 \) and \( 4 \)

In an n-type semiconductor, electrons are majority charge carriers and holes are minority charge carriers. The charge of an n-type semiconductor is?

• (1) negative
• (2) positive
• (3) neutral
• (4) depends on the dopant

The region in the output voltage versus input voltage graph where a transistor can be used as an amplifier is?

• (1) active region
• (2) cut-off region
• (3) saturation region
• (4) passive region

For an amplitude modulated wave, the maximum and minimum amplitudes are found to be \( 10 \) V and \( 2 \) V respectively. Then the modulation index is?

• (1) \( \frac{3}{4} \)
• (2) \( \frac{1}{5} \)
• (3) \( \frac{1}{3} \)
• (4) \( \frac{2}{3} \)

The wavelength of an electron is \( 10^3 \) nm. What is its momentum in kg m s\(^{-1}\)?

h = 6.625 x \(10^-34\)  Js
 

• (1) \( 6.625 \times 10^{-31} \)
• (2) \( 6.625 \times 10^{-37} \)
• (3) \( 6.625 \times 10^{-28} \)
• (4) \( 6.625 \times 10^{-34} \)

Two statements are given below:

Statement I: In H atom, the energy of 2s and 2p orbitals is the same.

Statement II: In He atom, the energy of 2s and 2p orbitals is the same.

• (1) Both statements I and II are correct
  (2) Both statements I and II are not correct
  (3) Statement I is correct but statement II is not correct
  (4) Statement I is not correct but statement II is correct

The set containing the elements with positive electron gain enthalpies is?

• (1) S, Se, Te
• (2) Kr, Xe, Rn
• (3) Cl, Br, I
• (4) K, Rb, Cs

Assertion (A): The ionic radii of \( Na^+ \) and \( F^- \) are the same.

Reason (R): Both \( Na^+ \) and \( F^- \) are isoelectronic species.

• (1) (A) and (R) are correct. (R) is the correct explanation of (A)
  (2) (A) and (R) are correct, but (R) is not the correct explanation of (A)
  (3) (A) is correct but (R) is not correct
  (4) (A) is not correct but (R) is correct

The number of lone pairs of electrons on the central atom of \( ClF_3, NF_3, SF_4, XeF_4 \) respectively are?

• (1) \( 0,1,0,2 \)
  (2) \( 2,1,0,0 \)
  (3) \( 2,1,1,2 \)
  (4) \( 2,1,1,0 \)

The hybridisation of the central atom of \( BF_3 \), \( SnCl_2 \), \( HgCl_2 \), respectively is?

• (1) \( sp^2, sp^2, sp \)
  (2) \( sp^3, sp^2, sp^2 \)
  (3) \( sp^3, sp, sp^2 \)
  (4) \( sp^3, sp, sp \)

The variation of volume of an ideal gas with its number of moles (\( n \)) is obtained as a graph at 300 K and 1 atm pressure. What is the slope of the graph?

• (1) \( 24.6 \) L
  (2) \( 24.6 \) L mol\(^{-1}\)
  (3) \( \frac{1}{24.6} \) L
  (4) \( \frac{1}{24.6} \) L\(^{-1}\) mol

Observe the following reaction:
\[ 2KClO_3 (s) \xrightarrow{\Delta} 2KCl (s) + 3O_2 (g) \]

In this reaction:

• (1) Cl is oxidized and O is reduced
  (2) Cl is reduced and O is oxidized
  (3) K is oxidized and O is reduced
  (4) K is reduced and Cl is also reduced

The \( \Delta_f H^\theta \) of \( AO_3(s) \), \( BO_2(s) \), and \( ABO_3(s) \) is -635, \( x \), and -1210 kJ mol\(^{-1}\) respectively. The reaction: ABO_3 (s) \rightarrow AO (s) + BO_2 (g)
Has an enthalpy change of \( \Delta_r H^\theta = 175 \) kJ mol\(^{-1}\). What is the value of \( x \) (in kJ mol\(^{-1}\))?

• (1) \( -750 \)
  (2) \( +400 \)
  (3) \( -400 \)
  (4) \( +750 \)

At 27°C, 100 mL of 0.5 M HCl is mixed with 100 mL of 0.4 M NaOH solution. To this resultant solution, 800 mL of distilled water is added. What is the pH of the final solution?

• (1) \( 12.0 \)
  (2) \( 2.0 \)
  (3) \( 1.3 \)
  (4) \( 1.0 \)

The proper conditions of storing \( H_2O_2 \) are:

• (1) Placing in wax lined plastic bottle and kept in dark
• (2) Placing in wax lined plastic bottle and exposed to light
• (3) Placing in wax lined plastic bottle containing traces of base
• (4) Placing in metal vessel and exposed to light

The standard electrode potentials \( E^\circ (V) \) for \( Li^+/Li \), \( Na^+/Na \) respectively are:

• (1) \( -3.04, -2.714 \)
• (2) \( -2.714, -3.04 \)
• (3) \( -3.04, -3.04 \)
• (4) \( -2.714, -2.714 \)

The alloy formed by beryllium with 'X' is used in the preparation of high-strength springs. 'X' is:

• (1) Al
• (2) Zn
• (3) Cu
• (4) Cr

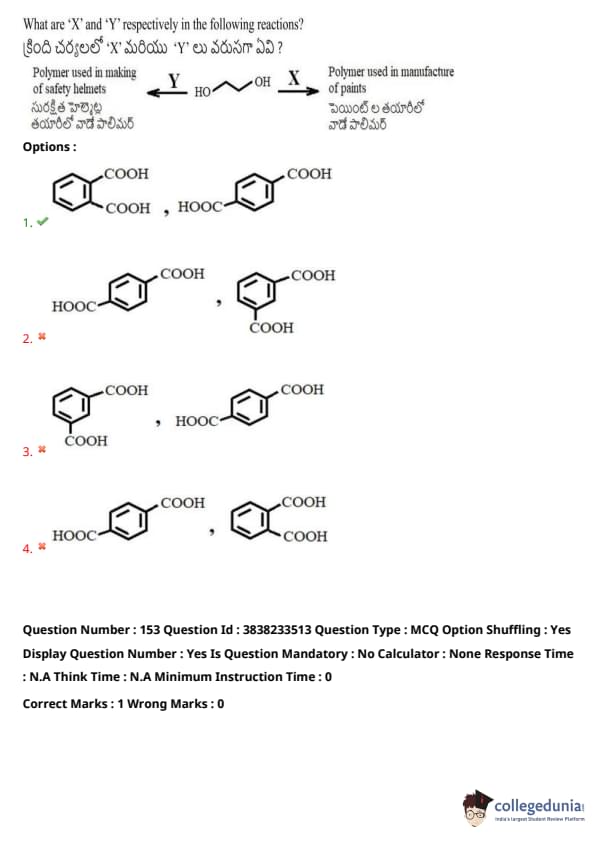
What are \( X \) and \( Y \) respectively in the following reactions?


X \xrightarrow{\text{CO B_2H_6 \xrightarrow{\text{NaH \xrightarrow{(C_2H_5)_2O Y

• (1) \( BH_3, 2CO; NaBO_2 \)
• (2) \( BH_3, CO; NaBH_4 \)
• (3) \( BH_3, CO; NaBO_2 \)
• (4) \( BH_3, CO; Na_2B_4O_7 \)

Which of the following statements are correct?
 

(i) \( CCl_4 \) undergoes hydrolysis easily.

(ii) Diamond has directional covalent bonds.

(iii)Fullerene is the thermodynamically most stable allotrope of carbon.

(iv)Glass is a man-made silicate.

• (1) \( i, iii \) only
• (2) \( ii, iv \) only
• (3) \( ii, iii, iv \) only
• (4) \( i, ii \) only

Which of the following industries generate non-biodegradable wastes?

• (1) Cotton mills
• (2) Paper mills
• (3) Thermal power plants
• (4) Textile factories

Possible number of isomers including stereoisomers for an organic compound with the molecular formula \( C_4H_9Br \) is:

• (1) 3
• (2) 4
• (3) 5
• (4) 2

The alkane which is next to methane in the homologous series can be prepared from which of the following reactions?

• (1) I, IV only
• (2) II, III only
• (3) I, III only
• (4) II, IV only

At high pressure and regulated supply of air, methane is heated with catalyst ‘X’ to give methanol and with catalyst ‘Y’ to give methanal. \( X \) and \( Y \) respectively are:

• (1) \( Mo_2O_3, Cu \)
• (2) \( Cu, Mo_2O_3 \)
• (3) \( V_2O_5, KMnO_4 \)
• (4) \( KMnO_4, Cr_2O_3 \)

What is ‘Y’ in the following set of reactions?
\[ C_4H_8 \xrightarrow{H_2O, H_2SO_4, 333K} X \xrightarrow{(i) O_3, (ii) Zn + H_2O} Y \]

Correct Answer: (2)
View Solution

The molecular formula of a crystal is \( AB_2O_4 \). Oxygen atoms form a close-packed lattice. Atoms of A occupy \( x% \) of tetrahedral voids and atoms of B occupy \( y% \) of octahedral voids. \( x \) and \( y \) are respectively:
 

• (1) \( 12.5%, 50% \)
• (2) \( 50%, 12.5% \)
• (3) \( 33.3%, 66.6% \)
• (4) \( 66.6%, 33.3% \)

At T(K), 0.1 moles of a non-volatile solute was dissolved in 0.9 moles of a volatile solvent. The vapour pressure of pure solvent is 0.9 bar. What is the vapour pressure (in bar) of the solution?
 

• (1) \( 0.89 \)
• (2) \( 0.81 \)
• (3) \( 0.79 \)
• (4) \( 0.71 \)

Two statements are given below:

Statement I: Molten NaCl is electrolysed using Pt electrodes. \( Cl_2 \) is liberated at the anode.

Statement II: Aqueous CuSO\(_4\) is electrolysed using Pt electrodes. \( O_2 \) is liberated at the cathode.

The correct answer is:

• (1) Both statement I and II are correct
• (2) Both statement I and II are not correct
• (3) Statement I is correct but statement II is not correct
• (4) Statement I is not correct but statement II is correct

For a first-order reaction, the graph between \( \log \frac{a}{(a - x)} \) (on y-axis) and time (in min, on x-axis) gave a straight line passing through the origin. The slope is \( 2 \times 10^{-3} \) min\(^{-1}\). What is the rate constant (in min\(^{-1}\))?
 

• (1) \( 2 \times 10^{-3} \)
• (2) \( \frac{2 \times 10^{-3}}{2.303} \)
• (3) \( 4.606 \times 10^{-3} \)
• (4) \( 0.5 \times 10^{-5} \)

In Haber’s process of manufacture of ammonia, the ‘catalyst’, the ‘promoter’, and ‘poison for the catalyst’ are respectively:
 

• (1) \( Fe, W, CO \)
• (2) \( Co, Mo, CO \)
• (3) \( Fe, Mo, CO_2 \)
• (4) \( Fe, Mo, CO \)

Among the following, the calcination process is:
 

• (1) 2Cu_2S + 3O_2 \xrightarrow{\Delta} 2Cu_2O + 2SO_2 \uparrow
• (2) Al_2O_3(s) + 2NaOH(aq) + 3H_2O(l) \rightarrow 2Na[Al(OH)_4](aq)
• (3) 2CuFeS_2 + O_2 \rightarrow Cu_2S + 2FeS + SO_2
• (4) Fe_2O_3 \cdot xH_2O(s) \xrightarrow{\Delta} Fe_2O_3(s) + xH_2O(g)

The correct order of boiling points of hydrogen halides is:

• (1) \( HF < HCl < HBr < HI \)
• (2) \( HI < HBr < HCl < HF \)
• (3) \( HCl < HBr < HI < HF \)
• (4) \( HBr < HCl < HI < HF \)

Observe the following reactions (unbalanced):

P_2O_3 + H_2O - X



P_4O_10 + H_2O - Y


The number of \( P=O \) bonds present in \( X, Y \) are respectively:
  (1) \( 1, 3 \)

• (2) \( 1, 2 \)
• (3) \( 2, 1 \)
• (4) \( 1, 1 \)

Carbon on reaction with hot conc. \( H_2SO_4 \), gives two oxides along with \( H_2O \). What is the nature of these two oxides?
 

• (1) Both are acidic
• (2) Both are basic
• (3) Both are neutral
• (4) Both are amphoteric

Which of the following orders is correct for the property given?
 

• (1) \( Cr < Mn < Fe \) - standard electrode potential value for \( M^{3+}/M^{2+} \)
• (2) \( Cr^{2+} < Mn^{2+} < Fe^{2+} \) - magnetic moments
• (3) \( VO_2^+ < Cr_2O_7^{2-} < MnO_4^- \) - oxidizing power
• (4) \( Ti < V < Cr \) - first ionization enthalpy

Arrange the following in increasing order of their crystal field splitting energy:

• (1) \( I < II < III < IV \)
• (2) \( IV < I < II < III \)
• (3) \( I < III < II < IV \)
• (4) \( IV < II < I < III \)

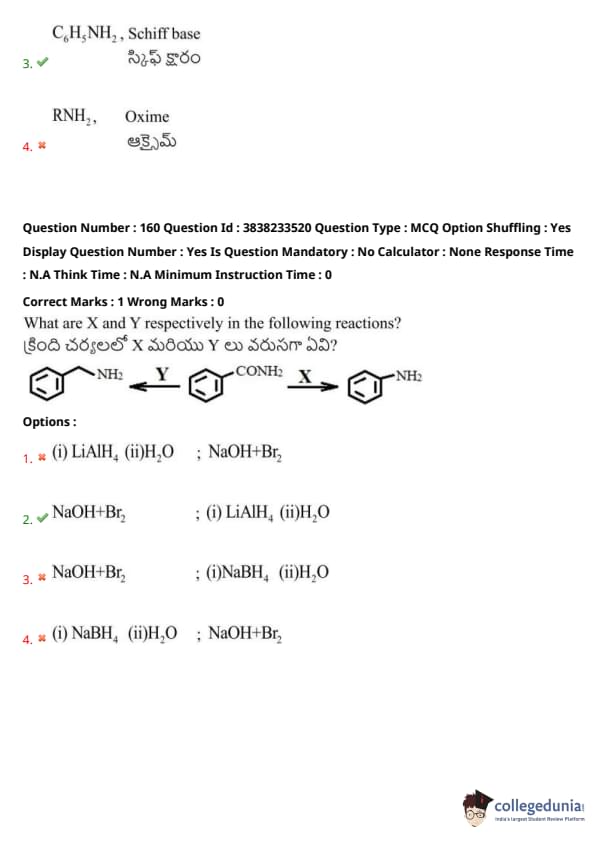
What are ‘X’ and ‘Y’ respectively in the following reactions?

Correct Answer: (1)
View Solution

Two statements are given below:

I. Milk sugar is a disaccharide of \( \alpha \)-D-galactose and \( \beta \)-D-glucose.

II. Sucrose is a disaccharide of \( \alpha \)-D-glucose and \( \beta \)-D-fructose.

The correct answer is:

• (1) Both statements I and II are correct
• (2) Both statements I and II are incorrect
• (3) Statement I is correct but statement II is incorrect
• (4) Statement I is incorrect but statement II is correct

The effects that aspirin can produce in the body are:





\flushleft

• (1) \( A, B, C \)
• (2) \( A, C, D \)
• (3) \( A, B, E \)
• (4) \( C, D, E \)

The reagent ‘X’ used in the following reaction to obtain a good yield of the product is:




\flushleft

• (1) \( KI, H_2SO_4 \)
• (2) \( KI, 95% \ H_3PO_4 \)
• (3) \( NaI, ZnCl_2 \)
• (4) \( HI \)

The \( C-O-H \) bond angle in A is \( X \) and \( C-O-C \) bond angle in B is \( Y \). What are X and Y?





\flushleft

• (1) \( X > 109^\circ 28' , Y > 109^\circ 28' \)
• (2) \( X < 109^\circ 28' , Y < 109^\circ 28' \)
• (3) \( X > 109^\circ 28' , Y = 109^\circ 28' \)
• (4) \( X < 109^\circ 28' , Y > 109^\circ 28' \)

IUPAC name of the following compound is:




\flushleft

• (1) 2-Methyl pentoxybenzene
• (2) 4-Methyl pentoxybenzene
• (3) Phenoxy-4-methylpentane
• (4) Phenoxy-2-methylpentane

The bromides formed by the cleavage of ethers A and B with HBr respectively are:

Correct Answer: (4)
View Solution

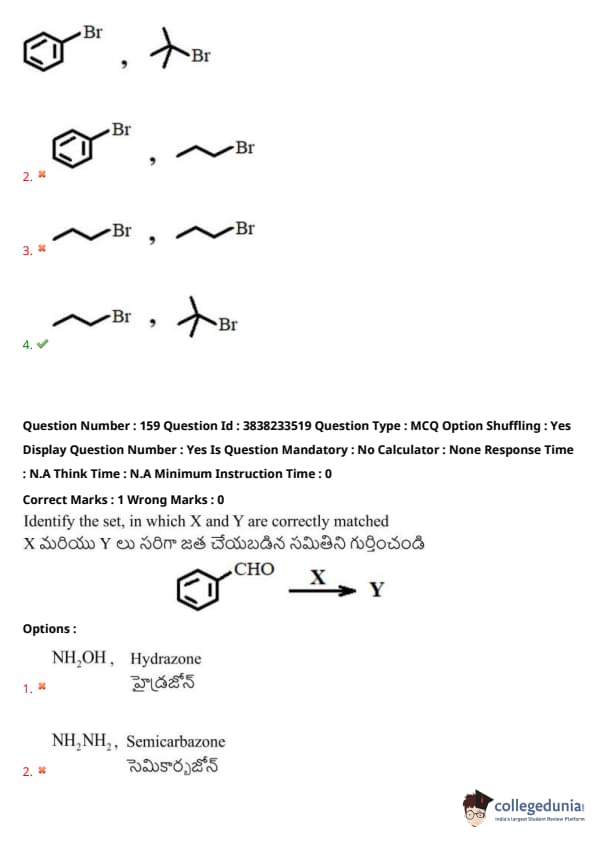
Identify the set, in which X and Y are correctly matched:




\flushleft

• (1) \( NH_2OH \), Hydrazone
• (2) \( NH_2NH_2 \), Semicarbazone
• (3) \( C_6H_5NH_2 \), Schiff base
• (4) \( RNH_2 \), Oxime

What are X and Y respectively in the following reactions?





\flushleft

• (1) \( (i) \ LiAlH_4, \ H_2O \ ; \ NaOH + Br_2 \)
• (2) \( NaOH + Br_2 \ ; \ (i) \ LiAlH_4, \ (ii) H_2O \)
• (3) \( NaOH + Br_2 \ ; \ (i) NaBH_4, \ (ii) H_2O \)
• (4) \( (i) NaBH_4, \ (ii) H_2O \ ; \ NaOH + Br_2 \)