TS EAMCET 2024 Question Paper May 10 Shift 1: Download MPC Question Paper with Solutions PDF

If the real valued function \( f(x) = \sin^{-1}(x^2 - 1) - 3\log_3(3^x - 2) \) is not defined for all \( x \in (-\infty, a] \cup (b, \infty) \), then what is \( 3^a + b^2 \)?

• (1) \( 5 \)
• (2) \( 6 \)
• (3) \( 3 \)
• (4) \( 4 \)

If \( f \) is a real valued function from \( A \) onto \( B \) defined by \( f(x) = \frac{1}{\sqrt{|x| - |x|}} \), then \( A \cap B \) is:

• (1) \( \emptyset \)
• (2) \( (-\infty, 0) \)
• (3) \( (0, \infty) \)
• (4) \( (-\infty, \infty) \)

Among the following four statements, the statement which is not true, for all \( n \in N \) is:

• (1) \( (2n + 7) < (n + 3)^2 \)
• (2) \( 1^2 + 2^2 + \dots + n^2 > \frac{n^3}{3} \)
• (3) \( 3.5^{2n+1} + 2^{3n+1} \) is divisible by 23
• (4) \( 2 + 7 + 12 + \dots + (5n - 3) = \frac{n(5n - 1)}{2} \)

If  x  y  y
    y  x  y 
    y  y  x  and

\( 5A^{-1} =

-3  2  2
2  -3  2
2  2  -3 , then \( A^2 - 4A \) is:

• (1) \( 5A^{-1} \)
• (2) \( 5I \)
• (3) \( 0 \)
• (4) \( I \)

If \( A = 9  3 0
             1  5  8

              7  6  2 and
\( A^T A^{-2} = a_{11}  a_{12}  a_{13}
                         a_{21}  a_{22}  a_{23}

                         a_{31}  a_{32}  a_{33} , then \( \sum_{1 \leq i \leq 3} \sum_{1 \leq j \leq 3} a_{ij} \) is:

• (1) \( 35 \)
• (2) \( 0 \)
• (3) \( 33 \)
• (4) \( 1 \)

If \( a \neq b \neq c \), then
\[ \Delta_1 = \begin{vmatrix} 1 & a^2 & bc
1 & b^2 & ca
1 & c^2 & ab \end{vmatrix}, \quad \Delta_2 = \begin{vmatrix} 1 & 1 & 1
a^2 & b^2 & c^2
a^3 & b^3 & c^3 \end{vmatrix} \]

and \( \frac{\Delta_1}{\Delta_2} = \frac{6}{11} \), then what is \( 11(a + b + c) \)?

• (1) \( 0 \)
• (2) \( 1 \)
• (3) \( ab + bc + ca \)
• (4) \( 6(ab + bc + ca) \)

The system of equations \( x + 3y + 7 = 0 \), \( 3x + 10y - 3z + 18 = 0 \), and \( 3y - 9z + 2 = 0 \) has:

• (1) unique solution
• (2) infinitely many solutions
• (3) no solution
• (4) finite number of solutions

If \( x \) and \( y \) are two positive real numbers such that \( x + iy = \frac{13\sqrt{5} + 12i}{(2 - 3i)(3 + 2i)} \), then \( 13y - 26x = \):

• (1) 28
• (2) 39
• (3) 42
• (4) 54

If \( z = x + iy \) and the point \( P \) represents \( z \) in the Argand plane, then the locus of \( z \) satisfying the equation \( |z-1| + |z+i| = 2 \) is:

• (1) \( 15x^2 - 2xy + 15y^2 - 16x + 16y - 48 = 0 \)
• (2) \( 3x^2 + 2xy + 3y^2 - 4x - 4y = 0 \)
• (3) \( 3x^2 - 2xy + 3y^2 - 4x + 4y = 0 \)
• (4) \( 15x^2 + 2xy + 15y^2 + 16x - 16y - 48 = 0 \)

One of the values of \( (-64i)^{5/6} \) is:

• (1) \( 32i \)
• (2) \( 16\sqrt{2}(1+i) \)
• (3) \( 32(1+i) \)
• (4) \( 16\sqrt{2} \)

If \( \alpha, \beta \) are the roots of the equation \( x + \frac{4}{x} = 2\sqrt{3} \), then \( \frac{2}{\sqrt{3}}\left| \alpha^{2024} - \beta^{2024} \right| \) is:

• (1) \( 2^{2024} \)
• (2) \( 2^{2025} \)
• (3) \( 2^{2023} \)
• (4) \( 2^{1012} \)

If \( \alpha, \beta \) are the real roots of the equation \( 12x^\frac{1}{3} - 25x^\frac{1}{6} + 12 = 0 \), if \( \alpha > \beta \), then \( 6\sqrt{\frac{\alpha}{\beta}} = \):

• (1) \( \frac{3}{2} \)
• (2) \( \frac{4}{3} \)
• (3) \( \frac{9}{8} \)
• (4) \( \frac{16}{9} \)

If the expression \( 7 + 6x - 3x^2 \) attains its extreme value \( \beta \) at \( x = \alpha \), then the sum of the squares of the roots of the equation \( x^2 + ax - \beta = 0 \) is:

• (1) \( 21 \)
• (2) \( -19 \)
• (3) \( 19 \)
• (4) \( -21 \)

If \( \alpha, \beta, \gamma \) are the roots of the equation \( x^3 + 3x^2 - 10x - 24 = 0 \). If \( \alpha > \beta > \gamma \) and \( \alpha^3 + 3\beta^2 - 10\gamma - 24 = 11k \), then \( k = \):

• (1) 1
• (2) 11
• (3) 5
• (4) 55

If \( \alpha, \beta, \gamma \) are the roots of the equation \( 8x^3 - 42x^2 + 63x - 27 = 0 \), If \( \beta < \gamma < \alpha \) and \( \beta, \gamma, \alpha \) are in geometric progression, then the extreme value of the expression \( \gamma x^2 + 4\beta x + \alpha \) is:

• (1) \( \frac{3}{4} \)
• (2) \( 3 \)
• (3) \( \frac{3}{2} \)
• (4) \( \frac{21}{4} \)

All the letters of the word 'COLLEGE' are arranged in all possible ways and all the seven letter words (with or without meaning) thus formed are arranged in the dictionary order. Then the rank of the word 'COLLEGE' is:

• (1) 119
• (2) 149
• (3) 176
• (4) 179

If all the possible 3-digit numbers are formed using the digits 1, 3, 5, 7, 9 without repeating any digit, then the number of such 3-digit numbers which are divisible by 3 is:

• (1) 6
• (2) 12
• (3) 18
• (4) 24

A question paper has 3 parts A, B, C. Part A contains 7 questions, part B contains 5 questions and Part C contains 3 questions. If a candidate is allowed to answer not more than 4 questions from part A; not more than 3 questions from part B and not more than 2 questions from part C, then the number of ways in which a candidate can answer exactly 7 questions is:

• (1) 4655
• (2) 4025
• (3) 3675
• (4) 2625

If \( p \) and \( q \) are the real numbers such that the 7th term in the expansion of \( \left( \frac{5}{p^3} \cdot \frac{3q}{7} \right)^8 \) is 700, then \( 49p^2 = \):

• (1) \( 4q^2 \)
• (2) \( 9q^2 \)
• (3) \( 16q^2 \)
• (4) \( 25q^2 \)

If \( T_4 \) represents the 4th term in the expansion of \( \left( 5x + \frac{7}{x} \right)^{-\frac{3}{2}} \) and \( x \not\in \left[ \frac{\sqrt{7}}{5}, \frac{\sqrt{7}}{5} \right] \), then \( \left( x^3 \cdot \sqrt{5x} \right) T_4 = \):

• (1) \( \frac{7^4}{2 \cdot 5^3} \)
• (2) \( - \frac{7^4}{2 \cdot 5^3} \)
• (3) \( - \frac{7^4}{2 \cdot 5^3} \)
• (4) \( \frac{7^4}{2 \cdot 5^3} \)

If \( \frac{2x^3 + 1}{2x^2 - x - 6} = ax + b + \frac{A}{px - 2} + \frac{B}{2x + q} \), then \( 51apB = \):

• (1) \( 23bqA \)
• (2) \( 69bqA \)
• (3) \( 7bqA \)
• (4) \( 17bqA \)

If \( \tan A = -\frac{60}{11} \) and A does not lie in the 4th quadrant. \( \sec B = \frac{41}{9} \) and B does not lie in the 1st quadrant. If \( \csc A + \cot B = K \), then \( 24K = \):

• (1) 11
• (2) 19
• (3) 40
• (4) 61

If \( \tan A + \tan B + \cot A + \cot B = \tan A \tan B - \cot A \cot B \) and \( 0^\circ < A + B < 270^\circ \), then \( A + B = \):

• (1) \( 45^\circ \)
• (2) \( 135^\circ \)
• (3) \( 150^\circ \)
• (4) \( 225^\circ \)

If \( \cos^2 84^\circ + \sin^2 126^\circ - \sin 84^\circ \cos 126^\circ = K \) and \( \cot A + \tan A = 2K \), then the possible values of \( \tan A \) are:

• (1) \( \frac{2}{3},\frac{3}{2} \)
• (2) \( \frac{1}{3}, 3 \)
• (3) \( \frac{1}{2}, 2 \)
• (4) \( \frac{3}{4}, \frac{4}{3} \)

The equation that is satisfied by the general solution of the equation \( 4 - 3 \cos \theta = 5 \sin \theta \cos \theta \) is:

• (1) \( 7 \sin^2 \theta + 3 \cos^2 \theta = 4 \)
• (2) \( \sin^2 \theta - 2 \cos \theta = \frac{1}{4} \)
• (3) \( \cot \theta - \tan \theta = \sec \theta \)
• (4) \( 1 + \sin^2 \theta = 3 \cos^2 \theta \)

If \( \sin^{-1}(4x) - \cos^{-1}(3x) = \frac{\pi}{6} \), then \( x = \):

• (1) \( \frac{\sqrt{3}}{2\sqrt{7}} \)
• (2) \( \frac{\sqrt{3}}{4\sqrt{7}} \)
• (3) \( \frac{\sqrt{3}}{2\sqrt{13}} \)
• (4) \( \frac{\sqrt{3}}{4\sqrt{13}} \)

If \( \sin h^{-1}(-\sqrt{3}) + \cos h^{-1}(2) = K \), then \( \cosh K = \):

• (1) \( \log(2 - \sqrt{3}) \)
• (2) \( \log(2 + \sqrt{3}) \)
• (3) \( 0 \)
• (4) \( 1 \)

In triangle ABC, if \( a = 4, b = 3, c = 2 \), then \( 2(a - b \cos C)(a - c \sec B) = \):

• (1) 0
• (2) 1
• (3) 2
• (4) 3

In triangle ABC, if \( A = 45^\circ \), \( C = 75^\circ \), and \( R = \sqrt{2} \), then the value of \( r \) is:

• (1) \( \frac{3 + \sqrt{3}}{\sqrt{3} + \sqrt{2} + 1} \)
• (2) \( \frac{\sqrt{3}}{\sqrt{3} + \sqrt{2} + 1} \)
• (3) \( \frac{\sqrt{3}}{\sqrt{6} + \sqrt{3} + 3} \)
• (4) \( \frac{\sqrt{3}}{\sqrt{3} + \sqrt{2} + 1} \)

P and Q are the points of trisection of the line segment AB. If the position vectors of A and B are \( 2\hat{i} - 5\hat{j} + 3\hat{k} \) and \( 4\hat{i} + \hat{j} - 6\hat{k} \) respectively, then the position vector of the point that divides PQ in the ratio 2:3 is:

• (1) \( \frac{1}{15} \left( 44\hat{i} - 33\hat{j} - 18\hat{k} \right) \)
• (2) \( \frac{1}{5} \left( 36\hat{i} - 26\hat{j} - 18\hat{k} \right) \)
• (3) \( \frac{1}{5} \left( 3\hat{i} + 7\hat{j} - 9\hat{k} \right) \)
• (4) \( \frac{1}{15} \left( -3\hat{i} - 7\hat{j} + 9\hat{k} \right) \)

The position vector of the point of intersection of the line joining the points \( \mathbf{i} - \mathbf{j} + \mathbf{k} \) and the line joining the points \( 2\mathbf{i} + \mathbf{j} - 6\mathbf{k} \), \( 3\mathbf{i} - \mathbf{j} - 7\mathbf{k} \) is:

• (1) \( \mathbf{i} - 3\mathbf{j} + 4\mathbf{k} \)
• (2) \( 4\mathbf{i} - 3\mathbf{j} - 8\mathbf{k} \)
• (3) \( \mathbf{i} + 3\mathbf{j} - 5\mathbf{k} \)
• (4) \( \mathbf{i} + \mathbf{j} - 2\mathbf{k} \)

If \( \mathbf{a} = 4\hat{i} + 5\hat{j} - 3\hat{k} \) and \( \mathbf{b} = 6\hat{i} - 2\hat{j} - 2\hat{k} \) are two vectors, then the magnitude of the component of \( \mathbf{b} \) parallel to \( \mathbf{a} \) is:

• (1) \( 2\sqrt{2} \)
• (2) \( 10\sqrt{2} \)
• (3) \( 4\sqrt{2} \)
• (4) \( 6\sqrt{2} \)

A plane \( \pi_1 \) passing through the point \( 3\hat{i} - 7\hat{j} + 5\hat{k} \) is perpendicular to the vector \( \hat{i} + 2\hat{j} - 2\hat{k} \) and another plane \( \pi_2 \) passing through the point \( 2\hat{i} + 7\hat{j} - 8\hat{k} \) is perpendicular to the vector \( 3\hat{i} + 2\hat{j} + 6\hat{k} \). If \( p_1 \) and \( p_2 \) are the perpendicular distances from the origin to the planes \( \pi_1 \) and \( \pi_2 \) respectively, then \( p_1 - p_2 \) is:

• (1) \( 1 \)
• (2) \( 2 \)
• (3) \( 3 \)
• (4) \( 4 \)

If \( \mathbf{a} = 2\overline{i} - \overline{j}, \overline{b} = 2\overline{j} - \overline{k}, \overline{c} = 2\overline{k} - \overline{i} \) are three vectors and \( \overline{d} \) is a unit vector perpendicular to \( \overline{c} \), If \( \overline{a}, \overline{b}, \overline{d} \) are coplanar vectors, then \( |\overline{d} \cdot \overline{b}| = \):

• (1) \( 0 \)
• (2) \( \frac{1}{\sqrt{14}} \)
• (3) \( \sqrt{\frac{2}{7}} \)
• (4) \( \sqrt{\frac{7}{2}} \)

If \( M_1 \) is the mean deviation from the mean of the discrete data \( 44, 5, 27, 20, 8, 54, 9, 14, 35 \) and \( M_2 \) is the mean deviation from the median of the same data, then \( M_1 - M_2 = \):

• (1) \( \frac{7}{9} \)
• (2) \( \frac{2}{3} \)
• (3) \( \frac{5}{9} \)
• (4) \( \frac{4}{9} \)

If two dice are thrown, then the probability of getting co-prime numbers on the dice is:

• (1) \( \frac{23}{36} \)
• (2) \( \frac{13}{36} \)
• (3) \( \frac{5}{6} \)
• (4) \( \frac{1}{6} \)

If two cards are drawn at random simultaneously from a well shuffled pack of 52 playing cards, then the probability of getting a card having a composite number and a card having a number which is a multiple of 3 is:

• (1) \( \frac{94}{663} \)
• (2) \( \frac{62}{663} \)
• (3) \( \frac{102}{663} \)
• (4) \( \frac{64}{663} \)

Bag \( P \) contains 3 white, 2 red, 5 blue balls and bag \( Q \) contains 2 white, 3 red, 5 blue balls. A ball is chosen at random from \( P \) and is placed in \( Q \). If a ball is chosen from bag \( Q \) at random, then the probability that it is a red ball is:

• (1) \( \frac{9}{50} \)
• (2) \( \frac{13}{45} \)
• (3) \( \frac{16}{55} \)
• (4) \( \frac{12}{35} \)

If the probability distribution of a random variable \( X \) is as follows, then the variance of \( X \) is:
\[ X = x \quad 2 \quad 3 \quad 5 \quad 9 \] \[ P(X = x) = k \quad 2k \quad 3k^2 \quad k^2 \]

• (1) \( \frac{61}{4} \)
• (2) \( \frac{7}{2} \)
• (3) 12
• (4) 3

The mean of a binomial variate \( X \sim B(n, p) \) is 1. If \( n > 2 \) and \( P(X = 2) = \frac{27}{128} \), then the variance of the distribution is:

• (1) \( \frac{3}{4} \)
• (2) \( \frac{1}{4} \)
• (3) \( \frac{4}{3} \)
• (4) 4

If the distance from a variable point \( P \) to the point \( (4,3) \) is equal to the perpendicular distance from \( P \) to the line \( x + 2y - 1 = 0 \), then the equation of the locus of the point \( P \) is:

• (1) \( 4x^2 + 4xy + y^2 - 38x + 26y + 124 = 0 \)
• (2) \( 4x^2 - 4xy + y^2 - 38x - 26y + 124 = 0 \)
• (3) \( 4x^2 - 4xy + y^2 + 38x + 26y + 124 = 0 \)
• (4) \( 4x^2 - 4xy - 38x + 26y + 124 = 0 \)

(0, k) is the point to which the origin is to be shifted by the translation of the axes so as to remove the first degree terms from the equation \( ax^2 - 2xy + by^2 - 2x + 4y + 1 = 0 \) and \( \frac{1}{2} \tan^{-1}(2) \) is the angle through which the coordinate axes are to be rotated about the origin to remove the \( xy \)-term from the given equation, then \( a + b = \):

• (1) \( 1 \)
• (2) \( -2 \)
• (3) \( 3 \)
• (4) \( -4 \)

If \( \beta \) is the angle made by the perpendicular drawn from origin to the line \( L = x + y - 2 = 0 \) with the positive X-axis in the anticlockwise direction. If \( a \) is the X-intercept of the line \( L = 0 \) and \( p \) is the perpendicular distance from the origin to the line \( L = 0 \), then \( \tan \beta + p^2 = \):

• (1) 1
• (2) 2
• (3) 3
• (4) 4

The line \( 2x + y - 3 = 0 \) divides the line segment joining the points \( A(1,2) \) and \( B(2,-1) \) in the ratio \( a:b \) at the point \( C \). If the point \( C \) divides the line segment joining the points \( P\left( \frac{b}{3a}, -3 \right) \) and \( Q\left( -3, \frac{-b}{3a} \right) \) in the ratio \( p:q \), then \( \frac{p}{q} + \frac{q}{p} = \):

• (1) \( \frac{29}{10} \)
• (2) \( \frac{17}{10} \)
• (3) 6
• (4) 5

If \( Q \) and \( R \) are the images of the point \( P(2,3) \) with respect to the lines \( x - y + 2 = 0 \) and \( 2x + y - 2 = 0 \) respectively, then \( Q \) and \( R \) lie on

• (1) the same side of the line \( 2x + y - 2 = 0 \)
• (2) the opposite sides of the line \( 2x - y - 2 = 0 \)
• (3) the same side of the line \( x + y + 2 = 0 \)
• (4) the opposite sides of the line \( x - y + 2 = 0 \)

If \( (2, -1) \) is the point of intersection of the pair of lines \[ 2x^2 + axy + 3y^2 + bx + cy - 3 = 0 \quad then \quad 3a + 2b + c = \]

• (1) \( 11 \)
• (2) \( 0 \)
• (3) \( 1 \)
• (4) \( 21 \)

If \( (l, k) \) is a point on the circle passing through the points \( (-1, 1) \), \( (0, -1) \), and \( (1, 0) \), and if \( k \neq 0 \), then find \( k \).

• (1) \( \frac{1}{2} \)
• (2) \( \frac{1}{3} \)
• (3) \( \frac{-1}{3} \)
• (4) \( \frac{-1}{2} \)

If the tangents \( x + y + k = 0 \) and \( x + ay + b = 0 \) drawn to the circle \( S : x^2 + y^2 + 2x - 2y + 1 = 0 \) are perpendicular to each other and \( k, b \) are both greater than 1, then find \( b - k \).

• (1) \( \sqrt{2} \)
• (2) 0
• (3) 2
• (4) \( \sqrt{2} \)

If \( (h, k) \) is the internal center of similitude of the circles \( x^2 + y^2 + 2x - 6y + 1 = 0 \) and \( x^2 + y^2 - 4x + 2y + 4 = 0 \), then find \( 4h \).

• (1) 0
• (2) 3
• (3) 1
• (4) 5

The slope of a common tangent to the circles \( x^2 + y^2 - 4x - 8y + 16 = 0 \) and \( x^2 + y^2 - 6x - 16y + 64 = 0 \) is:

• (1) 0
• (2) \( \frac{15}{8} \)
• (3) 1
• (4) \( \frac{17}{4} \)

The circles \(x^2 + y^2 + 2x - 6y - 6 = 0\) and \(x^2 + y^2 - 6x - 2y + k = 0\) are two intersecting circles and \(k\) is not an integer. If \( \theta \) is the angle between the two circles and \( \cos \theta = -\frac{5}{24} \), then find \( k \).

• (1) \( \frac{6}{5} \)
• (2) \( \frac{74}{9} \)
• (3) \( \frac{37}{3} \)
• (4) \( \frac{53}{7} \)

If \( (p, q) \) is the center of the circle which cuts the three circles \( x^2 + y^2 - 2x - 4y + 4 = 0 \), \( x^2 + y^2 + 2x - 4y + 1 = 0 \), and \( x^2 + y^2 - 4x - 2y - 11 = 0 \) orthogonally, then find \( p + q \).

• (1) 9
• (2) \( \frac{35}{4} \)
• (3) \( \frac{15}{2} \)
• (4) 7

If the focal chord of the parabola \( x^2 = 12y \) drawn through the point \( (3, 0) \) intersects the parabola at the points P and Q, then the sum of the reciprocals of the abscissae of the points P and Q is:

• (1) \( \frac{1}{4} \)
• (2) \( \frac{1}{5} \)
• (3) \( \frac{1}{3} \)
• (4) \( \frac{1}{8} \)

If the normal drawn at the point \( P(9, 9) \) on the parabola \( y^2 = 9x \) meets the parabola again at \( Q(a, b) \), then \( 2a + b = ? \)

• (1) 54
• (2) \( \frac{99}{2} \)
• (3) \( \frac{63}{2} \)
• (4) 27

The length of the latus rectum of the ellipse \( \frac{x^2}{a^2} + \frac{y^2}{b^2} = 1 \) \( (a > b) \) is \( \frac{8}{3} \). If the distance from the center of the ellipse to its focus is \( \sqrt{5} \), then \( \sqrt{a^2 + 6ab + b^2} = ? \)

• (1) 7
• (2) \( \sqrt{12} \)
• (3) \( \sqrt{3} \)
• (4) 11

S' is the focus of the ellipse \( \frac{x^2}{25} + \frac{y^2}{b^2} = 1, (b < 5) \) lying on the negative X-axis and \( P(\theta) \) is a point on this ellipse. If the distance between the foci of this ellipse is 8 and \( S'P = 7 \), then \( \theta \) is:

• (1) \( \frac{\pi}{6} \)
• (2) \( \frac{\pi}{3} \)
• (3) \( \frac{\pi}{4} \)
• (4) \( \frac{2\pi}{3} \)

The slope of the tangent drawn from the point \( (1,1) \) to the hyperbola \( 2x^2 - y^2 = 4 \) is:

• (1) 2
• (2) \( \frac{-2 \pm \sqrt{6}}{2} \)
• (3) \( -1 \pm \sqrt{6} \)
• (4) \( \frac{-2 \pm \sqrt{3}}{2} \)

The vertices of triangle \( \Delta ABC \) are \( A(2, 3, k) \), \( B(-1, k, -1) \), and \( C(4, -3, 2) \). If \( AB = AC \) and \( k > 0 \), then the triangle \( ABC \) is:

• (1) an equilateral triangle
• (2) a right-angled isosceles triangle
• (3) an isosceles triangle but not right angled
• (4) an obtuse angled isosceles triangle

If \( A(1, 2, -3) \), \( B(2, 3, -1) \), and \( C(3, 1, 1) \) are the vertices of triangle \( \Delta ABC \), then find \( \left| \frac{\cos A}{\cos B} \right|.\)

• (1) \( \frac{3\sqrt{3}}{4\sqrt{2}} \)
• (2) \( \frac{3\sqrt{3}}{\sqrt{7}} \)
• (3) \( \frac{4\sqrt{2}}{3\sqrt{3}} \)
• (4) \( \frac{\sqrt{7}}{3\sqrt{3}} \)

If \( a, b, c \) are the intercepts made on X, Y, Z-axes respectively by the plane passing through the points \( (1, 0, -2) \), \( (3, -1, 2) \), and \( (0, -3, 4) \), then \( 3a + 4b + 7c = \)?

• (1) \( -5 \)
• (2) \( 5 \)
• (3) \( -15 \)
• (4) \( 15 \)

If \( \lim_{x \to 4} \frac{2x^2 + (3+2a)x + 3a}{x^3 - 2x^2 - 23x + 60} = \frac{11}{9} \), then find \( \lim_{x \to a} \frac{x^2 + 9x + 20}{x^2 - x - 20} \).

• (1) \( -9 \)
• (2) \( -4 \)
• (3) \( -\frac{1}{4} \)
• (4) \( -\frac{1}{9} \)

If the function \( f(x) \) is given by \[ f(x) = \begin{cases} \frac{\tan(a(x-1))}{\frac{x-1}{x}}, & if 0 < x < 1
\frac{x^3-125}{x^2 - 25} , & if 1 \leq x \leq 4
\frac{b^x - 1}{x}, & if x > 4 \end{cases} \]
is continuous in its domain, then find \( 6a + 9b^4 \).

• (1) 284
• (2) 261
• (3) 214
• (4) 317

If \( y = \log \left[ \tan \left( \sqrt\frac{2x - 1}{2x + 1} \right) \right] \) for \( x > 0 \), then find \[ \left( \frac{dy}{dx} \right)_{x = 1}. \]

• (A) \( \frac{4\sqrt{2} \log 2}{9 \sin \left( \frac{2}{\sqrt{3}} \right)} \)
• (B) \( \frac{4\sqrt{2} \log 2}{9 \sin \left( \frac{\sqrt{3}}{2} \right)} \)
• (C) \( \frac{4\sqrt{3} \log 2}{9 \sin \left( \frac{2}{\sqrt{3}} \right)} \)
• (D) \( \frac{4\sqrt{2} \log 2}{9 \sin \left( \frac{\sqrt{3}}{2} \right)} \)

If \( y = \cos^{-1}\left( \frac{6x^2 - 2x^2 - 4}{2x^2 - 6x + 5} \right) \), then find \( \frac{dy}{dx} \).

• (1) \( \frac{2}{\sqrt{3x^2 - x^2 - 2}} \)
• (2) \( \frac{2}{3x^2 - 2} \)
• (3) \( \frac{2}{\sqrt{2x^2 - 6x + 5}} \)
• (4) \( \frac{2}{2x^2 - 6x + 5} \)

If \( \log y = y^{\log x} \), then \( \frac{dy}{dx} \) is:

• (1) \( \frac{y (\log y)^2}{x(1 - \log x \log y)} \)
• (2) \( \frac{y \log y}{x(1 - \log x \log y)} \)
• (3) \( \frac{y (1 - \log x \log y)}{x \log^2 x} \)
• (4) \( \frac{y}{x(1 - \log x \log y)} \)

If \( y = a \cos 3x + b e^{-x} \), then \( y'(3\sin 3x - \cos 3x) = \):

• (1) \( 10y' \sin 3x + 3y \sin 3x + 3 \cos 3x \)
• (2) \( 10y' \cos 3x + 3y \sin 3x \)
• (3) \( 10y' \cos 3x + 3y \sin 3x + 3 \sin 3x \)
• (4) \( 10y' \cos 3x + 3y \sin 3x + 3 \cos 3x \)

The approximate value of \( \sec 59^\circ \) obtained by taking \( 1^\circ = 0.0174 \) and \( \sqrt{3} = 1.732 \) is:

• (1) \( 1.9849 \)
• (2) \( 1.8493 \)
• (3) \( 1.9397 \)
• (4) \( 1.9948 \)

The equation of the normal drawn to the curve \( y^3 = 4x^5 \) at the point \( (4,16) \) is:

• (1) \( 20x + 3y = 128 \)
• (2) \( 20x - 3y = 32 \)
• (3) \( 3x - 20y + 308 = 0 \)
• (4) \( 3x + 20y = 332 \)

A point \( P \) is moving on the curve \( x^3 y^4 = 27 \). The x-coordinate of \( P \) is decreasing at the rate of 8 units per second. When the point \( P \) is at \( (2, 2) \), the y-coordinate of \( P \) is:

• (1) increases at the rate of 6 units per second
• (2) decreases at the rate of 6 units per second
• (3) increases at the rate of 4 units per second
• (4) decreases at the rate of 4 units per second

If the function \( f(x) = x^3 + ax^2 + bx + 40 \) satisfies the conditions of Rolle’s theorem on the interval \( [-5, 4] \) and \( -5, 4 \) are two roots of the equation \( f(x) = 0 \), then one of the values of \( c \) as stated in that theorem is:

• (1) 3
• (2) \( \frac{1 + \sqrt{67}}{3} \)
• (3) \( \frac{1 + \sqrt{65}}{3} \)
• (4) \( -2 \)

If \( x \) and \( y \) are two positive integers such that \( x + y = 24 \) and \( x^3 y^5 \) is maximum, then \( x^2 + y^2 \) is:

• (1) 288
• (2) 296
• (3) 306
• (4) 320

Evaluate the integral: \[ \int 4\cos^2 x - 5\sin^2 x \cos x \, dx. \]

• (1) \( \frac{1}{2} \cos x \sqrt{ (4 - 9 \sin^2 x)} + \frac{2}{3} \sin^{-1} \left( \frac{3 \sin x}{2} \right) + c \)
• (2) \( \frac{1}{2} \sin x \sqrt{(4 - 9 \sin^2 x)} + \frac{2}{3} \cos^{-1} \left( \frac{3 \cos x}{2} \right) + c \)
• (3) \( \frac{1}{2} \cos x \sqrt{(1 - 9 \cos^2 x)} + \frac{2}{3} \sin^{-1} \left( \frac{3 \cos x}{2} \right) + c \)
• (4) \( \frac{1}{2} \sin x (4 - 9 \cos^2 x) + \frac{2}{3} \sin^{-1} \left( \frac{3 \sin x}{2} \right) + c \)

Evaluate the integral: \[ \int \frac{4\tan^4 x + 3 \tan^2 x - 1}{\tan^2 x + 4} \, dx. \]

• (1) \( 4 \tan x - \frac{17}{4} \tan ^{-1} \frac{tan x}{4} \)
• (2) \( 4 \tan x - \frac{17}{4} \tan ^{-1} \frac{tan x}{2} \)
• (3) \( 4 \tan x - \frac{17}{2} \tan ^{-1} \frac{tan x}{2} \)
• (4) \( 2 \tan x - \frac{17}{2} \tan ^{-1} \frac{tan x}{2} \)

Evaluate the integral: \[ \int \frac{(\sin^4x + 2\cos^2x - 1) \cos x}{(1 + \sin x)^6} \, dx \]

• (1) \( \frac{\sin^6 x}{6(1 + \sin x)^6} + c \)
• (2) \( - \frac{\sin^6 x}{6(1 + \sin x)^6} + c \)
• (3) \( \frac{\cos^6 x}{6(1 + \sin x)^6} + c \)
• (4) \( - \frac{\cos^6 x}{6(1 + \sin x)^6} + c \)

Evaluate the integral: \[ \int (\log x)^3 \, dx \]

• (1) \( ( \log x)^3 - 3 (\log x)^2 + 6 \log x - 6 + c \)
• (2) \( x [ (\log x)^3 - 3 (\log x)^2 + 6 \log x - 6 ] + c \)
• (3) \( (x \log x)^3 - 3 (x \log x)^2 + 6x \log x - 6x + c \)
• (4) \( x [ (\log x)^3 - 3 (\log x)^2 + 6 \log x - 6 ] + c \)

Evaluate the integral: \[ \int \left( \sin^3 x + \cos^2 x \right)^2 \, dx \]

• (1) \( \frac{15 \pi}{16} + \frac{8}{15} \)
• (2) \( \frac{11 \pi}{16} + \frac{8}{15} \)
• (3) \( \frac{15 \pi}{16} + \frac{4}{15} \)
• (4) \( \frac{11 \pi}{16} + \frac{4}{15} \)

Evaluate the integral: \[ I = \int_{-\frac{\pi}{8}}^{\frac{\pi}{8}} \frac{\sin^4(4x)}{1 + e^{4x}} \, dx \]

• (1) \( \frac{3\pi}{128} \)
• (2) \( \frac{3\pi}{256} \)
• (3) \( \frac{3\pi}{64} \)
• (4) \( \frac{3\pi}{32} \)

The area of the region enclosed by the curves \( y^2 = 4(x+1) \) and \( y^2 = 5(x-4) \) is:

• (1) \( \frac{280}{3} \)
• (2) 150
• (3) 140
• (4) \( \frac{200}{3} \)

If A and B are arbitrary constants, then the differential equation having \[ y = Ae^{-x} + B \cos x \]
as its general solution is:

• (1) \( (\sin x - \cos x) \frac{d^2 y}{dx^2} + 2 \cos x \frac{dy}{dx} - (\sin x + \cos x) y = 0 \)
• (2) \( (\sin x - \cos x) \frac{d^2 y}{dx^2} + 2 \cos x \frac{dy}{dx} + (\sin x + \cos x) y = 0 \)
• (3) \( (\cos x + \sin x) \frac{d^2 y}{dx^2} + 2 \sin x \frac{dy}{dx} - (\sin x - \cos x) y = 0 \)
• (4) \( (\cos x - \sin x) \frac{d^2 y}{dx^2} - 2 \sin x \frac{dy}{dx} + (\cos x + \sin x) y = 0 \)

The general solution of the differential equation \[ \frac{dy}{dx} + \frac{\sin(2x + y)}{\cos x} + 2 = 0 \]
is:

• (1) \( (\sec x + \tan x)[\csc(2x + y) - \cot(2x + y)] = c \)
• (2) \( \sin(2x + y) \cos x = c \)
• (3) \( \cos(2x + y) \sin x = c \)
• (4) \( (\csc x - \cot x)(\sec(2x + y) - \tan(2x + y)) = c \)

Which of the following statements regarding the nature of physical laws is NOT correct?

• (1) All conserved quantities are necessarily scalars
• (2) The laws of nature do not change with time
• (3) The laws of nature are the same everywhere in the universe
• (4) The law of gravitation is the same both on the moon and the earth

The internal and external diameters of a hollow cylinder measured with vernier calipers are (5.73 \(\pm\) 0.01) cm and (6.01 \(\pm\) 0.01) cm respectively. Then the thickness of the cylinder wall is

• (1) (0.28 \(\pm\) 0.01) cm
• (2) (0.28 \(\pm\) 0.02) cm
• (3) (0.14 \(\pm\) 0.02) cm
• (4) (0.14 \(\pm\) 0.01) cm

A body moving with uniform acceleration travels a distance of 25 m in the fourth second and 37 m in the sixth second. The distance covered by the body in the next two seconds is

• (1) 63 m
• (2) 84 m
• (3) 49 m
• (4) 92 m

A body is projected from the ground at an angle of \( \tan^{-1}\sqrt{7} \) with the horizontal. At half of the maximum height, the speed of the body is \( n \) times the speed of projection. The value of \( n \) is

• (1) 2
  (2) \( \frac{1}{2} \)
• (3) \( \frac{4}{3} \)
• (4) \( \frac{3}{4} \)

An aircraft executes a horizontal loop of radius 9 km at a constant speed of 540 km/h. The wings of the aircraft are banked at an angle of

• (1) \( \sec^{-1}(4) \)
• (2) \( \cot^{-1}(4) \)
• (3) \( \tan^{-1}(4) \)
• (4) \( \sec^{-1}(4) \)

A body thrown vertically upwards from the ground reaches a maximum height ‘h’. The ratio of the kinetic and potential energies of the body at a height 40% of h from the ground is

• (1) 2:3
• (2) 3:2
• (3) 1:1
• (4) 4:9

A ball of mass 1.2 kg moving with a velocity of 12 ms\(^{-1}\) makes a one-dimensional collision with another stationary ball of mass 1.2 kg. If the coefficient of restitution is \( \frac{1}{\sqrt{2}} \), then the ratio of the total kinetic energy of the balls after the collision to the initial kinetic energy is

• (1) \( \frac{3}{4} \)
• (2) 1:1
• (3) 2:3
• (4) 3:5

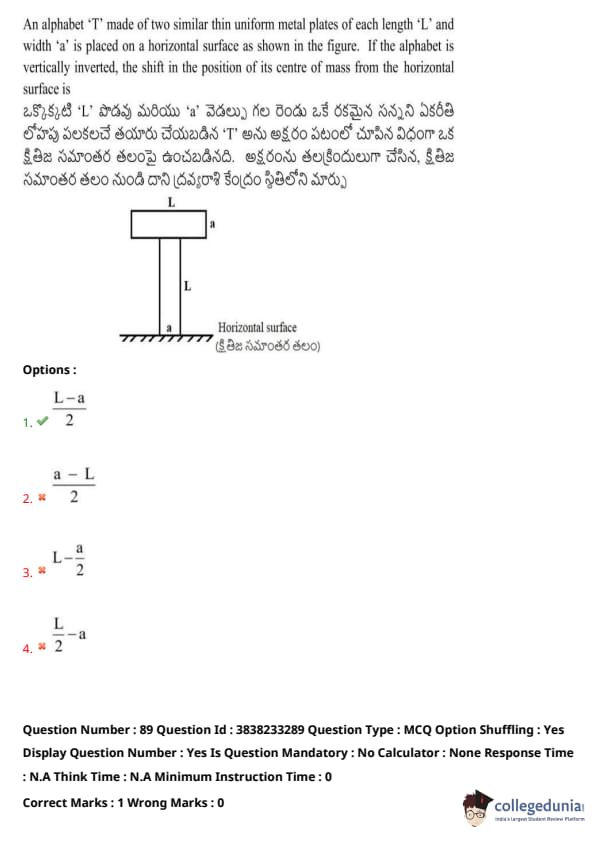
An alphabet ‘T’ made of two similar thin uniform metal plates of each length \( L \) and width \( a \) is placed on a horizontal surface as shown in the figure. If the alphabet is vertically inverted, the shift in the position of its center of mass from the horizontal surface is:

• (1) \( \frac{L - a}{2} \)
• (2) \( \frac{a - L}{2} \)
• (3) \( \frac{L - a}{2} \)
• (4) \( L - a \)

A solid sphere and a disc of same mass \(M\) and radius \(R\) are kept such that their curved surfaces are in contact and their centers lie along the same horizontal line. The moment of inertia of the two body system about an axis passing through their point of contact and perpendicular to the plane of the disc is:

• (1) \( \frac{53 MR^2}{20} \)
• (2) \( \frac{39 MR^2}{10} \)
• (3) \( \frac{29 MR^2}{10} \)
• (4) \( \frac{9 MR^2}{10} \)

If a body is dropped freely from a height of 20 m and reaches the surface of a planet with a velocity of 31.4 m/s, then the length of a simple pendulum that ticks seconds on the planet is:

• (1) \(1 \, m\)
• (2) \(0.625 \, m\)
• (3) \(2.5 \, m\)
• (4) \(2 \, m\)

Two stars of masses \( M \) and \( 2M \) that are at a distance \( d \) apart, are revolving one around another. The angular velocity of the system of two stars is:

• (1) \( \sqrt{\frac{4GM}{d^3}} \)
• (2) \( \sqrt{\frac{2GM}{d^3}} \)
• (3) \( \sqrt{\frac{9GM}{d^3}} \)
• (4) \( \sqrt{\frac{3GM}{d^3}} \)

A block of mass 2 kg is tied to one end of a 2 m long metal wire of 1.0 mm² area of cross-section and rotated in a vertical circle such that the tension in the wire is zero at the highest point. If the maximum elongation in the wire is 2 mm, the Young’s modulus of the metal is:

• (1) \( 1.0 \times 10^{11} \, Nm^{-2} \)
• (2) \( 1.2 \times 10^{11} \, Nm^{-2} \)
• (3) \( 2.0 \times 10^{11} \, Nm^{-2} \)
• (4) \( 0.2 \times 10^{11} \, Nm^{-2} \)

A big liquid drop splits into ‘n’ similar small drops under isothermal conditions, then in this process:

• (1) Volume decreases
• (2) Total surface area decreases
• (3) Energy is absorbed
• (4) Energy is liberated

A wooden cube of side 10 cm floats at the interface between water and oil with its lower surface 3 cm below the interface. If the density of oil is 0.9 g/cm³, the mass of the wooden cube is:

• (1) 940 g
• (2) 900 g
• (3) 1000 g
• (4) 930 g

37 g of ice at 0°C is mixed with 74 g of water at 70°C. The resultant temperature is:

• (1) 45°C
• (2) 70°C
• (3) 20°C
• (4) 35°C

The thickness of a uniform rectangular metal plate is 5 mm and the area of each surface is 3750 cm\(^2\). In steady state, the temperature difference between the two surfaces of the plate is 14°C. If the heat flowing through the plate in one second from one surface to the other surface is 42 J, then the thermal conductivity of the metal is:

• (1) \( 90 \, Wm^{-1}K^{-1} \)
• (2) \( 30 \, Wm^{-1}K^{-1} \)
• (3) \( 45 \, Wm^{-1}K^{-1} \)
• (4) \( 60 \, Wm^{-1}K^{-1} \)

The ratio of the specific heat capacities of a gas is 1.5. When the gas undergoes an adiabatic process, its volume is doubled and pressure becomes \( P_1 \). When the gas undergoes isothermal process, its volume is doubled and pressure becomes \( P_2 \). If \( P_1 = P_2 \), the ratio of the initial pressures of the gas when it undergoes adiabatic and isothermal processes is:

• (1) \( \sqrt{3}: \sqrt{2} \)
• (2) \( 1: 1 \)
• (3) \( \sqrt{3}:1 \)
• (4) \( \sqrt{2}:1 \)

A vessel contains hydrogen and nitrogen gases in the ratio 2:3 by mass. If the temperature of the mixture of the gases is 30°C, then the ratio of the average kinetic energies per molecule of hydrogen and nitrogen gases is:

• (1) \( 3:7 \)
• (2) \( 2:3 \)
• (3) \( 1:1 \)
• (4) \( 1:14 \)

The difference between the fundamental frequencies of an open pipe and a closed pipe of the same length is 100 Hz. The difference between the frequencies of the second harmonic of the open pipe and the third harmonic of the closed pipe is:

• (1) \( 100 \, Hz \)
• (2) \( 150 \, Hz \)
• (3) \( 200 \, Hz \)
• (4) \( 250 \, Hz \)

The displacement equations of sound waves produced by two sources are given by: \( y_1 = 5 \sin(400t) \) and \( y_2 = 8 \sin(408t) \), where \( t \) is time in seconds. If the waves are produced simultaneously, the number of beats produced per minute is:

• (1) \( 4 \)
• (2) \( 8 \)
• (3) \( 120 \)
• (4) \( 240 \)

When an object of height 12 cm is placed at a distance from a convex lens, an image of height 18 cm is formed on a screen. Without changing the positions of the object and the screen, if the lens is moved towards the screen, another clear image is formed on the screen. The height of this image is.

• (1) \(4 \, cm\)
• (2) \(6 \, cm\)
• (3) \(8 \, cm\)
• (4) \(10 \, cm\)

A thin plano-convex lens of focal length 73.5 cm has a circular aperture of diameter 8.4 cm. If the refractive index of the material of the lens is \( \frac{5}{3} \), then the thickness of the lens is nearly.

• (1) \(2.4 \, cm\)
• (2) \(2.4 \, mm\)
• (3) \(1.8 \, cm\)
• (4) \(1.8 \, mm\)

In Young's double slit experiment, intensity of light at a point on the screen where the path difference becomes \( \lambda \) is I. The intensity at a point on the screen where the path difference becomes \( \frac{\lambda}{3} \) is,

• (1) \( \frac{I}{4} \)
• (2) \( \frac{I}{3} \)
• (3) \( \frac{2I}{3} \)
• (4) \( \frac{I}{3} \)

Two point charges -10 µC and +5 µC are situated on the X-axis at \( x = 0 \) and \( x = \sqrt{2} \, m \). The point along the X-axis where the electric field becomes zero is.

• (1) \( x = \left( \sqrt{2} - 1 \right) \, m \)
• (2) \( x = 2 \left( \sqrt{2} - 1 \right) \, m \)
• (3) \( x = 2 \left( \sqrt{2} + 1 \right) \, m \)
• (4) \( x = \left( \sqrt{2} + 1 \right) \, m \)

A 10 µF capacitor is charged by a 100 V battery. It is disconnected from the battery and is connected to another uncharged capacitor of capacitance 30 µF. During this process, the electrostatic energy lost by the first capacitor is.

• (1) \( 5 \times 10^{-2} \, J \)
• (2) \( 1.25 \times 10^{-2} \, J \)
• (3) \( 2.75 \times 10^{-2} \, J \)
• (4) \( 3.75 \times 10^{-2} \, J \)

A conductor of length 1.5 m and area of cross-section \( 3 \times 10^{-5} \, m^2 \) has electrical resistance of 15 \( \Omega \). The current density in the conductor for an electric field of 21 \( V/m \) is.

• (1) \( 0.7 \times 10^6 \, A/m^2 \)
• (2) \( 0.7 \times 10^{-6} \, A/m^2 \)
• (3) \( 0.7 \times 10^{-5} \, A/m^2 \)
• (4) \( 0.7 \times 10^5 \, A/m^2 \)

The relation between the current \( i \) (in ampere) in a conductor and the time \( t \) (in second) is given by \( i = 12t + 9t^2 \). The charge passing through the conductor between the times \( t = 2 \, s \) and \( t = 10 \, s \) is.

• (1) \( 3720 \, C \)
• (2) \( 3648 \, C \)
• (3) \( 3600 \, C \)
• (4) \( 3552 \, C \)

A long straight rod of diameter 4 mm carries a steady current \( i \). The current is uniformly distributed across its cross-section. The ratio of the magnetic fields at distances 1 mm and 4 mm from the axis of the rod is.

• (1) 8:1
• (2) 1:4
• (3) 4:1
• (4) 1:1

A straight wire of length 20 cm carrying a current of \(\frac{3}{\pi ^2} \, A \) is bent in the form of a circle. The magnetic field at the centre of the circle is.

• (1) \( 8 \times 10^{-6} \, T \)
• (2) \( 3 \times 10^{-6} \, T \)
• (3) \( 12 \times 10^{-6} \, T \)
• (4) \( 6 \times 10^{-6} \, T \)

A circular coil carrying a current of 2.5 A is free to rotate about an axis in its plane perpendicular to an external magnetic field. When the coil is made to oscillate, the time period of oscillation is \( T \). If the current through the coil is 10 A, the time period of oscillation is.

• (1) \( T/2 \)
• (2) \( T \)
• (3) \( 2T \)
• (4) \( T/4 \)

A circular coil of area 200 cm\(^2\) and 50 turns is rotating about its vertical diameter with an angular speed of 40 rad/s in a uniform horizontal magnetic field of magnitude \(2 \times 10^{-2} \, T\). The maximum emf induced in the coil is.

• (1) \( 1.2 \, V \)
• (2) \( 0.8 \, V \)
• (3) \( 0.6 \, V \)
• (4) \( 0.3 \, V \)

An inductor and a resistor are connected in series to an AC source of 10 V. If the potential difference across the inductor is 6 V, then the potential difference across the resistor is

• (1) \( 4 \, V \)
• (2) \( 10 \, V \)
• (3) \( 6 \, V \)
• (4) \( 8 \, V \)

If the peak value of the magnetic field of an electromagnetic wave is \( 30 \times 10^{-9} \, T \), then the peak value of the electric field is

• (1) \( 3 \, Vm^{-1} \)
• (2) \( 12 \, Vm^{-1} \)
• (3) \( 6 \, Vm^{-1} \)
• (4) \( 9 \, Vm^{-1} \)

The de Broglie wavelength of a proton is twice the de Broglie wavelength of an alpha particle. The ratio of the kinetic energies of the proton and the alpha particle is:

• (1) \( 1:1 \)
• (2) \( 1:4 \)
• (3) \( 1:2 \)
• (4) \( 1:8 \)

The ratio of the centripetal accelerations of the electron in two successive orbits of hydrogen is 81:16. Due to a transition between these two states, the angular momentum of the electron changes by:

• (1) \( \frac{h}{3\pi} \)
• (2) \( \frac{3h}{\pi} \)
• (3) \( \frac{h}{2\pi} \)
• (4) \( \frac{2h}{\pi} \)

The operation of a nuclear reactor is said to be critical when the value of neutron multiplication factor \( K \) is

• (1) \( K = 0 \)
• (2) \( K > 1 \)
• (3) \( K = 1 \)
• (4) \( 0 < K < 1 \)

An \(\alpha\)-particle of energy \( E \) is liberated during the decay of a nucleus of mass number 236. The total energy released in this process is 236. The total energy released in this process is

• (1) \( 58E \)
• (2) \( 59E \)
• (3) \( \frac{58E}{59} \)
• (4) \( \frac{59E}{58} \)

The voltage gain of a transistor in common emitter configuration is 160. The resistances in base and collector sides of the circuit are 1k\( \Omega \) and 4k\( \Omega \), respectively. If the change in base current is 100\( \mu \)A, then the change in output current is

• (1) \( 4 mA \)
• (2) \( 4 \mu A \)
• (3) \( 40 mA \)
• (4) \( 40 \mu A \)

Normally a capacitor is connected across the output terminals of a rectifier to

• (1) convert AC to DC
• (2) convert DC to AC
• (3) to get a varying DC output
• (4) to get a steady DC output

The process of the loss of strength of a signal while propagating through a medium is

• (1) damping
• (2) attenuation
• (3) amplification
• (4) modulation

The wavenumber of the first spectral line of the Lyman series of He\(^+\) ion is \( x \) m\(^{-1}\). What is the wavenumber (in m\(^{-1}\)) of the second spectral line of the Balmer series of Li\(^{2+}\) ion?

• (1) \( \frac{9x}{16} \)
• (2) \( \frac{16x}{9} \)
• (3) \( \frac{8x}{27} \)
• (4) \( \frac{27x}{8} \)

The uncertainty in the determination of the position of a small ball of mass 10 g is \(10^{-33}\) m. With what % of accuracy can its speed be measured, if it has a speed of 52.5 m s\(^{-1}\)?

• (1) \( 1.0% \)
• (2) \( 20% \)
• (3) \( 10% \)
• (4) \( 2.0% \)

In which of the following ionic pairs, the second ion is smaller in size than the first ion?

• (1) \( Al^{3+}, Mg^{2+} \)
• (2) \( F^-, Na^+ \)
• (3) \( O^{2-}, N^{3-} \)
• (4) \( Mg^{2+}, Na^+ \)

The set of elements which obey the general electronic configuration \( (n-1)d^{10} ns^2 \) is:

• (1) \( Bh, Eu, Po \)
• (2) \( Ho, Er, Lu \)
• (3) \( Hs, Hg, W \)
• (4) \( Hs, Bi, Ba \)

Identify the set of molecules which are not in the correct order of their dipole moments.

• (1) \( HF > HCl > HBr \)
• (2) \( H_2O > H_2S > CO_2 \)
• (3) \( H_2S > HCl > HF \)
• (4) \( NH_3 > NF_3 > BF_3 \)

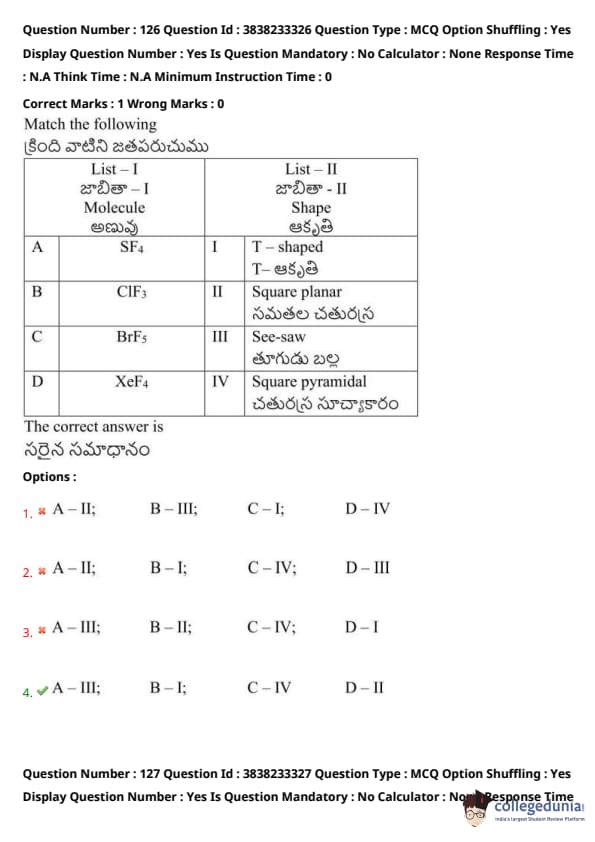
Match the following molecules with their respective molecular shapes:


\renewcommand{\arraystretch{1.3
\begin{tabular{|c|c|
\hline
List - I (Molecule) & List - II (Shape)

\hline
A) \( SF_4 \) & I) T - shaped

B) \( ClF_3 \) & II) Square planar

C) \( BrF_5 \) & III) See-saw

D) \( XeF_4 \) & IV) Square pyramidal

\hline
\end{tabular

• (1) A - II; B - III; C - I; D - IV
• (2) A - II; B - I; C - IV; D - III
• (3) A - III; B - I; C - IV; D - I
• (4) A - III; B - I; C - IV; D - II

At 400 K, an ideal gas is enclosed in a 0.5 m\(^3\) vessel at a pressure of 203 kPa. What is the change in temperature required (in K), if it occupies a volume of 0.2 m\(^3\) under a pressure of 304 kPa? (Nearest integer)

• (1) 240
• (2) 160
• (3) 120
• (4) 80

Match the following substances with their respective equivalent weights:


\renewcommand{\arraystretch{1.3
\begin{tabular{|c|c|
\hline
List - I (Substance) & List - II (Equivalent weight)

\hline
A) \( Na_2CO_3 \) & I) \( \frac{M}{5} \)

B) \( KMnO_4 | H^+ \) & II) \( \frac{M}{3} \)

C) \( K_2Cr_2O_7 | H^+ \) & III) \( \frac{M}{2} \)

D) \( KMnO_4 | H_2O \) & IV) \( \frac{M}{6} \)

\hline
\end{tabular

• (1) A - III; B - I; C - IV; D - II
• (2) A - III; B - IV; C - I; D - II
• (3) A - II; B - III; C - IV; D - I
• (4) A - IV; B - II; C - III; D - I

The standard enthalpy of combustion of C (graphite), H\(_2\) (g) and CH\(_3\)OH (l) respectively are \(-393\), \(-286\) and \(-726\) kJ mol\(^{-1}\). What is the standard enthalpy of formation of methanol?

• (1) \(-726\) kJ mol\(^{-1}\)
• (2) \(-239\) kJ mol\(^{-1}\)
• (3) \(-96\) kJ mol\(^{-1}\)
• (4) \(+96\) kJ mol\(^{-1}\)

Observe the following species:

(i) \( NH_3 \)
(ii) \( AlCl_3 \)
(iii) \( SnCl_4 \)
(iv) \( CO_2 \)
(v) \( Ag^+ \)
(vi) \( HSO_4^- \)

How many of the above species act as Lewis acids?

• (1) 5
• (2) 3
• (3) 4
• (4) 2

The normality of a 20-volume solution of hydrogen peroxide is:

• (1) 0.892 N
• (2) 1.785 N
• (3) 2.678 N
• (4) 3.570 N

Consider the following reactions:
\[ Cs + O_2 (excess) \rightarrow X \] \[ Cs + O_2 (limited) \rightarrow X \] \[ Na + O_2 \rightarrow Y \]

Identify the correct statement about \( X \) and \( Y \).

• (1) \( Y \) is monoxide and \( X \) is superoxide
• (2) \( Y \) is peroxide and \( X \) is peroxide
• (3) \( Y \) is peroxide and \( X \) is superoxide
• (4) \( Y \) is superoxide and \( X \) is peroxide

Choose the correct statements from the following:

I) In vapour phase, \( BeCl_2 \) exists as a chlorobridged dimer.

II) \( BeSO_4 \) is readily soluble in water.

III) \( BeO \) is completely basic in nature.

IV) \( BeCO_3 \), being unstable, is kept in the atmosphere of \( CO_2 \).

V) \( BeCO_3 \) is less soluble among all the carbonates of group 2 elements.

• (1) II, III, IV
• (2) I, II, IV
• (3) I, IV, V
• (4) II, III, V

Which of the following statements is correct regarding boric acid?

• (1) It acts as a weak Lewis acid by accepting \( OH^- \) from water.
• (2) It is a proton donor acid.
• (3) It is a strong tribasic acid.
• (4) It behaves as a Brønsted-Lowry acid in aqueous solution.

Assertion (A): Silicones are used for waterproofing of fabrics.

Reason (R): The repeating unit in silicones is

• (1) (A) and (R) are correct, but (R) is not the correct explanation of (A).
• (2) (A) and (R) are correct, (R) is the correct explanation of (A).
• (3) (A) is not correct but (R) is correct.
• (4) (A) is correct but (R) is not correct.

Acrolein (X) is one of the chemicals formed when \( O_3 \) and \( NO_2 \) react with unburnt hydrocarbons present in polluted air. The structure of 'X' is:

• (1) \( CH_3-CH=CH_2 \)
• (2) \( CH_2=CH-CHO \)
• (3) \( CH_2=CH-CN \)
• (4) \( CH_3CO(OO)NO_2 \)

An organic compound containing phosphorus on oxidation with \( Na_2O_2 \) gives a compound \( X \). When \( X \) is boiled with \( HNO_3 \) and treated with a reagent, it gives a yellow precipitate \( Y \). Identify \( X \) and \( Y \).

• (1) \( Na_3PO_4, (NH_4)_2MoO_3 \)
• (2) \( Na_3PO_4, (NH_4)_2MoO_4 \)
• (3) \( H_3PO_4, (NH_4)_2MoO_4 \)
• (4) \( Na_3PO_4, (NH_4)_3PO_4 \cdot 12MoO_3 \)

The correct IUPAC name of the given compound is:

• (1) 5-Amino-4-methyl-2-oxohex-3-en-1-ol
• (2) 4-Amino-2-methylpentanoic acid
• (3) 5-Amino-1-hydroxy-3-methylhex-3-en-2-one
• (4) 2-Amino-6-hydroxy-5-keto-4-methyl-3-hexene

The major product ‘Y’ in the given sequence of reactions is:

• (1) \( CH_3CH_2CH_2Br \)
• (2) \( CH_3CH(Br)CH_3 \)
• (3) \( CH_3COC_6H_5 \)
• (4) \( C_6H_5COBr \)

Compound ‘A’ on heating with sodalime gives propane. Identify the compound ‘A’.

• (1) \( CH_3-CH_2-CH_2OH \)
• (2) \( CH_3CH_2CO_2Na \)
• (3) \( CH_3CH_2CH_2CO_2Na \)
• (4) \( CH_3COCH_3 \)

An element with molar mass \( 2.7 \times 10^{-2} \) kg mol\(^{-1}\) forms a cubic unit cell with an edge length of 405 pm. If its density is \( 2.7 \times 10^3 \) kg m\(^{-3}\), the number of atoms present in one unit cell is:
(Given: \( N_A = 6.023 \times 10^{23} \) mol\(^{-1}\))

• (1) 2
• (2) 4
• (3) 6
• (4) 12

At 300 K, 0.06 kg of an organic solute is dissolved in 1 kg of water. The vapour pressure of the solution is 3.768 kPa. If the vapour pressure of pure water at that temperature is 3.78 kPa, what is the molar mass of the solute (in g mol\(^{-1}\))?

• (1) 180
• (2) 120
• (3) 340
• (4) 260

The molar conductivity of 0.02 M solution of an electrolyte is \( 124 \times 10^{-4} \) S m\(^{2}\) mol\(^{-1}\). What is the resistance of the same solution (in ohms), kept in a cell of cell constant 129 m\(^{-1}\)?

• (1) 390
• (2) 130
• (3) 260
• (4) 520

The decomposition of benzene diazonium chloride is a first-order reaction. The time taken for its decomposition to \( \frac{1}{4} \) and \( \frac{1}{10} \) of its initial concentration are \( t_{1/4} \) and \( t_{1/10} \) respectively. The value of \( \frac{t_{1/4}}{t_{1/10}} \times 100 \) is:
(Given: log 2 = 0.3)

• (1) 60
• (2) 30
• (3) 90
• (4) 45

10 mL of 0.5 M NaCl is required to coagulate 1L of \( Sb_2S_3 \) sol in 2 hours time. The flocculating value of NaCl (in millimoles) is:

• (1) 20
• (2) 10
• (3) 5
• (4) 15

Kaolinite is a silicate mineral of metal 'X' and calamine is a carbonate mineral of metal 'Y'. X and Y respectively are:

• (1) Fe, Cu
• (2) Zn, Al
• (3) Al, Zn
• (4) Zn, Cu

In the reaction: \[ NH_2CONH_2 + 2H_2O \rightarrow [X] \rightleftharpoons 2NH_3 + H_2O + [Y] \]
The hybridization of carbon in \( X \) and \( Y \) respectively are:

• (1) \( sp^2, sp \)
• (2) \( sp, sp^2 \)
• (3) \( sp^3, sp^2 \)
• (4) \( sp^2, sp^3 \)

Among the hydrides \( NH_3, PH_3, \) and \( BiH_3 \), the hydride with highest boiling point is \( X \) and the hydride with lowest boiling point is \( Y \). What are \( X \) and \( Y \) respectively?

• (1) \( PH_3, NH_3 \)
• (2) \( NH_3, PH_3 \)
• (3) \( BiH_3, PH_3 \)
• (4) \( NH_3, BiH_3 \)

Xenon (VI) fluoride on complete hydrolysis gives an oxide of xenon ‘O’. The total number of \( \sigma \) and \( \pi \) bonds in ‘O’ is:

• (1) 2
• (2) 4
• (3) 6
• (4) 8

In which of the following ions the spin-only magnetic moment is lowest?

• (1) \( [Ti(H_2O)_6]^{3+} \)
• (2) \( [Mn(H_2O)_6]^{2+} \)
• (3) \( [Ni(H_2O)_6]^{2+} \)
• (4) \( [Co(H_2O)_6]^{2+} \)

Identify the complex ion with electronic configuration \( t_{2g}^{3} e_{g}^{2} \).

• (1) \([Fe(H_2O)_6]^{3+}\)
• (2) \([Cr(H_2O)_6]^{3+}\)
• (3) \([Ni(H_2O)_6]^{2+}\)
• (4) \([Ti(H_2O)_6]^{3+}\)

Identify the structure of the polymer ‘P’ formed in the given reaction:

• (1)
• (2)
• (3)
• (4)

Which of the following vitamins is also called pyridoxine?

• (1) \( B_6 \)
• (2) \( B_{12} \)
• (3) \( B_2 \)
• (4) \( B_1 \)

The number of –OH groups present in the structures of bithionol, terpineol, and chloroxylenol is respectively:

• (1) 2, 1, 1
• (2) 1, 2, 1
• (3) 1, 1, 2
• (4) 2, 2, 1

Conversion of X to Y in the given reaction corresponds to:

• (1) Wurtz reaction
• (2) Fittig reaction
• (3) Wurtz-Fittig reaction
• (4) Sandmeyer reaction

Reaction of conversion of Y to Z in the given reaction corresponds to:

• (1) Reimer-Tiemann reaction
• (2) Kolbe’s reaction
• (3) Cannizzaro reaction
• (4) Stephen reaction

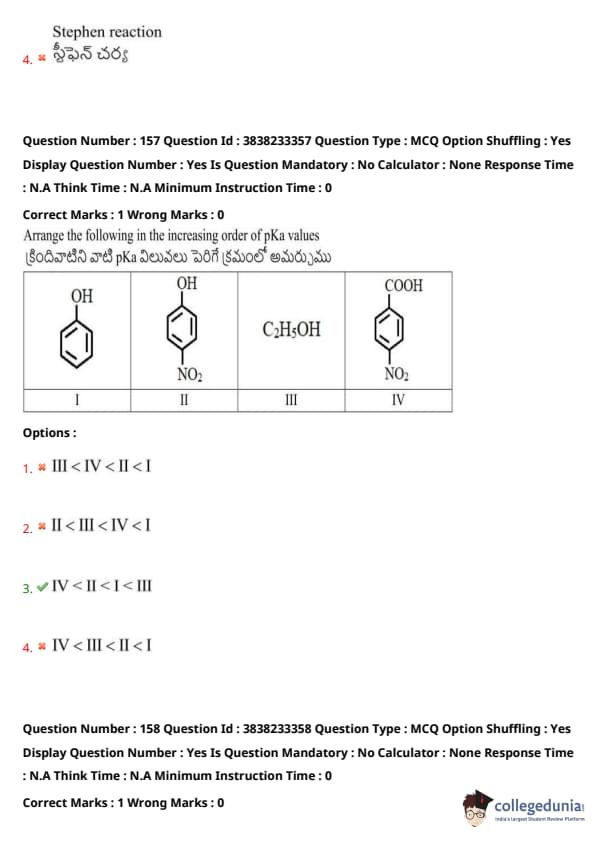
Arrange the following in the increasing order of pKa values.

• (1) \( III < IV < II < I \)
• (2) \( II < III < IV < I \)
• (3) \( IV < II < I < III \)
• (4) \( IV < III < II < I \)

What is 'C' in the following reaction sequence?

• (1) Propanone
• (2) 2-methyl-2-propanol
• (3) 2-methylprop-1-ene
• (4) But-2-enal

Identify the products R and S in the reaction sequence given.

• (1) \( (CH_3)_3Cl, CH_3OH \)
• (2) \( (CH_3)_3COH, CH_3I \)
• (3) \( (CH_3)_3COH, CH_3OH \)
• (4) \( (CH_3)_2C=CH_2, CH_3OH \)

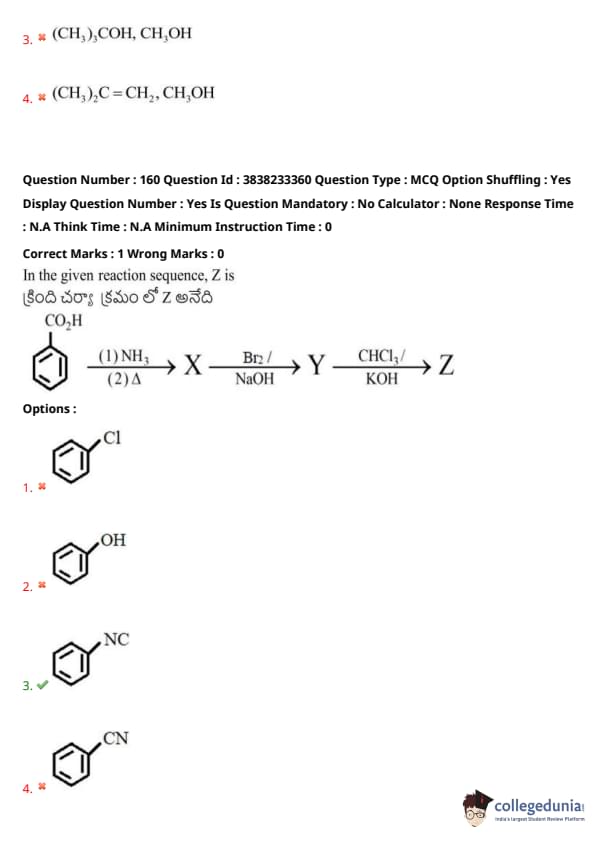
In the given reaction sequence, identify Z.

• (1)
• (2)
• (3)
• (4)