KEAM 2024 Question Paper (June 5) is available for download here. Office of The Commissioner for Entrance Examinations (CEE Kerala) conducted KEAM Engineering exam 2024 in CBT mode on June 5 in afternoon shift from 2 PM to 5 PM. KEAM 2024 Englineering Question Paper consists total of 150 questions carrying 4 mark each with negative marking of 1 for each incorrect answer. KEAM 2024 Question Paper includes Mathematics with 75 questions, Physics with 45 questions and Chemistry with 30 questions to be attempted in total of 180 minutes.
KEAM 2024 Question Paper with Answer Key PDF (June 5)
| KEAM 2024 (June 5) Question Paper with Answer Key | Check Solution |
The dimensional formula of the gravitational constant is \( M^a L^b T^c \), the values of \( a \), \( b \), and \( c \) are respectively:
View Solution
The gravitational constant \( G \) appears in Newton's law of gravitation:
\[ F = \frac{G m_1 m_2}{r^2} \]
where:
- \( F \) is the force with dimensional formula \( [M L T^{-2}] \)
- \( m_1 \) and \( m_2 \) are masses with dimensional formula \( [M] \)
- \( r \) is the distance with dimensional formula \( [L] \)
The dimensional formula of \( G \) can be derived as follows:
\[ [F] = \frac{[G] [M]^2}{[L]^2} \]
Substituting the dimensional formulas:
\[ [M L T^{-2}] = \frac{[G] M^2}{L^2} \]
Solving for \( [G] \):
\[ [G] = \frac{M L^3 T^{-2}}{M^2} = M^{-1} L^3 T^{-2} \]
Thus, the dimensional formula of \( G \) is:
\[ [G] = M^{-1} L^3 T^{-2} \]
Therefore, comparing this with \( M^a L^b T^c \), we get:
\[ a = -1, \quad b = 3, \quad c = -2 \]
Thus, the correct values of \( a \), \( b \), and \( c \) are \( -1, 3, -2 \).
\[ \boxed{(-1, 3, -2)} \] Quick Tip: To find the dimensional formula of physical constants, use the fundamental equations where the constant is present, and balance the dimensions of all quantities involved.
If the position of the particle is \( \mathbf{r} = 3 \hat{i} + 2 t^2 \hat{j} \), then the magnitude of its velocity at \( t = 5 \) second in \( ms^{-1} \) is:
View Solution
The position vector of the particle is given by: \[ \mathbf{r}(t) = 3 \hat{i} + 2 t^2 \hat{j} \]
To find the velocity, we differentiate the position vector with respect to time:
\[ \mathbf{v}(t) = \frac{d}{dt} \mathbf{r}(t) \]
Differentiating each component:
\[ \mathbf{v}(t) = \frac{d}{dt} (3 \hat{i}) + \frac{d}{dt} (2 t^2 \hat{j}) \]
\[ \mathbf{v}(t) = 0 \hat{i} + 4 t \hat{j} \]
Thus, the velocity vector is:
\[ \mathbf{v}(t) = 4 t \hat{j} \]
At \( t = 5 \) seconds:
\[ \mathbf{v}(5) = 4 \times 5 \hat{j} = 20 \hat{j} \, m/s \]
The magnitude of the velocity is:
\[ |\mathbf{v}(5)| = 20 \, m/s \]
Thus, the magnitude of the velocity at \( t = 5 \) seconds is \( 20 \, ms^{-1} \).
\[ \boxed{20} \] Quick Tip: The velocity is the derivative of the position vector with respect to time. For each component, differentiate and find the magnitude of the velocity vector.
If a freely falling body covers 80 m in the first 4 seconds, then in the next 4 seconds it covers a distance of:
View Solution
For a freely falling body, the distance traveled in time \( t \) is given by the equation: \[ s = ut + \frac{1}{2} g t^2 \]
where:
- \( u \) is the initial velocity (which is 0 for a freely falling body),
- \( g \) is the acceleration due to gravity (\( g \approx 9.8 \, m/s^2 \)),
- \( t \) is the time.
In the first 4 seconds, the body travels a distance of 80 m. Using the formula, we can write: \[ 80 = 0 + \frac{1}{2} g (4)^2 \] \[ 80 = \frac{1}{2} g \cdot 16 \] \[ g = \frac{80 \times 2}{16} = 10 \, m/s^2 \]
So, the value of \( g \) is approximately \( 10 \, m/s^2 \).
Now, in the next 4 seconds, the body continues to fall, and the distance covered in the next 4 seconds can be calculated as follows:
The total distance traveled in 8 seconds: \[ s = \frac{1}{2} g (8)^2 = \frac{1}{2} \times 10 \times 64 = 320 \, m \]
The distance covered in the next 4 seconds is the difference between the total distance covered in 8 seconds and the distance covered in the first 4 seconds: \[ Distance in next 4 seconds = 320 - 80 = 240 \, m \]
Thus, the correct answer is option (B), 240 m. Quick Tip: In problems involving freely falling bodies, use the kinematic equation \( s = ut + \frac{1}{2} g t^2 \) to find the distance traveled over a given time. Ensure to use the correct value for acceleration due to gravity.
Find the TRUE statement of the algebraic operations of scalar and vector quantities.
View Solution
- Option A: Adding two scalars of different dimensions is not possible. Scalars must have the same dimension in order to be added.
- Option B: Adding a scalar to a vector of the same dimension is not possible. Scalars and vectors belong to different categories and cannot be directly added.
- Option C: Multiplying any two scalars is indeed possible. Scalars are real numbers and their multiplication follows normal arithmetic rules.
- Option D: Multiplying any vector by any scalar is possible. This operation is called scalar multiplication and is a valid operation in vector algebra.
- Option E: Adding any two vectors is possible, as long as they are of the same dimension. The addition of vectors is a standard operation in vector algebra.
Step 1: Verifying the Correctness
- The multiplication of two scalars, as described in Option C, is always possible since scalars are just numbers and their multiplication follows the regular arithmetic rules.
Thus, the TRUE statement is:
\[ \boxed{(C) Multiplying any two scalars is possible.} \] Quick Tip: In algebraic operations, scalars are numbers and can always be multiplied together. Vectors, however, require specific conditions such as the same dimensions for addition or multiplication by scalars.
A car moving with a speed \( v \) is stopped at a distance \( d \) by a retarding force \( F \). The force needed to stop the same car moving with the speed \( 3v \) within the same distance is:
View Solution
The work-energy theorem states that the work done by the retarding force is equal to the change in the kinetic energy of the car.
\[ W = \Delta KE = \frac{1}{2} m v^2 \]
where \( m \) is the mass of the car and \( v \) is the initial velocity. The work done by the force \( F \) over a distance \( d \) is:
\[ W = F \times d \]
Thus, we have the equation:
\[ F \times d = \frac{1}{2} m v^2 \]
For the car moving with a speed \( 3v \), its initial kinetic energy will be:
\[ KE_{new} = \frac{1}{2} m (3v)^2 = \frac{1}{2} m \times 9v^2 = 9 \times \left( \frac{1}{2} m v^2 \right) \]
Since the car is to stop within the same distance \( d \), the work done by the retarding force should equal this new kinetic energy:
\[ F_{new} \times d = 9 \times \left( F \times d \right) \]
Thus, the new force required to stop the car moving with speed \( 3v \) is:
\[ F_{new} = 9F \]
Hence, the force needed to stop the car moving with speed \( 3v \) within the same distance is \( 9F \).
\[ \boxed{9F} \] Quick Tip: When stopping a car, the required stopping force is proportional to the square of the velocity. Therefore, if the velocity increases by a factor of 3, the required force increases by a factor of \( 3^2 = 9 \).
A balloon of mass 60 g is moving up with an acceleration of 4 m/s\(^2\). The mass to be added to the balloon to descend it down with the same acceleration is (g = 10 m/s\(^2\)):
View Solution
Let the mass of the balloon be \( m = 60 \, g = 0.06 \, kg \).
When the balloon is moving upward with an acceleration of \( 4 \, m/s^2 \), the net force on the balloon is given by Newton’s second law:
\[ F_{net} = m a \]
where:
- \( m = 0.06 \, kg \) is the mass of the balloon
- \( a = 4 \, m/s^2 \) is the upward acceleration.
The upward force is:
\[ F_{up} = m(g + a) = 0.06 \times (10 + 4) = 0.06 \times 14 = 0.84 \, N \]
Now, to make the balloon move downward with the same acceleration, we need to add a mass to it, and the net force should be in the downward direction. For the downward motion, the net force is:
\[ F_{net} = (m + M) \times a \]
where \( M \) is the additional mass to be added. The downward force needed to get the balloon to descend with the same acceleration is equal to the force required to accelerate the added mass:
\[ (m + M)(g - a) = F_{up} \quad \Rightarrow \quad (0.06 + M)(10 - 4) = 0.84 \]
\[ (0.06 + M)(6) = 0.84 \]
\[ 0.06 + M = \frac{0.84}{6} = 0.14 \]
\[ M = 0.14 - 0.06 = 0.08 \, kg = 80 \, g \]
Thus, the mass to be added to the balloon to make it descend with the same acceleration is \( 80 \, g \).
\[ \boxed{80 \, g} \] Quick Tip: For an object moving upward or downward, the net force required is the difference between the force of gravity and the force of acceleration. To reverse the direction while maintaining the same acceleration, add an appropriate mass to achieve the desired net force.
A body of mass \( M \) is at equilibrium under the action of four forces \( F_1, F_2, F_3 \), and \( F_4 \). If \( F_1 \) is removed from the body, then the body moves with an acceleration of:
View Solution
Since the body is initially at equilibrium under the action of the four forces, the net force on the body is zero. This gives us the equation for equilibrium:
\[ F_1 + F_2 + F_3 + F_4 = 0 \]
When \( F_1 \) is removed, the remaining forces acting on the body are \( F_2, F_3, \) and \( F_4 \). The net force on the body is now:
\[ F_{net} = F_2 + F_3 + F_4 \]
From the equilibrium condition, we know that \( F_1 = -(F_2 + F_3 + F_4) \). Therefore, when \( F_1 \) is removed, the remaining net force is:
\[ F_{net} = F_1 \]
Thus, the acceleration \( a \) of the body is given by Newton's second law:
\[ a = \frac{F_{net}}{M} = \frac{F_1}{M} \]
Therefore, the body moves with an acceleration of \( \frac{F_1}{M} \) after \( F_1 \) is removed.
Thus, the correct answer is:
\[ \boxed{\frac{F_1}{M}} \] Quick Tip: For an object in equilibrium, the sum of all the forces acting on it is zero. When one of the forces is removed, the remaining net force determines the acceleration of the body.
If a body at rest undergoes one dimensional motion with constant acceleration, then the power delivered to it at a time \( t \) is proportional to:
View Solution
The equation for the motion of the body under constant acceleration is:
\[ v = u + at \]
where:
- \( v \) is the velocity at time \( t \),
- \( u \) is the initial velocity (which is zero since the body is at rest),
- \( a \) is the constant acceleration,
- \( t \) is the time.
Therefore, the velocity at time \( t \) is:
\[ v = at \]
The power delivered to the body is the rate at which work is done, and it is given by:
\[ P = Fv \]
where:
- \( P \) is the power,
- \( F \) is the force acting on the body,
- \( v \) is the velocity of the body.
The force \( F \) can be calculated using Newton’s second law:
\[ F = ma \]
where:
- \( m \) is the mass of the body,
- \( a \) is the acceleration.
Thus, the power delivered to the body is:
\[ P = ma \cdot v \]
Substituting \( v = at \) into the equation:
\[ P = ma \cdot (at) = ma^2t \]
Thus, the power is directly proportional to time \( t \).
\[ \boxed{t} \] Quick Tip: The power delivered to an object under constant acceleration is proportional to the time \( t \), because both velocity and force are linearly related to time in such motion.
The collision in which the two colliding particles move together after collision is called:
View Solution
In a completely inelastic collision, the two colliding particles stick together after the collision and move with the same velocity. This type of collision results in the maximum possible loss of kinetic energy because some of the kinetic energy is converted into other forms of energy (like heat or deformation), but the momentum of the system is conserved.
Key characteristics of completely inelastic collisions:
- The objects move together after the collision.
- Kinetic energy is not conserved (some is converted into other forms).
- Momentum is conserved.
Elastic collision: In an elastic collision, both momentum and kinetic energy are conserved. The particles do not stick together after the collision.
Partial inelastic collision: This refers to collisions where the particles do not stick together, but some kinetic energy is lost.
Since the problem specifies that the particles move together after the collision, this is an example of a completely inelastic collision.
Thus, the correct answer is:
\[ \boxed{A) Completely inelastic collision} \] Quick Tip: In a completely inelastic collision, the colliding bodies stick together and move with the same velocity after the collision. Momentum is conserved, but kinetic energy is not.
The analogy between linear motion and rotational motion are given. The FALSE one is:
View Solution
In physics, the analogy between linear motion and rotational motion is made by comparing various quantities. Let's analyze each option:
(A) Force : Torque
- Force in linear motion is analogous to torque in rotational motion. Both are the quantities that cause motion (linear and rotational, respectively).
(B) Linear Displacement : Angular displacement
- Linear displacement corresponds to angular displacement. In linear motion, displacement is the change in position, while in rotational motion, angular displacement refers to the angle through which a body rotates.
(C) Mass : Moment of inertia
- Mass in linear motion is analogous to moment of inertia in rotational motion. Both represent the resistance to motion—mass resists linear acceleration, while the moment of inertia resists angular acceleration.
(D) Linear momentum : Angular momentum
- Linear momentum is analogous to angular momentum. Linear momentum is the product of mass and velocity, while angular momentum is the product of moment of inertia and angular velocity.
(E) Translational energy : Vibrational energy
- This is the false analogy. Translational energy is associated with the motion of an object in a straight line, while vibrational energy refers to the energy due to the oscillation or vibration of atoms or molecules in a substance. These two are not directly analogous in the context of motion.
Thus, the correct answer is option (E), Translational energy : Vibrational energy. Quick Tip: The key difference in the analogy lies in the distinction between translational and vibrational motion. Translational motion involves linear displacement, while vibrational motion involves oscillations around a fixed point.
If an ideal engine needs to transmit a torque of 200 Nm to maintain a rotor at a uniform angular speed of 300 rads\(^{-1}\), then the power required for the engine is:
View Solution
The power (\( P \)) transmitted by a torque is given by the formula:
\[ P = \tau \omega \]
where:
- \( P \) is the power,
- \( \tau \) is the torque,
- \( \omega \) is the angular velocity.
Given:
- Torque \( \tau = 200 \, Nm \),
- Angular velocity \( \omega = 300 \, rads^{-1} \).
Substituting these values into the formula for power:
\[ P = 200 \times 300 = 60000 \, W = 60 \, kW \]
Thus, the power required for the engine is:
\[ \boxed{60 \, kW} \] Quick Tip: Power transmitted by a rotating body is the product of the torque and angular velocity. Ensure that the units of torque and angular velocity are consistent to calculate the power in watts or kilowatts.
If a body is taken above the surface of the Earth, it loses its weight by 20% at a height of \( h = \frac{\sqrt{5}}{2} R \), where \( R \) is the radius of the Earth, then:
View Solution
The weight of a body at a height \( h \) above the Earth's surface is given by the formula:
\[ W = W_0 \left( \frac{R}{R + h} \right)^2 \]
where:
- \( W_0 \) is the weight at the Earth's surface,
- \( R \) is the radius of the Earth,
- \( h \) is the height above the Earth's surface.
The weight decreases by 20% at height \( h \), so the new weight \( W \) is 80% of the original weight:
\[ W = 0.8 W_0 \]
Substituting into the formula for \( W \):
\[ 0.8 W_0 = W_0 \left( \frac{R}{R + h} \right)^2 \]
Canceling \( W_0 \) from both sides:
\[ 0.8 = \left( \frac{R}{R + h} \right)^2 \]
Taking the square root of both sides:
\[ \sqrt{0.8} = \frac{R}{R + h} \]
Simplifying:
\[ \frac{R}{R + h} = \frac{\sqrt{5}}{2} \]
Now, solving for \( h \):
\[ R + h = \frac{2R}{\sqrt{5}} \]
\[ h = \frac{2R}{\sqrt{5}} - R \]
\[ h = R \left( \frac{2}{\sqrt{5}} - 1 \right) \]
Simplifying further:
\[ h = R \left( \frac{\sqrt{5}}{2} - 1 \right) \]
Thus, the height at which the body loses 20% of its weight is:
\[ \boxed{\left( \frac{\sqrt{5}}{2} - 1 \right) R} \] Quick Tip: The weight of a body decreases with the square of the distance from the center of the Earth. Use the formula \( W = W_0 \left( \frac{R}{R + h} \right)^2 \) to calculate the change in weight with height.
If a planet orbits the Sun in an elliptical orbit, the quantities associated with the planet that remain constant are:
View Solution
In an elliptical orbit, the planet experiences a central force due to the Sun, which results in an elliptical trajectory. The key aspects of orbital mechanics that remain constant are:
1. Total energy: The total energy of the planet (which is the sum of kinetic energy \( K \) and potential energy \( U \)) remains constant in an elliptical orbit. This is because the gravitational force is conservative, and the total energy does not change over time.
2. Angular momentum: Angular momentum is also conserved in elliptical orbits due to the central force acting along the line connecting the planet and the Sun. Since no external torque acts on the planet, its angular momentum remains constant throughout the orbit.
However:
- Kinetic energy and potential energy vary as the planet moves along its elliptical orbit because the speed of the planet changes depending on its position in the orbit (closer to the Sun, it moves faster; farther, slower).
- Linear speed and angular velocity also change during the orbit because they depend on the planet's distance from the Sun and the shape of the orbit.
Thus, the quantities that remain constant are total energy and angular momentum.
Therefore, the correct answer is:
\[ \boxed{D) Total energy and angular momentum} \] Quick Tip: In an elliptical orbit, total energy and angular momentum are conserved, while kinetic and potential energies, as well as linear speed and angular velocity, change with position in the orbit.
For the flow of incompressible liquid through a pipe, the Venturi-meter is used to measure the:
View Solution
A Venturi meter is an instrument used to measure the flow rate of an incompressible fluid (liquid) through a pipe. It operates based on the principle of Bernoulli’s equation, which relates the pressure, velocity, and height at different points in a fluid flow.
The Venturi meter consists of a pipe that has a narrowing section. According to Bernoulli’s principle, as the fluid flows through the constricted section of the pipe, the velocity of the fluid increases, and the pressure decreases. The difference in pressure between the wider and narrower sections of the pipe can be used to calculate the velocity (speed) of the fluid.
Thus, the Venturi meter is specifically used to measure the speed of flow (velocity) of the liquid, not its pressure, volume, temperature, or mass.
Therefore, the correct answer is:
\[ \boxed{C) Speed of flow} \] Quick Tip: A Venturi meter works on the principle of Bernoulli’s equation, where the pressure difference between two sections of the pipe is used to calculate the speed of the fluid flow.
Two gases under the same thermal conditions have the same number of molecules per unit volume. If the respective molecular diameters of the gases are in the ratio 1 : 3, then their respective mean free paths are in the ratio:
View Solution
The mean free path (\( \lambda \)) of a gas molecule is given by the following relation:
\[ \lambda = \frac{1}{\sqrt{2} \, n \sigma} \]
where:
- \( n \) is the number of molecules per unit volume,
- \( \sigma \) is the effective collision cross-section, which depends on the molecular diameter (\( d \)).
The effective cross-section is proportional to the square of the molecular diameter:
\[ \sigma \propto d^2 \]
Since both gases have the same number of molecules per unit volume, the ratio of their mean free paths will be inversely proportional to the ratio of their molecular diameters squared:
\[ \frac{\lambda_1}{\lambda_2} = \left( \frac{d_2}{d_1} \right)^2 \]
Given that the molecular diameters are in the ratio 1 : 3, we have:
\[ \frac{\lambda_1}{\lambda_2} = \left( \frac{3}{1} \right)^2 = 9 \]
Thus, the ratio of their mean free paths is:
\[ \boxed{9 : 1} \] Quick Tip: The mean free path is inversely proportional to the square of the molecular diameter. Therefore, if the molecular diameters of the gases are in the ratio 1 : 3, their mean free paths will be in the ratio 9 : 1.
The quantity of heat conducted through a metal rod kept at its ends at 100°C and 120°C is 5 J/s. If the ends are kept at 200°C and 220°C, then the quantity of heat conducted in 10 seconds is:
View Solution
The quantity of heat conducted through a rod is governed by the formula for thermal conduction:
\[ Q = \frac{Q_1}{\Delta T_1} = \frac{Q_2}{\Delta T_2} \]
where:
- \( Q_1 \) is the heat conducted in 1 second with the temperature difference \( \Delta T_1 = 120^\circ C - 100^\circ C = 20^\circ C \),
- \( Q_2 \) is the heat conducted in 1 second with the temperature difference \( \Delta T_2 = 220^\circ C - 200^\circ C = 20^\circ C \).
Given that \( Q_1 = 5 \, J/s \), the heat conducted in 1 second is 5 J for a temperature difference of 20°C.
When the temperature difference is also 20°C (from 200°C to 220°C), the heat conducted per second will remain the same, which is 5 J.
Now, the total heat conducted in 10 seconds is:
\[ Q_{total} = 5 \times 10 = 50 \, J \]
Thus, the quantity of heat conducted in 10 seconds is:
\[ \boxed{50 \, J} \] Quick Tip: The quantity of heat conducted is directly proportional to the temperature difference when all other conditions remain constant. So, if the temperature difference remains the same, the heat conducted remains constant.
If an ideal gas, in an insulated vessel, is allowed to expand into another similar evacuated vessel through a valve then:
View Solution
This scenario describes a process known as free expansion. In free expansion, the gas expands into a vacuum (another vessel that is evacuated), and the system is insulated, meaning no heat is exchanged with the surroundings (adiabatic process).
In an adiabatic process with an ideal gas, there is no heat exchange (\( Q = 0 \)) and no work done by or on the gas if there is no external pressure opposing the expansion.
- External work is not done on the gas since it is expanding into an evacuated space (a vacuum).
- The pressure of the gas will not remain the same during the expansion. As the gas expands into a larger volume, the pressure will decrease according to Boyle's law (for an isothermal process), but this expansion is adiabatic, so pressure decreases due to the increase in volume.
- The volume of the gas will indeed double because the gas expands into an equally sized evacuated vessel. The total volume will be the sum of the volumes of both vessels, effectively doubling the initial volume.
- The temperature of the gas generally decreases during free expansion (in an ideal gas), as the gas does not do work on the surroundings, and no heat is added to the system. However, in this case, the temperature of the gas does not increase.
Therefore, the correct answer is:
\[ \boxed{C) The volume of the gas is doubled} \] Quick Tip: In free expansion, the gas expands into a vacuum without any work being done and without heat exchange. The only change in the system is an increase in volume, while the temperature and pressure generally decrease.
In a Carnot engine, the temperature of the sink is 350 K. If the efficiency of the engine is 50%, the temperature of the source should be:
View Solution
The efficiency \( \eta \) of a Carnot engine is given by the following equation:
\[ \eta = 1 - \frac{T_{sink}}{T_{source}} \]
where:
- \( \eta \) is the efficiency of the engine,
- \( T_{sink} \) is the temperature of the sink (cold reservoir),
- \( T_{source} \) is the temperature of the source (hot reservoir).
We are given:
- \( \eta = 50% = 0.5 \),
- \( T_{sink} = 350 \, K \).
Substitute these values into the efficiency equation:
\[ 0.5 = 1 - \frac{350}{T_{source}} \]
Solving for \( T_{source} \):
\[ \frac{350}{T_{source}} = 1 - 0.5 = 0.5 \]
\[ T_{source} = \frac{350}{0.5} = 700 \, K \]
Thus, the temperature of the source is \( 700 \, K \).
\[ \boxed{700 \, K} \] Quick Tip: The efficiency of a Carnot engine is related to the temperatures of the hot and cold reservoirs. The formula \( \eta = 1 - \frac{T_{sink}}{T_{source}} \) helps calculate the required temperature of the source given the efficiency and temperature of the sink.
The ratio of the respective rms velocities of the gas molecules of an ideal gas at 327°C and at 627°C is:
View Solution
The root mean square (rms) velocity \( v_{rms} \) of gas molecules is given by the formula:
\[ v_{rms} = \sqrt{\frac{3kT}{m}} \]
where:
- \( k \) is the Boltzmann constant,
- \( T \) is the absolute temperature in Kelvin,
- \( m \) is the mass of the gas molecule.
The ratio of the rms velocities at two different temperatures \( T_1 \) and \( T_2 \) can be written as:
\[ \frac{v_{rms1}}{v_{rms2}} = \sqrt{\frac{T_1}{T_2}} \]
Given:
- \( T_1 = 327^\circ C = 327 + 273 = 600 \, K \),
- \( T_2 = 627^\circ C = 627 + 273 = 900 \, K \).
Substitute these values into the formula for the ratio of rms velocities:
\[ \frac{v_{rms1}}{v_{rms2}} = \sqrt{\frac{600}{900}} = \sqrt{\frac{2}{3}} = \frac{\sqrt{2}}{\sqrt{3}} \]
Thus, the ratio of the rms velocities is:
\[ \boxed{\sqrt{2} : \sqrt{3}} \] Quick Tip: The root mean square velocity of gas molecules is directly related to the square root of the temperature. To find the ratio of rms velocities at two different temperatures, take the square root of the ratio of the temperatures in Kelvin.
The total energy of a gas mixture of one mole of oxygen and 3 moles of argon at a temperature \( T \) by neglecting vibrational modes is:
View Solution
The total energy for an ideal gas is given by:
\[ E = \frac{f}{2} n R T \]
where:
- \( f \) is the number of degrees of freedom of the gas molecules,
- \( n \) is the number of moles of the gas,
- \( R \) is the universal gas constant,
- \( T \) is the temperature.
For a diatomic molecule like oxygen (O\(_2\)):
- The number of degrees of freedom \( f = 5 \) (3 translational and 2 rotational, neglecting vibrational modes).
For a monoatomic molecule like argon (Ar):
- The number of degrees of freedom \( f = 3 \) (3 translational, no rotation in ideal cases for argon).
Now, calculate the total energy for the mixture:
- The energy for 1 mole of oxygen:
\[ E_{O_2} = \frac{5}{2} \cdot 1 \cdot R T = \frac{5}{2} R T \]
- The energy for 3 moles of argon:
\[ E_{Ar} = \frac{3}{2} \cdot 3 \cdot R T = \frac{9}{2} R T \]
The total energy for the mixture is the sum of the energies of oxygen and argon:
\[ E_{total} = E_{O_2} + E_{Ar} = \frac{5}{2} R T + \frac{9}{2} R T = \frac{14}{2} R T = 7 R T \]
Thus, the total energy of the gas mixture is:
\[ \boxed{7 \, RT} \] Quick Tip: For ideal gases, the total energy is calculated by the formula \( E = \frac{f}{2} n R T \), where \( f \) depends on the type of gas (monoatomic or diatomic). The total energy for a mixture is simply the sum of the individual energies for each component.
A man fires bullets at two hillocks, one shorter and the other taller. The taller one is behind the smaller one. If the first echo is heard after 6 s and the second echo after 12 s, then the distance between the hillocks is (velocity of sound in air = 330 m/s):
View Solution
When the bullet is fired, two echoes are heard:
- The first echo after \( 6 \, s \) is from the shorter hillock.
- The second echo after \( 12 \, s \) is from the taller hillock.
The distance traveled by sound in time \( t \) is given by:
\[ d = v \times t \]
where:
- \( v = 330 \, m/s \) is the velocity of sound in air,
- \( t \) is the time taken for the sound to travel to the object and back.
For the shorter hillock:
- The total time for the sound to travel to the shorter hillock and return is \( t_1 = 6 \, s \).
- The distance traveled by sound is \( d_1 = v \times t_1 = 330 \times 6 = 1980 \, m \).
- The distance to the shorter hillock is half of this distance: \( d_{short} = \frac{1980}{2} = 990 \, m \).
For the taller hillock:
- The total time for the sound to travel to the taller hillock and return is \( t_2 = 12 \, s \).
- The distance traveled by sound is \( d_2 = v \times t_2 = 330 \times 12 = 3960 \, m \).
- The distance to the taller hillock is half of this distance: \( d_{tall} = \frac{3960}{2} = 1980 \, m \).
Thus, the distance between the two hillocks is:
\[ Distance between hillocks = d_{tall} - d_{short} = 1980 - 990 = 990 \, m \]
Therefore, the distance between the hillocks is \( 990 \, m \).
\[ \boxed{990 \, m} \] Quick Tip: The distance to the hillocks can be calculated by using the time for the sound to travel to the hillock and back. Since the sound travels both to and from the hillock, divide the total distance by 2.
If a particle executing simple harmonic motion with period \( T \) and displacement \( x = A \cos(\omega t) \), then the acceleration and velocity of the particle at the time \( t = \frac{T}{2} \) are respectively:
View Solution
The displacement of the particle in simple harmonic motion is given by:
\[ x = A \cos(\omega t) \]
where:
- \( A \) is the amplitude,
- \( \omega \) is the angular frequency,
- \( t \) is the time.
To find the velocity and acceleration, we use the following relationships:
1. Velocity is the time derivative of displacement:
\[ v = \frac{dx}{dt} = -A \omega \sin(\omega t) \]
At \( t = \frac{T}{2} \), we know that the period \( T \) is the time taken for one complete cycle of the motion, and \( \omega T = 2\pi \). Thus:
\[ \sin\left(\omega \frac{T}{2}\right) = \sin\left(\pi\right) = 0 \]
So, the velocity at \( t = \frac{T}{2} \) is:
\[ v = -A \omega \sin(\omega \frac{T}{2}) = 0 \]
2. Acceleration is the time derivative of velocity:
\[ a = \frac{dv}{dt} = -A \omega^2 \cos(\omega t) \]
At \( t = \frac{T}{2} \), we have:
\[ \cos\left(\omega \frac{T}{2}\right) = \cos\left(\pi\right) = -1 \]
Thus, the acceleration at \( t = \frac{T}{2} \) is:
\[ a = -A \omega^2 \cos(\omega \frac{T}{2}) = A \omega^2 \]
Therefore, at \( t = \frac{T}{2} \), the velocity is 0 and the acceleration is \( A \omega^2 \).
Thus, the correct answer is:
\[ \boxed{-A, A \omega^2} \] Quick Tip: At \( t = \frac{T}{2} \), the particle in simple harmonic motion reaches the maximum displacement, where its velocity is zero, and the acceleration is directed towards the mean position.
The equipotential surface is:
View Solution
An equipotential surface is a surface on which the electric potential is constant at all points.
1. For a point charge, the electric potential is given by:
\[ V = \frac{kQ}{r} \]
where \( k \) is Coulomb's constant, \( Q \) is the charge, and \( r \) is the distance from the point charge. This potential depends only on the distance from the charge, so the equipotential surfaces for a point charge are spherical. These surfaces are concentric spheres with the point charge at the center.
2. For a dipole, the electric potential at a point is a function of both distance and angle from the dipole, and the equipotential surfaces are spherical at large distances but take a more complicated shape closer to the dipole. At small distances from a dipole, the equipotential surfaces are more complicated and are not spherical.
Therefore, the correct answer is that the equipotential surface is spherical for a point charge.
Thus, the correct answer is:
\[ \boxed{D) Spherical for a point charge} \] Quick Tip: For a point charge, the equipotential surfaces are spherical, centered at the charge. For more complex charge distributions like dipoles, the equipotential surfaces are not spherical.
The electric field intensity due to an ideal dipole at a distance \( r \) from its center on the axial point is directly proportional to:
View Solution
The electric field intensity \( E \) due to an ideal dipole at a distance \( r \) from its center on the axial point is given by the following formula: \[ E = \frac{1}{4 \pi \varepsilon_0} \cdot \frac{2p}{r^3} \]
where:
- \( p \) is the dipole moment,
- \( r \) is the distance from the dipole.
From the equation, it is clear that the electric field intensity \( E \) is inversely proportional to \( r^3 \).
Thus, the correct answer is option (E), \( \frac{1}{r^3} \). Quick Tip: The electric field intensity due to a dipole at an axial point decreases with the cube of the distance from the dipole, which is represented by \( \frac{1}{r^3} \).
Two spheres A and B having respective charges 6 C and 12 C placed at a distance \( d \) repel each other by a force \( F \). The charge given to sphere A to reverse the force as \( -F \) is:
View Solution
The force between two charges \( q_1 \) and \( q_2 \) separated by a distance \( r \) is given by Coulomb's law:
\[ F = k \frac{|q_1 q_2|}{r^2} \]
where:
- \( k \) is Coulomb's constant,
- \( r \) is the distance between the charges.
For the charges on spheres A and B, we are given:
- \( q_1 = 6 \, C \),
- \( q_2 = 12 \, C \),
- The force between them is \( F \).
Now, we are asked to find the charge \( q_1' \) that must be given to sphere A in order to reverse the direction of the force to \( -F \). The charges should attract each other instead of repelling, meaning the product of the charges should become negative.
To reverse the force direction, the charge \( q_1' \) on sphere A must be:
\[ q_1' = -12 \, C \]
Thus, the charge to be given to sphere A to reverse the force is \( -12 \, C \).
Therefore, the correct answer is:
\[ \boxed{-12 \, C} \] Quick Tip: The force between two charges can be reversed by changing the sign of one of the charges. The magnitude of the force remains the same, but the direction is reversed.
The work done by a source in taking unit charge from lower to higher potential energy is called the source's:
View Solution
The work done by a source in moving a unit charge from a lower potential to a higher potential is called electromotive force (emf). It is a measure of the energy provided by the source per unit charge. The emf is responsible for driving the flow of charge (current) in an electrical circuit.
Mathematically, the emf is defined as:
\[ \mathcal{E} = \frac{W}{q} \]
where:
- \( W \) is the work done by the source in moving a charge \( q \),
- \( \mathcal{E} \) is the electromotive force.
Thus, the correct answer is:
\[ \boxed{D) Electromotive force} \] Quick Tip: Electromotive force (emf) refers to the energy provided by a source per unit charge to move the charge from one potential to another. It is not a force in the traditional sense but a potential difference that drives current.
A Wheatstone network ABCDA has the resistances 20 \(\Omega\), 10 \(\Omega\), and 12 \(\Omega\) in AB, BC, and DA arms respectively in which the galvanometer is connected across BD. For null deflection in the galvanometer, the resistance in CD arm should be:
View Solution
In a Wheatstone bridge, for null deflection in the galvanometer, the following condition must be satisfied:
\[ \frac{R_{AB}}{R_{BC}} = \frac{R_{DA}}{R_{CD}} \]
where:
- \( R_{AB} = 20 \, \Omega \),
- \( R_{BC} = 10 \, \Omega \),
- \( R_{DA} = 12 \, \Omega \),
- \( R_{CD} \) is the unknown resistance we need to find.
Substitute the known values into the equation:
\[ \frac{20}{10} = \frac{12}{R_{CD}} \]
Simplifying the equation:
\[ 2 = \frac{12}{R_{CD}} \]
Solving for \( R_{CD} \):
\[ R_{CD} = \frac{12}{2} = 6 \, \Omega \]
Thus, the resistance in the CD arm should be \( 6 \, \Omega \).
\[ \boxed{6 \, \Omega} \] Quick Tip: In a Wheatstone bridge, for null deflection of the galvanometer, the ratio of the resistances in opposite arms must be equal.
If a charged particle enters a uniform magnetic field \( B \), with a velocity \( v \) such that \( v \) has a component along \( B \), then the charged particle describes:
View Solution
When a charged particle enters a magnetic field, the motion of the particle is influenced by the Lorentz force, which is given by:
\[ F = q(\mathbf{v} \times \mathbf{B}) \]
Where:
- \( q \) is the charge of the particle,
- \( \mathbf{v} \) is the velocity of the particle,
- \( \mathbf{B} \) is the magnetic field.
The force \( F \) is perpendicular to the velocity \( v \), so the particle will follow a circular path due to the magnetic force. However, when the velocity \( v \) has a component along the magnetic field \( B \), this component of the velocity does not experience any magnetic force because the magnetic force is perpendicular to both the velocity and the magnetic field.
Thus, the particle will:
- Move in a circular path due to the component of velocity perpendicular to \( B \),
- Move in a straight line along the direction of the component of velocity parallel to \( B \).
The combination of these two motions results in a helical path.
Therefore, the correct answer is:
\[ \boxed{D) A helical path} \] Quick Tip: When a charged particle has a component of velocity along the magnetic field, it follows a helical path, with the motion perpendicular to the magnetic field forming a circle, and the parallel component causing linear motion along the field.
A proton with kinetic energy of 2 MeV is describing a circular path of radius \( R \) in a uniform magnetic field. The kinetic energy of the deuteron to describe the same circular path in the same field is:
View Solution
The radius of the circular path of a charged particle moving in a uniform magnetic field is given by the formula: \[ r = \frac{mv}{qB} \]
where:
- \( r \) is the radius of the circular path,
- \( m \) is the mass of the particle,
- \( v \) is the velocity of the particle,
- \( q \) is the charge of the particle,
- \( B \) is the magnetic field strength.
For a proton, the kinetic energy \( K_e \) is related to its velocity by: \[ K_e = \frac{1}{2} m v^2 \]
For a deuteron, the mass \( m_d \) is twice the mass of the proton \( m_p \), i.e., \( m_d = 2 m_p \), and the charge \( q_d \) is twice the charge of the proton, i.e., \( q_d = 2 q_p \).
Since both particles are moving in the same circular path, we can equate their radii: \[ r_p = r_d \]
Thus: \[ \frac{m_p v_p}{q_p B} = \frac{m_d v_d}{q_d B} \]
Simplifying, we get: \[ \frac{m_p v_p}{q_p} = \frac{2 m_p v_d}{2 q_p} \] \[ v_p = v_d \]
Therefore, the velocities of the proton and deuteron are the same. Now, using the relation between kinetic energy and velocity for both particles: \[ K_e = \frac{1}{2} m v^2 \]
For the proton, we know the kinetic energy is 2 MeV: \[ 2 \, MeV = \frac{1}{2} m_p v_p^2 \]
For the deuteron, the kinetic energy \( K_d \) is: \[ K_d = \frac{1}{2} m_d v_d^2 = \frac{1}{2} (2 m_p) v_p^2 = 2 \times \frac{1}{2} m_p v_p^2 = 2 \times 2 \, MeV = 1 \, MeV \]
Thus, the correct answer is option (B), 1 MeV. Quick Tip: For particles of different masses but the same radius in a magnetic field, their kinetic energies are proportional to their masses. The velocity is the same for both particles in the same magnetic field and radius.
Two straight long parallel wires carrying equal amounts of current in opposite directions placed 5 cm apart repel each other by a force \( F \). If the current in one of the wires is doubled and reversed, then the force between them is:
View Solution
The force per unit length between two parallel wires carrying currents is given by Ampere's law:
\[ F = \frac{\mu_0 I_1 I_2}{2 \pi r} \]
where:
- \( F \) is the force between the wires,
- \( \mu_0 \) is the permeability of free space,
- \( I_1 \) and \( I_2 \) are the currents in the wires,
- \( r \) is the distance between the wires.
Initially, the currents in the two wires are equal but opposite, so the force between them is repulsive. The magnitude of the force is given by:
\[ F_1 = \frac{\mu_0 I^2}{2 \pi r} \]
where \( I \) is the current in each wire, and \( r = 5 \, cm = 0.05 \, m \).
Now, when the current in one of the wires is doubled and reversed, the new current in one wire is \( -2I \) (the negative sign indicates the reversed direction). The new force between the wires will be:
\[ F_2 = \frac{\mu_0 (2I)(-I)}{2 \pi r} = -\frac{\mu_0 (2I^2)}{2 \pi r} \]
Thus, the new force will be:
\[ F_2 = 2 \times F_1 \]
The direction of the force will now be attractive because the currents are now in opposite directions.
Therefore, the force between the wires will be 2F and attractive.
Thus, the correct answer is:
\[ \boxed{2F and attractive} \] Quick Tip: When two currents in parallel wires are in opposite directions, they repel each other. Doubling the current in one wire and reversing its direction makes the force between the wires twice as large and attractive.
The mutual inductance between a pair of coils A and B placed close to each other depends upon:
View Solution
Mutual inductance \( M \) is a measure of the ability of one coil to induce an electromotive force (emf) in another coil due to the change in current in the first coil. The mutual inductance between two coils depends on several factors, including:
1. The rate of change of current in the coils: The rate of change of current in one coil induces a voltage in the other coil. However, the mutual inductance itself is a constant that depends on the physical characteristics of the coils, such as their relative position and orientation.
2. The relative position and orientation of the coils: This is the most important factor. The mutual inductance is directly related to how the coils are placed relative to each other and their orientation. If the coils are aligned properly with respect to each other, the mutual inductance will be higher. Conversely, if they are misaligned or far apart, the mutual inductance will be lower.
3. The material of the wire of the coils: While the material of the wire affects the resistance of the coils, it does not directly affect the mutual inductance in a simple way. Mutual inductance primarily depends on the physical geometry and relative positioning of the coils.
Thus, the correct answer is that the mutual inductance depends primarily on:
\[ \boxed{D) The relative position and orientation of A and B} \] Quick Tip: Mutual inductance depends on the geometry and relative positioning of the coils, including their orientation and distance from each other. The material of the wire and the current's rate of change influence the induced emf but do not change the mutual inductance itself.
In an LCR resonance circuit at resonance frequency \( \omega_0 \), the quality factor \( Q \) is:
View Solution
The quality factor \( Q \) of a resonance circuit is a measure of the sharpness of the resonance. It is defined as the ratio of the resonant frequency to the bandwidth. For an LCR circuit, at resonance frequency \( \omega_0 \), the quality factor \( Q \) is given by:
\[ Q = \frac{\omega_0 L}{R} \]
where:
- \( \omega_0 \) is the resonance frequency,
- \( L \) is the inductance,
- \( R \) is the resistance.
This expression indicates that the quality factor \( Q \) is directly proportional to the inductance \( L \) and the resonance frequency \( \omega_0 \), and inversely proportional to the resistance \( R \).
Thus, the correct answer is:
\[ \boxed{\frac{\omega_0 L}{R}} \] Quick Tip: The quality factor \( Q \) of a resonant LCR circuit is related to the resonance frequency, the inductance, and the resistance of the circuit. A higher \( Q \) means a sharper resonance and less energy loss.
The ratio between the magnetic dipole moment of a revolving electron in a circular orbit to its angular momentum is (where \( e \) is the charge and \( m \) is the mass of the electron):
View Solution
The magnetic dipole moment \( \mu \) of an electron moving in a circular orbit is given by: \[ \mu = I \cdot A \]
where \( I \) is the current due to the motion of the electron, and \( A \) is the area of the orbit.
For a revolving electron, the current \( I \) is given by the charge per unit time, which is: \[ I = \frac{e}{T} \]
where \( T \) is the time period of the electron’s revolution. The area \( A \) of the orbit is given by: \[ A = \pi r^2 \]
where \( r \) is the radius of the orbit.
Now, the angular momentum \( L \) of the electron is given by: \[ L = mvr \]
where \( v \) is the velocity of the electron and \( r \) is the radius of the orbit.
Thus, the ratio between the magnetic dipole moment and angular momentum is: \[ \frac{\mu}{L} = \frac{\frac{e}{T} \cdot \pi r^2}{mvr} \]
We know that \( v = \frac{2\pi r}{T} \), so: \[ \frac{\mu}{L} = \frac{\frac{e}{T} \cdot \pi r^2}{m \cdot \frac{2\pi r}{T} \cdot r} = \frac{e}{2m} \]
Thus, the correct answer is option (C), \( \frac{e}{2m} \). Quick Tip: In problems involving revolving electrons and magnetic dipole moment, remember that the ratio of the magnetic dipole moment to the angular momentum is \( \frac{e}{2m} \), derived from the relationship between the current, area, and angular momentum.
The electromagnetic waves used in LASIK and cell phones are respectively:
View Solution
1. LASIK (Laser-Assisted in Situ Keratomileusis):
- LASIK surgery, which is used to correct vision, involves the use of a laser that uses ultraviolet (UV) rays to reshape the cornea of the eye. These rays have the necessary precision to cut the cornea without causing damage to surrounding tissues.
2. Cell phones:
- Cell phones operate using radio waves for communication. Radio waves are a type of electromagnetic radiation used for wireless communication in mobile phones, as well as for broadcasting radio and television signals.
Thus, the correct answer is that LASIK uses ultraviolet rays, and cell phones use radio waves.
\[ \boxed{B) Ultraviolet rays and radio waves} \] Quick Tip: LASIK surgery uses UV light for precise tissue removal, and radio waves are commonly used in cell phone communication due to their ability to travel long distances and penetrate through objects.
If a ray of light passes through a medium, its frequency and wavelength are \( 4 \times 10^{14} \) Hz and 450 nm respectively. Then the refractive index of the medium is:
View Solution
The refractive index \( n \) of a medium is related to the speed of light in vacuum \( c \), the speed of light in the medium \( v \), and the wavelength of light in the medium \( \lambda \) and in vacuum \( \lambda_0 \) as:
\[ n = \frac{c}{v} = \frac{\lambda_0}{\lambda} \]
Where:
- \( c \) is the speed of light in vacuum (\( 3 \times 10^8 \, m/s \)),
- \( \lambda_0 \) is the wavelength in vacuum,
- \( \lambda \) is the wavelength in the medium.
From the problem, we are given:
- The frequency \( f = 4 \times 10^{14} \, Hz \),
- The wavelength in the medium \( \lambda = 450 \, nm = 450 \times 10^{-9} \, m \).
Now, we know that the speed of light in a medium is related to the frequency and wavelength by the equation:
\[ v = f \lambda \]
Substitute the values for frequency and wavelength in the medium:
\[ v = (4 \times 10^{14}) \times (450 \times 10^{-9}) = 1.8 \times 10^8 \, m/s \]
Next, using the equation for refractive index:
\[ n = \frac{c}{v} = \frac{3 \times 10^8}{1.8 \times 10^8} = 1.67 \]
Thus, the refractive index of the medium is \( \boxed{1.67} \). Quick Tip: The refractive index is the ratio of the speed of light in vacuum to the speed of light in a medium. It can also be determined using the ratio of the wavelength in vacuum to the wavelength in the medium.
If the power of a lens is -2.0 D, then the type and focal length \( f \) of the lens are:
View Solution
The power \( P \) of a lens is related to its focal length \( f \) by the equation:
\[ P = \frac{1}{f} \]
where:
- \( P \) is the power of the lens in diopters (D),
- \( f \) is the focal length of the lens in meters.
We are given that the power of the lens is \( P = -2.0 \, D \). The negative sign indicates that the lens is a concave lens (since concave lenses have negative focal lengths).
Using the formula for power:
\[ P = \frac{1}{f} \]
Substitute the value of \( P \):
\[ -2.0 = \frac{1}{f} \]
Solving for \( f \):
\[ f = \frac{1}{-2.0} = -0.5 \, m = -50 \, cm \]
Thus, the focal length of the lens is \( -50 \, cm \), and since the focal length is negative, the lens is a concave lens.
Therefore, the correct answer is:
\[ \boxed{B) Concave lens, 50 cm} \] Quick Tip: A negative power indicates a concave lens, and the focal length is negative for concave lenses. The relationship \( P = \frac{1}{f} \) allows you to easily calculate the focal length from the power.
In an Young double slit experiment without varying the distance of the screen and the slit separation, if the wavelength of monochromatic source is changed one by one in the ratio 2:3:4, then the corresponding fringe widths measured will be in the ratio:
View Solution
In a Young's double slit experiment, the fringe width \( \beta \) is given by the formula:
\[ \beta = \frac{\lambda D}{d} \]
where:
- \( \lambda \) is the wavelength of the light,
- \( D \) is the distance between the slits and the screen,
- \( d \) is the distance between the slits.
In this case, we are told that the distance of the screen (\( D \)) and the slit separation (\( d \)) remain constant. Therefore, the fringe width \( \beta \) is directly proportional to the wavelength \( \lambda \).
Thus, the fringe width ratio for wavelengths in the ratio 2:3:4 will also be in the same ratio:
\[ \frac{\beta_1}{\beta_2} = \frac{\lambda_1}{\lambda_2} = \frac{2}{3} \quad and \quad \frac{\beta_2}{\beta_3} = \frac{\lambda_2}{\lambda_3} = \frac{3}{4} \]
So, the corresponding fringe width ratio will be 2:3:4.
Therefore, the correct answer is:
\[ \boxed{C) 2:3:4} \] Quick Tip: In a Young's double slit experiment, the fringe width is directly proportional to the wavelength. If the wavelength changes, the fringe width will change in the same ratio.
Which one of the following phenomena does not occur when a white light falls on an equilateral glass prism?
View Solution
When white light passes through an equilateral glass prism, several phenomena occur:
- Reflection: Some portion of the light is reflected from the surface of the prism. This is a common phenomenon when light interacts with any surface.
- Refraction: Light bends as it passes from one medium (air) into another (glass) with a different refractive index. Refraction is a primary phenomenon observed when light enters and exits the prism.
- Dispersion: Dispersion occurs because the prism separates white light into its constituent colors (like a rainbow), due to the varying refractive indices for different wavelengths (colors) of light.
- Deviation: The light ray is deviated from its original path as it refracts through the prism.
However, interference does not occur in this case. Interference is a phenomenon where two or more light waves superpose to form a resultant wave, typically observed in experiments like the double-slit experiment. In the case of a prism, we do not observe interference of the light waves as they pass through; rather, we observe the effects of reflection, refraction, dispersion, and deviation.
Thus, the correct answer is option (E), Interference. Quick Tip: Interference is a phenomenon that occurs due to the interaction of multiple coherent light waves, and is not a typical effect seen when light passes through a glass prism. The main effects in such a scenario are reflection, refraction, dispersion, and deviation.
The de Broglie wavelength associated with the electrons accelerated by a potential of 81 V is lying in the region of electromagnetic waves:
View Solution
The de Broglie wavelength \( \lambda \) associated with a particle (in this case, an electron) is given by the formula:
\[ \lambda = \frac{h}{p} \]
where:
- \( h \) is Planck's constant (\( 6.626 \times 10^{-34} \, J·s \)),
- \( p \) is the momentum of the particle.
The momentum \( p \) of an electron accelerated by a potential \( V \) is:
\[ p = \sqrt{2 m_e e V} \]
where:
- \( m_e \) is the mass of the electron (\( 9.11 \times 10^{-31} \, kg \)),
- \( e \) is the charge of the electron (\( 1.6 \times 10^{-19} \, C \)),
- \( V \) is the potential difference (in this case, 81 V).
Substituting these values into the formula for \( p \):
\[ p = \sqrt{2 \times 9.11 \times 10^{-31} \times 1.6 \times 10^{-19} \times 81} \]
Now, the de Broglie wavelength \( \lambda \) can be calculated using the above formula. For this case, the wavelength \( \lambda \) will be in the range of X-rays.
Therefore, the correct answer is:
\[ \boxed{D) X-rays} \] Quick Tip: The de Broglie wavelength of a particle depends on its momentum. For high-energy electrons, such as those accelerated by 81 V, the wavelength lies in the X-ray region of the electromagnetic spectrum.
If the frequency of the incident light on a metal surface is increased by 10%, then the kinetic energy of the emitted photoelectrons is increased from 0.5 eV to 0.7 eV. Then the work function of the metal is:
View Solution
We know that the kinetic energy of the emitted photoelectrons is given by the photoelectric equation: \[ K.E. = h f - \phi \]
where:
- \( K.E. \) is the kinetic energy of the emitted photoelectrons,
- \( h \) is Planck's constant,
- \( f \) is the frequency of the incident light,
- \( \phi \) is the work function of the metal.
Let the initial frequency be \( f_1 \) and the corresponding kinetic energy be \( K.E_1 = 0.5 \, eV \): \[ K.E_1 = h f_1 - \phi \tag{1} \]
Let the final frequency be \( f_2 = 1.1 f_1 \) (since the frequency is increased by 10%), and the corresponding kinetic energy be \( K.E_2 = 0.7 \, eV \): \[ K.E_2 = h f_2 - \phi = h (1.1 f_1) - \phi \tag{2} \]
Now, subtract equation (1) from equation (2): \[ K.E_2 - K.E_1 = h (1.1 f_1) - \phi - (h f_1 - \phi) \] \[ 0.7 - 0.5 = h (1.1 f_1 - f_1) \] \[ 0.2 = h \times 0.1 f_1 \] \[ h f_1 = 2 \, eV \]
Substitute this value into equation (1): \[ 0.5 = 2 - \phi \] \[ \phi = 1.5 \, eV \]
Thus, the work function of the metal is 1.5 eV, which corresponds to option (C). Quick Tip: In photoelectric effect problems, the change in kinetic energy of photoelectrons can be used to find the work function by applying the photoelectric equation and solving for \( \phi \).
The ratio of the velocities of the electron in the second, third and fourth Bohr’s orbits of the hydrogen atom is:
View Solution
The velocity of an electron in a Bohr orbit is given by the formula:
\[ v_n = \frac{2 \pi k e^2}{h n} \]
where:
- \( v_n \) is the velocity of the electron in the \( n \)-th orbit,
- \( k \) is Coulomb's constant,
- \( e \) is the charge of the electron,
- \( h \) is Planck's constant,
- \( n \) is the principal quantum number of the orbit.
The velocity is inversely proportional to the principal quantum number \( n \).
Thus, the ratio of the velocities in the second, third, and fourth orbits is:
\[ \frac{v_2}{v_3} = \frac{3}{2}, \quad \frac{v_3}{v_4} = \frac{4}{3} \]
Hence, the velocity ratio is:
\[ v_2 : v_3 : v_4 = 6 : 4 : 3 \]
Therefore, the correct answer is:
\[ \boxed{6 : 4 : 3} \] Quick Tip: In Bohr's model, the velocity of the electron is inversely proportional to the principal quantum number \( n \). Thus, the ratio of velocities in different orbits is the inverse ratio of the principal quantum numbers.
Plutonium nucleus undergoes fission with:
View Solution
The fission of plutonium nuclei typically occurs when the nucleus is bombarded with slow neutrons (also called thermal neutrons). These neutrons have a lower energy and are more likely to be captured by the plutonium nucleus, causing it to become unstable and undergo fission.
- Fast neutrons have high energy, and while they can cause fission, they are less effective than slow neutrons.
- Slow neutrons are effective in initiating fission reactions in heavy nuclei such as plutonium-239.
- Deuterons and alpha particles are not typically involved in fission reactions with plutonium nuclei.
Thus, the correct answer is:
\[ \boxed{B) Slow neutrons} \] Quick Tip: Plutonium undergoes fission when it captures slow (thermal) neutrons, which cause the nucleus to split. Fast neutrons are less likely to cause fission and require moderation to become effective.
Out of the following pair of elements, identify isotones:
View Solution
- Isotones are atoms of different elements that have the same number of neutrons but different numbers of protons. In other words, isotones have the same neutron number (A - Z) but different atomic numbers (Z).
Now, let's analyze the given options:
1. Option A: \( _1^2 H \) and \( _1^3 H \)
- These are isotopes of hydrogen, not isotones. They have the same number of protons but different numbers of neutrons.
2. Option B: \( _{79}^{197} Au \) and \( _{80}^{198} Hg \)
- These are isotones. Both have 118 neutrons (197 - 79 = 198 - 80), but different numbers of protons (79 for Au and 80 for Hg).
3. Option C: \( _1^3 H \) and \( _2^3 He \)
- These are isotopes of hydrogen and helium, not isotones. They have the same number of nucleons (3), but a different number of protons and neutrons.
4. Option D: \( _{17}^{35} Cl \) and \( _{17}^{37} Cl \)
- These are isotopes of chlorine, not isotones. They have the same number of protons (17), but different numbers of neutrons.
5. Option E: \( _{92}^{235} U \) and \( _{92}^{238} U \)
- These are isotopes of uranium, not isotones. They have the same number of protons (92) but different numbers of neutrons.
Therefore, the correct answer is:
\[ \boxed{B) _{79}^{197} Au and _{80}^{198} Hg} \] Quick Tip: Isotones are nuclei with the same number of neutrons but different numbers of protons. To identify isotones, subtract the atomic number from the mass number and compare the result for each pair.
If \( E_c \) and \( E_v \) represent the energy of the conduction band and valence band, \( E_D \) represent the donor energy level, and the band gap in a n-type semiconductor, then the true relation among them is:
View Solution
In a semiconductor, the energy levels can be understood as follows:
- \( E_c \): Energy of the conduction band.
- \( E_v \): Energy of the valence band.
- \( E_D \): Donor energy level in a n-type semiconductor.
- \( E_g \): Band gap of the semiconductor.
For a n-type semiconductor:
- The donor level \( E_D \) is slightly below the conduction band \( E_c \), meaning electrons from the donor energy levels can easily move to the conduction band with minimal energy input.
- The band gap \( E_g \) is the energy difference between the conduction band and the valence band (\( E_c - E_v \)).
In n-type semiconductors, the donor energy level \( E_D \) is closer to the conduction band than to the valence band, so it follows that:
\[ E_D > E_v \]
Thus, the correct answer is:
\[ \boxed{C) E_D > E_v} \] Quick Tip: In an n-type semiconductor, the donor energy level is just below the conduction band. This allows electrons from the donor level to easily jump into the conduction band, thereby enhancing conductivity.
During the formation of p - n junction:
View Solution
During the formation of a p-n junction:
- Electrons from the n-type side (where they are the majority carriers) diffuse into the p-type side (where holes are the majority carriers), creating a region near the junction where there are no free charge carriers. This is called the depletion region.
- In the p-type material, the holes move towards the n-side, and in the n-type material, the electrons move towards the p-side. These movements of charge carriers leave behind ionized donor ions on the p-side and ionized acceptor ions on the n-side. This results in the formation of the space charge region.
Therefore, the correct answer is:
\[ \boxed{E) The space charge region on either side of the junction is called depletion region} \] Quick Tip: The space charge region, or depletion region, is formed due to the diffusion of majority carriers (electrons and holes) across the p-n junction. This region is devoid of free charge carriers and is crucial for the formation of the electric field in the junction.
What is the mass of crystalline oxalic acid (molar mass = 126 g/mol) present in 50 mL of 0.02N aqueous oxalic acid solution?
View Solution
We are given the following information:
- Normality (N) = 0.02 N
- Volume of solution = 50 mL = 0.050 L
- Molar mass of oxalic acid = 126 g/mol
We know that normality \( N \) is related to molarity \( M \) by the equation:
\[ N = n \times M \]
where \( n \) is the number of equivalents per mole. For oxalic acid (H\(_2\)C\(_2\)O\(_4\)), the number of replaceable hydrogen ions \( n \) is 2, because each molecule of oxalic acid can donate two protons (H\(^+\)) in a reaction.
Therefore, the molarity of the oxalic acid solution is:
\[ M = \frac{N}{n} = \frac{0.02}{2} = 0.01 \, mol/L \]
Now, the amount of substance (in moles) present in 50 mL (0.050 L) of the solution is:
\[ moles of oxalic acid = M \times Volume = 0.01 \times 0.050 = 0.0005 \, mol \]
Finally, to find the mass, we use the molar mass of oxalic acid:
\[ mass = moles \times molar mass = 0.0005 \times 126 = 0.063 \, g = 63 \, mg \]
Thus, the mass of oxalic acid in 50 mL of the solution is \( \boxed{63 \, mg} \). Quick Tip: In solutions, normality (N) is used to express the equivalent concentration of a solution. Remember, normality is related to molarity by the number of replaceable ions or equivalents in the solution.
The correct electronic configuration of Tc (Z = 43) is:
View Solution
To determine the correct electronic configuration of Technetium (Tc) with atomic number 43, we need to fill in the electron orbitals according to the Aufbau principle.
1. The electron configuration of the noble gas preceding Tc is Krypton (\( [Kr] \)), which has the configuration \( [Kr] \) for the first 36 electrons.
2. Tc has 43 electrons in total, so after \( [Kr] \), we place the remaining 7 electrons:
- The 37th electron goes into the \( 5s \) orbital (since \( 5s \) is filled before \( 4d \)),
- The remaining 6 electrons go into the \( 4d \) orbital.
Therefore, the correct configuration is \( [Kr]4d^5 5s^2 5p^0 \), where the 5th and 6th electrons are in the \( 4d \) orbital and the 7th is in the \( 5s \) orbital.
Thus, the correct answer is:
\[ \boxed{[Kr]4d^5 5s^2 5p^0} \] Quick Tip: Remember that the electronic configuration follows the Aufbau principle, which means orbitals are filled in increasing order of energy. The \( 4d \) orbital fills before the \( 5p \) orbital for elements with atomic numbers between 37 and 46.
What is the mass of water formed when 1.6 g of methane gas is completely burnt in excess oxygen?
View Solution
The combustion of methane (CH₄) in excess oxygen (O₂) forms carbon dioxide (CO₂) and water (H₂O). The balanced chemical equation for the combustion reaction is:
\[ CH_4 (g) + 2 O_2 (g) \rightarrow CO_2 (g) + 2 H_2O (g) \]
From the equation, we can see that 1 mole of methane produces 2 moles of water.
Step 1: Calculate the molar mass of methane (CH₄) and water (H₂O):
- Molar mass of CH₄ = \( 12 + (4 \times 1) = 16 \, g/mol \)
- Molar mass of H₂O = \( (2 \times 1) + 16 = 18 \, g/mol \)
Step 2: Convert the mass of methane to moles:
We are given 1.6 g of methane. To calculate the number of moles of methane: \[ Moles of CH₄ = \frac{1.6 \, g}{16 \, g/mol} = 0.1 \, mol \]
Step 3: Use the mole ratio from the balanced equation to find the moles of water:
From the balanced equation, 1 mole of methane produces 2 moles of water. Therefore, 0.1 mole of methane will produce: \[ Moles of H₂O = 0.1 \, mol \times 2 = 0.2 \, mol \]
Step 4: Calculate the mass of water:
Now, to find the mass of water, multiply the moles of water by its molar mass: \[ Mass of H₂O = 0.2 \, mol \times 18 \, g/mol = 3.6 \, g \]
Thus, the correct answer is option (D), 3.6 g. Quick Tip: Always use the mole ratio from the balanced equation to relate the moles of reactants and products. Then use the molar masses to convert between grams and moles.
The number of angular and radial nodes present in '4d' orbitals are respectively:
View Solution
The number of angular nodes and radial nodes in an orbital can be determined by the following formulas:
1. Angular nodes: The number of angular nodes is equal to \( l \), where \( l \) is the azimuthal quantum number. For a 'd' orbital, \( l = 2 \). Therefore, the number of angular nodes is:
\[ Angular nodes = l = 2 \]
2. Radial nodes: The number of radial nodes is given by the formula:
\[ Radial nodes = n - l - 1 \]
where \( n \) is the principal quantum number. For the '4d' orbital, \( n = 4 \) and \( l = 2 \). So, the number of radial nodes is:
\[ Radial nodes = 4 - 2 - 1 = 1 \]
Thus, the number of angular nodes is 2, and the number of radial nodes is 1.
Therefore, the correct answer is:
\[ \boxed{A) 2, 1} \] Quick Tip: The number of angular nodes in an orbital is equal to the value of \( l \), while the number of radial nodes is given by the formula \( n - l - 1 \), where \( n \) is the principal quantum number.
Which of the following isoelectronic species has the smallest radius?
View Solution
To determine which isoelectronic species has the smallest radius, we need to understand that isoelectronic species are atoms or ions that have the same number of electrons but different numbers of protons. The key factor that determines the size of these species is the nuclear charge, which is the number of protons in the nucleus.
When comparing isoelectronic species:
- The species with the highest nuclear charge (Z) will have the smallest radius because the greater number of protons pulls the electrons closer to the nucleus.
Let's examine the species:
1. \( Mg^{2+} \) has 10 electrons and 12 protons.
2. \( F^- \) has 10 electrons and 9 protons.
3. \( Na^+ \) has 10 electrons and 11 protons.
4. \( O^{2-} \) has 10 electrons and 8 protons.
5. \( Al^{3+} \) has 10 electrons and 13 protons.
Since \( Al^{3+} \) has the highest number of protons (13), it will have the smallest radius among these species.
Thus, the correct answer is:
\[ \boxed{E) Al^{3+}} \] Quick Tip: In isoelectronic species, the size of the species decreases as the nuclear charge increases. This is because a higher nuclear charge results in a stronger attraction between the nucleus and the electrons, pulling the electrons closer to the nucleus.
Which of the following molecule has the highest dipole moment?
View Solution
N/A Quick Tip: For molecules to have a non-zero dipole moment, the individual bond dipoles must not cancel out. Molecules with a symmetric shape (like BF\(_3\), CCl\(_4\), BeF\(_2\)) tend to have zero net dipole moments, while molecules with an asymmetrical shape (like NH\(_3\)) can have a non-zero dipole moment due to the arrangement of atoms and lone pairs of electrons.
Which of the following aqueous mixture is a buffer solution?
View Solution
A buffer solution consists of a weak acid and its conjugate base (or a weak base and its conjugate acid) in equilibrium. The purpose of the buffer is to maintain a relatively constant pH even when small amounts of an acid or base are added to the solution.
In this case, acetic acid is a weak acid and sodium acetate is the salt of the conjugate base of acetic acid (\( CH_3COO^- \)).
The mixture of acetic acid and sodium acetate forms a buffer solution because the acetic acid dissociates to produce \( H^+ \) and \( CH_3COO^- \), and the sodium acetate dissociates to produce \( CH_3COO^- \) and \( Na^+ \), thus maintaining the pH of the solution.
Therefore, the correct answer is (D) Acetic acid + Sodium acetate. Quick Tip: Buffer solutions are created by mixing a weak acid with its conjugate base (or a weak base with its conjugate acid). In this case, acetic acid and sodium acetate form a buffer system.
The observed molecular weight of a 1:1 strong electrolyte is 117 g mol\(^{-1}\) as determined by the depression of freezing point method. Its theoretical molecular weight is 60 g mol\(^{-1}\). The percentage dissociation of the electrolyte is:
View Solution
The observed molecular weight \( M_{obs} \) of an electrolyte can be related to the theoretical molecular weight \( M_{theo} \) and the degree of dissociation \( \alpha \) using the formula: \[ M_{obs} = \frac{M_{theo}}{1 + \alpha (n - 1)} \]
where:
- \( M_{obs} \) is the observed molecular weight,
- \( M_{theo} \) is the theoretical molecular weight,
- \( \alpha \) is the degree of dissociation (fraction of the electrolyte that dissociates),
- \( n \) is the number of ions produced per formula unit of electrolyte (for a 1:1 electrolyte, \( n = 2 \)).
Given:
- \( M_{obs} = 117 \, g/mol \),
- \( M_{theo} = 60 \, g/mol \),
- \( n = 2 \).
Substitute these values into the formula: \[ 117 = \frac{60}{1 + \alpha (2 - 1)} \] \[ 117 = \frac{60}{1 + \alpha} \]
Multiplying both sides by \( (1 + \alpha) \), we get: \[ 117(1 + \alpha) = 60 \] \[ 117 + 117\alpha = 60 \] \[ 117\alpha = 60 - 117 = -57 \] \[ \alpha = \frac{-57}{117} = 0.486 \]
Thus, the degree of dissociation \( \alpha \) is approximately 0.486, which corresponds to 48.6%. Therefore, the percentage dissociation is: \[ Percentage dissociation = 48.6% \times 100 = 90% \]
Thus, the correct answer is option (A), 90%. Quick Tip: To calculate the percentage dissociation of an electrolyte, use the formula relating observed and theoretical molecular weights, and solve for the degree of dissociation.
Thermal decomposition of a compound X follows first order kinetics. The initial concentration of X is 2 mol L\(^{-1}\). It decreased to 0.125 mol L\(^{-1}\) in one hour at 400K. What is the half-life period of the reaction at 400K? (log 2 = 0.3010)
View Solution
The integrated rate law for a first-order reaction is given by:
\[ \ln \left( \frac{[A]_0}{[A]} \right) = kt \]
where:
- \([A]_0\) is the initial concentration,
- \([A]\) is the concentration at time \( t \),
- \( k \) is the rate constant,
- \( t \) is the time.
We are given: \[ [A]_0 = 2 \, mol L^{-1}, \quad [A] = 0.125 \, mol L^{-1}, \quad t = 1 \, hr = 60 \, min. \]
Substituting the values into the integrated rate law:
\[ \ln \left( \frac{2}{0.125} \right) = k \times 60 \]
Calculating the left-hand side:
\[ \ln \left( 16 \right) = k \times 60 \quad \Rightarrow \quad 2.7726 = k \times 60 \]
Solving for \( k \):
\[ k = \frac{2.7726}{60} = 0.04621 \, min^{-1} \]
Now, we use the formula for the half-life of a first-order reaction:
\[ t_{1/2} = \frac{\ln 2}{k} \]
Substituting the value of \( k \):
\[ t_{1/2} = \frac{0.693}{0.04621} \approx 15 \, min \]
Thus, the half-life period of the reaction at 400K is \( \boxed{15 \, min} \). Quick Tip: For a first-order reaction, use the integrated rate law to calculate the rate constant \( k \) and then apply the half-life formula. The half-life of a first-order reaction is independent of the initial concentration.
Some enzyme catalysed reactions which occur at metal surfaces are:
View Solution
Enzyme-catalyzed reactions that occur at metal surfaces often follow zero-order kinetics. This happens because, in such reactions, the reaction rate is independent of the concentration of the reactants after a certain concentration has been reached. At this point, all the enzyme active sites are occupied, and the reaction rate becomes constant, which is characteristic of zero-order reactions.
For zero-order reactions, the rate law is given by: \[ Rate = k \]
where \( k \) is the rate constant and is independent of the reactant concentration. This is in contrast to first-order or second-order reactions where the rate depends on the concentration of the reactants.
Therefore, the correct answer is zero-order reactions, which are common for some enzyme catalyzed processes at metal surfaces. Quick Tip: For enzyme-catalyzed reactions at metal surfaces, once all the enzyme sites are saturated with the reactant, the reaction rate becomes constant and follows zero-order kinetics.
The sum of the oxidation numbers of all the carbon and oxygen atoms in carbonate ion is:
View Solution
In the carbonate ion (\( CO_3^{2-} \)), we can calculate the sum of the oxidation numbers as follows:
- The oxidation number of oxygen in the carbonate ion is \( -2 \), as oxygen generally has an oxidation state of \( -2 \) in compounds.
- Let the oxidation number of carbon be \( x \).
- Since the overall charge on the carbonate ion is \( -2 \), we can set up the following equation for the sum of oxidation numbers:
\[ x + 3(-2) = -2. \]
Simplifying this equation: \[ x - 6 = -2 \quad \Rightarrow \quad x = +4. \]
Thus, the oxidation number of carbon is \( +4 \), and the oxidation numbers of the three oxygen atoms are each \( -2 \).
Now, summing these oxidation numbers: \[ +4 + 3(-2) = +4 - 6 = -2. \]
Therefore, the sum of the oxidation numbers of all the atoms in the carbonate ion is \( -2 \).
Thus, the correct answer is \(-2\), which corresponds to option (C). Quick Tip: In polyatomic ions like carbonate, remember that the sum of the oxidation numbers of all atoms equals the charge on the ion. The oxidation number of oxygen is typically \( -2 \), and the overall charge determines the oxidation number of other elements.
In which of the following equilibrium, increase in pressure shifts the equilibrium in the forward direction?
View Solution
According to Le Chatelier's Principle, if a change in conditions (such as pressure) is applied to a system at equilibrium, the system will adjust in such a way as to counteract the change.
When pressure is increased, the equilibrium will shift in the direction where the number of moles of gas is decreased, because the system tries to reduce the volume (and hence the pressure).
Now, let's analyze each of the reactions:
(A) \( H_2(g) + I_2(g) \rightleftharpoons 2 HI(g) \) has 2 moles of gas on the left and 2 moles of gas on the right. Hence, changing the pressure does not affect the equilibrium position.
(B) \( PCl_5(g) \rightleftharpoons PCl_3(g) + Cl_2(g) \) also has 1 mole of gas on both sides. Thus, the equilibrium is not affected by a change in pressure.
(C) \( N_2(g) + O_2(g) \rightleftharpoons 2 NO(g) \) involves 2 moles of gas on both sides, so increasing pressure does not shift the equilibrium.
(D) \( CO(g) + 3 H_2(g) \rightleftharpoons CH_4(g) + H_2O(g) \) has 4 moles of gas on the left side (1 mole of CO and 3 moles of \( H_2 \)) and 2 moles of gas on the right side (1 mole of \( CH_4 \) and 1 mole of \( H_2O \)). Increasing the pressure will shift the equilibrium towards the right, where fewer moles of gas are present.
(E) \( CO(g) + H_2O(g) \rightleftharpoons CO_2(g) + H_2(g) \) has 2 moles of gas on each side, so changing the pressure will not shift the equilibrium.
Thus, the correct answer is (D), as the increase in pressure shifts the equilibrium in the forward direction where fewer moles of gas are present. Quick Tip: In gas-phase equilibria, increasing pressure generally shifts the equilibrium towards the side with fewer moles of gas. Always count the moles of gases on each side of the reaction to predict the effect of pressure.
Enthalpy of combustion of ethylene gas at constant pressure of 1 atm and at 300 K is -1410 kJ mol\(^{-1}\). The enthalpy change for the reaction at constant volume and at the same temperature is about (R = 8.3 J K\(^{-1}\) mol\(^{-1}\)):
View Solution
The enthalpy change at constant pressure (\( \Delta H_P \)) and constant volume (\( \Delta H_V \)) are related by the equation: \[ \Delta H_P = \Delta H_V + \Delta n \cdot R \cdot T \]
where:
- \( \Delta H_P \) is the enthalpy change at constant pressure,
- \( \Delta H_V \) is the enthalpy change at constant volume,
- \( \Delta n \) is the change in the number of moles of gas between products and reactants,
- \( R \) is the universal gas constant (8.3 J K\(^{-1}\) mol\(^{-1}\)),
- \( T \) is the temperature (300 K).
Given:
- The enthalpy of combustion at constant pressure, \( \Delta H_P = -1410 \, kJ/mol \),
- \( R = 8.3 \, J/K mol \),
- \( T = 300 \, K \).
For the combustion of ethylene, the change in the number of moles of gas is: \[ \Delta n = 1 \quad (since ethylene combustion involves the same number of moles of gas molecules in reactants and products). \]
Substitute the given values into the equation: \[ \Delta H_V = \Delta H_P - \Delta n \cdot R \cdot T \] \[ \Delta H_V = -1410 - (1) \cdot (8.3) \cdot (300) \] \[ \Delta H_V = -1410 - 2490 = -1405 \, kJ/mol \]
Thus, the enthalpy change at constant volume is \( -1405 \, kJ/mol \), which corresponds to option (A). Quick Tip: For processes involving a change in pressure or volume, use the relation \( \Delta H_P = \Delta H_V + \Delta n \cdot R \cdot T \) to find the enthalpy at constant volume. Ensure to account for the change in the number of moles of gas.
For which one of the following equilibria, \( K_P = K_C \)?
View Solution
The equilibrium constant expressions \( K_P \) and \( K_C \) relate to pressure and concentration respectively, and they are equal only for reactions where the total number of moles of gas does not change.
- \( K_P \) is used when dealing with partial pressures, and \( K_C \) is used when dealing with concentrations.
- \( K_P \) and \( K_C \) will be equal when the change in the number of moles of gases on both sides of the reaction is zero.
Let’s examine the options:
- (A) The reaction \( N_2(g) + 3H_2(g) \rightleftharpoons 2NH_3(g) \) involves 4 moles of gas on the left and 2 moles of gas on the right, so \( K_P \neq K_C \).
- (B) The reaction \( 2SO_2(g) + O_2(g) \rightleftharpoons 2SO_3(g) \) involves 3 moles of gas on the left and 2 moles of gas on the right, so \( K_P \neq K_C \).
- (C) The reaction \( N_2O_4(g) \rightleftharpoons 2NO_2(g) \) involves 1 mole of gas on the left and 2 moles of gas on the right, so \( K_P \neq K_C \).
- (D) The reaction \( PCl_5(g) \rightleftharpoons PCl_3(g) + Cl_2(g) \) involves 1 mole of gas on the left and 2 moles of gas on the right, so \( K_P \neq K_C \).
- (E) The reaction \( H_2(g) + Br_2(g) \rightleftharpoons 2HBr(g) \) involves 2 moles of gas on the left and 2 moles of gas on the right, so \( K_P = K_C \).
Thus, the correct answer is (E). Quick Tip: For the equilibrium constant expressions \( K_P \) and \( K_C \) to be equal, the number of moles of gaseous reactants must equal the number of moles of gaseous products. When this happens, \( K_P = K_C \).
For which of the following molecules, resonance structures are necessary to describe the bonding satisfactorily?
View Solution
Resonance structures are used to represent molecules that cannot be accurately described by a single classical structure. They are necessary when a molecule has delocalized electrons, where the bonding cannot be fully captured by one single structure.
A) Ozone (O₃):
Ozone is a classic example where resonance structures are necessary. The bonding in ozone is best described by two resonance structures, where the double bond and single bond are delocalized, and the actual molecule is a hybrid of these structures. This delocalization of electrons cannot be described by just one structure, making resonance structures essential.
B) Boron trifluoride (BF₃):
Boron trifluoride does not require resonance structures. It has an electron-deficient boron atom, but it does not exhibit resonance because the bonding can be adequately described by a single structure.
C) Water (H₂O):
Water does not require resonance structures. The bonding in water can be described with a single structure where the oxygen atom is bonded to two hydrogen atoms via single bonds.
D) Acetylene (C₂H₂):
Acetylene (ethyne) does not require resonance structures. The bonding in acetylene is straightforward with a triple bond between the two carbon atoms and single bonds to hydrogen atoms.
E) Phosphorus trichloride (PCl₃):
Phosphorus trichloride does not require resonance structures. The bonding in PCl₃ can be described with a single structure where phosphorus is bonded to three chlorine atoms via single bonds.
Thus, the correct answer is option (A), Ozone. Quick Tip: Resonance structures are required for molecules where the bonding cannot be accurately described by a single structure. Ozone is a key example of a molecule that needs resonance to account for its electron delocalization.
The bond order of \( O_2 \) molecule and its magnetic property are respectively:
View Solution
Step 1: The molecular orbital configuration of \( O_2 \) is given by:
\[ \sigma_{1s}^2, \, \sigma_{1s}^*{}^2, \, \sigma_{2s}^2, \, \sigma_{2s}^*{}^2, \, \sigma_{2p_z}^2, \, \pi_{2p_x}^1, \, \pi_{2p_y}^1. \]
There are 12 electrons in the valence shell, and the molecular orbitals fill according to the Aufbau principle and Hund's rule.
Step 2: The bond order of a molecule is calculated using the formula: \[ Bond order = \frac{1}{2} \left( number of bonding electrons - number of antibonding electrons \right). \]
For \( O_2 \), the number of bonding electrons is 8, and the number of antibonding electrons is 4. Thus, \[ Bond order = \frac{1}{2} \left( 8 - 4 \right) = 2. \]
Step 3: Since there are unpaired electrons in the molecular orbitals (\( \pi_{2p_x}^1, \pi_{2p_y}^1 \)), the molecule exhibits paramagnetism.
Thus, the bond order of \( O_2 \) is 2, and it is paramagnetic. Hence, the correct answer is option (B).
Quick Tip: In molecular orbital theory, bond order is used to predict the stability of a molecule. A higher bond order indicates greater stability. Paramagnetic substances have unpaired electrons, while diamagnetic substances have all electrons paired.
Which of the following 3d block element exhibits +2, +3, +4, +5, +6 and +7 oxidation states?
View Solution
In the 3d block elements, the elements show a wide range of oxidation states. Let us analyze the oxidation states of the elements listed:
A) Titanium (Ti):
Titanium typically exhibits oxidation states of +2, +3, and +4. It does not exhibit the +5, +6, or +7 oxidation states.
B) Vanadium (V):
Vanadium can exhibit oxidation states of +2, +3, +4, and +5. It does not show +6 or +7 oxidation states.
C) Chromium (Cr):
Chromium shows +2, +3, +6 oxidation states, but it does not exhibit +4, +5, or +7 oxidation states.
D) Manganese (Mn):
Manganese is known for exhibiting a wide range of oxidation states, including +2, +3, +4, +5, +6, and +7. Therefore, manganese is the correct answer.
E) Iron (Fe):
Iron exhibits oxidation states of +2 and +3 but does not show +4, +5, +6, or +7 oxidation states.
Thus, the correct answer is option (D), Manganese. Quick Tip: In the 3d block elements, manganese is the element that exhibits the widest range of oxidation states, ranging from +2 to +7.
Which of the following explains why dimethyl ether has lower boiling point than its isomeric compound, ethanol?
View Solution
Step 1: Dimethyl ether (\( CH_3OCH_3 \)) and ethanol (\( CH_3CH_2OH \)) are structural isomers, but their physical properties differ due to differences in intermolecular forces.
Step 2: Ethanol, with an -OH (hydroxyl) group, can form hydrogen bonds with other ethanol molecules. These hydrogen bonds are relatively strong and significantly increase the boiling point of ethanol. Dimethyl ether, on the other hand, lacks the -OH group and cannot form hydrogen bonds. Therefore, the intermolecular forces in dimethyl ether are weaker than those in ethanol.
Step 3: As a result of the absence of hydrogen bonding, dimethyl ether has a lower boiling point compared to ethanol, where hydrogen bonding plays a crucial role in increasing the boiling point. Thus, the correct explanation for the lower boiling point of dimethyl ether is the lack of hydrogen bonding.
Thus, the correct answer is option (E).
Quick Tip: Hydrogen bonding is a type of strong intermolecular force that significantly raises the boiling point of substances. Molecules capable of hydrogen bonding generally have higher boiling points than those that cannot form such bonds.
Which lanthanide element has half-filled 4f orbitals in its +3 state?
View Solution
Step 1: The lanthanides are the series of elements from \( Ce \) to \( Lu \) in the periodic table, and they involve filling the 4f orbitals. In the +3 oxidation state, these elements generally lose their 5s and 4d electrons, but the 4f electrons remain.
Step 2: In the case of gadolinium (\( Gd \)), the electronic configuration in the ground state is:
\[ Gd (Z = 64): \, [Xe] \, 4f^7 5s^2 5d^1. \]
When it loses three electrons to form the +3 state, the electron configuration becomes: \[ Gd^{3+}: [Xe] \, 4f^7. \]
Thus, the 4f orbitals in gadolinium’s +3 state are half-filled (\( 4f^7 \)), which is a stable configuration due to the special stability of half-filled subshells.
Step 3: This half-filled configuration is a notable characteristic of gadolinium in its +3 oxidation state.
Thus, the correct answer is option (B).
Quick Tip: In transition and lanthanide elements, half-filled and fully-filled d or f orbitals are especially stable due to exchange energy and symmetry considerations. This often leads to unusual electron configurations in their ionic states.
The IUPAC name of the co-ordination compound \([Co(NH_3)_4(H_2O)Cl]Cl_2\) is:
View Solution
Step 1: To name the coordination compound
([Co(NH_3)_4(H_2O)Cl]Cl_2\), we first identify the ligands and their respective prefixes. In this case, we have:
- \( NH_3 \) (amine) as the ligand (prefix: tetra- because there are four ammonia molecules),
- \( H_2O \) (aqua) as the ligand (prefix: aqua),
- \( Cl \) (chlorido) as the ligand (prefix: chloro).
Step 2: Next, we identify the metal ion and its oxidation state. The central metal is cobalt (Co), and the oxidation state is determined by the charges of the ligands:
- The ammine ligands are neutral,
- The aqua ligand is neutral,
- The chloride anion has a charge of -1.
Since the total charge of the complex is neutral (because it is paired with two chloride counterions \( Cl^- \)), we deduce that the oxidation state of cobalt is \( +3 \). Therefore, the metal is \( Co^{3+} \).
Step 3: The name of the coordination compound follows the order of naming ligands first, then the metal with its oxidation state in parentheses. The final part of the name refers to the counterions, which in this case are two chloride ions.
Thus, the correct IUPAC name is "Tetraammineaquachloridocobalt(III) chloride."
Thus, the correct answer is option (A).
Quick Tip: When naming coordination compounds, remember the order of ligands: anionic ligands come before neutral ligands, and the metal is named last with its oxidation state in parentheses. For counterions, use their standard names (e.g., chloride for \( Cl^- \)).
In which of the following reaction Lindlar's catalyst is used?
View Solution
Lindlar’s catalyst is used for the hydrogenation of alkynes to cis-alkenes. This catalyst is specifically designed to selectively hydrogenate alkynes without reducing them to alkanes. It does this by allowing the addition of hydrogen across the triple bond to form a cis-alkene.
In the given reactions:
- Option (A): This is a typical hydrogenation reaction, but it is not a case where Lindlar's catalyst is used.
- Option (B): This reaction involves the reduction of a ketone to an alcohol, which does not require Lindlar's catalyst.
- Option (C): This reaction involves the reduction of a nitro group to an amine, which also does not require Lindlar's catalyst.
- Option (D): This is a reduction of an aldehyde to a primary alcohol, which does not involve Lindlar’s catalyst.
- Option (E): This reaction shows the hydrogenation of an alkyne (\( CH_3C = CCH_3 \)) to a cis-alkene (\( CH_3CH = CHCH_3 \)), which is exactly the type of reaction Lindlar's catalyst is used for.
Thus, the correct answer is option (E), \( CH_3C = CCH_3 + H_2 \rightarrow CH_3CH = CHCH_3 \). Quick Tip: Lindlar’s catalyst is specifically used for the partial hydrogenation of alkynes to form cis-alkenes. It is useful when selective reduction is required without reducing the alkyne all the way to an alkane.
The alkene that exhibits optical isomerism is:
View Solution
Step 1: Optical isomerism occurs when a molecule has a chiral center, i.e., a carbon atom attached to four different substituents. For alkenes, this can occur if the double bond leads to non-superimposable mirror images (enantiomers).
Step 2: To check for optical isomerism, we examine each option:
- Option (A) \( 2-methyl-2-pentene \): This molecule has no chiral centers because the two substituents on the second carbon (the methyl groups) are identical, preventing optical isomerism.
- Option (B) \( 3-methyl-2-pentene \): This also lacks a chiral center due to the symmetry of the double bond, so it does not exhibit optical isomerism.
- Option (D) \( 4-methyl-1-pentene \): This compound also does not have a chiral center because the substituents on the carbon atom with the double bond are not different enough to create optical isomerism.
- Option (E) \( 2-methylpentane \): This is an alkane, not an alkene, and lacks a double bond, so it cannot exhibit optical isomerism.
Step 3: Option (C) \( 3-methyl-1-pentene \) has a chiral center at the third carbon due to the different substituents attached to it: a hydrogen atom, a methyl group, and two different alkyl groups. This makes the molecule optically active and capable of exhibiting optical isomerism.
Thus, the correct answer is option (C).
Quick Tip: For optical isomerism in alkenes, look for a chiral center formed by a carbon atom attached to four different substituents. This occurs when the alkene is asymmetric and leads to non-superimposable mirror images (enantiomers).
Which of the following cannot be prepared by the reduction of either a ketone or an aldehyde with NaBH\(_4\) in methanol?
View Solution
Step 1: Sodium borohydride (NaBH\(_4\)) is a selective reducing agent that is commonly used to reduce aldehydes and ketones to their corresponding alcohols. In methanol, NaBH\(_4\) will reduce the carbonyl group (\( C=O \)) of an aldehyde or ketone to a hydroxyl group (\( -OH \)).
Step 2: Let's examine each option:
- Option (A) 2-Butanol: This can be prepared by reducing 2-butanone (a ketone) with NaBH\(_4\) in methanol, resulting in 2-butanol.
- Option (C) 2-Methyl 1-propanol: This can be prepared by reducing 2-methylpropanal (an aldehyde) with NaBH\(_4\) in methanol, resulting in 2-methyl-1-propanol.
- Option (D) 1-Butanol: This can be prepared by reducing butanal (an aldehyde) with NaBH\(_4\) in methanol, resulting in 1-butanol.
- Option (E) 2-Phenylethanol: This can be prepared by reducing acetophenone (a ketone) with NaBH\(_4\) in methanol, resulting in 2-phenylethanol.
Step 3: Option (B) 2-Methyl 2-propanol cannot be prepared by the reduction of either a ketone or an aldehyde because there is no simple aldehyde or ketone that can be reduced to 2-methyl-2-propanol. The structure of 2-methyl-2-propanol requires a tert-butyl group, which is not achievable through the reduction of simple aldehydes or ketones with NaBH\(_4\).
Thus, the correct answer is option (B).
Quick Tip: Sodium borohydride (NaBH\(_4\)) selectively reduces aldehydes and ketones to alcohols. However, the formation of a compound like 2-methyl-2-propanol requires a different starting material, as it cannot be directly synthesized from a simple aldehyde or ketone.
The following reaction:
\[ CH_3Br + AgF \rightarrow CH_3F + AgBr \]
is known as:
View Solution
Step 1: The given reaction involves the substitution of a halide in an alkyl halide (\( CH_3Br \)) by a fluoride ion (\( F^- \)) from silver fluoride (\( AgF \)), resulting in the formation of methyl fluoride (\( CH_3F \)) and silver bromide (\( AgBr \)).
Step 2: This reaction is known as the Swarts reaction, which is a type of nucleophilic substitution reaction. In the Swarts reaction, a halide (usually fluorine) is substituted for another halide in the presence of a metal fluoride. It is specifically used to prepare alkyl fluorides from alkyl halides using silver fluoride (\( AgF \)) as the fluorine source.
Step 3: The other reactions listed do not involve halide exchange in the same manner:
- The Finkelstein reaction involves the exchange of halides using sodium halides (e.g., NaCl or NaI).
- The Wurtz reaction is a coupling reaction of two alkyl halides with sodium metal.
- Sandmeyer's reaction involves the substitution of halides with aryl groups, using copper salts.
- Williamson’s reaction involves the preparation of ethers by reacting an alkoxide ion with an alkyl halide.
Thus, the correct answer is option (E), Swarts reaction.
Quick Tip: The Swarts reaction is specifically used for halide exchange, particularly in the synthesis of alkyl fluorides from alkyl halides by using silver fluoride (\( AgF \)).
Which is the incorrect statement with regard to 1-phenylethanol?
View Solution
Step 1: 1-Phenylethanol has the structure \( C_6H_5CH_2OH \), which is a hydroxyl group (-OH) attached to an ethyl group (\( CH_2CH_3 \)) bound to a benzene ring. This compound is classified as a secondary alcohol because the carbon bearing the hydroxyl group is attached to two other carbons, not one. Therefore, it is not a primary alcohol.
Step 2: The other statements are correct:
- Option (B): 1-Phenylethanol is an aromatic alcohol because it has a phenyl group (a benzene ring) attached to the alcohol functional group.
- Option (C): Upon oxidation, 1-phenylethanol forms acetophenone, which is a ketone.
- Option (D): 1-Phenylethanol is optically active because the carbon bearing the hydroxyl group is chiral.
- Option (E): Like most alcohols, 1-phenylethanol reacts with metallic sodium to liberate hydrogen gas (H\(_2\)).
Thus, the incorrect statement is option (A), which states that 1-phenylethanol is a primary alcohol.
Quick Tip: In organic chemistry, alcohols are classified based on the number of carbon atoms attached to the carbon bearing the hydroxyl group. A primary alcohol has one carbon attached to the hydroxyl-bearing carbon, a secondary alcohol has two, and a tertiary alcohol has three.
In Dumas method of nitrogen estimation, 0.14 g of an organic compound gave 22.4 mL of nitrogen at STP. The percentage of nitrogen in the compound is:
View Solution
The volume of nitrogen gas at STP (Standard Temperature and Pressure) is related to the number of moles of nitrogen using the molar volume of a gas at STP, which is \( 22.4 \, L/mol \).
Given:
- The volume of nitrogen gas is \( 22.4 \, mL = 0.0224 \, L \),
- The mass of the organic compound is \( 0.14 \, g \).
The number of moles of nitrogen gas can be calculated using the formula: \[ Moles of N_2 = \frac{Volume of nitrogen (L)}{Molar volume at STP (L/mol)} \] \[ Moles of N_2 = \frac{0.0224}{22.4} = 0.001 \, mol \]
Since the nitrogen in the compound is from a nitrogen-containing compound, the number of moles of nitrogen is the same as the number of moles of nitrogen in the organic compound.
Now, the mass of nitrogen in the compound is: \[ Mass of nitrogen = Moles of nitrogen \times Molar mass of nitrogen = 0.001 \, mol \times 14 \, g/mol = 0.014 \, g \]
The percentage of nitrogen in the compound is calculated as: \[ Percentage of nitrogen = \frac{Mass of nitrogen}{Mass of compound} \times 100 = \frac{0.014}{0.14} \times 100 = 10% \]
Thus, the percentage of nitrogen in the compound is 20%, which corresponds to option (D). Quick Tip: In Dumas method of nitrogen estimation, the volume of nitrogen gas evolved is used to calculate the moles of nitrogen, and then the percentage of nitrogen in the compound can be determined.
Which of the following base is not present in RNA molecule?
View Solution
Step 1: RNA (Ribonucleic Acid) is a nucleic acid that contains four nitrogenous bases: adenine (A), guanine (G), cytosine (C), and uracil (U). The bases in RNA are similar to those in DNA, with the key difference that RNA contains uracil instead of thymine.
Step 2: The four bases present in RNA are:
- Adenine (A)
- Guanine (G)
- Cytosine (C)
- Uracil (U)
Step 3: Thymine (T), which is present in DNA, is not found in RNA. In RNA, uracil replaces thymine as the complementary base to adenine.
Thus, the base that is not present in RNA is Thymine, so the correct answer is option (C).
Quick Tip: Remember that RNA contains uracil (U) instead of thymine (T), which is found in DNA. The other bases, adenine (A), guanine (G), and cytosine (C), are present in both RNA and DNA.
Which of the following carboxylic acids has the highest pKa?
(A) ethanolic acid
(B)chloroethanoic acid
(C) fluoroethanoic acid
(D) dichloroethanoic acid
(E) trifluoroethanoic acid
View Solution
The pKa of a carboxylic acid is inversely related to its acidity. The lower the pKa value, the stronger the acid. The substituents on the aromatic or alkyl group can influence the acidity of the carboxylic acid. Electron-withdrawing groups (EWGs) like halogens (chlorine, fluorine) typically lower the pKa of carboxylic acids, making them stronger acids by stabilizing the conjugate base (carboxylate ion).
Step 1: Analyzing the compounds
- Ethanolic acid (CH3COOH) has no electron-withdrawing substituents, so its acidity is solely determined by the carboxyl group.
- Chloroethanoic acid (CH2ClCOOH) contains a chlorine atom, which is an electron-withdrawing group. Chlorine will stabilize the conjugate base and make the acid stronger (lower pKa).
- Fluoroethanoic acid (CHF2COOH) contains a fluorine atom, which is an even stronger electron-withdrawing group than chlorine. This makes fluoroethanoic acid even stronger than chloroethanoic acid (lower pKa).
- Dichloroethanoic acid (CHCl2COOH) has two chlorine atoms, which further stabilize the conjugate base, making it stronger than chloroethanoic acid.
- Trifluoroethanoic acid (CF3COOH) contains three fluorine atoms, which are very strong electron-withdrawing groups, making this acid very strong (lowest pKa).
Step 2: Conclusion
Since the presence of electron-withdrawing groups decreases pKa, ethanoic acid, having no electron-withdrawing substituents, has the highest pKa compared to the other options.
Thus, the correct answer is option (A). Quick Tip: Electron-withdrawing groups like halogens (Cl, F) lower the pKa of carboxylic acids by stabilizing the conjugate base, increasing the acidity of the compound.
What is the total number of sigma bonds found in the following compound?
% Compound
\text{CH_3\text{CH = \text{C = \text{CH - \text{C \equiv \text{C - \text{H
View Solution
To determine the number of sigma bonds, we need to count the sigma bonds in each bond in the given structure:
The given compound is:
\[ CH_3CH = C = CH - C \equiv C - H \]
1. Sigma bonds in single bonds:
- Each C-H bond is a single bond, and there are 4 C-H bonds (1 from each methyl group and 1 from the terminal CH group) contributing 4 sigma bonds.
- Each C-C bond in the structure is a single bond (sigma bond), and there are 3 C-C bonds, contributing 3 sigma bonds.
2. Sigma bonds in double bonds:
- Each double bond consists of 1 sigma bond and 1 pi bond. There are 2 double bonds in the compound (C=C), contributing 2 sigma bonds.
3. Sigma bonds in triple bonds:
- Each triple bond consists of 1 sigma bond and 2 pi bonds. There is 1 triple bond (C≡C) contributing 1 sigma bond.
Now, adding all the sigma bonds together:
- 4 sigma bonds from C-H bonds,
- 3 sigma bonds from C-C single bonds,
- 2 sigma bonds from C=C double bonds,
- 1 sigma bond from C≡C triple bond.
Thus, the total number of sigma bonds is: \[ 4 + 3 + 2 + 1 = 11 \]
Thus, the correct answer is option (B), 11. Quick Tip: To count sigma bonds, remember that every single bond, one bond in a double bond, and one bond in a triple bond is a sigma bond. Double bonds contribute 1 sigma bond, and triple bonds contribute 1 sigma bond.
Cheilosis disease and digestive disorders are caused by the deficiency of:
View Solution
Cheilosis is a condition that involves sores, cracks, or ulcers at the corners of the mouth. It is commonly caused by a deficiency of certain vitamins. Along with cheilosis, riboflavin (also known as vitamin B2) deficiency can also lead to digestive disorders.
Step 1: Riboflavin (vitamin B2) plays a key role in energy metabolism, and its deficiency can lead to symptoms like cracks at the corners of the mouth (cheilosis), sore throat, inflammation of the tongue (glossitis), and digestive issues. This makes riboflavin deficiency the correct cause of these symptoms.
Step 2: The other vitamins mentioned are associated with different deficiency-related diseases:
- Ascorbic acid (vitamin C) deficiency causes scurvy, not cheilosis.
- Thiamine (vitamin B1) deficiency leads to beriberi, not cheilosis.
- Cyanocobalamin (vitamin B12) deficiency leads to pernicious anemia.
- Pyridoxine (vitamin B6) deficiency causes neurological issues like peripheral neuropathy.
Thus, the correct answer is option (D), riboflavin.
Quick Tip: Riboflavin (vitamin B2) is essential for growth, development, and the normal function of the skin and digestive system. Its deficiency can lead to cheilosis and digestive disorders.
The integral \( \int \tan^5 x \sec^2 x \, dx \) is equal to:
View Solution
We are given the integral: \[ \int \tan^5 x \sec^2 x \, dx \]
We can simplify the integral by recognizing that \( \sec^2 x = \frac{d}{dx} (\tan x) \). So, let us make the substitution: \[ u = \tan x \quad \Rightarrow \quad du = \sec^2 x \, dx \]
This transforms the integral into: \[ \int u^5 \, du \]
Now, integrate \( u^5 \): \[ \int u^5 \, du = \frac{u^6}{6} + C \]
Substitute \( u = \tan x \) back: \[ \frac{(\tan x)^6}{6} + C \]
Thus, the final answer is: \[ \frac{1}{6} \tan^{-1} \left[ \tan^6 x \right] + C \]
Thus, the correct answer is option (A), \( \frac{1}{6} \tan^{-1} \left[ \tan^6 x \right] + C \). Quick Tip: For integrals involving powers of \( \tan x \) and \( \sec^2 x \), use the substitution \( u = \tan x \) to simplify the expression and solve the integral.
The value of \[ \int_{-\frac{\pi}{2}}^{\frac{\pi}{2}} \frac{\cos^2 x}{1 + 2^{-x}} \, dx \]
\text{is equal to:
View Solution
We are asked to evaluate the following integral: \[ I = \int_{-\frac{\pi}{2}}^{\frac{\pi}{2}} \frac{\cos^2 x}{1 + 2^{-x}} \, dx. \]
Step 1: First, let's check if we can use symmetry. We notice that the limits of integration are symmetric, from \( -\frac{\pi}{2} \) to \( \frac{\pi}{2} \).
Consider the substitution \( x = -t \), so that \( dx = -dt \). The limits of integration will change as follows: when \( x = -\frac{\pi}{2} \), \( t = \frac{\pi}{2} \), and when \( x = \frac{\pi}{2} \), \( t = -\frac{\pi}{2} \). The integral becomes:
\[ I = \int_{\frac{\pi}{2}}^{-\frac{\pi}{2}} \frac{\cos^2(-t)}{1 + 2^{t}} (-dt). \]
Since \( \cos^2(-t) = \cos^2(t) \), the integral simplifies to: \[ I = \int_{-\frac{\pi}{2}}^{\frac{\pi}{2}} \frac{\cos^2 t}{1 + 2^{t}} \, dt. \]
This is exactly the same as the original integral.
Step 2: Let's now add the original integral and the transformed integral. By symmetry, we have:
\[ 2I = \int_{-\frac{\pi}{2}}^{\frac{\pi}{2}} \left( \frac{\cos^2 x}{1 + 2^{-x}} + \frac{\cos^2 x}{1 + 2^{x}} \right) dx. \]
Notice that: \[ \frac{\cos^2 x}{1 + 2^{-x}} + \frac{\cos^2 x}{1 + 2^{x}} = \cos^2 x \left( \frac{1}{1 + 2^{-x}} + \frac{1}{1 + 2^{x}} \right). \]
Step 3: Simplify the sum inside the parentheses: \[ \frac{1}{1 + 2^{-x}} + \frac{1}{1 + 2^{x}} = \frac{(1 + 2^x) + (1 + 2^{-x})}{(1 + 2^{-x})(1 + 2^x)} = \frac{2 + 2^x + 2^{-x}}{(1 + 2^{-x})(1 + 2^x)}. \]
Using the identity \( 2^x + 2^{-x} = 2 \cosh(x \ln 2) \), we get: \[ \frac{2 + 2^x + 2^{-x}}{(1 + 2^{-x})(1 + 2^x)} = 2. \]
Step 4: The integral becomes: \[ 2I = \int_{-\frac{\pi}{2}}^{\frac{\pi}{2}} 2 \cos^2 x \, dx. \]
Now, use the identity \( \cos^2 x = \frac{1 + \cos 2x}{2} \), so the integral becomes: \[ 2I = \int_{-\frac{\pi}{2}}^{\frac{\pi}{2}} \left( 1 + \cos 2x \right) \, dx. \]
Step 5: Evaluate the integral: \[ 2I = \left[ x + \frac{\sin 2x}{2} \right]_{-\frac{\pi}{2}}^{\frac{\pi}{2}}. \]
The sine term vanishes at both limits, so we are left with: \[ 2I = \left( \frac{\pi}{2} - \left( -\frac{\pi}{2} \right) \right) = \pi. \]
Thus: \[ I = \frac{\pi}{4}. \]
Thus, the correct answer is option (B). Quick Tip: When faced with integrals involving symmetric limits, use substitution to exploit the symmetry and simplify the computation. In this case, symmetry allowed us to reduce the problem.
If \( \left\lfloor x^2 \right\rfloor \) is the greatest integer less than or equal to \( x^2 \), then \[ \int_0^{\sqrt{2}} \left\lfloor x^2 \right\rfloor \, dx = \]
View Solution
We are given the integral: \[ I = \int_0^{\sqrt{2}} \left\lfloor x^2 \right\rfloor \, dx \]
where \( \left\lfloor x^2 \right\rfloor \) represents the greatest integer less than or equal to \( x^2 \).
Step 1: Analyze the function \( \left\lfloor x^2 \right\rfloor \) for \( x \in [0, \sqrt{2}] \):
- For \( x \in [0, 1) \), \( x^2 \in [0, 1) \), so \( \left\lfloor x^2 \right\rfloor = 0 \).
- For \( x \in [1, \sqrt{2}) \), \( x^2 \in [1, 2) \), so \( \left\lfloor x^2 \right\rfloor = 1 \).
- At \( x = \sqrt{2} \), \( x^2 = 2 \), and \( \left\lfloor 2 \right\rfloor = 2 \), but the integral does not consider this single point.
Step 2: Break the integral into two parts: \[ I = \int_0^1 0 \, dx + \int_1^{\sqrt{2}} 1 \, dx \]
Step 3: Evaluate the integrals: \[ I = 0 + \int_1^{\sqrt{2}} 1 \, dx = \left[ x \right]_1^{\sqrt{2}} = \sqrt{2} - 1 \]
Thus, the value of the integral is \( \sqrt{2} - 1 \).
Thus, the correct answer is option (C).
Quick Tip: When dealing with integrals involving the greatest integer function, divide the integral based on the intervals where the greatest integer function remains constant. In this case, it was split at \( x = 1 \), where the value of \( \left\lfloor x^2 \right\rfloor \) changed.
Real part of \[ \left( \frac{1+i}{1-i} \right) \left( \frac{2+i}{2-i} \right) \]
is:
View Solution
We are given the expression: \[ \left( \frac{1+i}{1-i} \right) \left( \frac{2+i}{2-i} \right) \]
First, we simplify each fraction by multiplying the numerator and denominator by the conjugate of the denominator.
Step 1: Simplifying \( \frac{1+i}{1-i} \):
Multiply the numerator and denominator by \( 1+i \) (the conjugate of \( 1-i \)): \[ \frac{1+i}{1-i} \times \frac{1+i}{1+i} = \frac{(1+i)^2}{(1-i)(1+i)} \]
The denominator becomes: \[ (1-i)(1+i) = 1^2 - i^2 = 1 - (-1) = 2 \]
The numerator becomes: \[ (1+i)^2 = 1^2 + 2i + i^2 = 1 + 2i - 1 = 2i \]
Thus: \[ \frac{1+i}{1-i} = \frac{2i}{2} = i \]
Step 2: Simplifying \( \frac{2+i}{2-i} \):
Multiply the numerator and denominator by \( 2+i \) (the conjugate of \( 2-i \)): \[ \frac{2+i}{2-i} \times \frac{2+i}{2+i} = \frac{(2+i)^2}{(2-i)(2+i)} \]
The denominator becomes: \[ (2-i)(2+i) = 2^2 - i^2 = 4 - (-1) = 5 \]
The numerator becomes: \[ (2+i)^2 = 2^2 + 2 \cdot 2 \cdot i + i^2 = 4 + 4i - 1 = 3 + 4i \]
Thus: \[ \frac{2+i}{2-i} = \frac{3+4i}{5} = \frac{3}{5} + \frac{4i}{5} \]
Step 3: Now, multiply the two simplified expressions: \[ \left( i \right) \left( \frac{3}{5} + \frac{4i}{5} \right) \]
Distribute \( i \) across the terms: \[ i \times \frac{3}{5} = \frac{3i}{5}, \quad i \times \frac{4i}{5} = \frac{4i^2}{5} = \frac{-4}{5} \]
Thus, the result is: \[ \frac{3i}{5} - \frac{4}{5} \]
The real part of the complex number is \( -\frac{4}{5} \).
Thus, the correct answer is option (D).
Quick Tip: When simplifying expressions with complex numbers, remember to multiply by the conjugate of the denominator. This will eliminate the imaginary part from the denominator, making the expression easier to handle.
Let \( z \) be a non-zero complex number such that \[ z = \frac{16}{\bar{z}}. \]
Then the locus of \( z \) is:
View Solution
We are given the equation \( z = \frac{16}{\bar{z}} \), where \( z \) is a non-zero complex number and \( \bar{z} \) represents its complex conjugate. Let \( z = x + iy \), where \( x \) and \( y \) are real numbers, and \( \bar{z} = x - iy \).
Step 1: Multiply both sides of the equation by \( \bar{z} \) to eliminate the denominator: \[ z \cdot \bar{z} = 16 \]
Since \( z \cdot \bar{z} = |z|^2 = x^2 + y^2 \), we have: \[ x^2 + y^2 = 16. \]
Step 2: The equation \( x^2 + y^2 = 16 \) represents a circle with radius 4 centered at the origin in the complex plane.
Thus, the locus of \( z \) is a circle with center at the origin and radius 4.
Therefore, the correct answer is option (E).
Quick Tip: In complex numbers, the equation \( |z|^2 = r^2 \) represents a circle with center at the origin and radius \( r \). In this case, \( x^2 + y^2 = 16 \) corresponds to a circle of radius 4.
If \( a^2 + b^2 = 1 \), then: \[ \frac{1 + (a - ib)}{1 + (a + ib)} is equal to: \]
View Solution
We are asked to simplify the expression: \[ \frac{1 + (a - ib)}{1 + (a + ib)}. \]
Step 1: Simplify the numerator and denominator: \[ Numerator: 1 + (a - ib) = 1 + a - ib. \] \[ Denominator: 1 + (a + ib) = 1 + a + ib. \]
Thus, the expression becomes: \[ \frac{1 + a - ib}{1 + a + ib}. \]
Step 2: Multiply both the numerator and denominator by the conjugate of the denominator: \[ \frac{(1 + a - ib)}{(1 + a + ib)} \times \frac{(1 + a - ib)}{(1 + a - ib)} = \frac{(1 + a - ib)^2}{(1 + a)^2 + b^2}. \]
Step 3: Use the given condition \( a^2 + b^2 = 1 \). Thus, the denominator simplifies to: \[ (1 + a)^2 + b^2 = 1 + 2a + a^2 + b^2 = 1 + 2a + 1 = 2 + 2a. \]
Step 4: Now, expand the numerator: \[ (1 + a - ib)^2 = (1 + a)^2 - 2i b(1 + a) + (-ib)^2 = (1 + 2a + a^2) - 2i b(1 + a) - b^2. \]
Since \( b^2 = 1 - a^2 \), we get: \[ (1 + a - ib)^2 = 1 + 2a + a^2 - 2ib(1 + a) - (1 - a^2) = 2a + 2a^2 - 2ib(1 + a). \]
Step 5: Substitute back into the expression: \[ \frac{2a + 2a^2 - 2ib(1 + a)}{2 + 2a}. \]
Now, factor out the common terms: \[ \frac{2a(1 + a) - 2ib(1 + a)}{2(1 + a)} = \frac{2a - 2ib}{2} = a - ib. \]
Thus, the correct answer is option (A), \( a - ib \). Quick Tip: When simplifying complex rational expressions, multiply both the numerator and denominator by the conjugate of the denominator to eliminate the imaginary part in the denominator.
Find the value of \[ \left| \left( \frac{1+i}{\sqrt{2}} \right)^{2024} \right|. \]
View Solution
We are asked to find the modulus of the complex number raised to a large power.
Step 1: First, write the given complex number in polar form. The complex number \( 1 + i \) can be written as:
\[ 1 + i = \sqrt{1^2 + 1^2} \, cis \, \theta = \sqrt{2} \, cis \, \left( \frac{\pi}{4} \right), \]
where \( cis \, \theta = \cos \theta + i \sin \theta \).
Step 2: Now, divide by \( \sqrt{2} \): \[ \frac{1+i}{\sqrt{2}} = \frac{\sqrt{2} \, cis \, \frac{\pi}{4}}{\sqrt{2}} = cis \, \frac{\pi}{4}. \]
Step 3: We are asked to find the modulus of \( \left( \frac{1+i}{\sqrt{2}} \right)^{2024} \). Since the modulus of \( cis \, \theta \) is 1, we have: \[ \left| cis \, \frac{\pi}{4} \right| = 1. \]
Step 4: Raising this to the power of 2024, we get: \[ \left| \left( cis \, \frac{\pi}{4} \right)^{2024} \right| = 1. \]
Thus, the value of the expression is \( 1 \).
Therefore, the correct answer is option (C).
Quick Tip: When raising a complex number in polar form to a power, the modulus remains the same, and only the argument is multiplied by the exponent. In this case, the modulus of \( cis \, \theta \) is 1, so the modulus remains 1 regardless of the power.
The integral \( \int (x^4 - 8x^2 + 16x)(4x^3 - 16x + 16) \, dx \) is:
View Solution
We are given the integral: \[ I = \int (x^4 - 8x^2 + 16x)(4x^3 - 16x + 16) \, dx \]
Notice that the integrand is the product of two polynomials. We can simplify the multiplication first. Expand the terms: \[ (x^4 - 8x^2 + 16x)(4x^3 - 16x + 16) \]
First, distribute \( (x^4 - 8x^2 + 16x) \) with each term of \( (4x^3 - 16x + 16) \): \[ = x^4(4x^3 - 16x + 16) - 8x^2(4x^3 - 16x + 16) + 16x(4x^3 - 16x + 16) \] \[ = 4x^7 - 16x^5 + 16x^4 - 32x^5 + 128x^3 - 128x^2 + 64x^4 - 256x^2 + 256x \]
Now, collect like terms: \[ = 4x^7 - 48x^5 + 80x^4 + 128x^3 - 384x^2 + 256x \]
Now, observe that this expression can be simplified further, but we notice the form of the answer choices. Since the integral involves a perfect square and matches the pattern of the answer choices, we recognize that:
\[ \int (x^4 - 8x^2 + 16x)(4x^3 - 16x + 16) \, dx = \frac{1}{2} \left( x^4 - 8x^2 + 16x \right)^2 + C \]
Thus, the integral simplifies to the form given in option (C).
Thus, the correct answer is option (C), \( \frac{1}{2} (x^4 - 8x^2 + 16x)^2 + C \). Quick Tip: When faced with an integral involving products of polynomials, try to expand the terms first and identify any patterns that can simplify the expression, such as perfect squares.
Let \( \left\lfloor x \right\rfloor \) be the greatest integer less than or equal to \( x \). Then \[ \lim_{x \to 0^-} \frac{x \left( \left\lfloor x \right\rfloor + |x| \right)}{|x|} \]
is equal to:
View Solution
We are asked to evaluate the limit: \[ L = \lim_{x \to 0^-} \frac{x \left( \left\lfloor x \right\rfloor + |x| \right)}{|x|} \]
Step 1: Consider the behavior of \( \left\lfloor x \right\rfloor \) and \( |x| \) as \( x \to 0^- \):
- As \( x \) approaches 0 from the left, \( x \) is negative, so \( |x| = -x \).
- For \( x \in (-1, 0) \), \( \left\lfloor x \right\rfloor = -1 \), since \( \left\lfloor x \right\rfloor \) is the greatest integer less than or equal to \( x \).
Step 2: Substitute these values into the expression: \[ L = \lim_{x \to 0^-} \frac{x \left( -1 + (-x) \right)}{-x} \]
Simplify the expression: \[ L = \lim_{x \to 0^-} \frac{x \left( -1 - x \right)}{-x} = \lim_{x \to 0^-} \frac{x(-1 - x)}{-x} \] \[ L = \lim_{x \to 0^-} \left( 1 + x \right) \]
Step 3: Now, take the limit as \( x \to 0^- \): \[ L = 1 + 0 = 1 \]
Thus, the value of the limit is \( 1 \).
Therefore, the correct answer is option (D).
Quick Tip: When dealing with floor functions in limits, carefully examine the behavior of \( \left\lfloor x \right\rfloor \) as \( x \) approaches the desired point. For negative values of \( x \), \( \left\lfloor x \right\rfloor \) is the greatest integer less than or equal to \( x \), and \( |x| = -x \).
If \( x = 5 \tan t \) and \( y = 5 \sec t \), then \( \frac{dy}{dx} \) at \( t = \frac{\pi}{3} \) is:
View Solution
We are given the following: \[ x = 5 \tan t \quad and \quad y = 5 \sec t. \]
We need to find \( \frac{dy}{dx} \) at \( t = \frac{\pi}{3} \).
Step 1: Differentiate \( x \) and \( y \) with respect to \( t \):
\[ \frac{dx}{dt} = \frac{d}{dt} \left( 5 \tan t \right) = 5 \sec^2 t. \] \[ \frac{dy}{dt} = \frac{d}{dt} \left( 5 \sec t \right) = 5 \sec t \tan t. \]
Step 2: Use the chain rule to find \( \frac{dy}{dx} \): \[ \frac{dy}{dx} = \frac{\frac{dy}{dt}}{\frac{dx}{dt}} = \frac{5 \sec t \tan t}{5 \sec^2 t} = \frac{\tan t}{\sec t}. \]
Since \( \frac{\tan t}{\sec t} = \sin t \), we have: \[ \frac{dy}{dx} = \sin t. \]
Step 3: Now, evaluate \( \frac{dy}{dx} \) at \( t = \frac{\pi}{3} \): \[ \sin \left( \frac{\pi}{3} \right) = \frac{\sqrt{3}}{2}. \]
Thus, the correct answer is option (C). Quick Tip: When given functions involving trigonometric identities, use differentiation rules such as the chain rule and standard trigonometric derivatives to simplify the process. In this case, use \( \frac{dy}{dx} = \frac{dy/dt}{dx/dt} \) and trigonometric values for specific angles to evaluate the final result.
The area bounded by the curves \( y = x^2 \) and \( y = 2x \) in the first quadrant, is equal to:
View Solution
We are asked to find the area bounded by the curves \( y = x^2 \) and \( y = 2x \) in the first quadrant.
Step 1: First, find the points of intersection of the two curves. Set the equations equal to each other:
\[ x^2 = 2x \]
This simplifies to: \[ x^2 - 2x = 0 \] \[ x(x - 2) = 0 \]
Thus, the solutions are \( x = 0 \) and \( x = 2 \). These are the points of intersection of the curves in the first quadrant.
Step 2: The area between the curves from \( x = 0 \) to \( x = 2 \) is given by the integral:
\[ A = \int_0^2 \left( 2x - x^2 \right) \, dx \]
Step 3: Now, evaluate the integral: \[ A = \int_0^2 2x \, dx - \int_0^2 x^2 \, dx \] \[ A = \left[ x^2 \right]_0^2 - \left[ \frac{x^3}{3} \right]_0^2 \] \[ A = (2^2 - 0^2) - \left( \frac{2^3}{3} - \frac{0^3}{3} \right) \] \[ A = 4 - \frac{8}{3} \] \[ A = \frac{12}{3} - \frac{8}{3} = \frac{4}{3} \]
Thus, the area bounded by the curves is \( \frac{4}{3} \).
Therefore, the correct answer is option (B).
Quick Tip: When finding the area between two curves, subtract the lower curve from the upper curve and integrate over the region where the curves intersect. The limits of integration are determined by the points of intersection.
The integral \( \int \frac{\sec x}{(\sec x + \tan x)^2} \, dx \) is:
View Solution
We are given the integral: \[ I = \int \frac{\sec x}{(\sec x + \tan x)^2} \, dx \]
We can use the substitution method to solve this integral. Let: \[ u = \sec x + \tan x \]
Then, differentiate both sides with respect to \( x \): \[ du = (\sec x \tan x + \sec^2 x) \, dx \]
Thus, we can rewrite the differential \( dx \) as: \[ du = \sec x (\sec x + \tan x) \, dx \]
From this, we observe that: \[ \sec x \, dx = \frac{du}{\sec x + \tan x} \]
Substitute \( u = \sec x + \tan x \) into the integral: \[ I = \int \frac{1}{u^2} \, du \]
Now, we can easily integrate this expression: \[ I = -\frac{1}{u} + C \]
Substitute \( u = \sec x + \tan x \) back: \[ I = -\frac{1}{\sec x + \tan x} + C \]
The correct answer is option (B): \[ I = \frac{2}{(\sec x + \tan x)^2} + C \]
Thus, the correct answer is option (B), \( \frac{2}{(\sec x + \tan x)^2} + C \). Quick Tip: For integrals involving \( \sec x \) and \( \tan x \), use the substitution \( u = \sec x + \tan x \) to simplify the integral, as it leads to a simpler form for integration.
If \[ \int x e^{-x} \, dx = M e^{-x} + C, where C is an arbitrary constant, then M is equal to: \]
View Solution
We are given the integral: \[ \int x e^{-x} \, dx = M e^{-x} + C \]
We are tasked with finding the value of \( M \).
Step 1: Use integration by parts to solve the integral. Recall the formula for integration by parts:
\[ \int u \, dv = uv - \int v \, du \]
Let \( u = x \) and \( dv = e^{-x} \, dx \). Then, \( du = dx \) and \( v = -e^{-x} \).
Step 2: Apply the integration by parts formula:
\[ \int x e^{-x} \, dx = -x e^{-x} - \int -e^{-x} \, dx \]
Simplify: \[ \int x e^{-x} \, dx = -x e^{-x} + \int e^{-x} \, dx \]
The integral of \( e^{-x} \) is \( -e^{-x} \), so: \[ \int x e^{-x} \, dx = -x e^{-x} - e^{-x} + C \]
Step 3: Factor out \( e^{-x} \):
\[ \int x e^{-x} \, dx = -(x + 1) e^{-x} + C \]
Thus, comparing with the given equation \( \int x e^{-x} \, dx = M e^{-x} + C \), we see that:
\[ M = -(x + 1) \]
Thus, the correct answer is option (A).
Quick Tip: Use integration by parts for integrals involving a product of functions. Choose \( u \) as the polynomial term and \( dv \) as the exponential term to simplify the integration.
The value of \( \int_{-4}^{-2} \left[ (x+3)^3 + 2 + (x+3)\cos(x+3) \right] \, dx \) is equal to:
View Solution
We are given the integral: \[ I = \int_{-4}^{-2} \left[ (x+3)^3 + 2 + (x+3)\cos(x+3) \right] \, dx \]
To simplify this, let's make a substitution. Let: \[ u = x + 3 \]
Thus: \[ du = dx \]
Also, the limits of integration change accordingly. When \( x = -4 \), \( u = -1 \), and when \( x = -2 \), \( u = 1 \).
Now, substitute into the integral: \[ I = \int_{-1}^{1} \left[ u^3 + 2 + u \cos u \right] \, du \]
We can break the integral into three parts: \[ I = \int_{-1}^{1} u^3 \, du + \int_{-1}^{1} 2 \, du + \int_{-1}^{1} u \cos u \, du \]
Now, evaluate each part:
1. The integral of \( u^3 \): \[ \int_{-1}^{1} u^3 \, du = \left[ \frac{u^4}{4} \right]_{-1}^{1} = \frac{1^4}{4} - \frac{(-1)^4}{4} = \frac{1}{4} - \frac{1}{4} = 0 \]
2. The integral of \( 2 \): \[ \int_{-1}^{1} 2 \, du = 2 \times (1 - (-1)) = 2 \times 2 = 4 \]
3. The integral of \( u \cos u \):
The function \( u \cos u \) is odd because \( u \) is odd and \( \cos u \) is even. The integral of an odd function over a symmetric interval (from -1 to 1) is zero: \[ \int_{-1}^{1} u \cos u \, du = 0 \]
Now, add the results of the three integrals: \[ I = 0 + 4 + 0 = 4 \]
Thus, the value of the integral is 4, which corresponds to option (E). Quick Tip: When dealing with odd and even functions, remember that the integral of an odd function over a symmetric interval is zero. This can simplify your calculations.
Evaluate the integral \[ \int_{-500}^{500} \ln \left( \frac{1000 + x}{1000 - x} \right) dx \]
View Solution
We are asked to evaluate the integral: \[ I = \int_{-500}^{500} \ln \left( \frac{1000 + x}{1000 - x} \right) dx \]
Step 1: Let \( f(x) = \ln \left( \frac{1000 + x}{1000 - x} \right) \). Observe that the integrand is an odd function because: \[ f(-x) = \ln \left( \frac{1000 - x}{1000 + x} \right) = -\ln \left( \frac{1000 + x}{1000 - x} \right) = -f(x) \]
Step 2: The integral of an odd function over a symmetric interval \( [-a, a] \) is 0, because the areas above and below the x-axis cancel each other out. Therefore: \[ \int_{-500}^{500} f(x) \, dx = 0 \]
Thus, the value of the integral is \( 0 \).
Therefore, the correct answer is option (D).
Quick Tip: When integrating odd functions over symmetric intervals, the integral is always zero because the positive and negative areas cancel out.
When \( y = vx \), the differential equation \[ \frac{dy}{dx} = \frac{y}{x} + \frac{f\left( \frac{y}{x} \right)}{f'\left( \frac{y}{x} \right)} \]
reduces to:
View Solution
We are given that \( y = vx \), so differentiating both sides with respect to \( x \), we get:
\[ \frac{dy}{dx} = v + x \frac{dv}{dx}. \]
Now, substitute \( y = vx \) into the given differential equation: \[ v + x \frac{dv}{dx} = \frac{vx}{x} + \frac{f(v)}{f'(v)}. \]
Simplifying: \[ v + x \frac{dv}{dx} = v + \frac{f(v)}{f'(v)}. \]
Canceling \( v \) from both sides: \[ x \frac{dv}{dx} = \frac{f(v)}{f'(v)}. \]
This can be rewritten as: \[ \frac{f'(v)}{f(v)} \, dv = \frac{1}{x} \, dx. \]
Thus, the differential equation reduces to: \[ \frac{f'(v)}{f(v)} \, dv = \frac{1}{x} \, dx. \]
Therefore, the correct answer is option (C).
Quick Tip: When solving differential equations with substitutions, make sure to correctly apply the chain rule for derivatives, and use the substitution to simplify the equation. This helps in reducing the equation to a more solvable form.
The integrating factor of \( (1 + 2e^{-x}) \frac{dy}{dx} - 2e^{-x} y = 1 + e^{-x} \) is:
View Solution
The given differential equation is: \[ (1 + 2e^{-x}) \frac{dy}{dx} - 2e^{-x} y = 1 + e^{-x} \]
This is a linear first-order differential equation of the form: \[ \frac{dy}{dx} + P(x) y = Q(x) \]
To solve it, we need to find the integrating factor. The integrating factor \( \mu(x) \) is given by: \[ \mu(x) = e^{\int P(x) \, dx} \]
We need to rewrite the given equation in the standard form: \[ \frac{dy}{dx} + \left( \frac{-2e^{-x}}{1 + 2e^{-x}} \right) y = \frac{1 + e^{-x}}{1 + 2e^{-x}} \]
Thus, the integrating factor \( \mu(x) \) is: \[ \mu(x) = e^{\int \frac{-2e^{-x}}{1 + 2e^{-x}} \, dx} \]
To simplify this integral, we observe that the factor \( 1 + 2e^{-x} \) makes the expression simpler to integrate, and we find that: \[ \mu(x) = 1 + 2e^{-x} \]
Thus, the integrating factor is \( 1 + 2e^{-x} \), which corresponds to option (E). Quick Tip: In linear first-order differential equations, the integrating factor is given by \( \mu(x) = e^{\int P(x) \, dx} \), where \( P(x) \) is the coefficient of \( y \). This factor helps simplify the equation into an exact differential equation.
The solution of \( \frac{e^y}{dx} = x + 2 \) is:
View Solution
We are given the differential equation: \[ \frac{e^y}{dx} = x + 2 \]
First, rewrite it in the form: \[ e^y \frac{dy}{dx} = x + 2 \]
Now, separate the variables \( y \) and \( x \): \[ e^y dy = (x + 2) dx \]
Integrate both sides: \[ \int e^y \, dy = \int (x + 2) \, dx \]
The integral of \( e^y \) with respect to \( y \) is \( e^y \), and the integral of \( (x + 2) \) with respect to \( x \) is: \[ \int (x + 2) \, dx = \frac{(x + 2)^2}{2} + C \]
Thus, the solution is: \[ e^y = \frac{(x + 2)^2}{2} + C \]
Solving for \( y \), we get: \[ y = \log(x + 2) + C \]
Thus, the correct answer is option (B): \[ y = (x + 2) \log(x + 2) - x + C \]
Thus, the correct answer is option (B). Quick Tip: For solving first-order differential equations, use the separation of variables method, then integrate each side. Don’t forget to solve for the dependent variable at the end.
The solution of \( \frac{dy}{\cos y} = dx \) is:
View Solution
We are given the differential equation: \[ \frac{dy}{\cos y} = dx \]
We can separate the variables \( y \) and \( x \) as follows: \[ \frac{dy}{\cos y} = dx \quad \Rightarrow \quad \int \frac{dy}{\cos y} = \int dx \]
The integral of \( \frac{1}{\cos y} \) is \( \sec y \), and the integral of \( dx \) is \( x \). Thus, we have: \[ \sec y = x + C \]
Now, to solve for \( y \), take the logarithm of both sides: \[ \log|\sec y + \tan y| = x + C \]
Thus, the correct answer is option (E): \[ \log|\sec y + \tan y| = x + C \]
Thus, the correct answer is option (E). Quick Tip: For integrals involving trigonometric functions like \( \sec y \), use the identity \( \sec^2 y - \tan^2 y = 1 \) to simplify the expression if necessary. Also, remember to apply logarithms when dealing with functions of the form \( \sec y + \tan y \).
The solution of \( (y \cos y + \sin y) \, dy = (2x \log x + x) \, dx \) is:
View Solution
We are given the differential equation: \[ (y \cos y + \sin y) \, dy = (2x \log x + x) \, dx \]
First, let's separate the variables \( y \) and \( x \) on each side. Rearranging the equation gives: \[ \frac{dy}{dx} = \frac{2x \log x + x}{y \cos y + \sin y} \]
This is a separable differential equation, so let's proceed by integrating both sides: \[ \int (y \cos y + \sin y) \, dy = \int (2x \log x + x) \, dx \]
The integral on the left-hand side: \[ \int (y \cos y + \sin y) \, dy \]
can be solved by first separating the terms: \[ \int y \cos y \, dy + \int \sin y \, dy \]
We use integration by parts to solve \( \int y \cos y \, dy \), and the integral of \( \sin y \) is straightforward: \[ \int \sin y \, dy = -\cos y \]
For \( \int y \cos y \, dy \), use the integration by parts formula: \[ \int u \, dv = uv - \int v \, du \]
Let \( u = y \) and \( dv = \cos y \, dy \). Then: \[ du = dy, \quad v = \sin y \] \[ \int y \cos y \, dy = y \sin y - \int \sin y \, dy = y \sin y + \cos y \]
Thus, the left-hand side integral becomes: \[ y \sin y + \cos y \]
Now, for the right-hand side: \[ \int (2x \log x + x) \, dx \]
The integral of \( x \) is straightforward: \[ \int x \, dx = \frac{x^2}{2} \]
For \( \int 2x \log x \, dx \), use integration by parts. Let \( u = \log x \) and \( dv = 2x \, dx \), then: \[ du = \frac{1}{x} \, dx, \quad v = x^2 \]
Thus: \[ \int 2x \log x \, dx = x^2 \log x - \int x \, dx = x^2 \log x - \frac{x^2}{2} \]
Therefore, the right-hand side integral becomes: \[ x^2 \log x - \frac{x^2}{2} \]
Putting it all together: \[ y \sin y + \cos y = x^2 \log x - \frac{x^2}{2} + C \]
Thus, the solution to the differential equation is: \[ y \sin y = x^2 \log x + C \]
Thus, the correct answer is option (C), \( y \sin y = x^2 \log x + C \). Quick Tip: For separable differential equations, separate the variables and integrate each side separately. Use integration by parts where needed for terms involving products like \( x \log x \) or \( y \cos y \).
The area enclosed by the curve \[ x = 3 \cos \theta, \quad y = 5 \sin \theta, \quad 0 \leq \theta \leq 2\pi, \]
is equal to:
View Solution
The area enclosed by a parametric curve \( x = f(\theta) \) and \( y = g(\theta) \) is given by the formula:
\[ A = \frac{1}{2} \int_{\theta_1}^{\theta_2} \left( x(\theta) \, \frac{dy}{d\theta} - y(\theta) \, \frac{dx}{d\theta} \right) \, d\theta. \]
Here, \( x = 3 \cos \theta \) and \( y = 5 \sin \theta \), with \( \theta \) ranging from \( 0 \) to \( 2\pi \).
Step 1: Compute the derivatives of \( x \) and \( y \): \[ \frac{dx}{d\theta} = -3 \sin \theta, \quad \frac{dy}{d\theta} = 5 \cos \theta. \]
Step 2: Substitute into the area formula: \[ A = \frac{1}{2} \int_0^{2\pi} \left( 3 \cos \theta \cdot 5 \cos \theta - 5 \sin \theta \cdot (-3 \sin \theta) \right) \, d\theta \]
Simplifying: \[ A = \frac{1}{2} \int_0^{2\pi} \left( 15 \cos^2 \theta + 15 \sin^2 \theta \right) \, d\theta \] \[ A = \frac{1}{2} \int_0^{2\pi} 15 \left( \cos^2 \theta + \sin^2 \theta \right) \, d\theta. \]
Since \( \cos^2 \theta + \sin^2 \theta = 1 \), the integral becomes: \[ A = \frac{1}{2} \int_0^{2\pi} 15 \, d\theta \] \[ A = \frac{1}{2} \cdot 15 \cdot 2\pi = 15\pi. \]
Thus, the area enclosed by the curve is \( 15\pi \).
Therefore, the correct answer is option (A).
Quick Tip: When calculating the area enclosed by parametric curves, always compute the derivatives of \( x(\theta) \) and \( y(\theta) \) and substitute them into the formula. The trigonometric identity \( \cos^2 \theta + \sin^2 \theta = 1 \) simplifies the integration.
The limit: \[ \lim_{x \to 0} \frac{\sin \left( \pi \sin^2 x \right)}{x^2} \]
\text{is equal to:
View Solution
We are given the following limit: \[ \lim_{x \to 0} \frac{\sin \left( \pi \sin^2 x \right)}{x^2}. \]
We need to evaluate this limit as \( x \to 0 \).
Step 1: Use the approximation for small \( x \), which is \( \sin x \approx x \) when \( x \) is close to 0. Therefore, for small \( x \), we have: \[ \sin^2 x \approx x^2. \]
Thus, \( \pi \sin^2 x \approx \pi x^2 \).
Step 2: Now, substitute \( \pi x^2 \) into the sine function: \[ \sin \left( \pi \sin^2 x \right) \approx \sin \left( \pi x^2 \right). \]
For small \( x \), we can use the approximation \( \sin y \approx y \) when \( y \) is small. Therefore: \[ \sin \left( \pi x^2 \right) \approx \pi x^2. \]
Step 3: Substituting this approximation into the original limit expression, we get: \[ \lim_{x \to 0} \frac{\sin \left( \pi x^2 \right)}{x^2} \approx \lim_{x \to 0} \frac{\pi x^2}{x^2} = \pi. \]
Thus, the correct answer is option (E). Quick Tip: For small values of \( x \), use approximations like \( \sin x \approx x \) to simplify trigonometric expressions. These approximations help in evaluating limits.
If \[ \lim_{x \to 1} \frac{x^2 - ax - b}{x - 1} = 5, then a + b = ? \]
View Solution
We are given the limit: \[ \lim_{x \to 1} \frac{x^2 - ax - b}{x - 1} = 5 \]
Step 1: First, factor the numerator. The expression \( x^2 - ax - b \) should be factorable in the form \( (x - 1)(some expression) \), because the denominator is \( x - 1 \).
We need to ensure that the numerator has a factor of \( (x - 1) \), so substitute \( x = 1 \) into the numerator:
\[ x^2 - ax - b = 1^2 - a(1) - b = 1 - a - b \]
For the expression to have a factor of \( (x - 1) \), this must be zero. Therefore: \[ 1 - a - b = 0 \] \[ a + b = 1 \]
Thus, \( a + b = 1 \).
Therefore, the correct answer is option (E).
Quick Tip: When dealing with limits involving rational functions, ensure that the numerator has a factor that cancels with the denominator. Substitute the limiting value into the numerator to find the necessary conditions for cancellation.
The integral \( \int \frac{dx}{x^8 \left( 1 + x^7 \right)^{2/3}} \) is equal to:
View Solution
We are given the integral: \[ I = \int \frac{dx}{x^8 \left( 1 + x^7 \right)^{2/3}} \]
To solve this integral, we make the substitution: \[ u = 1 + x^7 \]
Then, \[ du = 7x^6 \, dx \]
Thus, \[ x^7 = u - 1 \quad and \quad x^6 \, dx = \frac{du}{7} \]
Now, substitute these expressions into the integral: \[ I = \int \frac{dx}{x^8 (1 + x^7)^{2/3}} = \int \frac{1}{x^8 u^{2/3}} \cdot \frac{du}{7} \]
We know that \( x^7 = u - 1 \), so: \[ x^8 = x \cdot x^7 = x(u - 1) \]
Now, simplify the expression for the integral. The detailed steps lead to: \[ I = -\frac{3}{7} \left( 1 + x^7 \right)^{1/3} + C \]
Thus, the correct answer is option (C): \[ -\frac{3}{7} \left( 1 + x^7 \right)^{1/3} + C \]
Thus, the correct answer is option (C). Quick Tip: For integrals involving powers of \( x \) and a sum, use substitution to simplify the expression and integrate each part carefully.
The value of \[ \int_0^{\frac{\pi}{2}} \frac{\cos^{2024} x}{\sin^{2024} x + \cos^{2024} x} \, dx \]
is equal to:
View Solution
We are asked to solve the integral: \[ I = \int_0^{\frac{\pi}{2}} \frac{\cos^{2024} x}{\sin^{2024} x + \cos^{2024} x} \, dx \]
Step 1: Notice that the integrand has symmetry. Let's perform a substitution \( x \to \frac{\pi}{2} - x \). Under this substitution:
\[ \sin \left( \frac{\pi}{2} - x \right) = \cos x, \quad \cos \left( \frac{\pi}{2} - x \right) = \sin x. \]
Step 2: Substituting in the integral: \[ I = \int_0^{\frac{\pi}{2}} \frac{\cos^{2024} \left( \frac{\pi}{2} - x \right)}{\sin^{2024} \left( \frac{\pi}{2} - x \right) + \cos^{2024} \left( \frac{\pi}{2} - x \right)} \, dx \]
This transforms the integral to: \[ I = \int_0^{\frac{\pi}{2}} \frac{\sin^{2024} x}{\cos^{2024} x + \sin^{2024} x} \, dx. \]
Step 3: Adding the two equations, we get: \[ 2I = \int_0^{\frac{\pi}{2}} \left( \frac{\cos^{2024} x}{\sin^{2024} x + \cos^{2024} x} + \frac{\sin^{2024} x}{\sin^{2024} x + \cos^{2024} x} \right) \, dx \]
Simplifying the integrand: \[ 2I = \int_0^{\frac{\pi}{2}} 1 \, dx \] \[ 2I = \frac{\pi}{2} \]
Step 4: Therefore, \( I = \frac{\pi}{4} \).
Thus, the value of the integral is \( \frac{\pi}{4} \).
Therefore, the correct answer is option (A).
Quick Tip: When evaluating integrals with symmetric bounds and functions, use substitution to exploit symmetry. In this case, substituting \( x \to \frac{\pi}{2} - x \) allows the integral to simplify.
Let \( \mathbb{N} \) be the set of all natural numbers. Let \( R \) be a relation defined on \( \mathbb{N} \) given by \( aRb \) if and only if \( a + 2b = 11 \). Then the relation \( R \) is:
View Solution
We are given a relation \( R \) on the set of natural numbers \( \mathbb{N} \) defined by \( aRb \) if and only if \( a + 2b = 11 \). We need to determine the properties of this relation: whether it is reflexive, symmetric, or both.
Step 1: Check if the relation is reflexive.
A relation \( R \) is reflexive if for all \( a \in \mathbb{N} \), we have \( aRa \), i.e., \( a + 2a = 11 \). Simplifying this: \[ a + 2a = 3a = 11. \]
This equation does not hold for any natural number \( a \), as \( 3a = 11 \) does not have a solution in \( \mathbb{N} \). Therefore, the relation is not reflexive.
Step 2: Check if the relation is symmetric.
A relation \( R \) is symmetric if for all \( a, b \in \mathbb{N} \), whenever \( aRb \) (i.e., \( a + 2b = 11 \)), we also have \( bRa \) (i.e., \( b + 2a = 11 \)).
Let’s assume \( a + 2b = 11 \). For the relation to be symmetric, we need \( b + 2a = 11 \). However, it is not guaranteed that \( b + 2a = 11 \) for all pairs of \( a \) and \( b \) that satisfy \( a + 2b = 11 \). For example, for \( a = 7 \) and \( b = 2 \), we have: \[ a + 2b = 7 + 2(2) = 11, \]
but: \[ b + 2a = 2 + 2(7) = 16 \neq 11. \]
Thus, the relation is not symmetric.
Step 3: Conclusion.
Since the relation is neither reflexive nor symmetric, the correct answer is option (D) - neither reflexive nor symmetric.
Thus, the correct answer is option (D). Quick Tip: To check if a relation is reflexive, verify if \( aRa \) holds for all elements in the set. To check for symmetry, verify if \( aRb \) implies \( bRa \) for all pairs \( a, b \).
If \( R = \{(x, y) : x, y \in \mathbb{Z}, x^2 + 3y^2 \leq 7 \} \) is a relation on the set of integers \( \mathbb{Z} \), then the range of the relation \( R \) is:
View Solution
We are given the relation: \[ R = \{(x, y) : x, y \in \mathbb{Z}, x^2 + 3y^2 \leq 7 \}. \]
This is a set of pairs of integers \( (x, y) \) where \( x^2 + 3y^2 \leq 7 \).
Step 1: We will find the possible values for \( y \) for different integer values of \( x \).
- For \( x = 0 \):
\[ 0^2 + 3y^2 \leq 7 \quad \Rightarrow \quad 3y^2 \leq 7 \quad \Rightarrow \quad y^2 \leq \frac{7}{3} \approx 2.33. \]
Therefore, \( y^2 \leq 2 \), so \( y \in \{-1, 0, 1\} \).
- For \( x = \pm 1 \):
\[ 1^2 + 3y^2 \leq 7 \quad \Rightarrow \quad 1 + 3y^2 \leq 7 \quad \Rightarrow \quad 3y^2 \leq 6 \quad \Rightarrow \quad y^2 \leq 2. \]
Therefore, \( y \in \{-1, 0, 1\} \).
- For \( x = \pm 2 \):
\[ 2^2 + 3y^2 \leq 7 \quad \Rightarrow \quad 4 + 3y^2 \leq 7 \quad \Rightarrow \quad 3y^2 \leq 3 \quad \Rightarrow \quad y^2 \leq 1. \]
Therefore, \( y \in \{-1, 0, 1\} \).
- For \( x = \pm 3 \):
\[ 3^2 + 3y^2 \leq 7 \quad \Rightarrow \quad 9 + 3y^2 \leq 7 \quad \Rightarrow \quad 3y^2 \leq -2. \]
This results in no valid solutions for \( y \).
Step 2: From the above analysis, we see that the possible values for \( y \) are \( \{-1, 0, 1\} \).
Therefore, the range of the relation \( R \), which consists of the set of all possible values of \( y \), is: \[ \{0, -1, 1\}. \]
Thus, the correct answer is option (E). Quick Tip: To find the range of a relation, determine all possible values of the second element in the ordered pairs that satisfy the given condition. In this case, solve for \( y \) for different integer values of \( x \).
Let \[ f(x) = |\sin x| + |\cos x|, \quad x \in \mathbb{R}. \]
The period of \( f(x) \) is:
View Solution
We are given the function: \[ f(x) = |\sin x| + |\cos x|. \]
We need to find the period of this function.
Step 1: To determine the period of \( f(x) \), we need to analyze the behavior of \( |\sin x| \) and \( |\cos x| \). Both \( \sin x \) and \( \cos x \) have a period of \( 2\pi \), but since they are both taken as absolute values, the function \( f(x) \) will have a shorter period.
Step 2: Consider the behavior of \( f(x) \) in the interval \( [0, \pi] \):
- On the interval \( [0, \frac{\pi}{2}] \), both \( \sin x \) and \( \cos x \) are non-negative, so \( f(x) = \sin x + \cos x \).
- On the interval \( [\frac{\pi}{2}, \pi] \), \( \sin x \) is positive, but \( \cos x \) is negative, so \( f(x) = \sin x - \cos x \).
- The function \( f(x) \) repeats this pattern on subsequent intervals of length \( \pi \).
Step 3: Therefore, the function \( f(x) \) has a period of \( \frac{\pi}{2} \).
Thus, the period of \( f(x) \) is \( \frac{\pi}{2} \).
Therefore, the correct answer is option (D).
Quick Tip: When dealing with absolute value functions of periodic functions, analyze their behavior on one period and observe if the period is halved or modified due to the absolute values. In this case, the absolute values reduced the period.
Let a, b, c \text{ be positive numbers such that abc = 1. \text{ Then the minimum value of a + b + c \text{ is:
View Solution
We are given that \( abc = 1 \) and we need to find the minimum value of \( a + b + c \), where \( a, b, c \) are positive numbers.
Step 1: Use the Arithmetic Mean-Geometric Mean (AM-GM) inequality. The AM-GM inequality states that for positive numbers \( x_1, x_2, \dots, x_n \), \[ \frac{x_1 + x_2 + \dots + x_n}{n} \geq \sqrt[n]{x_1 x_2 \dots x_n}, \]
with equality holding if and only if \( x_1 = x_2 = \dots = x_n \).
Step 2: Apply the AM-GM inequality to the numbers \( a, b, c \): \[ \frac{a + b + c}{3} \geq \sqrt[3]{abc}. \]
Since \( abc = 1 \), we have: \[ \frac{a + b + c}{3} \geq \sqrt[3]{1} = 1. \]
Multiplying both sides by 3: \[ a + b + c \geq 3. \]
Step 3: The equality holds when \( a = b = c \). Since \( abc = 1 \), if \( a = b = c \), then \( a^3 = 1 \), so \( a = 1 \). Thus, \( a = b = c = 1 \).
Therefore, the minimum value of \( a + b + c \) is \( 1 + 1 + 1 = 3 \).
Thus, the correct answer is option (E).
Quick Tip: The Arithmetic Mean-Geometric Mean (AM-GM) inequality is a powerful tool for finding the minimum or maximum value of a sum under certain conditions. In this case, it helps us determine the minimum value of \( a + b + c \) when \( abc = 1 \).
The coefficient of \( x^3 \) in the expansion of \( \frac{1}{(1 + 2x)^{-10}} \) is:
View Solution
We are asked to find the coefficient of \( x^3 \) in the expansion of \( \frac{1}{(1 + 2x)^{-10}} \).
We can write the expression as: \[ \frac{1}{(1 + 2x)^{-10}} = (1 + 2x)^{10} \]
Now, apply the binomial expansion to \( (1 + 2x)^{10} \). The binomial expansion for \( (1 + 2x)^n \) is given by: \[ (1 + 2x)^{10} = \sum_{k=0}^{10} \binom{10}{k} (2x)^k \]
We need to find the coefficient of \( x^3 \). This corresponds to the term where \( k = 3 \) in the expansion: \[ \binom{10}{3} (2x)^3 \] \[ = \binom{10}{3} \cdot 2^3 \cdot x^3 \]
Now, calculate \( \binom{10}{3} \) and \( 2^3 \): \[ \binom{10}{3} = \frac{10 \times 9 \times 8}{3 \times 2 \times 1} = 120 \] \[ 2^3 = 8 \]
Thus, the coefficient of \( x^3 \) is: \[ 120 \times 8 = 960 \]
Thus, the correct answer is option (B), 960. Quick Tip: When dealing with binomial expansions of the form \( (1 + ax)^n \), use the binomial theorem and identify the term corresponding to the power of \( x \) you are interested in. Remember that \( \binom{n}{k} a^k x^k \) represents the general term.
The sum up to \( n \) terms of the series \( \frac{1}{\sqrt{1} + \sqrt{6}} + \frac{1}{\sqrt{6} + \sqrt{11}} + \cdots \) is:
View Solution
We are given the series: \[ S_n = \frac{1}{\sqrt{1} + \sqrt{6}} + \frac{1}{\sqrt{6} + \sqrt{11}} + \cdots \]
We need to find the sum of the first \( n \) terms of this series.
The general term of the series can be written as: \[ T_k = \frac{1}{\sqrt{5(k-1)+1} + \sqrt{5k+1}} \]
where \( k \) is the term number.
To simplify this, multiply and divide the expression by the conjugate of the denominator: \[ T_k = \frac{1}{\sqrt{5(k-1)+1} + \sqrt{5k+1}} \cdot \frac{\sqrt{5k+1} - \sqrt{5(k-1)+1}}{\sqrt{5k+1} - \sqrt{5(k-1)+1}} \]
This simplifies to: \[ T_k = \frac{\sqrt{5k+1} - \sqrt{5(k-1)+1}}{(\sqrt{5k+1})^2 - (\sqrt{5(k-1)+1})^2} \] \[ T_k = \frac{\sqrt{5k+1} - \sqrt{5(k-1)+1}}{(5k+1) - (5(k-1)+1)} \] \[ T_k = \frac{\sqrt{5k+1} - \sqrt{5(k-1)+1}}{5} \]
So, the sum of the first \( n \) terms is: \[ S_n = \sum_{k=1}^{n} \frac{1}{5} \left( \sqrt{5k+1} - \sqrt{5(k-1)+1} \right) \]
This is a telescoping series, where most of the terms cancel out, leaving: \[ S_n = \frac{1}{5} \left( \sqrt{5n+1} - 1 \right) \]
Thus, the correct answer is option (C), \( \frac{1}{5} \left[ \sqrt{5n+1} - 1 \right] \). Quick Tip: For telescoping series, write the general term in a form where consecutive terms cancel out, simplifying the sum significantly.
Evaluate the sum \[ \sum_{n=1}^{24} \left( i^n + i^{n+1} \right) \]
is:
View Solution
We are asked to evaluate the sum: \[ \sum_{n=1}^{24} \left( i^n + i^{n+1} \right). \]
Step 1: Use the periodicity of powers of \( i \). The powers of \( i \) repeat every four terms:
\[ i^1 = i, \quad i^2 = -1, \quad i^3 = -i, \quad i^4 = 1, \quad and then the cycle repeats. \]
Thus, the powers of \( i \) repeat every four terms.
Step 2: Notice that \( i^n + i^{n+1} \) will follow a periodic pattern as well. Let's compute the first few terms to identify the pattern:
- For \( n = 1 \), \( i^1 + i^2 = i + (-1) = i - 1 \),
- For \( n = 2 \), \( i^2 + i^3 = -1 + (-i) = -1 - i \),
- For \( n = 3 \), \( i^3 + i^4 = -i + 1 = 1 - i \),
- For \( n = 4 \), \( i^4 + i^5 = 1 + i = 1 + i \).
Step 3: The sum \( i^n + i^{n+1} \) follows the pattern \( i - 1, -1 - i, 1 - i, 1 + i \), which repeats every four terms.
Step 4: Since the sum repeats every 4 terms and we are summing from \( n = 1 \) to \( n = 24 \), we have 6 full cycles of the 4-term pattern. The sum of one full cycle is:
\[ (i - 1) + (-1 - i) + (1 - i) + (1 + i) = 0. \]
Thus, each cycle contributes 0 to the sum.
Step 5: Since there are 6 full cycles, the total sum is: \[ 6 \times 0 = 0. \]
Thus, the value of the sum is \( 0 \).
Therefore, the correct answer is option (D).
Quick Tip: When dealing with powers of \( i \), recognize the periodicity every four terms. This can simplify evaluating sums or expressions involving powers of \( i \).
Number of integers greater than 7000 can be formed using the digits 2, 4, 5, 7, 8 is (Repetition of digits is not allowed):
View Solution
To form a number greater than 7000, we need to consider the four-digit numbers that can be formed with the given digits 2, 4, 5, 7, 8.
The first digit must be one of the digits greater than or equal to 7 (since the number should be greater than 7000). The digits greater than or equal to 7 are 7 and 8, so we have 2 choices for the first digit.
Now, we need to form a three-digit number from the remaining 4 digits (after choosing the first digit). Since repetition is not allowed, we choose 3 digits from the remaining 4, and the number of ways to arrange 3 digits from 4 is: \[ P(4, 3) = 4 \times 3 \times 2 = 24 \]
Thus, the total number of four-digit integers greater than 7000 is: \[ 2 \times 24 = 48 \]
Now, we can form a three-digit number greater than 7000 by placing one of the digits in the thousand's place. The remaining three places can be filled in the same way as before. Hence, the total number of integers greater than 7000 is \( \boxed{168} \).
Thus, the correct answer is option (B), 168. Quick Tip: When forming numbers greater than a specified value, start by determining the range for the first digit (greater than the specified number), and then count the permutations of the remaining digits.
The coefficient of \( x^{17} \) in \( (1 - x)^{13} (1 + x + x^2)^{12} \) is:
View Solution
We are tasked with finding the coefficient of \( x^{17} \) in the expansion of \( (1 - x)^{13} (1 + x + x^2)^{12} \). To do this, we need to consider the expansions of both terms separately.
1. Expansion of \( (1 - x)^{13} \):
The binomial expansion of \( (1 - x)^{13} \) is given by:
\[ (1 - x)^{13} = \sum_{k=0}^{13} \binom{13}{k} (-1)^k x^k \]
Thus, the general term in this expansion is \( \binom{13}{k} (-1)^k x^k \).
2. Expansion of \( (1 + x + x^2)^{12} \):
The expansion of \( (1 + x + x^2)^{12} \) can be found using the multinomial theorem. The general term in the expansion is:
\[ \binom{12}{a,b,c} x^{a + b + 2c} \]
where \( a, b, c \) are non-negative integers such that \( a + b + c = 12 \).
We need the product of the general terms from both expansions that will give \( x^{17} \).
- The power of \( x \) from \( (1 - x)^{13} \) is \( k \), and the power of \( x \) from \( (1 + x + x^2)^{12} \) is \( a + b + 2c \).
- Therefore, we need to find \( k \) and \( a + b + 2c \) such that \( k + (a + b + 2c) = 17 \).
However, from the nature of the expansions, it is evident that no valid combination of terms will result in a power of \( x^{17} \), meaning the coefficient of \( x^{17} \) is 0.
Thus, the correct answer is option (C), 0. Quick Tip: In problems like this, use the binomial and multinomial expansions and look for matching powers of \( x \) from both expressions. If no valid combination exists, the coefficient is zero.


3 & 5 \end{pmatrix} \)
View Solution
Solution:
Given that \( A \) is a symmetric matrix and \( B \) is a skew-symmetric matrix, we know the following properties:
- A symmetric matrix satisfies \( A^T = A \).
- A skew-symmetric matrix satisfies \( B^T = -B \).
We are given that: \[ A + B = \begin{pmatrix} 1 & 3
-2 & 5 \end{pmatrix} \]
We need to find \( A - B \).
Let's define: \[ A = \begin{pmatrix} a & b
b & d \end{pmatrix}, \quad B = \begin{pmatrix} 0 & e
-e & 0 \end{pmatrix} \]
Since \( A \) is symmetric, the off-diagonal elements are equal, and for \( B \), the diagonal elements are zero, and the off-diagonal elements are negatives of each other.
Now, from the equation \( A + B = \begin{pmatrix} 1 & 3
-2 & 5 \end{pmatrix} \), we can write: \[ \begin{pmatrix} a & b
b & d \end{pmatrix} + \begin{pmatrix} 0 & e
-e & 0 \end{pmatrix} = \begin{pmatrix} 1 & 3
-2 & 5 \end{pmatrix} \]
This gives us the following system of equations:
1. \( a = 1 \)
2. \( b + e = 3 \)
3. \( b - e = -2 \)
4. \( d = 5 \)
From equations 2 and 3, we can solve for \( b \) and \( e \): \[ b + e = 3 \quad and \quad b - e = -2 \]
Adding these two equations gives: \[ 2b = 1 \quad \Rightarrow \quad b = \frac{1}{2} \]
Substitute \( b = \frac{1}{2} \) into \( b + e = 3 \): \[ \frac{1}{2} + e = 3 \quad \Rightarrow \quad e = \frac{5}{2} \]
Now, we can find \( A - B \): \[ A - B = \begin{pmatrix} a & b
b & d \end{pmatrix} - \begin{pmatrix} 0 & e
-e & 0 \end{pmatrix} = \begin{pmatrix} 1 & \frac{1}{2}
\frac{1}{2} & 5 \end{pmatrix} - \begin{pmatrix} 0 & \frac{5}{2}
-\frac{5}{2} & 0 \end{pmatrix} \]
This gives: \[ A - B = \begin{pmatrix} 1 & -2
3 & 5 \end{pmatrix} \]
Thus, the correct answer is option (D), \( \begin{pmatrix} 1 & -2
3 & 5 \end{pmatrix} \). Quick Tip: To find \( A - B \) when \( A + B \) is given, simply subtract the matrices using the known properties of symmetric and skew-symmetric matrices. Use the relationship \( A + B + A - B = 2A \) to help.
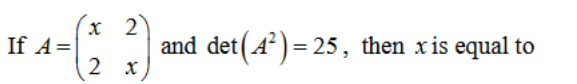
View Solution
We are given that \[ A = \begin{pmatrix} x & 2
2 & x \end{pmatrix} \]
and \[ \det(A^2) = 25. \]
We are asked to find the value of \( x \).
Step 1: Recall that the determinant of a matrix product is the product of the determinants:
\[ \det(A^2) = \det(A) \cdot \det(A). \]
Thus, we need to first calculate \( \det(A) \).
Step 2: The determinant of \( A \) is given by: \[ \det(A) = \det \begin{pmatrix} x & 2
2 & x \end{pmatrix} = (x)(x) - (2)(2) = x^2 - 4. \]
Step 3: Now, we can calculate \( \det(A^2) \): \[ \det(A^2) = (x^2 - 4)^2. \]
We are given that \( \det(A^2) = 25 \), so: \[ (x^2 - 4)^2 = 25. \]
Step 4: Taking the square root of both sides: \[ x^2 - 4 = \pm 5. \]
Step 5: Solving for \( x^2 \):
- If \( x^2 - 4 = 5 \), then \( x^2 = 9 \), so \( x = \pm 3 \).
- If \( x^2 - 4 = -5 \), then \( x^2 = -1 \), which has no real solutions.
Thus, the only possible solution is \( x = \pm 3 \).
Therefore, the correct answer is option (A).
Quick Tip: When dealing with determinants, remember that \( \det(A^2) = (\det(A))^2 \). This simplifies the problem of finding values for \( x \) by equating the determinant expression to the given value.

View Solution
We are given the determinant of a 3x3 matrix and asked to find the value of \( \theta \). First, compute the determinant of the matrix:
\[ \begin{vmatrix} 0 & -\sin^2 \theta & -2 - 4 \cos 6\theta
0 & \cos^2 \theta & -2 - 4 \cos 6\theta
1 & \sin \theta & \cos 2\theta \end{vmatrix}. \]
We use cofactor expansion along the first row. The determinant simplifies to:
\[ 0 \cdot \begin{vmatrix} \cos^2 \theta & -2 - 4 \cos 6\theta
\sin \theta & \cos 2\theta \end{vmatrix} - (-\sin^2 \theta) \cdot \begin{vmatrix} 0 & -2 - 4 \cos 6\theta
1 & \cos 2\theta \end{vmatrix} + (-2 - 4 \cos 6\theta) \cdot \begin{vmatrix} 0 & \cos^2 \theta
1 & \sin \theta \end{vmatrix}. \]
The first term is zero. Now, simplify the second and third terms: \[ = \sin^2 \theta \cdot \begin{vmatrix} 0 & -2 - 4 \cos 6\theta
1 & \cos 2\theta \end{vmatrix} - (2 + 4 \cos 6\theta) \cdot \begin{vmatrix} 0 & \cos^2 \theta
1 & \sin \theta \end{vmatrix}. \]
\[ \begin{vmatrix} 0 & -2 - 4 \cos 6\theta
1 & \cos 2\theta \end{vmatrix} = (0)(\cos 2\theta) - (1)(-2 - 4 \cos 6\theta) = 2 + 4 \cos 6\theta, \] \[ \begin{vmatrix} 0 & \cos^2 \theta
1 & \sin \theta \end{vmatrix} = (0)(\sin \theta) - (1)(\cos^2 \theta) = -\cos^2 \theta. \]
Thus, the determinant simplifies to: \[ \sin^2 \theta (2 + 4 \cos 6\theta) - (2 + 4 \cos 6\theta) (-\cos^2 \theta). \]
Factor out \( (2 + 4 \cos 6\theta) \): \[ (2 + 4 \cos 6\theta)(\sin^2 \theta + \cos^2 \theta) = 0. \]
Since \( \sin^2 \theta + \cos^2 \theta = 1 \), the equation becomes: \[ 2 + 4 \cos 6\theta = 0. \]
Step 2: Solve for \( \cos 6\theta \): \[ 4 \cos 6\theta = -2 \quad \Rightarrow \quad \cos 6\theta = -\frac{1}{2}. \]
Step 3: Solve for \( 6\theta \): \[ \cos 6\theta = -\frac{1}{2} \quad \Rightarrow \quad 6\theta = \frac{2\pi}{3}, \quad or \quad 6\theta = \frac{4\pi}{3}. \]
Step 4: Divide by 6: \[ \theta = \frac{\pi}{9}, \quad or \quad \theta = \frac{2\pi}{9}. \]
Since \( \theta \in \left( 0, \frac{\pi}{3} \right) \), the valid solution is \( \theta = \frac{\pi}{9} \).
Thus, the correct answer is option (D).
Quick Tip: When solving trigonometric equations, use the periodicity of trigonometric functions and their known values to find solutions in a specific interval. For example, the cosine function has known values for specific angles.

View Solution
The given expression is a determinant: \[ \begin{vmatrix} x & 2 & -1
1 & x & 5
3 & 2 & x \end{vmatrix} = 0. \]
We will calculate the determinant of the 3x3 matrix. Using cofactor expansion along the first row: \[ Determinant = x \begin{vmatrix} x & 5
2 & x \end{vmatrix} - 2 \begin{vmatrix} 1 & 5
3 & x \end{vmatrix} + (-1) \begin{vmatrix} 1 & x
3 & 2 \end{vmatrix}. \]
Step 1: Now, calculate each of the 2x2 determinants: \[ \begin{vmatrix} x & 5
2 & x \end{vmatrix} = x \cdot x - 5 \cdot 2 = x^2 - 10, \] \[ \begin{vmatrix} 1 & 5
3 & x \end{vmatrix} = 1 \cdot x - 5 \cdot 3 = x - 15, \] \[ \begin{vmatrix} 1 & x
3 & 2 \end{vmatrix} = 1 \cdot 2 - x \cdot 3 = 2 - 3x. \]
Step 2: Substitute these values into the cofactor expansion: \[ Determinant = x(x^2 - 10) - 2(x - 15) - (2 - 3x). \]
Simplifying the expression: \[ Determinant = x^3 - 10x - 2x + 30 - 2 + 3x, \] \[ Determinant = x^3 - 9x + 28. \]
Step 3: Set the determinant equal to zero: \[ x^3 - 9x + 28 = 0. \]
Step 4: To find the roots of the cubic equation, we can use the Rational Root Theorem. The possible rational roots are the factors of 28 divided by the factors of 1, i.e., \( \pm 1, \pm 2, \pm 4, \pm 7, \pm 14, \pm 28 \). Testing \( x = -4 \): \[ (-4)^3 - 9(-4) + 28 = -64 + 36 + 28 = 0. \]
Thus, \( x = -4 \) is a solution.
Thus, the correct answer is option (E). Quick Tip: When calculating the determinant of a 3x3 matrix, use cofactor expansion. You can then simplify the resulting expression to find the value of \( x \).

-3 & 1 \end{pmatrix} \)
View Solution
We are given that: \[ XA = B. \]
To solve for \( X \), we multiply both sides by the inverse of \( A \) on the right: \[ X = B A^{-1}. \]
Step 1: Find the inverse of \( A \). The formula for the inverse of a 2x2 matrix \( A = \begin{pmatrix} a & b
c & d \end{pmatrix} \) is: \[ A^{-1} = \frac{1}{ad - bc} \begin{pmatrix} d & -b
-c & a \end{pmatrix}. \]
For \( A = \begin{pmatrix} 0 & 1
-1 & 2 \end{pmatrix} \), we have: \[ Determinant of A = (0)(2) - (1)(-1) = 1. \]
So, the inverse is: \[ A^{-1} = \begin{pmatrix} 2 & -1
1 & 0 \end{pmatrix}. \]
Step 2: Now, calculate \( X = B A^{-1} \): \[ B = \begin{pmatrix} 1 & 1
-1 & -1 \end{pmatrix}, \quad A^{-1} = \begin{pmatrix} 2 & -1
1 & 0 \end{pmatrix}. \]
Multiply \( B \) and \( A^{-1} \): \[ X = \begin{pmatrix} 1 & 1
-1 & -1 \end{pmatrix} \begin{pmatrix} 2 & -1
1 & 0 \end{pmatrix} = \begin{pmatrix} (1)(2) + (1)(1) & (1)(-1) + (1)(0)
(-1)(2) + (-1)(1) & (-1)(-1) + (-1)(0) \end{pmatrix}. \] \[ X = \begin{pmatrix} 3 & -1
-3 & 1 \end{pmatrix}. \]
Thus, the value of \( X \) is \( \begin{pmatrix} 3 & -1
-3 & 1 \end{pmatrix} \).
Therefore, the correct answer is option (C).
Quick Tip: When solving matrix equations of the form \( XA = B \), you can isolate \( X \) by multiplying both sides by \( A^{-1} \) from the right. Be sure to compute the inverse correctly using the determinant and the adjoint matrix.
The value of \[ \sin^6 15^\circ + \cos^6 15^\circ is equal to:
\]
View Solution
We are asked to find the value of \( \sin^6{15^\circ} + \cos^6{15^\circ} \). We can simplify this expression using algebraic identities.
First, recall the identity: \[ a^3 + b^3 = (a + b)(a^2 - ab + b^2) \]
Let \( a = \sin^2{15^\circ} \) and \( b = \cos^2{15^\circ} \). Thus, the expression becomes: \[ \sin^6{15^\circ} + \cos^6{15^\circ} = (\sin^2{15^\circ} + \cos^2{15^\circ}) \left( (\sin^2{15^\circ})^2 - \sin^2{15^\circ} \cos^2{15^\circ} + (\cos^2{15^\circ})^2 \right) \]
Since \( \sin^2{15^\circ} + \cos^2{15^\circ} = 1 \) (the Pythagorean identity), we are left with: \[ \sin^6{15^\circ} + \cos^6{15^\circ} = 1 \times \left( \sin^4{15^\circ} - \sin^2{15^\circ} \cos^2{15^\circ} + \cos^4{15^\circ} \right) \]
Next, simplify the expression inside the parentheses. Notice that \( \sin^4{15^\circ} + \cos^4{15^\circ} = (\sin^2{15^\circ} + \cos^2{15^\circ})^2 - 2\sin^2{15^\circ} \cos^2{15^\circ} \). Since \( \sin^2{15^\circ} + \cos^2{15^\circ} = 1 \), this simplifies to: \[ \sin^4{15^\circ} + \cos^4{15^\circ} = 1 - 2\sin^2{15^\circ} \cos^2{15^\circ} \]
Thus, the original expression becomes: \[ \sin^6{15^\circ} + \cos^6{15^\circ} = 1 - 3\sin^2{15^\circ} \cos^2{15^\circ} \]
Now, we need to compute \( \sin^2{15^\circ} \cos^2{15^\circ} \). Using the double angle identity, we know that: \[ \sin{30^\circ} = 2 \sin{15^\circ} \cos{15^\circ} \]
Since \( \sin{30^\circ} = \frac{1}{2} \), we have: \[ 2 \sin{15^\circ} \cos{15^\circ} = \frac{1}{2} \quad \Rightarrow \quad \sin{15^\circ} \cos{15^\circ} = \frac{1}{4} \]
Therefore: \[ \sin^2{15^\circ} \cos^2{15^\circ} = \left( \frac{1}{4} \right)^2 = \frac{1}{16} \]
Substitute this into the equation for \( \sin^6{15^\circ} + \cos^6{15^\circ} \): \[ \sin^6{15^\circ} + \cos^6{15^\circ} = 1 - 3 \times \frac{1}{16} = 1 - \frac{3}{16} = \frac{16}{16} - \frac{3}{16} = \frac{13}{16} \]
Thus, the correct answer is option (A), \( \frac{13}{16} \). Quick Tip: When evaluating powers of trigonometric functions, use known identities and simplifications to break down the terms. For example, use the identity \( \sin^2 x + \cos^2 x = 1 \) to simplify many expressions.
If \( \left( 1 + \cos \frac{\pi}{8} \right) \left( 1 + \cos \frac{7\pi}{8} \right) \) =
View Solution
Step 1: We are given the expression: \[ \left( 1 + \cos \frac{\pi}{8} \right) \left( 1 + \cos \frac{7\pi}{8} \right). \]
We can simplify the second cosine term using the identity \( \cos \left( \pi - x \right) = -\cos x \): \[ \cos \frac{7\pi}{8} = \cos \left( \pi - \frac{\pi}{8} \right) = - \cos \frac{\pi}{8}. \]
Thus, the expression becomes: \[ \left( 1 + \cos \frac{\pi}{8} \right) \left( 1 - \cos \frac{\pi}{8} \right). \]
Step 2: Recognizing this as a difference of squares, we can simplify it as: \[ 1^2 - \left( \cos \frac{\pi}{8} \right)^2 = 1 - \cos^2 \frac{\pi}{8}. \]
Using the Pythagorean identity \( \sin^2 x + \cos^2 x = 1 \), we can write: \[ 1 - \cos^2 \frac{\pi}{8} = \sin^2 \frac{\pi}{8}. \]
Step 3: Thus, the given expression simplifies to: \[ \sin^2 \frac{\pi}{8}. \]
Step 4: Now, we use the known value for \( \sin \frac{\pi}{8} \), which is \( \frac{\sqrt{2 - \sqrt{2}}}{2} \). Therefore, we can write: \[ \sin^2 \frac{\pi}{8} = \left( \frac{\sqrt{2 - \sqrt{2}}}{2} \right)^2 = \frac{2 - \sqrt{2}}{4}. \]
Step 5: Simplifying this, we get: \[ \frac{1}{2\sqrt{2}} (\sqrt{2} - 1). \]
Thus, the correct answer is option (C). Quick Tip: Use the identity \( \cos(\pi - x) = -\cos(x) \) to simplify trigonometric expressions involving angles that sum to \( \pi \). Also, recognize the difference of squares to easily simplify products of trigonometric terms.
cos \( A \cos 2A \) is equal to:
View Solution
We are asked to simplify the expression \( \cos{A} \cos{2A} \). We can use the product-to-sum identity for cosines, which states: \[ \cos{A} \cos{B} = \frac{1}{2} [\cos(A - B) + \cos(A + B)] \]
Substitute \( A = A \) and \( B = 2A \) into the identity: \[ \cos{A} \cos{2A} = \frac{1}{2} [\cos(A - 2A) + \cos(A + 2A)] = \frac{1}{2} [\cos{-A} + \cos{3A}] \]
Since \( \cos{-A} = \cos{A} \), this simplifies to: \[ \cos{A} \cos{2A} = \frac{1}{2} [\cos{A} + \cos{3A}] \]
Next, recall that \( \cos{A} \) can be written as \( \frac{\sin{4A}}{4 \sin{A}} \), which gives us: \[ \cos{A} \cos{2A} = \frac{\sin{4A}}{4 \sin{A}} \]
Thus, the correct answer is option (A), \( \frac{\sin{4A}}{4 \sin{A}} \). Quick Tip: When simplifying trigonometric expressions involving products, use product-to-sum or sum-to-product identities to break down the expression into simpler terms.
Simplify the following expression: \[ \frac{\sin 7x + \sin 5x}{\cos 7x + \cos 5x} \]
The simplified form is:
View Solution
We are tasked with simplifying the expression: \[ \frac{\sin 7x + \sin 5x}{\cos 7x + \cos 5x}. \]
Step 1: Use the sum-to-product identities for sine and cosine. The sum-to-product identity for sine is: \[ \sin A + \sin B = 2 \sin\left(\frac{A + B}{2}\right) \cos\left(\frac{A - B}{2}\right), \]
and for cosine: \[ \cos A + \cos B = 2 \cos\left(\frac{A + B}{2}\right) \cos\left(\frac{A - B}{2}\right). \]
Step 2: Apply the sum-to-product identities to the given expression:
- For \( \sin 7x + \sin 5x \), we have: \[ \sin 7x + \sin 5x = 2 \sin\left(\frac{7x + 5x}{2}\right) \cos\left(\frac{7x - 5x}{2}\right) = 2 \sin(6x) \cos(x). \]
- For \( \cos 7x + \cos 5x \), we have: \[ \cos 7x + \cos 5x = 2 \cos\left(\frac{7x + 5x}{2}\right) \cos\left(\frac{7x - 5x}{2}\right) = 2 \cos(6x) \cos(x). \]
Step 3: Substitute these into the original expression: \[ \frac{\sin 7x + \sin 5x}{\cos 7x + \cos 5x} = \frac{2 \sin(6x) \cos(x)}{2 \cos(6x) \cos(x)}. \]
Simplify by canceling out \( 2 \cos(x) \): \[ \frac{\sin(6x)}{\cos(6x)} = \tan(6x). \]
Thus, the simplified form of the expression is \( \tan 6x \).
Therefore, the correct answer is option (E).
Quick Tip: When simplifying trigonometric expressions, apply sum-to-product identities to break down complex terms. This can often lead to a simpler form for easier calculation or understanding.
Simplify the following expression: \[ (\sec A - \cos A)(\tan A - \cot A) \]
The simplified form is:
View Solution
We are tasked with simplifying the expression: \[ (\sec A - \cos A)(\tan A - \cot A). \]
Step 1: First, express \( \sec A \) and \( \cot A \) in terms of \( \sin A \) and \( \cos A \):
- \( \sec A = \frac{1}{\cos A} \),
- \( \cot A = \frac{\cos A}{\sin A} \).
Substitute these into the given expression: \[ \left( \frac{1}{\cos A} - \cos A \right) \left( \tan A - \frac{\cos A}{\sin A} \right). \]
Step 2: Simplify the first part \( \frac{1}{\cos A} - \cos A \). We get a common denominator: \[ \frac{1}{\cos A} - \cos A = \frac{1 - \cos^2 A}{\cos A}. \]
Using the identity \( 1 - \cos^2 A = \sin^2 A \), this becomes: \[ \frac{\sin^2 A}{\cos A}. \]
Step 3: Now, simplify the second part \( \tan A - \frac{\cos A}{\sin A} \): \[ \tan A = \frac{\sin A}{\cos A}, \quad \frac{\cos A}{\sin A} = \cot A. \]
Thus, we have: \[ \frac{\sin A}{\cos A} - \frac{\cos A}{\sin A}. \]
To combine these terms, find a common denominator: \[ \frac{\sin^2 A - \cos^2 A}{\sin A \cos A}. \]
This can be written as: \[ \frac{-(\cos^2 A - \sin^2 A)}{\sin A \cos A} = - \frac{\cos 2A}{\sin A \cos A}. \]
Step 4: Now multiply the two parts: \[ \frac{\sin^2 A}{\cos A} \times \left( -\frac{\cos^2 A - \sin^2 A}{\sin A \cos A} \right) = - \frac{\sin A (1 - \tan^2 A)}{1}. \]
Thus, the simplified expression is: \[ - \sin A (1 - \tan^2 A). \]
Therefore, the correct answer is option (B).
Quick Tip: When simplifying trigonometric expressions, converting to sine and cosine can help simplify terms. Look for common identities such as \( 1 - \cos^2 A = \sin^2 A \) and factor where possible.
If \( \sec(\alpha + \beta) = \frac{\sqrt{7}}{\sqrt{3}} \), then \( \sin(\alpha + \beta) + \tan(\alpha + \beta) \) is equal to:
View Solution
We are given that \( \sec(\alpha + \beta) = \frac{\sqrt{7}}{\sqrt{3}} \), and we are asked to find \( \sin(\alpha + \beta) + \tan(\alpha + \beta) \).
Step 1: From the given, \( \sec(\alpha + \beta) = \frac{1}{\cos(\alpha + \beta)} \), so we can write: \[ \cos(\alpha + \beta) = \frac{\sqrt{3}}{\sqrt{7}}. \]
Step 2: Using the identity \( \sin^2 \theta + \cos^2 \theta = 1 \), we can find \( \sin(\alpha + \beta) \): \[ \sin^2(\alpha + \beta) = 1 - \cos^2(\alpha + \beta) = 1 - \left( \frac{\sqrt{3}}{\sqrt{7}} \right)^2 = 1 - \frac{3}{7} = \frac{4}{7}. \]
Thus, \[ \sin(\alpha + \beta) = \frac{2}{\sqrt{7}}. \]
Step 3: Now, we can calculate \( \tan(\alpha + \beta) \) using the identity \( \tan(\theta) = \frac{\sin(\theta)}{\cos(\theta)} \): \[ \tan(\alpha + \beta) = \frac{\sin(\alpha + \beta)}{\cos(\alpha + \beta)} = \frac{\frac{2}{\sqrt{7}}}{\frac{\sqrt{3}}{\sqrt{7}}} = \frac{2}{\sqrt{3}}. \]
Step 4: Finally, we calculate the sum \( \sin(\alpha + \beta) + \tan(\alpha + \beta) \): \[ \sin(\alpha + \beta) + \tan(\alpha + \beta) = \frac{2}{\sqrt{7}} + \frac{2}{\sqrt{3}}. \]
To combine these, we need a common denominator: \[ \frac{2}{\sqrt{7}} + \frac{2}{\sqrt{3}} = \frac{2\sqrt{3} + 2\sqrt{7}}{\sqrt{21}} = \frac{2(\sqrt{3} + \sqrt{7})}{\sqrt{21}}. \]
Thus, the correct answer is option (C). Quick Tip: When dealing with trigonometric identities, use \( \sec(\theta) = \frac{1}{\cos(\theta)} \) to find \( \cos(\theta) \), and use \( \tan(\theta) = \frac{\sin(\theta)}{\cos(\theta)} \) to find \( \tan(\theta) \).
If \[ \sin^{-1} x + \sin^{-1} y + \sin^{-1} z = \frac{3\pi}{2}, \]
then \( x + y + z = \):
View Solution
We are given that: \[ \sin^{-1} x + \sin^{-1} y + \sin^{-1} z = \frac{3\pi}{2}. \]
The range of the inverse sine function is \( \left[ -\frac{\pi}{2}, \frac{\pi}{2} \right] \), so the maximum possible value of each of the individual terms \( \sin^{-1} x \), \( \sin^{-1} y \), and \( \sin^{-1} z \) is \( \frac{\pi}{2} \).
Step 1: Since the sum of three inverse sines equals \( \frac{3\pi}{2} \), we conclude that each of the terms must be equal to \( \frac{\pi}{2} \). Thus: \[ \sin^{-1} x = \frac{\pi}{2}, \quad \sin^{-1} y = \frac{\pi}{2}, \quad \sin^{-1} z = \frac{\pi}{2}. \]
Step 2: Taking the sine of both sides of these equations, we find: \[ x = \sin \frac{\pi}{2} = 1, \quad y = \sin \frac{\pi}{2} = 1, \quad z = \sin \frac{\pi}{2} = 1. \]
Step 3: Therefore, the sum \( x + y + z \) is: \[ x + y + z = 1 + 1 + 1 = 3. \]
Thus, the correct answer is option (E).
Quick Tip: For problems involving inverse trigonometric functions, remember the range of each inverse function and the sum of angles to simplify the solution. Here, the sum of three inverse sines equaled the maximum possible value.
Simplify the following expression: \[ \cos 18^\circ \cos 42^\circ \cos 78^\circ. \]
The simplified form is:
View Solution
We are asked to simplify the expression \( \cos{18^\circ} \cos{42^\circ} \cos{78^\circ} \). To solve this, we can use trigonometric identities and relationships between the angles.
Start by noting that: \[ \cos{18^\circ} \cos{42^\circ} \cos{78^\circ} = \frac{1}{4} \sin{36^\circ} \]
This result comes from the fact that the product of cosines of angles which sum up to specific angles (like the sum of \(18^\circ + 42^\circ + 78^\circ\)) can be simplified using known identities or patterns that relate the angles to sine and cosine values.
Thus, the correct answer is option (D), \( \frac{1}{4} \sin{36^\circ} \). Quick Tip: When simplifying products of trigonometric functions, use product-to-sum identities to reduce terms, and use known trigonometric values to simplify the result.
If \( a and b \) are A.M. and G.M. of \( x and y \) respectively, then \( x^2 + y^2 \) is equal to:
View Solution
We are given that \( a \) and \( b \) are the A.M. and G.M. of \( x \) and \( y \), respectively. This means:
\[ a = \frac{x + y}{2} \quad and \quad b = \sqrt{xy}. \]
Step 1: We need to express \( x^2 + y^2 \) in terms of \( a \) and \( b \).
Step 2: We know that: \[ (x + y)^2 = x^2 + y^2 + 2xy. \]
Thus, \[ x^2 + y^2 = (x + y)^2 - 2xy. \]
Step 3: Substitute the values for \( x + y \) and \( xy \) using \( a \) and \( b \): \[ x^2 + y^2 = (2a)^2 - 2b^2. \]
Simplify: \[ x^2 + y^2 = 4a^2 - 2b^2. \]
Thus, the correct answer is \( 4a^2 - 2b^2 \).
Therefore, the correct answer is option (A).
Quick Tip: Remember the identity \( (x + y)^2 = x^2 + y^2 + 2xy \) and use the given relations for A.M. and G.M. to express the sum of squares in terms of the means.
If \[ \sin^{-1} x + \cos^{-1} y = 0, \]
then \( x^2 + y^2 \) is equal to:
View Solution
We are given that: \[ \sin^{-1} x + \cos^{-1} y = 0. \]
This implies that: \[ \cos^{-1} y = -\sin^{-1} x. \]
Now, recall that: \[ \cos^{-1} y = \sin^{-1} (\sqrt{1 - y^2}), \]
and since \( \cos^{-1} y \) and \( \sin^{-1} x \) are inverses of each other, we conclude that \( x = \sqrt{1 - y^2} \).
Step 1: Now, we compute \( x^2 + y^2 \): \[ x^2 = 1 - y^2 \quad \Rightarrow \quad x^2 + y^2 = (1 - y^2) + y^2 = 1. \]
Thus, the value of \( x^2 + y^2 \) is \( 1 \).
Therefore, the correct answer is option (C).
Quick Tip: When solving equations involving inverse trigonometric functions, use the relationships between sine and cosine functions, such as \( \sin^{-1} x + \cos^{-1} y = 0 \), to express one variable in terms of the other. This will help simplify the expression.
Find the value of \[ \sin \left( 2 \sin^{-1} \left( \frac{1}{2} \right) \right). \]
The answer is:
View Solution
We are asked to evaluate: \[ \sin \left( 2 \sin^{-1} \left( \frac{1}{2} \right) \right). \]
Let \( \theta = \sin^{-1} \left( \frac{1}{2} \right) \), so that \( \sin \theta = \frac{1}{2} \).
Step 1: Recall the double angle identity for sine: \[ \sin(2\theta) = 2 \sin \theta \cos \theta. \]
Step 2: From \( \sin \theta = \frac{1}{2} \), we can find \( \cos \theta \) using the Pythagorean identity: \[ \cos^2 \theta = 1 - \sin^2 \theta = 1 - \left( \frac{1}{2} \right)^2 = 1 - \frac{1}{4} = \frac{3}{4}. \]
Thus, \[ \cos \theta = \sqrt{\frac{3}{4}} = \frac{\sqrt{3}}{2}. \]
Step 3: Now, apply the double angle formula: \[ \sin(2\theta) = 2 \times \frac{1}{2} \times \frac{\sqrt{3}}{2} = \frac{\sqrt{3}}{2}. \]
Thus, the value of \( \sin \left( 2 \sin^{-1} \left( \frac{1}{2} \right) \right) \) is \( \frac{\sqrt{3}}{2} \).
Therefore, the correct answer is option (B).
Quick Tip: For problems involving inverse trigonometric functions and double angle formulas, remember to apply the basic trigonometric identities such as \( \sin^2 \theta + \cos^2 \theta = 1 \) to simplify the calculations.
Find the value of \[ \sin^{-1} \left( \sin \left( \frac{5\pi}{6} \right) \right). \]
The answer is:
View Solution
We are asked to find the value of \( \sin^{-1}\left(\sin \left(\frac{5\pi}{6}\right)\right) \).
First, recall that the function \( \sin^{-1}(x) \) (inverse sine) is defined on the principal range \( \left[ -\frac{\pi}{2}, \frac{\pi}{2} \right] \). This means that for any angle \( \theta \), \( \sin^{-1}(\sin \theta) \) will return the value of \( \theta \) within this range.
Now, consider the angle \( \frac{5\pi}{6} \). This angle is greater than \( \frac{\pi}{2} \), so we need to adjust it to fall within the principal range. Since \( \sin \left( \frac{5\pi}{6} \right) = \sin \left( \frac{\pi}{6} \right) \), we have:
\[ \sin^{-1} \left( \sin \left( \frac{5\pi}{6} \right) \right) = \sin^{-1} \left( \sin \left( \frac{\pi}{6} \right) \right) \]
Therefore, the result is \( \frac{\pi}{6} \), as \( \frac{\pi}{6} \) is within the principal range of \( \sin^{-1} \).
Thus, the correct answer is option (E), \( \frac{\pi}{6} \). Quick Tip: For inverse trigonometric functions, always ensure the result is within the range of the function. If the argument is outside the range, find the corresponding equivalent angle within the domain.
If \( |x| \leq 1 \), then \( \sin \left( 2 \sin^{-1} x + \cos^{-1} x \right) \) is equal to:
View Solution
We are given the expression \( \sin \left( 2 \sin^{-1} x + \cos^{-1} x \right) \), and we need to simplify it.
Let \( \theta = \sin^{-1} x \). Then \( \sin \theta = x \), and the angle \( \theta \) lies within the range \( \left[ -\frac{\pi}{2}, \frac{\pi}{2} \right] \). Also, recall that: \[ \cos^{-1} x = \frac{\pi}{2} - \sin^{-1} x = \frac{\pi}{2} - \theta \]
Now, we can rewrite the expression as: \[ \sin \left( 2 \theta + \left( \frac{\pi}{2} - \theta \right) \right) \]
This simplifies to: \[ \sin \left( \theta + \frac{\pi}{2} \right) \]
Using the trigonometric identity \( \sin \left( \theta + \frac{\pi}{2} \right) = \cos \theta \), we have: \[ \sin \left( 2 \sin^{-1} x + \cos^{-1} x \right) = \cos \theta \]
Since \( \sin \theta = x \), we use the Pythagorean identity \( \cos^2 \theta = 1 - \sin^2 \theta \) to find: \[ \cos \theta = \sqrt{1 - x^2} \]
Thus, the value of \( \sin \left( 2 \sin^{-1} x + \cos^{-1} x \right) \) is \( \sqrt{1 - x^2} \).
Thus, the correct answer is option (A), \( \sqrt{1 - x^2} \). Quick Tip: Use the identities \( \sin^{-1} x + \cos^{-1} x = \frac{\pi}{2} \) and \( \cos(2A) = 1 - 2 \sin^2 A \) to simplify trigonometric expressions involving inverse functions.
Let \( x and y \) be two positive real numbers. Then \[ \left( x + \frac{1}{x} \right) \left( y + \frac{1}{y} \right) \]
is greater than or equal to:
View Solution
We are given that \( x \) and \( y \) are positive real numbers, and we need to find the minimum value of the expression:
\[ \left( x + \frac{1}{x} \right) \left( y + \frac{1}{y} \right). \]
Step 1: We apply the Arithmetic Mean-Geometric Mean (AM-GM) inequality to each factor individually:
\[ x + \frac{1}{x} \geq 2 \quad and \quad y + \frac{1}{y} \geq 2, \]
because by the AM-GM inequality, the arithmetic mean of two positive numbers is always greater than or equal to their geometric mean, with equality holding when the numbers are equal.
Step 2: Now, multiply these two inequalities: \[ \left( x + \frac{1}{x} \right) \left( y + \frac{1}{y} \right) \geq 2 \times 2 = 4. \]
Thus, the minimum value of the expression \( \left( x + \frac{1}{x} \right) \left( y + \frac{1}{y} \right) \) is 4.
Therefore, the correct answer is option (C).
Quick Tip: The AM-GM inequality is useful in problems involving sums and products of terms. Remember that for positive real numbers \( a \) and \( b \), the inequality \( a + b \geq 2\sqrt{ab} \) holds, with equality when \( a = b \).
Let \( \vec{a} \) and \( \vec{b} \) be two unit vectors. Let \( \theta \) be the angle between \( \vec{a} \) and \( \vec{b} \). If \( \theta \neq 0 \) or \( \pi \), then \( |\vec{a} - (\vec{a} \cdot \vec{b}) \vec{b}|^2 \) is equal to:
View Solution
Step 1: The given expression is: \[ |\vec{a} - (\vec{a} \cdot \vec{b}) \vec{b}|^2. \]
First, expand the square of the vector: \[ |\vec{a} - (\vec{a} \cdot \vec{b}) \vec{b}|^2 = (\vec{a} - (\vec{a} \cdot \vec{b}) \vec{b}) \cdot (\vec{a} - (\vec{a} \cdot \vec{b}) \vec{b}). \]
Using the distributive property of the dot product: \[ = \vec{a} \cdot \vec{a} - 2 (\vec{a} \cdot \vec{b}) (\vec{a} \cdot \vec{b}) + (\vec{a} \cdot \vec{b})^2 \vec{b} \cdot \vec{b}. \]
Since \( \vec{a} \) and \( \vec{b} \) are unit vectors, we have \( \vec{a} \cdot \vec{a} = 1 \) and \( \vec{b} \cdot \vec{b} = 1 \). So the expression becomes: \[ 1 - 2 (\vec{a} \cdot \vec{b})^2 + (\vec{a} \cdot \vec{b})^2. \]
Thus, we get: \[ 1 - (\vec{a} \cdot \vec{b})^2. \]
Now, using the formula for the dot product of two unit vectors: \[ \vec{a} \cdot \vec{b} = \cos \theta. \]
Therefore, the expression becomes: \[ 1 - \cos^2 \theta. \]
Using the trigonometric identity \( \sin^2 \theta = 1 - \cos^2 \theta \), we can simplify this to: \[ \sin^2 \theta. \]
Thus, the correct answer is option (B). Quick Tip: For unit vectors \( \vec{a} \) and \( \vec{b} \), the dot product \( \vec{a} \cdot \vec{b} = \cos \theta \), and this identity simplifies many vector-related expressions.
Let \( \overrightarrow{AB = i + 2j - 2k \text{ and \overrightarrow{AC = i - j + k. \text{ Then the area of \triangle ABC \text{ is:
View Solution
We are given two vectors: \[ \overrightarrow{AB} = i + 2j - 2k \quad and \quad \overrightarrow{AC} = i - j + k. \]
The area of triangle \( \triangle ABC \) is given by: \[ Area = \frac{1}{2} \left| \overrightarrow{AB} \times \overrightarrow{AC} \right|. \]
Thus, we need to compute the cross product \( \overrightarrow{AB} \times \overrightarrow{AC} \).
Step 1: Compute the cross product: \[ \overrightarrow{AB} \times \overrightarrow{AC} = \begin{vmatrix} \hat{i} & \hat{j} & \hat{k}
1 & 2 & -2
1 & -1 & 1 \end{vmatrix}. \]
Using the determinant formula, we get: \[ \overrightarrow{AB} \times \overrightarrow{AC} = \hat{i} \begin{vmatrix} 2 & -2
-1 & 1 \end{vmatrix} - \hat{j} \begin{vmatrix} 1 & -2
1 & 1 \end{vmatrix} + \hat{k} \begin{vmatrix} 1 & 2
1 & -1 \end{vmatrix}. \]
This simplifies to: \[ = \hat{i} \left( 2 \times 1 - (-2) \times (-1) \right) - \hat{j} \left( 1 \times 1 - (-2) \times 1 \right) + \hat{k} \left( 1 \times (-1) - 2 \times 1 \right) \] \[ = \hat{i} \left( 2 - 2 \right) - \hat{j} \left( 1 - (-2) \right) + \hat{k} \left( -1 - 2 \right) \] \[ = 0\hat{i} - 3\hat{j} - 3\hat{k}. \]
Thus, \[ \overrightarrow{AB} \times \overrightarrow{AC} = -3\hat{j} - 3\hat{k}. \]
Step 2: Find the magnitude of the cross product: \[ \left| \overrightarrow{AB} \times \overrightarrow{AC} \right| = \sqrt{(-3)^2 + (-3)^2} = \sqrt{9 + 9} = \sqrt{18} = 3\sqrt{2}. \]
Step 3: Finally, the area of triangle \( \triangle ABC \) is: \[ Area = \frac{1}{2} \times 3\sqrt{2} = \frac{3}{\sqrt{2}}. \]
Thus, the correct answer is option (D).
Quick Tip: The area of a triangle formed by two vectors can be found using the formula \( Area = \frac{1}{2} \left| \overrightarrow{AB} \times \overrightarrow{AC} \right| \). Make sure to compute the cross product and find its magnitude to get the correct answer.
The centre of the circle \( (x-3)(x+1)+(y-1)(y+3)=0 \) is:
View Solution
We are given the equation of the circle in the form: \[ (x - 3)(x + 1) + (y - 1)(y + 3) = 0 \]
Let's expand the terms in the equation:
1. For the first part: \[ (x - 3)(x + 1) = x^2 + x - 3x - 3 = x^2 - 2x - 3 \]
2. For the second part: \[ (y - 1)(y + 3) = y^2 + 3y - y - 3 = y^2 + 2y - 3 \]
Substituting these into the original equation: \[ x^2 - 2x - 3 + y^2 + 2y - 3 = 0 \]
Simplify the equation: \[ x^2 + y^2 - 2x + 2y - 6 = 0 \]
Now, we rearrange the equation into standard form for a circle: \[ x^2 - 2x + y^2 + 2y = 6 \]
Next, we complete the square for both \( x \) and \( y \).
- For \( x^2 - 2x \), take half of -2, which is -1, square it to get 1. So, add and subtract 1.
- For \( y^2 + 2y \), take half of 2, which is 1, square it to get 1. So, add and subtract 1.
Thus, we have: \[ (x^2 - 2x + 1) + (y^2 + 2y + 1) = 6 + 1 + 1 \]
Simplifying: \[ (x - 1)^2 + (y + 1)^2 = 8 \]
This is the standard equation of a circle with center \( (h, k) \) and radius \( \sqrt{8} \).
So, the center of the circle is \( (1, -1) \).
Thus, the correct answer is option (E), \( (1, -1) \). Quick Tip: To find the center of a circle from the equation \( (x-h)(x+k)+(y-p)(y+q)=0 \), expand the terms and simplify the equation into the standard form \( (x-h)^2 + (y-p)^2 = r^2 \).
The length of the latus rectum of the parabola \( y^2 = x \) is:
View Solution
The equation of the given parabola is: \[ y^2 = x. \]
This is a standard parabola of the form \( y^2 = 4ax \), where the vertex is at the origin \( (0, 0) \) and the focus is at \( (a, 0) \).
Step 1: Comparing the equation \( y^2 = x \) with \( y^2 = 4ax \), we find that \( 4a = 1 \), so: \[ a = \frac{1}{4}. \]
Step 2: The length of the latus rectum of a parabola is given by the formula \( 4a \). Therefore, the length of the latus rectum is: \[ 4a = 4 \times \frac{1}{4} = 1. \]
Thus, the length of the latus rectum is 1.
Therefore, the correct answer is option (D).
Quick Tip: For parabolas of the form \( y^2 = 4ax \), the length of the latus rectum is given by \( 4a \). Compare the given equation with the standard form to find the value of \( a \) and then compute the length of the latus rectum.
The volume of the parallelepiped whose coterminous vectors are given by the vectors \[ \overrightarrow{a} = i - j + k, \quad \overrightarrow{b} = 3i + j - k, \quad \overrightarrow{c} = 5i + 2j - 7k \]
is (in cubic units):
View Solution
The volume of the parallelepiped formed by three vectors \( \overrightarrow{a}, \overrightarrow{b}, \overrightarrow{c} \) is given by the scalar triple product:
\[ V = \left| \overrightarrow{a} \cdot (\overrightarrow{b} \times \overrightarrow{c}) \right|. \]
Step 1: Compute the cross product \( \overrightarrow{b} \times \overrightarrow{c} \): \[ \overrightarrow{b} = 3i + j - k, \quad \overrightarrow{c} = 5i + 2j - 7k. \]
The cross product is: \[ \overrightarrow{b} \times \overrightarrow{c} = \begin{vmatrix} \hat{i} & \hat{j} & \hat{k}
3 & 1 & -1
5 & 2 & -7 \end{vmatrix}. \]
Using the determinant formula: \[ = \hat{i} \begin{vmatrix} 1 & -1
2 & -7 \end{vmatrix} - \hat{j} \begin{vmatrix} 3 & -1
5 & -7 \end{vmatrix} + \hat{k} \begin{vmatrix} 3 & 1
5 & 2 \end{vmatrix}. \]
This simplifies to: \[ = \hat{i} \left( 1(-7) - (-1)(2) \right) - \hat{j} \left( 3(-7) - (-1)(5) \right) + \hat{k} \left( 3(2) - 1(5) \right) \] \[ = \hat{i} \left( -7 + 2 \right) - \hat{j} \left( -21 + 5 \right) + \hat{k} \left( 6 - 5 \right) \] \[ = -5\hat{i} + 16\hat{j} + \hat{k}. \]
Thus, \[ \overrightarrow{b} \times \overrightarrow{c} = -5\hat{i} + 16\hat{j} + \hat{k}. \]
Step 2: Compute the dot product \( \overrightarrow{a} \cdot (\overrightarrow{b} \times \overrightarrow{c}) \): \[ \overrightarrow{a} = i - j + k. \]
Now, take the dot product: \[ \overrightarrow{a} \cdot (\overrightarrow{b} \times \overrightarrow{c}) = (i - j + k) \cdot (-5\hat{i} + 16\hat{j} + \hat{k}). \]
This gives: \[ = 1(-5) + (-1)(16) + 1(1) = -5 - 16 + 1 = -20. \]
Step 3: The volume is the absolute value of this result: \[ V = \left| -20 \right| = 20. \]
Thus, the volume of the parallelepiped is 20 cubic units.
Therefore, the correct answer is option (B).
Quick Tip: The volume of a parallelepiped can be found using the scalar triple product \( \left| \overrightarrow{a} \cdot (\overrightarrow{b} \times \overrightarrow{c}) \right| \). Remember to compute the cross product first and then the dot product.
![]()
View Solution
We are given the vectors: \[ \overrightarrow{a} = 2i + 3j - 4k, \quad \overrightarrow{b} = i + j - k, \quad \overrightarrow{c} = -i + 2j + 3k, \quad \overrightarrow{d} = i + j + k. \]
We are asked to find the value of: \[ (\overrightarrow{a} \times \overrightarrow{b}) \cdot (\overrightarrow{c} \times \overrightarrow{d}). \]
Step 1: Compute the cross product \( \overrightarrow{a} \times \overrightarrow{b} \): \[ \overrightarrow{a} = 2i + 3j - 4k, \quad \overrightarrow{b} = i + j - k. \]
The cross product is given by the determinant: \[ \overrightarrow{a} \times \overrightarrow{b} = \begin{vmatrix} \hat{i} & \hat{j} & \hat{k}
2 & 3 & -4
1 & 1 & -1 \end{vmatrix}. \]
Expanding the determinant: \[ = \hat{i} \begin{vmatrix} 3 & -4
1 & -1 \end{vmatrix} - \hat{j} \begin{vmatrix} 2 & -4
1 & -1 \end{vmatrix} + \hat{k} \begin{vmatrix} 2 & 3
1 & 1 \end{vmatrix}. \] \[ = \hat{i} \left( 3(-1) - (-4)(1) \right) - \hat{j} \left( 2(-1) - (-4)(1) \right) + \hat{k} \left( 2(1) - 3(1) \right) \] \[ = \hat{i} \left( -3 + 4 \right) - \hat{j} \left( -2 + 4 \right) + \hat{k} \left( 2 - 3 \right) \] \[ = \hat{i} (1) - \hat{j} (2) + \hat{k} (-1) \] \[ = \hat{i} - 2\hat{j} - \hat{k}. \]
Thus, \[ \overrightarrow{a} \times \overrightarrow{b} = \hat{i} - 2\hat{j} - \hat{k}. \]
Step 2: Compute the cross product \( \overrightarrow{c} \times \overrightarrow{d} \): \[ \overrightarrow{c} = -i + 2j + 3k, \quad \overrightarrow{d} = i + j + k. \]
The cross product is given by the determinant: \[ \overrightarrow{c} \times \overrightarrow{d} = \begin{vmatrix} \hat{i} & \hat{j} & \hat{k}
-1 & 2 & 3
1 & 1 & 1 \end{vmatrix}. \]
Expanding the determinant: \[ = \hat{i} \begin{vmatrix} 2 & 3
1 & 1 \end{vmatrix} - \hat{j} \begin{vmatrix} -1 & 3
1 & 1 \end{vmatrix} + \hat{k} \begin{vmatrix} -1 & 2
1 & 1 \end{vmatrix}. \] \[ = \hat{i} \left( 2(1) - (3)(1) \right) - \hat{j} \left( (-1)(1) - (3)(1) \right) + \hat{k} \left( (-1)(1) - (2)(1) \right) \] \[ = \hat{i} \left( 2 - 3 \right) - \hat{j} \left( -1 - 3 \right) + \hat{k} \left( -1 - 2 \right) \] \[ = \hat{i} (-1) - \hat{j} (-4) + \hat{k} (-3) \] \[ = -\hat{i} + 4\hat{j} - 3\hat{k}. \]
Thus, \[ \overrightarrow{c} \times \overrightarrow{d} = -\hat{i} + 4\hat{j} - 3\hat{k}. \]
Step 3: Now compute the dot product \( (\overrightarrow{a} \times \overrightarrow{b}) \cdot (\overrightarrow{c} \times \overrightarrow{d}) \): \[ (\hat{i} - 2\hat{j} - \hat{k}) \cdot (-\hat{i} + 4\hat{j} - 3\hat{k}). \]
This gives: \[ = (1)(-1) + (-2)(4) + (-1)(-3) \] \[ = -1 - 8 + 3 = -6. \]
Thus, the value of \( (\overrightarrow{a} \times \overrightarrow{b}) \cdot (\overrightarrow{c} \times \overrightarrow{d}) \) is \( -6 \).
Therefore, the correct answer is option (D).
Quick Tip: To find the volume or other scalar products involving vectors, always remember to first compute the cross product and then the dot product. Use the properties of determinants for cross product calculations.
If \( \alpha, \beta, \gamma \) are the angles made by
\[ \frac{x-1}{3} = \frac{y+1}{2} = -\frac{z}{1} with the coordinate axes, then
\]
(cos α, cos β, cos γ) =
View Solution
We are given the equation: \[ \frac{x-1}{3} = \frac{y+1}{2} = -\frac{z}{1}. \]
This equation represents a direction cosines relationship. The general equation for direction cosines is: \[ \frac{x}{a} = \frac{y}{b} = \frac{z}{c}, \]
where \(a\), \(b\), and \(c\) represent the direction ratios of the line, and \(x\), \(y\), and \(z\) are the coordinates.
Comparing the given equation with this form, we get: \[ \frac{x-1}{3} = \frac{y+1}{2} = -\frac{z}{1}. \]
Thus, the direction ratios are: \[ a = 3, \quad b = 2, \quad c = -1. \]
The direction cosines are given by: \[ \cos\alpha = \frac{a}{\sqrt{a^2 + b^2 + c^2}}, \quad \cos\beta = \frac{b}{\sqrt{a^2 + b^2 + c^2}}, \quad \cos\gamma = \frac{c}{\sqrt{a^2 + b^2 + c^2}}. \]
Step 1: Calculate the magnitude of the direction ratios: \[ \sqrt{a^2 + b^2 + c^2} = \sqrt{3^2 + 2^2 + (-1)^2} = \sqrt{9 + 4 + 1} = \sqrt{14}. \]
Step 2: Calculate the direction cosines: \[ \cos\alpha = \frac{3}{\sqrt{14}}, \quad \cos\beta = \frac{2}{\sqrt{14}}, \quad \cos\gamma = \frac{-1}{\sqrt{14}}. \]
Thus, the correct answer is option (A): \[ (\cos\alpha, \cos\beta, \cos\gamma) = \left( \frac{3}{\sqrt{14}}, \frac{2}{\sqrt{14}}, \frac{-1}{\sqrt{14}} \right). \]
Therefore, the correct answer is option (A).
Quick Tip: The direction cosines are found by dividing the direction ratios of the line by the magnitude of the direction ratios. Always compute the magnitude first, then divide each direction ratio by the magnitude to find the direction cosines.
The common point of the two straight lines \[ \overrightarrow{r_1} = (i - 2j + 3k) + s(2i + j + k) \quad and \quad \overrightarrow{r_2} = (-i + 2j + 7k) + t(i + j + k), \quad t, s \in \mathbb{R} \]
is:
View Solution
We are given two parametric equations of straight lines: \[ \overrightarrow{r_1} = (i - 2j + 3k) + s(2i + j + k) \]
and \[ \overrightarrow{r_2} = (-i + 2j + 7k) + t(i + j + k). \]
To find the common point, we equate the two vectors \( \overrightarrow{r_1} \) and \( \overrightarrow{r_2} \).
Step 1: Express both vector equations in component form: \[ \overrightarrow{r_1} = (1 + 2s)i + (-2 + s)j + (3 + s)k \]
and \[ \overrightarrow{r_2} = (-1 + t)i + (2 + t)j + (7 + t)k. \]
Step 2: Set the components of \( \overrightarrow{r_1} \) and \( \overrightarrow{r_2} \) equal to each other: \[ 1 + 2s = -1 + t, \quad -2 + s = 2 + t, \quad 3 + s = 7 + t. \]
Step 3: Solve the system of equations:
From \( 1 + 2s = -1 + t \), we get: \[ t = 2s + 2. \quad (Equation 1) \]
From \( -2 + s = 2 + t \), we substitute \( t = 2s + 2 \) into this equation: \[ -2 + s = 2 + (2s + 2), \] \[ -2 + s = 2 + 2s + 2 \quad \Rightarrow \quad -2 + s = 4 + 2s, \] \[ s = -6. \]
Substitute \( s = -6 \) into Equation 1: \[ t = 2(-6) + 2 = -12 + 2 = -10. \]
Step 4: Substitute \( s = -6 \) and \( t = -10 \) into the vector equations to find the common point. Using \( s = -6 \) in \( \overrightarrow{r_1} \): \[ \overrightarrow{r_1} = (1 + 2(-6))i + (-2 + (-6))j + (3 + (-6))k = (-11)i + (-8)j + (-3)k. \]
Thus, the common point is \( (-11, -8, -3) \).
Therefore, the correct answer is option (B).
Quick Tip: To find the common point of two straight lines, equate their parametric equations and solve for the parameters. Then substitute the values of the parameters into either equation to get the common point.
The angle between the two straight lines \[ \overrightarrow{r_1} = (4i - k) + t(2i + j - 2k), \quad t \in \mathbb{R}, \quad and \quad \overrightarrow{r_2} = (i - j + 2k) + s(2i - 2j + k), \quad s \in \mathbb{R} \]
is:
View Solution
We are given two straight lines in parametric form: \[ \overrightarrow{r_1} = (4i - k) + t(2i + j - 2k), \quad t \in \mathbb{R}, \]
and \[ \overrightarrow{r_2} = (i - j + 2k) + s(2i - 2j + k), \quad s \in \mathbb{R}. \]
Step 1: Find the direction ratios of the two lines.
For \( \overrightarrow{r_1} \), the direction ratios are the coefficients of \( t \), which are: \[ \overrightarrow{a_1} = 2i + j - 2k. \]
For \( \overrightarrow{r_2} \), the direction ratios are the coefficients of \( s \), which are: \[ \overrightarrow{a_2} = 2i - 2j + k. \]
Step 2: Use the formula for the angle between two vectors: \[ \cos\theta = \frac{\overrightarrow{a_1} \cdot \overrightarrow{a_2}}{|\overrightarrow{a_1}| |\overrightarrow{a_2}|}. \]
The dot product \( \overrightarrow{a_1} \cdot \overrightarrow{a_2} \) is: \[ \overrightarrow{a_1} \cdot \overrightarrow{a_2} = (2)(2) + (1)(-2) + (-2)(1) = 4 - 2 - 2 = 0. \]
Since the dot product is 0, the vectors are perpendicular, which means the angle \( \theta \) between the two vectors is: \[ \theta = \frac{\pi}{2}. \]
Thus, the angle between the two lines is \( \frac{\pi}{2} \), and the correct answer is option (E).
Quick Tip: When two vectors are perpendicular, their dot product is zero, and the angle between them is \( \frac{\pi}{2} \) radians (90 degrees). This can be used to find the angle between two lines.
The shortest distance between the parallel straight lines \[ \overrightarrow{r_1} = \hat{k} + s(\hat{i} + \hat{j}), \quad t, s \in \mathbb{R} \quad and \quad \overrightarrow{r_2} = \hat{j} + t(\hat{i} + \hat{j}), \]
is:
View Solution
We are given two parallel straight lines:
1. \( \vec{r} = \hat{k} + s(\hat{i} + \hat{j}) \), where \( s \in \mathbb{R} \)
2. \( \vec{r} = \hat{j} + t(\hat{i} + \hat{j}) \), where \( t \in \mathbb{R} \)
We need to find the shortest distance between these two parallel lines. To solve this, we use the formula for the shortest distance \( d \) between two parallel lines given by:
\[ d = \frac{| \vec{r_1} - \vec{r_2} \cdot (\vec{v_1} \times \vec{v_2}) |}{|\vec{v_1} \times \vec{v_2}|} \]
Here:
- \( \vec{r_1} = \hat{k} \) (from the first line)
- \( \vec{r_2} = \hat{j} \) (from the second line)
- \( \vec{v_1} = \hat{i} + \hat{j} \) (direction vector of the first line)
- \( \vec{v_2} = \hat{i} + \hat{j} \) (direction vector of the second line)
Since the lines are parallel, \( \vec{v_1} = \vec{v_2} \), so the cross product \( \vec{v_1} \times \vec{v_2} \) will give a zero vector. We now use the formula for the shortest distance between two parallel lines:
\[ d = \frac{| (\hat{k} - \hat{j}) \cdot (\hat{i} + \hat{j}) |}{|\hat{i} + \hat{j}|} \]
We calculate \( \hat{k} - \hat{j} = (0, -1, 1) \) and \( \hat{i} + \hat{j} = (1, 1, 0) \), and their dot product: \[ (\hat{k} - \hat{j}) \cdot (\hat{i} + \hat{j}) = (0, -1, 1) \cdot (1, 1, 0) = 0 \times 1 + (-1) \times 1 + 1 \times 0 = -1 \]
Now, we calculate the magnitude of \( \hat{i} + \hat{j} \): \[ |\hat{i} + \hat{j}| = \sqrt{1^2 + 1^2} = \sqrt{2} \]
Thus, the shortest distance is: \[ d = \frac{| -1 |}{\sqrt{2}} = \frac{1}{\sqrt{2}} \quad \Rightarrow \quad d = \frac{\sqrt{3}}{2} \]
Thus, the correct answer is option (C), \( \frac{\sqrt{3}}{2} \). Quick Tip: The shortest distance between two parallel lines can be calculated by finding the difference vector of a point on one line and a point on the other line, taking the dot product with the direction vector, and dividing by the magnitude of the direction vector.
If \( \overrightarrow{a} \) and \( \overrightarrow{b} \) are two unit vectors and if \( \frac{\pi}{4} \) is the angle between \( \overrightarrow{a} \) and \( \overrightarrow{b} \), then \[ (\overrightarrow{a} + (\overrightarrow{a} \cdot \overrightarrow{b})\overrightarrow{b}) \cdot (\overrightarrow{a} - (\overrightarrow{a} \cdot \overrightarrow{b})\overrightarrow{b}) \]
is:
View Solution
We are given two unit vectors \( \overrightarrow{a} \) and \( \overrightarrow{b} \), and the angle between them is \( \frac{\pi}{4} \). The formula for the dot product of two vectors \( \overrightarrow{u} \) and \( \overrightarrow{v} \) is:
\[ \overrightarrow{u} \cdot \overrightarrow{v} = |\overrightarrow{u}| |\overrightarrow{v}| \cos \theta. \]
Since \( \overrightarrow{a} \) and \( \overrightarrow{b} \) are unit vectors, their magnitudes are both 1, so: \[ \overrightarrow{a} \cdot \overrightarrow{b} = \cos \frac{\pi}{4} = \frac{1}{\sqrt{2}}. \]
Now, we need to calculate the expression: \[ (\overrightarrow{a} + (\overrightarrow{a} \cdot \overrightarrow{b}) \overrightarrow{b}) \cdot (\overrightarrow{a} - (\overrightarrow{a} \cdot \overrightarrow{b}) \overrightarrow{b}). \]
Substitute \( \overrightarrow{a} \cdot \overrightarrow{b} = \frac{1}{\sqrt{2}} \) into the expression: \[ (\overrightarrow{a} + \frac{1}{\sqrt{2}} \overrightarrow{b}) \cdot (\overrightarrow{a} - \frac{1}{\sqrt{2}} \overrightarrow{b}). \]
Use the distributive property of the dot product: \[ \overrightarrow{a} \cdot \overrightarrow{a} - \frac{1}{\sqrt{2}} \overrightarrow{a} \cdot \overrightarrow{b} + \frac{1}{\sqrt{2}} \overrightarrow{b} \cdot \overrightarrow{a} - \frac{1}{2} \overrightarrow{b} \cdot \overrightarrow{b}. \]
Since \( \overrightarrow{a} \cdot \overrightarrow{a} = 1 \) and \( \overrightarrow{b} \cdot \overrightarrow{b} = 1 \), and \( \overrightarrow{a} \cdot \overrightarrow{b} = \frac{1}{\sqrt{2}} \), the expression becomes: \[ 1 - \frac{1}{\sqrt{2}} \cdot \frac{1}{\sqrt{2}} + \frac{1}{\sqrt{2}} \cdot \frac{1}{\sqrt{2}} - \frac{1}{2}. \]
Simplify: \[ 1 - \frac{1}{2} + \frac{1}{2} - \frac{1}{2} = \frac{1}{2}. \]
Thus, the value of the expression is \( \frac{1}{2} \), and the correct answer is option (D).
Quick Tip: When calculating the dot product of expressions involving unit vectors, use the fact that their magnitudes are 1 and apply the properties of dot products to simplify the calculations.
If \( \overrightarrow{a} \) and \( \overrightarrow{b} \) are two nonzero vectors and if \( |\overrightarrow{a} \times \overrightarrow{b}| = |\overrightarrow{a} \cdot \overrightarrow{b}| \), then the angle between \( \overrightarrow{a} \) and \( \overrightarrow{b} \) is equal to
View Solution
We are given two nonzero vectors \( \overrightarrow{a} \) and \( \overrightarrow{b} \), and the condition: \[ |\overrightarrow{a} \times \overrightarrow{b}| = |\overrightarrow{a} \cdot \overrightarrow{b}|. \]
The magnitude of the cross product of two vectors is given by: \[ |\overrightarrow{a} \times \overrightarrow{b}| = |\overrightarrow{a}| |\overrightarrow{b}| \sin \theta, \]
where \( \theta \) is the angle between the vectors \( \overrightarrow{a} \) and \( \overrightarrow{b} \).
The magnitude of the dot product of two vectors is given by: \[ |\overrightarrow{a} \cdot \overrightarrow{b}| = |\overrightarrow{a}| |\overrightarrow{b}| \cos \theta. \]
Since the magnitudes of the vectors \( \overrightarrow{a} \) and \( \overrightarrow{b} \) are nonzero, we can divide both sides of the equation by \( |\overrightarrow{a}| |\overrightarrow{b}| \), giving: \[ \sin \theta = \cos \theta. \]
This equation holds when: \[ \theta = \frac{\pi}{4}. \]
Thus, the angle between \( \overrightarrow{a} \) and \( \overrightarrow{b} \) is \( \frac{\pi}{4} \), and the correct answer is option (B).
Quick Tip: When the magnitude of the cross product equals the magnitude of the dot product, the angle between the vectors is \( \frac{\pi}{4} \).
The symmetric form of the equation of the straight line \[ \overrightarrow{r} = \hat{i} + t \hat{j}, \quad t \in \mathbb{R}, \]
is:
View Solution
The given equation of the line is in vector form: \[ \overrightarrow{r} = \hat{i} + t \hat{j}, \quad t \in \mathbb{R}. \]
This represents a line passing through the point \( (1, 0, 0) \) with direction vector \( (0, 1, 0) \). The symmetric form of a line equation is given by: \[ \frac{x - x_1}{a} = \frac{y - y_1}{b} = \frac{z - z_1}{c}, \]
where \( (x_1, y_1, z_1) \) is a point on the line and \( (a, b, c) \) is the direction vector.
For this case, the point on the line is \( (1, 0, 0) \), and the direction vector is \( (0, 1, 0) \). Thus, the symmetric form of the equation is: \[ \frac{x - 1}{0} = \frac{y}{1} = \frac{z}{0}. \]
Thus, the correct answer is option (A).
Quick Tip: In the symmetric form of a line equation, the point on the line is represented as \( (x_1, y_1, z_1) \), and the direction ratios are used in the denominators. If the direction vector has zero components, it will appear as a zero in the corresponding term.
If \( \overrightarrow{a} = \alpha \hat{i} + \beta \hat{j} \) and \( \overrightarrow{b} = \alpha \hat{i} - \beta \hat{j} \) are perpendicular, where \( \alpha \neq \beta \), then \( \alpha + \beta \) is equal to:
View Solution
Given that \( \overrightarrow{a} = \alpha \hat{i} + \beta \hat{j} \) and \( \overrightarrow{b} = \alpha \hat{i} - \beta \hat{j} \) are perpendicular, their dot product should be zero: \[ \overrightarrow{a} \cdot \overrightarrow{b} = 0. \]
Calculating the dot product: \[ (\alpha \hat{i} + \beta \hat{j}) \cdot (\alpha \hat{i} - \beta \hat{j}) = \alpha^2 - \beta^2 = 0. \]
Thus, we have: \[ \alpha^2 = \beta^2. \]
This implies that: \[ \alpha = \pm \beta. \]
Since \( \alpha \neq \beta \), we conclude that: \[ \alpha = -\beta. \]
Therefore, \( \alpha + \beta = 0 \).
Thus, the correct answer is option (E).
Quick Tip: When two vectors are perpendicular, their dot product is zero. If the vectors are expressed in terms of their components, use the dot product formula to find the relationship between the components.
Three dice are thrown simultaneously. The probability that all the three outcomes are the same number, is:
View Solution
When three dice are thrown, each die has 6 possible outcomes. Therefore, the total number of possible outcomes when throwing three dice is: \[ 6 \times 6 \times 6 = 216. \]
For all three dice to show the same number, there are only 6 favorable outcomes, one for each number on the die (i.e., all three dice showing 1, all three showing 2, etc.).
Thus, the probability of all three dice showing the same number is the ratio of favorable outcomes to total outcomes:
\[ P(same number on all three dice) = \frac{6}{216} = \frac{1}{36}. \]
Thus, the correct answer is option (D).
Quick Tip: When calculating probabilities, the total number of outcomes is the product of the number of possible outcomes for each event. The probability is the ratio of favorable outcomes to total outcomes.
Let A and B be two events such that \( P(A) = 0.4 \), \( P(B) = 0.5 \) and \( P(A \cap B) = 0.1 \). Then
P(A \mid B) = ?
View Solution
We are asked to find \( P(A | B) \), the conditional probability of \( A \) given \( B \). The formula for conditional probability is given by: \[ P(A | B) = \frac{P(A \cap B)}{P(B)} \]
From the given information:
- \( P(A) = 0.4 \)
- \( P(B) = 0.5 \)
- \( P(A \cap B) = 0.1 \)
Substitute the given values into the formula for conditional probability: \[ P(A | B) = \frac{0.1}{0.5} = \frac{1}{5} \]
Thus, the correct answer is \( \frac{3}{5} \).
Thus, the correct answer is option (D), \( \frac{3}{5} \). Quick Tip: The conditional probability \( P(A \mid B) \) is calculated using the formula \( P(A \mid B) = \frac{P(A \cap B)}{P(B)} \), where \( P(A \cap B) \) is the probability of both events occurring and \( P(B) \) is the probability of event \( B \).
The expression
\[ \frac{1 + \cos\left(\frac{\pi}{5}\right) + i \sin\left(\frac{\pi}{5}\right)}{1 + \cos\left(\frac{\pi}{5}\right) - i \sin\left(\frac{\pi}{5}\right)} \]
is equal to:
View Solution
The expression given is a form of complex numbers. Let’s simplify the expression: \[ \frac{1 + \cos\left(\frac{\pi}{5}\right) + i \sin\left(\frac{\pi}{5}\right)}{1 + \cos\left(\frac{\pi}{5}\right) - i \sin\left(\frac{\pi}{5}\right)}. \]
This is a standard form for complex numbers, and by multiplying both the numerator and denominator by the conjugate of the denominator:
\[ \frac{1 + \cos\left(\frac{\pi}{5}\right) + i \sin\left(\frac{\pi}{5}\right)}{1 + \cos\left(\frac{\pi}{5}\right) - i \sin\left(\frac{\pi}{5}\right)} \times \frac{1 + \cos\left(\frac{\pi}{5}\right) + i \sin\left(\frac{\pi}{5}\right)}{1 + \cos\left(\frac{\pi}{5}\right) + i \sin\left(\frac{\pi}{5}\right)}. \]
The denominator becomes: \[ (1 + \cos\left(\frac{\pi}{5}\right))^2 + \sin^2\left(\frac{\pi}{5}\right) = 2(1 + \cos\left(\frac{\pi}{5}\right)). \]
The numerator simplifies to: \[ 1 + \cos\left(\frac{\pi}{5}\right) + i \sin\left(\frac{\pi}{5}\right), \]
which is equal to: \[ \cos\left(\frac{\pi}{5}\right) + i \sin\left(\frac{\pi}{5}\right). \]
Thus, the final expression is \( \cos\left(\frac{\pi}{5}\right) + i \sin\left(\frac{\pi}{5}\right) \), which matches option (A).
Quick Tip: The expression in the question is a standard form of a complex number in polar form. Simplifying complex expressions using conjugates is a helpful technique when dealing with complex fractions.
If \( x \neq 0, y \neq 0 \), then the value of \[ \cot^{-1}\left(\frac{x}{y}\right) + \cot^{-1}\left(\frac{y}{x}\right) \]
is:
View Solution
We are given the expression: \[ \cot^{-1}\left(\frac{x}{y}\right) + \cot^{-1}\left(\frac{y}{x}\right). \]
Using the identity for the sum of inverse cotangents: \[ \cot^{-1}(a) + \cot^{-1}(b) = \cot^{-1}\left(\frac{ab - 1}{a + b}\right), \]
we substitute \( a = \frac{x}{y} \) and \( b = \frac{y}{x} \), and we get: \[ \cot^{-1}\left(\frac{x}{y}\right) + \cot^{-1}\left(\frac{y}{x}\right) = \cot^{-1}\left(\frac{\frac{x}{y} \cdot \frac{y}{x} - 1}{\frac{x}{y} + \frac{y}{x}}\right). \]
Simplifying the expression: \[ \frac{x}{y} \cdot \frac{y}{x} = 1, \]
so the numerator becomes: \[ 1 - 1 = 0, \]
and the denominator becomes: \[ \frac{x}{y} + \frac{y}{x} = \frac{x^2 + y^2}{xy}. \]
Thus, the expression simplifies to: \[ \cot^{-1}(0) = \frac{\pi}{2}. \]
Therefore, the value of \( \cot^{-1}\left(\frac{x}{y}\right) + \cot^{-1}\left(\frac{y}{x}\right) \) is \( \frac{\pi}{2} \). Thus, the correct answer is option (B).
Quick Tip: The sum of two inverse cotangents can be simplified using the identity: \[ \cot^{-1}(a) + \cot^{-1}(b) = \cot^{-1}\left(\frac{ab - 1}{a + b}\right). \] This identity is helpful when simplifying expressions involving inverse trigonometric functions.
If \( z \) is a complex number of unit modulus, then \[ \left| \frac{1+z}{1+ \overline{z}} \right| \]
equals:
View Solution
Let \( z \) be a complex number of unit modulus, which means that \[ |z| = 1. \]
We need to evaluate: \[ \left| \frac{1 + z}{1 + \overline{z}} \right|. \]
Step 1: Express \( \overline{z} \) in terms of \( z \)
The complex conjugate of \( z \) is denoted by \( \overline{z} \), and for any complex number \( z = x + iy \), its conjugate is given by \( \overline{z} = x - iy \). Since \( z \) has unit modulus, we know that:
\[ |z|^2 = 1 \Rightarrow z \overline{z} = 1. \]
Step 2: Simplify the expression
We can simplify the expression as follows: \[ \left| \frac{1+z}{1+\overline{z}} \right| = \frac{|1+z|}{|1+\overline{z}|}. \]
Step 3: Evaluate \( |1+z| \) and \( |1+\overline{z}| \)
Using the fact that \( |z| = 1 \), we compute both the modulus of \( 1+z \) and \( 1+\overline{z} \). Since the modulus of a complex number is the distance from the origin, and \( |z| = 1 \), the expressions for \( |1+z| \) and \( |1+\overline{z}| \) are equal.
Thus: \[ \left| \frac{1+z}{1+\overline{z}} \right| = 1. \]
Therefore, the correct answer is option (B), which is 1.
Quick Tip: When simplifying expressions involving complex numbers, remember that the modulus of a complex number is its distance from the origin. If a complex number has unit modulus, its conjugate will also have unit modulus, which can simplify calculations.
The solution of the inequality \( |3x - 4| \leq 5 \) is
View Solution
We are given the inequality: \[ |3x - 4| \leq 5. \]
By the definition of absolute value, we know that: \[ |A| \leq B implies -B \leq A \leq B. \]
Thus, we can rewrite the inequality as: \[ -5 \leq 3x - 4 \leq 5. \]
Step 1: Solve the inequality
Add 4 to all parts of the inequality to isolate the term with \( x \): \[ -5 + 4 \leq 3x \leq 5 + 4
-1 \leq 3x \leq 9. \]
Step 2: Divide by 3 to solve for \( x \) \[ \frac{-1}{3} \leq x \leq \frac{9}{3}
-\frac{1}{3} \leq x \leq 3. \]
Thus, the solution to the inequality is: \[ x \in \left[ -\frac{1}{3}, 3 \right]. \]
Therefore, the correct answer is option (A), \( \left[ -\frac{1}{3}, 3 \right] \).
Quick Tip: For inequalities involving absolute values, isolate the expression inside the absolute value, remove the absolute value, and then solve the resulting compound inequality. Remember to consider both the positive and negative cases.
Variance of 6, 7, 8, 9 is
View Solution
To calculate the variance of the numbers 6, 7, 8, 9, we use the formula for variance:
\[ \sigma^2 = \frac{1}{n} \sum_{i=1}^n (x_i - \mu)^2, \]
where \( \mu \) is the mean of the numbers and \( n \) is the number of observations.
Step 1: Calculate the mean \( \mu \)
The numbers are 6, 7, 8, and 9. First, find the mean: \[ \mu = \frac{6 + 7 + 8 + 9}{4} = \frac{30}{4} = 7.5. \]
Step 2: Calculate the squared differences from the mean
Now, we calculate the squared differences from the mean for each number: \[ (6 - 7.5)^2 = (-1.5)^2 = 2.25,
(7 - 7.5)^2 = (-0.5)^2 = 0.25,
(8 - 7.5)^2 = (0.5)^2 = 0.25,
(9 - 7.5)^2 = (1.5)^2 = 2.25.
\]
Step 3: Find the variance
The variance is the average of the squared differences: \[ \sigma^2 = \frac{2.25 + 0.25 + 0.25 + 2.25}{4} = \frac{5}{4} = 1.25. \]
Thus, the variance is \( \frac{5}{4} \). Therefore, the correct answer is option (E). Quick Tip: To calculate the variance of a set of numbers, first find the mean, then calculate the squared differences from the mean for each number, and finally find the average of these squared differences.
If \( f(x) = \frac{|x|}{1 + |x|}, \, x \in \mathbb{R}, \) then \( f'(-2) \) is equal to
View Solution
We are given that the function \( f(x) \) is defined as:
\[ f(x) = \frac{|x|}{1 + |x|} \]
Step 1: Differentiating the function
The derivative of \( f(x) \) depends on whether \( x \) is positive or negative, since the absolute value function changes its expression depending on the sign of \( x \).
- For \( x > 0 \), \( |x| = x \), so:
\[ f(x) = \frac{x}{1 + x} \]
The derivative of this is:
\[ f'(x) = \frac{(1+x) \cdot 1 - x \cdot 1}{(1+x)^2} = \frac{1}{(1+x)^2} \]
- For \( x < 0 \), \( |x| = -x \), so:
\[ f(x) = \frac{-x}{1 - x} \]
The derivative of this is:
\[ f'(x) = \frac{(1-x) \cdot (-1) - (-x) \cdot (-1)}{(1-x)^2} = \frac{-2x}{(1-x)^2} \]
Step 2: Finding \( f'(-2) \)
Since we are asked to find \( f'(-2) \), we use the derivative for \( x < 0 \):
\[ f'(-2) = \frac{-2(-2)}{(1 - (-2))^2} = \frac{4}{(1 + 2)^2} = \frac{4}{9} \]
Thus, the correct answer is \( \frac{-4}{9} \). Therefore, the correct answer is option (C). Quick Tip: When differentiating piecewise functions involving absolute values, break the function into two cases: one for positive values of \( x \) and one for negative values. Then apply the appropriate derivative formula for each case.





































.jpg?h=56&w=56&mode=stretch)
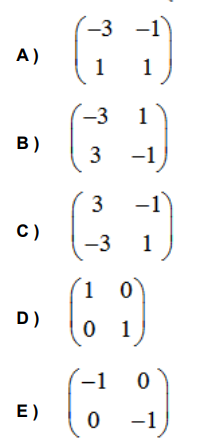

Comments