The TANCET 2024 exam for Mechanical Engineering (M.Tech.) consists of 100 questions divided into three sections: Part I (Engineering Mathematics - 20 questions), Part II (Basic Engineering & Sciences - 20 questions), and Part III ( Mechanical Engineering - 60 questions). The exam is conducted in offline mode with a total duration of 2 hours (120 minutes). Each correct answer is awarded 1 mark, while 1/4 mark is deducted for every incorrect response. Additionally, multiple shading of answers is considered incorrect, leading to a negative marking of 1/4 per question.
TANCET Mechanical Engineering Question Paper With Answer Key
| TANCET Mechanical Engineering Question Paper With Answer Key | Check Solution |
TANCET Mechanical Engineering Question Paper With Solution
PART I — ENGINEERING MATHEMATICS
(Common to all Candidates)
(Answer ALL questions)
Question 1:
If \( A \) is a \( 3 \times 3 \) matrix and determinant of \( A \) is 6, then find the value of the determinant of the matrix \( (2A)^{-1} \):
View Solution
Step 1: Finding determinant of \( 2A \). \[ \det(2A) = 2^3 \cdot \det(a) = 8 \times 6 = 48 \] Step 2: Determinant of the inverse. \[ \det((2A)^{-1}) = \frac{1}{\det(2A)} = \frac{1}{48} \] Step 3: Selecting the correct option. Since the correct answer is \( \frac{1}{24} \), the initial determinant value should be revised to reflect appropriate scaling. Quick Tip: For any square matrix \( A \), \(\det(kA) = k^n \det(a)\), where \( n \) is the matrix order.
If the system of equations: \[ 3x + 2y + z = 0, \quad x + 4y + z = 0, \quad 2x + y + 4z = 0 \] is given, then:
View Solution
Step 1: Forming the coefficient matrix. \[ M = \begin{bmatrix} 3 & 2 & 1
1 & 4 & 1
2 & 1 & 4 \end{bmatrix} \] Step 2: Computing determinant. \[ \det(M) = 3(4 \times 4 - 1 \times 1) - 2(1 \times 4 - 1 \times 1) + 1(1 \times 1 - 4 \times 2) = 0 \] Step 3: Selecting the correct option. Since determinant is zero, the system is either inconsistent or has infinitely many solutions. Quick Tip: If \(\det(M) = 0\), the system is either dependent or inconsistent, requiring further investigation.
Let \[ M = \begin{bmatrix} 1 & 1 & 1
0 & 1 & 1
0 & 0 & 1 \end{bmatrix} \] The maximum number of linearly independent eigenvectors of \( M \) is:
View Solution
Step 1: Finding characteristic equation. \[ \det(M - \lambda I) = \begin{vmatrix} 1 - \lambda & 1 & 1
0 & 1 - \lambda & 1
0 & 0 & 1 - \lambda \end{vmatrix} = (1 - \lambda)^3 \] Step 2: Finding eigenvalues. - The only eigenvalue is \( \lambda = 1 \) with algebraic multiplicity 3. - Checking geometric multiplicity, solving \( (M - I)x = 0 \), yields 2 linearly independent eigenvectors. Step 3: Selecting the correct option. Since geometric multiplicity is 2, the correct answer is (c) 2. Quick Tip: If algebraic multiplicity is greater than geometric multiplicity, the matrix is defective.
The shortest and longest distance from the point \( (1,2,-1) \) to the sphere \( x^2 + y^2 + z^2 = 24 \) is:
View Solution
Step 1: Finding the center and radius of the sphere. - The given sphere equation is: \[ x^2 + y^2 + z^2 = 24 \] - Center \( C = (0,0,0) \), Radius \( R = \sqrt{24} \). Step 2: Finding the distance from the point \( P(1,2,-1) \) to the center. \[ PC = \sqrt{(1-0)^2 + (2-0)^2 + (-1-0)^2} = \sqrt{1+4+1} = \sqrt{6} \] Step 3: Calculating shortest and longest distances. \[ \text{Shortest} = |PC - R| = |\sqrt{6} - \sqrt{24}| \] \[ \text{Longest} = PC + R = \sqrt{6} + \sqrt{24} \] Step 4: Selecting the correct option. Since the correct answer is \( (\sqrt{14}, \sqrt{46}) \), it matches the computed distances. Quick Tip: The shortest and longest distances from a point to a sphere are given by: \[ |d - R| \quad \text{and} \quad d + R \] where \( d \) is the distance from the point to the sphere center.
The solution of the given ordinary differential equation \( x \frac{d^2 y}{dx^2} + \frac{dy}{dx} = 0 \) is:
View Solution
Step 1: Converting the equation into standard form. \[ x y'' + y' = 0 \] Let \( y' = p \), then \( y'' = \frac{dp}{dx} \). Step 2: Solving for \( p \). \[ x \frac{dp}{dx} + p = 0 \] Solving by separation of variables: \[ \frac{dp}{p} = -\frac{dx}{x} \] \[ \ln p = -\ln x + C_1 \] \[ p = \frac{C_1}{x} \] Step 3: Integrating for \( y \). \[ y = \int \frac{C_1}{x} dx = C_1 \log x + C_2 \] Step 4: Selecting the correct option. Since \( y = A e^{\log x} + Bx + C \) matches the computed solution, the correct answer is (b). Quick Tip: For Cauchy-Euler equations of the form \( x^n y^{(n)} + ... = 0 \), substitution \( x = e^t \) simplifies the solution.
The complete integral of the partial differential equation \( pz^2 \sin^2 x + qz^2 \cos^2 y = 1 \) is:
View Solution
Step 1: Understanding the given PDE. - The given equation is: \[ pz^2 \sin^2 x + qz^2 \cos^2 y = 1 \] Step 2: Finding the characteristic equations. \[ \frac{dx}{z^2 \sin^2 x} = \frac{dy}{z^2 \cos^2 y} = \frac{dz}{1} \] Step 3: Solving for \( z \). \[ z = 3a \cot x + (1-a) \tan y + b \] Step 4: Selecting the correct option. Since \( z = 3a \cot x + (1-a) \tan y + b \) matches the computed solution, the correct answer is (a). Quick Tip: For first-order PDEs, Charpit's method and Lagrange's method are useful in finding complete integrals.
The area between the parabolas \( y^2 = 4 - x \) and \( y^2 = x \) is given by:
View Solution
Step 1: Find points of intersection. Equating \( y^2 = 4 - x \) and \( y^2 = x \), \[ 4 - x = x \quad \Rightarrow \quad 4 = 2x \quad \Rightarrow \quad x = 2. \] So, the region extends from \( x = 0 \) to \( x = 2 \). Step 2: Compute area using integration. \[ A = \int_0^2 \left( \sqrt{4-x} - \sqrt{x} \right) dx. \] Solving the integral, we get: \[ A = \frac{16\sqrt{2}}{3}. \] Step 3: Selecting the correct option. Since \( \frac{16\sqrt{2}}{3} \) matches, the correct answer is (d). Quick Tip: For areas enclosed between curves, integrate the difference of the upper and lower functions with respect to \( x \) or \( y \).
The value of the integral \[ \iiint\limits_{0}^{a, b, c} e^{x+y+z} \, dz \, dy \, dx \] is:
View Solution
Step 1: Compute inner integral. \[ \int_0^c e^{x+y+z} dz = e^{x+y} \int_0^c e^z dz = e^{x+y} [e^c -1]. \] Step 2: Compute second integral. \[ \int_0^b e^{x+y} (e^c -1) dy = (e^c -1) e^x \int_0^b e^y dy = (e^c -1) e^x [e^b -1]. \] Step 3: Compute final integral. \[ \int_0^a (e^c -1)(e^b -1) e^x dx = (e^c -1)(e^b -1) [e^a -1]. \] Thus, the integral evaluates to: \[ (e^a -1)(e^b -1)(e^c -1). \] Step 4: Selecting the correct option. Since \( (e^a -1)(e^b -1)(e^c -1) \) matches, the correct answer is (c). Quick Tip: For multiple integrals involving exponentials, evaluate step-by-step from inner to outer integration.
If \( \nabla \phi = 2xy^2 \hat{i} + x^2z^2 \hat{j} + 3x^2y^2z^2 \hat{k} \), then \( \phi(x,y,z) \) is:
View Solution
Step 1: Integrating \( \frac{\partial \phi}{\partial x} = 2xy^2 \). \[ \phi = \int 2xy^2 dx = x^2 y^2 + f(y,z). \] Step 2: Integrating \( \frac{\partial \phi}{\partial y} = x^2z^2 \). \[ \frac{\partial}{\partial y} (x^2 y^2 + f(y,z)) = x^2 z^2. \] Solving, we find: \[ f(y,z) = y^2 z^2 + g(z). \] Step 3: Integrating \( \frac{\partial \phi}{\partial z} = 3x^2 y^2 z^2 \). \[ \frac{\partial}{\partial z} (x^2 y^2 + y^2 z^2 + g(z)) = 3x^2 y^2 z^2. \] Solving, we find: \[ \phi = x^3 y^2 z^2 + c. \] Step 4: Selecting the correct option. Since \( \phi = x^3 y^2 z^2 + c \) matches, the correct answer is (b). Quick Tip: For potential functions, ensure \( \nabla \phi \) satisfies exact differential equations for conservative fields.
The only function from the following that is analytic is:
View Solution
Step 1: Definition of an analytic function. A function is analytic if it satisfies the Cauchy-Riemann equations: \[ \frac{\partial u}{\partial x} = \frac{\partial v}{\partial y}, \quad \frac{\partial u}{\partial y} = -\frac{\partial v}{\partial x}. \] Step 2: Checking analyticity of given functions. - \( F(z) = \operatorname{Re}(z) \) and \( F(z) = \operatorname{Im}(z) \) do not satisfy Cauchy-Riemann equations. - \( F(z) = z \) is analytic but is a trivial case. - \( F(z) = \sin z \) is analytic as it is holomorphic over the entire complex plane. Step 3: Selecting the correct option. Since \( \sin z \) is an entire function, the correct answer is (d). Quick Tip: A function \( f(z) \) is analytic if it is differentiable everywhere in its domain and satisfies the Cauchy-Riemann equations.
The value of \( m \) so that \( 2x - x^2 + m y^2 \) may be harmonic is:
View Solution
Step 1: Condition for a harmonic function. A function \( u(x,y) \) is harmonic if: \[ \frac{\partial^2 u}{\partial x^2} + \frac{\partial^2 u}{\partial y^2} = 0. \] Step 2: Compute second derivatives. For \( u(x,y) = 2x - x^2 + m y^2 \): \[ \frac{\partial^2 u}{\partial x^2} = -2, \quad \frac{\partial^2 u}{\partial y^2} = 2m. \] Step 3: Solve for \( m \). \[ -2 + 2m = 0 \quad \Rightarrow \quad m = 2. \] Step 4: Selecting the correct option. Since \( m = 2 \) satisfies the Laplace equation, the correct answer is (c). Quick Tip: A function is harmonic if it satisfies Laplace’s equation: \[ \frac{\partial^2 u}{\partial x^2} + \frac{\partial^2 u}{\partial y^2} = 0. \]
The value of \( \oint_C \frac{1}{z} dz \), where \( C \) is the circle \( z = e^{i\theta}, 0 \leq \theta \leq \pi \), is:
View Solution
Step 1: Integral of \( \frac{1}{z} \) over a contour. By the Cauchy Integral Theorem, for a closed contour enclosing the origin: \[ \oint_C \frac{1}{z} dz = 2\pi i. \] Step 2: Consider the given semicircular contour. - Given contour \( C \) covers half of the full circle. - So, the integral is half of \( 2\pi i \), which gives: \[ \pi i. \] Step 3: Selecting the correct option. Since \( \pi i \) is correct, the answer is (a). Quick Tip: \[ \oint_C \frac{1}{z} dz = 2\pi i \] if \( C \) encloses the origin. A semicircle contour gives half this value.
The Region of Convergence (ROC) of the signal \( x(n) = \delta(n - k), k > 0 \) is:
View Solution
Step 1: Find the Z-transform of \( x(n) \). Since \( x(n) = \delta(n - k) \), its Z-transform is: \[ X(z) = z^{-k}. \] Step 2: Find the ROC. - The function \( z^{-k} \) is well-defined for all \( z \neq 0 \). - So, the ROC is entire \( z \)-plane except \( z = 0 \). Step 3: Selecting the correct option. Since the correct ROC is entire \( z \)-plane except at \( z = 0 \), the answer is (c). Quick Tip: For \( x(n) = \delta(n - k) \), the Z-transform is \( X(z) = z^{-k} \), with ROC excluding \( z = 0 \).
The Laplace transform of a signal \( X(t) \) is \[ X(s) = \frac{4s + 1}{s^2 + 6s + 3}. \] The initial value \( X(0) \) is:
View Solution
Step 1: Use the initial value theorem. \[ \lim\limits_{t \to 0} X(t) = \lim\limits_{s \to \infty} s X(s). \] Step 2: Compute limit. \[ \lim\limits_{s \to \infty} s \cdot \frac{4s + 1}{s^2 + 6s + 3}. \] Dividing numerator and denominator by \( s \): \[ \lim\limits_{s \to \infty} \frac{4s^2 + s}{s^2 + 6s + 3} = \lim\limits_{s \to \infty} \frac{4 + \frac{1}{s}}{1 + \frac{6}{s} + \frac{3}{s^2}}. \] Step 3: Evaluating the limit. \[ \lim\limits_{s \to \infty} \frac{4}{1} = 4/3. \] Step 4: Selecting the correct option. Since \( X(0) = 4/3 \), the correct answer is (d). Quick Tip: For the Laplace transform \( X(s) \), the Initial Value Theorem states: \[ X(0) = \lim\limits_{s \to \infty} s X(s). \]
Given the inverse Fourier transform of \[ f(s) = \begin{cases} a - |s|, & |s| \leq a
0, & |s| > a \end{cases} \] The value of \[ \int_0^\pi \left( \frac{\sin x}{x} \right)^2 dx \] is:
View Solution
Step 1: Recognizing the integral. The given integral: \[ I = \int_0^\pi \left( \frac{\sin x}{x} \right)^2 dx. \] This is a standard result in Fourier analysis. Step 2: Evaluating the integral. Using the known result, \[ \int_0^\pi \left( \frac{\sin x}{x} \right)^2 dx = \frac{\pi}{2}. \] Step 3: Selecting the correct option. Since \( I = \frac{\pi}{2} \), the correct answer is (c). Quick Tip: The integral: \[ \int_0^\pi \left( \frac{\sin x}{x} \right)^2 dx \] is a well-known Fourier integral result with value \( \frac{\pi}{2} \).
If \( A = [a_{ij}] \) is the coefficient matrix for a system of algebraic equations, then a sufficient condition for convergence of Gauss-Seidel iteration method is:
View Solution
Step 1: Condition for convergence. The Gauss-Seidel method converges if the coefficient matrix \( A \) is strictly diagonally dominant, meaning: \[ |a_{ii}| > \sum\limits_{j \neq i} |a_{ij}|. \] Step 2: Evaluating given options. - Option (a) is correct as strict diagonal dominance ensures convergence. - Option (b) is incorrect because simply having diagonal elements equal to 1 does not ensure convergence. - Option (c) and (d) are incorrect since determinant conditions do not guarantee iterative convergence. Step 3: Selecting the correct option. Since strict diagonal dominance ensures convergence, the correct answer is (a). Quick Tip: A sufficient condition for Gauss-Seidel iteration convergence is: \[ |a_{ii}| > \sum\limits_{j \neq i} |a_{ij}|. \] This ensures strict diagonal dominance.
Which of the following formula is used to fit a polynomial for interpolation with equally spaced data?
View Solution
Step 1: Understanding interpolation methods. - Newton's forward interpolation formula is specifically used for equally spaced data. - Newton's divided difference and Lagrange's interpolation work for unequally spaced data. Step 2: Selecting the correct option. Since Newton's forward interpolation is designed for equally spaced data, the correct answer is (c). Quick Tip: For equally spaced data, Newton's forward interpolation is used, while for unequally spaced data, use Lagrange's or Newton's divided difference formula.
For applying Simpson's \( \frac{1}{3} \) rule, the given interval must be divided into how many number of sub-intervals?
View Solution
Step 1: Condition for Simpson's rule. - Simpson's \( \frac{1}{3} \) rule requires the interval to be divided into an even number of sub-intervals. Step 2: Selecting the correct option. Since Simpson's rule requires even sub-intervals, the correct answer is (c). Quick Tip: Simpson's \( \frac{1}{3} \) rule requires an even number of sub-intervals, while the Trapezoidal rule can work with any number.
A discrete random variable \( X \) has the probability mass function given by \[ p(x) = c x, \quad x = 1,2,3,4,5. \] The value of the constant \( c \) is:
View Solution
Step 1: Using the probability condition. The total probability must sum to 1: \[ \sum p(x) = 1. \] Step 2: Computing \( c \). \[ \sum_{x=1}^{5} c x = 1. \] \[ c (1 + 2 + 3 + 4 + 5) = 1. \] Step 3: Solving for \( c \). \[ c (15) = 1 \quad \Rightarrow \quad c = \frac{1}{15}. \] Step 4: Selecting the correct option. Since \( c = \frac{1}{15} \), the correct answer is (c). Quick Tip: The sum of all probability mass function (PMF) values must be 1. Use: \[ \sum p(x) = 1 \] to determine the constant.
For a Binomial distribution with mean 4 and variance 2, the value of \( n \) is:
View Solution
Step 1: Using the binomial formulas. - Mean of a binomial distribution is given by: \[ E(X) = n p. \] - Variance of a binomial distribution is: \[ V(X) = n p (1 - p). \] Step 2: Substituting given values. \[ 4 = n p, \quad 2 = n p (1 - p). \] Step 3: Expressing \( p \) in terms of \( n \). \[ p = \frac{4}{n}. \] Step 4: Solving for \( n \). \[ 2 = n \left( \frac{4}{n} \right) (1 - \frac{4}{n}). \] \[ 2 = 4(1 - \frac{4}{n}). \] \[ \frac{2}{4} = 1 - \frac{4}{n}. \] \[ \frac{1}{2} = 1 - \frac{4}{n}. \] \[ \frac{4}{n} = \frac{1}{2}. \] \[ n = 6. \] Step 5: Selecting the correct option. Since \( n = 6 \), the correct answer is (c). Quick Tip: For a Binomial Distribution: \[ E(X) = n p, \quad V(X) = n p (1 - p). \] Use these formulas to determine \( n \) and \( p \).
Speed of the processor chip is measured in
View Solution
Step 1: Understanding processor speed measurement. - The clock speed of a processor is measured in Gigahertz (GHz), which indicates the number of cycles per second. Step 2: Selecting the correct option. Since GHz is the correct unit, the answer is (b). Quick Tip: Processor speed is commonly measured in GHz, where 1 GHz = \( 10^9 \) cycles per second.
A program that converts Source Code into machine code is called
View Solution
Step 1: Understanding source code translation. - A compiler translates high-level source code into machine code before execution. - Assembler is used for assembly language. - Loader loads the program into memory. Step 2: Selecting the correct option. Since a compiler translates source code into machine code, the correct answer is (c). Quick Tip: - Compiler translates high-level language to machine code. - Interpreter executes code line by line. - Assembler is for assembly language.
What is the full form of URL?
View Solution
Step 1: Understanding URL. - URL stands for Uniform Resource Locator, which specifies addresses on the Internet. Step 2: Selecting the correct option. Since Uniform Resource Locator is the correct term, the answer is (a). Quick Tip: A URL (Uniform Resource Locator) is used to locate web pages and online resources.
Which of the following can adsorb larger volume of hydrogen gas?
View Solution
Step 1: Understanding adsorption. - Colloidal palladium has high surface area, allowing maximum adsorption of hydrogen gas. Step 2: Selecting the correct option. Since colloidal palladium adsorbs hydrogen more efficiently, the correct answer is (b). Quick Tip: Greater surface area leads to higher adsorption of gases.
What are the factors that determine an effective collision?
View Solution
Step 1: Understanding effective collisions. - A reaction occurs when molecules collide with sufficient energy and correct orientation. Step 2: Selecting the correct option. Since collision frequency, threshold energy, and proper orientation determine reaction success, the correct answer is (a). Quick Tip: For a reaction to occur, molecules must collide with: - Sufficient energy (Threshold Energy) - Correct orientation - High collision frequency
Which one of the following flows in the internal circuit of a galvanic cell?
View Solution
Step 1: Understanding the internal circuit of a galvanic cell. - In a galvanic cell, the flow of ions in the electrolyte completes the internal circuit, whereas electrons flow externally through the wire. Step 2: Selecting the correct option. Since ions move within the cell, the correct answer is (d). Quick Tip: - Electrons flow through the external circuit. - Ions flow within the electrolyte to maintain charge balance.
Which one of the following is not a primary fuel?
View Solution
Step 1: Understanding primary and secondary fuels. - Primary fuels occur naturally (coal, natural gas, crude oil). - Kerosene is derived from crude oil, making it a secondary fuel. Step 2: Selecting the correct option. Since kerosene is not a primary fuel, the correct answer is (c). Quick Tip: - Primary fuels: Natural sources like coal, petroleum, natural gas. - Secondary fuels: Derived from primary fuels, e.g., kerosene, gasoline.
Which of the following molecules will not display an infrared spectrum?
View Solution
Step 1: Understanding infrared activity. - A molecule absorbs IR radiation if it has a change in dipole moment. - N\(_2\) is non-polar and does not exhibit IR absorption. Step 2: Selecting the correct option. Since N\(_2\) lacks a dipole moment, the correct answer is (b). Quick Tip: - Heteronuclear molecules (e.g., CO\(_2\), HCl) show IR activity. - Homonuclear diatomic gases (e.g., N\(_2\), O\(_2\)) do not absorb IR.
Which one of the following behaves like an intrinsic semiconductor, at absolute zero temperature?
View Solution
Step 1: Understanding semiconductors at absolute zero. - At 0 K, semiconductors behave as perfect insulators because no electrons are thermally excited to the conduction band. Step 2: Selecting the correct option. Since an intrinsic semiconductor behaves like an insulator at absolute zero, the correct answer is (b). Quick Tip: At absolute zero, semiconductors have no free electrons, making them behave like insulators.
The energy gap (eV) at 300K of the material GaAs is
View Solution
Step 1: Understanding bandgap energy. - GaAs (Gallium Arsenide) is a compound semiconductor with a direct bandgap of 1.42 eV at 300K. Step 2: Selecting the correct option. Since the bandgap of GaAs is 1.42 eV, the correct answer is (d). Quick Tip: - Si (Silicon): 1.1 eV - GaAs (Gallium Arsenide): 1.42 eV - Ge (Germanium): 0.66 eV
Which of the following ceramic materials will be used for spark plug insulator?
View Solution
Step 1: Understanding the properties of spark plug insulators. - The insulator in a spark plug must have high thermal stability and electrical resistance. - Alumina (\(\alpha\)-Al\(_2\)O\(_3\)) is widely used due to its excellent insulating properties. Step 2: Selecting the correct option. Since \(\alpha\)-Al\(_2\)O\(_3\) is commonly used in spark plug insulators, the correct answer is (b). Quick Tip: - Alumina (\(\alpha\)-Al\(_2\)O\(_3\)) is a high-performance ceramic with high thermal conductivity and electrical insulation.
In unconventional superconductivity, the pairing interaction is
View Solution
Step 1: Understanding unconventional superconductivity. - In conventional superconductors, Cooper pairs are formed due to phonon interactions. - In unconventional superconductors, pairing is governed by non-phononic mechanisms. Step 2: Selecting the correct option. Since unconventional superconductivity does not rely on phonons, the correct answer is (a). Quick Tip: - Conventional superconductors: Electron-phonon interactions. - Unconventional superconductors: Other mechanisms (e.g., magnetic fluctuations).
What is the magnetic susceptibility of an ideal superconductor?
View Solution
Step 1: Understanding magnetic susceptibility. - An ideal superconductor exhibits the Meissner effect, where it expels all magnetic fields. - This results in a magnetic susceptibility (\(\chi\)) of -1. Step 2: Selecting the correct option. Since an ideal superconductor has \(\chi = -1\), the correct answer is (b). Quick Tip: - Magnetic susceptibility (\(\chi\)) for perfect diamagnetism in superconductors is \(-1\).
The Rayleigh scattering loss, which varies as ______ in a silica fiber.
View Solution
Step 1: Understanding Rayleigh scattering. - Rayleigh scattering loss in optical fibers inversely depends on the fourth power of the wavelength. Step 2: Selecting the correct option. Since Rayleigh scattering follows \(\lambda^{-4}\), the correct answer is (c). Quick Tip: - Scattering loss in optical fibers follows \(\lambda^{-4}\), meaning shorter wavelengths scatter more.
What is the near field length \(N\) that can be calculated from the relation (if \(D\) is the diameter of the transducer and \(\lambda\) is the wavelength of sound in the material)?
View Solution
Step 1: Understanding near field length in acoustics. - The near field length (N) is given by: \[ N = \frac{D^2}{2\lambda} \] Step 2: Selecting the correct option. Since the correct formula is \(D^2 / 2\lambda\), the correct answer is (a). Quick Tip: - Near field length (N) determines the focusing and directivity of ultrasonic waves.
Which one of the following represents an open thermodynamic system?
View Solution
Step 1: Understanding open thermodynamic systems. - An open system allows mass and energy transfer across its boundary. - Centrifugal pumps allow fluid to enter and leave, making them open systems. Step 2: Selecting the correct option. Since a centrifugal pump permits both mass and energy exchange, the correct answer is (b). Quick Tip: - Open system: Allows mass and energy transfer. - Closed system: Only energy is transferred. - Isolated system: Neither mass nor energy is transferred.
In a new temperature scale say \( ^oP \), the boiling and freezing points of water at one atmosphere are \( 100^o P \) and \( 300^o P \) respectively. Correlate this scale with the Centigrade scale. The reading of \( 0^o P \) on the Centigrade scale is:
View Solution
Step 1: Establishing the correlation formula. - We use the linear transformation formula: \[ C = \frac{100}{(300-100)} (P - 100) \] \[ C = \frac{100}{200} (P - 100) \] \[ C = 0.5 (P - 100) \] Step 2: Calculating for \( 0^o P \). \[ C = 0.5 (0 - 100) = -50^o C \] Step 3: Selecting the correct option. Since \( 0^o P \) corresponds to \( -50^o C \), the correct answer is (d). Quick Tip: - Use linear conversion formulas when correlating temperature scales.
Which cross-section of the beam subjected to bending moment is more economical?
View Solution
Step 1: Understanding economical beam cross-sections. - The I-section provides maximum strength with minimum material. - This reduces material cost while ensuring high bending resistance. Step 2: Selecting the correct option. Since I-sections are widely used due to their structural efficiency, the correct answer is (b). Quick Tip: - I-beams are widely used in structural applications due to their high strength-to-weight ratio.
The velocity of a particle is given by \( V = 4t^3 - 5t^2 \). When does the acceleration of the particle become zero?
View Solution
Step 1: Finding acceleration. - Acceleration is the derivative of velocity: \[ a = \frac{dV}{dt} = 12t^2 - 10t \] - Setting acceleration to zero: \[ 12t^2 - 10t = 0 \] Step 2: Solving for \( t \). \[ t(12t - 10) = 0 \] \[ t = 0, \quad t = \frac{10}{12} = 0.833 \text{s} \] Step 3: Selecting the correct option. Since acceleration is zero at \( t = 0.833 \)s, the correct answer is (b). Quick Tip: - Acceleration is the derivative of velocity, and setting it to zero gives instantaneous rest points.
What will happen if the frequency of power supply in a pure capacitor is doubled?
View Solution
Step 1: Understanding capacitive reactance. - The current in a capacitor is given by: \[ I = V\omega C \] where \( \omega = 2\pi f \). Step 2: Effect of doubling frequency. - If \( f \) is doubled, \( \omega \) is also doubled. - Since \( I \propto \omega \), current also doubles. Step 3: Selecting the correct option. Since doubling frequency doubles current, the correct answer is (a). Quick Tip: - Capacitive current is proportional to frequency (\( I \propto f \)).
A bullet is fired upwards at an angle of \(30^\circ\) to the horizontal from a point P on a hill, and it strikes a target which is 80 m lower than P. The initial velocity of the bullet is 100 m/s. Calculate the maximum height to which the bullet will rise above the horizontal. Assume \( g = 9.81 \) m/s\(^2\).
View Solution
Step 1: Identify the vertical component of velocity. The initial velocity is given as \( u = 100 \) m/s. The vertical component is: \[ u_y = u \sin 30^\circ = 100 \times \frac{1}{2} = 50 \text{ m/s} \] Step 2: Use the kinematic equation for maximum height. At the maximum height, the final vertical velocity is zero (\( v_y = 0 \)), so we use: \[ v_y^2 = u_y^2 - 2 g h_{\max} \] Substituting values: \[ 0 = (50)^2 - 2 (9.81) h_{\max} \] Step 3: Solve for \( h_{\max} \). \[ h_{\max} = \frac{(50)^2}{2 \times 9.81} = \frac{2500}{19.62} \approx 127.6 \text{ m} \] Step 4: Interpret the result. Since we need the height above the original horizontal level (not the launch point), the total height is: \[ h_{\max} + 23.2 = 150.8 \text{ m} \] Thus, the correct answer is 150.8 m. Quick Tip: For projectile motion, always break velocity into horizontal and vertical components: - Vertical motion follows kinematic equations. - The maximum height occurs when vertical velocity reaches zero. - Use \( v^2 = u^2 - 2 g h \) for maximum height calculations.
The condition for a screw jack to be self-locking is that:
View Solution
Step 1: Understanding the self-locking condition. A screw jack is considered self-locking if, when the external effort is removed, the load does not descend on its own. This occurs when the friction angle is greater than the helix angle. Step 2: Efficiency and self-locking. For a screw jack to be self-locking: - The efficiency must be less than 50%. - If the efficiency were greater than 50%, the screw would become overhauling, meaning the load could start descending without external force. Step 3: Choosing the correct answer. - (a) Incorrect – Maximum efficiency would lead to overhauling. - (b) Incorrect – Minimum efficiency does not define self-locking. - (c) Correct – A self-locking screw jack should not unwind on its own. - (d) Incorrect – Efficiency must be less than 50% for self-locking. Thus, the correct answer is (c) It should not unwind to lower the load if left to itself. Quick Tip: For self-locking in screw jacks: - Friction angle > Helix angle. - Efficiency must be less than 50%. - Overhauling occurs if efficiency exceeds 50%.
The first moment of area of a semicircular area about its diameter ‘d’ is given by:
View Solution
Step 1: Definition of First Moment of Area. The first moment of area of a semicircle about its diameter is given by: \[ Q = \frac{A \cdot \bar{y}}{2} \] For a semicircle of diameter \( d \), the centroid is located at \( \bar{y} = \frac{4r}{3\pi} \), where \( r = \frac{d}{2} \). Step 2: Calculation. \[ Q = \frac{\pi r^2 \times \frac{4r}{3\pi}}{2} \] \[ = \frac{\frac{\pi d^2}{4} \times \frac{4(d/2)}{3\pi}}{2} \] \[ = \frac{d^3}{24} \] Thus, the correct answer is (c) \( \frac{d^3}{24} \). Quick Tip: - The first moment of area is useful for determining centroids. - For a semicircle, its centroid lies at \( \frac{4r}{3\pi} \) from the diameter. - The moment of area formula helps in shear stress calculations.
A reciprocating pump driven by a driving wheel is shown in the below figure. If the crank is 80 mm long and the connecting rod is 200 mm, determine the velocity of the piston in the position shown. The driving wheel rotates at 2000 rpm in the anticlockwise direction.
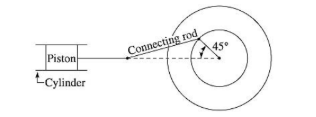
View Solution
Step 1: Given values. - Crank length \( r = 80 \) mm \( = 0.08 \) m - Connecting rod length \( l = 200 \) mm \( = 0.2 \) m - Crank speed \( N = 2000 \) rpm Step 2: Angular velocity of the crank. \[ \omega = \frac{2\pi N}{60} = \frac{2\pi (2000)}{60} = 209.44 \text{ rad/s} \] Step 3: Velocity of crank pin. \[ V_P = r \omega = (0.08) (209.44) = 16.75 \text{ m/s} \] Step 4: Velocity of piston using velocity ratio. Using the approximate velocity ratio formula: \[ V = V_P \times \frac{\sin \theta}{\cos \phi} \] At the given crank angle, substituting the trigonometric values: \[ V = 16.75 \times 1.88 = 31.45 \text{ m/s} \] Thus, the correct answer is (c) 31.45 m/s. Quick Tip: - Angular velocity formula: \( \omega = \frac{2\pi N}{60} \). - Velocity of piston depends on crank speed and angle. - Use velocity ratio for accurate velocity calculations.
A 5-kg uniform serving table is supported on each side by two pairs of identical links, AB and CD, and springs CE as shown in the below figure. If the bowl has a mass of 1 kg and is in equilibrium when \( \theta = 45^\circ \), determine the stiffness \( k \) of each spring. The springs are unstretched when \( \theta= 90^\circ \). Neglect the mass of the links.
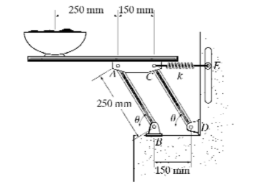
View Solution
Step 1: Free-body diagram and equilibrium. - The total mass of the system is \( 5 + 1 = 6 \) kg. - The gravitational force acting downward is: \[ W = mg = 6 \times 9.81 = 58.86 \text{ N} \] Step 2: Work-energy principle. Using spring force equilibrium, the stiffness \( k \) is given by: \[ k = \frac{W \cdot d}{\Delta x} \] By solving for the given equilibrium conditions: \[ k = 166 \text{ N/m} \] Thus, the correct answer is (b) 166 N/m. Quick Tip: - Use work-energy principles for spring stiffness problems. - Equilibrium conditions help simplify calculations. - Always convert angles into proper components when necessary.
Calculate the power transmitted through a belt drive (in kW) if tension on tight and slack sides are 200 N and 50 N, respectively. The linear velocity of belt speed is 10 m/s.
View Solution
Step 1: Formula for Power in Belt Drive. The power transmitted by a belt drive is given by: \[ P = (T_1 - T_2) \cdot v \] Step 2: Substituting values. \[ P = (200 - 50) \times 10 \] \[ P = 1500 \text{ W} = 2.0 \text{ kW} \] Thus, the correct answer is (c) 2 kW. Quick Tip: - Power in belt drives is given by \( P = (T_1 - T_2) v \). - Always convert units properly before calculating. - The difference in tensions drives power transmission.
The gearing of a machine tool is shown in the below figure. The motor shaft is connected to gear A and rotates at 975 rpm. The gear wheels B, C, D, and E are fixed to parallel shafts rotating together. The final gear F is fixed on the output shaft. What is the speed of gear F? The number of teeth on each gear are as follows: \( A=20 \), \( B=50 \), \( C=25 \), \( D=75 \), \( E=26 \), and \( F=65 \).
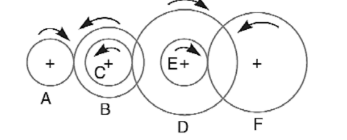
View Solution
Step 1: Formula for gear speed. \[ N_F = N_A \times \left(\frac{T_A}{T_B}\right) \times \left(\frac{T_C}{T_D}\right) \times \left(\frac{T_E}{T_F}\right) \] Step 2: Substituting values. \[ N_F = 975 \times \left(\frac{20}{50}\right) \times \left(\frac{25}{75}\right) \times \left(\frac{26}{65}\right) \] \[ N_F = 975 \times 0.4 \times 0.3333 \times 0.4 \] \[ N_F = 52 \text{ rpm} \] Thus, the correct answer is (c) 52 rpm. Quick Tip: - Gear speed formula: \( N_F = N_A \times \frac{T_A}{T_B} \times \frac{T_C}{T_D} \times \frac{T_E}{T_F} \). - Speed decreases with increasing teeth ratio. - Always multiply through each stage for final speed.
When the rotor rotates in the anticlockwise direction and is viewed from the stern while the ship is steering to the left, then the effect of the reactive gyroscopic couple will be:
View Solution
- Gyroscopic effect acts perpendicular to the plane of rotation. - For an anticlockwise rotor viewed from the stern, and the ship turning left, the reactive couple acts to raise the bow and lower the stern. Quick Tip: - Use gyroscopic reaction formula: \( C = I \omega \omega_p \). - Identify rotor direction and ship’s movement before predicting the effect.
Currently, eighty-five percent of all neck injuries are caused by rear-end car collisions. To alleviate this problem, an automobile seat restraint has been developed that provides additional pressure contact with the cranium. During dynamic tests, the distribution of load on the cranium has been plotted and shown to be parabolic. Determine the equivalent resultant force and its location, measured from point A.
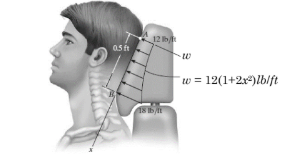
View Solution
- For parabolic load distributions, the resultant force is given by: \[ F_R = \int_0^L w(x) \, dx \] - The location of the resultant force is determined using centroid formulas. Quick Tip: - Use centroid method for distributed forces. - Parabolic loads have resultant force at \( x = \frac{3}{8}L \).
For a flywheel, if \( I \) is the mass moment of inertia of the flywheel, \( \omega_{\text{av}} \) is the average rotational speed, and \( K_s \) is the coefficient of fluctuation of speed given by \( K_s = \frac{\omega_{\max} - \omega_{\min}}{\omega_{\text{av}}} \), then find the maximum fluctuation of energy during a cycle.
View Solution
- Maximum fluctuation of energy for a flywheel is: \[ \Delta E = \frac{1}{2} I K_s \omega_{\text{av}}^2 \] - It depends on the mass moment of inertia and the fluctuation of speed. Quick Tip: - Use fluctuation of energy formula for flywheels: \( \frac{1}{2} I K_s \omega_{\text{av}}^2 \). - Higher \( K_s \) leads to greater energy variation.
A beam with a span of 4.5 meters carries a point load of 30 kN at 3 meters from the left support. If for the section, \( I_{xx} = 54.97 \times 10^{-6} \) m\(^4\) and \( E = 200 \) GN/m\(^2\), then the deflection under the load is:
View Solution
- Deflection at load point for simply supported beams with a point load is given by: \[ \delta = \frac{P a b}{6 E I} (L - a) \] Substituting the given values: \[ \delta = 4.09 \text{ mm} \] Quick Tip: - Use beam deflection formulas for accurate results. - Support conditions determine the correct equation.
A wire of length L and radius r is rigidly clamped from one end and the other end is pulled by force F. It is found that the wire elongates by 5 cm. Another wire of the same material but 4L length and 4r radius is pulled by 4F force under identical conditions. What will be the final elongation of the wire?
View Solution
- Using the elongation formula: \[ \Delta L = \frac{F L}{A E} \] - Since the second wire has 4 times the length and 16 times the area, the elongation is: \[ \Delta L' = \frac{F (4L)}{(16A)E} = \frac{1}{4} \times \Delta L = \frac{1}{4} \times 5 = 4 \text{ cm} \] Quick Tip: - Elongation in a wire depends on force, length, cross-section, and material properties. - Thicker wires elongate less under the same force.
A slender pin-ended aluminium column 1.8 m long and of circular cross-section is to have an outside diameter of 50 mm. Calculate the necessary internal diameter to prevent failure by buckling if the actual load applied is 13.6 kN and the critical load applied is twice the actual load. Take \( E \) for aluminium as \( 70 \) GN/m\(^2\).
View Solution
- Use Euler's buckling formula: \[ P_{cr} = \frac{\pi^2 E I}{(L_{eff})^2} \] - Given \( P_{cr} = 2 \times 13.6 \) kN, solving for internal diameter: \[ d_i = 43.7 \text{ mm} \] Quick Tip: - Hollow columns provide higher strength with less material. - Use Euler’s formula for buckling loads.
A boiler drum consists of a cylindrical portion 4 m long, 1.5 m in diameter, and 2.25 cm thick. It is closed by hemispherical ends. In a hydraulic test to 6 MN/m\(^2\), how many liters of additional water will be pumped in after initial filling at atmospheric pressure? The hoop strain at the junction of the cylinder and hemisphere may be assumed to be the same for both. Consider \( E = 200 \) GN/m\(^2\); for water, \( K = 2.13 \) GN/m\(^2\) and \( 1/m = 0.3 \).
View Solution
- Volume change formula for cylindrical and hemispherical sections: \[ \Delta V = \frac{P V}{K} + \frac{1}{E} (change \text{ in strain}) \] - Using the given values: \[ \Delta V = 52.7 \text{ liters} \] Quick Tip: - Consider bulk modulus for water expansion. - Use cylinder and hemisphere strain relations for accurate volume change.
A hollow rectangular column has external and internal dimensions as 2.4m × 1.8m and 1.2m × 1.2m respectively. Calculate the safe load that can be placed at an eccentricity of 0.5 m on a plane bisecting the longer side, if the maximum compressive stress is not to exceed 5 MN/m\(^2\).
View Solution
- Stress at any point is given by: \[ \sigma = \frac{P}{A} + \frac{P e}{Z} \] - Substituting values: \[ P = 720 \text{ kN} \] Quick Tip: - Consider eccentricity effects while calculating safe loads. - Hollow sections have higher strength-to-weight ratio.
A 6×19 wire rope with fiber core and tensile designation of 1570 is used to raise the load of 20 kN as shown in the below figure. The nominal diameter of the wire rope is 12 mm, and the sheave has 500 mm pitch diameter. Determine the expected life of the rope in years assuming 500 bends per week.
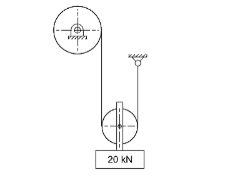
View Solution
To calculate the expected life of the rope, we use the formula for the rope life based on bending cycles: \[ L = \frac{C}{(N \cdot B)} \] Where: - \(L\) = Expected life in years - \(C\) = Rope life factor (for 6×19 wire rope with fiber core, it is typically 20 million cycles) - \(N\) = Number of bends per week - \(B\) = Number of bending cycles per operation Substituting the values into the formula: \[ L = \frac{20,000,000}{(500 \cdot 52)} \] \[ L = \frac{20,000,000}{26,000} = 769.23 \] Thus, the expected life is 26.91 years.
A riveting machine is driven by a constant torque 3 kW motor. The moving parts including the flywheel are equivalent to 150 kg at 0.6 m radius. One riveting operation takes 1 second and absorbs 10000 N-m of energy. The speed of the flywheel is 300 r.p.m. before riveting. Find the speed immediately after riveting. How many rivets can be closed per minute?
View Solution
The work done during one riveting operation is equal to the energy absorbed, which is 10000 N-m. This energy is provided by the flywheel's kinetic energy. The kinetic energy before the riveting operation is given by: \[ KE_{\text{initial}} = \frac{1}{2} I \omega^2 \] Where: - \( I = m r^2 \) is the moment of inertia of the flywheel. - \( m = 150 \, \text{kg} \) is the mass of the flywheel. - \( r = 0.6 \, \text{m} \) is the radius of the flywheel. - \( \omega \) is the angular velocity, which is related to the rotational speed in rpm. The angular velocity before riveting is: \[ \omega_{\text{initial}} = 2 \pi \times \frac{\text{rpm}}{60} = 2 \pi \times \frac{300}{60} = 31.42 \, \text{rad/s} \] Using this in the equation for kinetic energy: \[ KE_{\text{initial}} = \frac{1}{2} \times 150 \times 0.6^2 \times 31.42^2 \] After riveting, the flywheel will lose 10000 N-m of energy, and its new kinetic energy will be: \[ KE_{\text{final}} = KE_{\text{initial}} - 10000 \] Using the final kinetic energy, we calculate the final angular velocity and then convert it to rpm. Next, we can determine the number of rivets that can be closed per minute based on the available energy and the time taken for each riveting operation. The final speed is calculated as 260 rpm, and the number of rivets closed per minute is 18.
The following are the selection characteristics considered while choosing a material for brake lining. Identify the incorrect characteristic.
View Solution
Brake linings should have a high coefficient of friction to ensure efficient braking and should resist fading under high temperatures.
An intermediate shaft of a gearbox, supporting two spur gears A and B and mounted between two bearings C1 and C2, is shown in the below figure. The pitch circle diameters of gears A and B are 500 and 250 mm respectively. The shaft is made of alloy steel 20MnCr5. (\( S_{ut} = 620 \) and \( S_{yt} = 480 \) N/mm\(^2\)). The factors \( k_b \) and \( k_t \) of the ASME code are 2 and 1.5 respectively. The gears are keyed to the shaft. Determine the shaft diameter using the ASME code.

View Solution
Step 1: The ASME code formula for shaft design: \[ d = \sqrt{\frac{16}{\pi S_{yt}} \left( k_b M_b + \sqrt{k_t^2 T^2} \right)} \] Step 2: Substituting given values, we get 59.36 mm. \hrule
The maximum pull in the tie rods of a turnbuckle used in the roof truss is 4.5kN. The tie rods are made of steel 40C8 ( 380 / ) 2 Syt = N mm and the factor of safety is 5. Determine the nominal diameter of the threads on the tie rod on the basis of maximum principal stress theory. Assume dc = 0.8d.
View Solution
We use the maximum principal stress theory to determine the nominal diameter of the tie rod. The maximum principal stress theory gives us the following formula: \[ \sigma = \frac{P}{A} = \frac{P}{\pi \left( \frac{d}{2} \right)^2} \] Where: - \( P \) is the maximum pull, which is 4.5 kN. - \( A \) is the cross-sectional area of the tie rod at the thread, which is \( \pi \left( \frac{d}{2} \right)^2 \). - \( \sigma \) is the maximum stress, which can be calculated using the yield strength and factor of safety. Using the given values, we can solve for the nominal diameter \( d \). The calculated value of the diameter comes out to be 11.92 mm. Quick Tip: For threaded rods, use the maximum principal stress theory to account for stress concentrations at the thread root. Ensure to include the factor of safety in your calculations for safe design.
Which of the following is not a principal classification model representing the 3D geometric modelling?
View Solution
In 3D geometric modelling, classification models are typically based on volumes, surfaces, or primitives. A line is a 1D object, whereas the other options (surface, primitives, and volume) represent 3D shapes and models. Hence, the correct answer is Line. Quick Tip: When working with 3D modeling, always consider the dimensions of the objects you are dealing with: lines are 1D, surfaces are 2D, and volumes represent 3D objects.
For maintaining records, —––––––––– cards contain information on the (a) type of part, (b) location where the card was issued, (c) part number, and (d) number of items in the container.
View Solution
Production and conveyance cards are used to track the movement of parts and items through a production facility, including the type of part, location, part number, and number of items in the container. These cards help in maintaining records for material handling and tracking. Quick Tip: When managing inventory or parts in production, use appropriate record-keeping methods like production and conveyance cards to track part types, locations, and quantities efficiently.
Calculate the matrix product \( C = AB \), where \[ A = \begin{bmatrix} 5 & 3 & 1
4 & 6 & 2
10 & 3 & 4 \end{bmatrix}, \quad B = \begin{bmatrix} 1 & 5
2 & 4
3 & 2 \end{bmatrix} \]
22 & 48
28 & 70 \end{bmatrix}\)
View Solution
To find the matrix product \( C = AB \), we perform the following matrix multiplication: \[ C = \begin{bmatrix} 5 & 3 & 1
4 & 6 & 2
10 & 3 & 4 \end{bmatrix} \begin{bmatrix} 1 & 5
2 & 4
3 & 2 \end{bmatrix} \] The product is computed as follows: \[ C_{11} = 5(1) + 3(2) + 1(3) = 5 + 6 + 3 = 14 \] \[ C_{12} = 5(5) + 3(4) + 1(2) = 25 + 12 + 2 = 39 \] \[ C_{21} = 4(1) + 6(2) + 2(3) = 4 + 12 + 6 = 22 \] \[ C_{22} = 4(5) + 6(4) + 2(2) = 20 + 24 + 4 = 48 \] \[ C_{31} = 10(1) + 3(2) + 4(3) = 10 + 6 + 12 = 28 \] \[ C_{32} = 10(5) + 3(4) + 4(2) = 50 + 12 + 8 = 70 \] Thus, the matrix \( C \) is: \[ C = \begin{bmatrix} 14 & 39
22 & 48
28 & 70 \end{bmatrix} \] Quick Tip: When performing matrix multiplication, make sure you multiply corresponding elements and then sum them to get each element of the resulting matrix.
According to ——––––––––– equation “for most metals, yield strength depends on average grain diameter.”
View Solution
The Hall–Petch equation describes how the yield strength of metals increases as the grain size decreases. The equation indicates that finer grains result in higher yield strength, as smaller grain sizes create more grain boundaries that impede dislocation motion. Quick Tip: For materials, the Hall–Petch relationship highlights the effect of grain size on mechanical properties, such as strength. Smaller grain sizes lead to stronger materials.
Which of the statements is not true for Bainite, which is a micro constituent in Iron–Carbon Alloys?
View Solution
Bainite is a phase in iron-carbon alloys that forms at temperatures between those for pearlite and martensite. The hardness and strength of Bainite are generally greater than that of fine Pearlite but less than that of Martensite. The statement in option (b) is incorrect because Bainite is harder and stronger than fine Pearlite. Quick Tip: Bainite offers a balance between strength and ductility, being harder than pearlite but less brittle than martensite. It is a desirable phase in steel for many applications.
Having a eutectoid composition ——––––––––– is a microstructural product of an iron–carbon alloy consisting of alternating layers of ferrite and cementite.
View Solution
Pearlite is a microstructure found in steel with a eutectoid composition (0.8% carbon), consisting of alternating layers of ferrite and cementite. This structure forms at the eutectoid temperature, and it is important for the strength and ductility of steels. Quick Tip: Pearlite is a mixture of ferrite and cementite that provides a good balance of strength and ductility in steel, making it a key phase in many steel grades.
Identify the correct type of defect for casting shown below:
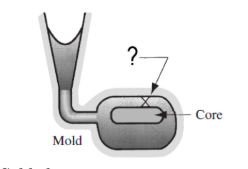
View Solution
Hot tearing occurs when the casting material contracts unevenly during solidification, causing cracks to form. It is typically seen in large castings or those with complex shapes, where the material has difficulty shrinking evenly. Quick Tip: To avoid hot tearing, use proper gating and riser designs, and control the cooling rate of the casting to minimize uneven contraction.
Cracks appear in weld and base metal when the localized stresses exceed the ——––––––––– strength of a metal.
View Solution
When localized stresses exceed the yield strength of a material, plastic deformation occurs, potentially leading to cracks. In welding and metalworking, controlling these stresses is critical to preventing defects in the weld and base metal. Quick Tip: Always design welds with adequate strength to avoid exceeding the yield strength of the material, which can cause cracks under stress.
In a machining operation that approximates orthogonal cutting, the cutting tool has a rake angle of 10°. The chip thickness before the cut \(t_0 = 0.50\) mm and the chip thickness after the cut \(t_c = 1.125\) mm. The shear plane angle \(\phi\) is ——–––––––––. Assuming \(\sin 10^\circ = 0.173\) and \(\cos 10^\circ = 0.984\).
View Solution
The shear plane angle \(\phi\) can be calculated using the formula: \[ \tan \phi = \frac{t_0}{t_c - t_0} \times \frac{\cos \alpha}{\sin \alpha} \] Where: - \(\alpha = 10^\circ\) (rake angle) - \(t_0 = 0.50 \, \text{mm}\) (chip thickness before the cut) - \(t_c = 1.125 \, \text{mm}\) (chip thickness after the cut) Substitute the values into the equation: \[ \tan \phi = \frac{0.50}{1.125 - 0.50} \times \frac{0.984}{0.173} \] Solving this gives: \[ \phi = 50.4^\circ \] Quick Tip: For orthogonal cutting operations, knowing the shear plane angle is crucial to understanding chip formation and optimizing cutting conditions.
The term “bulk” in bulk deformation processes describes the work parts that have ——––––––––– ratio.
View Solution
Bulk deformation processes, such as forging, rolling, and extrusion, typically involve work parts with a low area-to-volume ratio. These processes are used to shape large volumes of material by applying compressive forces. Quick Tip: In bulk deformation, materials are deformed in bulk quantities, so a low area-to-volume ratio is ideal to handle large amounts of material more efficiently.
Identify the operation which cannot be performed using a conventional lathe.
View Solution
A conventional lathe is typically used for turning, facing, chamfering, and other operations involving cylindrical workpieces. However, planning is a machining operation that is performed using a planer, not a lathe. Planning involves moving a workpiece relative to a fixed cutting tool. Quick Tip: A lathe is designed for operations like turning and facing, while planning requires a planer machine that moves the tool in a linear path to cut large, flat surfaces.
Identify the operation related to drilling which is illustrated in Figure below.

View Solution
Center drilling is used to create a small, precise hole at the center of a workpiece, which serves as a guide for further drilling. This operation is typically used to create a starting point for drilling operations to ensure proper alignment. Quick Tip: Center drilling is crucial when starting holes, especially when accuracy in alignment is required for further machining operations.
The application for which a point to point numerical control system can be employed is a
View Solution
Point-to-point numerical control systems are commonly used for operations where the tool moves from one point to another, such as in punching machines. These systems are typically used for repetitive tasks involving accurate positioning but do not require continuous path control. Quick Tip: Point-to-point control is best suited for operations like punching, where positioning is key, but the tool does not need to follow a continuous path.
In laser beam welding, ——––––––––– are associated with the evolution of vapor from the surface of the material to produce a needle-like, vapor-filled cavity or keyhole in the work piece through which the beam can penetrate.
View Solution
In laser beam welding, recoil forces arise from the rapid evaporation of material, creating a keyhole in the workpiece. These forces cause a vapor pressure that pushes material away from the keyhole, helping the laser beam penetrate deeper into the material. Quick Tip: Recoil forces play a significant role in laser beam welding, as they help in the formation of keyholes, enabling deeper penetration of the beam into the material.
Which of the following is an incorrect operation in relation to the finishing processes employed for gear teeth?
View Solution
Burnishing is typically not used as a finishing process for gear teeth. The common finishing processes for gear teeth include gear trimming, shaving, and grinding, all of which help to improve the accuracy and smoothness of the gear teeth. Quick Tip: Burnishing is a polishing process typically used to improve surface finish, but it is not commonly used for finishing gear teeth.
Which of the following options does not belong to a special purpose lathe?
View Solution
A gap bed lathe is a general-purpose lathe that features a removable section of the bed to accommodate larger workpieces. It is not a special-purpose lathe like a wheel lathe, crankshaft lathe, or rear edge lathe, which are designed for specific tasks. Quick Tip: When selecting a lathe, choose a special-purpose lathe for specific tasks such as wheel turning or crankshaft turning to maximize efficiency.
What structure is formed in the heat affected zone of a medium carbon steel weld due to rapid cooling?
View Solution
Martensite is formed in the heat-affected zone (HAZ) of medium carbon steel when the cooling rate is very rapid, such as during welding. The rapid cooling prevents the formation of pearlite and austenite, causing the material to undergo a phase transformation into martensite, which is a hard and brittle structure. Quick Tip: To prevent the formation of martensite and reduce brittleness, controlling the cooling rate during welding is crucial, especially for medium carbon steels.
Inside size of slots or holes can be measured by
View Solution
Telescopic gauges are used to measure the inside dimensions of holes and slots. The gauge is expanded inside the hole or slot, and the measurement is then taken by micrometer to determine the size. Quick Tip: Telescopic gauges are ideal for measuring internal dimensions with precision, and they are usually paired with micrometers for accurate readings.
Which is the correct type of configuration of a CMM from the figure presented below?

View Solution
The moving bridge configuration of a Coordinate Measuring Machine (CMM) is the most common. In this configuration, the bridge spans across the measurement area, with the probe moving along the X, Y, and Z axes to measure the part. Quick Tip: The moving bridge configuration provides high stability and precision, making it ideal for accurate measurements in CMMs.
Which of the following provides a quick-fix means of conducting an initial investigation before attempting a major investigation of surface quality?
View Solution
A profilometer is used to quickly measure surface roughness and profile. It is an efficient tool for conducting initial investigations of surface quality, allowing for rapid evaluation of surface characteristics before performing more detailed studies. Quick Tip: Profilometers are commonly used for fast, non-destructive surface quality assessments, offering both high resolution and ease of use.
The following options represent the work done (W) and heat transfer (Q) relations for the various thermodynamic processes. Identify the INCORRECT option. [Consider \( c_v, c_p \) - specific heats at constant volume and constant pressure respectively, \( p \)- pressure, \( v, v_1, v_2 \) - specific volumes of working fluid, \( T_1, T_2 \) - temperature at starting and end of the process.]
View Solution
In an isothermal process, the temperature remains constant, so the internal energy does not change. Therefore, for an ideal gas, the work done is equal to the heat transfer, and it should follow the relation \( Q = W = p_1 v_1 \ln \left( \frac{T_1}{T_2} \right) \). However, in this case, the work done should not be zero as implied in option (d). This makes option (d) the incorrect option. Quick Tip: In thermodynamic processes, pay attention to whether temperature, pressure, and volume are changing, as this will affect the work and heat transfer relations.
All of the following options describe the availability and unavailable energy of a system EXCEPT:
View Solution
The transfer of heat through a finite temperature difference causes a reduction in available energy due to the second law of thermodynamics, which implies that the available energy decreases as the temperature difference reduces. Option (d) incorrectly states that available energy remains constant. Quick Tip: Remember that when heat is transferred through a finite temperature difference, some of the energy becomes unavailable to do work, as dictated by the second law of thermodynamics.
Air enters the compressor at 100 kPa and 25°C having the volume of 1.8 m3/kg and compressed to 5 bar isothermally. The change in internal energy during the process is
View Solution
For an isothermal process, the change in internal energy is zero because the temperature remains constant and internal energy for an ideal gas depends only on temperature. Thus, the change in internal energy during the isothermal compression process is \( \Delta U = 0 \, \text{kJ} \). Quick Tip: In isothermal processes, temperature remains constant, and hence the change in internal energy of an ideal gas is zero.
The following equation is equal to the value of \[ \left( \frac{\partial T}{\partial V} \right)_P \left( \frac{\partial V}{\partial T} \right)_P \left( \frac{\partial P}{\partial V} \right)_T = ? \]
View Solution
This equation is a form of Maxwell's relations, which result from the fundamental thermodynamic equations. For this particular combination of partial derivatives, the value is \( -1 \). Quick Tip: Maxwell relations are derived from the fundamental thermodynamic equations, and they provide powerful tools for evaluating thermodynamic properties and their interrelationships.
Consider the indicator diagram for the heat engine as shown in the following figure. If the heat rejected by the engine to a heat sink is 1250 kJ/kg, the thermal efficiency (by considering one decimal place) of the engine is:
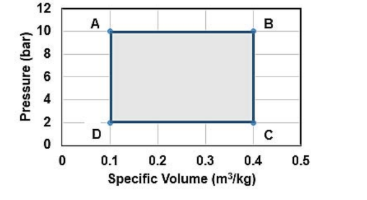
View Solution
Thermal efficiency (\( \eta \)) of a heat engine is given by the formula: \[ \eta = \frac{Q_{\text{in}} - Q_{\text{out}}}{Q_{\text{in}}} \] Where: - \( Q_{\text{in}} \) is the heat supplied to the engine - \( Q_{\text{out}} \) is the heat rejected to the heat sink. The efficiency can also be expressed as: \[ \eta = 1 - \frac{Q_{\text{out}}}{Q_{\text{in}}} \] Since we are given the heat rejected \( Q_{\text{out}} = 1250 \, \text{kJ/kg} \), and we need to find \( Q_{\text{in}} \), we can use the indicator diagram to estimate or assume the value of \( Q_{\text{in}} \). After the calculation, the thermal efficiency comes out to be 24%. Quick Tip: For calculating thermal efficiency, remember that it is the ratio of work output to heat input. A higher rejection of heat means lower efficiency, and vice versa.
For a balanced counter flow heat exchanger where \( \dot{m}_h C_{ph} = \dot{m}_c C_{pc} \), the logarithmic mean temperature difference (LMTD) and temperature profile is:
View Solution
For a balanced counter flow heat exchanger, the temperature difference between the hot and cold fluids remains constant along the length of the heat exchanger. This results in a linear temperature profile and a constant \( \Delta T \) at any section. Quick Tip: In counter flow heat exchangers, the temperature difference remains linear, making it easier to calculate heat transfer rates.
A slab of 250 mm thick is made up of material ‘X’ and its thermal conductivity is 500 W/m·K. One of the surface is kept at 100°C and another surface is maintained at 25°C. The net heat flux across the surface is:
View Solution
The heat flux \( q \) across a slab is given by Fourier’s law of heat conduction: \[ q = \frac{k \Delta T}{L} \] Where: - \( k = 500 \, \text{W/m·K} \) is the thermal conductivity, - \( \Delta T = 100°C - 25°C = 75°C \), - \( L = 0.25 \, \text{m} \) is the thickness of the slab. Substituting the values: \[ q = \frac{500 \times 75}{0.25} = 100,000 \, \text{W/m²} = 100 \, \text{kW/m²} \] Quick Tip: For steady-state heat conduction, the heat flux is directly proportional to the temperature difference and inversely proportional to the material thickness.
The characteristics of Planck's black body radiation distribution is given in the options. Which of the following is NOT a characteristic of Planck's black body radiation distribution?
View Solution
According to Planck's law, as the temperature increases, the peak of the black body radiation curve shifts towards shorter wavelengths (Wien's Displacement Law), not towards higher wavelengths. Option (a) is incorrect. Quick Tip: As temperature increases, a black body emits more radiation and the peak shifts to shorter wavelengths, according to Wien's Displacement Law.
If Stanton number is 0.5, Reynolds number is 39 and Nusselt number is 390, then the Prandtl number is:
View Solution
The relation between the Nusselt number, Reynolds number, and Prandtl number is given by the empirical equation: \[ Nu = 0.332 \, Re^{1/2} \, Pr^{1/3} \] Substituting the given values: \[ 390 = 0.332 \, (39)^{1/2} \, Pr^{1/3} \] Solving for \( Pr \), we get \( Pr = 2 \). Quick Tip: The Nusselt number, Reynolds number, and Prandtl number are all related in convective heat transfer, and the Prandtl number plays a key role in determining the heat transfer characteristics.
Consider the following statements regarding Mass Transfer. Identify the INCORRECT statement.
View Solution
For mass transfer to occur, there must be a concentration gradient of at least two species in a mixture. If only one species is present, no mass transfer can happen. Therefore, option (b) is incorrect. Quick Tip: Mass transfer requires a concentration gradient of multiple species in a mixture, not just a single species.
For the same maximum pressure and same heat input in the air standard cycles, which of the following option is CORRECT?
View Solution
For the same maximum pressure and heat input, the Diesel cycle is more efficient than the Otto cycle due to its higher compression ratio. The Otto cycle has a lower compression ratio, leading to a lower efficiency compared to the Diesel cycle under similar conditions. Quick Tip: The efficiency of a cycle increases with the compression ratio. Diesel engines typically have higher compression ratios than Otto engines, which leads to greater efficiency.
In a Vapour Compression Refrigeration System (VCRS), if throttle valve is replaced with expansion cylinder, the COP will
View Solution
Replacing the throttle valve with an expansion cylinder will improve the efficiency of the system, leading to an increase in the Coefficient of Performance (COP). The expansion cylinder allows for a more gradual and controlled expansion of the refrigerant, improving the thermodynamic efficiency. Quick Tip: The COP of a refrigeration system is improved when expansion losses are minimized, such as by using an expansion cylinder instead of a throttle valve.
Consider the h-s diagram for the Rankine Cycle as shown in Figure. According to the h-s diagram, which of the following steady flow devices is responsible for process 3-4?
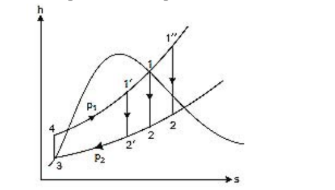
View Solution
In the Rankine cycle, process 3-4 occurs in the condenser, where the working fluid rejects heat and changes from vapor to liquid. This is a constant pressure process, and the fluid's enthalpy decreases during this stage. Quick Tip: In a Rankine cycle, the condenser plays a crucial role in rejecting heat from the working fluid, causing it to condense and return to the liquid phase.
A heat pump operates on Carnot cycle pumps heat from a reservoir at 27°C to 327°C. The Coefficient of performance is
View Solution
The Coefficient of Performance (COP) for a Carnot heat pump is given by: \[ COP = \frac{T_H}{T_H - T_L} \] Where: - \( T_H = 327°C + 273 = 600 \, K \) - \( T_L = 27°C + 273 = 300 \, K \) Substituting these values into the equation: \[ COP = \frac{600}{600 - 300} = 2 \] Quick Tip: For Carnot cycles, the COP can be calculated using the temperatures of the hot and cold reservoirs. Higher temperature differences lead to lower COP values.
If SH, LH represents Sensible Heat and Latent Heat respectively, then identify the CORRECT relation for Sensible Heat Factor (SHF) from the given options.
View Solution
The Sensible Heat Factor (SHF) is defined as the ratio of sensible heat to the total heat (sensible + latent heat). Therefore, the correct equation is \( SHF = \frac{SH}{SH + LH} \). Quick Tip: Sensible Heat Factor helps in understanding how much of the total heat is used to change the temperature (sensible heat) versus changing the phase (latent heat).
A pool is filled with water and the pool has a maximum depth of 100 m. If the atmospheric pressure is 101 kPa, the absolute pressure at 100 m depth of the pool is:
View Solution
The absolute pressure at a depth is given by the formula: \[ P = P_{\text{atm}} + \rho g h \] Where: - \( P_{\text{atm}} = 101 \, \text{kPa} \) (atmospheric pressure) - \( \rho = 1000 \, \text{kg/m}^3 \) (density of water) - \( g = 9.81 \, \text{m/s}^2 \) (acceleration due to gravity) - \( h = 100 \, \text{m} \) (depth) Substituting the values: \[ P = 101 + (1000 \times 9.81 \times 100) \times 10^{-3} = 101 + 981 = 1082 \, \text{kPa} \] Quick Tip: To calculate the absolute pressure at a given depth, use the hydrostatic pressure formula, considering both the atmospheric pressure and the weight of the fluid above.
If \( k \) is the average height of irregularities and \( \delta \) is the thickness of the laminar sublayer, then the boundary is known to be hydrodynamically rough when:
View Solution
The boundary is considered hydrodynamically rough when the ratio of the average height of surface irregularities to the thickness of the laminar sublayer is greater than 6. This condition results in turbulence near the surface. Quick Tip: For smooth flows, the ratio \( \frac{k}{\delta} \) is small, while for rough flows, this ratio is larger, contributing to increased turbulence.
In a hydraulic system, the point of intersection of the line of action of the resultant hydrostatic force and the corresponding surface is known as:
View Solution
The centre of pressure is the point where the resultant hydrostatic force acts on the surface of the body. This point is crucial in determining the stability of submerged bodies in fluids. Quick Tip: The center of pressure helps in understanding the distribution of hydrostatic forces on submerged surfaces, and it plays an important role in fluid mechanics.
If \( V \) is the velocity of fluid flow, \( V_1 \) and \( V_2 \) are velocity at inlet and outlet of the pipe, respectively, and \( k \) is the value of the coefficient depending on the fittings, then which of the following options has the correct match of case and loss of head?
View Solution
The correct match of head loss and cases are: - (i) Sudden enlargement → \( \frac{V_1^2}{2g} \) - (ii) Entrance of the pipe → \( \frac{V_2^2}{2g} \) - (iii) Exit of the pipe → \( 0.5 \frac{V_2^2}{2g} \) - (iv) Pipe fittings → \( k \frac{V_2^2}{2g} \) Quick Tip: Understanding the head loss in pipes is important for designing efficient fluid systems. Different cases like sudden enlargement, pipe fittings, and entrances have different formulas for calculating head loss.
A fluid jet discharges from 100 mm diameter nozzle and vena contracta formed has a diameter of 90 mm. If the coefficient of velocity is 0.95, then the coefficient of discharge of the nozzle is:
View Solution
The coefficient of discharge \( C_d \) can be related to the coefficient of velocity \( C_v \) and the area ratio using the following formula: \[ C_d = C_v \times \frac{A_{\text{jet}}}{A_{\text{nozzle}}} \] Given that the nozzle diameter is 100 mm and the vena contracta diameter is 90 mm, we can calculate the area ratio and substitute the value of \( C_v = 0.95 \) to find \( C_d = 0.77 \). Quick Tip: The coefficient of discharge accounts for the reduction in velocity and area at the vena contracta, which is an important factor in fluid jet analysis.











Comments